Wenn Sie kein Programm schreiben, verwenden Sie keine Programmiersprache

Leslie Lamport ist der Autor der grundlegenden Arbeit im Bereich des verteilten Rechnens, und Sie können ihn auch an den Buchstaben La in La TeX - „Lamport TeX“ erkennen. Dies ist das erste Mal, dass er 1979 das Konzept der konsistenten Konsistenz einführte, und sein Artikel „Wie man einen Multiprozessor-Computer herstellt, der Multiprozess-Programme korrekt ausführt“ gewann den Dijkstra-Preis (genauer gesagt, im Jahr 2000 wurde der Preis auf die alte Art und Weise genannt: „PODC Influential Paper Award "). Auf Wikipedia gibt es einen Artikel über ihn, in dem Sie weitere interessante Links finden. Wenn Sie mit der Lösung von Problemen bei Vorfällen oder Problemen der byzantinischen Generäle (BFT) zufrieden sind, sollten Sie verstehen, dass Lamport dahinter steckt.

Diese Habrastatia ist eine Übersetzung von Leslies Bericht auf dem Heidelberg Laureate Forum im Jahr 2018. Der Vortrag konzentriert sich auf formale Methoden zur Entwicklung komplexer und kritischer Systeme wie die Rosetta Space Probe oder Amazon Web Services-Engines. Das Anzeigen dieses Berichts ist für die Teilnahme an einer Frage- und Antwortrunde, die Leslie auf der Hydra-Konferenz abhalten wird, obligatorisch. Durch diese Habrastatia können Sie eine Stunde Zeit beim Ansehen eines Videos sparen. Wenn diese Einführung abgeschlossen ist, geben wir das Wort an den Autor weiter.

Es war einmal, Tony Hoar schrieb: "Jedes große Programm hat ein kleines Programm, das versucht, herauszukommen." Ich würde es so umformulieren: "In jedem großen Programm gibt es einen Algorithmus, der versucht, herauszukommen." Ich weiß jedoch nicht, ob Tony einer solchen Interpretation zustimmen würde.

Betrachten Sie als Beispiel den euklidischen Algorithmus zum Finden des größten gemeinsamen Teilers zweier positiver Ganzzahlen $$$(M, N)$ . In diesem Algorithmus weisen wir zu $$$x$ Wert $$$M$ , $$$N$ - Wert $$$y$ und subtrahieren Sie dann den kleinsten dieser Werte vom größten, bis sie gleich sind. Bedeutung von diesen $$$x$ und $$$y$ und wird der größte gemeinsame Faktor sein. Was ist der wesentliche Unterschied zwischen diesem Algorithmus und dem Programm, das ihn implementiert? In einem solchen Programm wird es viele Dinge auf niedriger Ebene geben: $$$M$ und $$$N$ es wird einen bestimmten Typ geben, BigInteger oder so ähnlich; Es ist notwendig, das Verhalten des Programms zu bestimmen, wenn $$$M$ und $$$N$ nicht positiv; und so weiter und so fort. Es gibt keinen klaren Unterschied zwischen den Algorithmen und den Programmen, aber auf der intuitiven Ebene spüren wir den Unterschied - die Algorithmen sind abstrakter, auf höherer Ebene. Und wie gesagt, in jedem Programm lebt ein Algorithmus, der versucht, herauszukommen. Normalerweise sind dies nicht die Algorithmen, über die wir im Algorithmuskurs informiert wurden. In der Regel ist dies ein Algorithmus, der nur für dieses spezielle Programm nützlich ist. Meistens ist es viel komplizierter als die in Büchern beschriebenen. Solche Algorithmen werden oft als Spezifikationen bezeichnet. In den meisten Fällen kommt dieser Algorithmus nicht heraus, weil der Programmierer seine Existenz nicht vermutet. Tatsache ist, dass dieser Algorithmus nicht sichtbar ist, wenn Sie sich auf Code, Typen, Ausnahmen, while Schleifen und mehr konzentrieren und nicht auf die mathematischen Eigenschaften von Zahlen. Ein auf diese Weise geschriebenes Programm ist schwer zu debuggen. Was bedeutet es also, einen Algorithmus auf Codeebene zu debuggen? Debugging-Tools dienen dazu, Fehler im Code und nicht im Algorithmus zu finden. Darüber hinaus ist ein solches Programm unwirksam, da Sie den Algorithmus erneut auf Codeebene optimieren.

Wie in fast jedem anderen Bereich der Wissenschaft und Technologie können diese Probleme durch mathematische Beschreibung gelöst werden. Es gibt viele Möglichkeiten, dies zu tun. Wir werden die nützlichsten davon in Betracht ziehen. Es funktioniert sowohl mit sequentiellen als auch parallelen (verteilten) Algorithmen. Diese Methode besteht darin, die Ausführung des Algorithmus als Folge von Zuständen und jeden Zustand als Zuweisung von Eigenschaften zu Variablen zu beschreiben. Beispielsweise wird der euklidische Algorithmus als eine Folge der folgenden Zustände beschrieben: Zuerst wird x der Wert M (Nummer 12) und y der Wert N (Nummer 18) zugewiesen. Dann subtrahieren wir den kleineren Wert vom größeren ( $$$x$ von $$$y$ ), was uns zum nächsten Zustand führt, in dem wir bereits wegnehmen $$$y$ von $$$x$ und die Ausführung des Algorithmus stoppt dabei: $$$[x \ linker Pfeil 12, \ linker Pfeil 18], [x \ linker Pfeil 12, \ linker Pfeil 6], [x \ linker Pfeil 6, \ linker Pfeil 6]$ .

Wir nennen eine Folge von Zustandsverhalten und ein Paar aufeinanderfolgender Zustände einen Schritt. Dann kann jeder Algorithmus durch eine Vielzahl von Verhaltensweisen beschrieben werden, die alle möglichen Varianten des Algorithmus darstellen. Für jedes spezifische M und N gibt es nur eine Ausführungsform, daher ist ein Satz von einem Verhalten ausreichend, um es zu beschreiben. Komplexere Algorithmen, insbesondere parallele, weisen viele Verhaltensweisen auf.

Viele Verhaltensweisen werden zunächst durch ein anfängliches Prädikat für Zustände beschrieben (ein Prädikat ist nur eine Funktion mit einem Booleschen Wert). und zweitens ein Prädikat des nächsten Zustands für Zustandspaare. Etwas Verhalten $$$s_1, s_2, s_3 ...$ tritt nur dann in viele Verhaltensweisen ein, wenn das ursprüngliche Prädikat für gilt $$$s_1$ und die Prädikate des nächsten Zustands gelten für jeden Schritt $$$(s_i, s_ {i + 1})$ . Versuchen wir, den euklidischen Algorithmus auf diese Weise zu beschreiben. Das anfängliche Prädikat hier ist: $$$(x = M) \ land (y = N)$ . Das Prädikat des nächsten Zustands für Zustandspaare wird durch die folgende Formel beschrieben:

Bitte seien Sie nicht beunruhigt - es sind nur sechs Zeilen enthalten. Es ist sehr einfach, sie herauszufinden, wenn Sie dies in der richtigen Reihenfolge tun. In dieser Formel beziehen sich Variablen ohne Striche auf den ersten Zustand, und Variablen mit Strichen sind dieselben Variablen im zweiten Zustand.

Wie Sie sehen können, steht in der ersten Zeile, dass im ersten Fall x im ersten Zustand größer als y ist. Nach einem logischen UND wird angegeben, dass der Wert von x im zweiten Zustand gleich dem Wert von x im ersten Zustand minus dem Wert von y im ersten Zustand ist. Nach einem weiteren logischen UND wird angegeben, dass der Wert von y im zweiten Zustand gleich dem Wert von y im ersten Zustand ist. All dies bedeutet, dass in dem Fall, in dem x größer als y ist, das Programm y von x subtrahiert und y unverändert lässt. Die letzten drei Zeilen beschreiben den Fall, in dem y größer als x ist. Beachten Sie, dass diese Formel falsch ist, wenn x gleich y ist. In diesem Fall gibt es keinen nächsten Status und das Verhalten wird beendet.

Wir haben den euklidischen Algorithmus also nur in zwei mathematischen Formeln beschrieben - und wir mussten uns mit keiner Programmiersprache herumschlagen. Was könnte schöner sein als diese beiden Formeln? Ersetzen Sie sie durch eine Formel. Verhalten $$$s_1, s_2, s_3 ...$ ist die Ausführung des euklidischen Algorithmus nur, wenn:

• $$$Init_E$ wahr für $$$s_1$ ,
• $$$Next_E$ wahr für jeden Schritt $$$(s_i, s_ {i + 1})$ .

Dies kann wie folgt als Prädikat für Verhaltensweisen geschrieben werden (wir werden es eine Eigenschaft nennen). Die erste Bedingung kann einfach ausgedrückt werden als $$$Init_E$ . Dies bedeutet, dass wir ein Zustandsprädikat nur dann als wahr für das Verhalten interpretieren, wenn es für den ersten Zustand wahr ist. Die zweite Bedingung lautet wie folgt: $$$\ square Next_E$ . Ein Quadrat bedeutet die Entsprechung zwischen den Prädikaten von Zustandspaaren und den Prädikaten des Verhaltens, d.h. $$$Next_E$ wahr für jeden Schritt im Verhalten. Infolgedessen sieht die Formel folgendermaßen aus: $$$Init_E \ land \ square Next_E$ .

Also haben wir den euklidischen Algorithmus mathematisch geschrieben. Im Wesentlichen handelt es sich lediglich um Definitionen oder Abkürzungen für $$$Init_E$ und $$$Next_E$ . Diese ganze Formel würde so aussehen:

Ist sie nicht schön? Leider ist Schönheit für Wissenschaft und Technologie kein entscheidendes Kriterium, aber es bedeutet, dass wir auf dem richtigen Weg sind.

Die Eigenschaft, die wir aufgeschrieben haben, gilt für einige Verhaltensweisen nur, wenn die beiden eben beschriebenen Bedingungen erfüllt sind. Bei $$$M = 12$ und $$$N = 18$ Sie gelten für das folgende Verhalten: $$$[x \ linker Pfeil 12, \ linker Pfeil 18], [x \ linker Pfeil 12, \ linker Pfeil 6], [x \ linker Pfeil 6, \ linker Pfeil 6]$ . Diese Bedingungen sind aber auch für kürzere Versionen desselben Verhaltens erfüllt: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6]$ . Und wir sollten sie nicht berücksichtigen, da dies nur separate Schritte des Verhaltens sind, das wir bereits betrachtet haben. Es gibt einen offensichtlichen Weg, sie loszuwerden: Ignorieren Sie einfach Verhaltensweisen, die in einem Zustand enden, für den mindestens ein nächster Schritt möglich ist. Dies ist jedoch nicht der richtige Ansatz. Wir brauchen eine allgemeinere Lösung. Außerdem funktioniert diese Bedingung nicht immer.

Eine Diskussion dieses Problems führt uns zu den Konzepten von Sicherheit und Aktivität. Die Sicherheitseigenschaft gibt an, welche Ereignisse gültig sind. Beispielsweise darf der Algorithmus den richtigen Wert zurückgeben. Die Aktivitätseigenschaft gibt an, welche Ereignisse früher oder später auftreten sollen. Beispielsweise sollte ein Algorithmus früher oder später einen Wert zurückgeben. Für den euklidischen Algorithmus lautet die Sicherheitseigenschaft wie folgt: $$$Init_E \ land \ square Next_E$ . Dazu muss eine Aktivitätseigenschaft hinzugefügt werden, um vorzeitige Stopps zu verhindern: $$$Init_E \ land \ square Next_E \ land L$ . In Programmiersprachen gibt es bestenfalls eine primitive Definition von Aktivität. Meistens wird Aktivität nicht einmal erwähnt, es wird einfach impliziert, dass der nächste Schritt im Programm stattfinden muss. Und um diese Eigenschaft hinzuzufügen, benötigen Sie einen ziemlich komplizierten Code. Mathematisch ist es sehr einfach, Aktivitäten auszudrücken (dafür wird nur dieses Quadrat benötigt), aber leider habe ich keine Zeit dafür - wir müssen unsere Diskussion auf Sicherheit beschränken.

Ein kleiner Exkurs nur für Mathematiker: Jede Eigenschaft ist eine Reihe von Verhaltensweisen, für die diese Eigenschaft gilt. Für jeden Satz von Sequenzen gibt es eine natürliche Topologie, die die folgende Distanzfunktion erstellt:

$$$s = 17, \ sqrt {2}, -2, \ pi, 10, 1/2 \\ t = 17, \ sqrt {2}, -2, e, 10, 1/$

Der Abstand zwischen diesen beiden Funktionen beträgt ¼, da der erste Unterschied zwischen ihnen beim vierten Element liegt. Je länger der Teil ist, in dem diese Sequenzen identisch sind, desto näher sind sie dementsprechend. Diese Funktion an sich ist nicht so interessant, aber sie erzeugt eine sehr interessante Topologie. In dieser Topologie sind Sicherheitseigenschaften geschlossene Mengen und Aktivitätseigenschaften dichte Mengen. In der Topologie besagt einer der Grundsätze, dass jede Menge der Schnittpunkt einer geschlossenen Menge und einer dichten Menge ist. Wenn wir uns daran erinnern, dass Eigenschaften Mengen von Verhaltensweisen sind, folgt aus diesem Satz, dass jede Eigenschaft eine Verbindung einer Sicherheitseigenschaft und einer Aktivitätseigenschaft ist. Dies ist eine Schlussfolgerung, die auch für Programmierer interessant sein wird.

Teilkorrektheit bedeutet, dass das Programm nur gestoppt werden kann, wenn es die richtige Antwort gibt. Die teilweise Korrektheit des euklidischen Algorithmus besagt, dass wenn die Ausführung abgeschlossen ist, dann $$$x = GCD (M, N)$ . Und unser Algorithmus vervollständigt die Ausführung, wenn $$$x = y$ . Mit anderen Worten, $$$(x = y) \ Rightarrow (x = GCD (M, N))$ . Die teilweise Korrektheit dieses Algorithmus bedeutet, dass diese Formel für alle Verhaltenszustände gilt. Fügen Sie am Anfang ein Symbol hinzu $$$\ square$ was bedeutet "für alle Schritte". Wie Sie sehen können, enthält die Formel keine Variablen mit einem Strich, daher hängt ihre Wahrheit vom ersten Zustand bei jedem Schritt ab. Und wenn für den ersten Zustand jedes Schritts etwas wahr ist, dann gilt diese Aussage für alle Zustände. Die teilweise Korrektheit des euklidischen Algorithmus wird durch jedes für den Algorithmus akzeptable Verhalten erfüllt. Wie wir gesehen haben, ist Verhalten zulässig, wenn die gerade angegebene Formel wahr ist. Wenn wir sagen, dass eine Eigenschaft erfüllt ist, bedeutet dies einfach, dass diese Eigenschaft aus einer Formel folgt. Ist das nicht wunderbar? Da ist sie:

$$$Init_E \ land \ square Next_E \ Rightarrow \ square ((x = y) \ Rightarrow (x = GCD (M, N)))$

Wir wenden uns der Invarianz zu. Das Quadrat mit den Klammern danach wird als Invarianzeigenschaft bezeichnet :

$$$Init_E \ land \ square Next_E \ Rightarrow \ color {red} {\ square ((x = y) \ Rightarrow (x = GCD (M, N)))}$

Der in Klammern nach dem Quadrat stehende Wert wird als Invariante bezeichnet :

$$$Init_E \ land \ square Next_E \ Rightarrow \ square (\ color {red} {(x = y) \ Rightarrow (x = GCD (M, N))})$

Wie kann man Invarianz beweisen? Zu beweisen $$$Init_E \ land \ square Next_E \ Rightarrow \ square I_E$ müssen Sie das für jedes Verhalten beweisen $$$s_1, s_2, s_3 ...$ die Folge $$$Init_E \ land \ square Next_E$ ist Wahrheit $$$I_e$ für jede Bedingung $$$s_j$ . Wir können dies durch Induktion beweisen, dafür müssen wir Folgendes beweisen:

1. von $$$Init_E \ land \ square Next_E$ Daraus folgt $$$I_e$ wahr für den Staat $$$s_1$ ;;
2. von $$$Init_E \ land \ square Next_E$ Daraus folgt, dass wenn $$$I_e$ wahr für den Staat $$$s_j$ dann auch noch
   wahr für den Staat $$$s_ {j + 1}$ .

Zuerst müssen wir das beweisen $$$Init_E$ impliziert $$$I_e$ . Weil die Formel das behauptet $$$Init_E$ wahr für den ersten Zustand bedeutet dies, dass $$$I_e$ wahr für den ersten Zustand. Weiter, wenn $$$Next_E$ wahr für jeden Schritt, und $$$I_e$ treu zu $$$s_j$ , $$$I_e$ wahr für $$$s_ {j + 1}$ , weil $$$\ square Next_E$ bedeutet das $$$Next_E$ wahr für jedes Paar von Zuständen. Das ist so geschrieben: $$$Next_E \ land I_E \ Rightarrow I'_E$ wo $$$I'_E$ - Das $$$I_e$ für alle Variablen mit einem Strich.

Eine Invariante, die die beiden Bedingungen erfüllt, die wir gerade bewiesen haben, wird als induktive Invariante bezeichnet . Teilkorrektheit ist nicht induktiv. Um seine Invarianz zu beweisen, müssen Sie die induktive Invariante finden, die sie impliziert. In unserem Fall ist die induktive Invariante wie folgt: $$$GCD (x, y) = GCD (M, N)$ .

Jede nachfolgende Aktion des Algorithmus hängt von seinem aktuellen Status ab und nicht von früheren Aktionen. Der Algorithmus erfüllt die Sicherheitseigenschaft, da die induktive Invariante darin erhalten bleibt. Der euklidische Algorithmus kann den größten gemeinsamen Nenner berechnen (d. H. Er stoppt nicht, bis er erreicht ist), da er eine Invariante hat $$$GCD (x, y) = GCD (M, N)$ . Um den Algorithmus zu verstehen, müssen Sie seine induktive Invariante kennen. Wenn Sie die Programmüberprüfung studiert haben, wissen Sie, dass der gerade gegebene Beweis einer Invariante nichts anderes als eine Methode zum Nachweis der teilweisen Korrektheit sequentieller Floyd-Hoare-Programme ist. Möglicherweise haben Sie auch von der Hoviki- Gris- Methode gehört , bei der es sich um die Erweiterung der Floyd-Hoar-Methode auf parallele Programme handelt. In beiden Fällen wird die induktive Invariante unter Verwendung der Programmanmerkung geschrieben. Und wenn Sie dies mit Hilfe der Mathematik und nicht mit einer Programmiersprache tun, geschieht dies äußerst einfach. Das ist das Herzstück der Hoviki-Gris-Methode. Die Mathematik macht komplexe Phänomene für das Verständnis viel zugänglicher, obwohl die Phänomene selbst natürlich nicht einfacher werden.

Schauen Sie sich die Formeln genauer an. Wenn wir in Mathe eine Formel mit Variablen geschrieben haben $$$x$ und $$$y$ Dies bedeutet nicht, dass andere Variablen nicht existieren. Sie können eine andere Gleichung hinzufügen, in der $$$y$ platziert in Bezug auf $$$z$ wird es nichts ändern. Nur die Formel sagt nichts über andere Variablen aus. Ich habe bereits gesagt, dass ein Zustand eine Zuweisung von Werten zu Variablen ist. Jetzt können Sie Folgendes hinzufügen: Beginnen Sie mit allen möglichen Variablen $$$x$ und $$$y$ und endet mit der Bevölkerung des Iran. Ich muss gestehen: als ich das die Formel sagte $$$Init_E \ land \ square Next_E$ beschreibt den euklidischen Algorithmus, den ich gelogen habe. Es beschreibt tatsächlich ein Universum, in dem Bedeutungen $$$x$ und $$$y$ repräsentieren die Ausführung des euklidischen Algorithmus. Der zweite Teil der Formel ( $$$\ square Next_E$ ) behauptet, dass sich jeder Schritt ändert $$$x$ oder $$$y$ . Mit anderen Worten, es beschreibt ein Universum, in dem sich die iranische Bevölkerung nur ändern kann, wenn sich die Bedeutung geändert hat $$$x$ oder $$$y$ . Daraus folgt, dass im Iran niemand geboren werden kann, nachdem die Ausführung des euklidischen Algorithmus abgeschlossen ist. Offensichtlich ist das nicht so. Dieser Fehler kann korrigiert werden, wenn wir gültige Schritte für welche haben $$$x$ und $$$y$ bleiben unverändert. Daher müssen wir unserer Formel einen weiteren Teil hinzufügen: $$$Init_E \ land \ square (Next_E \ lor (x '= x) \ land (y' = y))$ . Der Kürze halber schreiben wir es so: $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ . Diese Formel beschreibt ein Universum, das den euklidischen Algorithmus enthält. Die gleichen Änderungen müssen am Beweis der Invariante vorgenommen werden:

• Wir beweisen: $$$Init_E \ land \ color {red} {\ square [Next_E] _ {<x, y>}} \ Rightarrow \ square I_E$
• Mit Hilfe:
  
  1. $$$Init_E \ Rightarrow I_E$
  2. $$$\ color {red} {\ square [Next_E] _ {<x, y>}} \ land I_E \ Rightarrow I'_E$

Diese Änderung ist für die Sicherheit des euklidischen Algorithmus verantwortlich, da jetzt Verhaltensweisen bei welchen Werten möglich sind $$$x$ und $$$y$ nicht ändern. Diese Verhaltensweisen müssen mithilfe der Aktivitätseigenschaft beseitigt werden. Das ist ganz einfach, aber ich werde jetzt nicht darüber sprechen.

Sprechen Sie über die Implementierung. Angenommen, wir haben eine Art Maschine, die den euklidischen Algorithmus wie einen Computer implementiert. Es repräsentiert Zahlen als Arrays von 32-Bit-Wörtern. Für einfache Additions- und Subtraktionsoperationen benötigt sie viele Schritte, wie einen Computer. Wenn Sie die Aktivität noch nicht berühren, können wir uns eine solche Maschine auch anhand der Formel vorstellen $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ . Was meinen wir, wenn wir sagen, dass die euklidische Maschine den euklidischen Algorithmus implementiert? Dies bedeutet, dass die folgende Formel korrekt ist:

Seien Sie nicht beunruhigt, wir werden es jetzt der Reihe nach untersuchen. Es heißt, dass unsere Maschine einige Eigenschaften erfüllt ( $$$\ Rightarrow$ ) Diese Eigenschaft ist die euklidische Formel. $$$(Init_E \ land \ square [Next_E] _ {<x, y>}$ , Punkte sind Ausdrücke, die euklidische Maschinenvariablen enthalten, und $$$WITH$ Ist eine Substitution. Mit anderen Worten, die zweite Zeile ist die euklidische Formel, in der $$$x$ und $$$y$ durch Punkte ersetzt. In der Mathematik gibt es keine allgemein akzeptierte Notation für Substitution, daher musste ich mir diese selbst einfallen lassen. Im Wesentlichen die euklidische Formel ( $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ ) Ist eine Abkürzung für die Formel:

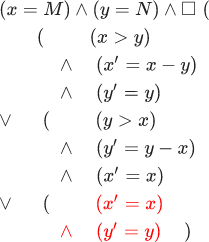
Rot hervorgehobener Teil der Formel erlaubt $$$x$ und $$$y$ in $$$(Init_E \ land \ square [Next_E] _ {\ color {red} {<x, y>}}$ bleib gleich.

Der beschriebene Ausdruck besagt nicht nur, dass die Maschine den euklidischen Algorithmus implementiert, sondern dass dies auch unter Berücksichtigung der angegebenen Substitutionen geschieht. Wenn Sie nur ein paar Programme nehmen und sagen, dass die Variablen dieser Programme in Beziehung stehen $$$x$ und $$$y$ - Es macht keinen Sinn zu sagen, dass all dies "den euklidischen Algorithmus implementiert". Es muss genau angegeben werden, wie der Algorithmus implementiert wird, warum nach allen Permutationen die Formel wahr wird. Jetzt habe ich keine Zeit zu zeigen, dass die oben beschriebene Definition korrekt ist, Sie müssen mein Wort dafür nehmen. Aber ich denke, Sie haben bereits erkannt, wie einfach und elegant es ist. Die Mathematik ist wirklich schön - damit konnten wir feststellen, was es bedeutet, dass ein Algorithmus einen anderen implementiert.

Um dies zu beweisen, ist es notwendig, eine geeignete Invariante zu finden $$$I_ {ME}$ Euklidische Autos. Dazu müssen folgende Bedingungen erfüllt sein:

1. $$$Init_ {ME} \ Rightarrow (Init_E, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$
2. $$$I_ {ME} \ land [Next_ {ME}] _ {<...>} \ Rightarrow ([Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow. ..)$

Wir werden uns jetzt nicht mit ihnen befassen, sondern nur darauf achten, dass dies gewöhnliche mathematische Formeln sind, wenn auch nicht die einfachsten. Invariant $$$I_ {ME}$ erklärt, warum die euklidische Maschine den euklidischen Algorithmus implementiert. Implementierung bedeutet, Variablen durch Ausdrücke zu ersetzen. Dies ist eine sehr häufige mathematische Operation. Im Programm kann eine solche Ersetzung jedoch nicht durchgeführt werden. Sie können a + b anstelle von x im Zuweisungsausdruck x = … , ein solcher Datensatz ist nicht sinnvoll. Wie kann man dann feststellen, dass ein Programm ein anderes implementiert? Wenn Sie nur an die Programmierung denken, ist dies nicht möglich. Im besten Fall finden Sie eine knifflige Definition, aber eine viel bessere Möglichkeit besteht darin, die Programme in mathematische Formeln zu übersetzen und die oben angegebene Definition zu verwenden. Ein Programm in eine mathematische Formel zu übersetzen bedeutet, dem Programm Semantik zu geben. Wenn die euklidische Maschine ein Programm ist, und $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ - also ihre mathematische Notation $$$(Init_E \ land \ square [Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$ zeigt uns, dass dies bedeutet, dass "das Programm den euklidischen Algorithmus implementiert". Programmiersprachen sind sehr komplex, daher ist diese Übersetzung des Programms in eine mathematische Sprache ebenfalls kompliziert, so dass wir dies in der Praxis nicht tun. Programmiersprachen sind einfach nicht dafür ausgelegt, Algorithmen darauf zu schreiben. , , , : , x y , . , , , .

- : , , , . , . — . . , . , — , . :

. $$$DecrementX$ ::

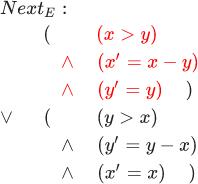
— $$$DecrementY$ ::

, :

.

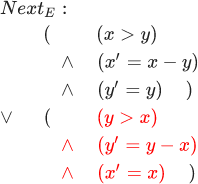
. Rosetta — , . Virtuoso. . TLA+, . , , . , (Eric Verhulst), . , TLA+, : « TLA+ . - C. TLA+ Virtuoso». Denken Sie über diese Figur nach. . , , , . . TLA+. , .

. Communications of the ACM ] , - Amazon . Amazon Web Services — , Amazon. , — TLA+. . -, , . , , . -, , . , — , , . -, , Amazon , . , 10% TLA+.

— Microsoft. TLA+ 2004 . 2015 TLA+, . . Amazon Web Services. Microsoft , , . : « , ». , Microsoft - . : « ». 2016-17 . TLA+, 150 , Azure ( Microsoft). Azure 2018 , , . : « , . , ». , , . - : , . , , .

, TLA+ . , TLA+, TLA+ Azure, , TLA+. , . , TLA+ , . Microsoft Cosmos DB, , . , . TLA+, , , TLA+.

TLA+ — . . TLA+ . , , . TLA+ , . : TLA+ , .

, . , , . , . Amazon Microsoft , . , .

, . — , . , Hydra 2019, 11-12 2019 -. .