🤸🏿 💯 🤲🏽 Optimale lineare Filterung: vom Gradientenabstieg bis zum adaptiven Filter 🧘 🙎🏽 🐣

Ich möchte das Thema Abstracts zum Master-Fach "Kommunikation und Signalverarbeitung" (TU Ilmenau) weiterentwickeln und eines der Hauptthemen des Kurses "Adaptive und Array-Signalverarbeitung" fortsetzen . Die Grundlagen der adaptiven Filterung.

Für wen dieser Artikel zuerst geschrieben wurde:

1) für eine Studentenbruderschaft einer einheimischen Spezialität ;
2) für Lehrer, die praktische Seminare vorbereiten, sich aber noch nicht für die Tools entschieden haben - nachfolgend finden Sie Beispiele in Python und Matlab / Octave ;
3) für alle, die sich für das Thema Filterung interessieren.

Was ist unter dem Schnitt zu finden:

1) Informationen aus der Theorie, die ich so kurz wie möglich zu ordnen versuchte, die mir aber informativ erscheinen;
2) Beispiele für die Verwendung von Filtern: insbesondere als Teil des Equalizers für das Antennenarray;
3) Links zu grundlegender Literatur und offenen Bibliotheken (in Python), die für die Forschung nützlich sein können.

Begrüßen Sie im Allgemeinen und lassen Sie uns alles nach Punkten sortieren.

Die nachdenkliche Person auf dem Foto ist vielen bekannt, glaube ich, Norbert Wiener. Zum größten Teil werden wir den Filter seines Namens untersuchen. Man kann jedoch nicht versäumen, unseren Landsmann zu erwähnen - Andrei Nikolaevich Kolmogorov, dessen Artikel von 1941 ebenfalls einen wesentlichen Beitrag zur Entwicklung der optimalen Filtertheorie leistete, die selbst in englischen Quellen als Kolmogorov-Wiener-Filtertheorie bezeichnet wird .

Was erwägen wir?

Heute betrachten wir ein klassisches Filter mit einer endlichen Impulsantwort (FIR, endliche Impulsantwort), die durch die folgende einfache Schaltung beschrieben werden kann (Abb. 1).

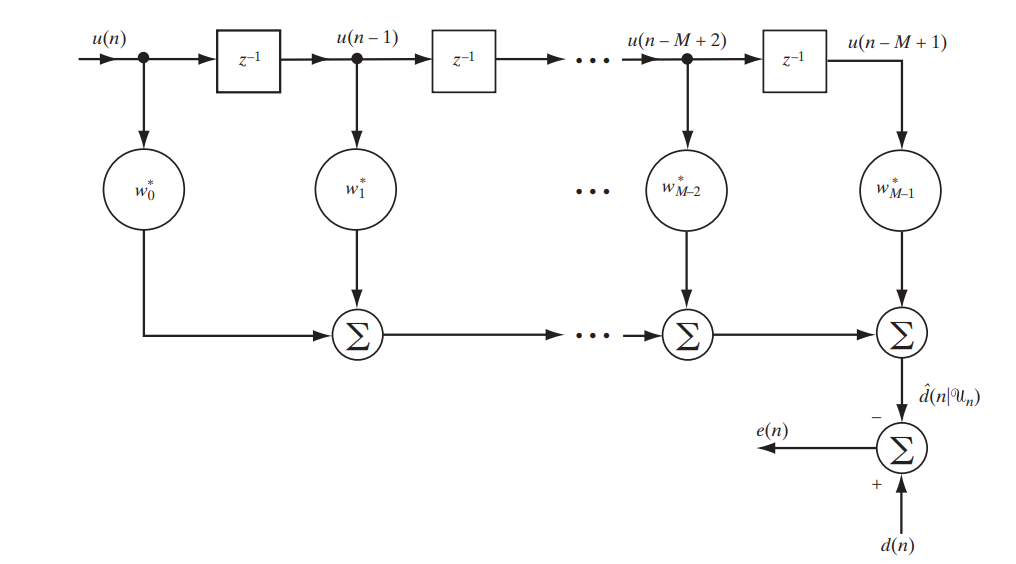
Abb. 1. Das FIR-Filterschema zur Untersuchung des Wiener-Filters. [1. S.117]

Wir werden in Matrixform schreiben, was genau am Ausgang dieses Standes sein wird:

$e (n) = d (n) - \ hat {d} (n | \ mathcal {U} _n) = d (n) - \ mathbf {w} ^ H \ mathbf {u} \ qquad (1)$

Entschlüsseln Sie die Notation:

Ist die Differenz (Fehler) zwischen dem gegebenen und dem empfangenen Signal
Ist ein vordefiniertes Signal
$\ mathbf {u}$ Ist ein Vektor von Abtastwerten oder mit anderen Worten ein Signal am Eingang des Filters
$\ hat {d} (n | \ mathcal {U} _n)$ Ist das Signal am Filterausgang
$\ mathbf {w} ^ H.$ - Dies ist eine hermitische Konjugation des Filterkoeffizientenvektors. - In ihrer optimalen Auswahl liegt die Anpassungsfähigkeit des Filters

Sie haben wahrscheinlich bereits vermutet, dass wir den kleinsten Unterschied zwischen dem gegebenen und dem gefilterten Signal anstreben werden, dh den kleinsten Fehler. Dies bedeutet, dass wir vor einer Optimierungsaufgabe stehen.

Was werden wir optimieren?

Um zu optimieren oder vielmehr zu minimieren, meinen wir nicht nur den Fehler, den mittleren quadratischen Fehler ( MSE - Mean Sqared Error ):

$MSE: J (\ mathbf {w}) = E \ {e (n) ^ 2 \} \ qquad (2)$

wo $J (\ mathbf {w})$ bezeichnet die Kostenfunktion des Vektors der Filterkoeffizienten und $E \ {* \}$ bezeichnet mat. Warten.

Das Quadrat ist in diesem Fall sehr angenehm, da es bedeutet, dass wir mit dem Problem der konvexen Programmierung konfrontiert sind (ich google nur ein solches Analogon der englischen konvexen Optimierung ), was wiederum ein einzelnes Extremum impliziert (in unserem Fall ein Minimum).

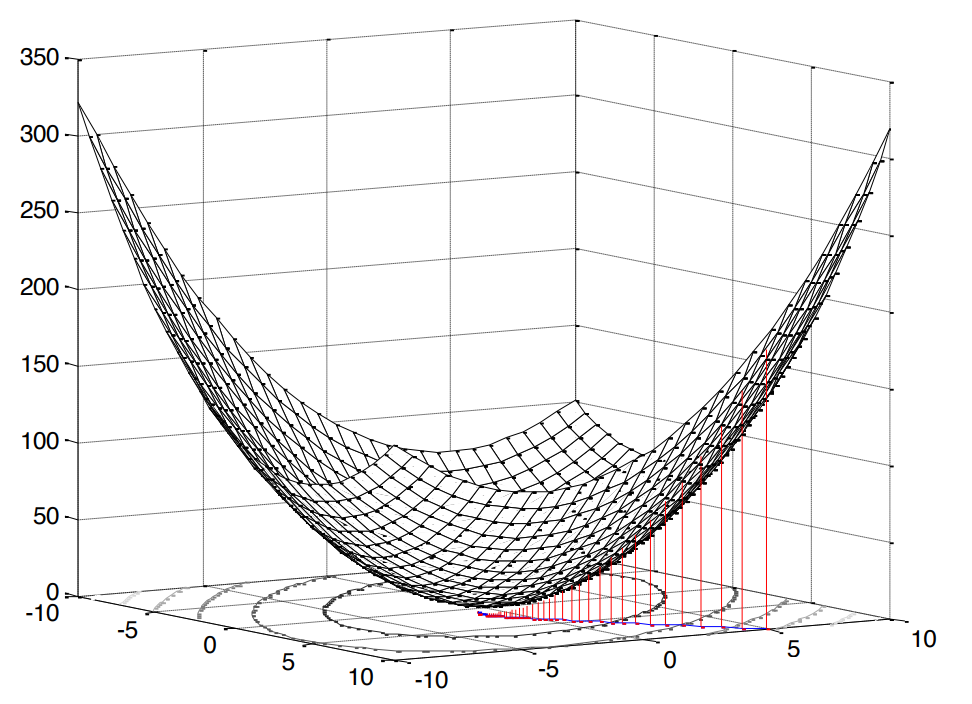
Abb. 2. Die Oberfläche des mittleren quadratischen Fehlers .

Unsere Fehlerfunktion hat eine kanonische Form [1, S. 121]:

$J (\ mathbf {w}) = \ sigma ^ 2_d - \ mathbf {w} ^ H \ mathbf {p} - \ mathbf {p} ^ H \ mathbf {w} + \ mathbf {w} ^ H \ mathbf { R} \ mathbf {w} \ qquad (3)$

wo $\ sigma ^ 2_d$ Ist die Varianz des erwarteten Signals, $\ mathbf {p} = E \ {\ mathbf {u} (n) d ^ * (n) \}$ Ist der Kreuzkorrelationsvektor zwischen dem Eingangsvektor und dem erwarteten Signal und $\ mathbf {R} = E \ {\ mathbf {u} (n) \ mathbf {u} ^ H (n) \}$ Ist die Autokorrelationsmatrix des Eingangssignals.

Die Schlussfolgerung dieser Formel ist hier (ich habe es klarer versucht).

Wie oben erwähnt, haben wir ein Extremum (Minimum), wenn wir über konvexe Programmierung sprechen. Um den minimalen Wert der Kostenfunktion (den minimalen quadratischen Mittelwertfehler) zu ermitteln, reicht es aus, die Tangente der Steigung der Tangente oder mit anderen Worten die partielle Ableitung in Bezug auf unsere untersuchte Variable zu ermitteln:

$\ frac {\ delta J (\ mathbf {w})} {\ delta w ^ *} = - \ mathbf {p} + \ mathbf {R} \ mathbf {w} \ qquad (4)$

Im besten Fall ( $\ mathbf {w} = \ mathbf {w} _ {opt}$ ) sollte der Fehler natürlich minimal sein, was bedeutet, dass wir die Ableitung mit Null gleichsetzen:

$\ mathbf {R} \ mathbf {w} _ {opt} = \ mathbf {p} \ qquad (5)$

Eigentlich ist es hier unser Ofen, von dem aus wir weiter tanzen werden: Vor uns liegt ein System linearer Gleichungen .

Wie werden wir uns entscheiden?

Es sollte sofort angemerkt werden, dass beide Lösungen, die wir unten betrachten werden, in diesem Fall theoretisch und lehrreich sind, da $\ mathbf {R}$ und $\ mathbf {p}$ im Voraus bekannt (dh wir hatten die angebliche Fähigkeit, ausreichende Statistiken zu sammeln, um diese zu berechnen). Die Analyse solcher vereinfachten Beispiele hier ist jedoch das Beste, was Sie sich vorstellen können, um die grundlegenden Ansätze zu verstehen.

Analytische Lösung

Dieses Problem kann sozusagen in der Stirn gelöst werden - mit inversen Matrizen:

$\ mathbf {w} _ {opt} = \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (6)$

Ein solcher Ausdruck heißt Wiener-Hopf-Gleichung - er ist für uns immer noch als Referenz nützlich.

Um völlig akribisch zu sein, wäre es wahrscheinlich korrekter, diesen Fall allgemein aufzuschreiben, d. H. nicht mit $^ {-}$ und mit ( Pseudo-Invert ):
$\ mathbf {R} ^ + = \ mathbf {R} ^ H (\ mathbf {R} \ mathbf {R} ^ H) ^ {- 1}$

Die Autokorrelationsmatrix kann jedoch nicht nicht quadratisch oder singulär sein, daher glauben wir zu Recht, dass es keinen Widerspruch gibt.

Aus dieser Gleichung ist es analytisch möglich, abzuleiten, wie hoch der Mindestwert der Kostenfunktion sein wird (d. H. In unserem Fall MMSE - minimaler mittlerer quadratischer Fehler):

$J_ {min} = J (\ mathbf {w} _ {opt}) = \ sigma ^ 2_d - \ mathbf {p} ^ H \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (7)$

Die Ableitung der Formel ist hier (ich habe auch versucht, sie bunter zu machen).

Nun, es gibt eine Lösung.

Iterative Lösung

Ja, es ist jedoch möglich, ein lineares Gleichungssystem zu lösen, ohne die Autokorrelationsmatrix iterativ zu invertieren ( um Berechnungen zu speichern ). Betrachten Sie zu diesem Zweck die native und verständliche Methode des Gradientenabfalls ( Methode des steilsten / Gradientenabstiegs ).

Das Wesen des Algorithmus kann auf Folgendes reduziert werden:

Wir setzen die gewünschte Variable auf einen Standardwert (z. B. $\ mathbf {w} (0) = \ mathbf {0}$ )
Wähle einen Schritt $\ mu$ (Wie genau wir uns entscheiden, werden wir weiter unten besprechen).
Und dann gehen wir sozusagen mit einem bestimmten Schritt entlang unserer ursprünglichen Oberfläche (in unserem Fall ist dies die MSE-Oberfläche) hinunter $\ mu$ und eine bestimmte Geschwindigkeit, die durch die Größe des Gradienten bestimmt wird.

Daher der Name: Gefälle - Gefälle oder steilste - schrittweise Abfahrt - Abfahrt.

Der Gradient in unserem Fall ist bereits bekannt: Wir haben ihn tatsächlich gefunden, als wir die Kostenfunktion differenzierten (die Oberfläche ist konkav, vergleiche mit [1, S. 220]). Wir schreiben, wie die Formel für die iterative Aktualisierung der gewünschten Variablen (Filterkoeffizienten) aussehen wird [1, S. 220]:

$\ mathbf {w} (n + 1) = \ mathbf {w} (n) - \ mu [- \ mathbf {p} + \ mathbf {R} \ mathbf {w} (n)] \ qquad (8)$

wo Ist die Iterationsnummer.

Lassen Sie uns nun über die Auswahl einer Schrittgröße sprechen.

Wir listen die offensichtlichen Prämissen auf:

Schritt kann nicht negativ oder Null sein
Der Schritt sollte nicht zu groß sein, sonst konvergiert der Algorithmus nicht (er springt sozusagen von Kante zu Kante, ohne ins Extreme zu fallen).
Der Schritt kann natürlich sehr klein sein, aber dies ist auch nicht ganz wünschenswert - der Algorithmus wird mehr Zeit aufwenden

In Bezug auf den Wiener Filter wurden Einschränkungen natürlich schon vor langer Zeit gefunden [1, S. 222-226]:

$0 <\ mu <\ frac {2} {\ lambda_ {max}} \ qquad (9)$

wo $\ lambda_ {max}$ Ist der größte Eigenwert der Autokorrelationsmatrix $\ mathbf {R}$ .

Eigenwerte und Vektoren sind übrigens ein eigenständiges interessantes Thema im Zusammenhang mit der linearen Filterung. Für diesen Fall gibt es sogar einen ganzen Eigenfilter (siehe Anhang 1).

Aber das ist zum Glück noch nicht alles. Es gibt auch eine optimale, adaptive Lösung:

$\ mu (n) = \ frac {\ mathbf {\ gamma} (n) ^ H \ mathbf {\ gamma} (n)} {\ mathbf {\ gamma} (n) ^ H \ mathbf {R} \ mathbf { \ gamma} (n)} \ qquad (10)$

wo $\ mathbf {\ gamma} (n) = \ mathbf {p} - \ mathbf {R} \ mathbf {w} (n)$ Ist ein negativer Gradient. Wie aus der Formel ersichtlich ist, wird der Schritt in jede Iteration neu berechnet, dh angepasst.

Die Schlussfolgerung der Formel ist hier (viel Mathematik - schauen Sie sich nur die berüchtigten Nerds wie ich an).

Okay, für die zweite Entscheidung haben wir auch die Bühne bereitet.

Aber ist es mit Beispielen möglich?

Aus Gründen der Klarheit werden wir eine kleine Simulation durchführen. Wir werden Python 3.6.4 verwenden .

Ich werde gleich sagen, dass diese Beispiele Teil einer der Hausaufgaben sind, von denen jede den Schülern innerhalb von zwei Wochen zur Lösung angeboten wird. Ich habe den Teil unter Python umgeschrieben (um die Sprache unter den Funkingenieuren bekannt zu machen). Vielleicht werden Sie im Web auf einige andere Optionen anderer ehemaliger Studenten stoßen.

import numpy as np import matplotlib.pyplot as plt from scipy.linalg import toeplitz def convmtx(h,n): return toeplitz(np.hstack([h, np.zeros(n-1)]),\ np.hstack([h[0], np.zeros(n-1)])) def MSE_calc(sigmaS, R, p, w): w = w.reshape(w.shape[0], 1) wH = np.conj(w).reshape(1, w.shape[0]) p = p.reshape(p.shape[0], 1) pH = np.conj(p).reshape(1, p.shape[0]) MSE = sigmaS - np.dot(wH, p) - np.dot(pH, w) + np.dot(np.dot(wH, R), w) return MSE[0, 0] def mu_opt_calc(gamma, R): gamma = gamma.reshape(gamma.shape[0], 1) gammaH = np.conj(gamma).reshape(1, gamma.shape[0]) mu_opt = np.dot(gammaH, gamma) / np.dot(np.dot(gammaH, R), gamma) return mu_opt[0, 0]

Wir werden unser lineares Filter für das Kanalentzerrungsproblem verwenden , dessen Hauptzweck darin besteht, die verschiedenen Auswirkungen dieses Kanals auf das Nutzsignal zu nivellieren.

Der Quellcode kann hier oder hier in einer Datei heruntergeladen werden (ja, ich hatte so ein Hobby - Wikipedia bearbeiten).

Systemmodell

Angenommen, es gibt ein Antennenarray (wir haben es bereits in einem Artikel über MUSIK untersucht ).

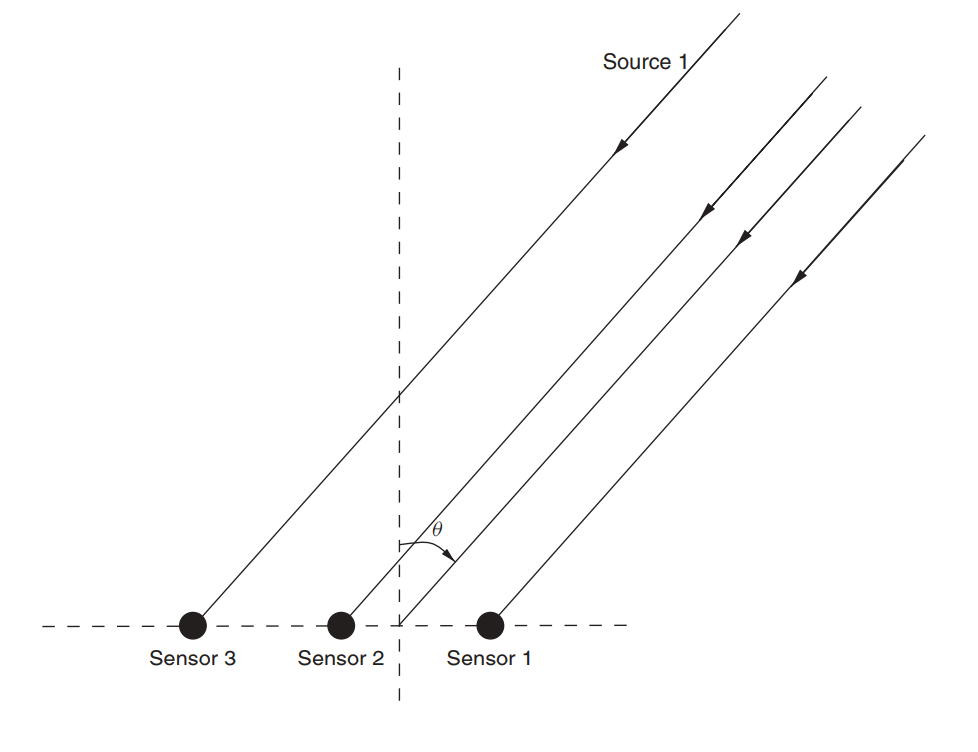
Abb. 3. Nicht gerichtetes lineares Antennenarray (ULAA - Uniform Linear Antenna Array) [2, S. 32].

Definieren Sie die anfänglichen Gitterparameter:

 M = 5 #    (number of sensors)

In diesem Artikel werden wir so etwas wie einen Breitbandkanal mit Fading betrachten , dessen charakteristisches Merkmal die Mehrwegeausbreitung ist . In solchen Fällen wird normalerweise ein Ansatz angewendet, bei dem jeder Strahl mit einer Verzögerung einer bestimmten Größe modelliert wird (Abb. 4).

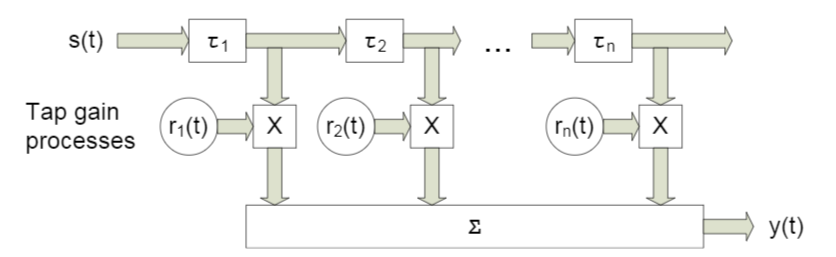
Abb. 4. Das Modell des Breitbandkanals mit n festen Verzögerungen. [3, S. 29]. Wie Sie verstehen, spielen bestimmte Bezeichnungen keine Rolle - im Folgenden werden wir etwas andere verwenden.

Das Modell des empfangenen Signals für einen Sensor wird wie folgt ausgedrückt:

$x (n) = \ sum_ {l = 0} ^ Lh (l) s (n-l) + \ nu (n)$

In diesem Fall gibt die Referenznummer an, h (l) Ist die Antwort des Kanals entlang des l- ten Strahls, L ist die Anzahl der Verzögerungsregister, s ist das übertragene (nützliche) Signal, $\ nu (n)$ - additives Rauschen.

Für mehrere Sensoren hat die Formel folgende Form:

$\ mathbf {x} (n) = \ mathbf {H} \ mathbf {s} (n) + \ mathbf {\ nu} (n)$

wo $\ mathbf {x} (n)$ und $\ mathbf {\ nu} (n)$ - Dimension haben $M \ mal 1$ Dimension $\ mathbf {H}$ ist gleich $M \ mal (M-L)$ und die Dimension $\ mathbf {s} (n)$ gleich $(M-L) \ mal 1$ .

Angenommen, jeder Sensor empfängt aufgrund des Einfalls der Welle in einem Winkel auch ein Signal mit einer bestimmten Verzögerung. Matrix $\ mathbf {H}$ In unserem Fall ist es eine Faltungsmatrix für den Antwortvektor für jeden Strahl. Ich denke, der Code wird klarer:

 h = np.array([0.722-1j*0.779, -0.257-1j*0.722, -0.789-1j*1.862]) L = len(h)-1 # number of signal sources H = convmtx(h,ML) print(H.shape) print(H)

Die Schlussfolgerung wird sein:

 >>> (5, 3) >>> array([[ 0.722-0.779j, 0. +0.j , 0. +0.j ], [-0.257-0.722j, 0.722-0.779j, 0. +0.j ], [-0.789-1.862j, -0.257-0.722j, 0.722-0.779j], [ 0. +0.j , -0.789-1.862j, -0.257-0.722j], [ 0. +0.j , 0. +0.j , -0.789-1.862j]])

Als nächstes legen wir die Anfangsdaten für das Nutzsignal und das Rauschen fest:

 sigmaS = 1 #    (the signal's s(n) power) sigmaN = 0.01 #   (the noise's n(n) power)

Nun kommen wir zu Korrelationen.

 Rxx = (sigmaS)*(np.dot(H,np.matrix(H).H))+(sigmaN)*np.identity(M) p = (sigmaS)*H[:,0] p = p.reshape((len(p), 1))

Die Ableitung der Formeln hier (auch ein Blatt für die verzweifeltsten).

Wir finden eine Lösung für Wiener:

 # Solution of the Wiener-Hopf equation: wopt = np.dot(np.linalg.inv(Rxx), p) MSEopt = MSE_calc(sigmaS, Rxx, p, wopt)

Fahren wir nun mit der Gradientenabstiegsmethode fort.

Finden Sie den größten Eigenwert, damit die obere Grenze des Schritts daraus abgeleitet werden kann (siehe Formel (9)):

 lamda_max = max(np.linalg.eigvals(Rxx))

Stellen wir nun einige Schritte ein, die einen bestimmten Bruchteil des Maximums ausmachen:

 coeff = np.array([1, 0.9, 0.5, 0.2, 0.1]) mus = 2/lamda_max*coeff # different step sizes

Definieren Sie die maximale Anzahl von Iterationen:

 N_steps = 100

Führen Sie den Algorithmus aus:

 MSE = np.empty((len(mus), N_steps), dtype=complex) for mu_idx, mu in enumerate(mus): w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): w = w - mu*(np.dot(Rxx, w) - p) MSE[mu_idx, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Jetzt machen wir dasselbe, aber für den adaptiven Schritt (Formel (10)):

 MSEoptmu = np.empty((1, N_steps), dtype=complex) w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): gamma = p - np.dot(Rxx,w) mu_opt = mu_opt_calc(gamma, Rxx) w = w - mu_opt*(np.dot(Rxx,w) - p) MSEoptmu[:, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Sie sollten so etwas bekommen:

Zeichnen

 x = [i for i in range(1, N_steps+1)] plt.figure(figsize=(5, 4), dpi=300) for idx, item in enumerate(coeff): if item == 1: item = '' plt.loglog(x, np.abs(MSE[idx, :]),\ label='$\mu = '+str(item)+'\mu_{max}$') plt.loglog(x, np.abs(MSEoptmu[0, :]),\ label='$\mu = \mu_{opt}$') plt.loglog(x, np.abs(MSEopt*np.ones((len(x), 1), dtype=complex)),\ label = 'Wiener solution') plt.grid(True) plt.xlabel('Number of steps') plt.ylabel('Mean-Square Error') plt.title('Steepest descent') plt.legend(loc='best') plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

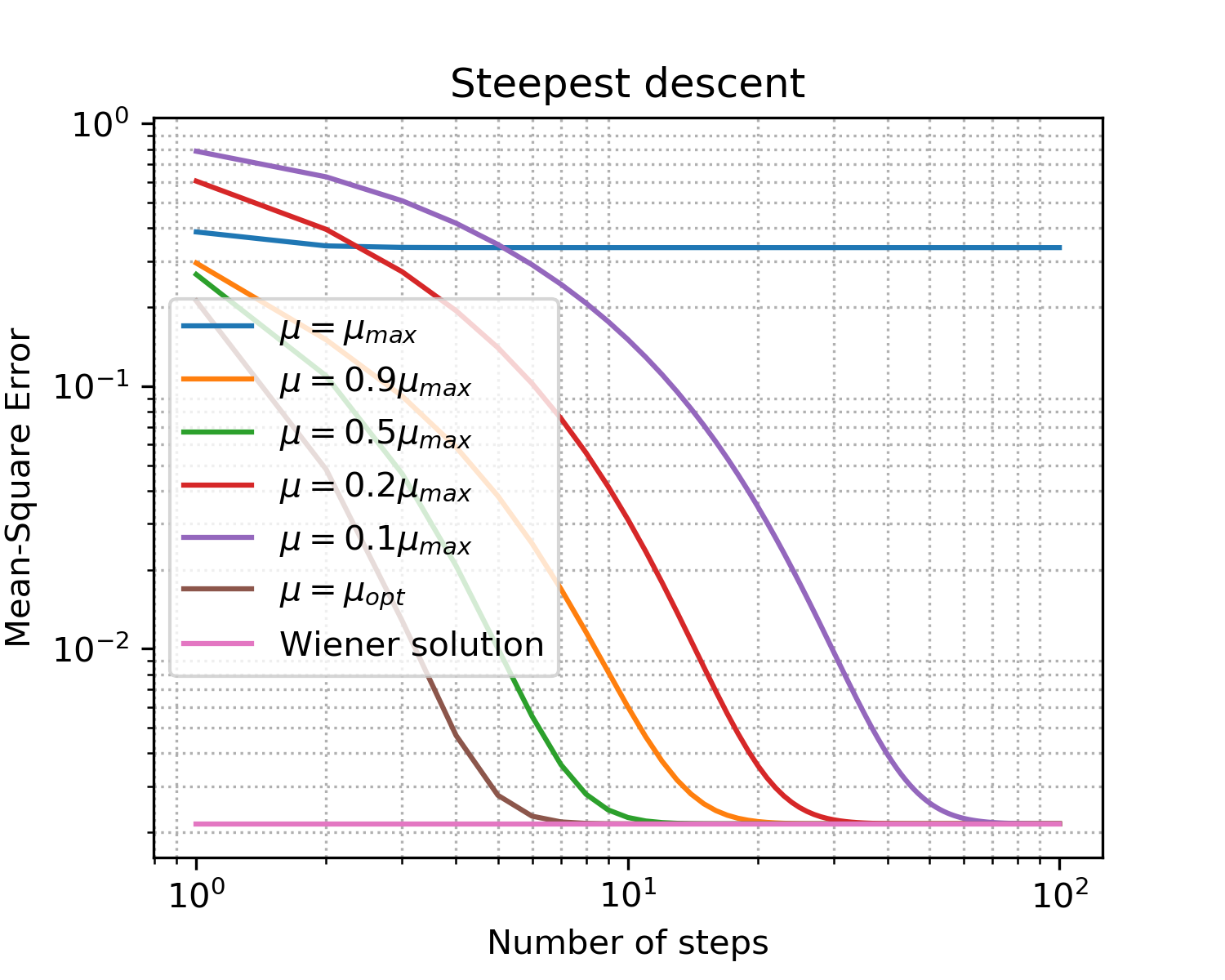
Abb. 5. Lernkurven für Schritte unterschiedlicher Größe.

Befestigungen, um die wichtigsten Punkte beim Gefälle hervorzuheben:

Wie erwartet ergibt der optimale Schritt die schnellste Konvergenz.
bedeutet nicht mehr besser: Nachdem wir die Obergrenze überschritten haben, haben wir überhaupt keine Konvergenz erreicht.

Also haben wir den optimalen Vektor der Filterkoeffizienten gefunden, der die Effekte des Kanals am besten ausgleicht - wir haben den Equalizer trainiert .

Gibt es etwas näher an der Realität?

Natürlich! Wir haben bereits mehrfach gesagt, dass das Sammeln von Statistiken (d. H. Das Berechnen von Korrelationsmatrizen und Vektoren) in Echtzeitsystemen alles andere als ein erschwinglicher Luxus ist. Die Menschheit hat sich jedoch an diese Schwierigkeiten angepasst: Anstelle eines deterministischen Ansatzes in der Praxis werden adaptive Ansätze verwendet. Sie können in zwei große Gruppen eingeteilt werden [1, S. 246]:

probabilistisch (stochastisch) (z. B. SG - stochastischer Gradient)
und basierend auf der Methode der kleinsten Quadrate (z. B. LMS - Least Mean Squares oder RLS - Recursive Least Squares)

Das Thema der adaptiven Filter ist in der Open-Source-Community gut vertreten (Beispiele für Python):

Im zweiten Beispiel gefällt mir besonders die Dokumentation. Seien Sie jedoch vorsichtig! Als ich das Padasip- Paket getestet habe , hatte ich Schwierigkeiten beim Umgang mit komplexen Zahlen (standardmäßig ist float64 dort impliziert). Möglicherweise können bei der Arbeit mit einigen anderen Implementierungen dieselben Probleme auftreten.

Algorithmen haben natürlich ihre eigenen Vor- und Nachteile, deren Summe den Umfang des Algorithmus bestimmt.

Werfen wir einen kurzen Blick auf die Beispiele: Wir werden die drei Algorithmen SG , LMS und RLS betrachten , die wir bereits erwähnt haben (wir werden in der MATLAB-Sprache modellieren - ich gestehe, es gab bereits Leerzeichen und schreiben alles in Einheitlichkeitspython um, um ... na ja ...).

Eine Beschreibung der LMS- und RLS- Algorithmen finden Sie beispielsweise im Padasip- Dock.

Eine Beschreibung der SG finden Sie hier.

Der Hauptunterschied zum Gradientenabstieg ist ein variabler Gradient:

$\ mathbf {w} [n] = \ mathbf {w} [n-1] + \ mu \ left (\ mathbf {\ hat {p}} [n] - \ mathbf {\ hat {R}} _ {xx } [n] \ mathbf {w} [n-1] \ right)$

bei

$\ mathbf {\ hat {R}} _ {xx} [n] = \ frac {1} {n} \ left ((n-1) \ mathbf {\ hat {R}} _ {xx} [n-1 ] + \ mathbf {x} [n] \ mathbf {x} [n] ^ H \ rechts)$

$\ mathbf {\ hat {p}} [n] = \ frac {1} {n} \ left ((n-1) \ mathbf {\ hat {p}} [n-1] + \ mathbf {x} [ n] d [n] ^ * \ rechts)$

1) Ein ähnlicher Fall wie oben.

Quellen (MatLab / Octave).

Quellen können hier heruntergeladen werden .

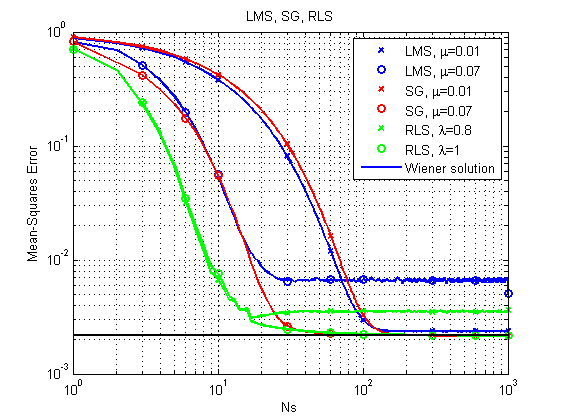
Abb. 6. Lernkurven für LMS, RLS und SG.

Es ist sofort zu bemerken, dass der LMS-Algorithmus aufgrund seiner relativen Einfachheit im Prinzip möglicherweise nicht zu einer optimalen Lösung mit einem relativ großen Schritt kommt. RLS liefert das schnellste Ergebnis, kann aber auch mit einem relativ kleinen Vergessensfaktor versagen. Bisher geht es SG gut, aber schauen wir uns ein anderes Beispiel an.

2) Der Fall, wenn sich der Kanal zeitlich ändert.

Quellen (MatLab / Octave).

Quellen können hier heruntergeladen werden .

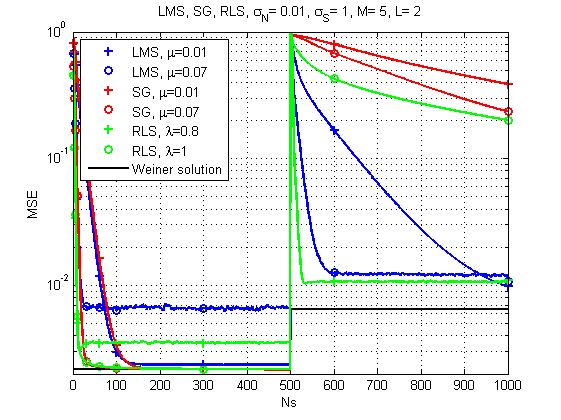
Abb. 7. Lernkurven für LMS, RLS und SG (Kanalwechsel im Laufe der Zeit).

Und hier ist das Bild schon viel interessanter: Mit einer starken Veränderung in der Reaktion des Kanals scheint LMS bereits die zuverlässigste Lösung zu sein. Wer hätte das gedacht. Obwohl RLS mit dem richtigen Vergessensfaktor auch ein akzeptables Ergebnis liefert.

Ein paar Worte zur Leistung.

Ja, natürlich hat jeder Algorithmus seine eigene spezifische Rechenkomplexität, aber nach meinen Messungen kann meine alte Maschine ein Ensemble für ungefähr 120 μs pro Iteration bei LMS und SG und ungefähr 250 μs pro Iteration bei RLS bewältigen. Das heißt, der Unterschied ist im Allgemeinen vergleichbar.

Und das ist alles für heute. Vielen Dank an alle, die geschaut haben!

Literatur

Haykin SS Adaptive Filtertheorie. - Pearson Education India, 2005.
Haykin, Simon und KJ Ray Liu. Handbuch zur Array-Verarbeitung und zu Sensornetzwerken. Vol. 63. John Wiley & Sons, 2010. pp. 102-107
Arndt, D. (2015). On Channel Modeling für den mobilen Satellitenempfang an Land (Dissertation).

Anhang 1

Eigenfilter

Das Hauptziel eines solchen Filters ist die Maximierung des Signal-Rausch-Verhältnisses (SNR).

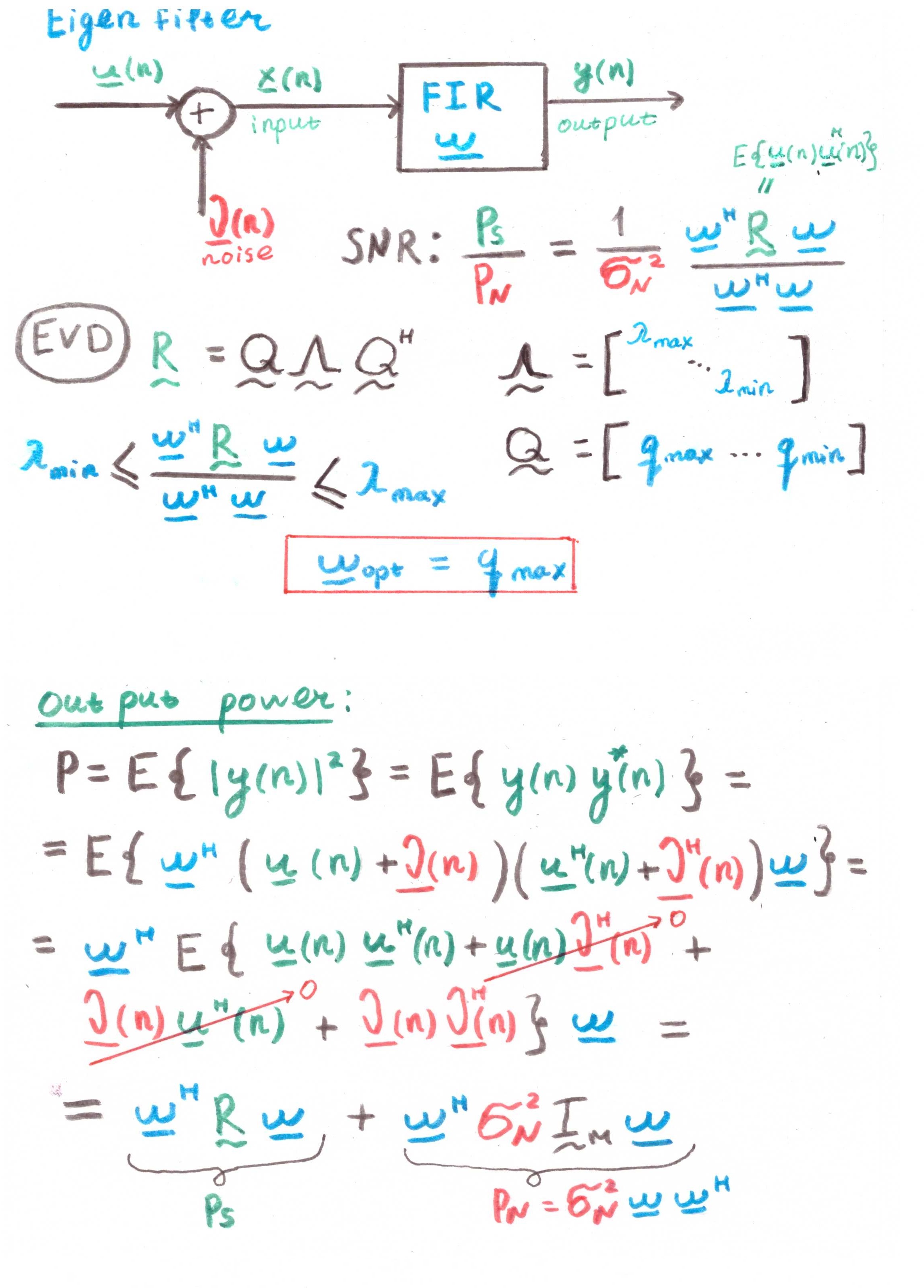
Nach dem Vorhandensein von Korrelationen in den Berechnungen zu urteilen, ist dies jedoch eher ein theoretisches Konstrukt als eine praktische Lösung.

Optimale lineare Filterung: vom Gradientenabstieg bis zum adaptiven Filter