Eine kurze Einführung in Markov-Ketten

Im Jahr 1998 veröffentlichten Lawrence Page, Sergey Brin, Rajiv Motwani und Terry Vinograd den Artikel „Das PageRank-Zitierranking: Ordnung ins Web bringen“, in dem der mittlerweile berühmte PageRank-Algorithmus beschrieben wurde, der zur Grundlage von Google wurde. Nach etwas weniger als zwei Jahrzehnten wurde Google ein Riese, und obwohl sich sein Algorithmus stark weiterentwickelt hat, ist PageRank immer noch das „Symbol“ für Google-Ranking-Algorithmen (obwohl nur wenige Menschen wirklich sagen können, wie viel Gewicht der Algorithmus heute benötigt). .

Aus theoretischer Sicht ist es interessant festzustellen, dass eine der Standardinterpretationen des PageRank-Algorithmus auf einem einfachen, aber grundlegenden Konzept von Markov-Ketten basiert. Aus dem Artikel werden wir sehen, dass Markov-Ketten leistungsstarke Werkzeuge für die stochastische Modellierung sind, die für jeden Datenwissenschaftler nützlich sein können. Insbesondere werden wir solche grundlegenden Fragen beantworten: Was sind Markov-Ketten, welche guten Eigenschaften besitzen sie und was kann mit ihrer Hilfe getan werden?

Kurzer Rückblick

Im ersten Abschnitt geben wir die grundlegenden Definitionen an, die zum Verständnis der Markov-Ketten erforderlich sind. Im zweiten Abschnitt betrachten wir den Sonderfall von Markov-Ketten in einem endlichen Zustandsraum. Im dritten Abschnitt betrachten wir einige der elementaren Eigenschaften von Markov-Ketten und veranschaulichen diese Eigenschaften anhand vieler kleiner Beispiele. Schließlich verknüpfen wir im vierten Abschnitt die Markov-Ketten mit dem PageRank-Algorithmus und sehen anhand eines künstlichen Beispiels, wie Markov-Ketten zum Einordnen der Knoten eines Graphen verwendet werden können.

Hinweis Um diesen Beitrag zu verstehen, müssen Sie die Grundlagen der Wahrscheinlichkeit und der linearen Algebra kennen. Insbesondere werden die folgenden Konzepte verwendet: bedingte Wahrscheinlichkeit , Eigenvektor und Formel mit voller Wahrscheinlichkeit .

---

Was sind Markov-Ketten?

Zufallsvariablen und zufällige Prozesse

Bevor wir das Konzept der Markov-Ketten einführen, erinnern wir uns kurz an die grundlegenden, aber wichtigen Konzepte der Wahrscheinlichkeitstheorie.

Erstens ist eine Zufallsvariable X außerhalb der Sprache der Mathematik eine Größe, die durch das Ergebnis eines Zufallsphänomens bestimmt wird. Das Ergebnis kann eine Zahl (oder "Ähnlichkeit einer Zahl", beispielsweise Vektoren) oder etwas anderes sein. Zum Beispiel können wir eine Zufallsvariable als Ergebnis eines Würfelwurfs (Zahl) oder als Ergebnis eines Münzwurfs definieren (keine Zahl, es sei denn, wir bezeichnen beispielsweise "Adler" als 0, aber "Schwänze" als 1). Wir erwähnen auch, dass der Raum möglicher Ergebnisse einer Zufallsvariablen diskret oder stetig sein kann: Beispielsweise ist eine normale Zufallsvariable stetig und eine Poisson-Zufallsvariable diskret.

Ferner können wir einen zufälligen Prozess (auch als stochastisch bezeichnet) als eine Menge von Zufallsvariablen definieren, die durch die Menge T indiziert werden, die häufig unterschiedliche Zeitpunkte bezeichnet (im Folgenden werden wir dies annehmen). Die beiden häufigsten Fälle: T kann entweder eine Menge natürlicher Zahlen (zufälliger Prozess mit diskreter Zeit) oder eine Menge reeller Zahlen (zufälliger Prozess mit kontinuierlicher Zeit) sein. Wenn wir beispielsweise jeden Tag eine Münze werfen, legen wir einen zufälligen Prozess mit diskreter Zeit fest, und der sich ständig ändernde Wert einer Option an der Börse legt einen zufälligen Prozess mit kontinuierlicher Zeit fest. Zufällige Variablen zu verschiedenen Zeitpunkten können unabhängig voneinander sein (ein Beispiel mit einem Münzwurf) oder eine gewisse Abhängigkeit aufweisen (ein Beispiel mit dem Optionswert). Darüber hinaus können sie einen kontinuierlichen oder diskreten Zustandsraum haben (den Raum möglicher Ergebnisse zu jedem Zeitpunkt).


Verschiedene Arten von Zufallsprozessen (diskret / kontinuierlich in Raum / Zeit).

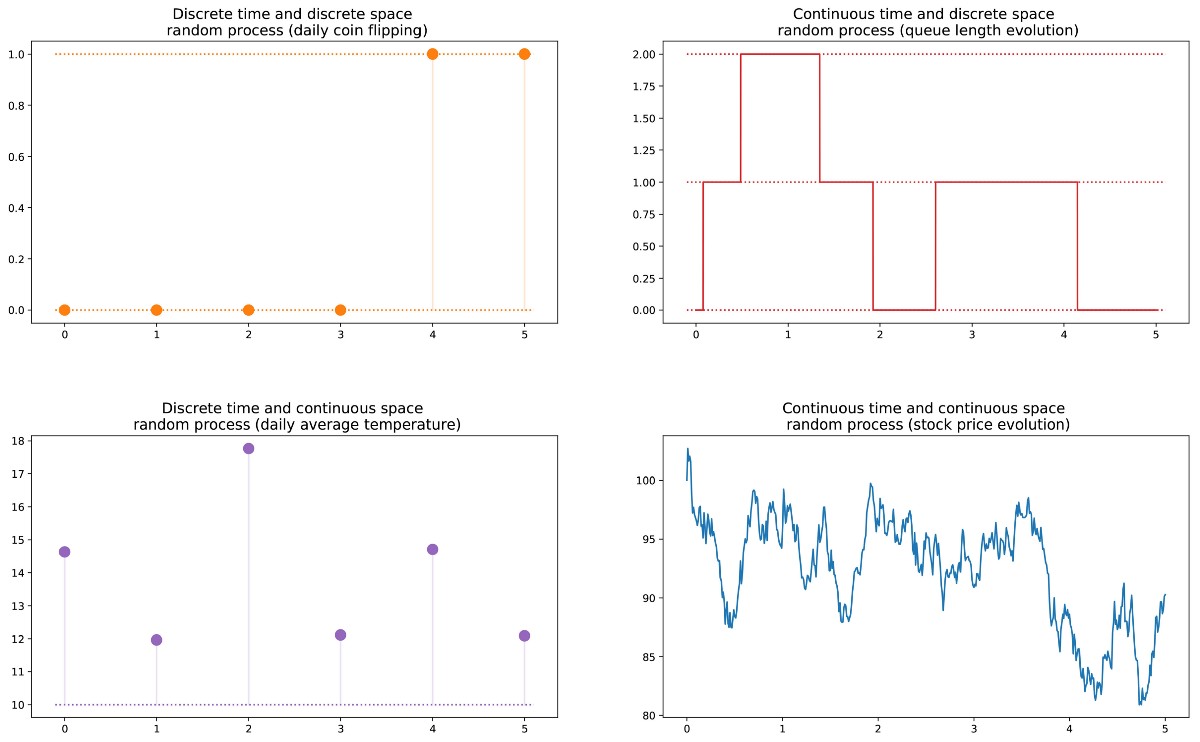
Markov-Eigenschaft und Markov-Kette

Es gibt bekannte Familien zufälliger Prozesse: Gaußsche Prozesse, Poisson-Prozesse, autoregressive Modelle, Modelle mit gleitendem Durchschnitt, Markov-Ketten und andere. Jeder dieser Einzelfälle hat bestimmte Eigenschaften, die es uns ermöglichen, sie besser zu untersuchen und zu verstehen.

Eine der Eigenschaften, die das Studium eines zufälligen Prozesses erheblich vereinfacht, ist die Markov-Eigenschaft. Wenn wir es in einer sehr informellen Sprache erklären, sagt uns die Markov-Eigenschaft, dass wir, wenn wir den Wert kennen, der durch einen zufälligen Prozess zu einem bestimmten Zeitpunkt erhalten wird, keine zusätzlichen Informationen über das zukünftige Verhalten des Prozesses erhalten und andere Informationen über seine Vergangenheit sammeln. In einer mathematischeren Sprache: Zu jedem Zeitpunkt hängt die bedingte Verteilung zukünftiger Zustände eines Prozesses mit gegebenen aktuellen und vergangenen Zuständen nur vom aktuellen Zustand ab und nicht von vergangenen Zuständen (die Eigenschaft des Speichermangels ). Ein zufälliger Prozess mit einer Markov-Eigenschaft wird als Markov-Prozess bezeichnet .


Die Markov-Eigenschaft bedeutet, dass wir, wenn wir den aktuellen Status zu einem bestimmten Zeitpunkt kennen, keine zusätzlichen Informationen über die Zukunft benötigen, die aus der Vergangenheit stammen.

Basierend auf dieser Definition können wir die Definition von "homogenen Markov-Ketten mit diskreter Zeit" formulieren (im Folgenden werden wir sie der Einfachheit halber "Markov-Ketten" nennen). Die Markov-Kette ist ein Markov-Prozess mit diskreter Zeit und einem diskreten Zustandsraum. Eine Markov-Kette ist also eine diskrete Folge von Zuständen, von denen jeder aus einem diskreten Zustandsraum (endlich oder unendlich) stammt und die Markov-Eigenschaft erfüllt.

Mathematisch können wir die Markov-Kette wie folgt bezeichnen:


wobei zu jedem Zeitpunkt der Prozess seine Werte aus einer diskreten Menge E bezieht, so dass


Dann impliziert die Markov-Eigenschaft, dass wir haben


Beachten Sie erneut, dass diese letzte Formel die Tatsache widerspiegelt, dass für die Chronologie (wo ich jetzt bin und wo ich vorher war) die Wahrscheinlichkeitsverteilung des nächsten Zustands (wo ich der nächste sein werde) vom aktuellen Zustand abhängt, jedoch nicht von früheren Zuständen.

Hinweis In diesem Einführungsbeitrag haben wir beschlossen, nur über einfache homogene Markov-Ketten mit diskreter Zeit zu sprechen. Es gibt jedoch auch inhomogene (zeitabhängige) Markov-Ketten und / oder zeitkontinuierliche Ketten. In diesem Artikel werden solche Variationen des Modells nicht berücksichtigt. Es ist auch erwähnenswert, dass die obige Definition einer Markov-Eigenschaft extrem vereinfacht ist: Die wahre mathematische Definition verwendet das Konzept der Filterung, das weit über unsere einführende Kenntnis des Modells hinausgeht.

Wir charakterisieren die Zufallsdynamik einer Markov-Kette

Im vorherigen Unterabschnitt haben wir die allgemeine Struktur einer Markov-Kette kennengelernt. Mal sehen, was wir brauchen, um eine bestimmte "Instanz" eines solchen zufälligen Prozesses festzulegen.

Zunächst stellen wir fest, dass die vollständige Bestimmung der Eigenschaften eines zufälligen Prozesses mit diskreter Zeit, die die Markov-Eigenschaft nicht erfüllt, schwierig sein kann: Die Wahrscheinlichkeitsverteilung zu einem bestimmten Zeitpunkt kann von einem oder mehreren Momenten in der Vergangenheit und / oder Zukunft abhängen. All diese möglichen Zeitabhängigkeiten können möglicherweise die Erstellung einer Prozessdefinition erschweren.

Aufgrund der Markov-Eigenschaft ist die Dynamik der Markov-Kette jedoch recht einfach zu bestimmen. Und in der Tat. wir müssen nur zwei Aspekte bestimmen: die anfängliche Wahrscheinlichkeitsverteilung (d. h. die Wahrscheinlichkeitsverteilung zum Zeitpunkt n = 0), bezeichnet mit


und die Übergangswahrscheinlichkeitsmatrix (die uns die Wahrscheinlichkeiten gibt, dass der Zustand zum Zeitpunkt n + 1 der nächste für einen anderen Zustand zum Zeitpunkt n für ein beliebiges Zustandspaar ist), bezeichnet mit


Wenn diese beiden Aspekte bekannt sind, ist die vollständige (probabilistische) Dynamik des Prozesses klar definiert. Tatsächlich kann die Wahrscheinlichkeit eines Ergebnisses des Prozesses dann zyklisch berechnet werden.

Beispiel: Angenommen, wir möchten die Wahrscheinlichkeit wissen, dass die ersten drei Zustände des Prozesses Werte haben (s0, s1, s2). Das heißt, wir wollen die Wahrscheinlichkeit berechnen


Hier wenden wir die Formel für die Gesamtwahrscheinlichkeit an, die besagt, dass die Wahrscheinlichkeit des Erhaltens (s0, s1, s2) gleich der Wahrscheinlichkeit des Erhaltens des ersten s0-fachen der Wahrscheinlichkeit des Erhaltens von s1 ist, vorausgesetzt, wir haben zuvor das s0-fache der Wahrscheinlichkeit des Erhaltens von s2 unter Berücksichtigung der Tatsache erhalten, dass wir haben früher in der Reihenfolge s0 und s1. Mathematisch kann dies geschrieben werden als


Und dann wird eine Vereinfachung offenbart, die durch die Markov-Annahme bestimmt wird. Tatsächlich erhalten wir bei langen Ketten stark bedingte Wahrscheinlichkeiten für die letzteren Zustände. Im Fall von Markov-Ketten können wir diesen Ausdruck jedoch vereinfachen, indem wir die Tatsache ausnutzen, dass


auf diese Weise bekommen


Da sie die probabilistische Dynamik des Prozesses vollständig charakterisieren, können viele komplexe Ereignisse nur auf der Grundlage der anfänglichen Wahrscheinlichkeitsverteilung q0 und der Übergangswahrscheinlichkeitsmatrix p berechnet werden. Erwähnenswert ist auch eine weitere grundlegende Verbindung: der Ausdruck der Wahrscheinlichkeitsverteilung zum Zeitpunkt n + 1, ausgedrückt in Bezug auf die Wahrscheinlichkeitsverteilung zum Zeitpunkt n

Markov-Ketten in endlichen Zustandsräumen

Matrix- und Graphendarstellung

Hier nehmen wir an, dass die Menge E eine endliche Anzahl möglicher Zustände N hat:


Dann kann die anfängliche Wahrscheinlichkeitsverteilung als ein Zeilenvektor q0 der Größe N beschrieben werden, und Übergangswahrscheinlichkeiten können als eine Matrix p der Größe N durch N beschrieben werden, so dass


Der Vorteil dieser Notation besteht darin, dass wir die Wahrscheinlichkeitsverteilung in Schritt n durch den Zeilenvektor qn so bezeichnen, dass seine Komponenten spezifiziert werden


dann bleiben einfache Matrixrelationen erhalten


(hier werden wir den Beweis nicht betrachten, aber es ist sehr einfach, ihn zu reproduzieren).


Wenn wir den Zeilenvektor rechts, der die Wahrscheinlichkeitsverteilung zu einem bestimmten Zeitpunkt beschreibt, mit der Übergangswahrscheinlichkeitsmatrix multiplizieren, erhalten wir die Wahrscheinlichkeitsverteilung zum nächsten Zeitpunkt.

Wie wir sehen, wird der Übergang der Wahrscheinlichkeitsverteilung von einer gegebenen Stufe zur nächsten einfach als die richtige Multiplikation des Zeilenvektors der Wahrscheinlichkeiten des Anfangsschritts mit der Matrix p definiert. Darüber hinaus impliziert dies, dass wir haben


Die zufällige Dynamik einer Markov-Kette in einem endlichen Zustandsraum kann leicht als normalisierter orientierter Graph dargestellt werden, so dass jeder Knoten des Graphen ein Zustand ist und für jedes Zustandspaar (ei, ej) eine Kante existiert, die von ei nach ej geht, wenn p (ei, ej) )> 0. Dann ist der Kantenwert die gleiche Wahrscheinlichkeit p (ei, ej).

Beispiel: ein Leser unserer Website

Lassen Sie uns dies alles anhand eines einfachen Beispiels veranschaulichen. Betrachten Sie das alltägliche Verhalten eines fiktiven Besuchers einer Site. Jeden Tag hat er drei mögliche Bedingungen: Der Leser besucht die Site an diesem Tag nicht (N), der Leser besucht die Site, liest jedoch nicht den gesamten Beitrag (V), und der Leser besucht die Site und liest einen gesamten Post (R). Wir haben also den folgenden Zustandsraum:


Angenommen, dieser Leser hat am ersten Tag eine 50% ige Chance, nur auf die Site zuzugreifen, und eine 50% ige Chance, die Site zu besuchen und mindestens einen Artikel zu lesen. Der Vektor, der die anfängliche Wahrscheinlichkeitsverteilung beschreibt (n = 0), sieht dann folgendermaßen aus:


Stellen Sie sich auch vor, dass die folgenden Wahrscheinlichkeiten eingehalten werden:

• Wenn der Leser einen Tag nicht besucht, besteht eine Wahrscheinlichkeit von 25%, ihn am nächsten Tag nicht zu besuchen, eine Wahrscheinlichkeit von 50%, ihn nur zu besuchen, und eine Wahrscheinlichkeit von 25%, den Artikel zu besuchen und zu lesen
• Wenn der Leser die Website eines Tages besucht, aber nicht liest, hat er eine 50% ige Chance, sie am nächsten Tag erneut zu besuchen und den Artikel nicht zu lesen, und eine 50% ige Chance, sie zu besuchen und zu lesen
• Wenn ein Leser einen Artikel am selben Tag besucht und liest, hat er eine 33% ige Chance, sich am nächsten Tag nicht anzumelden (ich hoffe, dieser Beitrag hat keinen solchen Effekt!) , eine 33% ige Chance, sich nur auf der Website anzumelden, und 34%, den Artikel erneut zu besuchen und zu lesen

Dann haben wir die folgende Übergangsmatrix:


Aus dem vorherigen Unterabschnitt wissen wir, wie wir für diesen Leser die Wahrscheinlichkeit jedes Zustands am nächsten Tag berechnen können (n = 1).


Die probabilistische Dynamik dieser Markov-Kette kann wie folgt grafisch dargestellt werden:


Präsentation in Form eines Diagramms der Markov-Kette, das das Verhalten unseres erfundenen Besuchers der Website modelliert.

Eigenschaften von Markov-Ketten

In diesem Abschnitt werden wir nur auf einige der grundlegendsten Eigenschaften oder Merkmale von Markov-Ketten eingehen. Wir werden nicht auf mathematische Details eingehen, sondern einen kurzen Überblick über interessante Punkte geben, die untersucht werden müssen, um Markov-Ketten zu verwenden. Wie wir gesehen haben, kann im Fall eines endlichen Zustandsraums die Markov-Kette als Graph dargestellt werden. In Zukunft werden wir die grafische Darstellung verwenden, um einige Eigenschaften zu erklären. Vergessen Sie jedoch nicht, dass diese Eigenschaften nicht unbedingt auf den Fall eines endlichen Zustandsraums beschränkt sind.

Zersetzbarkeit, Periodizität, Unwiderruflichkeit und Wiederherstellbarkeit

Beginnen wir in diesem Unterabschnitt mit mehreren klassischen Methoden zur Charakterisierung eines Zustands oder einer gesamten Markov-Kette.

Zunächst erwähnen wir, dass die Markov-Kette nicht zusammensetzbar ist, wenn es möglich ist, einen Zustand von einem anderen Zustand aus zu erreichen (dies ist nicht in einem Schritt erforderlich). Wenn der Zustandsraum endlich ist und die Kette als Graph dargestellt werden kann, können wir sagen, dass der Graph einer nicht zusammensetzbaren Markov-Kette stark verbunden ist (Graphentheorie).


Darstellung der Eigenschaft der Unzusammensetzbarkeit (Irreduzibilität). Die Kette links kann nicht gekürzt werden: von 3 oder 4 können wir nicht in 1 oder 2 gelangen. Die Kette rechts (eine Kante wird hinzugefügt) kann gekürzt werden: Jeder Zustand kann von jedem anderen aus erreicht werden.

Ein Zustand hat eine Periode k, wenn beim Verlassen für eine Rückkehr in diesen Zustand die Anzahl der Zeitschritte ein Vielfaches von k ist (k ist der größte gemeinsame Teiler aller möglichen Längen von Rückkehrpfaden). Wenn k = 1 ist, sagen sie, dass der Zustand aperiodisch ist und die gesamte Markov-Kette aperiodisch ist, wenn alle ihre Zustände aperiodisch sind. Im Fall einer irreduziblen Markov-Kette können wir auch erwähnen, dass, wenn ein Zustand aperiodisch ist, alle anderen ebenfalls aperiodisch sind.


Darstellung der Periodizitätseigenschaft. Die Kette links ist periodisch mit k = 2: Wenn Sie einen Zustand verlassen, erfordert die Rückkehr immer die Anzahl der Schritte multipliziert mit 2. Die Kette rechts hat eine Periode von 3.

Ein Staat ist unwiderruflich, wenn beim Verlassen des Staates eine Wahrscheinlichkeit ungleich Null besteht, dass wir niemals zu ihm zurückkehren werden. Umgekehrt gilt ein Staat als rückzahlbar, wenn wir wissen, dass wir nach Verlassen des Staates in Zukunft mit Wahrscheinlichkeit 1 zu ihm zurückkehren können (wenn er nicht unwiderruflich ist).


Abbildung der Rückgabe- / Unwiderruflichkeitseigenschaft. Die Kette auf der linken Seite hat die folgenden Eigenschaften: 1, 2 und 3 sind unwiderruflich (wenn wir diese Punkte verlassen, können wir nicht absolut sicher sein, dass wir zu ihnen zurückkehren) und haben eine Periode von 3, und 4 und 5 sind rückzahlbar (wenn wir diese Punkte verlassen, sind wir absolut sicher dass wir eines Tages zu ihnen zurückkehren werden) und eine Periode von 2 haben. Die Kette auf der rechten Seite hat eine weitere Rippe, wodurch die gesamte Kette rückzahlbar und aperiodisch wird.

Für den Rückgabezustand können wir die durchschnittliche Rückgabezeit berechnen, die die erwartete Rückgabezeit beim Verlassen des Zustands ist. Beachten Sie, dass selbst die Wahrscheinlichkeit einer Rückgabe 1 beträgt. Dies bedeutet nicht, dass die erwartete Rückgabezeit endlich ist. Daher können wir unter allen Rückkehrzuständen zwischen positiven Rückkehrzuständen (mit einer endlichen erwarteten Rückkehrzeit) und Null-Rückkehrzuständen (mit einer unendlichen erwarteten Rückkehrzeit) unterscheiden.

Stationäre Verteilung, Randverhalten und Ergodizität

In diesem Unterabschnitt betrachten wir Eigenschaften, die einige Aspekte der (zufälligen) Dynamik charakterisieren, die von der Markov-Kette beschrieben wird.

Die Wahrscheinlichkeitsverteilung π über den Zustandsraum E wird als stationäre Verteilung bezeichnet, wenn sie den Ausdruck erfüllt


Da haben wir


Dann erfüllt die stationäre Verteilung den Ausdruck


Per Definition ändert sich die stationäre Wahrscheinlichkeitsverteilung nicht über die Zeit. Das heißt, wenn die Anfangsverteilung q stationär ist, ist sie in allen nachfolgenden Zeitstufen gleich. Wenn der Zustandsraum endlich ist, kann p als Matrix und π als Zeilenvektor dargestellt werden, und dann erhalten wir


Dies drückt erneut die Tatsache aus, dass sich die stationäre Wahrscheinlichkeitsverteilung nicht mit der Zeit ändert (wie wir sehen, können wir durch Multiplizieren der Wahrscheinlichkeitsverteilung rechts mit p die Wahrscheinlichkeitsverteilung in der nächsten Zeitstufe berechnen). Beachten Sie, dass eine nicht zusammensetzbare Markov-Kette genau dann eine stationäre Wahrscheinlichkeitsverteilung aufweist, wenn einer ihrer Zustände eine positive Rendite aufweist.

Eine weitere interessante Eigenschaft im Zusammenhang mit der stationären Wahrscheinlichkeitsverteilung ist wie folgt. Wenn die Kette eine positive Rendite (dh eine stationäre Verteilung) und eine aperiodische Verteilung aufweist, konvergiert die Wahrscheinlichkeitsverteilung der Kette unabhängig von den anfänglichen Wahrscheinlichkeiten, wenn die Zeitintervalle gegen unendlich tendieren: Sie sagen, dass die Kette eine begrenzende Verteilung hat , was nichts anderes ist. als stationäre Verteilung. Im Allgemeinen kann es so geschrieben werden:


Wir betonen noch einmal, dass wir keine Annahmen über die anfängliche Wahrscheinlichkeitsverteilung treffen: Die Wahrscheinlichkeitsverteilung der Kette reduziert sich unabhängig von den Anfangsparametern auf eine stationäre Verteilung (Gleichgewichtsverteilung der Kette).

Schließlich ist Ergodizität eine weitere interessante Eigenschaft im Zusammenhang mit dem Verhalten der Markov-Kette. Wenn die Markov-Kette nicht zusammensetzbar ist, wird auch gesagt, dass sie „ergodisch“ ist, weil sie den folgenden ergodischen Satz erfüllt. Angenommen, wir haben eine Funktion f (.), Die vom Zustandsraum E zur Achse geht (dies kann zum Beispiel der Preis sein, in jedem Zustand zu sein). Wir können den Durchschnittswert bestimmen, der diese Funktion entlang einer bestimmten Trajektorie bewegt (zeitlicher Durchschnitt). Für den n-ten ersten Term wird dies als bezeichnet


Wir können auch den Durchschnittswert der Funktion f auf der Menge E berechnen, gewichtet mit der stationären Verteilung (räumlicher Durchschnitt), die bezeichnet wird


Dann sagt uns der Ergodensatz, dass, wenn die Flugbahn unendlich lang wird, der Zeitmittelwert gleich dem räumlichen Durchschnitt ist (gewichtet mit der stationären Verteilung). Die Ergodizitätseigenschaft kann wie folgt geschrieben werden:


Mit anderen Worten bedeutet dies, dass in der früheren Grenze das Verhalten der Trajektorie unbedeutend wird und nur das langfristige stationäre Verhalten bei der Berechnung des zeitlichen Durchschnitts wichtig ist.

Kehren wir zum Beispiel mit dem Site Reader zurück

Betrachten Sie erneut das Beispiel des Site-Readers. In diesem einfachen Beispiel ist es offensichtlich, dass die Kette nicht zusammensetzbar und aperiodisch ist und alle ihre Zustände positiv zurückgegeben werden können.

Um zu zeigen, welche interessanten Ergebnisse mit Markov-Ketten berechnet werden können, betrachten wir die durchschnittliche Zeit der Rückkehr zum Zustand R (der Zustand „besucht die Site und liest den Artikel“). Mit anderen Worten, wir möchten die folgende Frage beantworten: Wenn unser Leser eines Tages die Website besucht und einen Artikel liest, wie viele Tage müssen wir dann durchschnittlich warten, bis er zurückkommt und den Artikel liest? Versuchen wir, ein intuitives Konzept für die Berechnung dieses Werts zu erhalten.

Zuerst bezeichnen wir


Wir wollen also m (R, R) berechnen. Wenn wir über das erste Intervall sprechen, das nach dem Verlassen von R erreicht wurde, erhalten wir


Dieser Ausdruck erfordert jedoch, dass wir für die Berechnung von m (R, R) m (N, R) und m (V, R) kennen. Diese beiden Größen können auf ähnliche Weise ausgedrückt werden:


Wir haben also 3 Gleichungen mit 3 Unbekannten und nach dem Lösen erhalten wir m (N, R) = 2,67, m (V, R) = 2,00 und m (R, R) = 2,54. Die durchschnittliche Zeit, um zum Zustand R zurückzukehren, beträgt dann 2,54. Das heißt, unter Verwendung der linearen Algebra konnten wir die durchschnittliche Zeit bis zur Rückkehr in den Zustand R berechnen (sowie die durchschnittliche Übergangszeit von N nach R und die durchschnittliche Übergangszeit von V nach R).

Lassen Sie uns zum Abschluss dieses Beispiels sehen, wie die stationäre Verteilung der Markov-Kette aussehen wird. Um die stationäre Verteilung zu bestimmen, müssen wir die folgende Gleichung der linearen Algebra lösen:


Das heißt, wir müssen den linken Eigenvektor p finden, der dem Eigenvektor 1 zugeordnet ist. Wenn wir dieses Problem lösen, erhalten wir die folgende stationäre Verteilung:


Stationäre Verteilung im Beispiel mit dem Site Reader.

Sie können auch feststellen, dass π (R) = 1 / m (R, R) ist, und wenn ein wenig reflektiert wird, dann ist diese Identität ziemlich logisch (aber wir werden nicht im Detail darüber sprechen).

Da die Kette nicht zusammensetzbar und aperiodisch ist, bedeutet dies, dass die Wahrscheinlichkeitsverteilung auf lange Sicht gegen eine stationäre Verteilung konvergiert (für alle Anfangsparameter). Mit anderen Worten, unabhängig vom Ausgangszustand des Lesers der Site erhalten wir, wenn wir lange genug warten und zufällig einen Tag auswählen, die Wahrscheinlichkeit π (N), dass der Leser die Site an diesem Tag nicht besucht, die Wahrscheinlichkeit π (V), dass Der Leser wird vorbeischauen, aber den Artikel nicht lesen, und die Wahrscheinlichkeit ist π®, dass der Leser vorbeischaut und den Artikel liest. Um die Eigenschaft der Konvergenz besser zu verstehen, werfen wir einen Blick auf die folgende Grafik, die die Entwicklung der Wahrscheinlichkeitsverteilungen ausgehend von verschiedenen Startpunkten und (schnell) der Konvergenz zu einer stationären Verteilung zeigt:


3 (, ) ().

: PageRank

PageRank! , , PageRank, , , . , .

-

PageRank versucht, das folgende Problem zu lösen: Wie ordnen wir einen vorhandenen Satz (wir können davon ausgehen, dass dieser Satz bereits durch eine Abfrage gefiltert wurde) mithilfe von Links, die bereits zwischen den Seiten vorhanden sind?

Um dieses Problem zu lösen und Seiten ordnen zu können, führt PageRank ungefähr den folgenden Prozess aus. Wir glauben, dass sich ein beliebiger Internetnutzer zum ersten Mal auf einer der Seiten befindet. Dann beginnt dieser Benutzer zufällig, sich zu bewegen, indem er auf jede Seite eines der Links klickt, die zu einer anderen Seite des betreffenden Satzes führen (es wird angenommen, dass alle Links, die außerhalb dieser Seiten führen, verboten sind). Auf jeder Seite haben alle gültigen Links die gleiche Wahrscheinlichkeit zu klicken.

So definieren wir die Markov-Kette: Seiten sind mögliche Zustände, Übergangswahrscheinlichkeiten werden durch Links von Seite zu Seite festgelegt (so gewichtet, dass auf jeder Seite alle verknüpften Seiten die gleiche Auswahlwahrscheinlichkeit haben), und die Eigenschaften des Speichermangels werden eindeutig durch das Benutzerverhalten bestimmt. Wenn wir auch annehmen, dass die gegebene Kette positiv zurückgegeben und aperiodisch ist (kleine Tricks werden verwendet, um diese Anforderungen zu erfüllen), dann konvergiert die Wahrscheinlichkeitsverteilung der „aktuellen Seite“ auf lange Sicht zu einer stationären Verteilung. Das heißt, unabhängig von der ersten Seite hat jede Seite nach langer Zeit eine (fast feste) Wahrscheinlichkeit, aktuell zu werden, wenn wir einen zufälligen Zeitpunkt wählen.

Der PageRank basiert auf der folgenden Hypothese: Die wahrscheinlichsten Seiten in einer stationären Verteilung sollten auch die wichtigsten sein (wir besuchen diese Seiten häufig, da sie Links von Seiten erhalten, die auch während Übergängen häufig besucht werden). Dann bestimmt die stationäre Wahrscheinlichkeitsverteilung den PageRank-Wert für jeden Zustand.

Künstliches Beispiel

Um dies viel klarer zu machen, schauen wir uns ein künstliches Beispiel an. Angenommen, wir haben eine winzige Website mit 7 Seiten mit den Bezeichnungen 1 bis 7, und die Links zwischen diesen Seiten entsprechen der folgenden Spalte.


Aus Gründen der Klarheit sind die Wahrscheinlichkeiten jedes Übergangs in der oben gezeigten Animation nicht gezeigt. Da jedoch davon ausgegangen wird, dass „Navigation“ ausschließlich zufällig sein sollte (dies wird als „zufälliges Gehen“ bezeichnet), können die Werte leicht anhand der folgenden einfachen Regel reproduziert werden: Für eine Site mit K ausgehenden Links (Seite mit K Links zu anderen Seiten) die Wahrscheinlichkeit jedes ausgehenden Links gleich 1 / K. Das heißt, die Übergangswahrscheinlichkeitsmatrix hat die Form:


wobei die Werte von 0,0 der Einfachheit halber durch "." ersetzt werden. Bevor wir weitere Berechnungen durchführen, können wir feststellen, dass diese Markov-Kette nicht zusammensetzbar und aperiodisch ist, dh auf lange Sicht konvergiert das System zu einer stationären Verteilung. Wie wir gesehen haben, kann diese stationäre Verteilung berechnet werden, indem das folgende Problem des linken Eigenvektors gelöst wird


Auf diese Weise erhalten wir für jede Seite die folgenden PageRank-Werte (stationäre Verteilungswerte)


PageRank-Werte berechnet für unser künstliches Beispiel von 7 Seiten.

Dann ist das PageRank-Ranking dieser winzigen Website 1> 7> 4> 2> 5 = 6> 3.

---

Schlussfolgerungen

Wichtigste Ergebnisse aus diesem Artikel:

• Zufallsprozesse sind Sätze von Zufallsvariablen, die häufig nach Zeit indiziert sind (Indizes geben häufig diskrete oder kontinuierliche Zeit an).
• Für einen zufälligen Prozess bedeutet die Markov-Eigenschaft, dass für einen bestimmten Strom die Wahrscheinlichkeit der Zukunft nicht von der Vergangenheit abhängt (diese Eigenschaft wird auch als „Speichermangel“ bezeichnet).
• Die zeitdiskrete Markov-Kette besteht aus zufälligen Prozessen mit zeitdiskreten Indizes, die die Markov-Eigenschaft erfüllen
• ( , …)
• PageRank ( ) -, ; ( , , , )

, , . , , ( , , ), ( - ), ( ), ( ), .

Natürlich sind die enormen Möglichkeiten, die Markov-Ketten im Hinblick auf Modellierung und Berechnung bieten, viel größer als die in dieser bescheidenen Übersicht berücksichtigten. Wir hoffen daher, dass wir das Interesse des Lesers wecken konnten, diese Tools weiter zu untersuchen, die einen wichtigen Platz im Arsenal eines Wissenschaftlers und Datenexperten einnehmen.