Es ist kein Geheimnis, dass eine der Lieblingsbeschäftigungen eines Softwareentwicklers darin besteht, Arbeitgeber zu befragen. Wir alle tun dies von Zeit zu Zeit und aus ganz anderen Gründen. Und die offensichtlichste davon - die Arbeitssuche - ist meiner Meinung nach nicht die häufigste. Die Teilnahme an einem Interview ist eine gute Möglichkeit, um fit zu bleiben, vergessene Grundlagen zu wiederholen und etwas Neues zu lernen. Und wenn Sie erfolgreich sind, steigern Sie auch das Selbstvertrauen. Wir langweilen uns, setzen uns in einem sozialen Netzwerk wie
"LinkedIn" den Status "offen für Angebote" - und die Armee der Personalmanager greift bereits unsere Posteingänge für eingehende Nachrichten an.

Während all dieses Chaos vor sich geht, stehen wir vor vielen Fragen, die, wie sie auf der anderen Seite des implizit zusammengebrochenen Vorhangs sagen, „eine Glocke läuten“ und deren Details sich hinter dem
Nebel des Krieges verbergen. Sie werden meistens nur bei Tests mit Algorithmen und Datenstrukturen (persönlich hatte ich solche Daten überhaupt nicht) und bei Interviews abgerufen.
Eine der häufigsten Fragen in einem Interview für einen Programmierer jeder Spezialisierung sind Listen. Zum Beispiel einfach verknüpfte Listen. Und verwandte grundlegende Algorithmen. Zum Beispiel eine Kehrtwende. Und normalerweise passiert das irgendwie so: "Gut, aber wie würden Sie eine einfach verknüpfte Liste erweitern?" Die Hauptsache ist, den Antragsteller mit dieser Frage zu überraschen.
All dies veranlasste mich, diese kurze Rezension zur ständigen Erinnerung und Erbauung zu schreiben. Also, Witze beiseite, siehe da!
Einfach verknüpfte Liste
Eine verknüpfte Liste ist eine der grundlegenden
Datenstrukturen . Jedes Element (oder jeder Knoten) davon besteht tatsächlich aus gespeicherten Daten und Verknüpfungen zu benachbarten Elementen. Eine einfach verknüpfte Liste speichert nur einen Link zum nächsten Element in der Struktur, und eine
doppelt verknüpfte Liste enthält einen Link zum nächsten und vorherigen. Eine solche Organisation von Daten ermöglicht es ihnen, sich in einem beliebigen Speicherbereich zu befinden (im Gegensatz beispielsweise zu einem
Array , dessen Elemente sich alle nacheinander im Speicher befinden sollten).
Zu Listen gibt es natürlich noch viel mehr zu sagen: Sie können kreisförmig sein (d. H. Das letzte Element speichert eine Verknüpfung zum ersten) oder nicht (d. H. Es gibt keine Verknüpfung zum letzten Element). Listen können eingegeben werden, d.h. Daten des gleichen Typs enthalten oder nicht. Und so weiter und so fort.
Versuchen Sie besser, Code zu schreiben. Zum Beispiel können Sie sich einen Listenknoten vorstellen:
final class Node<T> { let payload: T var nextNode: Node? init(payload: T, nextNode: Node? = nil) { self.payload = payload self.nextNode = nextNode } }
"Allgemein" ist ein Typ, der Nutzdaten eines beliebigen Typs im Feld "
payload speichern kann.
Die Liste selbst wird durch ihren ersten Knoten erschöpfend identifiziert:
final class SinglyLinkedList<T> { var firstNode: Node<T>? init(firstNode: Node<T>? = nil) { self.firstNode = firstNode } }
Der erste Knoten wird als optional deklariert, da die Liste möglicherweise leer ist.
Theoretisch müssen Sie in der Klasse natürlich alle erforderlichen Methoden implementieren - Einfügen, Löschen, Zugriff auf Knoten usw., aber wir werden es ein anderes Mal tun. Gleichzeitig werden wir prüfen, ob die Verwendung von struct (mit der Apple uns durch unser Beispiel aktiv ermutigt) eine bessere Wahl ist, und möglicherweise an den Ansatz „Copy-on-Write“ erinnern.Single-Linked-List-Spread
Der erste Weg. Zyklus
Es ist Zeit, zur Sache zu kommen, für die wir heute hier sind! Und der effektivste Weg, damit umzugehen, sind zwei Wege. Die erste ist eine einfache Schleife vom ersten bis zum letzten Knoten.
Der Zyklus arbeitet mit drei Variablen, denen vor Beginn der Wert des vorherigen, aktuellen und nächsten Knotens zugewiesen wird. (In diesem Moment ist der Wert des vorherigen Knotens natürlich leer.) Der Zyklus beginnt mit der Überprüfung, ob der nächste Knoten nicht leer ist. In diesem Fall wird der Hauptteil des Zyklus ausgeführt. In der Schleife geschieht keine Magie: Am aktuellen Knoten wird dem Feld, das sich auf das nächste Element bezieht, eine Verknüpfung mit dem vorherigen Element zugewiesen (bei der ersten Iteration wird der Wert der Verknüpfung zurückgesetzt, was dem Stand der Dinge im letzten Knoten entspricht). Nun und weiter werden den Variablen, die dem vorherigen, aktuellen und nächsten Knoten entsprechen, neue Werte zugewiesen. Nach dem Verlassen der Schleife wird dem aktuellen (d. H. Dem letzten im Allgemeinen iterierbaren) Knoten dem nächsten Knoten ein neuer Verbindungswert zugewiesen, weil Das Verlassen der Schleife erfolgt genau in dem Moment, in dem der letzte Knoten in der Liste aktuell wird.
In Worten klingt das alles natürlich seltsam und unverständlich, daher ist es besser, sich den Code anzusehen:
extension SinglyLinkedList { func reverse() { var previousNode: Node<T>? = nil var currentNode = firstNode var nextNode = firstNode?.nextNode while nextNode != nil { currentNode?.nextNode = previousNode previousNode = currentNode currentNode = nextNode nextNode = currentNode?.nextNode } currentNode?.nextNode = previousNode firstNode = currentNode } }
Zur Überprüfung verwenden wir eine Liste von Knoten, deren Nutzdaten einfache
Ganzzahlkennungen sind. Erstellen Sie eine Liste mit zehn Elementen:
let node = Node(payload: 0)
Alles scheint in Ordnung zu sein, aber wir sind Menschen, keine Computer, und es wäre schön, wenn wir einen visuellen Beweis für die Richtigkeit der erstellten Liste und des oben beschriebenen Algorithmus erhalten würden. Vielleicht reicht ein einfacher Druck. Um die Ausgabe lesbar zu machen, fügen wir
CustomStringConvertible Knoten die Implementierung des
CustomStringConvertible Protokolls mit einer Ganzzahl-
CustomStringConvertible :
extension Node: CustomStringConvertible where T == Int { var description: String { let firstPart = """ Node \(Unmanaged.passUnretained(self).toOpaque()) has id \(payload) and """ if let nextNode = nextNode { return firstPart + " next node \(nextNode.payload)." } else { return firstPart + " no next node." } } }
... und die entsprechende Liste, um alle Knoten der Reihe nach anzuzeigen:
extension SinglyLinkedList: CustomStringConvertible where T == Int { var description: String { var description = """ List \(Unmanaged.passUnretained(self).toOpaque()) """ if firstNode != nil { description += " has nodes:\n" var node = firstNode while node != nil { description += (node!.description + "\n") node = node!.nextNode } return description } else { return description + " has no nodes." } } }
Die Zeichenfolgendarstellung unserer Typen enthält eine Adresse im Speicher und eine Ganzzahlkennung. Mit ihnen organisieren wir den Druck der generierten Liste von zehn Knoten:
print(String(describing: list))
Erweitern Sie diese Liste und drucken Sie sie erneut aus:
list.reverse() print(String(describing: list))
Möglicherweise stellen Sie fest, dass sich die Adressen im Speicher der Liste und der Knoten nicht geändert haben und die Knoten der Liste in umgekehrter Reihenfolge gedruckt werden. Verweise auf das nächste Element des Knotens verweisen jetzt auf das vorherige (das heißt, das nächste Element des Knotens "5" ist jetzt nicht "6", sondern "4"). Und das heißt, wir haben es geschafft!
Der zweite Weg. Rekursion
Der zweite bekannte Weg, dieselbe Kehrtwende
durchzuführen, basiert auf
Rekursion . Um es zu implementieren, deklarieren wir eine Funktion, die den ersten Knoten der Liste übernimmt und den „neuen“ ersten Knoten zurückgibt (der der letzte war).
Der Parameter und der Rückgabewert sind optional, da er innerhalb dieser Funktion auf jedem nachfolgenden Knoten immer wieder aufgerufen wird, bis er leer ist (d. H. Bis das Ende der Liste erreicht ist). Dementsprechend muss im Hauptteil der Funktion geprüft werden, ob der Knoten, auf dem die Funktion aufgerufen wird, leer ist und ob dieser Knoten Folgendes aufweist. Wenn nicht, gibt die Funktion zurück, was an das Argument übergeben wurde.
Eigentlich habe ich ehrlich versucht, den vollständigen Algorithmus in Worten zu beschreiben, aber am Ende habe ich fast alles gelöscht, weil das Ergebnis unmöglich zu verstehen wäre. Flussdiagramme zu zeichnen und die Schritte des Algorithmus formal zu beschreiben - auch in diesem Fall halte ich es nicht für sinnvoll, da es für Sie und mich bequemer ist, den
Swift- Code einfach zu lesen und zu verstehen:
extension SinglyLinkedList { func reverseRecursively() { func reverse(_ node: Node<T>?) -> Node<T>? { guard let head = node else { return node } if head.nextNode == nil { return head } let reversedHead = reverse(head.nextNode) head.nextNode?.nextNode = head head.nextNode = nil return reversedHead } firstNode = reverse(firstNode) } }
Der Algorithmus selbst wird zur Vereinfachung des Aufrufs von einer Methode des Typs der tatsächlichen Liste "umbrochen".
Es sieht kürzer aus, ist aber meiner Meinung nach schwerer zu verstehen.
Wir rufen diese Methode für das Ergebnis des vorherigen Spread auf und drucken ein neues Ergebnis:
list.reverseRecursively() print(String(describing: list))
Aus der Ausgabe ist ersichtlich, dass sich nicht alle Adressen im Speicher erneut geändert haben und die Knoten nun in der ursprünglichen Reihenfolge folgen (dh sie werden erneut "bereitgestellt"). Und das heißt, wir haben es wieder richtig gemacht!
Schlussfolgerungen
Wenn Sie sich die Umkehrmethoden genau ansehen (oder ein Experiment mit Anrufzählung durchführen), werden Sie feststellen, dass die Schleife im ersten Fall und der interne (rekursive) Methodenaufruf im zweiten Fall einmal weniger auftreten als die Anzahl der Knoten in der Liste (in unserem Fall neun) mal). Sie können auch darauf achten, was im ersten Fall um die Schleife herum geschieht - dieselbe Reihenfolge von Zuweisungen - und im zweiten Fall auf den ersten, nicht rekursiven Methodenaufruf. Es stellt sich heraus, dass in beiden Fällen der „Kreis“ für eine Liste von zehn Knoten genau zehnmal wiederholt wird. Wir haben also eine lineare
Komplexität für beide Algorithmen -
O (n) .
Im Allgemeinen werden die beiden beschriebenen Algorithmen als die effektivsten zur Lösung dieses Problems angesehen. In Bezug auf die Komplexität der Berechnungen ist es nicht möglich, einen Algorithmus mit einem niedrigeren Wert zu entwickeln: Auf die eine oder andere Weise müssen Sie jeden Knoten "besuchen", um dem in der Verbindung gespeicherten einen neuen Wert zuzuweisen.
Ein weiteres erwähnenswertes Merkmal ist die „zugewiesene Speicherkomplexität“. Beide vorgeschlagenen Algorithmen erzeugen eine feste Anzahl neuer Variablen (drei im ersten Fall und eine im zweiten). Dies bedeutet, dass die Menge des zugewiesenen Speichers nicht von den quantitativen Eigenschaften der Eingabedaten abhängt und durch eine konstante Funktion - O (1) beschrieben wird.
Im zweiten Fall ist dies jedoch nicht der Fall. Die Gefahr einer Rekursion besteht darin, dass jedem rekursiven Aufruf auf dem
Stapel zusätzlicher Speicher zugewiesen wird. In unserem Fall entspricht die Rekursionstiefe der Menge der Eingabedaten.
Und schließlich habe ich beschlossen, ein wenig mehr zu experimentieren: Auf einfache und primitive Weise habe ich die absolute Ausführungszeit von zwei Methoden für eine unterschiedliche Menge von Eingabedaten gemessen. So:
let startDate = Date().timeIntervalSince1970
Und das habe ich bekommen (das sind die Rohdaten vom
Spielplatz ):
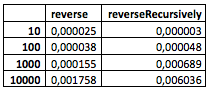
(Leider hat mein Computer die größeren Werte nicht gemeistert.)
Was kann man vom Tisch sehen? Noch nichts Besonderes. Es fällt zwar bereits auf, dass sich die rekursive Methode bei einer relativ geringen Anzahl von Knoten etwas schlechter verhält, aber irgendwo zwischen 100 und 1000 zeigt sie sich besser.
Ich habe den gleichen einfachen Test auch in einem vollwertigen
„Xcode“ -Projekt versucht. Die Ergebnisse sind wie folgt:

Zunächst ist zu erwähnen, dass die Ergebnisse nach Aktivierung des „aggressiven“ Optimierungsmodus erzielt wurden, der auf die Ausführungsgeschwindigkeit (
-Ofast )
-Ofast , weshalb die Zahlen teilweise so klein sind. Interessant ist auch, dass sich in diesem Fall die rekursive Methode etwas besser zeigte, im Gegenteil, nur bei sehr kleinen Eingabedatengrößen und bereits bei einer Liste von 100 Knoten verliert die Methode. Von 100.000 hat er das Programm abnormal beendet.
Fazit
Ich habe versucht, ein eher klassisches Thema aus der Sicht meiner bevorzugten Programmiersprache zu behandeln, und ich hoffe, Sie waren neugierig, den Fortschritt ebenso wie mich selbst zu verfolgen. Ich bin auch sehr froh, wenn Sie auch etwas Neues gelernt haben - dann habe ich definitiv meine Zeit in diesem Artikel verschwendet (anstatt zu sitzen und
Fernsehsendungen anzusehen ).
Wenn jemand den Wunsch hat, meine sozialen Aktivitäten zu verfolgen, finden Sie hier einen Link zu meinem „Twitter“ , wo zunächst Links zu meinen neuen Posts und ein wenig mehr vorhanden sind.