Wenn der vorherige Artikel eher geimpft wurde, ist es jetzt an der Zeit, Julias Parallelisierungsfunktionen auf ihrem Computer zu testen.
Mehrkern- oder verteilte Verarbeitung
Die Implementierung von Parallel Computing mit verteiltem Speicher wird vom Distributed Modul als Teil der mit Julia gelieferten Standardbibliothek bereitgestellt. Die meisten modernen Computer verfügen über mehr als einen Prozessor, und mehrere Computer können geclustert werden. Mit der Leistung dieser mehreren Prozessoren können Sie viele Berechnungen schneller durchführen. Die Leistung wird von zwei Hauptfaktoren beeinflusst: der Geschwindigkeit der Prozessoren selbst und der Geschwindigkeit ihres Speicherzugriffs. Im Cluster ist es offensichtlich, dass diese CPU auf demselben Computer (Knoten) den schnellsten Zugriff auf RAM hat. Vielleicht noch überraschender ist, dass solche Probleme bei einem typischen Multi-Core-Laptop aufgrund von Unterschieden in der Geschwindigkeit des Hauptspeichers und des Caches relevant sind. Daher sollte eine gute Multiprozessorumgebung es Ihnen ermöglichen, den "Besitz" eines Teils des Speichers durch einen bestimmten Prozessor zu steuern. Julia bietet eine Messaging-basierte Multiprozessor-Umgebung, mit der Programme gleichzeitig auf mehreren Prozessen in verschiedenen Speicherdomänen ausgeführt werden können.
Julias Messaging-Implementierung unterscheidet sich von anderen Umgebungen wie MPI [1] . Die Kommunikation in Julia erfolgt normalerweise in eine Richtung, was bedeutet, dass der Programmierer in einem Zwei-Prozess-Vorgang nur einen Prozess explizit steuern muss. Darüber hinaus sehen diese Vorgänge normalerweise nicht wie "Senden einer Nachricht" und "Empfangen einer Nachricht" aus, sondern ähneln eher Vorgängen einer höheren Ebene, z. B. Aufrufen von benutzerdefinierten Funktionen.
Die verteilte Programmierung in Julia basiert auf zwei Grundelementen: Fernverbindungen und Fernaufrufe . Eine Remoteverbindung ist ein Objekt, das von jedem Prozess aus verwendet werden kann, um auf ein in einem bestimmten Prozess gespeichertes Objekt zu verweisen. Ein Fernaufruf ist eine Anforderung eines Prozesses, eine bestimmte Funktion gemäß bestimmten Argumenten eines anderen (möglicherweise gleichen) Prozesses aufzurufen.
Remoteverbindungen gibt es in zwei Formen: Future und RemoteChannel .
Ein Fernanruf gibt Future und führt dies sofort aus. Der Prozess, der den Anruf getätigt hat, fährt mit dem nächsten Vorgang fort, während der Remote-Anruf an einer anderen Stelle stattfindet. Sie können warten, bis der Remote-Aufruf mit dem Befehl wait für die zurückgegebene Future , und Sie können den vollständigen Wert des Ergebnisses auch mit fetch abrufen .
Auf der anderen Seite haben wir RemoteChannels, die neu geschrieben werden. Beispielsweise können mehrere Prozesse ihre Verarbeitung unter Bezugnahme auf denselben Remote-Kanal koordinieren. Jedem Prozess ist eine Kennung zugeordnet. Der Prozess, der die interaktive Julia-Eingabeaufforderung bereitstellt, hat immer die Kennung 1. Die Prozesse, die standardmäßig für gleichzeitige Vorgänge verwendet werden, werden als "Worker" bezeichnet. Wenn es nur einen Prozess gibt, wird Prozess 1 als funktionierend betrachtet. Andernfalls werden alle Prozesse außer Prozess 1 als Arbeiter betrachtet.

Kommen wir dazu. julia -pn mit julia -pn postscript bietet n Workflows auf dem lokalen Computer. In der Regel ist es sinnvoll, dass n der Anzahl der CPU-Threads (logischen Kerne) auf dem Computer entspricht. Beachten Sie, dass das Argument -p das verteilte Modul implizit lädt.
Wie starte ich ein Postscript?Konsolenoperationen sollten für Linux-Benutzer unkompliziert sein. Dieses Schulungsprogramm richtet sich an unerfahrene Benutzer von Windows.
Terminal Julia (REPL) bietet die Möglichkeit, Systembefehle zu verwenden:
julia> pwd() # "C:\\Users\\User\\AppData\\Local\\Julia-1.1.0" julia> cd("C:/Users/User/Desktop") # julia> run(`calc`) # # Windows. # Process(`calc`, ProcessExited(0))
Mit diesen Befehlen können Sie Julia von Julia aus starten, aber es ist besser, sich nicht mitreißen zu lassen
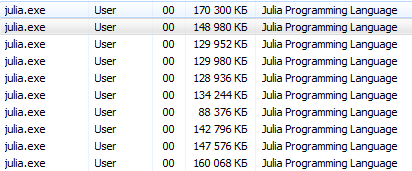
Es wäre korrekter, cmd von julia / bin / aus auszuführen und dort den Befehl julia -p 2 oder eine Option für Liebhaber des Startens über eine Verknüpfung C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4 Erstellen Sie auf dem Desktop ein Notizblockdokument mit den folgenden Inhalten C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4 ( geben Sie die Adresse und Anzahl der Prozesse an ) und speichern Sie es als Textdokument mit dem Namen run.bat . Hier, jetzt auf Ihrem Desktop, befindet sich eine Julia-Startsystemdatei für 4 Kerne.
Sie können eine andere Methode verwenden (besonders relevant für Jupyter ):
using Distributed addprocs(2)
$ ./julia -p 2 julia> r = remotecall(rand, 2, 2, 2) Future(2, 1, 4, nothing) julia> s = @spawnat 2 1 .+ fetch(r) Future(2, 1, 5, nothing) julia> fetch(s) 2×2 Array{Float64,2}: 1.18526 1.50912 1.16296 1.60607
Das erste Argument für Remotecall ist die aufgerufene Funktion.
Die meisten gleichzeitigen Programme in Julia beziehen sich nicht auf bestimmte Prozesse oder die Anzahl der verfügbaren Prozesse, aber ein Fernaufruf wird als Schnittstelle auf niedriger Ebene betrachtet, die eine genauere Steuerung bietet.
Das zweite Argument für remotecall ist die Kennung des Prozesses, der die Arbeit remotecall , und die verbleibenden Argumente werden an die aufgerufene Funktion übergeben. Wie Sie sehen können, haben wir in der ersten Zeile Prozess 2 gebeten, eine zufällige 2 x 2-Matrix zu erstellen, und in der zweiten Zeile haben wir darum gebeten, 1 hinzuzufügen. Das Ergebnis beider Berechnungen ist in zwei Futures verfügbar, r und s. Das Spawnat-Makro wertet den Ausdruck im zweiten Argument für den im ersten Argument angegebenen Prozess aus. Manchmal benötigen Sie möglicherweise einen fernberechneten Wert. Dies geschieht normalerweise, wenn Sie von einem Remote-Objekt lesen, um die für den nächsten lokalen Vorgang erforderlichen Daten abzurufen. remotecall_fetch gibt es eine remotecall_fetch Funktion. Dies entspricht dem fetch (remotecall (...)) , ist jedoch effizienter.
Denken Sie daran, dass getindex(r, 1,1) gleich r[1,1] , sodass dieser Aufruf das erste Element des zukünftigen r abruft.
Die remotecall Remote- remotecall nicht besonders praktisch. Das @spawn Makro erleichtert die @spawn . Es arbeitet mit einem Ausdruck, nicht mit einer Funktion, und wählt aus, wo die Operation für Sie ausgeführt werden soll:
julia> r = @spawn rand(2,2) Future(2, 1, 4, nothing) julia> s = @spawn 1 .+ fetch(r) Future(3, 1, 5, nothing) julia> fetch(s) 2×2 Array{Float64,2}: 1.38854 1.9098 1.20939 1.57158
Beachten Sie, dass wir 1 .+ Fetch(r) anstelle von 1 .+ r Dies liegt daran, dass wir nicht wissen, wo der Code ausgeführt wird. Im allgemeinen Fall kann es daher erforderlich sein, r abzurufen, um r in den Additionsprozess zu verschieben. In diesem Fall ist @spawn intelligent genug, um Berechnungen für den Prozess durchzuführen, dem r , sodass der Abruf nicht betriebsbereit ist (es wird keine Arbeit geleistet). (Es ist erwähnenswert, dass Spawn nicht eingebaut ist, sondern in Julia als Makro definiert ist. Sie können Ihre eigenen solchen Konstrukte definieren.)
Es ist wichtig zu beachten, dass Future nach dem Extrahieren seinen Wert lokal zwischenspeichert. Weitere Aufrufe zum Abrufen bedeuten keinen Netzwerksprung. Nachdem alle verweisenden Futures ausgewählt wurden, wird der gelöschte gespeicherte Wert gelöscht.
@async ähnelt @spawn , führt jedoch Aufgaben nur im lokalen Prozess aus. Wir verwenden es, um für jeden Prozess eine „Feed“ -Aufgabe zu erstellen. Jede Aufgabe wählt den nächsten Index aus, der berechnet werden muss, wartet dann auf den Abschluss des Prozesses und wiederholt sich, bis uns die Indizes ausgehen.
Bitte beachten Sie, dass die Feeder-Tasks erst ausgeführt werden, wenn die Haupt-Task das Ende des @ sync- Blocks erreicht hat. Danach übergibt sie die Kontrolle und wartet auf den Abschluss aller lokalen Tasks, bevor sie von der Funktion zurückkehrt.
Ab Version 0.7 können Feeder-Tasks den Status über nextidx gemeinsam nutzen, da alle im selben Prozess ausgeführt werden. Selbst wenn Aufgaben gemeinsam geplant werden, kann in einigen Kontexten eine Blockierung erforderlich sein, z. B. bei asynchronen E / A. Dies bedeutet, dass die remotecall_fetch nur an genau definierten Punkten erfolgt: in diesem Fall, wenn remotecall_fetch . Dies ist der aktuelle Implementierungsstatus und kann sich in zukünftigen Versionen von Julia ändern, da es so konzipiert ist, dass bis zu N Aufgaben in M Prozessen oder M: N Threading ausgeführt werden können . Dann benötigen wir ein Modell, um Sperren für nextidx zu erhalten / freizugeben, da es nicht sicher ist, mehrere Prozesse gleichzeitig Ressourcen lesen und schreiben zu lassen.
Ihr Code muss für jeden Prozess verfügbar sein, der ihn ausführt. Geben Sie beispielsweise an der Julia-Eingabeaufforderung Folgendes ein:
julia> function rand2(dims...) return 2*rand(dims...) end julia> rand2(2,2) 2×2 Array{Float64,2}: 0.153756 0.368514 1.15119 0.918912 julia> fetch(@spawn rand2(2,2)) ERROR: RemoteException(2, CapturedException(UndefVarError(Symbol("#rand2")) Stacktrace: [...]
Prozess 1 kannte die Funktion rand2, Prozess 2 jedoch nicht. In den meisten Fällen laden Sie Code aus Dateien oder Paketen herunter und können flexibel steuern, welche Prozesse den Code laden. Betrachten Sie die Datei DummyModule.jl , die den folgenden Code enthält:
module DummyModule export MyType, f mutable struct MyType a::Int end f(x) = x^2+1 println("loaded") end
Um in allen Prozessen auf DummyModule.jl zu DummyModule.jl muss DummyModule.jl in jedem Prozess geladen werden. Ein Aufruf zum include ('DummyModule.jl') lädt es nur für einen Prozess. Verwenden Sie zum @everywhere in jeden Prozess das Makro @everywhere (führen Sie Julia mit julia -p 2 aus):
julia> @everywhere include("DummyModule.jl") loaded From worker 3: loaded From worker 2: loaded
Wie üblich macht dies DummyModule nicht für Prozesse zugänglich, die verwendet oder importiert werden müssen. Wenn ein DummyModule in den Umfang eines Prozesses einbezogen wird, ist es in keinem anderen enthalten:
julia> using .DummyModule julia> MyType(7) MyType(7) julia> fetch(@spawnat 2 MyType(7)) ERROR: On worker 2: UndefVarError: MyType not defined ⋮ julia> fetch(@spawnat 2 DummyModule.MyType(7)) MyType(7)
Es ist jedoch weiterhin möglich, MyType an den Prozess zu senden, der das DummyModule geladen hat, auch wenn es nicht im Gültigkeitsbereich liegt:
julia> put!(RemoteChannel(2), MyType(7)) RemoteChannel{Channel{Any}}(2, 1, 13)
Die Datei kann beim Start mit dem Flag -L auch in mehrere Prozesse vorgeladen werden, und das Treiberskript kann zur Steuerung von Berechnungen verwendet werden:
julia -p <n> -L file1.jl -L file2.jl driver.jl
Der Julia-Prozess, der das Treiberskript im obigen Beispiel ausführt, hat die Kennung 1, genau wie der Prozess, der die interaktive Eingabeaufforderung bereitstellt. Wenn DummyModule.jl keine separate Datei, sondern ein Paket ist, lädt die Verwendung von DummyModule DummyModule.jl in allen Prozessen, überträgt es jedoch nur in den Bereich des Prozesses, für den die Verwendung aufgerufen wurde.
Starten und Verwalten von Workflows
Die grundlegende Julia-Installation unterstützt zwei Arten von Clustern:
- Der mit der Option -p angegebene lokale Cluster, wie oben gezeigt.
- Cluster-Computer mit der Option --machine-file. Dies verwendet die SSH-Anmeldung ohne Kennwort, um Julia-Workflows (auf demselben Pfad wie der aktuelle Host) auf den angegebenen Computern zu starten.

Die Funktionen addprocs , rmprocs , worker und andere stehen als Softwaretool zum Hinzufügen, Entfernen und Abfragen von Prozessen in einem Cluster zur Verfügung.
julia> using Distributed julia> addprocs(2) 2-element Array{Int64,1}: 2 3
Das Distributed Modul muss explizit in den Hauptprozess geladen werden, bevor addprocs . Es wird automatisch für Workflows verfügbar. Beachten Sie, dass Worker weder das ~/.julia/config/startup.jl noch ihren globalen Status (z. B. globale Variablen, Definitionen neuer Methoden und geladene Module) mit einem der anderen ausgeführten Prozesse synchronisieren. Andere Arten von Clustern können unterstützt werden, indem Sie Ihren eigenen ClusterManager schreiben, wie unten im Abschnitt ClusterManager beschrieben .
Datenaktionen
Das Senden von Nachrichten und das Verschieben von Daten machen den größten Teil des Overheads in einem verteilten Programm aus. Die Reduzierung der Anzahl der Nachrichten und der gesendeten Datenmenge ist entscheidend für die Erzielung von Leistung und Skalierbarkeit. Dazu ist es wichtig, die Datenbewegung zu verstehen, die von Julias verschiedenen verteilten Programmierkonstrukten ausgeführt wird.
fetch kann als explizite Datenverschiebungsoperation betrachtet werden, da es die Bewegung eines Objekts direkt zum lokalen Computer anfordert. @spawn (und mehrere verwandte Konstrukte) verschieben ebenfalls Daten, dies ist jedoch nicht so offensichtlich, sodass es als implizite Datenverschiebungsoperation bezeichnet werden kann. Betrachten Sie diese beiden Ansätze zum Erstellen und Quadrieren einer Zufallsmatrix:
Wegzeiten:
julia> A = rand(1000,1000); julia> Bref = @spawn A^2; [...] julia> fetch(Bref);
Methode zwei:
julia> Bref = @spawn rand(1000,1000)^2; [...] julia> fetch(Bref);
Der Unterschied scheint trivial zu sein, ist aber aufgrund des Verhaltens von @spawn tatsächlich ziemlich bedeutend. Bei der ersten Methode wird eine Zufallsmatrix lokal erstellt und dann an einen anderen Prozess gesendet, wo sie quadriert wird. Bei der zweiten Methode wird eine Zufallsmatrix für einen anderen Prozess erstellt und quadriert. Daher sendet die zweite Methode viel weniger Daten als die erste. In diesem Spielzeugbeispiel sind die beiden Methoden leicht zu unterscheiden und auszuwählen. In einem realen Programm kann das Entwerfen von Datenbewegungen jedoch sehr teuer und wahrscheinlich eine Messung sein.
Wenn der erste Prozess beispielsweise die Matrix A benötigt, ist die erste Methode möglicherweise besser. Wenn die Berechnung von A teuer ist und nur den aktuellen Prozess verwendet, kann es unvermeidlich sein, ihn auf einen anderen Prozess zu verschieben. Wenn der aktuelle Prozess zwischen spawn und fetch(Bref) nur sehr wenig gemeinsam hat, ist es möglicherweise besser, die Parallelität vollständig zu beseitigen. Oder stellen Sie sich vor, dass rand(1000, 1000) durch eine teurere Operation ersetzt wurde. Dann könnte es sinnvoll sein, nur für diesen Schritt eine weitere spawn Anweisung hinzuzufügen.
Globale Variablen
Ausdrücke, die remote über Spawn ausgeführt werden, oder Schließungen, die für die Remote-Ausführung mit remotecall , können sich auf globale Variablen beziehen. Globale Bindungen im Hauptmodul werden etwas anders behandelt als globale Bindungen in anderen Modulen. Betrachten Sie das folgende Codefragment:
A = rand(10,10) remotecall_fetch(()->sum(A), 2)
In diesem Fall MUSS die sum im Remote-Prozess definiert werden. Beachten Sie, dass A eine globale Variable ist, die im lokalen Arbeitsbereich definiert ist. Worker 2 hat im Hauptabschnitt keine Variable mit dem Namen A Durch das Senden der Schließfunktion () -> sum(A) für Worker 2 wird Main.A 2 definiert. Main.A bleibt auf Worker 2 auch nach Rückgabe des Aufrufs remotecall_fetch .

Remote-Aufrufe mit eingebetteten globalen Referenzen (nur im Hauptmodul) verwalten globale Variablen wie folgt:
- Neue globale Bindungen werden an Zielarbeitsstationen erstellt, wenn sie als Teil eines Remote-Aufrufs referenziert werden.
- Globale Konstanten werden auch auf Remote-Knoten als Konstanten deklariert.
- Globals werden nur im Rahmen eines Fernanrufs und nur dann an den Zielmitarbeiter erneut gesendet, wenn sich ihr Wert geändert hat. Darüber hinaus synchronisiert der Cluster keine globalen Bindungen zwischen Knoten. Zum Beispiel:
A = rand(10,10) remotecall_fetch(()->sum(A), 2)
Die Ausführung des obigen Fragments führt dazu, dass Main.A auf Mitarbeiter 2 einen anderen Wert als Main.A auf Mitarbeiter 3 hat, während der Wert von Main.A auf Knoten 1 Null ist.
Wie Sie wahrscheinlich verstanden haben, können solche Aktionen für Worker nicht ausgeführt werden, obwohl der mit globalen Variablen verknüpfte Speicher erfasst werden kann, wenn sie dem Master-Gerät neu zugewiesen werden, da die Bindungen weiterhin funktionieren. klar! kann verwendet werden, um bestimmte globale Variablen manuell nothing zuzuweisen, wenn sie nicht mehr benötigt werden. Dadurch wird der ihnen im Rahmen des normalen Speicherbereinigungszyklus zugeordnete Speicher freigegeben. Daher sollten Programme beim Zugriff auf globale Variablen in Remote-Aufrufen vorsichtig sein. In der Tat ist es, wann immer möglich, besser, sie überhaupt zu vermeiden. Wenn Sie auf globale Variablen verweisen müssen, sollten Sie let Blöcke verwenden, um globale Variablen zu lokalisieren. Zum Beispiel:
julia> A = rand(10,10); julia> remotecall_fetch(()->A, 2); julia> B = rand(10,10); julia> let B = B remotecall_fetch(()->B, 2) end; julia> @fetchfrom 2 InteractiveUtils.varinfo() name size summary ––––––––– ––––––––– –––––––––––––––––––––– A 800 bytes 10×10 Array{Float64,2} Base Module Core Module Main Module
Es ist leicht zu erkennen, dass die globale Variable A für Worker 2 definiert ist, B als lokale Variable geschrieben ist und daher die Bindung für B für Worker 2 nicht vorhanden ist.
Parallele Schleifen

Glücklicherweise erfordern viele nützliche Parallelitätsberechnungen keine Datenverschiebung. Ein typisches Beispiel ist eine Monte-Carlo-Simulation, bei der mehrere Prozesse gleichzeitig unabhängige Simulationstests verarbeiten können. Wir können @spawn , um Münzen in zwei Prozesse zu @spawn . Schreiben Sie zuerst die folgende Funktion in count_heads.jl :
function count_heads(n) c::Int = 0 for i = 1:n c += rand(Bool) end c end
Die Funktion count_heads addiert einfach n zufällige Bits. So können wir einige Tests auf zwei Maschinen durchführen und die Ergebnisse addieren:
julia> @everywhere include_string(Main, $(read("count_heads.jl", String)), "count_heads.jl") julia> a = @spawn count_heads(100000000) Future(2, 1, 6, nothing) julia> b = @spawn count_heads(100000000) Future(3, 1, 7, nothing) julia> fetch(a)+fetch(b) 100001564
Dieses Beispiel zeigt ein leistungsstarkes und häufig verwendetes paralleles Programmiermuster. Viele Iterationen werden unabhängig voneinander in mehreren Prozessen ausgeführt, und dann werden ihre Ergebnisse unter Verwendung einer Funktion kombiniert. Der Vereinigungsprozess wird als Reduktion bezeichnet, da er normalerweise den Tensorrang reduziert: Der Vektor von Zahlen wird auf eine Zahl reduziert, oder die Matrix wird auf eine Zeile oder Spalte usw. reduziert. Im Code sieht dies normalerweise so aus: Muster x = f(x, v [i]) , wobei x die Batterie ist, f die Reduktionsfunktion ist und v[i] die zu reduzierenden Elemente sind.
Es ist wünschenswert, dass f assoziativ ist, damit es keine Rolle spielt, in welcher Reihenfolge die Operationen ausgeführt werden. Bitte beachten Sie, dass unsere Verwendung dieser Vorlage mit count_heads verallgemeinert sein kann. Wir haben zwei explizite spawn Anweisungen verwendet, die die Parallelität auf zwei Prozesse beschränken. Um eine beliebige Anzahl von Prozessen auszuführen, können wir eine parallele for Schleife verwenden, die im verteilten Speicher arbeitet und mit verteiltem Speicher in Julia geschrieben werden kann , zum Beispiel:
nheads = @distributed (+) for i = 1:200000000 Int(rand(Bool)) end
( (+) ). . .
, for , . , , , . , , . , :
a = zeros(100000) @distributed for i = 1:100000 a[i] = i end
, . , . , Shared Arrays , , :
using SharedArrays a = SharedArray{Float64}(10) @distributed for i = 1:10 a[i] = i end
«» , :
a = randn(1000) @distributed (+) for i = 1:100000 f(a[rand(1:end)]) end
f , . , , . , Future , . Future , fetch , , @sync , @sync distributed for .
, (, , ). , , Julia pmap . , :
julia> M = Matrix{Float64}[rand(1000,1000) for i = 1:10]; julia> pmap(svdvals, M);
pmap , . , distributed for , , , . pmap , distributed . distributed for .
(Shared Arrays)

Shared Arrays . DArray , SharedArray . DArray , ; , SharedArray .
SharedArray — , , . Shared Array SharedArrays , . SharedArray ( ) , , . SharedArray , . , Array , SharedArray , sdata . AbstractArray sdata , sdata Array . :
SharedArray{T,N}(dims::NTuple; init=false, pids=Int[])
N - T dims , pids . , , pids ( , ).
init initfn(S :: SharedArray) , . , init , .
:
julia> using Distributed julia> addprocs(3) 3-element Array{Int64,1}: 2 3 4 julia> @everywhere using SharedArrays julia> S = SharedArray{Int,2}((3,4), init = S -> S[localindices(S)] = myid()) 3×4 SharedArray{Int64,2}: 2 2 3 4 2 3 3 4 2 3 4 4 julia> S[3,2] = 7 7 julia> S 3×4 SharedArray{Int64,2}: 2 2 3 4 2 3 3 4 2 7 4 4
SharedArrays.localindices . , , :
julia> S = SharedArray{Int,2}((3,4), init = S -> S[indexpids(S):length(procs(S)):length(S)] = myid()) 3×4 SharedArray{Int64,2}: 2 2 2 2 3 3 3 3 4 4 4 4
, , . Zum Beispiel:
@sync begin for p in procs(S) @async begin remotecall_wait(fill!, p, S, p) end end end
. pid , , ( S ), pid .
«»:
q[i,j,t+1] = q[i,j,t] + u[i,j,t]
, , , , , : q [i,j,t] , q[i,j,t+1] , , , q[i,j,t] , q[i,j,t+1] . . . , (irange, jrange) , :
julia> @everywhere function myrange(q::SharedArray) idx = indexpids(q) if idx == 0
:
julia> @everywhere function advection_chunk!(q, u, irange, jrange, trange) @show (irange, jrange, trange)
SharedArray
julia> @everywhere advection_shared_chunk!(q, u) = advection_chunk!(q, u, myrange(q)..., 1:size(q,3)-1)
, :
julia> advection_serial!(q, u) = advection_chunk!(q, u, 1:size(q,1), 1:size(q,2), 1:size(q,3)-1);
@distributed :
julia> function advection_parallel!(q, u) for t = 1:size(q,3)-1 @sync @distributed for j = 1:size(q,2) for i = 1:size(q,1) q[i,j,t+1]= q[i,j,t] + u[i,j,t] end end end q end;
, :
julia> function advection_shared!(q, u) @sync begin for p in procs(q) @async remotecall_wait(advection_shared_chunk!, p, q, u) end end q end;
SharedArray , ( julia -p 4 ):
julia> q = SharedArray{Float64,3}((500,500,500)); julia> u = SharedArray{Float64,3}((500,500,500));
JIT- @time :
julia> @time advection_serial!(q, u); (irange,jrange,trange) = (1:500,1:500,1:499) 830.220 milliseconds (216 allocations: 13820 bytes) julia> @time advection_parallel!(q, u); 2.495 seconds (3999 k allocations: 289 MB, 2.09% gc time) julia> @time advection_shared!(q,u); From worker 2: (irange,jrange,trange) = (1:500,1:125,1:499) From worker 4: (irange,jrange,trange) = (1:500,251:375,1:499) From worker 3: (irange,jrange,trange) = (1:500,126:250,1:499) From worker 5: (irange,jrange,trange) = (1:500,376:500,1:499) 238.119 milliseconds (2264 allocations: 169 KB)
advection_shared! , , .
, . , , .
, , , .
- Julia
, , , .
, , -. , wo — . - , .. , .
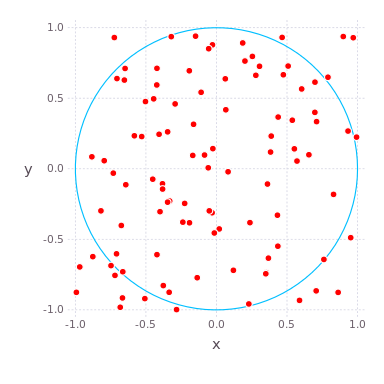
( , ) ( ) , , , . , , . compute_pi (N) , , .
function compute_pi(N::Int)
, , . : , , 25 .
Julia Pi.jl ( Sublime Text , ):
C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4 julia> include("C:/Users/User/Desktop/Pi.jl")
using Distributed addprocs(4)
Jupyter
Pi.jl @everywhere function compute_pi(N::Int) n_landed_in_circle = 0
, :
julia> @time parallel_pi_computation(1000000000, ncores = 1) 6.818123 seconds (1.96 M allocations: 99.838 MiB, 0.42% gc time) 3.141562892 julia> @time parallel_pi_computation(1000000000, ncores = 1) 5.081638 seconds (1.12 k allocations: 62.953 KiB) 3.141657252 julia> @time parallel_pi_computation(1000000000, ncores = 2) 3.504871 seconds (1.84 k allocations: 109.382 KiB) 3.1415942599999997 julia> @time parallel_pi_computation(1000000000, ncores = 4) 3.093918 seconds (1.12 k allocations: 71.938 KiB) 3.1416889400000003 julia> pi ? = 3.1415926535897...
JIT - — . , Julia . , ( Multi-Threading, Atomic Operations, Channels Coroutines).
Nützliche Links
, , . MPI.jl MPI ,
DistributedArrays.jl .
GPU, :
- ( C) OpenCL.jl CUDAdrv.jl OpenCL CUDA.
- ( Julia) CUDAnative.jl CUDA .
- , , CuArrays.jl CLArrays.jl
- , ArrayFire.jl GPUArrays.jl
- -
- Kynseed
, , . !