Sich entwickelnde zelluläre Automaten

Verbinden Sie die zellulären Automaten mit dem genetischen Algorithmus und sehen Sie, was passiert.

Der Artikel enthält Gif (Verkehr!) Und kontrastierende Bilder. Epileptiker können einen epileptischen Anfall haben.

Regeln für zellulare Automaten

Der einfachste zellulare Automat ist ein eindimensionaler zellularer Automat (es gibt auch nulldimensionale Automaten - wir werden weiter unten darauf eingehen). In einem eindimensionalen zellularen Automaten haben wir ein eindimensionales Array, dessen Zellen (Zellen) einen von zwei Zuständen annehmen können (1/0, wahr / falsch, weiß / schwarz, lebend / tot). Der nächste Zustand der Zelle in dem Array wird gemäß einer Regel durch den aktuellen Zustand der Zelle und den Zustand zweier benachbarter Zellen bestimmt.

Insgesamt existiert $$$2 ^ 3 = 8$Kombinationen von Zellzuständen und zwei benachbarten Zellen:



Als nächstes schreiben wir für jede der Kombinationen den Zustand der Zelle für die nächste Iteration (für den nächsten Zustand des Automaten) auf:



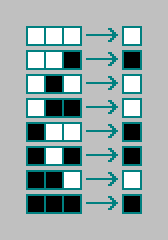
Ich habe eine Regel für einen Mobilfunkautomaten. Die Regeln für eindimensionale zellulare Automaten sind mit 8 Bit („Wolframcode“) codiert. Insgesamt existiert $$$2 ^ 8 = 256$elementare zelluläre Automaten:



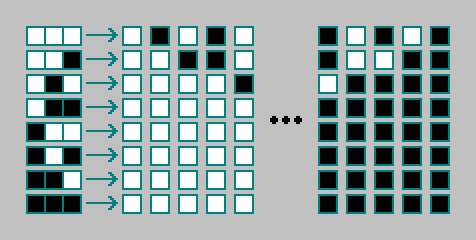
256 Maschinen können manuell aussortiert werden. Wir werden nicht auf sie eingehen. Wir berechnen die Anzahl der vorhandenen Regeln für zweidimensionale zellulare Automaten.

Ein zweidimensionaler zellularer Automat verwendet ein zweidimensionales Array. Jede Zelle hat 8 Nachbarn in der Nähe von Moore (es gibt auch ein von Neumann-Viertel, in dem diagonale Zellen nicht berücksichtigt werden. Wir werden dies im Artikel nicht berücksichtigen):



Der Einfachheit halber schreiben wir die Zellen in eine Zeile (wir werden die ausgewählte Reihenfolge später im Artikel verwenden):



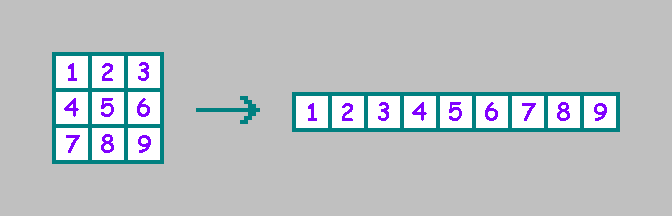
Für einen zweidimensionalen zellularen Automaten existiert $$$2 ^ 9 = 512$Kombinationen von Zellzuständen und 8 benachbarten Zellen:



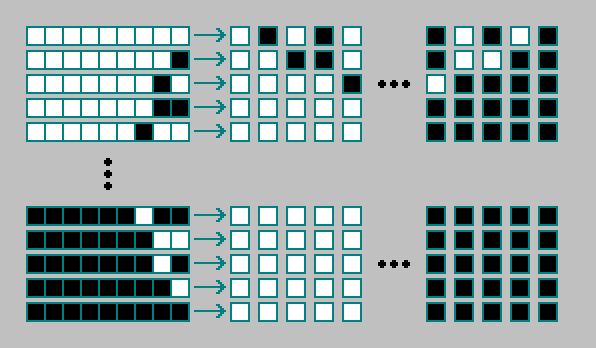
Die Regel für einen zweidimensionalen zellularen Automaten ist mit 512 Bit codiert. Insgesamt existiert $$$2 ^ {512}$zweidimensionale zelluläre Automaten:



Nummer:

$$

$$2 ^ {512} \ ca. 1.340781 \ times10 ^ {154}$$

mehr Atome im beobachtbaren Universum ( $$$10 ^ {80}$)
Manuell kann diese Anzahl von Maschinen nicht aussortiert werden. Wenn wir jede Sekunde einen Automaten betrachten würden - während der Existenz des Universums hätten wir es geschafft, alles zu betrachten $$$\ ca. 4.35 \ times10 ^ {17}$automatische Maschinen.

Einfache Aufzählung funktioniert nicht, aber mit Hilfe eines genetischen Algorithmus können wir Automaten finden, die bestimmten vordefinierten Kriterien am besten entsprechen.

Wir werden in JavaScript programmieren. Alle Codefragmente sind unter Spoilern versteckt, um Leser, die mit Programmiersprachen nicht vertraut sind, nicht zu verwirren.

Zweidimensionaler zellularer Automat

Wir schreiben einen zweidimensionalen zellularen Automaten mit einer Zufallsregel. Wir werden die Regel im Regelarray speichern, dessen Länge Regelgröße = 512 ist:


Als nächstes füllen Sie den Ausgangszustand der Maschine mit einem zufälligen Haus:


(hier und weiter im Artikel wird als Breite und Höhe der Maschine eine Zufallszahl genommen - nicht sehr groß und nicht sehr klein ungerade Zahl 89)

Die Funktion, die den folgenden Zustand des Automaten berechnet, sieht folgendermaßen aus (um ihn nicht zu verunreinigen, wurde die Initialisierung der Zeichenfläche entfernt):


Die Variablen xm und xp speichern die X-Koordinaten des Nachbarn links und des Nachbarn rechts (x minus und x plus). Die Variablen ym und yp speichern die entsprechenden Y-Koordinaten.

Hier:


Wir legen die periodischen Randbedingungen fest (das Feld des Automaten ist die Oberfläche des Torus).

Weiter:


Schreiben Sie in der obigen Reihenfolge den Inhalt der Zellen in eine Zeichenfolge. Wir übersetzen die Zeichenfolge in eine Dezimalzahl. Für diese Kombination finden wir im Regelarray den Zustand, den die Zelle mit den x- und y-Koordinaten annehmen soll.


Ersetzen Sie nach allen Iterationen den vorherigen Status des Automaten durch einen neuen:


Wir zeichnen einen Automaten mit der Funktion setInterval:


Im Browser ausführen

Ich empfehle, die Maschine 10 bis 20 Mal mit zufälligen Regeln zu starten, bevor Sie den Artikel weiterlesen.

Wir können die Maschine sehr lange mit verschiedenen Zufallsregeln betreiben. Das Bild, das wir erhalten, unterscheidet sich nicht vom Bild auf dem Fernsehbildschirm, wenn kein Signal vorliegt:



Als nächstes wollen wir unseren „Fernseher“ mithilfe des genetischen Algorithmus einrichten.

Genetischer Algorithmus

Die Größe der ursprünglichen Population beträgt 200 Maschinen (Einzelpersonen). Für Regeln verwenden wir anstelle eines eindimensionalen Regelarrays ein zweidimensionales Populationsarray. Der erste Index (n) ist die Nummer des Individuums in der Bevölkerung.


Das Fitness-Array enthält die Fitness-Koeffizienten jedes Einzelnen. Dieses Array wird im Auswahlprozess ausgefüllt. Nach der Auswahl beginnen wir den Evolutionsprozess.

Evolutionsprozess

Aus unserer Bevölkerung nehmen wir die Hälfte der am besten angepassten Personen (entsprechend dem Fitnesskoeffizienten). Die verbleibende Hälfte wird zerstört. Als nächstes nehmen wir zwei überlebende Individuen und kreuzen sie.



Wählen Sie zum Überqueren eine zufällige Position in den Genotypen zweier Vorfahren aus. Vor dieser Position nehmen wir Gene von einem Vorfahren, nach dieser Position - von einem anderen. Wir setzen die ausgewählten Gene im Genotyp einem Nachkommen zu. Die restlichen Gene sind für einen anderen. Wir platzieren zwei Vorfahren und zwei Nachkommen in einer neuen Population. Gleichzeitig nimmt jeder Einzelne einmal an der Überfahrt teil.

Mutationen. Mit einer Wahrscheinlichkeit von 5% mutiert (zufällig invertiert) ein zufällig ausgewähltes Gen in jedem Individuum. Wenn Sie die Wahrscheinlichkeit von Mutationen erhöhen, gibt es erfolgreichere Mutanten. Gleichzeitig hat eine erfolgreiche Mutante möglicherweise keine Zeit, erfolgreiche Nachkommen zu hinterlassen, bevor sie erneut erfolglos mutiert. Wir werden später auf dieses Problem zurückkommen.

Natürliche Auslese

Vor Beginn des Evolutionsprozesses muss eine Auswahl getroffen werden. Die Auswahl kann sowohl natürlich als auch künstlich sein. Die künstliche Auswahl erfolgt manuell - etwas später. Für die natürliche Selektion legen wir einige Kriterien fest und wählen die Maschinen aus, die den angegebenen Kriterien am besten entsprechen.

Welche Kriterien können im Voraus festgelegt werden? Nimm den einfachsten. Unser „Fernseher“ blinkt zu stark. Wir speichern zwei Zustände des zellularen Automaten - bei 99 und bei 100 Iterationen. Zählen Sie die Anzahl der Zellen, die sich nicht geändert haben. Die resultierende Zahl wird als Fitnesskoeffizient verwendet. Ein Kriterium reicht uns natürlich nicht aus. Es ist einfach, manuell den Automaten auszuwählen, der das gegebene Kriterium am besten erfüllt: den Automaten [0,0,0, ..., 0] und den Automaten [1,1,1, ..., 1]. Bei der ersten Iteration werden diese beiden Automaten mit Nullen oder Einsen gefüllt und ändern ihren Status nicht mehr. Wir definieren das zweite Kriterium: Die Differenz zwischen der Anzahl von 0 und 1 (Zellen) in der Maschine überschreitet 100 nicht (die Anzahl wird "vom Bulldozer" genommen).

array1 - Zustand des Automaten bei der 99. Iteration. array2 - bei der 100. Iteration:


Wir fangen an. Die optimale Lösung wurde im 421. Evolutionszyklus gefunden. In der Grafik sehen Sie den Fortschritt:



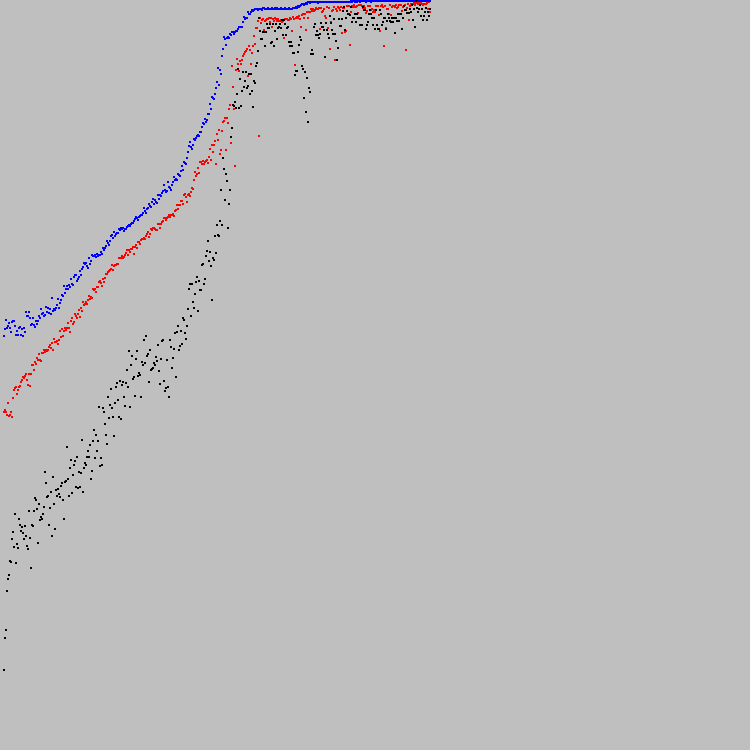
Der Graph ist entlang der Y-Achse skaliert. Der untere Punkt ist 0, der höchste Punkt ist 7921. Offensichtlich ist 7921 die optimale Lösung (alle Zellen in der 89x89-Maschine erfüllen das angegebene Kriterium). Nach 100 Iterationen ändert keine Zelle ihren Status.

Die blauen Punkte in der Grafik sind die besten Personen in der Bevölkerung. Rotweine sind die schlechtesten (nur Personen, die das zweite Kriterium erfüllen, werden berücksichtigt). Schwarze Punkte - der durchschnittliche Fitnesskoeffizient für die gesamte Bevölkerung (unter Berücksichtigung von Personen, die das zweite Kriterium nicht erfüllen). Das zweite Kriterium (das Gleichgewicht zwischen Weiß und Schwarz) ist sehr schwierig. Einige Automaten erfüllen das zweite Kriterium auch nach 421 Evolutionszyklen nicht. Daher liegen schwarze Punkte unter rot.

Der Genpool der Population (Individuen entlang der Y-Achse, Gene entlang der X-Achse):



Mal sehen, welchen Kanal unser "Fernseher" gefangen hat:



Die gefundene Lösung ist nicht die einzig optimale. Wenn wir die Evolution (mit zufälligen anfänglichen Genotypen) wiederholen, werden wir andere optimale Lösungen finden. Einer von ihnen:



Ändern Sie die Auswahlkriterien.

Wir werden die Anzahl der Zellen betrachten, für die ein Muster in der Nähe von Moore der Ordnung 2 erscheint. Nehmen wir das einfachste Muster:



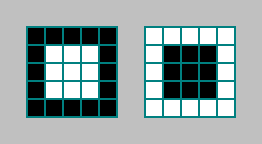
Dieses Kriterium ist insofern interessant, als wir 25 Zellen überprüfen, während der Automat den Zustand der Zelle basierend auf den Zuständen von 9 Zellen berechnet.

Das Kriterium ist sehr streng. Wenn wir einen zufälligen Automaten nehmen, sieht es nach 100 Iterationen folgendermaßen aus:



Keine einzige Zelle in einem solchen Automaten erfüllt das gegebene Kriterium. Deshalb mildern wir das Kriterium ein wenig:

1. Machen wir einen Fehler im Muster.
2. Wir werden nicht bei der letzten Iteration nach dem Muster suchen, sondern bei den letzten 50 Iterationen.

Das zweite Kriterium (das Gleichgewicht zwischen Weiß und Schwarz) wird entfernt.

Wir fangen an. Grafik:



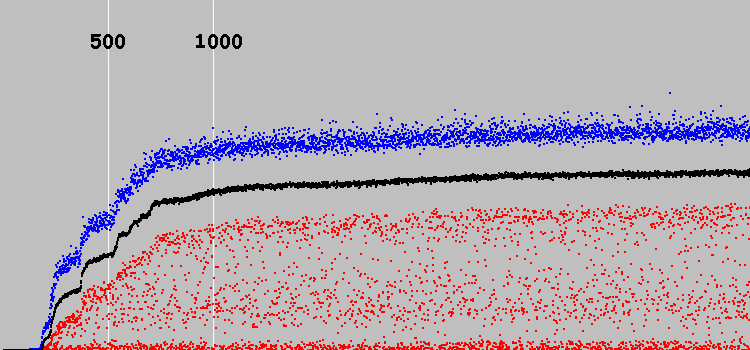
Die y-Achse ist beliebig. (In der vorherigen Maschine ist die optimale Lösung 7921. In dieser Maschine ungefähr 30.)
X-Achse - 3569 Evolutionszyklen. Zwei weiße vertikale Linien markieren 500 und 1000 Evolutionszyklen.
Blaue Punkte - das beste Individuum in der Bevölkerung, rot - das schlechteste, schwarz - das durchschnittliche Verhältnis für die gesamte Bevölkerung.

Die Lösung wurde in den ersten 500 Evolutionszyklen gefunden. In den nächsten 500 Zyklen verbessert sich die Lösung. Und dann entwickelt sich das System praktisch nicht mehr weiter.

In den drei folgenden Bildern: 500 Zyklen, 1000 Zyklen und 3569 Evolutionszyklen:



Genpool (3569):



In der Dynamik:



In der Abbildung unten sehen Sie, wie der Oszillator (Segelflugzeug) in dieser Maschine gebildet wird:



Wir können die Maschine mit dem Anfangszustand starten, in dem eine Zelle gefüllt ist. Korrigieren Sie als Nächstes alle Kombinationen von Zellen, die in den folgenden Iterationen des Automaten gefunden wurden. Ein Array von Genen (der Genotyp eines Automaten) ist ein Array aller möglichen Kombinationen. Nachdem wir nur die auftretenden Kombinationen isoliert haben, können wir leicht alle Gene feststellen, die an der Bildung des Oszillators beteiligt sind. Graue Balken sind Gene, die nicht an der Bildung des Oszillators beteiligt sind:



Mutationen in diesen Genen wurzeln nicht, weil sie die Musterbildung stören.

In unserer Maschine wird ein Muster (Quadrat) nur um eine schwarze Zelle gebildet. Versuchen wir, den Evolutionsprozess zusammen mit dem zweiten Kriterium zu starten: Der Unterschied zwischen der Anzahl der weißen und schwarzen Zellen überschreitet 400 nicht.

Wir beginnen 3569 Evolutionszyklen. Grafik:



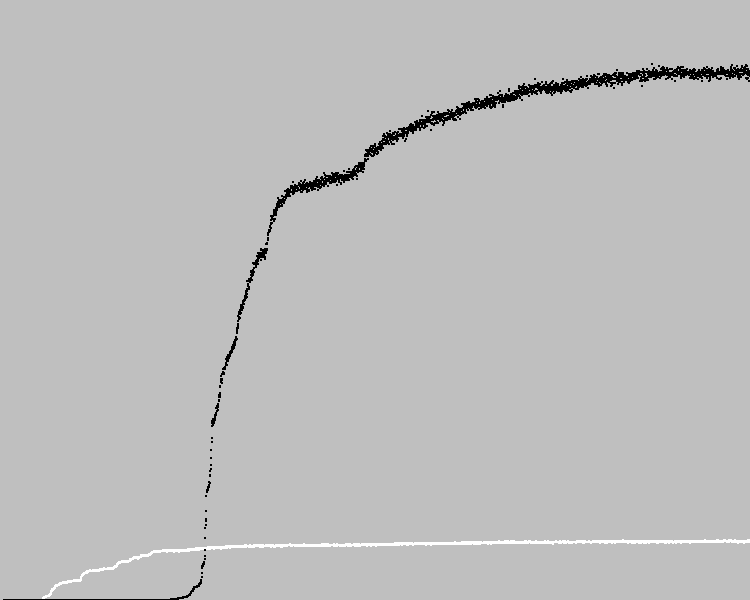
Schwarze Punkte in der Grafik sind der durchschnittliche Fitnesskoeffizient in einer Population. Weiße Punkte - der durchschnittliche Fitnesskoeffizient der vorherigen Maschine. Es wurde eine Lösung mit einem Fehler im Muster gefunden.

Genpool:



100 erste Iterationen:



Letzte (100) Iteration:



Ein bisschen nicht das Ergebnis, das wir erwartet hatten. Es gibt schwarze Quadrate, weiß - nein. Verschärfen Sie das zweite Kriterium: Die Differenz zwischen der Anzahl der weißen und schwarzen Zellen überschreitet 100 nicht.

Wir beginnen 14865 Evolutionszyklen.
Die Grafik vergleicht die durchschnittlichen Fitnesskoeffizienten der Populationen. Blaue Punkte sind unser Maschinengewehr. Weiß und Schwarz sind frühere Maschinen.



Ein Automat entwickelt sich so heftig, dass es den Anschein hat, als würde er sich überhaupt nicht entwickeln. Das zweite Diagramm ist entlang der Y-Achse skaliert. Zwei weiße Linien - 500 und 1000 Zyklen.



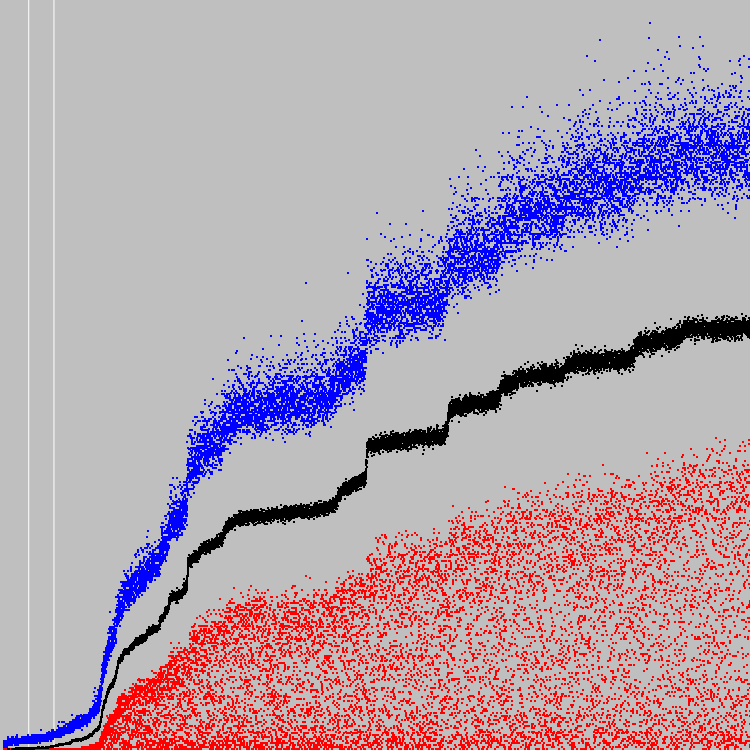
Bei der besten Person entsprechen durchschnittlich 6 Zellen einem bestimmten Kriterium.

Schauen wir uns eine zufällige Maschine aus einer Population an.
50 Iterationen:



Letzte (50) Iteration:



Kein akzeptables Ergebnis gefunden. Das zweite Kriterium erschwert die Suche, daher werden wir es ablehnen (wir werden es später in diesem Artikel nicht verwenden). Lassen wir dieses Muster und suchen nach ein paar anderen Mustern.

Muster:



Wir fangen an. 3000 Evolutionszyklen. Grafik:



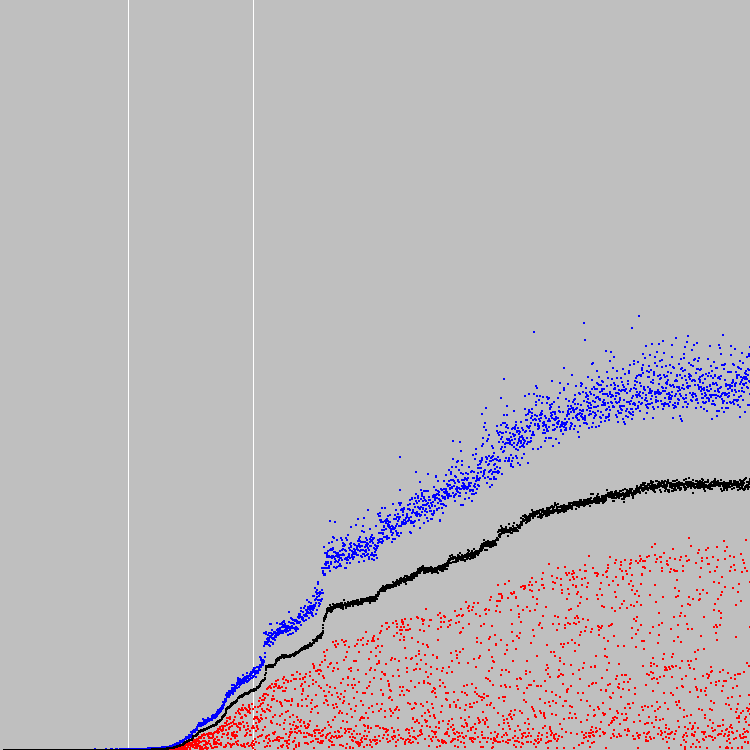
Genpool:



In der Dynamik (100 Iterationen):



Letzte (100) Iteration:



Muster:



In früheren Maschinen durften wir einen Fehler im Muster machen. Lassen Sie uns diesmal nach dem genauen Muster suchen.

Wir beginnen 4549 Evolutionszyklen. Grafik:



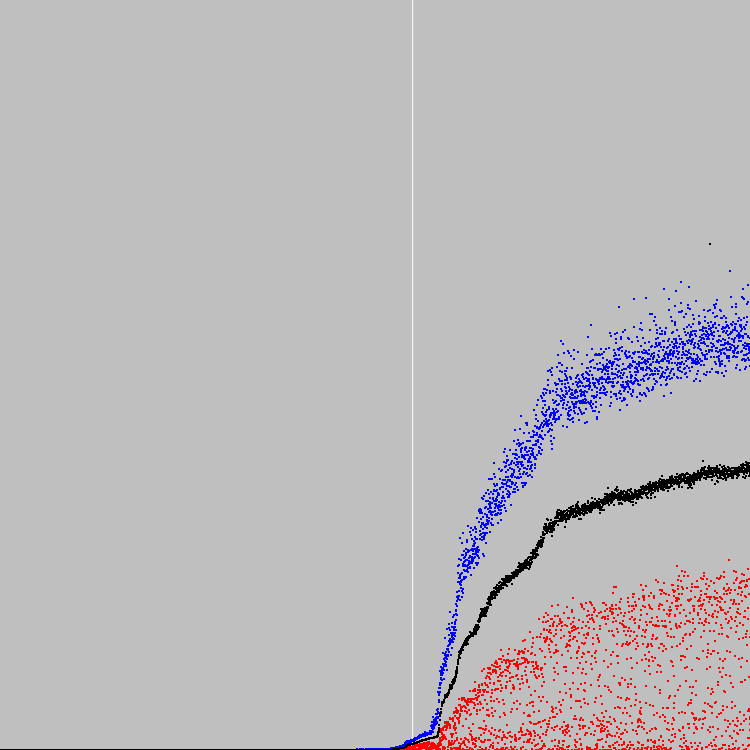
Weiße vertikale Linie - 2500 Evolutionszyklen. Zu diesem Zeitpunkt (etwas früher) begann die Fitness der Bevölkerung schnell zu wachsen. Die Bevölkerung wurde gerettet, um eine Zwischenlösung zu finden. Die Zwischenlösung erwies sich als viel interessanter als die Lösung im 4549. Evolutionszyklus.

Lösung im 4549. Evolutionszyklus gefunden:



Es gibt 100 Iterationen auf Gif. Nach einer bestimmten Anzahl von Iterationen (ca. 500-2000) ist der Zustand des Automaten fast vollständig geordnet (Höhe und Breite des Automaten werden speziell durch ungerade Zahlen ausgewählt, so dass der Automat nicht vollständig geordnet werden konnte):



Ein Automat mit geraden Seitengrößen nimmt nach einer bestimmten Anzahl von Iterationen einen vollständig geordneten Zustand an. Automatisch 90x90, ungefähr 1200 Iterationen:



Zwischenlösung (gefunden im 2500. Evolutionszyklus):



Dieser Automat weiß auch, wie man einen bestimmten chaotischen Anfangszustand in einen bestimmten Zustand endlicher Ordnung verarbeitet (der endgültige geordnete Zustand ist eine Verschiebung des Musters entlang der X-Achse nach links + mehrere Oszillatorzellen).

Die 16x16-Maschine hat in ungefähr 100 Iterationen aussortiert:



32x32 - ungefähr 1000 Iterationen:



64x64 - ungefähr 6000 Iterationen:



90x90 - ungefähr 370000 Iterationen:



11x11 (ungerade Abmessungen des Automatenfeldes) - ungefähr 178700 Iterationen:



Das 13x13-Sturmgewehr wurde nicht in akzeptabler Zeit optimiert.

In der Abbildung unten zeigt die Maschine im Feld 256x256 bei der 100.000sten Iteration:



Ich empfehle, diesen Automaten in Dynamik über ein großes Feld zu betrachten - es ist sehr interessant, den Prozess der Chaos-Selbstorganisation in diesem Automaten zu beobachten: in einem Browser ausführen

Genpool der Zwischenpopulation:



Durch einen Neustart des Evolutionsprozesses können Sie andere Lösungen finden. Einer von ihnen:





Ein anderes Muster:



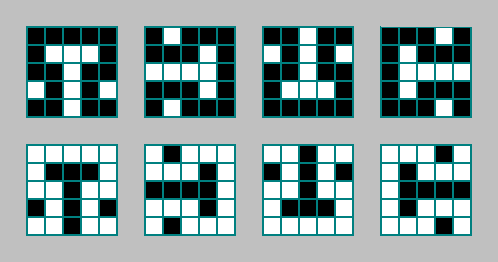
Lassen Sie uns bei der Suche nach einem Muster erneut einen Fehler machen (ohne Fehler entwickelt sich das System mit dem ausgewählten Muster nicht weiter).

Wir fangen an. 5788 Evolutionszyklen. Grafik:



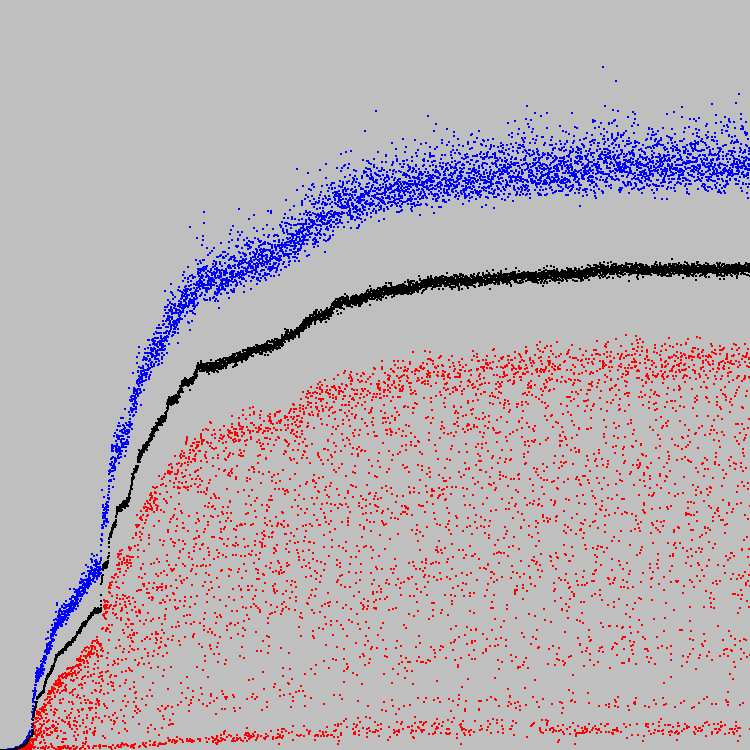
Die Skala ist beliebig.

Genpool:



In der Dynamik:



Der geordnete Zustand des Automaten (Musterverschiebung entlang der Y-Achse + mehrere Oszillatorzellen nach oben):



Es ist viel interessanter, nicht die Maschine selbst zu beobachten, sondern die Mutanten, die in dieser Population vorkommen:



Auf Gif ist die Maschine 256x256. 200 Iterationen. Die verbleibenden Iterationen können im Browser angezeigt werden .

Man könnte mit natürlicher Auslese enden und zu künstlich übergehen, aber ich möchte zeigen, wie viel $$$2 ^ {512}$eine riesige Anzahl. Unter dieser Anzahl von Automaten finden wir einen Automaten, der ein bestimmtes Muster zeichnet (mit einer gewissen Genauigkeit für komplexere Muster).

Das folgende Muster:



In früheren Experimenten haben wir die Summe der Zellen gezählt, um die ein Muster gebildet wird (wenn mit einem Fehler, addieren Sie 1 zur Summe, wenn ohne Fehler, addieren Sie 2). Die resultierende Menge wurde als Fitnessfaktor für den genetischen Algorithmus verwendet.

Bei einem komplexeren Muster funktioniert diese Methode nicht. Ein Automat, bei dem eine kleinere Anzahl von Zellen einem bestimmten Kriterium besser entspricht (die Anzahl von Zellen, die dem Muster in der Nähe der Zelle entsprechen), verliert jedes Mal gegen einen Automaten, bei dem eine größere Anzahl von Zellen einem bestimmten Kriterium weniger genau entspricht. Wie im Beispiel mit den obigen Quadraten:



Für das gewünschte Muster betrachten wir bei der 100. Iteration jedes Automaten in der Population, der von jeder Zelle umgeben ist, die Anzahl der Zellen, die mit dem Muster übereinstimmen. Wir werden nur das beste Ergebnis für jede Maschine erzielen. Die Anzahl der Zellen, die dem Muster entsprechen, wird als Fitnessfaktor verwendet. Das Muster besteht aus 7x17 = 119 Zellen. Diese Zahl wird als optimale Lösung angesehen. 6000 Evolutionszyklen ermöglichten es uns, einen Automaten zu finden, der ein Muster mit 5 Fehlern zeichnet (114 Zellen stimmen mit dem Muster überein).

Grafik in beliebigem Maßstab:



Ein Anstieg des Prozentsatzes der Mutationen beeinträchtigte die Fitness der Bevölkerung nicht.

Es gibt viele Mutanten im Genpool der Bevölkerung:



Ein zufälliger Automat aus einer Population in der Dynamik:



Die beste Maschine bei der 100. Iteration:



Gesuchte und gefundene Muster:



Nachdem man mit den Auswahlkriterien, der Größe des Automatenfeldes und dem Prozentsatz der Mutationen gespielt hatte, stellte sich heraus, dass sich die Population verbesserte und ein Automat gefunden wurde, der nur 3 Fehler im Muster macht.

Genpool:



Maschine bei der 100. Iteration:



Gesuchte und gefundene Muster:





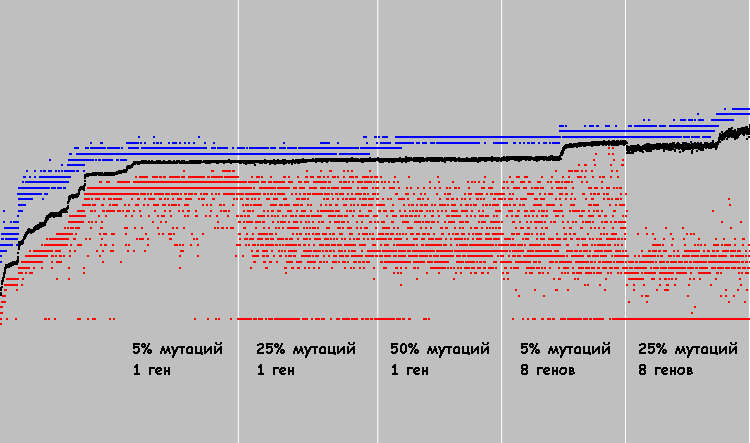
In vier Diagrammen können Sie sehen, wie sich das System mit unterschiedlichen Mutationswahrscheinlichkeiten entwickelt (1 Gen mutiert):



Rote Punkte sind der durchschnittliche Fitnesskoeffizient in einer Population. Schwarze Punkte sind der Fitnesskoeffizient jedes Einzelnen. 3000 Evolutionszyklen für jedes System.

Genpools von Populationen (in derselben Reihenfolge):









Automaten bei der 100. Iteration:









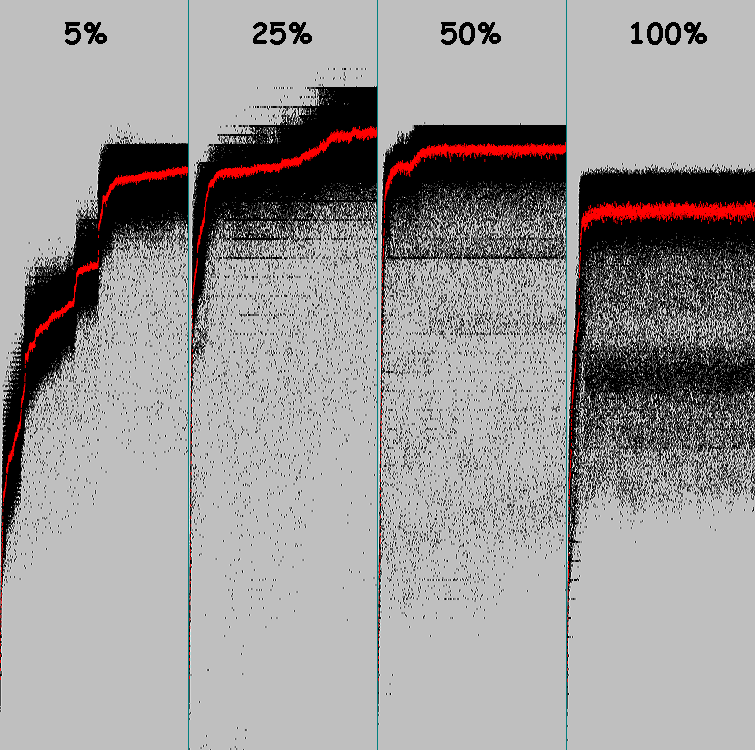
Lassen Sie uns ein weiteres Experiment durchführen. Das Muster ist das gleiche. Die anfänglichen Genotypen sind mit zufälligen Genen gefüllt. Die Wahrscheinlichkeit von Mutationen beträgt 5%. 1 bis 8 Gene mutieren (für jedes Individuum wird eine zufällige Anzahl mutierender Gene genommen). 100 Evolutionszyklen.



Die Grafik ist eine Wärmekarte. Die Punktgröße im Diagramm beträgt 5 Pixel. Der Ursprung ist die obere linke Ecke.
Auf der Y-Achse (von 0 bis 100) - Evolutionszyklen. Auf der X-Achse (von 0 bis 119) - die Anzahl der Zellen, die mit dem Muster übereinstimmen (für jedes Individuum in der Population erhalten wir das beste Ergebnis). Die Helligkeit des Punktes ist die Anzahl der Personen mit dem angegebenen Ergebnis (X-Koordinate).

Führen Sie den genetischen Algorithmus viermal mit denselben Parametern aus (100 Zyklen, 5% Mutationen, bis zu 8 Gene mutieren). In der Grafik beginnen alle 5:



Die folgenden 5 Starts: 25% Mutationen, bis zu 8 Gene mutieren:



Die Stichprobe ist klein, aber wir können Rückschlüsse auf die Wirksamkeit der Erhöhung des Prozentsatzes der Mutationen ziehen.

Als nächstes werde ich die Ineffizienz der im Artikel verwendeten Kreuzungsmethode zeigen.

Zuvor verwendete Methode:



Anstatt den Genotyp in zwei Teile zu teilen, erben Nachkommen zufällige Ahnengene:



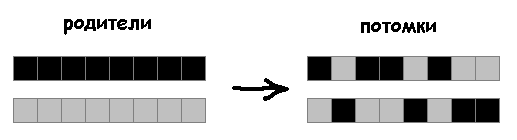
5% Mutationen:



25%:



Als nächstes werden wir diese Methode der Kreuze verwenden.

Darauf mit natürlichem Selektionsfinish. Wenn jemand interessante Ideen zu den Kriterien für die natürliche Selektion hat, äußern Sie diese bitte in den Kommentaren.

Für die künstliche Selektion werden zelluläre Automaten zweiter Ordnung verwendet .

Mobilfunkautomat zweiter Ordnung

Betrachten Sie einen nulldimensionalen zellularen Automaten erster Ordnung (alle oben betrachteten zellularen Automaten sind erster Ordnung). Ein nulldimensionaler zellularer Automat besteht aus einer Zelle. Eine Zelle kann sich in einem von zwei Zuständen befinden. Der nächste Zustand der Zelle (t) wird durch den aktuellen Zustand der Zelle (t-1) bestimmt. Insgesamt gibt es 4 nulldimensionale zellulare Automaten (darunter einen Oszillator):



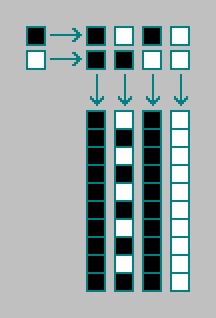
In einem zellularen Automaten zweiter Ordnung wird der nächste Zustand der Zelle (t) durch den aktuellen Zustand (t-1) und den vorherigen Zustand der Zelle (t-2) bestimmt. Insgesamt gibt es 4 Kombinationen von zwei Zellzuständen. $$$2 ^ {4} = $ 1$- die Anzahl der nulldimensionalen zellularen Automaten zweiter Ordnung:



Solche zellularen Automaten weisen komplexere Oszillatoren auf.

$$$2 ^ {8} = 256$zelluläre Automaten dritter Ordnung:



$$$2 ^ {16} = 65536$Zellularautomaten vierter Ordnung können nicht in einem Bild gezeigt werden.

Suche nach Zellenautomaten $$$n$-te Ordnung mit einer Schwingungsperiode gleich $$$n$- Die Aufgabe ist nicht trivial und äußerst interessant. Dieses Thema verdient einen separaten Artikel.

In zweidimensionalen eindimensionalen zellulären Automaten wird der folgende Zustand einer Zelle durch den aktuellen Zustand von drei Zellen und den vorherigen Zustand einer Zelle bestimmt:



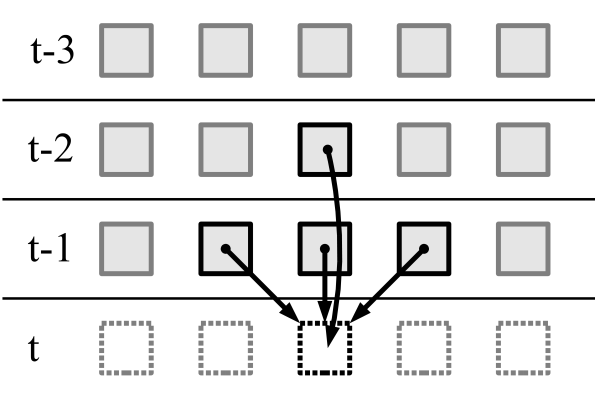
Es gibt $$$2 ^ {16} = 65536$eindimensionale zelluläre Automaten zweiter Ordnung.

Code:



Zellularautomaten zweiter Ordnung zeichnen komplexere Muster als Zellularautomaten erster Ordnung.

In den folgenden Bildern sind mehrere Zufallsmaschinen zweiter Ordnung (auf der linken Seite des Bildes - im Zustand t-1 ist eine Zelle rechts gefüllt - für die Zufallszustände t-1 und t-2 ist der Binärcode der Inhalt des

Regelarrays ): 0011111011001000:


0101101110011110: 0110000110010010: 0110011010010110


:


1110011010010110:


0110111010000101:


1111101001110110:


1001010001100000: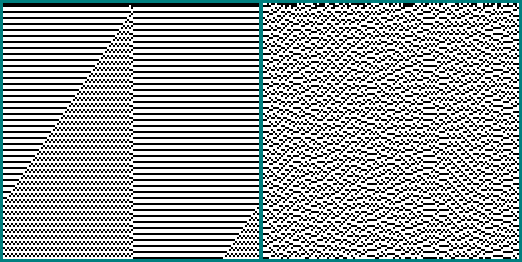


Dieselbe


Maschine 256x256:



512x512



Andere Maschinen sind hier zu sehen:
Eindimensionale Mobilfunkmaschine zweiter Ordnung.
Eindimensionaler zellularer Automat dritter Ordnung.

Eindimensionale zelluläre Automaten zweiter Ordnung finden sich in Wolframs Buch A New Kind of Science.

Künstliche Selektion

Wie ein eindimensionaler zellularer Automat zweiter Ordnung verwenden wir in einem zweidimensionalen zellularen Automaten zweiter Ordnung eine zusätzliche Zelle aus dem vorherigen (t-2) Zustand des Automaten.

Der Einfachheit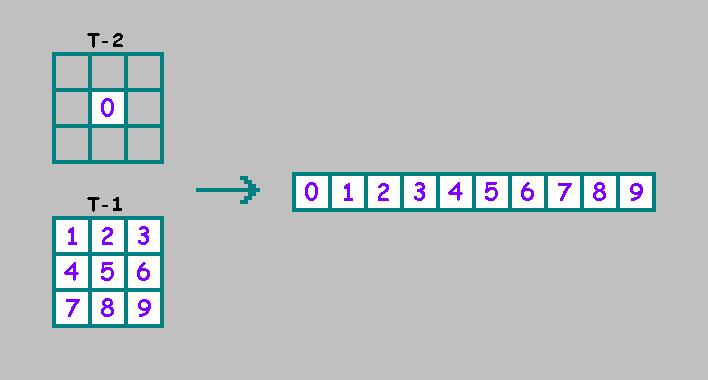



halber platzieren wir diese Zelle am Anfang der Binärzeile: Die Bequemlichkeit liegt in der Tatsache, dass der Automat, wenn die erste und die zweite Hälfte des Genotyps zusammenfallen, als Automat erster Ordnung betrachtet werden kann:



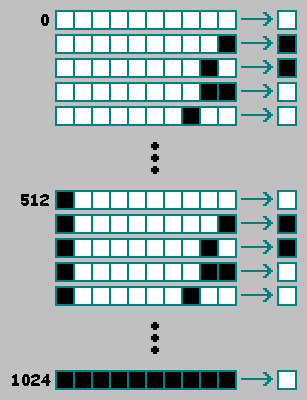Durch Hinzufügen einer Zelle haben wir die Anzahl der vorhandenen Automaten in erhöht$$ mal.$2^{512}$
$$- die Anzahl der vorhandenen zweidimensionalen Automaten zweiter Ordnung. Für die natürliche Selektion haben wir ein Kriterium bestimmt und Automaten anhand dieses Kriteriums verglichen. Bei der künstlichen Auswahl wählen wir die Maschinen manuell nach einem undeutlichen Prinzip aus: "Diese Maschine ist interessant, aber das ist nicht sehr." Mit diesem Prinzip können Sie nicht die beste Maschine unter zufälligen Maschinen auswählen:Es gibt verschiedene Möglichkeiten, dieses Problem zu lösen. Ich schlage vor, vier Möglichkeiten in Betracht zu ziehen.$2^{512} \times 2^{512} = 2^{1024}$

1. Im Ausgangszustand der Maschine ist eine Zelle gefüllt

Eine Möglichkeit besteht darin, die Entwicklung eines zellularen Automaten zu beobachten, in dessen Ausgangszustand eine Zelle gefüllt ist.

Wir füllen die anfängliche Population mit zufälligen Maschinen. Mehrere Maschinen aus der ursprünglichen Grundgesamtheit (jeweils 30 Iterationen):





Eine kleine Anzahl von Automaten mit weniger chaotischem Verhalten ist in der Bevölkerung vorhanden. Wir werden sie für die Kreuzung auswählen:





20 zufällige Maschinen aus der ursprünglichen Population (Zustand der Maschinen bei der 30. Iteration):



Nach drei Evolutionszyklen:



Nach acht Evolutionszyklen:



Acht Evolutionszyklen reichten aus, um die gesamte Population mit einer Maschine mit einem bestimmten Merkmal zu füllen (eine Maschine, die Dreiecke zeichnet). .

2. Der Genotyp ist teilweise gefüllt

Wenn das Verhältnis von Einheiten und Nullen im Genotyp verletzt wird, wird das Verhältnis von Einheiten und Nullen im Phänotyp verletzt.

Im Genotyp (Regel) des Automaten werden die folgenden Zellzustände für alle möglichen Kombinationen der Zelle und benachbarter Zellen aufgezeichnet. Wenn der Genotyp mehr Nullen (oder Einsen) enthält, sammeln sich Nullen (oder Einsen) in den folgenden Zuständen des Automaten an. Es ist interessant, die Korrelation zwischen dem Verhältnis von Einsen und Nullen im Genotyp und dem Verhältnis von Einsen und Nullen im Phänotyp zu untersuchen.

Erstellen Sie ein Diagramm.

Erstellen Sie eine Population von 200 Maschinen. Wir füllen die Genotypen mit Nullen (1024 Gene im Genotyp eines zweidimensionalen Automaten zweiter Ordnung). Weiter $$Gene sind mit Einheiten gefüllt. Für die erste Bevölkerung$n$$$ für die 513. Bevölkerung$n=0$$$$n=512$ . Entlang der Achse $$ist die Bevölkerungszahl. Entlang der Achse$x$$$ markiert (mit weißen Punkten) das Verhältnis von Einsen und Nullen im Genpool der Population. Wir haben eine Hyperbel:Für jeden Automaten (mit einer Feldgröße von 89x89) betrachten wir 100 Iterationen. Bei der 100. Iteration zählen wir die Anzahl der Einsen und Nullen im Zustand (Phänotyp) jedes Automaten. Wir markieren in der Grafik das Verhältnis von Einheiten und Nullen (die Gesamtzahl aller Einheiten wird durch die Gesamtzahl aller Nullen geteilt). Wir haben eine Kurve:Anstelle des Gesamtverhältnisses von Einsen und Nullen in allen Phänotypen können Sie das Verhältnis von Einsen und Nullen in jedem Phänotyp betrachten:Auf der linken Seite des Diagramms befinden sich Punkte mit der größten Abweichung vom Durchschnittswert. Es kann angenommen werden, dass dies Automaten sind, in deren Genotypen das Null-Gen gleich Eins ist. Angenommen - geprüft. Wir setzen das Null-Gen immer gleich Null. 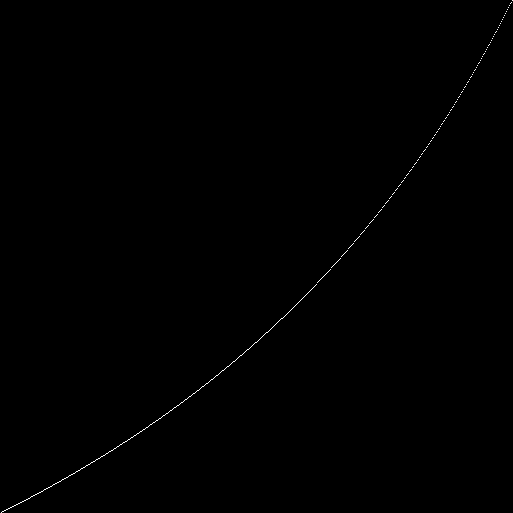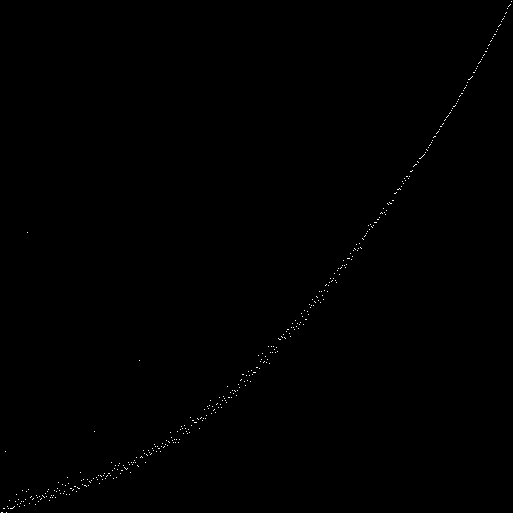Wir zeichnen ein neues Diagramm:$y$















Vergleichen Sie mit Maschinen, bei denen das Null-Gen immer gleich Eins ist:



Bei Maschinen zweiter Ordnung gibt es ein weiteres Null-Gen - das 512. Gen. Mal sehen, wie dieses Gen den Phänotyp beeinflusst.

Das 0. und 512. Gen sind immer Null: Das



0. Gen ist immer Null. Das 512. Gen ist immer gleich eins:



Um unsere geschätzten Epileptiker nicht noch einmal zu verspotten, werden das 0. und 512. Gen in der Anfangspopulation des genetischen Algorithmus mit Nullen gefüllt.

Schauen wir uns die Maschinen an, die wir durch Setzen von Nullen auf das 0. und 512. Gen beseitigt haben.

Die ersten 8 Zustände eines Automaten, in denen nur das 0. Gen gefüllt ist (das Null-Gen ist Eins, der Rest sind Nullen): Ein



Automat, in dem nur das 512. Gen



gefüllt ist : Ein Automat, in dem nur das 0. und 512. Gen gefüllt sind:



Lassen Sie uns eine Stelle in der Grafik herausgreifen, an der sich die Population in Gruppen aufteilt:



An dieser Stelle sind die Genotypen zu 25% gefüllt.

Vergleichen Sie zwei Populationen.

Erste Bevölkerung. 30 zufällige Maschinen bei der 1000. Iteration. Genotypen sind zu 50% voll (512 Einheiten und 512 Nullen):



Die zweite Population. 30 zufällige Maschinen bei der 1000. Iteration. Die Genotypen sind zu 25% voll (256 Einheiten und 768 Nullen):



Die zweite Population ist für die künstliche Selektion geeignet. Wir können einige der Zeichen in solchen Maschinen leicht hervorheben. Zum Beispiel: "dunkler", "weniger chaotisch" (Automaten, in denen weiße Zellen gruppiert sind) usw.

Wir wählen "dunkler". Die Wahrscheinlichkeit von Mutationen beträgt 10%, bis zu 4 Gene mutieren. Nach der ersten Auswahl:



Nach der zweiten Auswahl:



Ein interessanter Automat erschien in der Bevölkerung.

256x256, Zustand der Maschine bei der 1000. Iteration: Die



Maschine füllt allmählich die Population.

Nach der achten Auswahl:



Eine weitere interessante Maschine erschien.

256x256, Zustand des Automaten bei der 1000. Iteration:



Population nach dreizehn Auswahlen:



Mehrere Automaten aus dieser Population. 256x256, 1000. Iteration für alle. Unter dem Bild befindet sich ein Link, auf den Sie klicken können, um die Maschine in der Dynamik anzuzeigen:


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.

3. Conway-Automatikmaschine und dergleichen

Der bekannteste zweidimensionale zellulare Automat erster Ordnung ist das Conway-Automatenspiel „Life“ .

Die Regeln für den Conway-Automaten lauten wie folgt:
Wenn sich 3 lebende Zellen um eine tote Zelle befinden, wird die Zelle zum Leben erweckt (ansonsten bleibt sie tot).
Wenn sich 2 oder 3 lebende Zellen um eine lebende Zelle befinden, bleibt die Zelle am Leben (andernfalls stirbt sie ab).
Eine tote Zelle ist 0, eine lebende Zelle ist 1.

Um eine Zelle herum können 0 bis 8 lebende Zellen sein. Nach 9 Optionen rund um die lebende und um die tote Zelle. Wir schreiben alle Optionen in das r-Array:



Die erste Hälfte des Arrays ist für eine tote Zelle, die zweite für eine lebende Zelle.

Wir können die Regel des Conway-Automaten für alle möglichen (512) Kombinationen einer Zelle und 8 benachbarter Zellen beschreiben:





Kopieren Sie für einen Automaten zweiter Ordnung die zweite Hälfte des Regelarrays aus der ersten:



Wir starten die Maschine mit der angegebenen Regel. Wir sehen die charakteristischen Segelflugzeuge und Oszillatoren. Mehrere Iterationen dieses Automaten: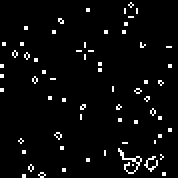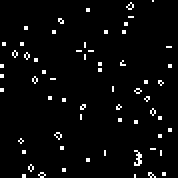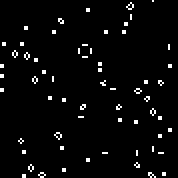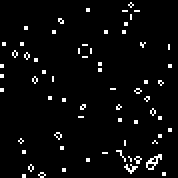



Array r besteht aus 18 Zellen. Es gibt$$ Automaten ähnlich dem Conway-Automaten (die nach denselben Regeln geschrieben werden können: die Anzahl der von den Toten umgebenen lebenden Zellen, in denen die Zelle zum Leben erweckt wird, und die Anzahl der lebenden Zellen in der lebenden Umgebung, in der die Zelle stirbt).Sie können siehieransehen(standardmäßig startet der Conway-Automat, die Schaltfläche „Regel ändern“ füllt das r-Array zufällig aus).Mehrere zufällige Maschinen (Binärcode - Array r):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111$2^{18}=262144$































Für einen genetischen Algorithmus können Sie als Genotyp als Array r ( $$Kombinationen) und das Regelarray ($2^{18}$$$ Kombinationen der ersten Ordnung für die zellulären Automaten und$2^{512}$$$ - für einen zellularen Automaten zweiter Ordnung).$2^{1024}$

$$ist eine relativ kleine Zahl. Mit dieser Nummer können Sie die Regel für die Maschine manuell auswählen, ohne einen genetischen Algorithmus zu verwenden (was Conway tatsächlich getan hat). Wenn Sie das Regelarray mit zufälligen Maschinen dieses Typs füllen und dieses Array als Genotyp verwenden, kann das Experiment bis zu einem gewissen Grad als nicht erfolgreich angesehen werden (genug, um die Ergebnisse dieses Experiments im Artikel nicht anzuzeigen). In den Regeln derartiger zellularer Automaten gibt es Symmetrie. Zum Beispiel für die folgenden Zellkombinationen:$2^{18}$






Der Zustand der Zelle bei der nächsten Iteration ist der gleiche. Nach der ersten Kreuzung wird die Symmetrie in den Regeln der Nachkommen gebrochen. Vorfahren sammeln Mutationen an, die auch die Symmetrie zerstören. Eine Verletzung der Symmetrie im Genotyp führt zu einer Verletzung der Symmetrie im Phänotyp.

Man kann die Manifestation dieser Symmetrie im Phänotyp sehen, wenn eine Zelle im Anfangszustand des Automaten gefüllt ist.

Lass uns ein Experiment machen. Um die Symmetrie aufrechtzuerhalten, verwenden wir das r-Array als Genotyp. 5% Mutationen, 1 Gen mutiert. Im Ausgangszustand ist eine Zelle gefüllt.

30 zufällige Maschinen aus der Grundgesamtheit. Der Zustand der Automaten bei der 30. Iteration:



Versuchen wir, solche Automaten zu isolieren, die sich am langsamsten aus einer Zelle entwickeln (wachsen).







Nach der ersten Auswahl wurden Automaten entfernt, die sich nicht entwickeln:



In der neuen Population gibt es mehrere solcher Automaten (die sich nicht entwickeln) - dies sind erfolglose Nachkommen und Mutanten.

Als nächstes werden wir hauptsächlich Maschinen mit weißem Hintergrund auswählen (Zellen, zu denen sich die Maschine nicht entwickelt hat).


Grundgesamtheit nach der zweiten Auswahl:



3 Auswahlen:



5 Auswahlen:



8 Auswahlen:



13 Auswahlen:



Dieselben Maschinen bei der 60. Iteration:



21 Auswahlen. Der Zustand der Automaten bei der 30. Iteration: Der



Zustand der Automaten bei der 60. Iteration:



34 Auswahlen. Zustand der Automaten bei der 30. Iteration:



Zustand der Automaten bei der 60. Iteration:



Außerdem entwickelt sich das System nicht weiter. Drei Automaten aus dieser Population (jeweils 100 Iterationen):

[1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,1]


[1 , 0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1]


[1,0,0,1,1,0,0, 1,1,0,1,0,1,1,0,1,1,1]


Zum Vergleich eine Zufallsmaschine:

[1,0,0,1,1,1,0,1,1,1,0, 0,1,1,0,0,0,1]

4. Conway-Automat und dergleichen (2)

In Maschinen mit den Regeln des Conway-Typs zählen wir die Anzahl der lebenden (Einheiten) Zellen in der Nähe von Moore. Diese Nachbarschaft kann in 4 Paare unterteilt werden und die Anzahl der lebenden Zellen in diesen Paaren zählen: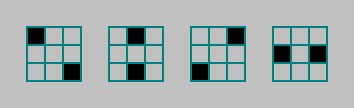



Somit erhöhen wir die Anzahl der Automaten, behalten aber die Symmetrie im Phänotyp bei.

Jedes Paar kann 0 bis 2 lebende Zellen haben. Par 4. Anzahl der Kombinationen$$$3^4=81$ .Nach der 81. Kombination um die lebende und um die tote Zelle. Insgesamt existiert$$ Automaten dieses Typs. Nummer:$2^{162}$

$$

$$2^{162}\approx5.846\times10^{48}$$

Es ist vollständig astronomisch und passt zu einem genetischen Algorithmus.

Die Genotypgröße jedes Individuums beträgt 162 Gene:


Als nächstes malen wir diese Regel für alle möglichen Kombinationen einer Zelle und acht benachbarter Zellen:


Wir werden das Regelarray verwenden, wenn wir den nächsten Zustand des Automaten berechnen. Wir rufen die Funktion fillrule () nach dem Laden der Seite und nach dem Aufrufen der Funktion evolute () auf.

Die anfängliche Bevölkerung sieht chaotisch aus. 30 zufällige Maschinen, die 1000. Iteration:



Dieses Chaos variiert geringfügig in der Dynamik und die Maschinen eignen sich gut zur Auswahl, aber machen wir es einfacher - wir werden die „dunkelsten“ auswählen.

Bevölkerung nach fünf Auswahlen:



Als nächstes können Sie nach Maschinen mit den komplexesten Oszillatoren suchen. Der gesamte Prozess des Auslegens ist sinnlos. Im Folgenden sind einige der interessantesten Automaten aufgeführt, die mit dem genetischen Algorithmus gefunden wurden.

256x256, 10000. Iteration für alle. Unter dem Bild befindet sich ein Link, auf den Sie klicken können, um die Maschine in der Dynamik anzuzeigen:


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.


Ansicht in Dynamik.

Ein Stück?

Und hier können Sie herumspielen:

Zweidimensionale zellulare Automaten zweiter Ordnung.

Schnittstelle:



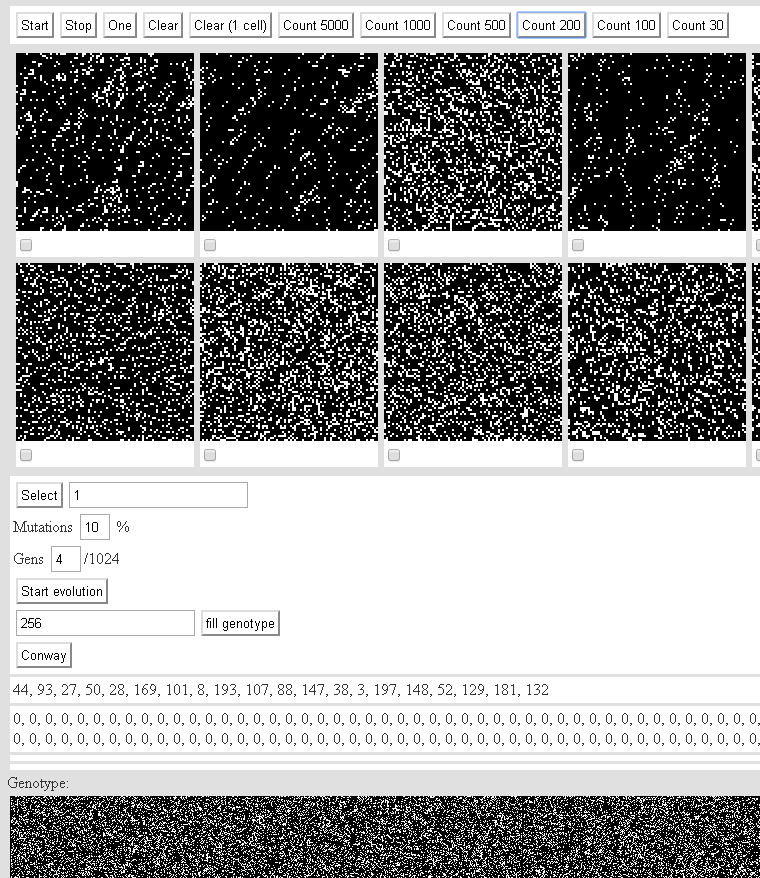Die Schaltfläche Start startet die Maschinen.
Stop - stoppt.
Eins ist eine Iteration.
Löschen - stoppt die Maschine und füllt den Ausgangszustand mit einem Zufall.
Löschen (1 Zelle) - stoppt die Maschine und füllt eine Zelle im Ausgangszustand.
Die verbleibenden Schaltflächen in dieser Zeile zählen die angegebene Anzahl von Iterationen für jeden Automaten.
Das Rendern eines Automaten auf Leinwand verbraucht die gesamte Leistung. Wenn Sie schnell 200 Iterationen berechnen müssen, klicken Sie auf "Anzahl 200". Wir klicken nicht auf die Schaltfläche "Anzahl 5000" - der Browser kann sie aufhängen.

Unter 20 zufälligen Maschinen (Populationsgröße - 200 Maschinen). Unter den Kontrollkästchen der Verkaufsautomaten. Wir markieren die interessantesten. Drücken Sie Auswahl - die Fitness des Geräts erhöht sich um die rechts angegebene Zahl.
Mutationen - die Wahrscheinlichkeit von Mutationen.
Gens ist die Anzahl der mutierenden Gene.

Evolution starten - Startet den Mechanismus von Kreuzen und Mutationen.

Genotyp füllen - füllt die angegebene Anzahl von Genen im Genotyp jedes Automaten.
Conway - füllt die Bevölkerung mit Maschinen vom Typ Konveevsky.

Nachfolgend zwei Zeilen: Die
Nummern der angezeigten Maschinen.
Der Inhalt des Fenotype-Arrays.

Der Genpool der Bevölkerung ist noch geringer.

Alle Fortschritte werden im lokalen Speicher gespeichert.

Sie können hier mit Sturmgewehren vom Typ Konveevsky (mit denen, die zuletzt im Artikel betrachtet wurden) spielen:

4. Conway-Automat und dergleichen (2).