Forschungsarbeit ist vielleicht der interessanteste Teil unserer Ausbildung. Die Idee ist, sich auch an der Universität in die gewählte Richtung zu versuchen. Beispielsweise forschen Studierende aus den Bereichen Software Engineering und Maschinelles Lernen häufig im Unternehmen (hauptsächlich JetBrains oder Yandex, aber nicht nur).
In diesem Beitrag werde ich über mein Projekt in der Informatik sprechen. Im Rahmen der Arbeit habe ich Ansätze zur Lösung eines der bekanntesten NP-harten Probleme untersucht und in die Praxis umgesetzt:
das Vertex-Covering-Problem .
Ein interessanter Ansatz für NP-schwierige Probleme ist nun die Entwicklung schnell parametrisierter Algorithmen. Ich werde versuchen, Sie auf den neuesten Stand zu bringen, einige einfache parametrisierte Algorithmen zu erklären und eine leistungsstarke Methode zu beschreiben, die mir sehr geholfen hat. Ich habe meine Ergebnisse bei der PACE Challenge vorgestellt: Nach den Ergebnissen offener Tests nimmt meine Entscheidung den dritten Platz ein und die endgültigen Ergebnisse werden am 1. Juli bekannt gegeben.

Über mich
Mein Name ist Vasily Alferov, ich beende jetzt das dritte Jahr der HSE - St. Petersburg. Ich habe Algorithmen seit meiner Schulzeit geliebt, als ich an der Moskauer Schule 179 studierte und erfolgreich an Informatikwettbewerben teilnahm.
Die endgültige Anzahl von Spezialisten für parametrisierte Algorithmen geht an die Bar ...
Ein Beispiel stammt aus dem Buch "Parametrisierte Algorithmen".Stellen Sie sich vor, Sie sind ein Barwächter in einer kleinen Stadt. Jeden Freitag kommt die Hälfte der Stadt in Ihre Bar, um sich zu entspannen, was Ihnen große Probleme bereitet: Sie müssen gewalttätige Besucher aus der Bar werfen, um Kämpfe zu verhindern. Am Ende stört es Sie und Sie beschließen, vorbeugende Maßnahmen zu ergreifen.
Da Ihre Stadt klein ist, wissen Sie mit Sicherheit, welche Besucherpaare sich sehr wahrscheinlich streiten, wenn sie gemeinsam an die Bar kommen. Sie haben eine Liste von
n Leuten, die heute Abend in die Bar kommen werden. Sie beschließen, keine Stadtbewohner in die Bar zu lassen, damit niemand kämpft. Gleichzeitig wollen Ihre Vorgesetzten keine Gewinne verlieren und sind unglücklich, wenn Sie nicht mehr als
k Leute an die Bar lassen.
Leider ist die Herausforderung, vor der Sie stehen, eine klassische NP-schwierige Aufgabe. Sie können es als
Vertex-Abdeckung oder als Vertex-Abdeckungsproblem kennen. Für solche Probleme sind im allgemeinen Fall Algorithmen unbekannt, die in einer akzeptablen Zeit arbeiten. Um genau zu sein, sagt die unbewiesene und ziemlich starke Hypothese der ETH (Exponential Time Hypothesis), dass dieses Problem nicht rechtzeitig gelöst werden kann
Das heißt, was merklich besser ist als eine erschöpfende Suche, kann man sich nicht vorstellen. Lassen Sie zum Beispiel
n = 1000 Personen planen, zu Ihrer Bar zu kommen. Dann wird eine vollständige Suche durchgeführt
Optionen, die es ungefähr gibt
- wahnsinnig viel. Glücklicherweise hat Ihr Leitfaden ein Limit von
k = 10 festgelegt , sodass die Anzahl der Kombinationen, über die Sie iterieren müssen, viel geringer ist: Die Anzahl der Teilmengen von zehn Elementen beträgt
. Dies ist bereits besser, zählt aber auch für einen leistungsstarken Cluster nicht für den Tag.
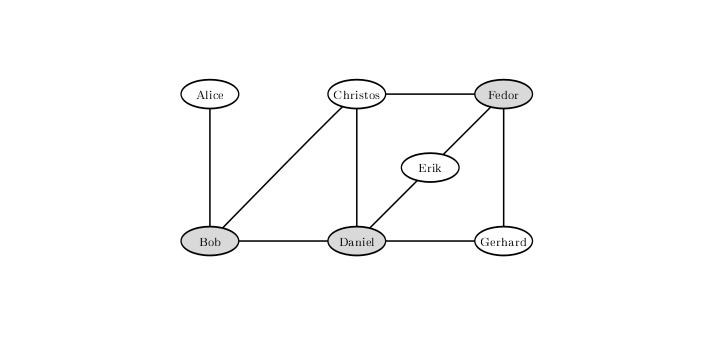
Um die Möglichkeit eines Kampfes mit einer solchen Konfiguration angespannter Beziehungen zwischen den Besuchern der Bar auszuschließen, dürfen Sie Bob, Daniel und Fedor nicht zulassen. Eine Lösung, bei der nur noch zwei über Bord bleiben, gibt es nicht.
Bedeutet das, dass es Zeit ist, sich zu ergeben und alle hereinzulassen? Betrachten wir andere Optionen. Nun, zum Beispiel können Sie nicht nur diejenigen hereinlassen, die wahrscheinlich mit einer sehr großen Anzahl von Menschen kämpfen. Wenn jemand mit mindestens
k + 1 von einer anderen Person kämpfen kann, können Sie ihn definitiv nicht hereinlassen, sonst müssen Sie nicht alle
k + 1 Stadtbewohner zulassen, mit denen er kämpfen kann, was die Führung definitiv verärgert.
Mögest du alles wegwerfen, was du nach diesem Prinzip kannst. Dann können alle anderen mit nicht mehr als
k Leuten kämpfen. Wenn Sie
k Leute aus ihnen herauswerfen, können Sie nicht mehr als verhindern
Konflikte. Also, wenn alles mehr als
Wenn eine Person in mindestens einen Konflikt verwickelt ist, können Sie sie sicherlich nicht alle verhindern. Da Sie natürlich sicher sind, dass keine Konflikte auftreten, müssen Sie alle Teilmengen von zehn von zweihundert Personen aussortieren. Es gibt ungefähr
und so viele Vorgänge können bereits im Cluster aussortiert werden.
Wenn es sicher ist, völlig konfliktfreie Persönlichkeiten zu nehmen, was ist dann mit denen, die nur in einen Konflikt verwickelt sind? Tatsächlich können sie auch eingelassen werden, indem die Türen vor ihrem Gegner geschlossen werden. In der Tat, wenn Alice nur mit Bob in Konflikt steht, dann werden wir nicht verlieren, wenn wir zwei von ihnen in Alice lassen: Bob mag andere Konflikte haben, aber Alice hat sie definitiv nicht. Darüber hinaus macht es für uns keinen Sinn, beides nicht zuzulassen. Nach solchen Operationen nicht mehr
Gäste mit einem ungelösten Schicksal: alles was wir haben
Konflikte, bei jeweils zwei Teilnehmern und jeweils an mindestens zwei. Es bleibt also nur zu klären
Optionen, die durchaus für einen halben Tag auf einem Laptop berechnet werden können.
In der Tat kann durch einfaches Denken noch attraktivere Bedingungen erreicht werden. Beachten Sie, dass wir definitiv alle Streitigkeiten lösen müssen, dh aus jedem Konfliktpaar, um mindestens eine Person auszuwählen, die wir nicht zulassen. Betrachten Sie diesen Algorithmus: Nehmen Sie jeden Konflikt, aus dem wir einen Teilnehmer löschen, und beginnen Sie rekursiv mit dem Rest, löschen Sie dann einen anderen und beginnen Sie auch rekursiv. Da wir bei jedem Schritt jemanden werfen, ist der Rekursionsbaum eines solchen Algorithmus ein Binärbaum der Tiefe
k , daher arbeitet der Algorithmus insgesamt für
Dabei ist
n die Anzahl der Eckpunkte und
m die Anzahl der Kanten. In unserem Beispiel sind dies ungefähr zehn Millionen, die in Sekundenbruchteilen nicht nur auf einem Laptop, sondern sogar auf einem Mobiltelefon gezählt werden.
Das obige Beispiel ist ein Beispiel eines
parametrisierten Algorithmus . Parametrisierte Algorithmen sind Algorithmen, die während
f (k) poly (n) arbeiten , wobei
p ein Polynom ist,
f eine beliebige berechenbare Funktion ist und
k ein Parameter ist, der möglicherweise viel kleiner als die Größe des Problems ist.
Alle Diskussionen vor diesem Algorithmus geben ein Beispiel für die
Kernelisierung , eine der gängigen Techniken zum Erstellen parametrisierter Algorithmen. Die Kernelisierung ist eine Reduzierung der Größe einer Aufgabe auf einen Wert, der durch eine Funktion eines Parameters begrenzt ist. Die resultierende Aufgabe wird oft als Kernel bezeichnet. Durch einfaches Überlegen von Scheitelpunktgraden haben wir einen quadratischen Kernel für das Vertex-Cover-Problem erhalten, der durch die Größe der Antwort parametrisiert wird. Es gibt andere Parameter, die für diese Aufgabe ausgewählt werden können (z. B. Vertex Cover Above LP), aber wir werden genau einen solchen Parameter diskutieren.
Tempo Herausforderung
Der Wettbewerb
PACE Challenge (Parametrisierte Algorithmen und Computational Experiments Challenge) begann 2015, um eine Verbindung zwischen parametrisierten Algorithmen und Ansätzen herzustellen, die in der Praxis zur Lösung von Computerproblemen verwendet werden. Die ersten drei Wettbewerbe waren dem
Ermitteln der
Baumbreite des Diagramms (
Treewidth ), dem
Ermitteln des
Steiner-Baums (
Steiner-Baum ) und dem
Ermitteln vieler Scheitelpunkte sowie dem Schneiden von Zyklen (
Feedback Vertex Set ) gewidmet. In diesem Jahr war eine der Aufgaben, bei denen man seine Stärken ausprobieren konnte, das oben beschriebene Problem der oberen Abdeckung.
Der Wettbewerb wird von Jahr zu Jahr beliebter. Wenn Sie den vorläufigen Daten glauben, haben dieses Jahr nur 24 Teams am Wettbewerb teilgenommen, um das Problem der Vertex-Abdeckung zu lösen. Es ist erwähnenswert, dass der Wettbewerb nicht mehrere Stunden und nicht einmal eine Woche, sondern mehrere Monate dauert. Die Teams haben die Möglichkeit, Literatur zu studieren, ihre ursprüngliche Idee zu entwickeln und zu versuchen, sie umzusetzen. In der Tat ist dieser Wettbewerb eine Forschungsarbeit. Ideen für die effektivsten Lösungen und die Vergabe von Gewinnern werden in Verbindung mit der
IPEC- Konferenz (Internationales Symposium für parametrisierte und exakte Berechnungen) auf dem größten jährlichen algorithmischen Treffen in Europa
ALGO abgehalten . Weitere Informationen zum Wettbewerb selbst finden Sie auf der
Website . Die Ergebnisse der vergangenen Jahre finden Sie
hier .
Lösungsschema
Um das Problem der Scheitelpunktabdeckung zu lösen, habe ich versucht, parametrisierte Algorithmen anzuwenden. Sie bestehen normalerweise aus zwei Teilen: Vereinfachungsregeln (die idealerweise zur Kernelisierung führen) und Aufteilungsregeln. Vereinfachungsregeln verarbeiten Eingaben in Polynomzeit vor. Der Zweck der Anwendung solcher Regeln besteht darin, das Problem auf ein äquivalentes Problem kleinerer Größe zu reduzieren. Vereinfachungsregeln sind der teuerste Teil des Algorithmus, und die Anwendung dieses bestimmten Teils führt zur Gesamtarbeitszeit
anstelle der einfachen Polynomzeit. In unserem Fall basieren die Aufteilungsregeln auf der Tatsache, dass Sie für jeden Scheitelpunkt entweder ihren oder ihren Nachbarn als Antwort nehmen müssen.
Das allgemeine Schema lautet wie folgt: Wir wenden die Vereinfachungsregeln an, wählen dann einen Scheitelpunkt aus und führen zwei rekursive Aufrufe durch: Im ersten nehmen wir ihn als Antwort und im anderen nehmen wir alle seine Nachbarn. Dies ist das, was wir entlang dieses Gipfels als Aufteilen (Brunching) bezeichnen.
Genau eine Ergänzung zu diesem Schema wird im nächsten Absatz vorgenommen.
Ideen zum Aufteilen von Regeln
Lassen Sie uns diskutieren, wie Sie einen Scheitelpunkt auswählen, entlang dessen die Aufteilung erfolgt.
Die Hauptidee ist im algorithmischen Sinne sehr gierig: Nehmen wir den Peak des maximalen Grades und teilen ihn durch ihn auf. Warum scheint es so besser? Weil wir im zweiten Zweig des rekursiven Aufrufs so viele Scheitelpunkte auf diese Weise entfernen. Sie können davon ausgehen, dass ein kleines Diagramm erhalten bleibt und wir schnell daran arbeiten werden.
Dieser Ansatz mit den bereits diskutierten einfachen Kernelisierungstechniken ist nicht schlecht, er löst einige Tests mit einer Größe von mehreren tausend Eckpunkten. Zum Beispiel funktioniert es jedoch nicht gut für kubische Graphen (dh Graphen, deren Grad an jedem Scheitelpunkt drei beträgt).
Es gibt eine andere Idee, die auf einer ziemlich einfachen Idee basiert: Wenn der Graph getrennt wird, kann das Problem mit den verbundenen Komponenten unabhängig gelöst werden, indem die Antworten am Ende kombiniert werden. Dies ist übrigens die kleine versprochene Änderung des Schemas, die die Lösung erheblich beschleunigen wird: Früher haben wir in diesem Fall für das Produkt der Zeiten gearbeitet, in denen die Antworten der Komponenten gezählt wurden, und jetzt arbeiten wir für die Menge. Und um das Brunch zu beschleunigen, müssen Sie einen verbundenen Graphen in einen nicht verbundenen verwandeln.
Wie kann man das machen? Wenn das Diagramm einen Artikulationspunkt enthält, muss entlang dieses gewandert werden. Ein Artikulationspunkt ist ein solcher Scheitelpunkt, dass der Graph beim Entfernen die Konnektivität verliert. Finden Sie in der Grafik alle Punkte des Gelenks können ein klassischer Algorithmus in linearer Zeit sein. Dieser Ansatz beschleunigt das Brunch erheblich.
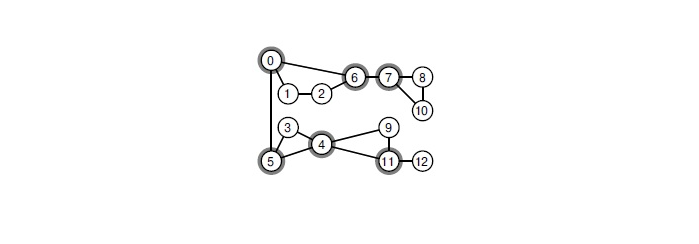
Wenn Sie einen der ausgewählten Scheitelpunkte entfernen, wird das Diagramm in verbundene Komponenten zerlegt.
Wir werden es tun, aber ich will mehr. Suchen Sie beispielsweise im Diagramm nach kleinen Scheitelpunktabschnitten und teilen Sie diese entlang der Scheitelpunkte auf. Der effektivste Weg, den minimalen globalen Scheitelpunktabschnitt zu finden, ist die Verwendung des Gomori-Hu-Baums, der in kubischer Zeit erstellt wird. Bei der PACE Challenge beträgt eine typische Diagrammgröße mehrere tausend Eckpunkte. In diesem Szenario müssen Milliarden von Operationen an jedem Scheitelpunkt des Rekursionsbaums ausgeführt werden. Es stellt sich heraus, dass es einfach unmöglich ist, das Problem in der vorgegebenen Zeit zu lösen.
Versuchen wir, die Lösung zu optimieren. Der minimale Scheitelpunktabschnitt zwischen einem Scheitelpunktpaar kann durch jeden Algorithmus ermittelt werden, der den maximalen Fluss konstruiert. Sie können den Dinitz-
Algorithmus in einem solchen Netzwerk ausführen, in der Praxis funktioniert er sehr schnell. Ich habe den Verdacht, dass es theoretisch möglich ist, eine Schätzung für die Arbeitszeit nachzuweisen
das ist schon ganz akzeptabel.
Ich habe mehrmals versucht, nach Schnitten zwischen Paaren zufälliger Eckpunkte zu suchen und den ausgeglichensten daraus zu ziehen. Leider ergab dies bei den offenen PACE Challenge-Tests schlechte Ergebnisse. Ich verglich es mit einem Algorithmus, der entlang der Eckpunkte des maximalen Grades verstreut war, und begann sie mit einer Einschränkung der Abstiegstiefe. Nachdem der Algorithmus versucht hatte, den Schnitt auf diese Weise zu finden, blieben größere Graphen übrig. Dies ist darauf zurückzuführen, dass sich die Schnitte als sehr unausgeglichen herausstellten: Nach dem Entfernen von 5-10 Spitzen konnten nur 15-20 abgespalten werden.
Es ist erwähnenswert, dass Artikel über theoretisch die schnellsten Algorithmen viel fortgeschrittenere Techniken zur Auswahl von Scheitelpunkten für die Aufteilung verwenden. Solche Techniken haben eine sehr komplexe Implementierung und oft schlechte Zeit- und Gedächtnisgrade. Ich konnte mich nicht von ihnen unterscheiden, was für die Praxis durchaus akzeptabel war.
So wenden Sie Vereinfachungsregeln an
Wir haben bereits Ideen für die Kernelisierung. Ich möchte Sie daran erinnern:
- Wenn es einen isolierten Scheitelpunkt gibt, löschen Sie ihn.
- Wenn es einen Scheitelpunkt vom Grad 1 gibt, löschen Sie ihn und nehmen Sie den Nachbarn als Antwort.
- Wenn es einen Scheitelpunkt mit einem Grad von mindestens k + 1 gibt , nehmen Sie ihn als Antwort.
Bei den ersten beiden ist alles klar, bei der dritten gibt es einen Trick. Wenn wir im Comic-Bar-Problem eine Einschränkung von oben für
k erhalten haben , müssen Sie in der PACE-Challenge nur die Scheitelpunktabdeckung mit der Mindestgröße finden. Dies ist eine typische Umwandlung eines Suchproblems in ein Entscheidungsproblem, häufig zwischen den beiden Arten von Aufgaben, die keinen Unterschied machen. In der Praxis kann es einen Unterschied geben, wenn wir einen Problemlöser für die Scheitelpunktabdeckung schreiben. Zum Beispiel wie im dritten Absatz.
In Bezug auf die Implementierung gibt es zwei Möglichkeiten, dies zu tun. Der erste Ansatz heißt Iterative Vertiefung. Es besteht aus Folgendem: Wir können mit einer vernünftigen Einschränkung der Antwort von unten beginnen und dann unseren Algorithmus ausführen, wobei diese Einschränkung als Einschränkung der Antwort von oben verwendet wird, ohne dass die Rekursion niedriger als diese Einschränkung ist. Wenn wir eine Antwort finden, ist diese garantiert optimal, andernfalls können Sie diese Grenze um eins erhöhen und erneut beginnen.
Ein anderer Ansatz besteht darin, eine aktuelle optimale Antwort zu speichern und nach einer kleineren Antwort zu suchen. Wenn diese gefunden wird, ändern Sie diesen Parameter
k , um überschüssige Zweige in der Suche mehr abzuschneiden.
Nachdem ich mehrere nächtliche Experimente durchgeführt hatte, entschied ich mich für eine Kombination dieser beiden Methoden: Zuerst führte ich meinen Algorithmus mit einer gewissen Einschränkung der Suchtiefe aus (wählte ihn so aus, dass er im Vergleich zur Hauptlösung eine unbedeutende Zeit in Anspruch nimmt) und verwendete die beste Lösung, die als Einschränkung von oben gefunden wurde auf die Antwort - das heißt auf genau diese
k .
Eckpunkte des Grades 2
Mit Eckpunkten der Grade 0 und 1 haben wir es herausgefunden. Es stellt sich heraus, dass dies auch mit Eckpunkten des Grades 2 möglich ist, aber dafür erfordert der Graph komplexere Operationen.
Um dies zu erklären, müssen Sie die Peaks irgendwie identifizieren. Wir nennen einen Scheitelpunkt 2. Grades den Scheitelpunkt
v und seine Nachbarn die Scheitelpunkte
x und
y . Dann haben wir zwei Fälle.
- Wenn x und y Nachbarn sind. Dann können Sie die Antwort x und y aufnehmen und v löschen. In der Tat müssen als Antwort mindestens zwei Eckpunkte aus diesem Dreieck genommen werden, und wir werden sicherlich nicht verlieren, wenn wir x und y nehmen : Sie haben wahrscheinlich mehr Nachbarn, v jedoch nicht.
- Wenn x und y keine Nachbarn sind. Dann wird angegeben, dass alle drei Eckpunkte zu einem zusammengeklebt werden können. Die Idee ist, dass es in diesem Fall eine optimale Antwort gibt, bei der wir entweder v oder beide Eckpunkte x und y nehmen . Darüber hinaus müssen wir im ersten Fall alle Nachbarn x und y als Antwort nehmen, und im zweiten Fall ist dies nicht erforderlich. Dies ist genau dann der Fall, wenn wir den geklebten Scheitelpunkt nicht als Antwort nehmen und wenn wir ihn nehmen. Es bleibt nur zu beachten, dass in beiden Fällen die Antwort von einer solchen Operation um eins abnimmt.
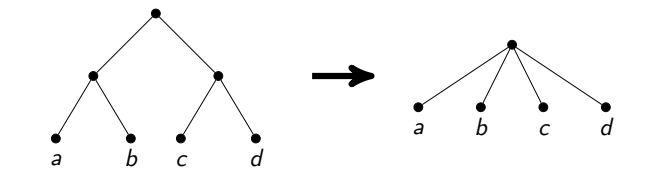
Es ist erwähnenswert, dass ein solcher Ansatz für eine ehrliche lineare Zeit ziemlich schwierig genau umzusetzen ist. Das Kleben von Scheitelpunkten ist eine schwierige Operation. Sie müssen die Listen der Nachbarn kopieren. Wenn Sie dies nachlässig tun, kann es zu einer asymptotisch nicht optimalen Betriebszeit kommen (z. B. wenn Sie nach jedem Kleben viele Kanten kopieren). Ich entschied mich dafür, nach ganzen Pfaden von Eckpunkten des Grades 2 zu suchen und eine Reihe von Sonderfällen zu analysieren, wie z. B. Schleifen von solchen Eckpunkten oder von allen solchen Eckpunkten außer einem.
Außerdem muss diese Operation reversibel sein, damit wir während der Rückkehr von der Rekursion das Diagramm in seiner ursprünglichen Form wiederherstellen. Um dies sicherzustellen, habe ich die Listen der Kanten der zusammengeführten Scheitelpunkte nicht gelöscht. Danach wusste ich nur, auf welche Kanten gerichtet werden sollte. Diese Implementierung von Graphen erfordert ebenfalls Genauigkeit, bietet jedoch eine ehrliche lineare Zeit. Und für Diagramme mit mehreren Zehntausenden von Kanten passt es vollständig in den Prozessor-Cache, was große Geschwindigkeitsvorteile bietet.
Linearer Kern
Schließlich der interessanteste Teil des Kernels.
Denken Sie zunächst daran, dass in zweigeteilten Graphen die minimale Scheitelpunktabdeckung angestrebt werden kann
. Verwenden Sie dazu den
Hopcroft-Karp- Algorithmus, um dort die maximale Übereinstimmung zu finden, und verwenden Sie dann den
Koenig-Egerwari- Satz.
Die Idee eines linearen Kernels lautet wie folgt: Zuerst teilen wir den Graphen, dh anstelle jedes Scheitelpunkts
v erhalten wir zwei Scheitelpunkte
und
und anstelle jeder Kante
u - v haben wir zwei Kanten
und
. Das resultierende Diagramm ist zweiteilig. Wir finden darin die minimale Scheitelpunktabdeckung. Einige Eckpunkte des Originaldiagramms gelangen zweimal dorthin, andere nur einmal und andere nie. Das Nemhauser-Trotter-Theorem besagt, dass es in diesem Fall möglich ist, Scheitelpunkte zu entfernen, die nicht einmal getroffen wurden, und diejenigen zu beantworten, die zweimal getroffen wurden. Darüber hinaus sagt sie, dass Sie von den verbleibenden Spitzen (die einmal getroffen wurden) mindestens die Hälfte zurücknehmen müssen.
Wir haben gerade gelernt, nicht mehr als
2k Eckpunkte in einem Diagramm zu belassen. Wenn der Rest der Antwort mindestens die Hälfte aller Scheitelpunkte ist, sind die gesamten Scheitelpunkte dort nicht mehr als
2k .
Hier habe ich einen kleinen Schritt nach vorne gemacht. Es ist klar, dass der auf diese Weise konstruierte Kernel davon abhängt, welche Art von minimaler Scheitelpunktabdeckung in dem zweigeteilten Graphen wir genommen haben. Ich würde gerne davon ausgehen, dass die Anzahl der verbleibenden Eckpunkte minimal ist. Bisher wussten sie nur rechtzeitig, wie es geht.
. Ich habe die Implementierung dieses Algorithmus rechtzeitig gefunden
Somit kann dieser Kern in Graphen von Hunderttausenden von Eckpunkten in jeder Verzweigungsstufe durchsucht werden.
Ergebnis
Die Praxis zeigt, dass meine Lösung bei Tests mit mehreren hundert Eckpunkten und mehreren tausend Kanten gut funktioniert. Bei solchen Tests ist zu erwarten, dass in einer halben Stunde eine Lösung gefunden werden kann. Die Wahrscheinlichkeit, in einem akzeptablen Zeitraum eine Antwort zu finden, steigt im Prinzip, wenn der Graph viele Eckpunkte mit einem hohen Grad aufweist, z. B. Grad 10 und höher.
Um am Wettbewerb teilnehmen zu können, mussten Entscheidungen an
optil.io gesendet
werden . Gemessen an der dort präsentierten
Platte liegt meine Entscheidung für offene Tests auf dem dritten von zwanzig Plätzen mit einem großen Vorsprung vor dem zweiten. Um ganz ehrlich zu sein, ist nicht ganz klar, wie Entscheidungen beim Wettbewerb selbst bewertet werden: Zum Beispiel besteht meine Entscheidung weniger Tests als die Entscheidung auf dem vierten Platz, aber für diejenigen, die sie bestehen, funktioniert sie schneller.
Ergebnisse zu geschlossenen Tests werden am 1. Juli bekannt gegeben.