⛪️ 💉 🎦 Die Welt der dreidimensionalen Hypersphäre. Geodätische Strahlverfolgung in einem geschlossenen Universum mit sphärischer Geometrie 🤱🏾 🧘🏼 😜

Möchten Sie die Welt mit den Augen einer Kreatur sehen, die in einem kompakten geschlossenen Universum mit sphärischer Geometrie lebt? Die Welt ohne Nacht sehen? Eine Welt, in der der andere Pol des Planeten am Himmel sichtbar ist? Eine Welt, in der es keinen Unterschied zwischen einer Sonnen- und einer Mondfinsternis gibt? Willkommen bei Katze!

Einführung Zweidimensionale geschlossene Welt

Um besser zu verstehen, was als nächstes passieren wird, stellen Sie sich vor, Sie sind ein zweidimensionales Wesen und leben in einer zweidimensionalen Welt, die eine Kugel darstellt. Wie wirst du deine Welt wahrnehmen? Beginnen wir mit der Bestimmung der Position der Körper. Sie können den Punkt deklarieren, an dem Sie das „Zentrum des Universums“ sind, zwei zueinander senkrechte Einheitsvektoren auswählen und das resultierende kartesische Koordinatensystem in der Nähe des „Zentrums des Universums“ verwenden.

Wenn Sie sich jedoch vom "Zentrum des Universums" entfernen, werden seltsame Dinge passieren. Was Sie als senkrechte Linien mit einem gewissen Abstand vom "Zentrum des Universums" wahrgenommen haben, wird zu dem, was Sie als parallele Linien wahrnehmen ...

... und parallele Linien schneiden sich.

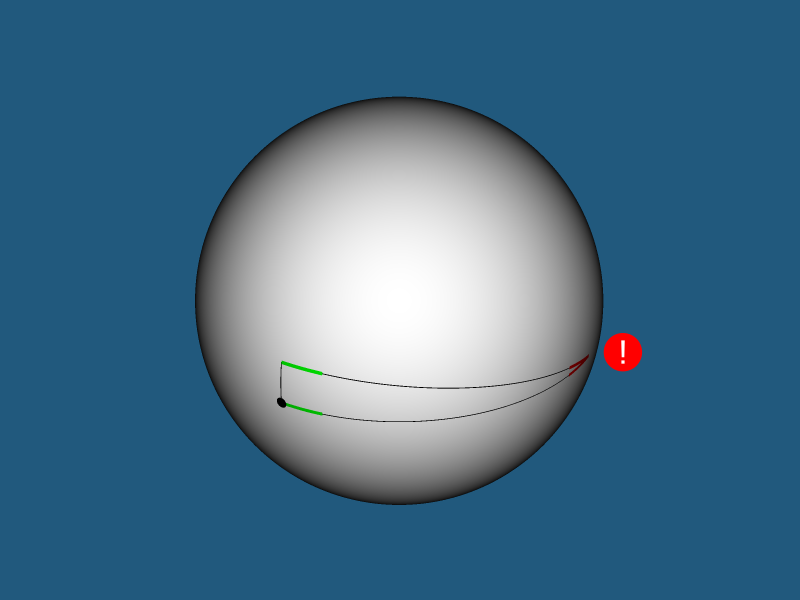
Der Grund ist einfach - was Sie als gerade Linie wahrnehmen, ist eigentlich ein großer Kreis - die geodätische Linie der Kugel. Daher ist das kartesische Koordinatensystem ungeeignet, um die Position von Körpern in Ihrer Welt zu bestimmen - wenn Sie sich vom "Zentrum des Universums" entfernen, verliert es seine Bedeutung.

Sie müssen ein anderes Koordinatensystem wählen, das für die Verwendung in Ihrer Welt besser geeignet ist - polar . Dieses Koordinatensystem ist natürlich und konsistent. In der Tat - der Winkel zwischen der Polarachse und der Richtung zum Körper bleibt unabhängig von der Entfernung zum Körper konstant.

In der Lage zu sein, die Position von Körpern zu bestimmen, können wir Ihre Welt mental erforschen und einige Effekte beschreiben, die auftreten, wenn Sie sich vom "Zentrum des Universums" entfernen und weil Ihre Welt eine Kugel ist.

Die umgekehrte Perspektive . Wenn sich ein Körper vom "Zentrum des Universums" entfernt, nimmt normalerweise seine Winkelgröße ab. In einer Entfernung von mehr als einem Viertel der Länge der geodätischen Linie vom "Zentrum des Universums" mit der Entfernung des Körpers nimmt jedoch seine Winkelgröße zu. Dieser Effekt beruht auf der Tatsache, dass der Abstand zwischen den geodätischen Linien der Kugel zum Äquator zunimmt und nachdem der Äquator abnimmt. Ein Körper, der im gleichen Abstand vom Äquator entfernt ist, hat die gleiche Winkelgröße, unabhängig davon, auf welcher Seite er vom Äquator liegt. Und diese Winkelgröße ist größer als die Winkelgröße des Körpers am Äquator.

Den Körper über den ganzen Himmel strecken. Hier wird der Begriff ganzer Himmel in der Bedeutung verwendet - das gesamte Sichtfeld eines zweidimensionalen Wesens (oben und unten oder vorne und hinten). Befindet sich der Körper in der Nähe des Punktes gegenüber dem "Zentrum des Universums", werden Sie, wo immer Sie hinschauen, Ihren Blick auf diesen Körper richten. Der Körper wird keinen Punkt haben, der nicht gesehen werden konnte - jeder Punkt hat einen Platz am Himmel. Dies ist der ultimative Fall des umgekehrten perspektivischen Effekts.

Symmetrische Transformation tel. Wenn sich der Körper in einem Abstand von mehr als der halben Länge der geodätischen Linie vom "Zentrum des Universums" befindet, wird dieser Körper symmetrisch transformiert - die linke und rechte Seite des Körpers wechseln die Position. Normalerweise fallen die linken und rechten Strahlen, die vom "Zentrum des Universums" ausgestrahlt werden, auf die linke und rechte Seite des Körpers. In einem Abstand von der halben Länge der geodätischen Linie vom "Zentrum des Universums" kreuzen sich die Strahlen und fallen nach dem Überqueren auf die gegenüberliegenden Seiten des Körpers.

Die zweite Vorwärts- und Rückwärtsperspektive. Dieser Effekt wird auch beobachtet, wenn sich der Körper in einer Entfernung befindet, die größer als die Hälfte der Länge der geodätischen Linie vom "Zentrum des Universums" ist. In Abständen von der Hälfte bis zu drei Vierteln der Länge der geodätischen Linie vom "Zentrum des Universums" nimmt seine Winkelgröße wieder ab, wenn sich der Körper entfernt (direkte Perspektive). In Abständen von drei Vierteln bis zur gesamten Länge der geodätischen Linie vom „Zentrum des Universums“ nimmt seine Winkelgröße wieder zu, wenn sich der Körper entfernt (umgekehrte Perspektive). Dieser Effekt sowie der inverse perspektivische Effekt sind mit einer Änderung des Abstands zwischen den geodätischen Linien der Kugel verbunden. Auf dem Weg zurück zum "Zentrum des Universums" nimmt der Abstand zwischen den geodätischen Linien der Kugel zum Äquator nach dem Äquator zu und ab.

Doppel. Jeder Körper in Ihrer Welt hat ein Doppel - wenn Sie einen Körper vor sich sehen, können Sie beim Umdrehen seine gegenüberliegende Seite sehen (Doppel). Ein Strahl, der auf einem langen Weg ausgestrahlt wird, umrundet Ihre Welt und tritt in den Rücken des Körpers ein. Es sollte beachtet werden, dass die Oberfläche des Doppels der Teil der Oberfläche ist, den Sie nicht vor sich sehen, und dass er symmetrisch transformiert wird. Hier wird der Begriff Oberfläche in der Bedeutung verwendet - der Grenze eines zweidimensionalen Körpers, der von einem zweidimensionalen Wesen wahrgenommen wird -, wie er auf einen Kreis angewendet wird. Es handelt sich tatsächlich um einen Kreisbogen, der von einem zweidimensionalen Wesen als Segment wahrgenommen wird. Aus Gründen der Klarheit werden wir jedoch nicht nur den Bogen, sondern auch den dahinter liegenden Teil des Kreises hervorheben.

Der Durchgang des Körpers durch einen Punkt gegenüber dem "Zentrum des Universums". Da der Effekt der Dehnung des Körpers bis zum ganzen Himmel sehr ungewöhnlich ist, werden wir ihn genauer betrachten. In den Figuren: die Nachbarschaft eines Punktes gegenüber dem "Zentrum des Universums".

Es ist zu sehen, dass:

Erstens nimmt die Körperoberfläche vor Ihnen zu (blau gestrichen) und die hinter Ihnen ab (blau gestrichen). Gleichzeitig haben beide Oberflächen die gleichen Winkelabmessungen - das heißt, die Oberfläche des vor Ihnen befindlichen Körpers wird zusammengezogen (der größte Teil der Oberfläche liegt in jedem Grad) und die hinter Ihnen liegende Fläche wird gedehnt (der gesamte kleinere Teil der Oberfläche liegt in jedem Grad).
Wenn der Körper einen Punkt gegenüber dem "Zentrum des Universums" berührt, beträgt die Winkelgröße beider Oberflächen 180 Grad - eine Hälfte des Himmels (vor Ihnen) nimmt die gesamte Oberfläche des Körpers ein, und die zweite Hälfte des Himmels (hinter Ihnen) wird von einem Punkt auf der Rückseite des Körpers besetzt
Während das Zentrum des Körpers mit dem Punkt gegenüber dem "Zentrum des Universums" ausgerichtet ist, erfolgt der Vorgang des umgekehrten Ziehens und Dehnens
Wenn sich der Körper an einem Punkt gegenüber dem "Zentrum des Universums" befindet, ist seine Oberfläche unverzerrt über den gesamten Himmel gespannt
Der Körper, der von einem Punkt gegenüber dem "Zentrum des Universums" gleitet, sieht ähnlich aus

Doppelter Horizont. Stellen Sie sich vor, Sie leben auf einem zweidimensionalen Planeten. Wenn Sie nach unten schauen, sehen Sie die Oberfläche Ihrer Seite des Planeten, und wenn Sie nach oben schauen, sehen Sie ... die Oberfläche der Rückseite des Planeten. Darüber hinaus wird es sehr eng - Sie können sowohl die Oberfläche der Rückseite des Planeten als auch den Teil der Oberfläche Ihrer Seite des Planeten sehen, der sich hinter Ihrem Rücken hinter dem Horizont befindet - Sie können dies alles über Ihrem Kopf sehen. Der Himmel wird in Form eines fadenschmalen Streifens dargestellt, der von oben und unten von den Horizonten Ihres und der Rückseite des Planeten eingeklemmt wird. Dies ist eine Kombination aus der Wirkung, den Körper über den ganzen Himmel zu strecken, und der Wirkung eines Doppels. Im Allgemeinen können Sie in Ihrer Welt, wenn nichts Ihren Blick behindert, Ihren Nacken direkt vor sich sehen ... einen so gesunden Nacken in all seinen Details ... der sich über den ganzen Himmel erstreckt).

Eine Welt ohne Nacht. Stellen Sie sich vor, der zweidimensionale Planet, auf dem Sie leben, dreht sich um einen zweidimensionalen Stern. Das Licht, das ein Stern auf einem kurzen Weg ausstrahlt, fällt auf die Tagesseite des Planeten. Gleichzeitig geht das Licht, das ein Stern auf einem langen Weg ausstrahlt, um Ihre Welt und fällt auf die Nachtseite des Planeten. Die Nacht existiert nicht mehr. Alles, was bleibt, sind Sonnenuntergänge und Sonnenaufgänge, die gleichzeitig auftreten werden - wenn die Seite des Sterns, die Ihnen zugewandt ist, über den Horizont hinausgeht, steigt die Rückseite des Sterns hinter Ihnen hinter dem Horizont auf. Natürlich können Sie den wahren Sonnenuntergang und die Morgendämmerung entlang des Weges hervorheben, an dem das Licht vorbeigegangen ist, aber es wird fast unmöglich sein, sie von Doppelbetten zu unterscheiden.

Es gibt auch einen Extremfall. Wenn der Planet Pech hat und sich am Punkt des gegenüberliegenden Sterns befindet, wird der Stern bis zum ganzen Himmel ausgedehnt, aber es wird problematisch sein, ihn zu bewundern, da das gesamte vom Stern emittierte Licht auf den Planeten fällt (ohne Lichtabsorption und -streuung durch das interplanetare Medium).

Sonnen- und Mondfinsternisse. Stellen Sie sich vor, ein zweidimensionaler natürlicher Satellit dreht sich um einen zweidimensionalen Planeten, auf dem Sie leben. Wenn ein Satellit zwischen einen Planeten und einen Stern gerät, fällt sein Schatten auf den Planeten. Andererseits wird der Planet gleichzeitig zwischen dem vom Stern auf einem langen Weg emittierten Licht und dem Satelliten, dh dem Schatten des Planeten, der auf den Satelliten fällt. Eine gleichzeitige Sonnen- und Mondfinsternis tritt auf. Natürlich ist es möglich, die wahren Sonnen- und Mondfinsternisse entlang der Länge des Weges, durch den das Licht ging, zu unterscheiden, aber es wird praktisch unmöglich sein, sie von Zwillingen zu unterscheiden. In den Schatten zu fallen, der während der Sonnenfinsternisse auf den Planeten und seinen Satelliten fällt, ist der einzige Weg, in Ihrer Welt im Dunkeln zu sein.

Dreidimensionale geschlossene Welt

Oben haben wir die wunderbare Welt eines zweidimensionalen Wesens untersucht. Was ist mit uns dreidimensionalen Wesen? Was ist die Geometrie des Universums ? Leider kann die Wissenschaft diese Frage noch nicht beantworten. Hauptsächlich stören die Eigenschaften und die Größe des Universums . Versuchen wir, der Wissenschaft zu helfen. Wir wählen als Kandidaten das interessanteste geschlossene Universum mit sphärischer Geometrie aus und untersuchen es visuell. Werden wir Effekte für ein zweidimensionales Analogon entdecken? Vielleicht lernen wir etwas Neues? Etwas, das Sie nicht erwartet hatten? Oder sogar sehen, was wir jeden Tag sehen, aber nicht darauf achten? Wie wird ein solches Universum aussehen?

Modell

Wir werden die Welt erforschen, die eine dreidimensionale Hypersphäre (3-Kugel) ist - das heißt eine Kugel, die im vierdimensionalen Raum liegt. Wir wählen einen Objekttyp für die Visualisierung - eine Kugel (eine 2-Kugel, die zu einer 3-Kugel gehört).

Grundlegende Konzepte und Beziehungen

Kartesische Koordinaten im vierdimensionalen Raum - wir werden sie als bezeichnen

$(x_0, x_1, x_2, x_3)$ - das ist eigentlich

$(x, y, z, w)$ .

Hypersphärische Koordinaten im vierdimensionalen Raum (wir verwenden nur Winkel, da der Radius unserer Welt eine Konstante sein wird) - wir bezeichnen sie als

$(a_0, a_1, a_2)$ - das ist eigentlich

$(\ phi, \ theta, \ psi)$ .

3-Kugel am Ursprung zentriert - eine Menge von Punkten, deren Radiusvektor eine Länge hat, die dem Radius der 3-Kugel entspricht

$R$ Ist unsere Welt

$\ quad \ quad x_0 ^ 2 + x_1 ^ 2 + x_2 ^ 2 + x_3 ^ 2 = R ^ 2$

2-Kugel, die zur 3-Kugel gehört - eine Menge von Punkten, deren Radiusvektor eine Länge hat, die dem Radius der 3-Kugel entspricht

$R$ und bildet ein 2-Kugel-Zentrum mit einem Radiusvektor

$c$ Winkel gleich dem Winkelradius der 2-Kugel

$r_a$ Sind unsere Visualisierungsobjekte

$\ quad \ quad x_0 c_0 + x_1 c_1 + x_2 c_2 + x_3 c_3 = R ^ 2 \ cos r_a$

wo

$\ quad \ quad r_a = r / R$

$\ quad \ quad r$ - geodätischer Radius einer 2-Kugel

Geodätischer, Winkel- und bedingter Radius - um besser zu verstehen, was es ist, betrachten Sie ein zweidimensionales Analogon einer 2-Kugel, die zu einer 3-Kugel gehört - eines Kreises, der zu einer Kugel gehört.

Der rote Bogen in der Abbildung ist der geodätische Radius des Kreises

$r$ . Die rote Ecke auf der rechten Seite der Figur ist der Winkelradius des Kreises

$r_a = r / R$ . Die Höhe des Dreiecks auf der rechten Seite der Figur ist der bedingte Radius des Kreises

$r_n = R \ sin r_a$ .

Übergang von hypersphärischen Koordinaten

$(a_0, a_1, a_2)$ zu kartesisch

$(x_0, x_1, x_2, x_3)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

wo

$\ quad \ quad a_0$ variiert von

$0$ vorher

$2 \ pi$

$\ quad \ quad a_1$ variiert von

$0$ vorher

$\ pi$

$\ quad \ quad a_2$ variiert von

$0$ vorher

$\ pi$

Der Schnittpunkt der geodätischen Linie einer 3-Kugel mit einer 2-Kugel, die zu einer 3-Kugel gehört.
Dieses Verhältnis wird für die Strahlverfolgung verwendet. Es gebe eine geodätische Linie, die sich vom Pol der 3-Kugel erstreckt

$(0, 0, 0, R)$ in der durch Winkel definierten Richtung

$a_0$ und

$a_1$ - Diese Winkel stimmen mit den Winkeln überein, die die Richtung im dreidimensionalen Raum in der Nähe des 3-Kugel-Pols bestimmen

$(0, 0, 0, R)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

Vereinfachung haben wir (1)

$\ quad \ quad x_0 = r_0 \ sin a_2$

$\ quad \ quad x_1 = r_1 \ sin a_2$

$\ quad \ quad x_2 = r_2 \ sin a_2$

$\ quad \ quad x_3 = r_3 \ cos a_2$

wo

$\ quad \ quad r_0 = R \ sin a_1 \ cos a_0$

$\ quad \ quad r_1 = R \ sin a_1 \ sin a_0$

$\ quad \ quad r_2 = R \ cos a_1$

$\ quad \ quad r_3 = R$

Ersetzen von (1) in der Gleichung der 2-Kugel und Vereinfachen haben wir (2)

$\ quad \ quad A \ sin a_2 + B \ cos a_2 = C$

wo

$\ quad \ quad A = r_0 c_0 + r_1 c_1 + r_2 c_2$

$\ quad \ quad B = r_3 c_3$

$\ quad \ quad C = R ^ 2 \ cos r_a$

Wenn wir (1) in die Gleichung der 3-Kugel einsetzen und vereinfachen, haben wir (3)

$\ quad \ quad D \ sin ^ 2 a_2 + E \ cos ^ 2 a_2 = F$

wo

$\ quad \ quad D = r_0 ^ 2 + r_1 ^ 2 + r_2 ^ 2$

$\ quad \ quad E = r_3 ^ 2$

$\ quad \ quad F = R ^ 2$

ausdrücken von (2)

$\ cos a_2$ wir haben

$\ quad \ quad \ cos a_2 = (C - A \ sin a_2) / B$

Ersetzen in (3)

$\ cos a_2$ wir haben

$\ quad \ quad D \ sin ^ 2 a_2 + E / B ^ 2 (C - A \ sin a_2) ^ 2 = F$

Vereinfachung haben wir

$\ quad \ quad a \ sin ^ 2 a_2 + b \ sin a_2 + c = 0$

wo

$\ quad \ quad m = E / B ^ 2$

$\ quad \ quad a = m A ^ 2 + D$

$\ quad \ quad b = -2 m A C$

$\ quad \ quad c = m C ^ 2 - F$

Ein Punkt auf der Fortsetzung der geodätischen Linie einer 3-Kugel, die durch zwei Punkte verläuft.
Diese Beziehung wird verwendet, um die Texturkoordinaten und die externe Normalen an einem beliebigen Punkt der zur 3-Kugel gehörenden 2-Kugel zu finden. Lass

$\ quad \ quad O$ - 3-Kugel-Zentrum

$\ quad \ quad A$ - Zentrum der 2-Kugel

$\ quad \ quad B$ Ist ein beliebiger Punkt der 2-Kugel

$\ quad \ quad C$ - der gewünschte Punkt liegt auf der Fortsetzung der geodätischen Linie

$AB$ in einem kleinen Winkelabstand

$\ delta$ von Punkt

$B$

$\ quad \ quad D$ - Schnittpunkt der Linien

$AB$ und

$OC$

$\ quad \ quad E$ - der Schnittpunkt der Linie, die durch den Punkt verläuft

$D$ senkrecht zur Geraden

$AB$ und eine Linie, die durch einen Punkt verläuft

$O$ parallel zu gerade

$AB$

$\ quad \ quad r_a$ - Winkelradius einer 2-Kugel

$\ quad \ quad a = (\ pi - r_a) / 2$

$\ quad \ quad b = a - \ delta$
Wenn

$r_a> \ pi$ dann sollte es gesetzt werden

$r_a = 2 \ pi - r_a$ und

$\ delta = - \ delta$
Wird finden

$\ vec {OD}$

$\ quad \ quad \ vec {OD} = \ vec {OA} + \ vec {AB} / | \ vec {AB} | \ cdot | \ vec {AD} |$

wo

$\ quad \ quad | \ vec {AD} | = | \ vec {AB} | / 2 + | \ vec {OE} |$

$\ quad \ quad | \ vec {OE} | = | \ vec {DE} | / \ tan b$

$\ quad \ quad | \ vec {DE} | = R \ sin a$

wird finden

$\ vec {OC}$

$\ quad \ quad \ vec {OC} = \ vec {OD} / | \ vec {OD} | \ cdot R$

Beleuchtung

Wir werden zwei Beleuchtungsmodelle verwenden.

Einfaches Beleuchtungsmodell. In diesem Modell hängt die Helligkeit eines Oberflächenpunkts vom Kosinus des Winkels zwischen der äußeren Normalen zur Oberfläche und der Richtung zum Betrachter ab. Wir werden es verwenden, wenn wir Bilder für erklärendes Material erstellen. Tatsächlich ist dies ein Modell mit einer Punktlichtquelle, die sich dort befindet, wo sich der Beobachter befindet, wobei die Helligkeit eines Oberflächenpunkts nicht von der Entfernung zur Lichtquelle abhängt.

Realistisches Beleuchtungsmodell. Dieses Modell verfügt über eine spezielle Punktlichtquelle. Wir werden es verwenden, um realistische Bilder zu erstellen. Dieses Modell kann den Einfluss des Wellenfrontbereichs auf die Helligkeit eines Oberflächenpunkts berücksichtigen (tatsächlich den Einfluss des Abstands zur Lichtquelle). In einem geschlossenen Universum mit sphärischer Geometrie ist die Wellenfrontfläche direkt proportional zum Quadrat des bedingten Radius der Kugel mit einem geodätischen Radius, der dem Abstand vom Oberflächenpunkt zur Lichtquelle entspricht. Mit der Entfernung von der Lichtquelle nimmt die Wellenfrontfläche zum Äquator zu (Lichtstrahlen divergieren) und nachdem der Äquator abgenommen hat (Lichtstrahlen konvergieren, fokussieren). Nach dem Passieren des Punktes gegenüber dem "Zentrum des Universums" erfolgt der umgekehrte Vorgang: Die Lichtstrahlen divergieren zuerst und konvergieren dann wieder. Darüber hinaus kann dieses Modell Wahrnehmungsmerkmale berücksichtigen ( Weber-Fechner-Gesetz ).

Um das Bild zu erstellen, verwenden wir die Rückstrahlverfolgung . Damit das Modell interaktiv ist (wir werden unsere Welt untersuchen und uns darin bewegen), muss das Bild in Echtzeit erstellt werden. Daher werden wir die Berechnungen im Fragment-Shader durchführen (wir verwenden WebGL). Wir implementieren die Schnittstelle in JavaScript.

Texturen

Textur earth.jpg von hier

Textur moon.jpg von hier

Textur sun.png von hier

Erste Bekanntschaft

Wir werden eine dreidimensionale geschlossene Welt mit einer geodätischen Linienlänge von 100 schaffen - damit wir leichter navigieren können - der Äquator unserer Welt befindet sich in einer Entfernung von 25 (ein Viertel der Länge der geodätischen Linie) und der gegenüberliegende Pol unserer Welt in einer Entfernung von 50 (die halbe Länge der geodätischen Linie). Wir platzieren einen Planeten in unserer Welt und malen Teile seiner Oberfläche in Farben, je nachdem in welchen Oktanten sie fallen:

Oktant	X-Zeichen	Y-Zeichen	Z-Zeichen	Farbe
Ich	+	+	+	Rot (Rot)
II	- -	+	+	Grün (Grün)
III	- -	- -	+	Blau ( B lue)
IV	+	- -	+	Orange
V.	+	+	- -	Blau ( C yan)
VI	- -	+	- -	Lila ( M agenta)
VII	- -	- -	- -	Gelb (gelb)
VIII	+	- -	- -	Weiß

Als Haupttextur verwenden wir die Textur eines 3x6-Schachbretts, dh jede Parallele und jeder Meridian durchlaufen genau 12 Zellen. Als alternative Textur verwenden wir die Textur des Globus. Unten sehen Sie Bilder eines Vorbeiflugs an unserem Planeten.

Eine Momentaufnahme des Nordpols. Die X-Achse ist nach rechts gerichtet, die Y-Achse ist nach oben gerichtet, die Z-Achse ist auf uns gerichtet. Wenn Sie eine alternative Textur anwenden, können Sie Folgendes sehen:

Auf der rechten Seite befindet sich der Pazifik
Oben - Nordamerika
links - der Atlantik
unten - Eurasien

Bilder vom Flug vom Nordpol zum Äquator und vom Äquator zum Südpol.

Momentaufnahme des Südpols. Die X-Achse ist nach rechts gerichtet, die Y-Achse ist nach unten gerichtet, die Z-Achse ist von uns weg gerichtet. Wenn Sie eine alternative Textur anwenden, können Sie Folgendes sehen:

Rechts - Pazifik, Neuseeland, Australien
von oben - Indischer Ozean
links - Atlantik, Afrika
unten - Südamerika

Visuelle Studie

Wir werden eine visuelle Untersuchung unserer Welt durchführen, um Analoga der Effekte zu entdecken, die wir in einer zweidimensionalen geschlossenen Welt entdeckt haben.

Doppel. Wie im zweidimensionalen Analogon wird jeder Körper in unserer Welt ein Doppel haben - wenn wir den Nordpol vor uns sehen und dann umdrehen, können wir ... den Südpol sehen. Die Kontraktion der Oberfläche des Doppels macht sich dadurch bemerkbar, dass wir nah genug am Planeten sind.

Ein Experiment, bei dem sich der Beobachter vom Planeten entfernt (die Zahl in der oberen linken Ecke jedes Bildes gibt den Abstand zwischen dem Beobachter und dem Planeten an).

Es ist zu sehen, dass:

anfangs nimmt die Winkelgröße des Planeten ab - dies ist die übliche direkte Perspektive
Wenn der Planet dann den Äquator unserer Welt passiert hat (Entfernung mehr als 25), nimmt seine Winkelgröße zu - dies ist der Effekt der entgegengesetzten Perspektive, die uns vertraut ist
Wenn wir zum gegenüberliegenden Pol unserer Welt kriechen, sehen wir eine verengte Oberfläche (Abstand 46,875).
Wenn sich der Planet am gegenüberliegenden Pol unserer Welt befindet (Entfernung 50), erstreckt er sich bis zum ganzen Himmel
Wenn wir vom gegenüberliegenden Pol unserer Welt gleiten, sehen wir eine gestreckte Oberfläche (Abstand 53,125).
Nachdem der Planet den entgegengesetzten Pol unserer Welt passiert hat, sieht er symmetrisch transformiert aus - der rote Oktant hat sich mit dem blauen geändert und so weiter
dann nimmt die Winkelgröße des Planeten ab (Abstand von 50 bis 75) und nimmt dann zu (Abstand von 75 bis 100) - dies ist der bekannte Effekt der zweiten Vorwärts- und Rückwärtsperspektive

Artefakte. Bei der Verwendung des Modells wurde festgestellt, dass während des Durchgangs des Planeten durch die vom Beobachter in Entfernungen von 25, 50 und 75 liegenden Punkte Artefakte auftreten können - die Haare können auf dem Planeten „wachsen“ oder sogar „zerbröckeln“. Anscheinend berücksichtigt meine Mathematik etwas nicht)

Ein Bild des Planeten in der Nähe des gegenüberliegenden Pols unserer Welt (eine Weitwinkel-Linse wurde verwendet). Die Oberfläche des Planeten vor uns ist sehr verengt - Sie können nicht nur die gesamte nördliche Hemisphäre sehen, sondern auch einen Teil der südlichen Hemisphäre hinter dem Äquator. Die Oberfläche des Planeten hinter uns ist sehr gespannt - der Südpol ist gut sichtbar. Beide Oberflächen strecken sich aufeinander zu und versuchen, uns in eine Kugelschale einzuschließen und uns ein Bild eines Planeten zu zeigen, der sich über den Himmel erstreckt.

Ein Experiment, bei dem der Betrachter nach oben schaut (die Zahl in der oberen linken Ecke jedes Bildes ist der Winkel zwischen der Abwärtsrichtung und dem Blick).

Auf den Bildern:

Zuerst erscheint der Horizont unserer Seite des Planeten
dann sehen wir einen zweiten Horizont darüber, wo wir finden, was sich auf unserer Seite des Planeten hinter unserem Rücken hinter dem Horizont befindet
Wenn wir nach oben schauen, sehen wir die Rückseite des Planeten

Doppelhorizontbild (verwendetes Weitwinkelobjektiv). Der Himmelsstreifen ist groß genug, weil wir uns auf einer Höhe von etwa 50 km befinden.

Ein Bild des Himmels über dem Kopf (ein Weitwinkelobjektiv wurde verwendet).

Eine Welt ohne Nacht.
Der Einfachheit halber werden wir unseren Planeten Erde, seinen natürlichen Satelliten - den Mond und den Stern, um den sie sich drehen - die Sonne nennen. Die Proportionen der Größen von Sonne, Erde, Mond und ihrer Umlaufbahnen zur Klarheit werden nicht beobachtet.
Im Bild: Die Grenze zwischen Tag- und Nachtseite des Planeten, die durch den Atlantik führt. Gleichzeitig sind die abnehmende und wachsende Erde sichtbar. Die Jungs, die auf den Mondbasen unserer Welt sitzen, sehen ein ungefähr ähnliches Bild.

Zur Animation: Die Bewegung der Grenze zwischen Tag- und Nachtseite der Erde. Sie können die Überlappung der Sonne durch die Erdscheibe sehen, die von den Sonnenstrahlen beleuchtet wird, die auf einem langen Weg freigesetzt werden.

Sonnen- und Mondfinsternisse.
Im Bild: Der Mond taucht aus dem Schatten der Erde auf. Die Grenzen zwischen Tag- und Nachtseite der Erde und des Mondes sind sichtbar.

Zur Animation: Sonnen- und Mondfinsternisse.

Es ist zu sehen, dass:

Erstens wirft die Erde einen Schatten auf den Mond und der Mond wirft einen Schatten auf die Erde
dann kommt der Mond aus dem Schatten der Erde und der Schatten des Mondes verlässt die Erdoberfläche
dann kehrt der Schatten des Mondes zur Erdoberfläche zurück und der Mond tritt wieder in den Schatten der Erde ein
Die Grenze zwischen der Tag- und der Nachtseite des Mondes ist nicht sichtbar, wenn der Mond von der Erdscheibe bedeckt ist, da sich die uns zugewandte Seite des Mondes immer noch im Schatten der Erde befindet

Zur Animation: Die Bewegung der Grenzen zwischen Tag- und Nachtseite der Erde und des Mondes kombiniert mit Sonnen- und Mondfinsternissen. Die Leute, die die Observatorien am Lagrange-Punkt L ₂ in unserer Welt bedienen, sehen ungefähr das gleiche Bild.) Natürlich, wenn wir die Rotation der Erde vernachlässigen.

Im Bild: Morgengrauen auf der ISS in unserer Welt)

Fazit

Wofür ist das alles? Ich wollte die Welt nur wirklich mit den Augen einer Kreatur sehen, die in einem kompakten geschlossenen Universum mit sphärischer Geometrie lebt. Diese wunderbare Welt ohne die Symbole von Christoffel und dergleichen zu kennen und dabei im Rahmen des allgemeinen Kurses der höheren Mathematik zu bleiben. Das Ergebnis liegt vor Ihnen. Alles scheint zu funktionieren. Hoffe du hattest einen interessanten und schönen Tag!

Quellcode .

Arbeitsmodell (offen auf dem PC, nicht für mobile Geräte).

Für diejenigen, die sich für das Thema interessieren, gibt es einen großartigen Artikel, der über die erstaunlichen Phänomene spricht, die im realen Universum beobachtet werden können: Wie man ein Schwarzes Loch zeichnet. Geodätische Strahlverfolgung in gekrümmter Raumzeit .

Die Welt der dreidimensionalen Hypersphäre. Geodätische Strahlverfolgung in einem geschlossenen Universum mit sphärischer Geometrie

Einführung Zweidimensionale geschlossene Welt

Dreidimensionale geschlossene Welt

Modell

Erste Bekanntschaft

Visuelle Studie

Fazit

More articles: