🚭 👨🏿‍🎓 🐵 Logistik der Maßnahme zur getrennten Sammlung von Wertstoffen ✋🏻 🧦 🙆🏻

Anstatt mitzumachen

Wenn die Prozesse der Abfallsammlung und -verarbeitung in Russland vollständig angepasst sind, ist es nicht leicht zu sagen, aber ich möchte jetzt nicht an der Wiederauffüllung von Deponien teilnehmen. Daher gibt es in vielen großen Städten auf die eine oder andere Weise Freiwilligenbewegungen, die sich mit einer bestimmten getrennten Sammlung befassen.

In Nowosibirsk findet eine solche Aktivität im Rahmen der Kampagne „Grünes Eichhörnchen“ statt, bei der die Bürger der Umwelt einmal im Monat zu einem bestimmten Zeitpunkt angesammelten recycelbaren Hausmüll an vorbestimmte Orte bringen. Gleichzeitig kommt dort ein gemieteter LKW an, der die gesammelten und sortierten wiederverwertbaren Materialien zum Standort bringt, von wo aus sie zwischen verschiedenen Verarbeitungsunternehmen verteilt werden. Die Aktion besteht seit 2014, und seitdem hat die Anzahl der Sammelstellen für Wertstoffe sowie deren Volumen erheblich zugenommen. Für das Lkw-Routing reichte ein Blick nicht aus, und wir begannen, Optimierungsmodelle zu entwickeln, um die Transportkosten zu minimieren. Das erste dieser Modelle ist Gegenstand dieses Artikels.

In Abschnitt 1 werde ich das Schema für die Organisation der Aktion detailliert und mit Abbildungen beschreiben. Ferner wird in Abschnitt 2 die Aufgabe der Minimierung der Transportkosten als die Aufgabe formalisiert, das Problem der Routenführung heterogener Fahrzeuge mit Zeitfenstern zu lösen. Abschnitt 3 befasst sich mit der Lösung dieses Problems unter Verwendung eines frei verteilten Pakets zur Lösung gemischter ganzzahliger linearer mathematischer Programmierprobleme GLPK.

1. Die Aktion "Grünes Eichhörnchen"

Seit 2014 führt die Living Earth- Initiativgruppe eine monatliche Kampagne durch, um die Sammlung von recyceltem Eichhörnchen in Nowosibirsk zu trennen. Zum Zeitpunkt des Schreibens wird das Recycling mit einer Reihe von Vorbehalten als Kunststoffabfall mit der Bezeichnung PET, PE, PP, PS, Glas, Aluminium, Eisen, Haushaltsgeräte, Altpapier und mehr akzeptiert. Mehr als 50 Freiwillige beteiligen sich an der Vorbereitung und Durchführung der Aktion. Die Aktion ist nicht kommerziell, die Teilnahme daran ist kostenlos und bedeutet keine finanzielle Belohnung.

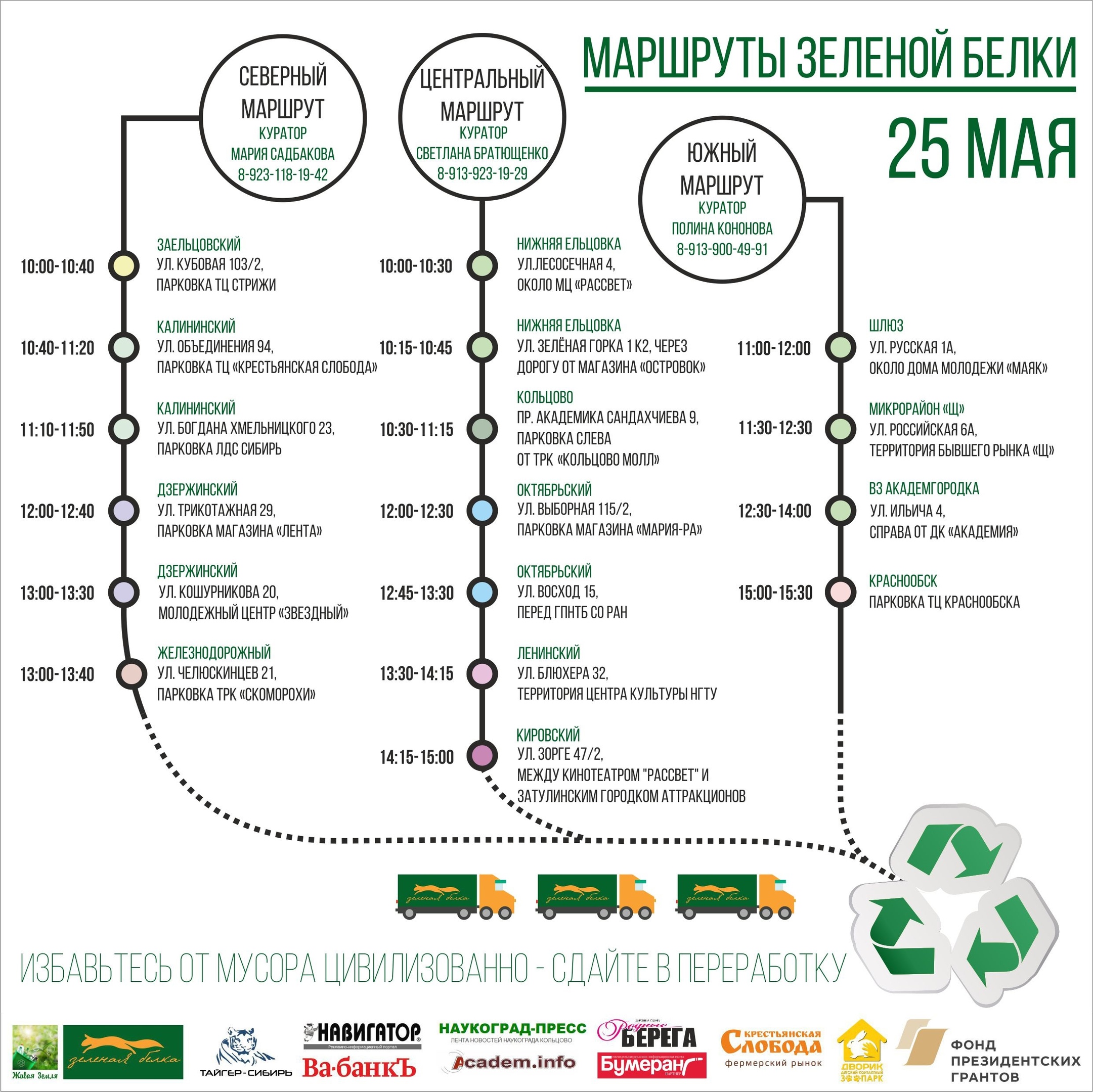
Punkte

Die Aktion findet an 17 Punkten der Stadt statt, die sich in einem Zeitraum von 15 bis 90 Minuten in vom Auto zurückgelegten Entfernungen voneinander befinden. Einer dieser Punkte auf dem Foto: Taschen links entlang der Wand, um verschiedene Plastikfraktionen zu sammeln, rechts - ein Lastwagen, in den in Zukunft alles geladen wird, und in der Mitte - ein Freiwilliger mit Ohren.

Bild

Alle Aktivitäten an diesem Punkt werden von Kuratoren organisiert, die Einschränkungen hinsichtlich des Zeitpunkts haben, zu dem sie bereit sind, ihre Aufgaben zu erfüllen. Bei der Planung einer Aktion geben die Kuratoren das Zeitintervall an, in dem die Aktion an ihrem Punkt durchgeführt werden muss.

Es gibt auch Daten zu den durchschnittlichen Mengen an Wertstoffen, die an jedem Punkt gesammelt wurden.

Routen

Die Punkte sind in Routen organisiert, die nacheinander von einem LKW gefahren werden. LKW-Bewegungen werden von Streckenleitern überwacht, die die Betriebsumgebung überwachen und Entscheidungen über die Behandlung besonderer Ereignisse treffen.

Bild

Lastwagen

Sie werden im Rahmen von Vorschlägen zur stündlichen Vermietung von Frachtfahrzeugen gemeinsam vermietet. Es ist nicht möglich, den Kunststoff an Ort und Stelle zu verdichten, daher ist der Hauptparameter, der den LKW charakterisiert, das Volumen der Karosserie. Die Tragfähigkeit ist in unserem Fall kein begrenzender Faktor.

Die Hauptkosten der Maßnahme hängen mit der Zahlung der Lkw-Vermietung zusammen. Daher ist ihre Reduzierung entscheidend für die Existenz und Entwicklung unseres Anteils, der institutionelle Bedeutung im Sinne der Bildung von Vorstellungen über verantwortungsvollen Konsum erlangt. Als nächstes wird ein Ansatz zur Lösung dieses Problems beschrieben, der auf der Anwendung diskreter Optimierungsmethoden basiert, nämlich der mathematischen Programmierung.

2. Formalisierung

Bei der Konstruktion des mathematischen Modells bleiben wir im Rahmen linearer Programme mit gemischten ganzen Zahlen, für die das Verständnis der Algebra der Klasse 7 ausreicht.

Die einzige Schwierigkeit kann mit der Verwendung von abstrakten Notations- und Summationszeichen in Formeln verbunden sein. Ich hoffe, dies schreckt Leser nicht ab, die selten auf mathematische Texte stoßen.

Im Optimierungsmodell können vier Komponenten unterschieden werden:

die Bildung von Gruppen von Punkten, die eine separate Route bilden;
Definition einer Schaltung für jede der Gruppen;
Erfüllung der Anforderungen für die Ankunftszeit des Lastwagens an jedem Punkt;
Bestimmung des LKW-Typs, der für die Wartung der einzelnen Strecken benötigt wird.

Wir betrachten jeden der Teile und führen die erforderliche Notation nach Bedarf ein.

Punktgruppierung

Lass

V = \ {1, \ dots, n \}

$V = \ {1, \ dots, n \}$ Es gibt viele Indizes von Sammelstellen für wiederverwertbare Materialien, und der Ort, an dem gesammelte Wertstoffe transportiert werden - wir nennen es ein Depot - hat einen Index von 0. Put

\ bar {V} = V \ cup \ {0 \}

$\ bar {V} = V \ cup \ {0 \}$

Jede Punktgruppe bildet eine eigene Route. Durch

R

$R$ bezeichnen den Satz von Routennummern.

Lass die Menge

z_{i r}, i i n I, r i n R

$z_ {ir}, i \ in I, r \ in R$ gleich eins, wenn der Punkt

i

$i$ in der Route mit der Nummer enthalten

r

$r$ und sonst Null. Dann die Anforderung, dass der Punkt

i i n V

$i \ in V$ muss eine der Routen eingeben kann als geschrieben werden

s u m_{r i n R} z_{i r} = z_{i 1} + z_{i 2} + d o t s + z_{i n} = 1.

$\ sum_ {r \ in R} z_ {ir} = z_ {i1} + z_ {i2} + \ dots + z_ {in} = 1.$

Das Depot muss alle Routen eingeben:

z_{0 r} = 1, r i n R

$z_ {0r} = 1, r \ in R$

Feinheiten

Leider verursacht eine solche Aufzeichnung Rechenprobleme, die mit der Symmetrie des zulässigen Bereichs verbunden sind. Es kann durch Hinzufügen einer Reihe von Einschränkungen beseitigt werden, die die Wahl einer lexikographisch minimalen Zerlegung gewährleisten. Sie können hier zum Beispiel mehr auf Russisch lesen.

1 - z_{i r} l e q s u m_{j = 1}^{i - 1} l e f t (1 - s u m_{k = 1}^{r - 1} z_{j k} r i g h t) + s u m_{k = 1}^{r - 1} z_{i k}, q u a d i i n I, r i n R, r l e q i .

$1-z_ {ir} \ leq \ sum_ {j = 1} ^ {i-1} \ left (1- \ sum_ {k = 1} ^ {r-1} z_ {jk} \ right) + \ sum_ { k = 1} ^ {r-1} z_ {ik}, \ quad i \ in I, r \ in R, r \ leq i.$

Definition eines Umweges

Routen sind eine abwechselnde Folge von Punkten und Kreuzungen zwischen ihnen. Formal beginnen sie alle an einem der Punkte des Sets

V

$V$ und im Depot enden, ist es jedoch einfacher anzunehmen, dass alle Routen zyklisch sind. Diese Annahme ändert nichts an der Essenz, sondern macht alle Scheitelpunkte gleich: In diesem Fall gibt es keine Endscheitelpunkte, sie sind alle Transitscheitelpunkte.

Für Punkte

i, j i n b a r V

$i, j \ in \ bar {V}$ und Route

r i n R

$r \ in R$ Richten Sie eine Variable ein

x_{i j r}

$x_ {ijr}$ gleich eins, wenn in der Route mit Nummer

r

$r$ LKW fährt vom Punkt ab

i

$i$ auf den Punkt

j

$j$ und sonst Null.

Dann müssen wir zunächst den LKW auf der Strecke bewegen

r i n R

$r \ in R$ besuchte den Punkt

i i n V

$i \ in V$ wenn sie nach der Aufteilung in Gruppen in die Gruppe mit der Nummer fiel

r

$r$ ::

s u m_{j i n b a r V} x_{j i r} = z_{i r}, q u a d i i n b a r V, r i n R .

$\ sum_ {j \ in \ bar {V}} x_ {jir} = z_ {ir}, \ quad i \ in \ bar {V}, r \ in R.$

Zweitens der LKW nach der Ankunft am Punkt

i i n b a r V

$i \ in \ bar {V}$ muss sie verlassen.

s u m_{j i n b a r V} x_{j i r} = s u m_{j i n b a r V} x_{i j r}, q u a d i i n b a r V, r i n R . .

$\ sum_ {j \ in \ bar {V}} x_ {jir} = \ sum_ {j \ in \ bar {V}} x_ {ijr}, \ quad i \ in \ bar {V}, r \ in R. .$

Möglicherweise stellen Sie fest, dass diese Einschränkungen die Mengen zulassen

x_{i j r}

$x_ {ijr}$ Definieren Sie Routen, die eine Reihe von disjunkten Schleifen sind. Routen dieser Art sind natürlich nicht sinnvoll, und eine Reihe von Einschränkungen sind erforderlich, um dies zu vermeiden.

Über die Beseitigung von Subzyklen

Eine Möglichkeit könnte darin bestehen, nicht negative Hilfsgrößen einzuführen

f_{i j r}, i, j i n b a r V, r i n R

$f_ {ijr}, i, j \ in \ bar {V}, r \ in R$ Der Satz von Beziehungen, der unter Verwendung dieser Größen aufgezeichnet wird, eliminiert Wertekombinationen

x_{i j r}

$x_ {ijr}$ Definieren von Routen, die keine verbundene Schleife sind.

s u m_{i i n V} f_{0 j r} = s u m_{i i n V} z_{i r}, q u a d r i n R,

$\ sum_ {i \ in V} f_ {0jr} = \ sum_ {i \ in V} z_ {ir}, \ quad r \ in R,$

f_{i j r} l e q n x_{i j r}, q u a d i i n b a r V, j i n b a r V, r i n R,

$f_ {ijr} \ leq nx_ {ijr}, \ quad i \ in \ bar {V}, j \ in \ bar {V}, r \ in R,$

s u m_{j i n b a r V} f_{j i r} = s u m_{j i n b a r V} f_{i j r} + z_{i r}, q u a d i i n V, r i n R .

$\ sum_ {j \ in \ bar {V}} f_ {jir} = \ sum_ {j \ in \ bar {V}} f_ {ijr} + z_ {ir}, \ quad i \ in V, r \ in R.$

Diese Verhältnisse geben den Fluss vom Depot zu den übrigen Routenpunkten an. An jedem Zwischenpunkt wird eine Durchflusseinheit absorbiert. Damit das Netzwerk einen Leistungsfluss hat, der der Anzahl der Punkte minus eins entspricht, muss die Route verbunden werden.

Erfüllung der Anforderungen zum Zeitpunkt der Ankunft des LKW an jedem Punkt

Mit anderen Worten, Sie müssen Punkte nur innerhalb der von den Kuratoren angegebenen Zeitfenster besuchen. Durch

B_{i}

$B_i$ und

E_{i}

$E_i$ bezeichnen jeweils den Beginn und das Ende des Zeitintervalls, in dem der Kurator des Punktes

i

$i$ kann daran teilnehmen.

Um die Umsetzung dieser Einschränkungen zu verfolgen, benötigen wir Informationen über die Zeit, die der LKW während Stopps und Überfahrten auf der Route verbringt. Durch

L_{i}, i i n V

$L_i, i \ in V$ bezeichnen die Ladedauer am Punkt

i

$i$ und durch

D_{i j}, i, j i n b a r V

$D_ {ij}, i, j \ in \ bar {V}$ - Zeit der Bewegung von einem Punkt

i

$i$ auf den Punkt

j

$j$ Wir reservieren das

D_{0 i} = 0

$D_ {0i} = 0$ für alle

i i n b a r V

$i \ in \ bar {V}$ und kann im Allgemeinen durchgeführt werden

D_{i j} n e q D_{j i}

$D_ {ij} \ neq D_ {ji}$ für jeden

i n e q j

$i \ neq j$

Wir führen nicht negative Variablen ein

a_{i}, i i n b a r V

$a_i, i \ in \ bar {V}$ und

w_{i r}, i i n b a r V, r i n R

$w_ {ir}, i \ in \ bar {V}, r \ in R$ gleich Ankunftszeiten und Wartezeiten am Punkt

i

$i$ beim Fahren entlang einer Route

r

$r$ jeweils. Für die eingegebenen Werte sollten die folgenden Beziehungen erfüllt sein.

Die Wartezeit darf nicht kürzer sein als die zum Laden erforderliche Zeit

w_{i r} g e q L_{i} z_{i r}, q u a d i i n b a r V, r i n R,

$w_ {ir} \ geq L_iz_ {ir}, \ quad i \ in \ bar {V}, r \ in R,$

und gleich Null, wenn der Punkt nicht zur Route gehört

r

$r$

w_{i r} l e q M z_{i r}, q u a d i i n b a r V, r i n R,

$w_ {ir} \ leq Mz_ {ir}, \ quad i \ in \ bar {V}, r \ in R,$

Ankunftszeit am Punkt

j

$j$ berechnet zu geeigneten Zeiten für den vorherigen Punkt

i

$i$ Hier ist eine ziemlich große Konstante

M

$M$ wird verwendet, um unnötige Abhängigkeiten beim Wechsel zwischen zu beseitigen

i

$i$ und

j

$j$ nicht getan.

a_{i} + s u m_{r i n R} w_{i r} + D_{i j} l e q a_{j} + M (1 - s u m_{r i n R} x_{i j r}), q u a d i i n I, j i n V,

$a_i + \ sum_ {r \ in R} w_ {ir} + D_ {ij} \ leq a_j + M (1 - \ sum_ {r \ in R} x_ {ijr}), \ quad i \ in I, j \ in V,$

Die Ankunft und Abfahrt des LKW muss innerhalb des vom Kurator angegebenen Intervalls erfolgen.

a_{i} g e q B_{i}, q u a d i i n V,

$a_i \ geq B_i, \ quad i \ in V,$

a_{i} + s u m_{r i n R} w_{i r} l e q E_{i}, q u a d i i n V .

$a_i + \ sum_ {r \ in R} w_ {ir} \ leq E_i, \ quad i \ in V.$

Bestimmen des LKW-Typs, der für die Wartung jeder Route benötigt wird
Bezeichnen Sie die vielen Arten von LKWs, die von gemietet werden können

T

$T$ LKW-Typ

t i n T

$t \ in T$ gekennzeichnet durch Körpervolumen

C_{t}

$C_t$ und die Kosten für eine Stunde Miete

P_{t}

$P_t$ Mindestmietdauer für LKWs

t

$t$ bezeichnen mit

U_{t}^{0}

$U_t ^ 0$ Die Menge der am Punkt gesammelten Wertstoffe

i i n V

$i \ in V$ bezeichnen mit

G_{i}

$G_i$

Wir führen Variablen ein

y_{t r}, t i n T, r i n R

$y_ {tr}, t \ in T, r \ in R$ gleich eins, wenn LKW-Typ

t

$t$ Service Route mit Nummer zugeordnet

r

$r$ und sonst Null.

Ganzzahlige Variablen

u_{t r}, t i n T, r i n R

$u_ {tr}, t \ in T, r \ in R$ Stellen Sie den Zeitpunkt für die Anmietung eines LKW-Typs ein

t

$t$ die Route mit Nummer bedienen

r

$r$
Für jede Route

r i n R

$r \ in R$ müssen Sie den LKW-Typ zuweisen:

s u m_{t i n T} y_{t r} = 1, q u a d r i n R

$\ sum_ {t \ in T} y_ {tr} = 1, \ quad r \ in R$

In Übereinstimmung mit der Aufteilung der Punkte zwischen Routen können sich einige Routen als trivial herausstellen, dh nur Depots enthalten. Wenn die Route

r

$r$ nicht trivial, dann wird der ihm zugewiesene LKW mindestens vermietet

U_{t}^{0}

$U_t ^ 0$ Stunden.

u_{t r} g e q U_{t}^{0} (y_{t r} - s u m_{i i n V} z_{i r}), q u a d t i n T, r i n R .

$u_ {tr} \ geq U_t ^ 0 (y_ {tr} - \ sum_ {i \ in V} z_ {ir}), \ quad t \ in T, r \ in R.$

Gleichzeitig sollte die Mietdauer auch die Gesamtdauer des Parkens und der Bewegung entlang der Strecke überschreiten.

u_{t r} g e q s u m_{i i n V} s u m_{j i n b a r V} D_{i j} x_{i j r} + s u m_{i i n b a r V} w_{i r} - M (1 - y_{t r}), q u a d r i n R, t i n T .

$u_ {tr} \ geq \ sum_ {i \ in V} \ sum_ {j \ in \ bar {V}} D_ {ij} x_ {ijr} + \ sum_ {i \ in \ bar {V}} w_ { ir} -M (1-y_ {tr}), \ quad r \ in R, t \ in T.$

Fügen Sie Einschränkungen für die Eigenschaft hinzu: Wenn der LKW vom Typ ist

t

$t$ nicht einer Route zugeordnet

r

$r$ ist seine Mietzeit Null.

u_{t r} l e q M y_{t r} .

$u_ {tr} \ leq My_ {tr}.$

Alle an Routenpunkten gesammelten Wertstoffe sollten auf die Rückseite des Lastwagens passen.

s u m_{i i n V} G_{i} z_{i r} l e q s u m_{t i n T} C_{t} y_{t r}, q u a d r i n R .

$\ sum_ {i \ in V} G_iz_ {ir} \ leq \ sum_ {t \ in T} C_ty_ {tr}, \ quad r \ in R.$

Schließlich ist es unser Ziel, die Kosten für die Anmietung von LKWs zu minimieren, die unter Verwendung der eingeführten Bezeichnungen wie folgt geschrieben werden

s u m_{t i n T} s u m_{r i n R} P_{t} u_{t r}

$\ sum_ {t \ in T} \ sum_ {r \ in R} P_tu_ {tr}$

Suche nach einer Lösung

Es ist leicht zu überprüfen, ob alle im Optimierungsmodell enthaltenen Ausdrücke lineare Funktionen von Variablen sind. Um die genauen und ungefähren Lösungen zu finden, können Sie Standardpakete zur Lösung von Programmierproblemen mit gemischten Ganzzahlen wie Gurobi , CPLEX , Xpress , ORtools , verwenden. SCIP , BLIS usw.
Wir schreiben ein Modell zur Minimierung der Transportkosten in der GMPL-Sprache. Dadurch können wir das kostenlose GLPK- Paket für unsere Zwecke verwenden. Um Code zu schreiben und das Modell zu debuggen, ist es praktisch, die GUSEK- Entwicklungsumgebung herunterzuladen, deren Zusammensetzung bereits GLPK enthält.

GUSEK sieht so aus:

Bild

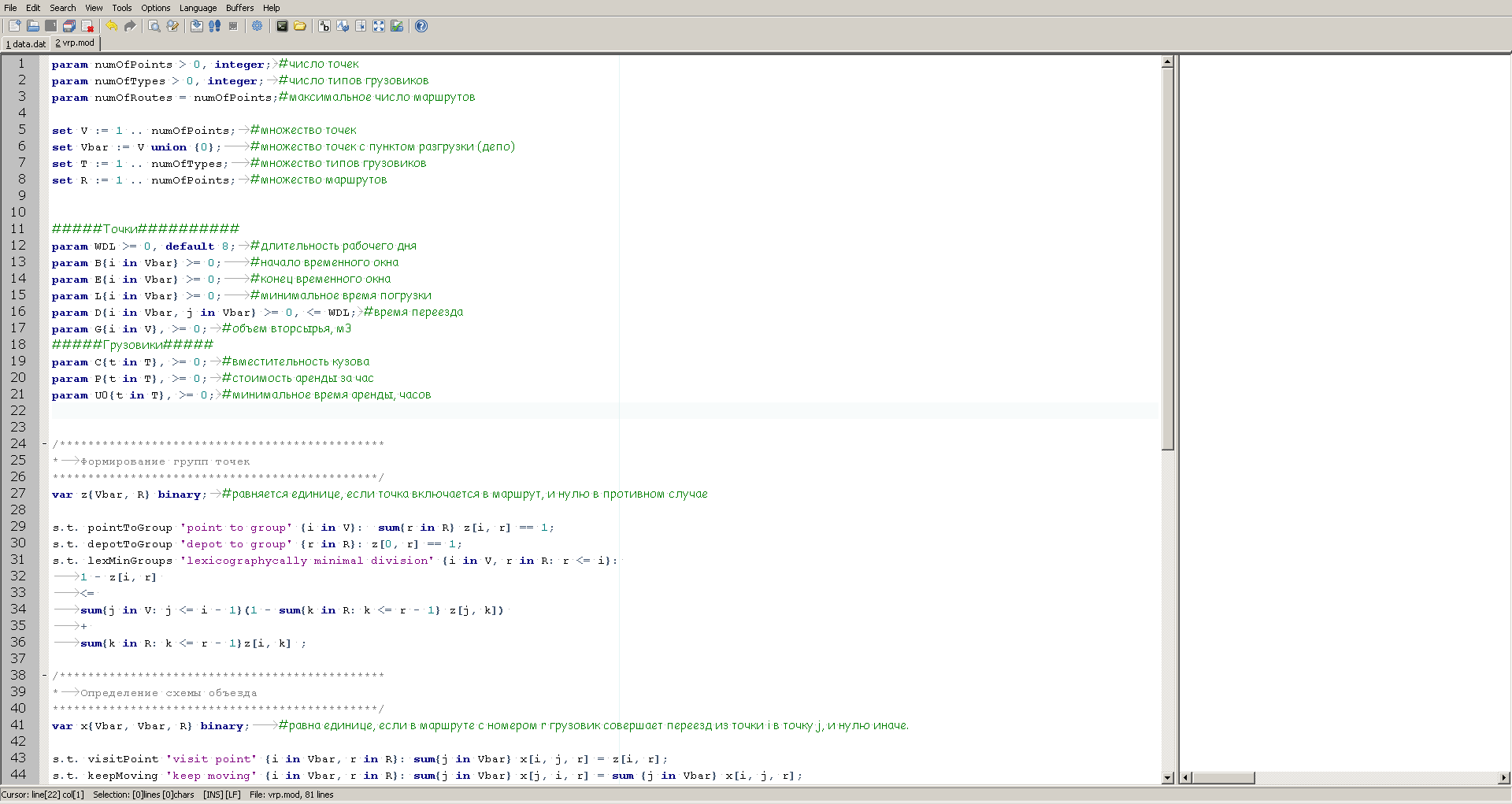
Links sehen wir eine Beschreibung des Modells und rechts ein Fenster zur Anzeige von Informationen über den Berechnungsfortschritt, die der Solver nach dem Start liefert.

Vollständige Beschreibung des Modells

param numOfPoints > 0, integer; #  param numOfTypes > 0, integer; #   param numOfRoutes = numOfPoints;#   set V := 1 .. numOfPoints; #  set Vbar := V union {0}; #     () set T := 1 .. numOfTypes; #   set R := 1 .. numOfPoints; #  ############### param WDL >= 0, default 8; #   param B{i in Vbar} >= 0; #   param E{i in Vbar} >= 0; #   param L{i in Vbar} >= 0; #   param D{i in Vbar, j in Vbar} >= 0, <= WDL; #  param G{i in V}, >= 0; # , 3 ########## param C{t in T}, >= 0; #  param P{t in T}, >= 0; #    param U0{t in T}, >= 0; #  ,  /********************************************** *    **********************************************/ var z{Vbar, R} binary; # ,     ,      st pointToGroup 'point to group' {i in V}: sum{r in R} z[i, r] == 1; st depotToGroup 'depot to group' {r in R}: z[0, r] == 1; st lexMinGroups 'lexicographycally minimal division' {i in V, r in R: r <= i}: 1 - z[i, r] <= sum{j in V: j <= i - 1}(1 - sum{k in R: k <= r - 1} z[j, k]) + sum{k in R: k <= r - 1}z[i, k] ; /********************************************** *    **********************************************/ var x{Vbar, Vbar, R} binary; # ,    c  r      i   j,   . st visitPoint 'visit point' {i in Vbar, r in R}: sum{j in Vbar} x[i, j, r] = z[i, r]; st keepMoving 'keep moving' {i in Vbar, r in R}: sum{j in Vbar} x[j, i, r] = sum {j in Vbar} x[i, j, r]; var f{Vbar, Vbar, R} >= 0; #,  . st flowFromDepot 'flow from depot' {r in R}: sum{i in V} f[0, i, r] == sum{i in V} z[i, r]; st flowAlongActiveArcs 'flow along active arcs' {i in Vbar, j in Vbar, r in R}: f[i, j, r] <= numOfPoints * x[i, j, r]; st flowConservation 'flow conservation' {i in V, r in R}: sum{j in Vbar} f[j, i, r] == sum{j in Vbar} f[i, j, r] + z[i, r]; var a{i in V} >= 0; #     var w{i in Vbar, r in R} >= 0; #     st wait 'wait'{i in Vbar, r in R}: w[i, r] >= L[i] * z[i, r]; st dontWait 'dont wait'{i in Vbar, r in R}: w[i, r] <= (E[i] - B[i]) * z[i, r]; st arrivalTime 'arrival time' {i in V, j in V}: a[i] + sum{r in R}w[i, r] + D[i,j] <= a[j] + 3 * WDL * (1 - sum{r in R} x[i, j, r]); st arriveAfter 'arrive after' {i in V}: a[i] >= B[i]; st departBefore 'depart before' {i in V}: a[i] + sum{r in R}w[i, r] <= E[i]; /********************************************** *   ,       **********************************************/ var y{t in T, r in R}, binary; # ,    t       r,   . var u{t in T, r in R}, integer, >= 0; #    t,     rst assignVehicle 'assign vehicle' {r in R}: sum{t in T} y[t,r] == 1; st rentTime 'rent time' {r in R, t in T}: u[t, r] >= sum{i in V, j in Vbar}D[i, j] * x[i, j, r] + sum{i in Vbar}w[i, r] - WDL * (1 - y[t, r]); st minRentTime 'minimal rent time' {r in R, t in T}: u[t, r] >= U0[t] * (y[t, r] - sum{i in V}z[i, r]); st noRent 'no rent' {t in T, r in R}: u[t, r] <= WDL * y[t, r]; st fitCapacity 'fit capacity' {r in R}: sum{i in V} G[i] * z[i, r] <= sum{t in T} C[t] * y[t, r]; minimize rentCost: sum{t in T, r in R} P[t] * u[t, r]; solve; /********************************************** *     **********************************************/ printf{i in V, r in R} (if 0.1 < z[i,r] then "point %s to group %s\n" else ""), i, r, z[i,r]; printf{r in R, i in Vbar, j in Vbar} (if 0.1 < x[i, j, r] then "route %s: %s -> %s\n" else ""), r, i, j; printf{i in V} "point %s arrive between %s and %s (actual = %s)\n", i, B[i], E[i], a[i]; end;

Für einen schnellen Start füge ich auch Daten aus meinem Kopf hinzu, die für die Verwendung im Modell vorbereitet wurden:

Daten eingeben

 data; param numOfPoints := 9; #  param numOfTypes := 6; #   ############### param : B E L := 0 0 8 1 1 0 8 1 2 0 8 1 3 0 8 1 4 0 8 1 5 0 8 1 6 0 8 1 7 0 8 1 8 0 8 1 9 0 8 1; param D default 0 : 0 1 2 3 4 5 6 7 8 9 := 0 . . . . . . . . . . 1 0.1 0.3 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 2 0.3 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 3 0.4 0.3 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 4 0.4 0.4 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 5 0.1 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 6 0.5 0.5 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 7 0.3 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 8 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 9 0.5 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1; param G := 1 1 2 2 3 1 4 2 5 1 6 2 7 1 8 2 9 1; ########## param : C P := 1 8 500 2 10 500 3 14 600 4 18 650 5 25 700 6 35 800; param U0 default 2; #  ,  end;

Nach dem Kopieren des Modellcodes in eine Datei mit dem Namen, z. B. model.mod, und den Eingabedaten in die Datei data.dat kann alles ausgeführt werden. Wir setzen eine Grenze für die Berechnungszeit von 100 Sekunden (dies geschieht mit dem Schlüssel --tmlim [Zeit in Sekunden]), übertragen den Pfad mit den Eingabedaten in die Datei (mit dem Schlüssel -d [Dateipfad]).

Bild

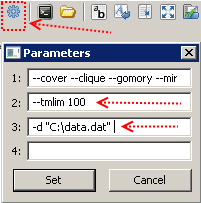
und drücken Sie F5. Bei Erfolg werden im rechten Fenster Nachrichten angezeigt, und nach hundert Sekunden haben wir die beste Lösung, die GLPK in der vorgegebenen Zeit gefunden hat.

Bild

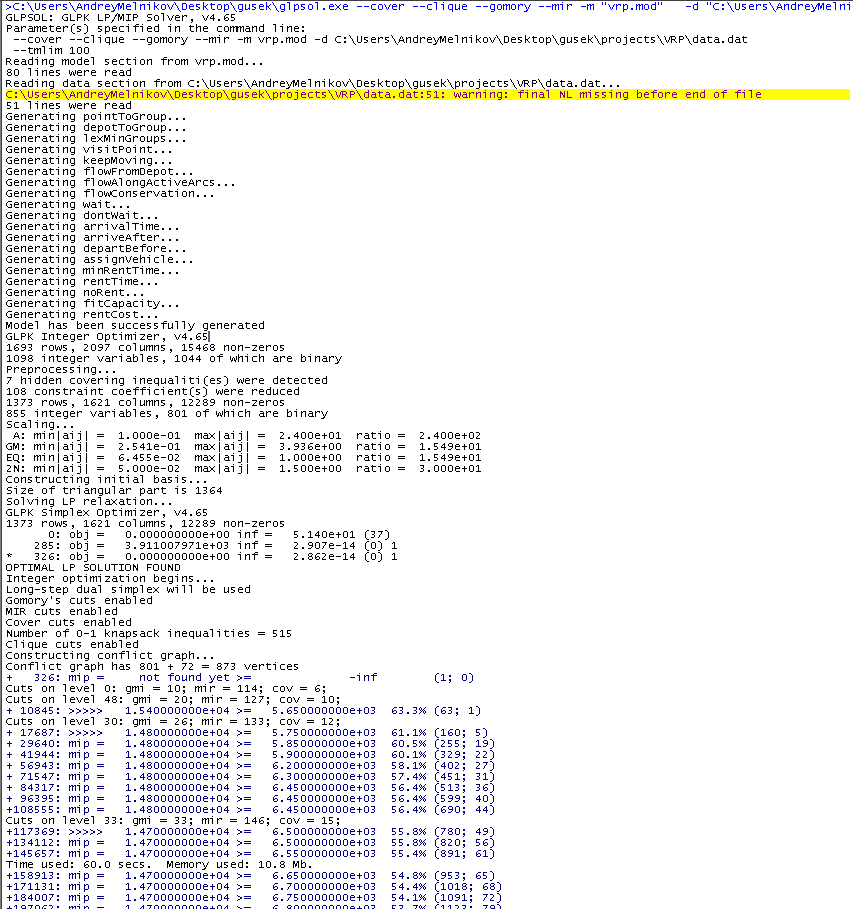
Im blauen Text interessiert uns die Bedeutung nach der Inschrift "mip =". Wie Sie sehen können, nimmt sie von Zeit zu Zeit ab. Alle neuen Lösungen sind in Arbeit, deren bester Wert in dieser Spalte angezeigt wird (bisher sind es 14700). Die nächste Zahl ist die Untergrenze für die beste existierende, d. H. Optimale Lösung. Die Schätzung wird zunächst deutlich unterschätzt, aber im Laufe der Zeit verfeinert, dh erhöht. Die Werte links und rechts konvergieren und die relative Lücke zwischen ihnen zum Zeitpunkt des Screenshots beträgt 54,1%. Sobald diese Zahl Null wird, beweist der Algorithmus, dass die beste gefundene Lösung die bestmögliche ist. Es ist nicht immer gerechtfertigt, in der Praxis auf dieses Ereignis zu warten, und zwar nicht nur, weil es lange dauert, sondern es ist auch wichtig zu reservieren, dass eine gute Lösung in der Regel relativ schnell ist und die Hauptzeitkosten mit der Verfeinerung der Schätzung verbunden sind, die erforderlich ist, um das bestmögliche Ergebnis zu erzielen.

Anstelle einer Schlussfolgerung

Routing-Probleme sind äußerst rechenintensiv, und mit der Zunahme der Anzahl der zu besuchenden Punkte wächst die Zeit, die ein Löser benötigt, um eine Lösung zu finden und seine Optimalität zu beweisen, schnell. Für relativ kleine Beispiele kann der Löser jedoch in angemessener Zeit einen erfolgreichen Satz von Routen erstellen und zur Unterstützung der Entscheidungsfindung verwendet werden. Die Analyse der vom Modell vorgeschlagenen Routing-Optionen hat uns dabei geholfen, signifikante Möglichkeiten zur Kostenreduzierung zu entdecken. Dies ist entscheidend für die Existenz und Entwicklung des Bestands.

Unsere weiteren Bemühungen gingen dahin, mit Unsicherheit in Bezug auf die Menge der an den Punkten gesammelten Wertstoffe zu arbeiten. Wir entwickeln eine Reihe stochastischer Programmiermodelle, um strategische und operative Entscheidungen im Lkw-Routing zu treffen. Wenn sich das Thema als relevant herausstellt und Interesse weckt, werde ich auch darüber schreiben, denn bald müssen wir uns alle wesentlich gründlicher mit Umweltfragen befassen, und ich wünsche uns viel Erfolg.

Logistik der Maßnahme zur getrennten Sammlung von Wertstoffen

Anstatt mitzumachen

1. Die Aktion "Grünes Eichhörnchen"

2. Formalisierung

Suche nach einer Lösung

Anstelle einer Schlussfolgerung

More articles: