Neuronale Netze und tiefes Lernen, Kapitel 1: Verwenden neuronaler Netze zum Erkennen handgeschriebener Zahlen

Hinweis

Hier ist eine Übersetzung von Michael Nielsens kostenlosem Online-Buch Neural Networks and Deep Learning, das unter der Creative Commons Attribution-NonCommercial 3.0 Unported License vertrieben wird . Die Motivation für die Erstellung war die erfolgreiche Erfahrung bei der Übersetzung eines Programmierlehrbuchs, Expressive JavaScript . Das Buch über neuronale Netze ist ebenfalls sehr beliebt, Autoren von englischsprachigen Artikeln zitieren es aktiv. Ich habe ihre Übersetzungen nicht gefunden, außer der Übersetzung des Anfangs des ersten Kapitels mit Abkürzungen .

Wer sich beim Autor des Buches bedanken möchte, kann dies auf seiner offiziellen Seite per Überweisung per PayPal oder Bitcoin tun. Um den Übersetzer auf Habré zu unterstützen, gibt es ein Formular "um den Autor zu unterstützen".

Einführung

In diesem Tutorial erfahren Sie ausführlich über Konzepte wie:

• Neuronale Netze - ein hervorragendes Software-Paradigma, das unter dem Einfluss der Biologie erstellt wurde und es dem Computer ermöglicht, anhand von Beobachtungen zu lernen.
• Deep Learning ist ein leistungsfähiger Satz von Trainingstechniken für neuronale Netze.

Neuronale Netze (NS) und Deep Learning (GO) bieten heute die beste Lösung für viele Probleme in den Bereichen Bilderkennung, Sprache und Verarbeitung natürlicher Sprache. In diesem Tutorial lernen Sie viele der Schlüsselkonzepte kennen, die NS und GO zugrunde liegen.

Worum geht es in diesem Buch?

NS ist eines der besten Software-Paradigmen, die jemals vom Menschen erfunden wurden. Mit einem Standard-Programmieransatz teilen wir dem Computer mit, was zu tun ist, teilen große Aufgaben in viele kleine auf und bestimmen genau die Aufgaben, die der Computer problemlos ausführen kann. Im Falle der Nationalversammlung hingegen sagen wir dem Computer nicht, wie das Problem zu lösen ist. Er selbst lernt dies auf der Grundlage von "Beobachtungen" der Daten und "erfindet" seine eigene Lösung für das Problem.

Automatisiertes datenbasiertes Lernen klingt vielversprechend. Bis 2006 wussten wir jedoch nicht, wie wir die Nationalversammlung so ausbilden sollten, dass sie mit Ausnahme einiger Sonderfälle über die traditionelleren Ansätze hinausgehen konnte. Im Jahr 2006 wurden Trainingstechniken der sogenannten tiefe neuronale Netze (GNS). Jetzt sind diese Techniken als Deep Learning (GO) bekannt. Sie wurden weiterentwickelt, und heute haben GNS und GO bei vielen wichtigen Aufgaben im Zusammenhang mit Computer Vision, Spracherkennung und Verarbeitung natürlicher Sprache erstaunliche Ergebnisse erzielt. In großem Umfang werden sie von Unternehmen wie Google, Microsoft und Facebook bereitgestellt.

Der Zweck dieses Buches ist es, Ihnen zu helfen, die Schlüsselkonzepte neuronaler Netze, einschließlich moderner GO-Techniken, zu beherrschen. Nachdem Sie mit dem Tutorial gearbeitet haben, schreiben Sie einen Code, der NS und GO verwendet, um komplexe Probleme der Mustererkennung zu lösen. Sie haben eine Grundlage für den Einsatz von NS und Zivilschutz bei der Lösung Ihrer eigenen Probleme.

Prinzipbasierter Ansatz

Eine der Überzeugungen, die dem Buch zugrunde liegen, ist, dass es besser ist, ein solides Verständnis der Schlüsselprinzipien der Nationalversammlung und der Zivilgesellschaft zu erlangen, als Wissen aus einer langen Liste verschiedener Ideen zu gewinnen. Wenn Sie die wichtigsten Ideen gut verstehen, werden Sie schnell andere neue Materialien verstehen. In der Sprache des Programmierers können wir sagen, dass wir die grundlegende Syntax, Bibliotheken und Datenstrukturen der neuen Sprache studieren werden. Möglicherweise erkennen Sie nur einen kleinen Teil der gesamten Sprache - viele Sprachen verfügen über immense Standardbibliotheken - Sie können jedoch neue Bibliotheken und Datenstrukturen schnell und einfach verstehen.

Daher ist dieses Buch kategorisch kein Lehrmaterial zur Verwendung einer bestimmten Bibliothek für die Nationalversammlung. Wenn Sie nur lernen möchten, wie man mit der Bibliothek arbeitet, lesen Sie das Buch nicht! Finden Sie die Bibliothek, die Sie benötigen, und arbeiten Sie mit Schulungsunterlagen und Dokumentationen. Aber denken Sie daran: Obwohl dieser Ansatz den Vorteil hat, das Problem sofort zu lösen, reicht es nicht aus, wenn Sie nur verstehen möchten, was genau in der Nationalversammlung geschieht, wenn Sie Ideen beherrschen möchten, die in vielen Jahren relevant sein werden Modebibliothek. Sie müssen die verlässlichen und langfristigen Ideen verstehen, die der Arbeit der Nationalversammlung zugrunde liegen. Technologie kommt und geht und Ideen halten ewig.

Praktischer Ansatz

Wir werden die Grundprinzipien am Beispiel einer bestimmten Aufgabe untersuchen: einem Computer das Erkennen handgeschriebener Zahlen beibringen. Mit herkömmlichen Programmieransätzen ist diese Aufgabe äußerst schwer zu lösen. Wir können es jedoch recht gut mit einem einfachen NS und mehreren Dutzend Codezeilen ohne spezielle Bibliotheken lösen. Darüber hinaus werden wir dieses Programm schrittweise verbessern und dabei immer mehr Schlüsselideen zur Nationalversammlung und zum Zivilschutz einbeziehen.

Dieser praktische Ansatz bedeutet, dass Sie einige Programmiererfahrung benötigen. Sie müssen jedoch kein professioneller Programmierer sein. Ich habe Python-Code (Version 2.7) geschrieben, der auch dann klar sein sollte, wenn Sie keine Python-Programme geschrieben haben. Während des Studiums erstellen wir eine eigene Bibliothek für die Nationalversammlung, die Sie für Experimente und Weiterbildungen verwenden können. Der gesamte Code kann hier heruntergeladen werden . Wenn Sie das Buch fertiggestellt haben oder gerade lesen, können Sie eine der vollständigeren Bibliotheken für die Nationalversammlung auswählen, die für die Verwendung in diesen Projekten angepasst sind.

Die mathematischen Anforderungen zum Verständnis des Materials sind recht durchschnittlich. Die meisten Kapitel haben mathematische Teile, aber normalerweise sind es elementare Algebra- und Funktionsgraphen. Manchmal verwende ich fortgeschrittenere Mathematik, aber ich habe das Material so strukturiert, dass Sie es verstehen können, auch wenn Ihnen einige Details entgehen. Der größte Teil der Mathematik wird in Kapitel 2 verwendet, das ein wenig Matanalyse und lineare Algebra erfordert. Für diejenigen, denen sie nicht vertraut sind, beginne ich Kapitel 2 mit einer Einführung in die Mathematik. Wenn Sie Schwierigkeiten haben, überspringen Sie einfach das Kapitel bis zur Nachbesprechung. Mach dir auf keinen Fall Sorgen.

Ein Buch ist selten gleichzeitig auf ein Verständnis der Prinzipien und einen praktischen Ansatz ausgerichtet. Ich glaube jedoch, dass es besser ist, auf der Grundlage der Grundgedanken der Nationalversammlung zu studieren. Wir werden Arbeitscode schreiben und nicht nur abstrakte Theorie studieren, sondern Sie können diesen Code untersuchen und erweitern. Auf diese Weise verstehen Sie die Grundlagen, sowohl Theorie als auch Praxis, und können weiter lernen.

Übungen und Aufgaben

Autoren technischer Bücher warnen den Leser oft, dass er einfach alle Übungen absolvieren und alle Probleme lösen muss. Wenn ich solche Warnungen vorlese, wirken sie immer etwas seltsam. Wird mir etwas Schlimmes passieren, wenn ich keine Übungen mache und Probleme löse? Nein, natürlich. Ich werde nur durch weniger tiefes Verständnis Zeit sparen. Manchmal lohnt es sich. Manchmal nicht.

Was ist es wert, mit diesem Buch gemacht zu werden? Ich rate Ihnen, die meisten Übungen zu absolvieren, aber nicht die meisten Aufgaben zu lösen.

Die meisten Übungen müssen abgeschlossen werden, da dies grundlegende Überprüfungen für ein angemessenes Verständnis des Materials sind. Wenn Sie die Übung nicht relativ einfach durchführen können, müssen Sie etwas Grundlegendes übersehen haben. Natürlich, wenn Sie wirklich in irgendeiner Art von Übung stecken - lassen Sie es fallen, vielleicht ist dies eine Art kleines Missverständnis, oder vielleicht habe ich etwas schlecht formuliert. Wenn Ihnen die meisten Übungen jedoch Schwierigkeiten bereiten, müssen Sie das vorherige Material höchstwahrscheinlich erneut lesen.

Aufgaben sind eine andere Sache. Sie sind schwieriger als Übungen, und mit einigen werden Sie es schwer haben. Das ist ärgerlich, aber natürlich ist Geduld angesichts einer solchen Enttäuschung der einzige Weg, das Thema wirklich zu verstehen und aufzunehmen.

Ich empfehle daher nicht, alle Probleme zu lösen. Besser noch - holen Sie sich Ihr eigenes Projekt. Möglicherweise möchten Sie NS verwenden, um Ihre Musiksammlung zu klassifizieren. Oder um den Wert von Aktien vorherzusagen. Oder etwas anderes. Aber finden Sie ein interessantes Projekt für Sie. Und dann können Sie die Aufgaben aus dem Buch ignorieren oder sie lediglich als Inspiration für die Arbeit an Ihrem Projekt verwenden. Bei Problemen mit Ihrem eigenen Projekt lernen Sie mehr als nur mit einer beliebigen Anzahl von Aufgaben zu arbeiten. Emotionales Engagement ist ein Schlüsselfaktor für die Meisterleistung.

Natürlich, obwohl Sie vielleicht kein solches Projekt haben. Es ist in Ordnung. Lösen Sie Aufgaben, für die Sie eine intrinsische Motivation empfinden. Verwenden Sie Material aus dem Buch, um Ideen für persönliche kreative Projekte zu finden.

Kapitel 1

Das menschliche visuelle System ist eines der Weltwunder. Betrachten Sie die folgende Folge handgeschriebener Zahlen:



Die meisten Leute werden sie leicht lesen, wie 504192. Aber diese Einfachheit täuscht. In jeder Gehirnhälfte hat eine Person einen primären visuellen Kortex , auch als V1 bekannt, der 140 Millionen Neuronen und zig Milliarden Verbindungen zwischen ihnen enthält. Gleichzeitig ist nicht nur V1 am menschlichen Sehen beteiligt, sondern eine ganze Reihe von Gehirnregionen - V2, V3, V4 und V5 -, die an einer immer komplexer werdenden Bildverarbeitung beteiligt sind. Wir haben einen Supercomputer in unseren Köpfen, der seit Hunderten von Millionen von Jahren von der Evolution abgestimmt und perfekt darauf ausgelegt ist, die sichtbare Welt zu verstehen. Das Erkennen handgeschriebener Zahlen ist nicht so einfach. Es ist nur so, dass wir Menschen erstaunlicherweise überraschend gut erkennen, was unsere Augen uns zeigen. Aber fast alle diese Arbeiten werden unbewusst ausgeführt. Und normalerweise legen wir keinen Wert darauf, welche schwierige Aufgabe unsere visuellen Systeme lösen.

Die Schwierigkeit, visuelle Muster zu erkennen, wird deutlich, wenn Sie versuchen, ein Computerprogramm zu schreiben, um Zahlen wie die oben genannten zu erkennen. Was in unserer Ausführung einfach erscheint, erweist sich plötzlich als äußerst komplex. Das einfache Konzept, wie wir die Formen erkennen - „die Neun hat oben eine Schleife und unten rechts den vertikalen Balken“ - ist für einen algorithmischen Ausdruck gar nicht so einfach. Wenn Sie versuchen, diese Regeln klar zu formulieren, geraten Sie schnell in einen Sumpf von Ausnahmen, Fallstricken und besonderen Anlässen. Die Aufgabe scheint hoffnungslos.

NS-Ansatz zur Lösung des Problems auf andere Weise. Die Idee ist, die vielen handgeschriebenen Zahlen zu nehmen, die als Lehrbeispiele bekannt sind.



und entwickeln Sie ein System, das aus diesen Beispielen lernen kann. Mit anderen Worten, die Nationalversammlung verwendet Beispiele, um automatisch handschriftliche Regeln zur Erkennung von Ziffern zu erstellen. Darüber hinaus kann das Netzwerk durch Erhöhen der Anzahl von Trainingsbeispielen mehr über handschriftliche Zahlen erfahren und deren Genauigkeit verbessern. Obwohl ich oben nur 100 Fallstudien zitiert habe, können wir vielleicht ein besseres Handschrifterkennungssystem mit Tausenden oder sogar Millionen und Milliarden von Fallstudien erstellen.

In diesem Kapitel werden wir ein Computerprogramm schreiben, das das NS-Lernen zum Erkennen handgeschriebener Zahlen implementiert. Das Programm wird nur 74 Zeilen lang sein und keine speziellen Bibliotheken für die Nationalversammlung verwenden. Dieses kurze Programm kann jedoch handschriftliche Zahlen mit einer Genauigkeit von mehr als 96% erkennen, ohne dass ein menschliches Eingreifen erforderlich ist. Darüber hinaus werden wir in zukünftigen Kapiteln Ideen entwickeln, mit denen die Genauigkeit auf 99% oder mehr verbessert werden kann. Tatsächlich leisten die besten kommerziellen NS so gute Arbeit, dass sie von Banken zur Bearbeitung von Schecks und von der Post zur Erkennung von Adressen verwendet werden.

Wir konzentrieren uns auf die Erkennung von Handschriften, da dies ein großartiger Prototyp einer Aufgabe zum Studium von NS ist. Ein solcher Prototyp ist ideal für uns: Es ist eine schwierige Aufgabe (das Erkennen handgeschriebener Zahlen ist keine leichte Aufgabe), aber nicht so kompliziert, dass eine äußerst komplexe Lösung oder immense Rechenleistung erforderlich ist. Darüber hinaus ist dies eine großartige Möglichkeit, komplexere Techniken wie GO zu entwickeln. Daher werden wir in dem Buch ständig auf die Aufgabe der Handschrifterkennung zurückkommen. Später werden wir diskutieren, wie diese Ideen auf andere Aufgaben des Computer-Sehens, auf die Spracherkennung, die Verarbeitung natürlicher Sprache und andere Bereiche angewendet werden können.

Wenn der Zweck dieses Kapitels nur darin bestand, ein Programm zum Erkennen handgeschriebener Zahlen zu schreiben, wäre das Kapitel natürlich viel kürzer! Dabei werden wir jedoch viele Schlüsselideen im Zusammenhang mit NS entwickeln, darunter zwei wichtige Arten von künstlichen Neuronen ( Perzeptron und Sigmoidneuron) und den Standard-NS-Lernalgorithmus, den stochastischen Gradientenabstieg . Im Text konzentriere ich mich darauf, zu erklären, warum alles so gemacht wird, und Ihr Verständnis der Nationalversammlung zu formen. Dies erfordert ein längeres Gespräch, als wenn ich nur die grundlegenden Mechanismen des Geschehens vorgestellt hätte, aber es kostet ein tieferes Verständnis, das Sie haben werden. Unter anderem - am Ende des Kapitels werden Sie verstehen, was ein Zivilschutz ist und warum er so wichtig ist.

Perceptrons

Was ist ein neuronales Netzwerk? Zunächst werde ich über eine Art künstliches Neuron sprechen, das Perzeptron. Perceptrons wurden in den 1950er und 60er Jahren vom Wissenschaftler Frank Rosenblatt erfunden, inspiriert von den frühen Arbeiten von Warren McCallock und Walter Pitts . Heutzutage werden andere Modelle künstlicher Neuronen häufiger verwendet - in diesem Buch, und die meisten modernen Arbeiten zu NS verwenden hauptsächlich das Sigmoidmodell des Neurons. Wir werden sie bald treffen. Um zu verstehen, warum Sigmoidneuronen auf diese Weise definiert werden, lohnt es sich, Zeit mit der Analyse des Perzeptrons zu verbringen.

Wie funktionieren Perzeptrone? Das Perzeptron empfängt mehrere Binärzahlen x ₁ , x ₂ , ... und gibt eine Binärzahl an:



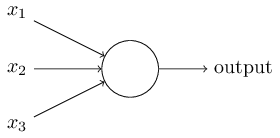
In diesem Beispiel hat das Perzeptron drei Eingangsnummern, x ₁ , x ₂ , x ₃ . Im Allgemeinen kann es mehr oder weniger davon geben. Rosenblatt schlug eine einfache Regel zur Berechnung des Ergebnisses vor. Er führte Gewichte w ₁ , w ₂ und reelle Zahlen ein und drückte die Bedeutung der entsprechenden Eingabezahlen für die Ergebnisse aus. Die Ausgabe eines Neurons, 0 oder 1, wird dadurch bestimmt, ob eine gewichtete Summe kleiner oder größer als ein bestimmter Schwellenwert ist [Schwellenwert] $$$\ sum_j w_jx_j$ . Wie Gewichte ist der Schwellenwert eine reelle Zahl, ein Parameter eines Neurons. In mathematischen Begriffen:

$$

$$output = \ begin {Fälle} 0 ~ if ~ \ sum_j w_jx_j \ leq Schwelle \\ 1 ~ wenn ~ \ sum_j w_jx_j> Schwelle \ Ende {Fälle} \ tag {1}$$

Das ist die ganze Beschreibung des Perzeptrons!

Dies ist das grundlegende mathematische Modell. Ein Perzeptron kann als Entscheidungsträger betrachtet werden, indem Beweise abgewogen werden. Lassen Sie mich Ihnen ein nicht sehr realistisches, aber einfaches Beispiel geben. Nehmen wir an, das Wochenende steht vor der Tür und Sie haben gehört, dass in Ihrer Stadt ein Käsefestival stattfinden wird. Du magst Käse und versuchst zu entscheiden, ob du zum Festival gehst oder nicht. Sie können eine Entscheidung treffen, indem Sie drei Faktoren abwägen:

1. Ist das Wetter gut?
2. Möchte Ihr Partner mit Ihnen gehen?
3. Ist das Festival weit entfernt von öffentlichen Verkehrsmitteln? (Du hast kein Auto)

Diese drei Faktoren können als binäre Variablen x ₁ , x ₂ , x _{3 dargestellt werden} . Zum Beispiel x ₁ = 1, wenn das Wetter gut ist, und 0, wenn es schlecht ist. x ₂ = 1, wenn Ihr Partner gehen möchte, und 0, wenn nicht. Gleiches gilt für x ₃ .

Nehmen wir an, Sie sind so ein Fan von Käse, dass Sie bereit sind, zum Festival zu gehen, auch wenn Ihr Partner nicht daran interessiert ist und es schwierig ist, dorthin zu gelangen. Aber vielleicht hasst du nur schlechtes Wetter und bei schlechtem Wetter gehst du nicht zum Festival. Sie können Perzeptrone verwenden, um einen solchen Entscheidungsprozess zu modellieren. Eine Möglichkeit besteht darin, das Gewicht w ₁ = 6 für das Wetter und w ₂ = 2, w ₃ = 2 für andere Bedingungen zu wählen. Ein größerer Wert von w ₁ bedeutet, dass das Wetter für Sie viel wichtiger ist als die Frage, ob Ihr Partner zu Ihnen kommt oder die Nähe des Festivals zu einem Zwischenstopp. Angenommen, Sie wählen den Schwellenwert 5 für das Perzeptron. Mit diesen Optionen implementiert das Perzeptron das gewünschte Entscheidungsmodell und gibt 1 bei gutem Wetter und 0 bei schlechtem Wetter. Der Wunsch des Partners und die Nähe des Anschlags beeinflussen den Ausgabewert nicht.

Durch Ändern von Gewichten und Schwellenwerten können wir verschiedene Entscheidungsmodelle erhalten. Nehmen wir zum Beispiel die Schwelle 3. Dann entscheidet das Perzeptron, dass Sie zum Festival gehen müssen, entweder bei schönem Wetter oder wenn sich das Festival in der Nähe einer Bushaltestelle befindet und Ihr Partner sich bereit erklärt, mit Ihnen zu gehen. Mit anderen Worten, das Modell ist anders. Wenn Sie die Schwelle senken, möchten Sie mehr zum Festival gehen.

Offensichtlich ist das Perzeptron kein vollständiges menschliches Entscheidungsmodell! Dieses Beispiel zeigt jedoch, wie ein Perzeptron verschiedene Arten von Beweisen abwägen kann, um Entscheidungen zu treffen. Es scheint möglich, dass ein komplexes Netzwerk von Perzeptronen sehr komplexe Entscheidungen treffen kann:



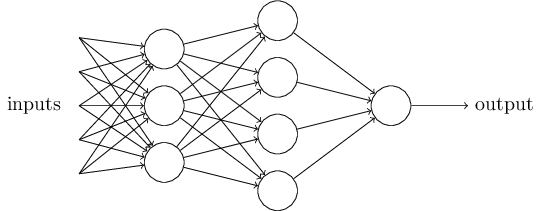
In diesem Netzwerk trifft die erste Spalte von Perzeptronen - was wir die erste Schicht von Perzeptronen nennen - drei sehr einfache Entscheidungen, wobei die eingegebenen Beweise abgewogen werden. Was ist mit Perzeptronen aus der zweiten Schicht? Jeder von ihnen trifft eine Entscheidung und wägt die Ergebnisse der ersten Entscheidungsebene ab. Auf diese Weise kann das Perzeptron der zweiten Schicht eine Entscheidung auf einer komplexeren und abstrakteren Ebene treffen als das Perzeptron der ersten Schicht. Und noch komplexere Entscheidungen können von Perzeptronen auf der dritten Ebene getroffen werden.Auf diese Weise kann ein mehrschichtiges Netzwerk von Perzeptronen komplexe Entscheidungen treffen.

Als ich das Perzeptron bestimmte, sagte ich übrigens, dass es nur einen Ausgabewert hat. Im oberen Netzwerk sehen die Perzeptrone jedoch so aus, als hätten sie mehrere Ausgabewerte. Tatsächlich haben sie nur einen Ausweg. Viele Ausgabepfeile sind nur eine bequeme Möglichkeit, um zu zeigen, dass die Ausgabe des Perzeptrons als Eingabe mehrerer anderer Perzeptrone verwendet wird. Dies ist weniger umständlich als das Zeichnen eines einzelnen Verzweigungsausgangs.

Vereinfachen wir die Beschreibung von Perzeptronen. Zustand$$$\sum_j w_jx_j > treshold$ungeschickt, und wir können uns auf zwei Änderungen am Datensatz einigen, um ihn zu vereinfachen. Das erste ist aufzunehmen$$$\sum_j w_jx_j$ als skalares Produkt, $$$w \cdot x = \sum_j w_jx_j$wobei w und x Vektoren sind, deren Komponenten Gewichte bzw. Eingabedaten sind. Die zweite besteht darin, die Schwelle auf einen anderen Teil der Ungleichung zu übertragen und durch einen Wert zu ersetzen, der als Perzeptronverschiebung [Bias] bekannt ist.$$$b \equiv −threshold$ . Wenn wir die Verschiebung anstelle eines Schwellenwerts verwenden, können wir die Perzeptronregel neu schreiben:

$$

$$output = \begin{cases} 0 ~ if ~ w \cdot x + b \leq 0 \\ 1 ~ if ~ w \cdot x + b > 0 \end{cases} \tag{2}$$

Der Versatz kann als Maß dafür dargestellt werden, wie einfach es ist, am Ausgang des Perzeptrons einen Wert von 1 zu erhalten. In biologischer Hinsicht ist die Verschiebung ein Maß dafür, wie einfach es ist, das Perzeptron zur Aktivierung zu bringen. Ein Perzeptron mit einer sehr großen Vorspannung ist extrem einfach zu geben 1. Bei einer sehr großen negativen Vorspannung ist dies jedoch schwierig. Offensichtlich ist die Einführung von Bias eine kleine Änderung in der Beschreibung von Perzeptronen, aber später werden wir sehen, dass dies zu einer weiteren Vereinfachung der Aufzeichnung führt. Daher werden wir weiterhin nicht den Schwellenwert verwenden, sondern immer den Offset.

Ich habe Perzeptrone im Hinblick auf die Methode zum Abwägen von Beweisen für die Entscheidungsfindung beschrieben. Eine andere Methode ihrer Verwendung ist die Berechnung elementarer logischer Funktionen, die wir normalerweise als Hauptberechnungen betrachten, wie z. B. AND, OR und NAND. Nehmen wir zum Beispiel an, wir haben ein Perzeptron mit zwei Eingängen, deren Gewicht jeweils -2 beträgt und dessen Versatz 3 beträgt. Hier ist es: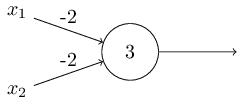



Eingang 00 ergibt Ausgang 1, weil (−2) ∗ 0 + (- 2 ) ∗ 0 + 3 = 3 ist größer als Null. Dieselben Berechnungen besagen, dass die Eingänge 01 und 10 1 ergeben. Aber 11 am Eingang ergibt 0 am Ausgang, da (−2) ∗ 1 + (- 2) ∗ 1 + 3 = −1, kleiner als Null. Daher implementiert unser Perzeptron die NAND-Funktion!

Dieses Beispiel zeigt, dass Perzeptrone verwendet werden können, um grundlegende Logikfunktionen zu berechnen. Tatsächlich können wir Perzeptron-Netzwerke verwenden, um alle logischen Funktionen im Allgemeinen zu berechnen. Tatsache ist, dass das NAND- Logikgatter universell für Berechnungen ist - es ist möglich, beliebige Berechnungen auf seiner Basis zu erstellen. Beispielsweise können Sie NAND-Gatter verwenden, um eine Schaltung zu erstellen, die zwei Bits x ₁ und x ₂ hinzufügt . Berechnen Sie dazu die bitweise Summe$$$x_1 \oplus x_2$sowie das Übertragsflag , das 1 ist, wenn sowohl x ₁ als auch x ₂ 1 sind - das heißt, das Übertragsflag ist einfach das Ergebnis der bitweisen Multiplikation x ₁ x ₂ :



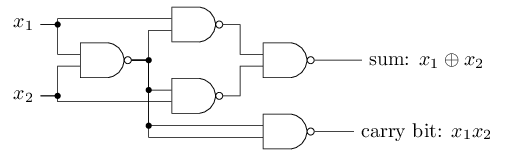Um das äquivalente Netzwerk von Perzeptronen zu erhalten, ersetzen wir alle NAND-Gatter durch Perzeptrone durch zwei Eingaben, deren Gewicht jeweils -2 beträgt, und mit einem Versatz von 3. Hier ist das resultierende Netzwerk. Beachten Sie, dass ich das Perzeptron entsprechend dem unteren rechten Ventil bewegt habe, um das Zeichnen von Pfeilen zu vereinfachen:



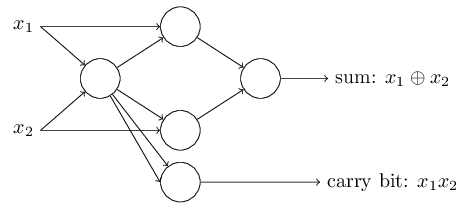Ein bemerkenswerter Aspekt dieses Perzeptron-Netzwerks ist, dass der Ausgang des am weitesten links stehenden zweimal als Eingang nach unten verwendet wird. Als ich das Modell des Perzeptrons definierte, erwähnte ich nicht die Zulässigkeit eines solchen Doppelausgangsschemas an derselben Stelle. In der Tat ist es nicht wirklich wichtig. Wenn wir dies nicht zulassen möchten, können wir einfach zwei Zeilen mit einer Gewichtung von -2 zu einer mit einer Gewichtung von -4 kombinieren. (Wenn Ihnen dies nicht offensichtlich erscheint, hören Sie auf und beweisen Sie es sich selbst). Nach dieser Änderung sieht das Netzwerk wie folgt aus: Alle nicht zugewiesenen Gewichte sind gleich -2, alle Offsets sind gleich 3 und ein Gewicht -4 ist markiert:



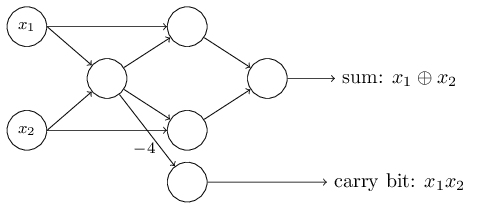Eine solche Aufzeichnung von Perzeptronen, die eine Ausgabe, aber keine Eingaben haben:



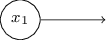ist nur eine Abkürzung. Dies bedeutet nicht, dass er keine Eingaben hat. Um dies zu verstehen, nehmen wir an, wir haben ein Perzeptron ohne Eingaben. Dann wäre die gewichtete Summe ∑ _j w _j x _j immer Null, also würde das Perzeptron 1 für b> 0 und 0 für b ≤ 0 geben. Das heißt, das Perzeptron würde nur einen festen Wert geben und nicht das, was wir brauchen (x ₁ im Beispiel) oben). Es ist besser, die eingegebenen Perzeptrone nicht als Perzeptrone zu betrachten, sondern als spezielle Einheiten, die einfach definiert werden, um die gewünschten Werte x ₁ , x ₂ , ... zu erzeugen.

Das Addiererbeispiel zeigt, wie ein Perzeptron-Netzwerk verwendet werden kann, um eine Schaltung zu simulieren, die viele NAND-Gatter enthält. Und da diese Tore für Berechnungen universell sind, sind Perzeptrone für Berechnungen universell.

Die rechnerische Vielseitigkeit von Perzeptronen ist sowohl ermutigend als auch enttäuschend. Es ist ermutigend sicherzustellen, dass das Perzeptron-Netzwerk genauso leistungsfähig ist wie jedes andere Computergerät. Enttäuschend, was den Eindruck erweckt, dass Perzeptrone nur eine neue Art von NAND-Logikgatter sind. So lala Entdeckung!

Die Situation ist jedoch tatsächlich besser. Es stellt sich heraus, dass wir Trainingsalgorithmen entwickeln können, mit denen die Gewichte und Verschiebungen des Netzwerks von künstlichen Neuronen automatisch angepasst werden können. Diese Anpassung erfolgt als Reaktion auf externe Reize, ohne dass ein Programmierer direkt eingreifen muss. Diese Lernalgorithmen ermöglichen es uns, künstliche Neuronen auf eine Weise zu verwenden, die sich radikal von gewöhnlichen Logikgattern unterscheidet. Anstatt eine Schaltung explizit von NAND-Gattern und anderen zu registrieren, können unsere neuronalen Netze einfach lernen, wie man Probleme löst, manchmal solche, für die es äußerst schwierig wäre, eine reguläre Schaltung direkt zu entwerfen.

Sigmoidneuronen

Lernalgorithmen sind großartig. Wie kann man jedoch einen solchen Algorithmus für ein neuronales Netzwerk entwickeln? Angenommen, wir haben ein Netzwerk von Perzeptronen, mit denen wir uns in der Lösung eines Problems schulen möchten. Angenommen, die Eingabe in das Netzwerk kann Pixel eines gescannten Bildes einer handgeschriebenen Ziffer sein. Und wir möchten, dass das Netzwerk die Gewichte und Offsets kennt, die zur korrekten Klassifizierung der Zahlen erforderlich sind. Um zu verstehen, wie ein solches Training funktionieren kann, stellen wir uns vor, dass wir ein bestimmtes Gewicht (oder eine bestimmte Tendenz) im Netzwerk geringfügig ändern. Wir möchten, dass diese kleine Änderung zu einer kleinen Änderung der Netzwerkleistung führt. Wie wir bald sehen werden, ermöglicht diese Eigenschaft das Lernen. Schematisch wollen wir Folgendes (offensichtlich ist ein solches Netzwerk zu einfach, um Handschrift zu erkennen!):



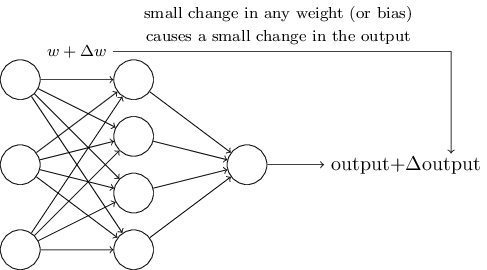
Wenn eine kleine Änderung des Gewichts (oder der Verzerrung) zu einer kleinen Änderung des Ausgabeergebnisses führen würde, könnten wir die Gewichte und Verzerrungen so ändern, dass sich unser Netzwerk ein wenig näher an dem verhält, was wir wollen. Nehmen wir zum Beispiel an, das Netzwerk hat das Bild fälschlicherweise "8" zugewiesen, obwohl es "9" hätte sein sollen. Wir könnten herausfinden, wie eine kleine Änderung des Gewichts und der Verschiebung vorgenommen werden kann, damit das Netzwerk der Klassifizierung des Bildes als „9“ ein Stück näher kommt. Und dann würden wir dies wiederholen und immer wieder Gewichte und Verschiebungen ändern, um das beste und beste Ergebnis zu erzielen. Das Netzwerk würde lernen.

Das Problem ist, dass dies nicht der Fall ist, wenn sich Perzeptrone im Netzwerk befinden. Eine kleine Änderung der Gewichte oder der Verschiebung eines Perzeptrons kann manchmal zu einer Änderung seiner Ausgabe in das Gegenteil führen, beispielsweise von 0 auf 1. Ein solcher Flip kann das Verhalten des restlichen Netzwerks auf sehr komplizierte Weise ändern. Und selbst wenn jetzt unsere „9“ richtig erkannt wird, hat sich das Verhalten des Netzwerks mit allen anderen Bildern wahrscheinlich auf eine schwer zu kontrollierende Weise vollständig geändert. Aus diesem Grund ist es schwer vorstellbar, wie wir Gewichte und Offsets schrittweise anpassen können, damit sich das Netzwerk allmählich dem gewünschten Verhalten nähert. Vielleicht gibt es einen klugen Weg, um dieses Problem zu umgehen. Es gibt jedoch keine einfache Lösung für das Problem, ein Netzwerk von Perzeptronen zu lernen.

Dieses Problem kann umgangen werden, indem ein neuer Typ eines künstlichen Neurons namens Sigmoid-Neuron eingeführt wird. Sie ähneln Perzeptronen, sind jedoch so modifiziert, dass kleine Änderungen der Gewichte und Offsets nur zu geringen Änderungen der Ausgabe führen. Dies ist eine grundlegende Tatsache, die es dem Netzwerk von Sigmoidneuronen ermöglicht, zu lernen.

Lassen Sie mich ein Sigmoid-Neuron beschreiben. Wir werden sie auf die gleiche Weise wie Perzeptrone zeichnen:



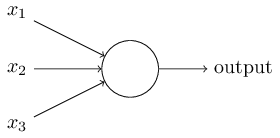
Es hat den gleichen Eingang x ₁ , x ₂ , ... Aber anstatt gleich 0 oder 1 zu sein, können diese Eingänge einen beliebigen Wert im Bereich von 0 bis 1 haben. Beispielsweise ist ein Wert von 0,638 eine gültige Eingabe für Sigmoidneuron (CH). Genau wie das Perzeptron hat SN Gewichte für jeden Eingang, w ₁ , w ₂ , ... und die Gesamtvorspannung b. Sein Ausgabewert ist jedoch nicht 0 oder 1. Es ist σ (w⋅x + b), wobei σ das Sigmoid ist.

Übrigens wird σ manchmal als logistische Funktion bezeichnet , und diese Klasse von Neuronen wird als logistische Neuronen bezeichnet. Es ist nützlich, sich an diese Terminologie zu erinnern, da diese Begriffe von vielen Menschen verwendet werden, die mit neuronalen Netzen arbeiten. Wir werden uns jedoch an die Sigmoid-Terminologie halten.

Die Funktion ist wie folgt definiert:

$$

$$\ sigma (z) \ equiv \ frac {1} {1 + e ^ {- z}} \ tag {3}$$

In unserem Fall wird der Ausgabewert des Sigmoidneurons mit den Eingabedaten x ₁ , x ₂ , ... durch die Gewichte w ₁ , w ₂ , ... und den Versatz b wie folgt betrachtet:

$$

$$\ frac {1} {1 + exp (- \ sum_j w_jx_j - b)} \ tag {4}$$

Auf den ersten Blick scheint CH völlig anders zu sein als Neuronen. Das algebraische Aussehen eines Sigmoid kann verwirrend und dunkel erscheinen, wenn Sie nicht damit vertraut sind. Tatsächlich gibt es viele Ähnlichkeiten zwischen Perzeptronen und SN, und die algebraische Form eines Sigmoid erweist sich eher als technisches Detail als als ernstes Hindernis für das Verständnis.

Um die Ähnlichkeiten zum Perzeptronmodell zu verstehen, nehmen wir an, dass z ≡ w ⋅ x + b eine große positive Zahl ist. Dann ist e - z ≤ 0, daher ist σ (z) ≤ 1. Mit anderen Worten, wenn z = w ≤ x + b groß und positiv ist, beträgt die SN-Ausbeute ungefähr 1, wie im Perzeptron. Angenommen, z = w ⋅ x + b ist groß mit einem Minuszeichen. Dann ist e - z → ∞ und σ (z) ≈ 0. Für großes z mit einem Minuszeichen nähert sich das Verhalten des SN also auch dem Perzeptron. Und nur wenn w ⋅ x + b eine durchschnittliche Größe hat, werden gravierende Abweichungen vom Perzeptronmodell beobachtet.

Was ist mit der algebraischen Form von σ? Wie verstehen wir ihn? Tatsächlich ist die genaue Form von σ nicht so wichtig - die Form der Funktion im Diagramm ist wichtig. Da ist sie:



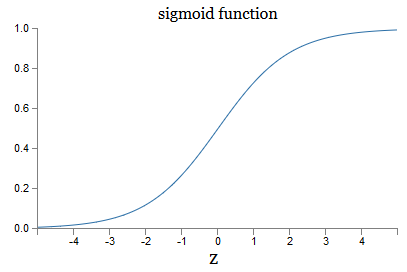
Dies ist eine reibungslose Version der Schrittfunktion:



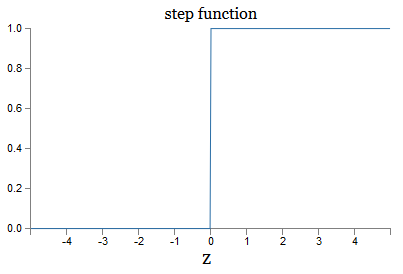
Wenn σ schrittweise wäre, wäre das SN ein Perzeptron, da es abhängig vom Vorzeichen w ⋅ x + b 0 oder 1 Ausgang haben würde (tatsächlich ergibt das Perzeptron bei z = 0 0 und die Schrittfunktion - 1 an diesem Punkt müsste also die Funktion geändert werden).

Mit der reellen Funktion σ erhalten wir ein geglättetes Perzeptron. Und die Hauptsache hier ist die Glätte der Funktion, nicht ihre genaue Form. Glätte bedeutet, dass kleine Änderungen der Δw _j -Gewichte und δb-Offsets kleine Änderungen der Δ-Ausgabe des Ausgangs ergeben. Die Algebra sagt uns, dass die Δ-Ausgabe wie folgt gut angenähert ist:

$$

$$\ Delta output \ approx \ sum_j \ frac {\ partielle Ausgabe} {\ partielle w_j} \ Delta w_j + \ frac {\ partielle Ausgabe} {\ partielle b} \ Delta b \ tag {5}$$

Wenn die Summation über allen Gewichten w _j liegt und ∂output / ∂w _j und ∂output / ∂b die partiellen Ableitungen der Ausgabe in Bezug auf w _j bzw. b bezeichnen. Keine Panik, wenn Sie sich in der Gesellschaft privater Derivate unsicher fühlen! Obwohl die Formel mit all diesen partiellen Ableitungen kompliziert aussieht, sagt sie tatsächlich etwas ganz Einfaches (und Nützliches) aus: Δoutput ist eine lineare Funktion, die von den Gewichten und Vorspannungen von Δw _j und Δb abhängt. Seine Linearität macht es einfach, kleine Änderungen der Gewichte und Offsets auszuwählen, um jede gewünschte kleine Ausgangsvorspannung zu erzielen. Obwohl SNs im qualitativen Verhalten Perzeptronen ähnlich sind, erleichtern sie das Verständnis, wie die Ausgabe durch Ändern von Gewichten und Verschiebungen geändert werden kann.

Wenn die allgemeine Form σ für uns wichtig ist und nicht ihre genaue Form, warum verwenden wir dann eine solche Formel (3)? Tatsächlich werden wir später manchmal Neuronen betrachten, deren Ausgabe f (w ⋅ x + b) ist, wobei f () eine andere Aktivierungsfunktion ist. Die Hauptsache, die sich ändert, wenn sich die Funktion ändert, ist der Wert der partiellen Ableitungen in Gleichung (5). Es stellt sich heraus, dass die Verwendung von σ bei der Berechnung dieser partiellen Ableitungen die Algebra erheblich vereinfacht, da Exponenten bei der Differenzierung sehr schöne Eigenschaften haben. In jedem Fall wird σ häufig bei der Arbeit mit neuronalen Netzen verwendet, und am häufigsten wird in diesem Buch eine solche Aktivierungsfunktion verwendet.

Wie ist das Ergebnis der Arbeit von CH zu interpretieren? Offensichtlich besteht der Hauptunterschied zwischen den Perzeptronen und dem CH darin, dass der CH nicht nur 0 oder 1 ausgibt. Ihre Ausgabe kann eine beliebige reelle Zahl von 0 bis 1 sein, sodass Werte wie 0,173 oder 0,689 gültig sind. Dies kann beispielsweise nützlich sein, wenn der Ausgabewert beispielsweise die durchschnittliche Helligkeit der Pixel des am Eingang des NS empfangenen Bildes anzeigen soll. Aber manchmal kann es unpraktisch sein. Angenommen, die Netzwerkausgabe soll sagen, dass "Bild 9 eingegeben wurde" oder "Eingabebild nicht 9". Offensichtlich wäre es einfacher, wenn die Ausgabewerte 0 oder 1 wären, wie bei einem Perzeptron. In der Praxis können wir uns jedoch darauf einigen, dass ein Ausgabewert von mindestens 0,5 am Eingang „9“ und ein Wert unter 0,5 „nicht 9“ bedeutet. Ich werde immer ausdrücklich auf das Bestehen solcher Vereinbarungen hinweisen.

Übungen

• CH simuliert Perzeptrone, Teil 1

Angenommen, wir nehmen alle Gewichte und Offsets aus einem Netzwerk von Perzeptronen und multiplizieren sie mit einer positiven Konstante c> 0. Zeigen Sie, dass sich das Netzwerkverhalten nicht ändert.

• CH simuliert Perzeptrone, Teil 2

Nehmen wir an, wir haben die gleiche Situation wie im vorherigen Problem - ein Netzwerk von Perzeptronen. Angenommen, die Eingabedaten für das Netzwerk sind ausgewählt. Wir brauchen keinen bestimmten Wert, die Hauptsache ist, dass er fest ist. Angenommen, die Gewichte und Verschiebungen sind so, dass w⋅x + b ≠ 0 ist, wobei x der Eingabewert eines beliebigen Perzeptrons des Netzwerks ist. Jetzt ersetzen wir alle Perzeptrone im Netzwerk durch SN und multiplizieren die Gewichte und Verschiebungen mit der positiven Konstante c> 0. Zeigen Sie, dass im Grenzwert c → ∞ das Verhalten des Netzwerks vom SN genau das gleiche ist wie das der Perzeptron-Netzwerke. Wie wird diese Aussage verletzt, wenn für eines der Perzeptrone w⋅x + b = 0 ist?

Neuronale Netzwerkarchitektur

Im nächsten Abschnitt werde ich ein neuronales Netzwerk vorstellen, das eine gute Klassifizierung handgeschriebener Zahlen ermöglicht. Zuvor ist es hilfreich, die Terminologie zu erläutern, mit der wir auf verschiedene Teile des Netzwerks verweisen können. Angenommen, wir haben das folgende Netzwerk:



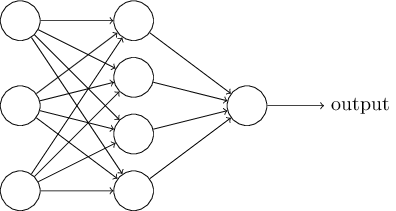
Wie bereits erwähnt, wird die am weitesten links liegende Schicht im Netzwerk als Eingabeschicht bezeichnet, und ihre Neuronen werden als Eingangsneuronen bezeichnet. Die am weitesten rechts stehende oder Ausgangsschicht enthält Ausgangsneuronen oder, wie in unserem Fall, ein Ausgangsneuron. Die mittlere Schicht wird als versteckt bezeichnet, da ihre Neuronen weder eingegeben noch ausgegeben werden. Der Begriff "versteckt" mag etwas mysteriös klingen - als ich ihn zum ersten Mal hörte, entschied ich, dass er eine tiefe philosophische oder mathematische Bedeutung haben sollte - er bedeutet jedoch nur "weder Eingang noch Ausgang". Das obige Netzwerk hat nur eine versteckte Schicht, aber einige Netzwerke haben mehrere versteckte Schichten. Im folgenden vierschichtigen Netzwerk gibt es beispielsweise zwei versteckte Schichten:



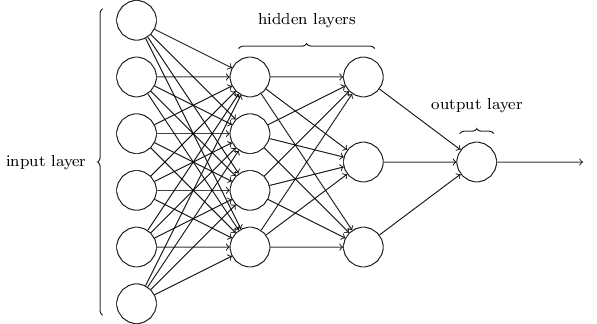
Dies mag verwirrend sein, aber aus historischen Gründen werden solche mehrschichtigen Netzwerke manchmal als mehrschichtige Perzeptrone, MLPs, bezeichnet, obwohl sie eher aus Sigmoidneuronen als aus Perzeptronen bestehen. Ich werde eine solche Terminologie nicht verwenden, weil sie verwirrend ist, aber ich muss vor ihrer Existenz warnen.

Das Entwerfen von Eingabe- und Ausgabeebenen ist manchmal eine einfache Aufgabe. Nehmen wir zum Beispiel an, wir versuchen festzustellen, ob die handschriftliche Zahl "9" bedeutet oder nicht. Eine natürliche Netzwerkschaltung codiert die Helligkeit der Bildpixel in den Eingangsneuronen. Wenn das Bild schwarzweiß mit einer Größe von 64 x 64 Pixel ist, haben wir 64 x 64 = 4096 Eingangsneuronen mit einer Helligkeit im Bereich von 0 bis 1. Die Ausgabeebene enthält nur ein Neuron, dessen Wert kleiner als 0,5 bedeutet, dass "Ein" Die Eingabe war nicht 9 ", aber Werte mehr bedeuten, dass" die Eingabe 9 war ".

Während das Entwerfen von Eingabe- und Ausgabeebenen oft eine einfache Aufgabe ist, kann das Entwerfen versteckter Ebenen eine schwierige Kunst sein. Insbesondere ist es nicht möglich, den Prozess der Entwicklung versteckter Ebenen mit wenigen einfachen Faustregeln zu beschreiben. Forscher der Nationalversammlung haben viele heuristische Regeln für das Design verborgener Schichten entwickelt, die dazu beitragen, das gewünschte Verhalten neuronaler Netze zu erreichen. Eine solche Heuristik kann beispielsweise verwendet werden, um zu verstehen, wie ein Kompromiss zwischen der Anzahl der verborgenen Ebenen und der für das Training des Netzwerks verfügbaren Zeit erzielt werden kann. Später werden wir auf einige dieser Regeln stoßen.

Bisher haben wir NSs diskutiert, bei denen die Ausgabe einer Schicht als Eingabe für die nächste verwendet wird. Solche Netze werden neuronale Netze mit direkter Verteilung genannt. Dies bedeutet, dass es keine Schleifen im Netzwerk gibt - Informationen werden immer weitergeleitet und niemals zurückgemeldet. Wenn wir Schleifen hätten, würden wir auf Situationen stoßen, in denen das Eingabesigmoid von der Ausgabe abhängen würde. Es wäre schwer zu verstehen, und wir erlauben solche Schleifen nicht.

Es gibt jedoch andere Modelle künstlicher NS, bei denen Rückkopplungsschleifen verwendet werden können. Diese Modelle werden als wiederkehrende neuronale Netze (RNS) bezeichnet. Die Idee dieser Netzwerke ist, dass ihre Neuronen für begrenzte Zeiträume aktiviert werden. Diese Aktivierung kann andere Neutronen stimulieren, die etwas später auch für eine begrenzte Zeit aktiviert werden können. Dies führt zur Aktivierung der folgenden Neuronen, und im Laufe der Zeit erhalten wir eine Kaskade aktivierter Neuronen. Schleifen in solchen Modellen stellen keine Probleme dar, da die Ausgabe eines Neurons seinen Eintritt zu einem späteren Zeitpunkt und nicht sofort beeinflusst.

RNSs waren nicht so einflussreich wie NSs der direkten Verteilung, insbesondere weil Trainingsalgorithmen für RNSs bisher weniger Potenzial haben. Das RNS bleibt jedoch weiterhin äußerst interessant. Im Geiste der Arbeit sind sie dem Gehirn viel näher als NS der direkten Verteilung. Es ist möglich, dass das RNS wichtige Probleme lösen kann, die mit Hilfe der Direktverteilung NS mit großen Schwierigkeiten gelöst werden können. Um den Umfang unserer Studie einzuschränken, werden wir uns jedoch auf die am weitesten verbreitete NS der Direktverteilung konzentrieren.

Einfaches Netzwerk zur Klassifizierung von Tinte

Nachdem wir die neuronalen Netze definiert haben, kehren wir zur Handschrifterkennung zurück. Die Aufgabe, handgeschriebene Zahlen zu erkennen, kann in zwei Unteraufgaben unterteilt werden. Zunächst möchten wir einen Weg finden, ein Bild mit vielen Ziffern in eine Folge von Einzelbildern aufzuteilen, von denen jedes eine Ziffer enthält. Zum Beispiel möchten wir das Bild teilen



in sechs getrennte



Wir Menschen können dieses Segmentierungsproblem leicht lösen, aber es ist für ein Computerprogramm schwierig, das Bild korrekt aufzuteilen. Nach der Segmentierung muss das Programm jede einzelne Ziffer klassifizieren. So möchten wir beispielsweise, dass unser Programm die erste Ziffer erkennt



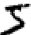
es ist 5.

Wir werden uns darauf konzentrieren, ein Programm zur Lösung des zweiten Problems zu erstellen, der Klassifizierung einzelner Zahlen. Es stellt sich heraus, dass das Problem der Segmentierung nicht so schwer zu lösen ist, sobald wir einen guten Weg finden, einzelne Ziffern zu klassifizieren. Es gibt viele Ansätze zur Lösung des Segmentierungsproblems. Eine davon besteht darin, viele verschiedene Arten der Bildsegmentierung unter Verwendung des Klassifikators einzelner Ziffern auszuprobieren und jeden Versuch zu bewerten. Die Versuchssegmentierung wird sehr geschätzt, wenn der Klassifizierer einzelner Ziffern mit der Klassifizierung aller Segmente vertraut ist, und niedrig, wenn er Probleme in einem oder mehreren Segmenten hat. Die Idee ist, dass wenn der Klassifikator irgendwo Probleme hat, dies höchstwahrscheinlich bedeutet, dass die Segmentierung falsch ist. Diese Idee und andere Optionen können für eine gute Lösung des Segmentierungsproblems verwendet werden. Anstatt uns um die Segmentierung zu kümmern, konzentrieren wir uns auf die Entwicklung eines NS, der eine interessantere und komplexere Aufgabe lösen kann, nämlich das Erkennen einzelner handgeschriebener Zahlen.

Um einzelne Ziffern zu erkennen, verwenden wir NS aus drei Ebenen:



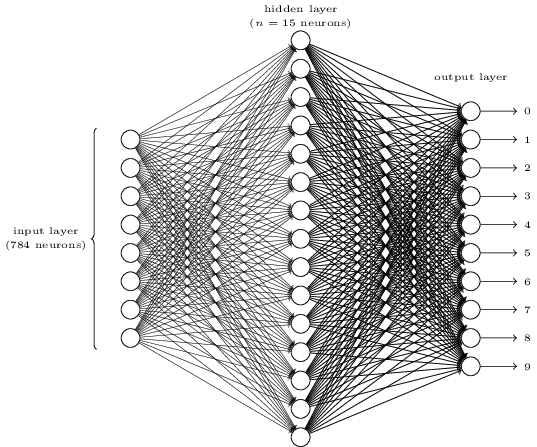
Die Eingangsnetzwerkschicht enthält Neuronen, die verschiedene Werte der Eingangspixel codieren. Wie im nächsten Abschnitt angegeben wird, bestehen unsere Trainingsdaten aus vielen Bildern gescannter handgeschriebener Ziffern mit einer Größe von 28 x 28 Pixel, sodass die Eingabeebene 28 x 28 = 784 Neuronen enthält. Der Einfachheit halber habe ich die meisten 784 Neuronen im Diagramm nicht angegeben. Eingehende Pixel sind Schwarzweiß, wobei ein Wert von 0,0 Weiß anzeigt, 1,0 Schwarz anzeigt und Zwischenwerte zunehmend dunklere Graustufen anzeigen.

Die zweite Schicht des Netzwerks ist ausgeblendet. Wir bezeichnen die Anzahl der Neuronen in dieser Schicht n und werden mit verschiedenen Werten von n experimentieren. Das obige Beispiel zeigt eine kleine verborgene Schicht, die nur n = 15 Neuronen enthält.

Es gibt 10 Neuronen in der Ausgabeschicht des Netzwerks. Wenn das erste Neuron aktiviert ist, dh sein Ausgabewert ist ≈ 1, bedeutet dies, dass das Netzwerk glaubt, dass die Eingabe 0 war. Wenn das zweite Neuron aktiviert ist, glaubt das Netzwerk, dass die Eingabe 1 war. Und so weiter. Genau genommen nummerieren wir die Ausgangsneuronen von 0 bis 9 und schauen uns an, welche von ihnen den maximalen Aktivierungswert hatten. Wenn dies beispielsweise Neuron Nr. 6 ist, dann glaubt unser Netzwerk, dass die Eingabe Nummer 6 war. Und so weiter.

Sie fragen sich vielleicht, warum wir zehn Neuronen verwenden müssen. Schließlich wollen wir wissen, welche Ziffer von 0 bis 9 dem Eingabebild entspricht. Es wäre natürlich, nur 4 Ausgangsneuronen zu verwenden, von denen jedes einen Binärwert annehmen würde, abhängig davon, ob sein Ausgangswert näher an 0 oder 1 liegt. Vier Neuronen wären ausreichend, da 2 ⁴ = 16, mehr als 10 mögliche Werte. Warum sollte unser Netzwerk 10 Neuronen verwenden? Ist das unwirksam? Die Basis dafür ist empirisch; Wir können beide Varianten des Netzwerks ausprobieren, und es stellt sich heraus, dass für diese Aufgabe ein Netzwerk mit 10 Ausgangsneuronen besser darauf trainiert ist, Zahlen zu erkennen als ein Netzwerk mit 4. Es bleibt jedoch die Frage, warum 10 Ausgangsneuronen besser sind. Gibt es eine Heuristik, die uns im Voraus sagen würde, dass 10 Ausgangsneuronen anstelle von 4 verwendet werden sollten?

Um zu verstehen, warum, ist es nützlich, darüber nachzudenken, was ein neuronales Netzwerk tut. Betrachten Sie zunächst die Option mit 10 Ausgangsneuronen. Wir konzentrieren uns auf das erste Ausgangsneuron, das versucht zu entscheiden, ob das eingehende Bild Null ist. Er tut dies, indem er Beweise aus einer verborgenen Schicht abwägt. Was machen versteckte Neuronen? Angenommen, das erste Neuron in der verborgenen Schicht bestimmt, ob das Bild so etwas enthält:



Er kann dies tun, indem er Pixeln, die zu diesem Bild passen, große Gewichte und dem Rest kleine Gewichte zuweist. Nehmen wir auf die gleiche Weise an, dass das zweite, dritte und vierte Neuron in der verborgenen Schicht suchen, ob das Bild ähnliche Fragmente enthält:



Wie Sie vielleicht erraten haben, ergeben diese vier Fragmente zusammen das Bild 0, das wir zuvor gesehen haben:



Wenn also die vier versteckten Neuronen aktiviert sind, können wir daraus schließen, dass die Zahl 0 ist. Dies ist natürlich nicht der einzige Beweis dafür, dass dort 0 angezeigt wurde - wir können 0 auf viele andere Arten erhalten (indem wir diese Bilder leicht verschieben oder leicht verzerren). Wir können jedoch mit Sicherheit sagen, dass wir zumindest in diesem Fall den Schluss ziehen können, dass am Eingang 0 war.

Wenn wir davon ausgehen, dass das Netzwerk so funktioniert, können wir plausibel erklären, warum es besser ist, 10 Ausgangsneuronen anstelle von 4 zu verwenden. Wenn wir 4 Ausgangsneuronen hätten, würde das erste Neuron versuchen, zu entscheiden, was das bedeutendste Bit der eingehenden Ziffer ist. Und es gibt keine einfache Möglichkeit, das wichtigste Bit mit den oben angegebenen einfachen Formen zu verknüpfen. Es ist kaum vorstellbar, warum Teile der Form einer Ziffer in irgendeiner Weise mit dem wichtigsten Teil der Ausgabe zusammenhängen.

All dies wird jedoch nur durch Heuristiken unterstützt. Nichts spricht dafür, dass ein dreischichtiges Netzwerk wie gesagt funktionieren sollte und versteckte Neuronen einfache Komponenten von Formen finden sollten. Vielleicht findet der knifflige Lernalgorithmus einige Gewichte, mit denen wir nur 4 Ausgangsneuronen verwenden können. Als Heuristik funktioniert meine Methode jedoch gut und kann Ihnen viel Zeit bei der Entwicklung einer guten NS-Architektur sparen.

Übungen

• , . , . . , 3 , ( ) 0,99, 0,01.

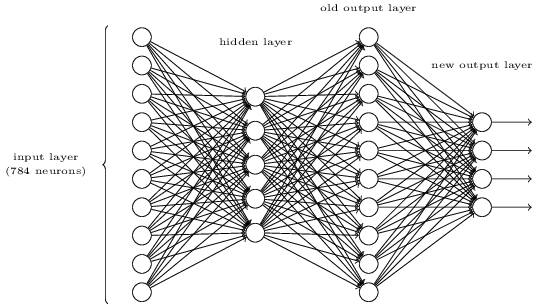Wir haben also das NA-Schema - wie lernt man, Zahlen zu erkennen? Das erste, was wir brauchen, sind Trainingsdaten, die sogenannten Trainingsdatensatz. Wir werden das MNIST-Kit verwenden, das Zehntausende gescannter Bilder handgeschriebener Zahlen und deren korrekte Klassifizierung enthält. Der Name MNIST wurde aufgrund der Tatsache erhalten, dass es sich um eine modifizierte Teilmenge der beiden Datensätze handelt, die von NIST , dem US-amerikanischen National Institute of Standards and Technology, gesammelt wurden . Hier einige Bilder von MNIST:



Dies sind die gleichen Zahlen, die zu Beginn des Kapitels als Erkennungsaufgabe angegeben wurden. Wenn wir die NS überprüfen, werden wir sie natürlich bitten, die falschen Bilder zu erkennen, die bereits im Trainingsset enthalten waren!

MNIST-Daten bestehen aus zwei Teilen. Das erste enthält 60.000 Bilder für das Training. Dies sind gescannte Manuskripte von 250 Personen, von denen die Hälfte Angestellte des US Census Bureau und die andere Hälfte Schüler waren. Die Bilder sind schwarzweiß und messen 28 x 28 Pixel. Der zweite Teil des MNIST-Datensatzes besteht aus 10.000 Bildern zum Testen des Netzwerks. Dies ist auch ein Schwarzweißbild mit 28 x 28 Pixel. Wir werden diese Daten verwenden, um zu bewerten, wie gut das Netzwerk gelernt hat, Zahlen zu erkennen. Um die Qualität der Bewertung zu verbessern, wurden diese Zahlen von weiteren 250 Personen herangezogen, die nicht an der Aufzeichnung des Schulungssatzes teilnahmen (obwohl dies auch Mitarbeiter des Büros und Schüler waren). Dies hilft uns sicherzustellen, dass unser System die Handschrift von Personen erkennen kann, die es während des Trainings nicht getroffen hat.

Die Trainingseingabe wird mit x bezeichnet. Es ist zweckmäßig, jedes Eingabebild x als einen Vektor mit 28x28 = 784 Messungen zu behandeln. Jeder Wert innerhalb des Vektors gibt die Helligkeit eines Pixels im Bild an. Wir werden den Ausgabewert als y = y (x) bezeichnen, wobei y ein zehndimensionaler Vektor ist. Wenn zum Beispiel ein bestimmtes Trainingsbild x 6 enthält, ist y (x) = (0,0,0,0,0,0,1,0,0,0) ^T der Vektor, den wir benötigen. T ist eine Transponierungsoperation, die einen Zeilenvektor in einen Spaltenvektor verwandelt.

Wir wollen einen Algorithmus finden, der es uns ermöglicht, nach solchen Gewichten und Offsets zu suchen, so dass sich die Netzwerkausgabe für alle Trainingseingaben x y (x) nähert. Um die Annäherung an dieses Ziel zu quantifizieren, definieren wir eine Kostenfunktion (manchmal auch als Verlustfunktion bezeichnet);; Im Buch werden wir die Kostenfunktion verwenden, aber einen anderen Namen beachten):

$$

$$C(w, b) = \frac{1}{2n} \sum_x || y(x) – a ||^2 \tag{6}$$

Hier bezeichnet w einen Satz von Netzwerkgewichten, b ist ein Satz von Offsets, n ist die Anzahl von Trainingseingabedaten, a ist der Vektor von Ausgangsdaten, wenn x Eingabedaten sind, und die Summe durchläuft alle Trainingseingabedaten x. Die Ausgabe hängt natürlich von x, w und b ab, aber der Einfachheit halber habe ich diese Abhängigkeit nicht bezeichnet. Die Notation || v || bedeutet die Länge des Vektors v. Wir werden C eine quadratische Kostenfunktion nennen; manchmal wird es auch als Standardfehler oder MSE bezeichnet. Wenn Sie sich C genau ansehen, können Sie sehen, dass es nicht negativ ist, da alle Mitglieder der Summe nicht negativ sind. Außerdem werden die Kosten von C (w, b) klein, dh C (w, b) ≤ 0, genau dann, wenn y (x) für alle Trainingseingabedaten x ungefähr gleich dem Ausgangsvektor a ist. Unser Algorithmus funktionierte also gut, wenn es uns gelang, Gewichte und Offsets so zu finden, dass C (w, b) ≈ 0 war. Und umgekehrt funktionierte er schlecht, wenn C (w,b) groß - Dies bedeutet, dass y (x) für eine große Menge an Eingabe nicht mit der Ausgabe übereinstimmt. Es stellt sich heraus, dass das Ziel des Trainingsalgorithmus darin besteht, die Kosten von C (w, b) als Funktion von Gewichten und Offsets zu minimieren. Mit anderen Worten, wir müssen eine Reihe von Gewichten und Offsets finden, die den Wert der Kosten minimieren. Wir werden dies mit einem Algorithmus tun, der Gradientenabstieg genannt wird.

Warum brauchen wir einen quadratischen Wert? Interessieren wir uns nicht hauptsächlich für die Anzahl der vom Netzwerk korrekt erkannten Bilder? Ist es möglich, diese Zahl einfach direkt zu maximieren und den Zwischenwert des quadratischen Wertes nicht zu minimieren? Das Problem ist, dass die Anzahl der korrekt erkannten Bilder keine glatte Funktion der Gewichte und Offsets des Netzwerks ist. Zum größten Teil ändern kleine Änderungen der Gewichte und Offsets nicht die Anzahl der korrekt erkannten Bilder. Aus diesem Grund ist es schwer zu verstehen, wie Gewichte und Vorspannungen geändert werden können, um die Effizienz zu verbessern. Wenn wir eine reibungslose Kostenfunktion verwenden, ist es für uns leicht zu verstehen, wie kleine Änderungen an Gewichten und Offsets vorgenommen werden können, um die Kosten zu verbessern. Daher konzentrieren wir uns zuerst auf den quadratischen Wert und untersuchen dann die Klassifizierungsgenauigkeit.

Selbst wenn wir bedenken, dass wir eine reibungslose Kostenfunktion verwenden möchten, könnte es Sie dennoch interessieren, warum wir die quadratische Funktion für Gleichung (6) gewählt haben. Ist es nicht möglich, es willkürlich zu wählen? Wenn wir eine andere Funktion wählen würden, würden wir vielleicht einen völlig anderen Satz von Minimierungsgewichten und Offsets erhalten? Eine vernünftige Frage, und später werden wir die Kostenfunktion erneut untersuchen und einige Korrekturen daran vornehmen. Die quadratische Kostenfunktion eignet sich jedoch hervorragend, um die grundlegenden Dinge beim Erlernen von NS zu verstehen. Daher werden wir uns vorerst daran halten.

Zusammenfassend: Unser Ziel beim Training von NS ist es, Gewichte und Offsets zu finden, die die quadratische Kostenfunktion C (w, b) minimieren. Die Aufgabe ist gut gestellt, hat aber bisher viele ablenkende Strukturen - die Interpretation von w und b als Gewichte und Offsets, die im Hintergrund verborgene Funktion σ, die Wahl der Netzwerkarchitektur, MNIST und so weiter. Es stellt sich heraus, dass wir viel verstehen können, den größten Teil dieser Struktur ignorieren und uns nur auf den Aspekt der Minimierung konzentrieren. Daher werden wir vorerst die spezielle Form der Kostenfunktion, die Kommunikation mit der Nationalversammlung usw. vergessen. Stattdessen werden wir uns vorstellen, dass wir nur eine Funktion mit vielen Variablen haben und diese minimieren wollen. Wir werden eine Technologie namens Gradientenabstieg entwickeln, mit der solche Probleme gelöst werden können. Und dann kommen wir zu einer bestimmten Funktion zurück,was wir für die Nationalversammlung minimieren wollen.

Nehmen wir an, wir versuchen, eine Funktion C (v) zu minimieren. Es kann eine beliebige Funktion mit reellen Werten vieler Variablen sein. V = v ₁ , v ₂ , ... Beachten Sie, dass ich die Notation w und b durch v ersetzt habe, um zu zeigen, dass es sich um eine beliebige Funktion handeln kann - wir sind nicht mehr von HC besessen. Es ist nützlich sich vorzustellen, dass eine Funktion C nur zwei Variablen hat - v ₁ und v ₂ :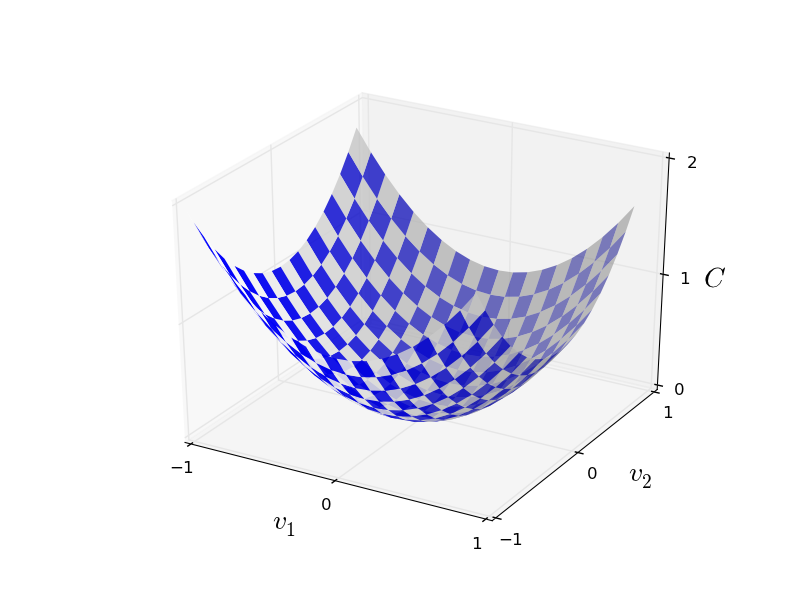



Wir möchten herausfinden, wo C ein globales Minimum erreicht. Natürlich können wir mit der oben gezeichneten Funktion den Graphen studieren und das Minimum finden. In diesem Sinne habe ich Ihnen vielleicht eine zu einfache Funktion gegeben! Im allgemeinen Fall kann C eine komplexe Funktion vieler Variablen sein, und es ist normalerweise unmöglich, nur den Graphen zu betrachten und das Minimum zu finden.

Eine Möglichkeit, das Problem zu lösen, besteht darin, mithilfe der Algebra das Minimum analytisch zu ermitteln. Wir können die Ableitungen berechnen und versuchen, sie zu verwenden, um das Extremum zu finden. Wenn wir Glück haben, funktioniert dies, wenn C eine Funktion von einer oder zwei Variablen ist. Bei einer großen Anzahl von Variablen wird dies jedoch zu einem Albtraum. Und für NSs benötigen wir oft viel mehr Variablen - für die größten NSs hängen die Kostenfunktionen auf komplexe Weise von Milliarden von Gewichten und Verschiebungen ab. Die Verwendung von Algebra zur Minimierung dieser Funktionen schlägt fehl!

(Nachdem ich festgestellt hatte, dass es für uns bequemer wäre, C als Funktion zweier Variablen zu betrachten, sagte ich zweimal in zwei Absätzen: „Ja, aber was ist, wenn es sich um eine Funktion einer viel größeren Anzahl von Variablen handelt?“ Ich entschuldige mich. Glauben Sie uns, dass es wirklich nützlich sein wird, C als Funktion darzustellen Bei zwei Variablen fällt dieses Bild manchmal auseinander, weshalb die beiden vorherigen Absätze benötigt wurden. Für mathematische Überlegungen ist es häufig erforderlich, mehrere intuitive Darstellungen zu jonglieren und gleichzeitig zu lernen, wann die Darstellung verwendet werden kann und wann nicht ZYA.)

Okay, das bedeutet, dass Algebra nicht funktioniert. Glücklicherweise gibt es eine großartige Analogie, die einen gut funktionierenden Algorithmus bietet. Wir stellen uns unsere Funktion als Tal vor. Mit dem neuesten Zeitplan wird es nicht so schwierig sein. Und wir stellen uns einen Ball vor, der am Hang des Tals entlang rollt. Unsere Erfahrung zeigt uns, dass der Ball irgendwann ganz nach unten rutschen wird. Vielleicht können wir diese Idee nutzen, um das Minimum einer Funktion zu finden? Wir wählen zufällig den Startpunkt für einen imaginären Ball aus und simulieren dann die Bewegung des Balls, als würde er auf den Grund des Tals rollen. Wir können diese Simulation einfach verwenden, indem wir die Ableitungen (und möglicherweise die zweiten Ableitungen) von C zählen - sie erzählen uns alles über die lokale Form des Tals und damit darüber, wie unser Ball rollt.

Basierend auf dem, was Sie geschrieben haben, könnten Sie denken, dass wir Newtons Bewegungsgleichungen für den Ball aufschreiben, die Auswirkungen von Reibung und Schwerkraft berücksichtigen und so weiter. Tatsächlich werden wir dieser Analogie mit dem Ball nicht so nahe kommen - wir entwickeln einen Algorithmus zur Minimierung von C und keine exakte Simulation der Gesetze der Physik! Diese Analogie sollte unsere Vorstellungskraft anregen und unser Denken nicht einschränken. Anstatt in die komplexen Details der Physik einzutauchen, stellen wir die Frage: Wenn wir für einen Tag zu Gott ernannt würden, würden wir unsere eigenen Gesetze der Physik erstellen und dem Ball sagen, wie er rollen soll, welches Gesetz oder welche Bewegungsgesetze wir wählen würden, damit der Ball immer weiter rollt Talboden?

Um das Problem zu klären, werden wir darüber nachdenken, was passiert, wenn wir den Ball um eine kleine Strecke Δv ₁ in Richtung von v ₁ bewegenund einen kleinen Abstand Δv ₂ in Richtung von v ₂ . Die Algebra sagt uns, dass sich C wie folgt ändert:

$$

$$\Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2 \tag{7}$$

Wir werden einen Weg finden, solche Δv ₁ und Δv ₂ so zu wählen , dass ΔC kleiner als Null ist; Das heißt, wir werden sie so auswählen, dass der Ball nach unten rollt. Um zu verstehen, wie dies zu tun ist, ist es nützlich, Δv als den Vektor der Änderungen zu definieren, dh Δv ≡ (Δv ₁ , Δv ₂ ) ^T , wobei T die Transponierungsoperation ist, die Zeilenvektoren in Spaltenvektoren umwandelt. Wir definieren auch den Gradientenvektor C als partielle Ableitungen (∂S / ∂V ₁ , ∂S / ∂V ₂ ) ^T . Wir bezeichnen den Gradientenvektor mit ∇:

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2})^T \tag{8}$$

Bald werden wir die Änderung von ΔC durch Δv und den Gradienten ∇C umschreiben. In der Zwischenzeit möchte ich etwas klarstellen, weshalb die Leute oft am Gefälle hängen. Wenn sie sich zum ersten Mal mit ∇C trafen, verstehen die Leute manchmal nicht, wie sie das Symbol wahrnehmen sollen ∇. Was bedeutet das konkret? Tatsächlich können Sie ∇C sicher als ein einzelnes mathematisches Objekt betrachten - einen zuvor definierten Vektor - der einfach mit zwei Zeichen geschrieben wird. Unter diesem Gesichtspunkt ist ∇ wie das Schwenken einer Flagge, die besagt, dass "∇C ein Gradientenvektor ist". Es gibt fortgeschrittenere Gesichtspunkte, unter denen ∇ als unabhängige mathematische Einheit betrachtet werden kann (zum Beispiel als Differenzierungsoperator), aber wir brauchen sie nicht.

Mit solchen Definitionen kann Ausdruck (7) wie folgt umgeschrieben werden:

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{9}$$

Diese Gleichung hilft zu erklären, warum ∇C als Gradientenvektor bezeichnet wird: Sie verbindet die Änderungen in v mit den Änderungen in C, genau wie von einer Entität namens Gradienten erwartet. [dt. Gradient - Abweichung / ca. trans.] Es ist jedoch interessanter, dass diese Gleichung es uns ermöglicht zu sehen, wie man Δv so wählt, dass ΔC negativ ist. Nehmen wir an, wir wählen

$$

$$\Delta v = - \eta \nabla C \tag{10}$$

Dabei ist η ein kleiner positiver Parameter (Lerngeschwindigkeit). Dann sagt uns Gleichung (9), dass ΔC ≈ - η ∇C ⋅C = - η || ∇C || ² .Seit || ∇C || ² ≥ 0, dies stellt sicher, dass ΔC ≤ 0, dh C, die ganze Zeit abnimmt, wenn wir v ändern, wie in (10) vorgeschrieben (natürlich als Teil der Näherung aus Gleichung (9)). Und genau das brauchen wir! Daher nehmen wir Gleichung (10), um das "Bewegungsgesetz" des Balls in unserem Gradientenabstiegsalgorithmus zu bestimmen. Das heißt, wir werden Gleichung (10) verwenden, um den Δv-Wert zu berechnen, und dann werden wir den Ball auf diesen Wert bewegen:

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{11}$$

Dann wenden wir diese Regel erneut für den nächsten Schritt an. Wenn wir die Wiederholung fortsetzen, werden wir C senken, bis wir hoffentlich ein globales Minimum erreichen.

Zusammenfassend lässt sich sagen, dass der Gradientenabstieg durch sequentielle Berechnung des Gradienten ∇ C und die anschließende Verschiebung in die entgegengesetzte Richtung erfolgt, was zu einem „Sturz“ entlang des Talhangs führt. Dies kann wie folgt visualisiert werden: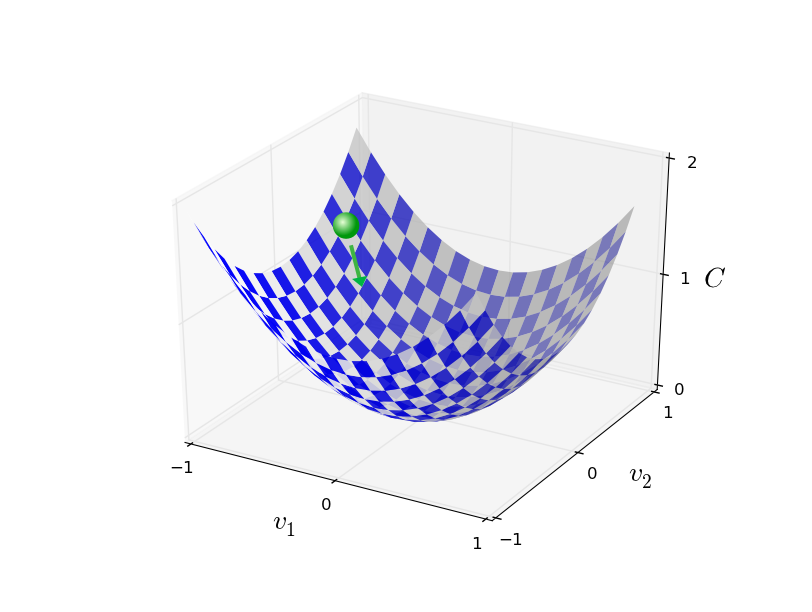



Beachten Sie, dass mit dieser Regel der Gradientenabstieg keine echte physische Bewegung reproduziert. Im wirklichen Leben hat der Ball einen Impuls, der es ihm ermöglichen kann, über den Hang zu rollen oder sogar für einige Zeit aufzurollen. Erst nach der Arbeit der Reibungskraft wird garantiert, dass der Ball das Tal hinunter rollt. Unsere Auswahlregel Δv sagt nur "runter". Eine ziemlich gute Regel, um das Minimum zu finden!

Damit der Gradientenabstieg korrekt funktioniert, müssen wir einen ausreichend kleinen Wert der Lerngeschwindigkeit η wählen, damit Gleichung (9) eine gute Annäherung darstellt. Andernfalls kann sich herausstellen, dass ΔC> 0 ist - nichts Gutes! Gleichzeitig ist es nicht erforderlich, dass η zu klein ist, da dann die Änderungen von Δv winzig sind und der Algorithmus zu langsam arbeitet. In der Praxis ändert sich η so, dass Gleichung (9) eine gute Annäherung ergibt und der Algorithmus nicht zu langsam arbeitet. Später werden wir sehen, wie es funktioniert.

Ich erklärte den Gradientenabstieg, wenn Funktion C nur von zwei Variablen abhing. Aber alles funktioniert auf die gleiche Weise, wenn C eine Funktion vieler Variablen ist. Angenommen, sie hat m Variablen, v ₁ , ..., v _m. Dann ist die Änderung von & Dgr; C, die durch eine kleine Änderung von & Dgr; v = (& Dgr; v ₁ , ..., & Dgr ; v _m ) ^{T verursacht} wird

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{12}$$

wobei der Gradient ∇C der Vektor ist

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1},…, \frac{\partial C}{\partial v_m})^T \tag{13}$$

Wie bei zwei Variablen können wir wählen

$$

$$\Delta v = - \eta \nabla C \tag{14}$$

und stellen Sie sicher, dass unser ungefährer Ausdruck (12) für ΔC negativ ist. Dies gibt uns die Möglichkeit, den Gradienten auf ein Minimum zu reduzieren, selbst wenn C eine Funktion vieler Variablen ist, und die Aktualisierungsregel immer wieder anzuwenden.

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{15}$$

Diese Aktualisierungsregel kann als definierender Gradientenabstiegsalgorithmus betrachtet werden. Es gibt uns eine Methode zum wiederholten Ändern der Position von v auf der Suche nach dem Minimum der Funktion C. Diese Regel funktioniert nicht immer - verschiedene Dinge können schief gehen und verhindern, dass der Gradientenabstieg das globale Minimum von C findet - wir werden in den folgenden Kapiteln auf diesen Punkt zurückkommen. In der Praxis funktioniert der Gradientenabstieg jedoch häufig sehr gut, und wir werden sehen, dass dies in der Nationalversammlung ein wirksamer Weg ist, um die Kostenfunktion zu minimieren und daher das Netzwerk zu trainieren.

In gewissem Sinne kann der Gradientenabstieg als optimale minimale Suchstrategie angesehen werden. Angenommen, wir versuchen, Δv in eine Position zu bewegen, um C zu minimieren. Dies entspricht der Minimierung von ΔC ≈ ∇C ⋅ Δv. Wir werden die Schrittgröße so begrenzen, dass || Δv || = ε für eine kleine Konstante ε> 0. Mit anderen Worten, wir möchten eine kleine Strecke fester Größe zurücklegen und versuchen, die Bewegungsrichtung zu finden, die C so weit wie möglich verringert. Es kann bewiesen werden, dass die Wahl von Δv zur Minimierung von ∇C ⋅ Δv Δv = -η∇C ist, wobei η = ε / || ∇C || durch die Einschränkung || Δv || bestimmt wird = ε. Der Gradientenabstieg kann daher als ein Weg angesehen werden, kleine Schritte in die Richtung zu unternehmen, in der C am meisten abnimmt.

Übungen

• . : — , , , .
• , , . , ? ?

Die Menschen haben viele Optionen für den Gradientenabstieg untersucht, einschließlich solcher, die einen echten physischen Ball genauer reproduzieren. Solche Optionen haben ihre Vorteile, aber auch einen großen Nachteil: Die Notwendigkeit, die zweiten partiellen Ableitungen von C zu berechnen, die viele Ressourcen verbrauchen können. Um dies zu verstehen, nehmen wir an, dass wir alle zweiten partiellen Ableitungen ∂ ² C / ∂v _j ∂v _k berechnen müssen . Wenn die Variablen v _j Millionen sind, müssen wir ungefähr eine Billion (eine Million Quadrat) zweite partielle Ableitungen berechnen (tatsächlich eine halbe Billion, da ∂ ² C / ∂v _j ∂v _k = ∂ ² C / ∂v _k ∂v _j. Aber du hast die Essenz verstanden). Dies erfordert viele Rechenressourcen. Es gibt Tricks, um dies zu vermeiden, und die Suche nach Alternativen zum Gradientenabstieg ist ein Bereich aktiver Forschung. In diesem Buch werden wir jedoch den Gradientenabstieg und seine Varianten als Hauptansatz für das Erlernen von NS verwenden.

Wie wenden wir Gradientenabstieg auf NA-Lernen an? Wir müssen es verwenden, um nach Gewichten w _k und Offsets b _l zu suchen , die die Kostengleichung (6) minimieren. Schreiben wir die Aktualisierungsregel für den Gradientenabstieg neu, indem wir die Variablen v _j durch Gewichte und Offsets ersetzen . Mit anderen Worten, jetzt hat unsere „Position“ die Komponenten w _k und b _l , und der Gradientenvektor ∇C hat die entsprechenden Komponenten ∂C / ∂w_k und ∂C / ∂b _l . Nachdem wir unsere Update-Regel mit neuen Komponenten geschrieben haben, erhalten wir:

$$

$$w_k \rightarrow w'_k = w_k - \eta \frac{\partial C}{\partial w_k} \tag{16}$$

$$

$$b_l \rightarrow b'_l = b_l - \eta \frac{\partial C}{\partial b_l} \tag{17}$$

Durch erneutes Anwenden dieser Aktualisierungsregel können wir „bergab rollen“ und mit etwas Glück die Mindestkostenfunktion finden. Mit anderen Worten, diese Regel kann verwendet werden, um die Nationalversammlung auszubilden.

Es gibt mehrere Hindernisse für die Anwendung der Gradientenabstiegsregel. Wir werden sie in den folgenden Kapiteln genauer untersuchen. Aber im Moment möchte ich nur ein Problem erwähnen. Um es zu verstehen, kehren wir zum quadratischen Wert in Gleichung (6) zurück. Beachten Sie, dass diese Kostenfunktion wie folgt aussieht: C = 1 / n ∑ _x C _x , dh es sind die durchschnittlichen Kosten C _x ≡ (|| y (x) - a || ² ) / 2 für einzelne Trainingsbeispiele. In der Praxis müssen wir zur Berechnung des Gradienten ∇C die Gradienten ∇C _x berechnengetrennt für jede Trainingseingabe x und dann mitteln, ∇C = 1 / n ∑ _x ∇C _x . Leider wird es sehr lange dauern, wenn die Menge an Eingaben sehr groß ist, und ein solches Training wird langsam sein.

Um das Lernen zu beschleunigen, können Sie den stochastischen Gradientenabstieg verwenden. Die Idee ist, den ∇C-Gradienten durch Berechnen von ∇C _x für eine kleine Zufallsstichprobe von Trainingseingaben näherungsweise zu berechnen . Durch die Berechnung ihres Durchschnitts können wir schnell eine gute Schätzung des tatsächlichen Gradienten ∇C erhalten, was dazu beiträgt, den Gradientenabstieg und damit das Training zu beschleunigen.

Eine genauere Formulierung des stochastischen Gradientenabfalls erfolgt durch Zufallsstichprobe einer kleinen Anzahl von m Trainingseingabedaten. Wir werden diese zufälligen Daten X ₁ , X ₂ , .., X _m nennen und es ein Minipaket nennen. Wenn die Stichprobengröße m groß genug ist, liegt der Durchschnittswert von ∇C _{X j} nahe genug am Durchschnitt aller ∇Cx, d. H.

$$

$$\frac{\sum^m_{j=1} \nabla C_{X_j}}{m} \approx \frac{\sum_x \nabla C_x}{n} = \nabla C \tag{18}$$

Dabei geht der zweite Betrag über den gesamten Satz von Trainingsdaten. Durch den Austausch von Teilen erhalten wir

$$

$$\nabla C \approx \frac{1}{m} \sum^m_{j=1} \nabla C_{X_j} \tag{19}$$

Dies bestätigt, dass wir den Gesamtgradienten schätzen können, indem wir die Gradienten für ein zufällig ausgewähltes Minipack berechnen.

Um dies direkt mit dem Training von NS in Verbindung zu bringen, nehmen wir an, dass w _k und b _l die Gewichte und Verschiebungen unseres NS bezeichnen. Dann wählt der stochastische Gradientenabstieg ein zufälliges Minipaket von Eingabedaten aus und lernt daraus

$$

$$w_k \rightarrow w'_k = w_k - \frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial w_k} \tag{20}$$

$$

$$b_l \rightarrow b'_l = b_l - \frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial b_l} \tag{21}$$

Wo ist die Summe aller Trainingsbeispiele X _j im aktuellen Minipaket? Dann wählen wir ein anderes zufälliges Minipaket aus und studieren es. Und so weiter, bis wir alle Trainingsdaten erschöpft haben, was als Ende der Trainingsära bezeichnet wird. In diesem Moment beginnen wir eine neue Ära des Lernens.

Übrigens ist anzumerken, dass sich die Vereinbarungen bezüglich der Skalierung der Kostenfunktion und der Aktualisierung der Gewichte und Offsets in einem Minipaket unterscheiden. In Gleichung (6) haben wir die Kostenfunktion 1 / n-mal skaliert. Manchmal lassen die Leute 1 / n weg, indem sie die Kosten für einzelne Trainingsbeispiele addieren, anstatt den Durchschnitt zu berechnen. Dies ist nützlich, wenn die Gesamtzahl der Trainingsbeispiele nicht im Voraus bekannt ist. Dies kann beispielsweise passieren, wenn zusätzliche Daten in Echtzeit angezeigt werden. Auf die gleiche Weise lassen die Mini-Paket-Aktualisierungsregeln (20) und (21) manchmal das 1 / m-Mitglied vor der Summe weg. Konzeptionell hat dies keine Auswirkungen, da es einer Änderung der Lerngeschwindigkeit η entspricht. Beim Vergleich verschiedener Werke lohnt es sich jedoch, darauf zu achten.

Ein stochastischer Gradientenabstieg kann als politische Abstimmung betrachtet werden: Es ist viel einfacher, eine Stichprobe in Form eines Minipakets zu entnehmen, als einen Gradientenabstieg auf eine vollständige Stichprobe anzuwenden - genau wie eine Umfrage am Ausgang eines Standorts einfacher ist als eine vollständige Wahl durchzuführen. Wenn unser Trainingssatz beispielsweise wie MNIST eine Größe von n = 60.000 hat und wir eine Stichprobe eines Minipakets mit der Größe m = 10 erstellen, beschleunigen wir die Gradientenschätzung um das 6000-fache! Natürlich wird die Schätzung nicht ideal sein - es wird statistische Schwankungen geben -, aber sie muss nicht ideal sein: Wir müssen uns nur in die Richtung bewegen, in der C abnimmt, was bedeutet, dass wir den Gradienten nicht genau berechnen müssen. In der Praxis ist der stochastische Gradientenabstieg eine gängige und leistungsstarke Unterrichtstechnik für die Nationalversammlung und die Grundlage der meisten Unterrichtstechnologien, die wir als Teil des Buches entwickeln werden.

• - 1. , x w _k → w′ _k = w _k − η ∂C _x / ∂w _k b _l → b′ _l = b _l − η ∂C _x / ∂b _l . . Usw. , -, . - ( ). - - 20.

Lassen Sie mich diesen Abschnitt mit einer Diskussion über ein Thema beenden, das manchmal Menschen stört, die zum ersten Mal auf einen Gradientenabstieg gestoßen sind. In NS ist der Wert von C eine Funktion vieler Variablen - aller Gewichte und Offsets - und bestimmt gewissermaßen die Oberfläche in einem sehr mehrdimensionalen Raum. Die Leute beginnen zu denken: "Ich muss all diese zusätzlichen Dimensionen visualisieren." Und sie beginnen sich Sorgen zu machen: "Ich kann nicht in vier Dimensionen navigieren, ganz zu schweigen von fünf (oder fünf Millionen)." Haben sie eine besondere Qualität, die die „echte“ Supermathematik hat? Natürlich nicht. Selbst professionelle Mathematiker können sich den vierdimensionalen Raum nicht gut vorstellen - wenn überhaupt. Sie gehen zu Tricks und entwickeln andere Möglichkeiten, um darzustellen, was passiert. Genau das haben wir getan:Wir haben die algebraische (und nicht die visuelle) Darstellung von ΔC verwendet, um zu verstehen, wie man sich bewegt, damit C abnimmt. Menschen, die gute Arbeit mit einer Vielzahl von Dimensionen leisten, haben eine große Bibliothek ähnlicher Techniken im Kopf. Unser algebraischer Trick ist nur ein Beispiel. Diese Techniken sind möglicherweise nicht so einfach wie wir es gewohnt sind, wenn wir drei Dimensionen visualisieren. Wenn Sie jedoch eine Bibliothek ähnlicher Techniken erstellen, beginnen Sie, in höheren Dimensionen gut zu denken. Ich werde nicht auf Details eingehen, aber wenn Sie interessiert sind, mögen Sie vielleichtWas sind wir gewohnt, wenn wir drei Dimensionen visualisieren, aber wenn Sie eine Bibliothek ähnlicher Techniken erstellt haben, beginnen Sie, in höheren Dimensionen gut zu denken. Ich werde nicht auf Details eingehen, aber wenn Sie interessiert sind, mögen Sie vielleichtWas sind wir gewohnt, wenn wir drei Dimensionen visualisieren, aber wenn Sie eine Bibliothek ähnlicher Techniken erstellt haben, beginnen Sie, in höheren Dimensionen gut zu denken. Ich werde nicht auf Details eingehen, aber wenn Sie interessiert sind, mögen Sie vielleichtEine Diskussion einiger dieser Techniken durch professionelle Mathematiker, die es gewohnt sind, in höheren Dimensionen zu denken. Obwohl einige der besprochenen Techniken recht komplex sind, sind die meisten der besten Antworten intuitiv und für jedermann zugänglich.

Implementierung eines Netzwerks zur Klassifizierung von Zahlen

Ok, jetzt schreiben wir ein Programm, das lernt, handgeschriebene Ziffern anhand des stochastischen Gradientenabfalls und der Trainingsdaten von MNIST zu erkennen. Wir werden dies mit einem kurzen Programm in Python 2.7 tun, das nur aus 74 Zeilen besteht! Als erstes müssen wir die MNIST-Daten herunterladen. Wenn Sie git verwenden, können Sie sie erhalten, indem Sie das Repository dieses Buches klonen:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git

Wenn nicht, laden Sie den Code über den Link herunter.

Als ich zuvor MNIST-Daten erwähnte, sagte ich übrigens, dass sie in 60.000 Trainingsbilder und 10.000 Testbilder unterteilt sind. Dies ist die offizielle Beschreibung von MNIST. Wir werden die Daten etwas anders brechen. Wir werden die Überprüfungsbilder unverändert lassen, aber den Schulungssatz in zwei Teile aufteilen: 50.000 Bilder, mit denen wir die Nationalversammlung schulen, und einzelne 10.000 Bilder zur zusätzlichen Bestätigung. Wir werden sie zwar nicht verwenden, aber später werden sie uns nützlich sein, wenn wir die Konfiguration einiger Hyperparameter des NS verstehen - die Lerngeschwindigkeit usw. -, die unser Algorithmus nicht direkt auswählt. Obwohl bestätigende Daten nicht Teil der ursprünglichen MNIST-Spezifikation sind, verwenden viele MNIST auf diese Weise, und im Bereich HC ist die Verwendung bestätigender Daten üblich. Wenn ich jetzt von den „MNIST-Trainingsdaten“ spreche, meine ich unsere 50.000 Karitnoks, nicht die ursprünglichen 60.000.

Zusätzlich zu MNIST-Daten benötigen wir eine Python-Bibliothek namens Numpy für schnelle lineare Algebra-Berechnungen. Wenn Sie es nicht haben, können Sie es vom Link nehmen .

Bevor ich Ihnen das gesamte Programm vorstelle, möchte ich die Hauptfunktionen des Codes für NS erläutern. Den zentralen Platz nimmt die Netzwerkklasse ein, mit der wir die Nationalversammlung vertreten. Hier ist der Initialisierungscode für das Netzwerkobjekt:

 class Network(object): def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] 

Das Größenarray enthält die Anzahl der Neuronen in den entsprechenden Schichten. Wenn wir also ein Netzwerkobjekt mit zwei Neuronen in der ersten Schicht, drei Neuronen in der zweiten Schicht und einem Neuron in der dritten Schicht erstellen möchten, schreiben wir es folgendermaßen:

 net = Network([2, 3, 1]) 

Die Offsets und Gewichte im Netzwerkobjekt werden zufällig mit der Numpy-Funktion np.random.randn initialisiert, die eine Gaußsche Verteilung mit einer mathematischen Erwartung von 0 und einer Standardabweichung von 1 erzeugt. Diese zufällige Initialisierung gibt unserem stochastischen Gradientenabstiegsalgorithmus einen Ausgangspunkt. In den folgenden Kapiteln finden Sie die besten Möglichkeiten zum Initialisieren von Gewichten und Offsets. Dies reicht jedoch vorerst aus. Beachten Sie, dass der Netzwerkinitialisierungscode davon ausgeht, dass die erste Schicht von Neuronen eingegeben wird, und ihnen keine Verzerrung zuweist, da sie nur zur Berechnung der Ausgabe verwendet werden.

Beachten Sie auch, dass Offsets und Gewichte als Array von Numpy-Matrizen gespeichert werden. Zum Beispiel ist net.weights [1] eine Numpy-Matrix, die die Gewichte speichert, die die zweite und dritte Schicht von Neuronen verbinden (dies ist nicht die erste und zweite Schicht, da in Python die Nummerierung der Elemente des Arrays von Grund auf neu erfolgt). Da das Schreiben von net.weights [1] zu lange dauert, bezeichnen wir diese Matrix als w. Dies ist eine solche Matrix, dass w _jk das Gewicht der Verbindung zwischen dem k-ten Neuron in der zweiten Schicht und dem j-ten Neuron in der dritten Schicht ist. Eine solche Reihenfolge der Indizes j und k mag seltsam erscheinen - wäre es nicht logischer, sie zu tauschen? Der große Vorteil einer solchen Aufzeichnung besteht jedoch darin, dass der Aktivierungsvektor der dritten Schicht von Neuronen erhalten wird:

$$

$$a '= \ sigma (wa + b) \ tag {22}$$

Schauen wir uns diese ziemlich reiche Gleichung an. a ist der Aktivierungsvektor der zweiten Schicht von Neuronen. Um a 'zu erhalten, multiplizieren wir a mit der Gewichtsmatrix w und addieren den Verschiebungsvektor b. Dann wenden wir das Sigmoid σ Element für Element auf jedes Element des Vektors wa + b an (dies wird als Vektorisierung der Funktion σ bezeichnet). Es ist leicht zu überprüfen, ob Gleichung (22) das gleiche Ergebnis wie Regel (4) für die Berechnung eines Sigmoidneurons liefert.

Übung

• Schreiben Sie Gleichung (22) in Komponentenform und stellen Sie sicher, dass sie das gleiche Ergebnis wie Regel (4) für die Berechnung eines Sigmoidneurons liefert.

Vor diesem Hintergrund ist es einfach, Code zu schreiben, der die Ausgabe eines Netzwerkobjekts berechnet. Wir beginnen mit der Definition eines Sigmoid:

 def sigmoid(z): return 1.0/(1.0+np.exp(-z)) 

Beachten Sie, dass Numpy, wenn der z-Parameter ein Numpy-Vektor oder -Array ist, das Sigmoid-Element automatisch anwendet, dh in Vektorform.

Fügen Sie der Netzwerkklasse eine direkte Weitergabemethode hinzu, die a aus dem Netzwerk als Eingabe verwendet und die entsprechende Ausgabe zurückgibt. Es wird angenommen, dass der Parameter a (n, 1) Numpy ndarray ist, kein Vektor (n,). Hier ist n die Anzahl der Eingangsneuronen. Wenn Sie versuchen, den Vektor (n,) zu verwenden, erhalten Sie seltsame Ergebnisse.

Das Verfahren wendet einfach Gleichung (22) auf jede Schicht an:

  def feedforward(self, a): """       "a"""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a 

Natürlich brauchen wir sie von Netzwerkobjekten, um sie zu lernen. Dazu geben wir ihnen die SGD-Methode, die einen stochastischen Gradientenabstieg implementiert. Hier ist sein Code. An einigen Stellen ist es ziemlich mysteriös, aber im Folgenden werden wir es genauer analysieren.

  def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) 

training_data ist eine Liste von Tupeln "(x, y)", die die Trainingseingabe und die gewünschte Ausgabe darstellen. Die Variablen epochs und mini_batch_size geben die Anzahl der zu lernenden Epochen und die Größe der zu verwendenden Minipakete an. eta - Lerngeschwindigkeit, η. Wenn test_data festgelegt ist, wird das Netzwerk nach jeder Ära anhand der Verifizierungsdaten ausgewertet und der aktuelle Fortschritt wird angezeigt. Dies ist nützlich, um den Fortschritt zu verfolgen, verlangsamt jedoch die Arbeit erheblich.

Der Code funktioniert so. In jeder Epoche mischt er zunächst versehentlich Trainingsdaten und zerlegt sie dann in Minipakete der richtigen Größe. Dies ist eine einfache Möglichkeit, eine Stichprobe von Trainingsdaten zu erstellen. Dann wenden wir für jeden mini_batch einen Schritt des Gradientenabfalls an. Dies erfolgt über den Code self.update_mini_batch (mini_batch, eta), der die Netzwerkgewichte und -versätze gemäß einer Iteration des Gradientenabfalls aktualisiert, wobei nur Trainingsdaten in mini_batch verwendet werden. Hier ist der Code für die update_mini_batch-Methode:

  def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] 

Der größte Teil der Arbeit wird von der Leitung erledigt.

  delta_nabla_b, delta_nabla_w = self.backprop(x, y) 

Es ruft einen Backpropagation-Algorithmus auf - eine schnelle Methode, um den Gradienten einer Kostenfunktion zu berechnen. Update_mini_batch berechnet diese Steigungen einfach für jedes Trainingsbeispiel aus mini_batch und aktualisiert dann self.weights und self.biases.

Bisher werde ich keinen Code für self.backprop demonstrieren. Wir werden im nächsten Kapitel mehr über Backpropagation erfahren, und es wird self.backprop-Code geben. Angenommen, es verhält sich vorerst wie angegeben und gibt einen geeigneten Gradienten für die mit dem Trainingsbeispiel x verbundenen Kosten zurück.

Schauen wir uns das gesamte Programm an, einschließlich erklärender Kommentare. Mit Ausnahme der Funktion self.backprop spricht das Programm für sich selbst - die Hauptarbeit erledigen self.SGD und self.update_mini_batch. Die self.backprop-Methode verwendet mehrere zusätzliche Funktionen, um den Gradienten zu berechnen, nämlich sigmoid_prime, der die Ableitung des Sigmoid berechnet, und self.cost_derivative, die ich hier nicht beschreiben werde. Sie können sich ein Bild davon machen, indem Sie sich den Code und die Kommentare ansehen. Im nächsten Kapitel werden wir sie genauer betrachten. Denken Sie daran, dass das Programm zwar lang erscheint, der größte Teil des Codes jedoch aus Kommentaren besteht, die das Verständnis erleichtern. Tatsächlich besteht das Programm selbst nur aus 74 Nicht-Codezeilen - nicht leer und keine Kommentare. Der gesamte Code ist auf GitHub verfügbar .

 """ network.py ~~~~~~~~~~           .      .     ,    .   ,       . """ ####  #   import random #   import numpy as np class Network(object): def __init__(self, sizes): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].               0    1. ,      ,       ,        . """ self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] def feedforward(self, a): """   ,  ``a`` -  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) #   delta = self.cost_derivative(activations[-1], y) * \ sigmoid_prime(zs[-1]) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """ l      ,      . l = 1    , l = 2 – ,   .    ,   python      .""" for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def evaluate(self, test_data): """    ,      .    –          .""" test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data] return sum(int(x == y) for (x, y) in test_results) def cost_derivative(self, output_activations, y): """    ( C_x /  a)   .""" return (output_activations-y) ####   def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

Wie gut erkennt das Programm handschriftliche Zahlen? Beginnen wir mit dem Laden der MNIST-Daten. Wir werden dies mit dem kleinen Hilfsprogramm mnist_loader.py tun, das ich unten beschreiben werde. Führen Sie die folgenden Befehle in der Python-Shell aus:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Dies kann natürlich in einem separaten Programm erfolgen, aber wenn Sie parallel zu einem Buch arbeiten, ist dies einfacher.

Richten Sie nach dem Herunterladen der MNIST-Daten ein Netzwerk von 30 versteckten Neuronen ein. Wir werden dies tun, nachdem wir das oben beschriebene Programm importiert haben, das als Netzwerk bezeichnet wird:

 >>> import network >>> net = network.Network([784, 30, 10]) 

Schließlich verwenden wir den stochastischen Gradientenabstieg für das Training von Trainingsdaten für 30 Epochen mit einer Minipaketgröße von 10 und einer Lerngeschwindigkeit von η = 3,0:

 >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Wenn Sie Code parallel zum Lesen eines Buches ausführen, beachten Sie, dass die Ausführung einige Minuten dauert. Ich schlage vor, Sie starten alles, lesen weiter und überprüfen regelmäßig, was das Programm produziert. Wenn Sie es eilig haben, können Sie die Anzahl der Epochen verringern, indem Sie die Anzahl der versteckten Neuronen verringern oder nur einen Teil der Trainingsdaten verwenden. Der endgültige Arbeitscode funktioniert schneller: Diese Python-Skripte sollen Ihnen helfen, die Funktionsweise des Netzwerks zu verstehen, und sind nicht leistungsstark! Und natürlich kann das Netzwerk nach dem Training auf fast jeder Computerplattform sehr schnell arbeiten. Wenn wir dem Netzwerk beispielsweise eine gute Auswahl an Gewichten und Offsets beibringen, kann es problemlos für die Arbeit mit JavaScript in einem Webbrowser oder als native Anwendung auf einem mobilen Gerät portiert werden. In jedem Fall wird ungefähr die gleiche Schlussfolgerung aus dem Programm gezogen, das das neuronale Netzwerk trainiert. Sie schreibt die Anzahl der korrekt erkannten Testbilder nach jeder Trainingsära. Wie Sie sehen, erreicht es auch nach einer Ära eine Genauigkeit von 9.129 von 10.000, und diese Zahl wächst weiter:

Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000

Es stellt sich heraus, dass das trainierte Netzwerk einen Prozentsatz der korrekten Klassifizierung von maximal 95 - 95,42% ergibt! Ein ziemlich vielversprechender erster Versuch. Ich warne Sie, dass Ihr Code nicht unbedingt genau die gleichen Ergebnisse liefert, da wir das Netzwerk mit zufälligen Gewichten und Offsets initialisieren. Für dieses Kapitel habe ich den besten von drei Versuchen ausgewählt.

Lassen Sie uns das Experiment neu starten, indem Sie die Anzahl der versteckten Neuronen auf 100 ändern. Wenn Sie den Code gleichzeitig mit dem Lesen ausführen, denken Sie daran, dass dies ziemlich viel Zeit in Anspruch nimmt (auf meinem Computer dauert jede Ära mehrere zehn Sekunden). Daher ist es besser, parallel zu lesen mit Codeausführung.

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Dies verbessert natürlich das Ergebnis auf 96,59%. Zumindest in diesem Fall hilft die Verwendung von mehr versteckten Neuronen, bessere Ergebnisse zu erzielen.

Die Rückmeldungen der Leser deuten darauf hin, dass die Ergebnisse dieses Experiments sehr unterschiedlich sind und einige Lernergebnisse viel schlechter sind. Verwenden Sie Techniken aus Kapitel 3, um die Vielfalt der Arbeitseffizienz von einem Lauf zum anderen erheblich zu verringern.

Um diese Genauigkeit zu erreichen, musste ich natürlich eine bestimmte Anzahl von Epochen für das Lernen, die Größe des Minipakets und die Lerngeschwindigkeit η auswählen. Wie oben erwähnt, werden sie als Hyperparameter unserer Nationalversammlung bezeichnet, um sie von einfachen Parametern (Gewichte und Offsets) zu unterscheiden, die der Algorithmus während des Trainings anpasst. Wenn wir Hyperparameter schlecht wählen, erhalten wir schlechte Ergebnisse. Nehmen wir zum Beispiel an, wir haben die Lernrate η = 0,001 gewählt:

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data) 

Die Ergebnisse sind viel weniger beeindruckend:

Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000

Sie können jedoch feststellen, dass die Netzwerkeffizienz im Laufe der Zeit langsam zunimmt. Dies deutet darauf hin, dass Sie versuchen können, die Lerngeschwindigkeit beispielsweise auf 0,01 zu erhöhen. In diesem Fall sind die Ergebnisse besser, was darauf hinweist, dass die Geschwindigkeit weiter erhöht werden muss (wenn die Änderung die Situation verbessert, ändern Sie sich weiter!). Wenn Sie dies mehrmals tun, werden wir schließlich zu η = 1,0 (und manchmal sogar 3,0) gelangen, was unseren früheren Experimenten nahe kommt. Obwohl wir Hyperparameter anfangs schlecht ausgewählt haben, haben wir zumindest genügend Informationen gesammelt, um unsere Parameterauswahl verbessern zu können.

Im Allgemeinen ist das Debuggen von NA eine komplizierte Angelegenheit. Dies ist insbesondere dann der Fall, wenn die Auswahl der anfänglichen Hyperparameter zu Ergebnissen führt, die das zufällige Rauschen nicht überschreiten. Angenommen, wir versuchen, eine erfolgreiche Architektur mit 30 Neuronen zu verwenden, ändern jedoch die Lerngeschwindigkeit auf 100,0:

 >>> net = network.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data) 

Am Ende stellt sich heraus, dass wir zu weit gegangen sind und zu viel Geschwindigkeit genommen haben:

Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000

Stellen Sie sich nun vor, wir nähern uns dieser Aufgabe zum ersten Mal. Natürlich wissen wir aus frühen Experimenten, dass es richtig wäre, die Lerngeschwindigkeit zu verringern. Wenn wir uns dieser Aufgabe jedoch zum ersten Mal nähern würden, hätten wir keine Ergebnisse, die uns zur richtigen Lösung führen könnten. Könnten wir anfangen zu denken, dass wir vielleicht die falschen Anfangsparameter für Gewichte und Offsets gewählt haben und es für das Netzwerk schwierig ist zu lernen? Oder haben wir nicht genügend Trainingsdaten, um ein aussagekräftiges Ergebnis zu erzielen? Vielleicht haben wir nicht genug Epochen gewartet? Vielleicht kann ein neuronales Netzwerk mit einer solchen Architektur einfach nicht lernen, handgeschriebene Zahlen zu erkennen? Vielleicht ist die Lerngeschwindigkeit zu langsam? Wenn Sie sich der Aufgabe zum ersten Mal nähern, haben Sie nie Vertrauen.

Daraus lohnt es sich, eine Lektion zu lernen, dass das Debuggen von NS keine triviale Aufgabe ist, und dies ist wie das reguläre Programmieren Teil der Kunst. Sie müssen diese Debugging-Technik lernen, um gute Ergebnisse von NS zu erhalten. Im Allgemeinen müssen wir eine Heuristik entwickeln, um gute Hyperparameter und eine gute Architektur auszuwählen. Wir werden dies im Buch ausführlich diskutieren, einschließlich der Auswahl der obigen Hyperparameter.

Übung

• Versuchen Sie, ein Netzwerk aus nur zwei Schichten - Eingabe und Ausgabe ohne Verstecktheit - mit 784 bzw. 10 Neuronen zu erstellen. Trainieren Sie das Netzwerk mit stochastischem Gefälle. Welche Klassifizierungsgenauigkeit erhalten Sie?

Ich habe zuvor die Details zum Laden von MNIST-Daten übersprungen. Es passiert ganz einfach. Hier ist der Code, um das Bild zu vervollständigen. Datenstrukturen werden in den Kommentaren beschrieben - alles ist einfach, Tupel und Arrays von Numpy ndarray-Objekten (wenn Sie mit solchen Objekten nicht vertraut sind, stellen Sie sie sich als Vektoren vor).

 """ mnist_loader ~~~~~~~~~~~~      MNIST.       ``load_data``  ``load_data_wrapper``.  , ``load_data_wrapper`` -  ,     . """ ####  #  import cPickle import gzip #  import numpy as np def load_data(): """  MNIST   ,  ,    . ``training_data``      .    .  numpy ndarray  50 000 .   –     numpy ndarray  784 ,  28 * 28 = 784    MNIST.  –  numpy ndarray  50 000 .   –   0  9   ,    . ``validation_data``  ``test_data`` ,    10 000 .    ,           ``training_data``.    - ``load_data_wrapper()``. """ f = gzip.open('../data/mnist.pkl.gz', 'rb') training_data, validation_data, test_data = cPickle.load(f) f.close() return (training_data, validation_data, test_data) def load_data_wrapper(): """ ,  ``(training_data, validation_data, test_data)``.   ``load_data``,         .  , ``training_data`` -    50 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   . ``y`` -  10- numpy.ndarray,   ,     ``x``. ``validation_data``  ``test_data`` -  ,   10 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   ,  ``y`` -   ,  ,   ( ),  ``x``. ,  ,           .         .""" tr_d, va_d, te_d = load_data() training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]] training_results = [vectorized_result(y) for y in tr_d[1]] training_data = zip(training_inputs, training_results) validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]] validation_data = zip(validation_inputs, va_d[1]) test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]] test_data = zip(test_inputs, te_d[1]) return (training_data, validation_data, test_data) def vectorized_result(j): """ 10-    1.0   j     .      (0..9)     .""" e = np.zeros((10, 1)) e[j] = 1.0 return e 

Ich sagte, dass unser Programm ziemlich gute Ergebnisse erzielt. Was bedeutet das?Gut im Vergleich zu was? Es ist nützlich, die Ergebnisse einiger einfacher, grundlegender Tests zu haben, mit denen Sie einen Vergleich anstellen können, um zu verstehen, was „gute Ergebnisse“ bedeuten. Das einfachste Basislevel wäre natürlich eine zufällige Vermutung. Dies kann in etwa 10% der Fälle erfolgen. Und wir zeigen ein viel besseres Ergebnis!

Was ist mit einem weniger trivialen Basislevel? Schauen wir uns an, wie dunkel das Bild ist. Beispielsweise ist Bild 2 normalerweise dunkler als Bild 1, einfach weil es mehr dunkle Pixel hat, wie in den folgenden Beispielen gezeigt:



Daraus folgt, dass wir die durchschnittliche Dunkelheit für jede Ziffer von 0 bis 9 berechnen können. Wenn wir ein neues Bild erhalten, berechnen wir dessen Dunkelheit und wir vermuten, dass es eine Zahl mit der nächsten durchschnittlichen Dunkelheit zeigt. Dies ist eine einfache Prozedur, die einfach zu programmieren ist, daher werde ich keinen Code schreiben - bei Interesse liegt sie auf GitHub . Dies ist jedoch eine ernsthafte Verbesserung im Vergleich zu zufälligen Vermutungen - der Code erkennt 2.225 von 10.000 Bildern korrekt, dh er ergibt eine Genauigkeit von 22,25%.

Es ist nicht schwer, andere Ideen zu finden, die eine Genauigkeit im Bereich von 20 bis 50% erreichen. Nachdem Sie etwas mehr gearbeitet haben, können Sie 50% überschreiten. Um jedoch eine viel größere Genauigkeit zu erzielen, ist es besser, maßgebliche MO-Algorithmen zu verwenden. Probieren wir einen der bekanntesten Algorithmen aus, die Support Vector Method oder SVM. Wenn Sie mit SVM nicht vertraut sind, machen Sie sich keine Sorgen, wir müssen diese Details nicht verstehen. Wir verwenden nur eine Python-Bibliothek namens scikit-learn, die eine einfache Schnittstelle zur schnellen C-Bibliothek für SVM bietet, die als LIBSVM bekannt ist .

Wenn wir den SVM-Klassifikator scikit-learn mit den Standardeinstellungen ausführen, erhalten wir die korrekte Klassifizierung von 9.435 von 10.000 (der Code ist unter dem Link verfügbar) Dies ist bereits eine große Verbesserung gegenüber dem naiven Ansatz, Bilder nach Dunkelheit zu klassifizieren. Dies bedeutet, dass SVM ungefähr so ​​gut funktioniert wie unser NS, nur ein bisschen schlechter. In den folgenden Kapiteln werden wir uns mit neuen Techniken vertraut machen, mit denen wir unsere NS so verbessern können, dass sie die SVM deutlich übertreffen.

Das ist aber noch nicht alles.Ergebnis 9 435 von 10 000 aus scikit-learn ist für die Standardeinstellungen angegeben. SVM verfügt über viele Parameter, die angepasst werden können, und Sie können nach Parametern suchen, die dieses Ergebnis verbessern. Ich werde nicht auf Details eingehen, sie können in dem Artikel von Andreas Müller gelesen werden . Er zeigte, dass durch Arbeiten zur Optimierung der Parameter eine Genauigkeit von mindestens 98,5% erreicht werden kann. Mit anderen Worten, eine gut abgestimmte SVM macht nur eine Ziffer aus 70 Fehlern. Ein gutes Ergebnis! Kann NA mehr erreichen?

Es stellt sich heraus, dass sie es können. Heute überholt ein gut abgestimmter NS jede andere bekannte Technologie in der MNIST-Lösung, einschließlich SVM. Rekord für 20139.979 von 10.000 Bildern korrekt klassifiziert. Und wir werden die meisten dafür verwendeten Technologien in diesem Buch sehen. Diese Genauigkeit liegt nahe am Menschen und übertrifft sie vielleicht sogar, da einige Bilder von MNIST selbst für Menschen schwer zu entziffern sind, zum Beispiel: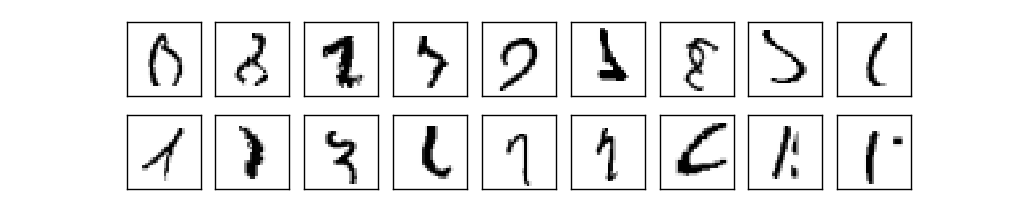



Ich denke, Sie werden zustimmen, dass es schwierig ist, sie zu klassifizieren! Bei solchen Bildern im MNIST-Datensatz ist es überraschend, dass der NS alle 10.000 Bilder mit Ausnahme von 21 korrekt erkennen kann. Normalerweise glauben Programmierer, dass das Lösen einer solch komplexen Aufgabe einen komplexen Algorithmus erfordert. Aber auch die NS ist am WerkDer Rekordhalter verwendet ziemlich einfache Algorithmen, bei denen es sich um kleine Abweichungen von den in diesem Kapitel untersuchten handelt. Die gesamte Komplexität wird während des Trainings automatisch basierend auf den Trainingsdaten angezeigt. In gewissem Sinne ist die Moral unserer Ergebnisse und derjenigen, die in komplexeren Werken enthalten sind, die für einige Aufgaben

komplexer Algorithmus ≤ einfacher Trainingsalgorithmus + gute Trainingsdaten

Zu tiefem Lernen

Obwohl unser Netzwerk eine beeindruckende Leistung zeigt, wird dies auf mysteriöse Weise erreicht. Gewichte und Mischnetzwerke werden automatisch erkannt. Wir haben also keine vorgefertigte Erklärung dafür, wie das Netzwerk das tut, was es tut. Gibt es eine Möglichkeit, die Grundprinzipien der Klassifizierung durch ein Netzwerk handgeschriebener Zahlen zu verstehen? Und ist es angesichts dieser Möglichkeiten möglich, das Ergebnis zu verbessern?

Wir formulieren diese Fragen strenger um: Nehmen wir an, dass sich die NS in einigen Jahrzehnten in künstliche Intelligenz (KI) verwandeln wird. Werden wir verstehen, wie diese KI funktioniert? Vielleicht bleiben die Netzwerke mit ihren Gewichten und Offsets für uns unverständlich, da sie automatisch zugewiesen werden. In den ersten Jahren der KI-Forschung hofften die Menschen, dass der Versuch, KI zu schaffen, uns auch helfen würde, die Prinzipien zu verstehen, die der Intelligenz zugrunde liegen, und vielleicht sogar die Arbeit des menschlichen Gehirns. Am Ende kann sich jedoch herausstellen, dass wir weder das Gehirn noch die Funktionsweise der KI verstehen werden!

Um diese Probleme zu lösen, erinnern wir uns an die Interpretation künstlicher Neuronen, die ich zu Beginn des Kapitels gegeben habe - dass dies eine Möglichkeit ist, Beweise abzuwägen. Angenommen, wir möchten feststellen, ob sich das Gesicht einer Person auf einem Bild befindet:







Dieses Problem kann auf die gleiche Weise wie die Handschrifterkennung angegangen werden: Die Verwendung von Bildpixeln als Eingabe für den NS und die Ausgabe des NS ist ein Neuron, das sagt: "Ja, das ist ein Gesicht" oder "Nein, das ist kein Gesicht" ".

Angenommen, wir tun dies, ohne jedoch einen Lernalgorithmus zu verwenden. Wir werden versuchen, manuell ein Netzwerk zu erstellen und die entsprechenden Gewichte und Offsets auszuwählen. Wie können wir das angehen? Wenn wir die Nationalversammlung vergessen, können wir die Aufgabe für einen Moment in Unteraufgaben unterteilen: Hat das Bild der Augen in der oberen linken Ecke? Gibt es ein Auge in der oberen rechten Ecke? Gibt es eine mittlere Nase? Gibt es einen Mund in der Mitte? Gibt es oben Haare? Usw.

Wenn die Antworten auf mehrere dieser Fragen positiv sind oder sogar „wahrscheinlich ja“, schließen wir, dass das Bild möglicherweise ein Gesicht hat. Umgekehrt, wenn die Antworten nein sind, gibt es wahrscheinlich keine Person.

Dies ist natürlich eine ungefähre Heuristik und weist viele Mängel auf. Vielleicht ist das ein kahlköpfiger Mann, und er hat keine Haare. Vielleicht können wir nur einen Teil des Gesichts oder das Gesicht in einem Winkel sehen, so dass einige Teile des Gesichts geschlossen sind. Die Heuristik legt jedoch nahe, dass wir, wenn wir Teilprobleme mit Hilfe neuronaler Netze lösen können, möglicherweise NSs für die Gesichtserkennung erstellen können, indem wir Netze für Unteraufgaben kombinieren. Das Folgende ist eine mögliche Architektur eines solchen Netzwerks, in dem Subnetze durch Rechtecke angezeigt werden. Dies ist kein völlig realistischer Ansatz zur Lösung des Gesichtserkennungsproblems: Er wird benötigt, um die Arbeit neuronaler Netze intuitiv zu verstehen.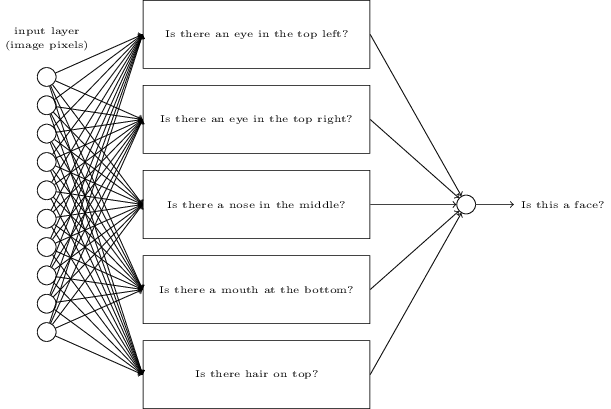


In den Rechtecken gibt es Unteraufgaben: Hat das Bild der Augen in der oberen linken Ecke? Gibt es ein Auge in der oberen rechten Ecke? Gibt es eine mittlere Nase? Gibt es einen Mund in der Mitte? Gibt es oben Haare? Usw.

Es ist möglich, dass Subnetze auch in Komponenten zerlegt werden können. Nehmen Sie die Frage nach einem Auge in der oberen linken Ecke. Es kann unterschieden werden in Fragen wie: "Gibt es eine Augenbraue?", "Gibt es Wimpern?", "Gibt es eine Pupille?" usw. Natürlich sollten Fragen Informationen über den Ort enthalten - "Befindet sich die Augenbraue oben links über der Pupille?" Usw. - aber vereinfachen wir dies zunächst. Daher kann das Netzwerk, das die Frage nach der Anwesenheit des Auges beantwortet, in die Komponenten zerlegt werden:


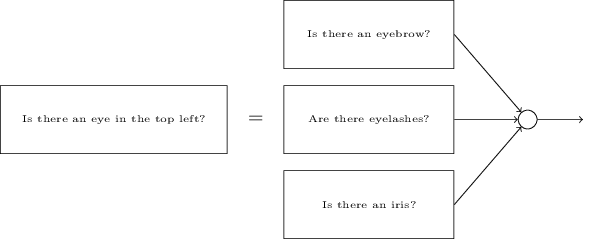"Gibt es eine Augenbraue?", "Gibt es Wimpern?", "Gibt es eine Pupille?"

Diese Fragen können in kleinen Schritten in kleine Schichten unterteilt werden. Daher werden wir mit Subnetzen arbeiten, die so einfache Fragen beantworten, dass sie auf Pixelebene leicht zerlegt werden können. Diese Fragen können beispielsweise das Vorhandensein oder Fehlen einfacher Formen an bestimmten Stellen des Bildes betreffen. Einzelne Neuronen, die mit Pixeln assoziiert sind, können auf sie reagieren.

Das Ergebnis ist ein Netzwerk, das sehr komplexe Fragen - ob sich eine Person im Bild befindet - in sehr einfache Fragen zerlegt, die auf der Ebene der einzelnen Pixel beantwortet werden können. Sie wird dies durch eine Abfolge von vielen Ebenen tun, in denen die ersten Ebenen sehr einfache und spezifische Fragen zum Bild beantworten und die letzteren eine Hierarchie komplexerer und abstrakterer Konzepte erstellen. Netzwerke mit einer solchen Mehrschichtstruktur - zwei oder mehr verborgene Schichten - werden als Deep Neural Networks (GNS) bezeichnet.

Natürlich habe ich nicht darüber gesprochen, wie man dieses rekursive Subnetz macht. Es wird definitiv unpraktisch sein, Gewichte und Offsets manuell auszuwählen. Wir möchten Trainingsalgorithmen verwenden, damit das Netzwerk automatisch Gewichte und Offsets - und durch sie die Hierarchien von Konzepten - basierend auf Trainingsdaten lernt. In den 1980er und 1990er Jahren versuchten Forscher, stochastischen Gradientenabstieg und Backpropagation zu verwenden, um GNS zu trainieren. Leider gelang es ihnen mit Ausnahme einiger spezieller Architekturen nicht. Die Netzwerke trainierten, aber sehr langsam, und in der Praxis war es zu langsam, um irgendwie verwendet zu werden.

Seit 2006 wurden verschiedene Technologien entwickelt, um STS zu trainieren. Sie basieren auf stochastischem Gradientenabstieg und Rückausbreitung, enthalten aber auch neue Ideen. Sie durften viel tiefere Netzwerke trainieren - heute trainieren die Leute leise Netzwerke mit 5-10 Schichten. Und es stellt sich heraus, dass sie viele Probleme viel besser lösen als flache NS, dh Netzwerke mit einer verborgenen Schicht. Der Grund ist natürlich, dass STS eine komplexe Hierarchie von Konzepten erstellen kann. Dies ähnelt der Verwendung modularer Schemata und Abstraktionsideen durch Programmiersprachen, um komplexe Computerprogramme zu erstellen. Um einen tiefen NS mit einem flachen NS zu vergleichen, muss man ungefähr eine Programmiersprache vergleichen, die Funktionsaufrufe mit einer Sprache ausführen kann, die dies nicht tut. Abstraktion in der NS sieht nicht so aus wie in Programmiersprachen,hat aber die gleiche Bedeutung.