Lassen Sie es ein abstraktes Experiment geben, in dessen Verlauf ein bestimmtes Ereignis auftreten kann. Dieses Experiment wurde fünfmal durchgeführt, und in vier von ihnen fand das gleiche Ereignis statt. Welche Schlussfolgerungen können aus diesen 4/5 gezogen werden?

Es
gibt eine Bernoulli-Formel , die die Antwort gibt, mit welcher Wahrscheinlichkeit 4 von 5 mit einer bekannten Anfangswahrscheinlichkeit auftreten. Aber sie gibt keine Antwort, wie hoch war die anfängliche Wahrscheinlichkeit, wenn sich herausstellte, dass die Ereignisse 4 von 5 waren. Lassen wir die Bernoulli-Formel beiseite.
Lassen Sie uns ein einfaches kleines Programm erstellen, das die Wahrscheinlichkeitsprozesse für einen solchen Fall simuliert und basierend auf dem Ergebnis der Berechnungen einen Graphen erstellt.
void test1() { uint sz_ar_events = 50;
Den Code für dieses Programm finden Sie
hier zusammen mit den Zusatzfunktionen.
Die Berechnung wurde in Excel geworfen und ein Zeitplan erstellt.

Diese Version des Graphen kann als Wahrscheinlichkeitsdichteverteilung des Wahrscheinlichkeitswertes bezeichnet werden. Seine Fläche entspricht der Einheit, die in diesem Hügel verteilt ist.
Um das Bild zu vervollständigen, möchte ich erwähnen, dass dieses Diagramm dem Diagramm gemäß der Bernoulli-Formel des Wahrscheinlichkeitsparameters entspricht und die Anzahl der Experimente mit N + 1 multipliziert.
Weiter im Text, wo ich einen Bruchteil der Form k / n im Artikel verwende, ist dies keine Unterteilung, dies sind k Ereignisse aus n Experimenten, um nicht jedes Mal k aus n zu schreiben.
Weiter. Es ist möglich, die Anzahl der Experimente zu erhöhen und einen engeren Bereich des Ortes der Hauptwerte des Wahrscheinlichkeitswertes zu erhalten, aber unabhängig davon, wie sie erhöht werden, wird dieser Bereich nicht mit einer bekannten Wahrscheinlichkeit auf den Nullbereich reduziert.
Die folgende Grafik zeigt die Verteilungen für 4/5, 7/9, 11/14 und 24/30. Je enger die Fläche ist, desto höher ist der Hügel, dessen Fläche eine konstante Einheit ist. Diese Beziehungen wurden gewählt, weil sie alle ungefähr 0,8 sind und nicht weil genau diese bei 0,8 der Anfangswahrscheinlichkeit auftreten können. Ausgewählt, um zu demonstrieren, welcher Bereich möglicher Werte auch bei 30 durchgeführten Experimenten erhalten bleibt.
Der Programmcode für dieses Diagramm ist
hier .

Daraus folgt, dass in der Realität die experimentelle Wahrscheinlichkeit nicht genau bestimmt werden kann, aber wir können nur den Bereich des möglichen Ortes einer solchen Größe annehmen, wobei die Genauigkeit davon abhängt, wie viele Messungen durchgeführt wurden.
Unabhängig davon, wie viele Experimente durchgeführt werden, besteht immer die Möglichkeit, dass die anfängliche Wahrscheinlichkeit sowohl 0,0001 als auch 0,9999 beträgt. Der Einfachheit halber werden extrem unwahrscheinliche Werte verworfen. Und wir nehmen zum Beispiel 95% des Hauptbereichs des Verteilungsplans.
So etwas nennt man Konfidenzintervalle. Ich habe keine Empfehlungen dazu erhalten, wie viel und warum Interesse übrig bleiben sollte. Für die Wettervorhersage benötigen Sie weniger, um mehr Space Shuttles zu starten. Sie erwähnen normalerweise auch nicht, welches Konfidenzintervall dennoch für die Wahrscheinlichkeit von Ereignissen verwendet wird und ob es überhaupt verwendet wird.
In meinem Programm wird hier die Berechnung der Grenzen des Konfidenzintervalls durchgeführt.
Es stellte sich heraus, dass die Wahrscheinlichkeit des Ereignisses durch die Wahrscheinlichkeitsdichte des Wahrscheinlichkeitswertes bestimmt wird, und es ist immer noch erforderlich, einen Prozentsatz des Bereichs der Hauptwerte darauf zu legen, damit Sie zumindest definitiv sagen können, welche Wahrscheinlichkeit das untersuchte Ereignis hat.
Nun zu einem realeren Experiment.
Lassen Sie alle sich mit einer Münze langweilen, werfen Sie diese Münze und holen Sie sich 4 von 5 Tropfen mit dem Schwanz - ein sehr realer Fall. Tatsächlich ist dies nicht ganz das Gleiche wie etwas höher beschrieben. Wie unterscheidet sich das vom vorherigen Experiment?
Das vorherige Experiment wurde unter der Annahme beschrieben, dass die Wahrscheinlichkeit des Ereignisses gleichmäßig über das Intervall von 0 bis 1 verteilt werden kann. Im Programm wird dies durch die Zeile
double Wahrscheinlichkeit = get_random_real_0_1 () angegeben; . Es gibt jedoch keine Münzen mit einer Wahrscheinlichkeit des Fallens, beispielsweise 0,1 oder 0,9 sind immer auf einer Seite.
Wenn Sie tausend verschiedene Münzen von gewöhnlich bis zu den am meisten gekrümmten nehmen und für jede eine Messung des Verlusts durchführen, indem Sie sie tausendmal oder öfter werfen, zeigt dies, dass sie wirklich auf einer Seite im Bereich von 0,4 bis 0,6 herausfallen (dies sind Zufallszahlen, werde ich nicht aber ich suche 1000 Münzen und werfe jeweils 1000 Mal).
Wie ändert diese Tatsache das Programm zur Simulation der Wahrscheinlichkeiten einer bestimmten Münze, für die 4 von 5 Schwänzen empfangen wurden?
Angenommen, die einseitige Verteilung des Verlusts für Münzen wird als Annäherung an den Graphen der Normalverteilung mit den Parametern Durchschnitt = 0,5, Standardabweichung = 0,1 beschrieben. (In der Grafik unten ist es schwarz dargestellt).
Wenn ich in einem Programm die Erzeugung der Anfangswahrscheinlichkeit gemäß der angegebenen Regel von gleichmäßig verteilt auf verteilt ändere, erhalte ich die folgenden Grafiken:
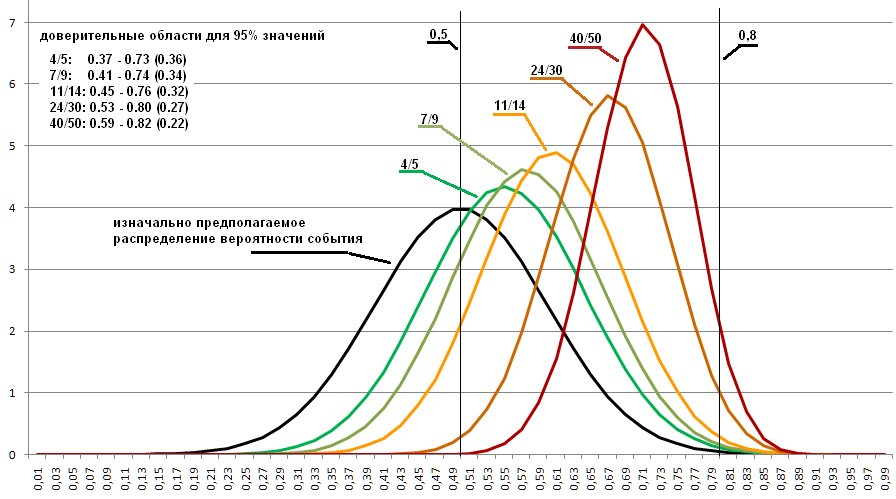
Der Code für diese Option ist
hier .
Es ist ersichtlich, dass sich die Verteilungen stark verschoben haben und nun einen etwas anderen Bereich bestimmen, in dem die gewünschte Wahrscheinlichkeit sehr wahrscheinlich ist. Wenn also bekannt ist, welche Wahrscheinlichkeiten für diese Dinge existieren, von denen wir eine messen möchten, kann dies das Ergebnis etwas verbessern.
Infolgedessen bedeutet 4/5 nichts, und selbst 50 der durchgeführten Experimente sind nicht sehr informativ. Dies sind nur sehr wenige Informationen, um festzustellen, welche Wahrscheinlichkeit dem Experiment noch zugrunde liegt.
== Update ==
Wie
jzha in den Kommentaren erwähnte, können diese Graphen, eine Person, die Mathematik sehr gut kennt, auch unter Verwendung exakter Formeln konstruiert werden. Der Zweck dieses Artikels ist es jedoch, so klar wie möglich zu demonstrieren, wie das, was jeder im Alltag Wahrscheinlichkeit nennt, gebildet wird.
Um es mit exakten Formeln zu erstellen, müssen die verfügbaren Daten zur Wahrscheinlichkeitsverteilung aller Münzen durch Annäherung an die Beta-Verteilung berücksichtigt und durch Berechnung der Verteilungen die Berechnungen bereits abgeleitet werden. Ein solches Schema enthält zahlreiche Erklärungen dazu, und wenn ich es hier beschreibe, wird es sich eher um einen Artikel über mathematische Berechnungen als um alltägliche Wahrscheinlichkeiten handeln.
Wie man die Formeln bekommt, beschreibt einen Sonderfall mit einer Münze, siehe Kommentare von
jzha .