Wie kann die LZ4-Dekomprimierung in ClickHouse beschleunigt werden?

Wenn Sie Abfragen in ClickHouse ausführen , stellen Sie möglicherweise fest, dass der Profiler häufig die Funktion LZ_decompress_fast oben LZ_decompress_fast . Was ist los? Bei dieser Frage haben wir uns gefragt, wie wir den besten Komprimierungsalgorithmus auswählen sollen.

ClickHouse speichert Daten in komprimierter Form. Bei der Ausführung von Abfragen versucht ClickHouse, so wenig wie möglich zu tun, um CPU-Ressourcen zu schonen. In vielen Fällen sind alle potenziell zeitaufwändigen Berechnungen bereits gut optimiert, und der Benutzer hat eine gut durchdachte Abfrage geschrieben. Dann müssen Sie nur noch eine Dekomprimierung durchführen.



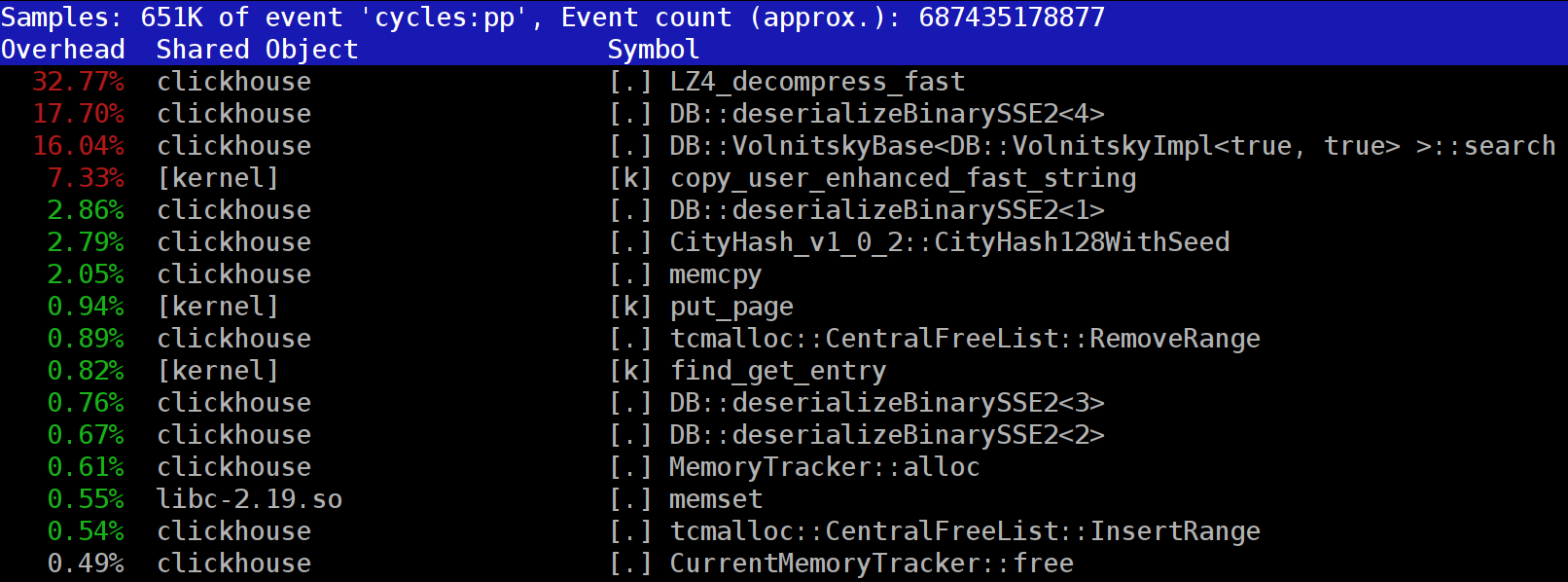
Warum wird die LZ4-Dekomprimierung zum Engpass? LZ4 scheint ein extrem leichter Algorithmus zu sein : Die Datendekomprimierungsrate beträgt je nach Daten normalerweise 1 bis 3 GB / s pro Prozessorkern. Dies ist viel schneller als das typische Festplattensubsystem. Darüber hinaus verwenden wir alle verfügbaren CPU-Kerne, und die Dekomprimierung wird linear über alle physischen Kerne skaliert.

Es sind jedoch zwei Punkte zu beachten. Zunächst werden komprimierte Daten von der Festplatte gelesen, die Dekomprimierungsgeschwindigkeit wird jedoch als Menge nicht komprimierter Daten angegeben. Wenn das Komprimierungsverhältnis groß genug ist, kann fast nichts von den Datenträgern gelesen werden. Es wird jedoch viele dekomprimierte Daten geben, was sich natürlich auf die CPU-Auslastung auswirkt: Im Fall von LZ4 ist der zum Dekomprimieren von Daten erforderliche Arbeitsaufwand nahezu proportional zum Volumen der dekomprimierten Daten selbst.

Zweitens, wenn Daten zwischengespeichert werden, müssen Sie möglicherweise überhaupt keine Daten von Datenträgern lesen. Sie können sich auf den Seitencache verlassen oder Ihren eigenen Cache verwenden. Das Caching ist in spaltenorientierten Datenbanken effizienter, da nur häufig verwendete Spalten im Cache verbleiben. Aus diesem Grund scheint LZ4 häufig ein Engpass in Bezug auf die CPU-Auslastung zu sein.

Dies wirft zwei weitere Fragen auf. Erstens, wenn die Dekomprimierung uns verlangsamt, lohnt es sich zunächst, Daten zu komprimieren? Diese Spekulation ist in der Praxis jedoch irrelevant. Bis vor kurzem bot die ClickHouse-Konfiguration nur zwei Datenkomprimierungsoptionen - LZ4 und Zstandard . Standardmäßig wird LZ4 verwendet. Durch die Umstellung auf Zstandard wird die Komprimierung stärker und langsamer. Es gab jedoch keine Option zum vollständigen Deaktivieren der Komprimierung, da davon ausgegangen wird, dass LZ4 eine angemessene minimale Komprimierung bietet, die immer verwendet werden kann. (Genau deshalb liebe ich LZ4.)

Aber dann erschien im internationalen ClickHouse-Support-Chat ein mysteriöser Fremder, der sagte, er habe ein sehr schnelles Festplattensubsystem (mit NVMe-SSD), und Dekomprimierung ist das einzige, was seine Abfragen verlangsamt. Es wäre also schön, Daten ohne speichern zu können Komprimierung Ich antwortete, dass wir diese Option nicht haben, aber es wäre einfach hinzuzufügen. Einige Tage später erhielten wir eine Pull-Anfrage, die die Komprimierungsmethode none implementiert. Ich habe den Mitwirkenden gebeten, darüber zu berichten, inwieweit diese Option zur Beschleunigung von Abfragen beigetragen hat. Die Antwort war, dass sich diese neue Funktion in der Praxis als nutzlos herausstellte, da die unkomprimierten Daten zu viel Speicherplatz beanspruchten und nicht in diese NVMe-Laufwerke passten.

Die zweite Frage, die sich stellt, lautet: Wenn ein Cache vorhanden ist, warum nicht zum Speichern bereits dekomprimierter Daten verwenden? Dies ist eine praktikable Möglichkeit, die in vielen Fällen die Notwendigkeit einer Dekompression beseitigt. ClickHouse hat auch einen Cache wie diesen: den Cache dekomprimierter Blöcke . Aber es ist schade, viel RAM dafür zu verschwenden. Daher ist es normalerweise nur sinnvoll, kleine, sequentielle Abfragen zu verwenden, bei denen nahezu identische Daten verwendet werden.

Unsere Schlussfolgerung ist, dass es immer vorzuziehen ist, Daten in komprimiertem Format zu speichern. Schreiben Sie Daten immer im komprimierten Format auf die Festplatte. Übertragen Sie Daten auch mit Komprimierung über das Netzwerk. Meiner Meinung nach ist die Standardkomprimierung auch dann gerechtfertigt, wenn Daten innerhalb eines einzelnen Rechenzentrums in einem 10-GB-Netzwerk ohne Überzeichnung übertragen werden, während die Übertragung unkomprimierter Daten zwischen Rechenzentren einfach nicht akzeptabel ist.

Warum LZ4?

Warum LZ4 wählen? Könnten wir nicht etwas noch Leichteres wählen? Theoretisch könnten wir, und das ist ein guter Gedanke. Aber schauen wir uns die Klasse der Algorithmen an, zu denen LZ4 gehört.

Erstens ist es generisch und passt den Datentyp nicht an. Wenn Sie beispielsweise im Voraus wissen, dass Sie ein Array von Ganzzahlen haben, können Sie einen der VarInt-Algorithmen verwenden, wodurch die CPU effektiver genutzt wird. Zweitens ist LZ4 nicht übermäßig von Datenmodellannahmen abhängig. Angenommen, Sie haben eine geordnete Zeitreihe von Sensorwerten, ein Array von Gleitkommazahlen. Wenn Sie dies berücksichtigen, können Sie Deltas zwischen diesen Zahlen berechnen und sie dann mit einem generischen Algorithmus komprimieren, was zu einem höheren Komprimierungsverhältnis führt.

Sie werden keine Probleme haben, LZ4 mit Byte-Arrays oder Dateien zu verwenden. Natürlich hat es eine Spezialisierung (dazu später mehr), und in einigen Fällen ist seine Verwendung sinnlos. Aber wenn wir es einen Allzweckalgorithmus nennen, sind wir der Wahrheit ziemlich nahe. Wir sollten beachten, dass LZ4 dank seines internen Designs den RLE- Algorithmus automatisch als Sonderfall implementiert.

Die wichtigere Frage ist jedoch, ob LZ4 der hinsichtlich der Gesamtgeschwindigkeit und der Kompressionsstärke optimalste Algorithmus dieser Klasse ist. Optimale Algorithmen werden als Pareto-Grenze bezeichnet, was bedeutet, dass es keinen anderen Algorithmus gibt, der auf eine Weise definitiv besser und auf andere Weise nicht schlechter ist (und auch für eine Vielzahl von Datensätzen). Einige Algorithmen sind schneller, führen jedoch zu einem geringeren Komprimierungsverhältnis, während andere eine stärkere Komprimierung aufweisen, sich jedoch langsamer komprimieren oder dekomprimieren lassen.

Um ehrlich zu sein, ist LZ4 nicht wirklich die Pareto-Grenze - es gibt einige Optionen, die nur ein kleines bisschen besser sind. Schauen Sie sich zum Beispiel LZTURBO von einem Entwickler mit dem Spitznamen powturbo an . Dank der encode.ru- Community (dem größten und möglicherweise einzigen Forum zur Datenkomprimierung) besteht kein Zweifel an der Zuverlässigkeit der Ergebnisse. Leider verteilt der Entwickler den Quellcode oder die Binärdateien nicht. Sie stehen nur einer begrenzten Anzahl von Personen zum Testen oder für viel Geld zur Verfügung (obwohl es so aussieht, als hätte noch niemand dafür bezahlt). Schauen Sie sich auch Lizard (früher LZ5) und Density an . Sie funktionieren möglicherweise etwas besser als LZ4, wenn Sie eine bestimmte Komprimierungsstufe auswählen. Eine weitere wirklich interessante Option ist LZSSE . Lesen Sie diesen Artikel jedoch zu Ende, bevor Sie ihn lesen.

Wie funktioniert lz4?

Schauen wir uns an, wie LZ4 im Allgemeinen funktioniert. Dies ist eine der Implementierungen des LZ77-Algorithmus. L und Z stellen die Namen der Entwickler dar (Lempel und Ziv), und 77 steht für das Jahr 1977, als der Algorithmus veröffentlicht wurde. Es gibt viele andere Implementierungen: QuickLZ, FastLZ, BriefLZ, LZF, LZO sowie gzip und zip, wenn niedrige Komprimierungsstufen verwendet werden.

Ein mit LZ4 komprimierter Datenblock enthält eine Folge von Einträgen (Befehlen oder Anweisungen) zweier Typen:

1. Literale: "Nehmen Sie die folgenden N Bytes wie sie sind und kopieren Sie sie in das Ergebnis".
2. Übereinstimmung: "Nehmen Sie N Bytes aus dem dekomprimierten Ergebnis, beginnend mit dem Versatzwert relativ zur aktuellen Position".

Beispiel. Vor der Komprimierung:

 Hello world Hello 

Nach der Komprimierung:

 literals 12 "Hello world " match 5 12 

Wenn wir einen komprimierten Block nehmen und den Cursor durch diesen bewegen, während wir diese Befehle ausführen, erhalten wir als Ergebnis die ursprünglichen unkomprimierten Daten.

So werden Daten also im Grunde genommen dekomprimiert. Die Grundidee ist klar: Um eine Komprimierung durchzuführen, codiert der Algorithmus eine wiederholte Folge von Bytes unter Verwendung von Übereinstimmungen.

Einige Eigenschaften sind auch klar. Dieser byteorientierte Algorithmus zerlegt keine einzelnen Bytes. es kopiert sie nur in ihrer Gesamtheit. Dies unterscheidet sich von der Entropiecodierung. Zum Beispiel ist zstd eine Kombination aus LZ77 und Entropiecodierung.

Beachten Sie, dass der komprimierte Block nicht zu groß sein sollte. Die Größe wird gewählt, um zu vermeiden, dass während der Dekomprimierung viel RAM verschwendet wird, um zu vermeiden, dass der Direktzugriff in der komprimierten Datei (die aus einer großen Anzahl komprimierter Blöcke besteht) zu stark verlangsamt wird. Manchmal passt der Block in einen CPU-Cache. Sie können beispielsweise 64 KB auswählen, damit die Puffer für komprimierte und nicht komprimierte Daten in den L2-Cache passen, wobei die Hälfte noch frei ist.

Wenn wir eine größere Datei komprimieren müssen, können wir die komprimierten Blöcke verketten. Dies ist auch praktisch, um zusätzliche Daten (wie eine Prüfsumme) mit jedem komprimierten Block zu speichern.

Der maximale Versatz für das Match ist begrenzt. In LZ4 liegt die Grenze bei 64 Kilobyte. Dieser Betrag wird als Schiebefenster bezeichnet. Dies bedeutet, dass Übereinstimmungen in einem Fenster von 64 Kilobyte vor dem Cursor gefunden werden können, das mit dem Cursor verschoben wird, wenn er sich vorwärts bewegt.

Schauen wir uns nun an, wie Daten komprimiert werden oder mit anderen Worten, wie übereinstimmende Sequenzen in einer Datei gefunden werden. Sie können immer ein Suffix verwenden (es ist großartig, wenn Sie tatsächlich davon gehört haben). Es gibt Methoden, die gewährleisten, dass sich die längste Übereinstimmung nach der Komprimierung in den vorhergehenden Bytes befindet. Dies wird als optimales Parsen bezeichnet und bietet nahezu das beste Komprimierungsverhältnis für einen komprimierten Block mit festem Format. Es gibt jedoch bessere Ansätze, z. B. eine ausreichend gute Übereinstimmung zu finden, die nicht unbedingt die längste ist. Der effizienteste Weg, dies zu finden, ist die Verwendung einer Hash-Tabelle.

Dazu iterieren wir den Cursor durch den ursprünglichen Datenblock und nehmen einige Bytes nach dem Cursor (sagen wir 4 Bytes). Wir hashen sie und setzen den Offset vom Anfang des Blocks (wo die 4 Bytes entnommen wurden) in die Hash-Tabelle. Der Wert 4 heißt "min-match" - mit dieser Hash-Tabelle können wir Übereinstimmungen von mindestens 4 Bytes finden.

Wenn wir uns die Hash-Tabelle ansehen und sie bereits einen übereinstimmenden Datensatz enthält und der Offset das Schiebefenster nicht überschreitet, prüfen wir, wie viele weitere Bytes nach diesen 4 Bytes übereinstimmen. Vielleicht gibt es noch viel mehr Spiele. Es ist auch möglich, dass es eine Kollision in der Hash-Tabelle gibt und nichts übereinstimmt, aber das ist keine große Sache. Sie können den Wert in der Hash-Tabelle einfach durch einen neuen ersetzen. Kollisionen in der Hash-Tabelle führen einfach zu einem niedrigeren Komprimierungsverhältnis, da weniger Übereinstimmungen vorhanden sind. Diese Art von Hash-Tabelle (mit fester Größe und ohne Auflösung von Kollisionen) wird übrigens als "Cache-Tabelle" bezeichnet. Dieser Name ist sinnvoll, da die Cache-Tabelle im Falle einer Kollision einfach den alten Eintrag vergisst.

Eine Herausforderung für den aufmerksamen Leser. Nehmen wir an, dass die Daten ein Array von UInt32-Zahlen im Little-Endian-Format sind, das einen Teil einer Folge natürlicher Zahlen darstellt: 0, 1, 2 ... Erklären Sie, warum diese Daten bei Verwendung von LZ4 (der Größe der komprimierten Daten) nicht komprimiert werden ist nicht kleiner als die unkomprimierten Daten).

Wie man alles beschleunigt

Deshalb möchte ich die LZ4-Dekomprimierung beschleunigen. Mal sehen, wie die Dekomprimierungsschleife aussieht. Hier ist es im Pseudocode:

 while (...) {    read(input_pos, literal_length, match_length);    copy(output_pos, input_pos, literal_length);    output_pos += literal_length;    read(input_pos, match_offset);    copy(output_pos, output_pos - match_offset,        match_length);    output_pos += match_length; } 

Das LZ4-Format ist so konzipiert, dass sich Literale und Übereinstimmungen in einer komprimierten Datei abwechseln. Offensichtlich steht das Literal immer an erster Stelle (weil es von Anfang an keinen Ort gibt, an dem man ein Match spielen kann). Daher werden ihre Längen zusammen codiert.

Es ist eigentlich etwas komplizierter. Ein Byte wird aus der Datei gelesen und dann in zwei Halbbytes (Halbbytes) aufgeteilt, die die codierten Zahlen 0 bis 15 enthalten. Wenn die entsprechende Zahl nicht 15 ist, wird angenommen, dass sie die Länge des Literals und der Übereinstimmung ist. jeweils. Und wenn es 15 ist, ist die Länge länger und es wird in den folgenden Bytes codiert. Dann wird das nächste Byte gelesen und sein Wert zur Länge addiert. Wenn es gleich 255 ist, wird dasselbe mit dem nächsten Byte gemacht.

Beachten Sie, dass das maximale Komprimierungsverhältnis für das LZ4-Format 255 nicht erreicht. Eine weitere nutzlose Beobachtung ist, dass die zweimalige Verwendung von LZ4 das Komprimierungsverhältnis verbessert, wenn Ihre Daten sehr redundant sind.

Wenn wir die Länge eines Literals (und dann die Übereinstimmungslänge und den Übereinstimmungsversatz) lesen, reicht es aus, nur zwei Speicherblöcke zu kopieren, um es zu dekomprimieren.

So kopieren Sie einen Speicherblock

Es scheint, als könnten Sie einfach die memcpy Funktion verwenden, mit der Speicherblöcke kopiert werden. Dies ist jedoch nicht der optimale Ansatz und nicht wirklich angemessen.

Die Verwendung von memcpy ist nicht optimal, weil:

1. Es befindet sich normalerweise in der libc-Bibliothek (und die libc-Bibliothek ist normalerweise dynamisch verknüpft, sodass der memcpy-Aufruf indirekt über PLT erfolgt).
2. Es wird vom Compiler nicht eingefügt, wenn das Größenargument zur Kompilierungszeit unbekannt ist.
3. Es ist sehr aufwendig, die Reste eines Speicherblocks, die nicht Vielfache der Maschinenwortlänge oder des Maschinenregisters sind, korrekt zu verarbeiten.

Der letzte Punkt ist der wichtigste. Angenommen, wir haben die memcpy-Funktion gebeten, genau 5 Bytes zu kopieren. Es wäre großartig, 8 Bytes sofort mit zwei movq-Anweisungen zu kopieren.

Hello world Hello wo ...
^^^^^ ^^^ - src
^^^^^ ^^^ - dst

Aber dann werden wir drei zusätzliche Bytes kopieren, also werden wir außerhalb der Puffergrenzen schreiben. Die memcpy Funktion hat keine Berechtigung dazu, da sie einige Daten in unserem Programm überschreiben und zu einem Speicher-Stomping-Fehler führen kann. Und wenn wir an eine nicht ausgerichtete Adresse schreiben, können diese zusätzlichen Bytes auf einer nicht zugewiesenen Seite des virtuellen Speichers oder auf einer Seite ohne Schreibzugriff landen. Das würde uns einen Segmentierungsfehler geben (das ist gut).

In unserem Fall können wir jedoch fast immer zusätzliche Bytes schreiben. Wir können zusätzliche Bytes im Eingabepuffer lesen, solange sich die zusätzlichen Bytes vollständig darin befinden. Unter den gleichen Bedingungen können wir die zusätzlichen Bytes in den Ausgabepuffer schreiben, da wir sie bei der nächsten Iteration weiterhin überschreiben.

Diese Optimierung ist bereits in der ursprünglichen Implementierung von LZ4 enthalten:

 inline void copy8(UInt8 * dst, const UInt8 * src) {    memcpy(dst, src, 8); /// Note that memcpy isn't actually called here. } inline void wildCopy8(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) {    do    {        copy8(dst, src);        dst += 8;        src += 8;    } while (dst < dst_end); } 

Um diese Optimierung nutzen zu können, müssen wir nur sicherstellen, dass wir weit genug von den Puffergrenzen entfernt sind. Dies sollte nichts kosten, da wir bereits nach Pufferüberlauf suchen. Die Verarbeitung der letzten Bytes, der "verbleibenden" Daten, kann nach der Hauptschleife erfolgen.

Es gibt jedoch noch einige Nuancen. Das Kopieren erfolgt zweimal in der Schleife: mit einem Literal und einer Übereinstimmung. Bei Verwendung der Funktion LZ4_decompress_fast (anstelle von LZ4_decompress_safe ) wird die Prüfung jedoch nur einmal durchgeführt, wenn das Literal kopiert werden muss. Die Überprüfung wird beim Kopieren der Übereinstimmung nicht durchgeführt, aber die Spezifikation für das LZ4-Format enthält Bedingungen, die es Ihnen ermöglichen, dies zu vermeiden:

Die letzten 5 Bytes sind immer Literale.
Die letzte Übereinstimmung muss mindestens 12 Byte vor dem Ende des Blocks beginnen.
Folglich kann ein Block mit weniger als 13 Bytes nicht komprimiert werden.

Speziell ausgewählte Eingabedaten können zu einer Speicherbeschädigung führen. Wenn Sie die Funktion LZ4_decompress_fast verwenden, benötigen Sie Schutz vor fehlerhaften Daten. Zumindest sollten Sie Prüfsummen für die komprimierten Daten berechnen. Wenn Sie Schutz vor Hackern benötigen, verwenden Sie die Funktion LZ4_decompress_safe . Andere Optionen: Verwenden Sie eine kryptografische Hash-Funktion als Prüfsumme (obwohl dies wahrscheinlich die Leistung beeinträchtigt). reservieren Sie mehr Speicher für Puffer; Ordnen Sie Speicher für Puffer mit einem separaten mmap Aufruf zu und erstellen Sie eine Schutzseite.

Wenn ich Code sehe, der 8 Datenbytes kopiert, frage ich mich sofort, warum genau 8 Bytes. Sie können 16 Bytes mit SSE-Registern kopieren:

 inline void copy16(UInt8 * dst, const UInt8 * src) { #if __SSE2__    _mm_storeu_si128(reinterpret_cast<__m128i *>(dst),        _mm_loadu_si128(reinterpret_cast<const __m128i *>(src))); #else    memcpy(dst, src, 16); #endif } inline void wildCopy16(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) {    do    {        copy16(dst, src);        dst += 16;        src += 16;    } while (dst < dst_end); } 

Das gleiche gilt für das Kopieren von 32 Byte für AVX und 64 Byte für AVX-512. Außerdem können Sie die Schleife mehrmals abrollen. Wenn Sie sich jemals angesehen haben, wie memcpy implementiert ist, ist dies genau der Ansatz, der verwendet wird. (Übrigens wird der Compiler die Schleife in diesem Fall nicht entrollen oder vektorisieren, da hierfür umfangreiche Überprüfungen eingefügt werden müssen.)

Warum hat die ursprüngliche LZ4-Implementierung dies nicht getan? Erstens ist nicht klar, ob dies besser oder schlechter ist. Der resultierende Gewinn hängt von der Größe der zu kopierenden Blöcke ab. Wenn sie also alle kurz sind, würde dies zusätzliche Arbeit für nichts bedeuten. Und zweitens werden die Bestimmungen im LZ4-Format ruiniert, die dazu beitragen, unnötige Verzweigungen in der internen Schleife zu vermeiden.

Wir werden diese Option jedoch vorerst berücksichtigen.

Schwieriges Kopieren

Kehren wir zur Frage zurück, ob es immer möglich ist, Daten auf diese Weise zu kopieren. Angenommen, wir müssen eine Übereinstimmung kopieren, dh ein Stück Speicher aus dem Ausgabepuffer nehmen, der sich in einem gewissen Versatz hinter dem Cursor befindet, und ihn an die Cursorposition kopieren.

Stellen Sie sich einen einfachen Fall vor, in dem Sie 5 Bytes mit einem Versatz von 12 kopieren müssen:

Hello world ...........
^^^^^ - src
^^^^^ - dst

Hello world Hello wo ...
^^^^^ - src
^^^^^ - dst

Es gibt jedoch einen schwierigeren Fall, wenn wir einen Speicherblock kopieren müssen, der länger als der Offset ist. Mit anderen Worten, es enthält einige Daten, die noch nicht in den Ausgabepuffer geschrieben wurden.

Kopieren Sie 10 Bytes mit einem Offset von 3:

abc .............
^^^^^^^^^^ - src
^^^^^^^^^^ - dst

abc abcabcabca ...
^^^^^^^^^^ - src
^^^^^^^^^^ - dst

Wir haben alle Daten während des Komprimierungsprozesses, und eine solche Übereinstimmung kann durchaus gefunden werden. Die memcpy Funktion eignet sich nicht zum Kopieren, da sie den Fall nicht unterstützt, wenn sich Bereiche von Speicherblöcken überlappen. Die memmove Funktion funktioniert auch nicht, da der Speicherblock, aus dem die Daten entnommen werden sollen, noch nicht vollständig initialisiert wurde. Wir müssen auf die gleiche Weise kopieren, als würden wir Byte für Byte kopieren.

 op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; ... 

So funktioniert es:

a bc a ............
^ - src
^ - dst

a b ca b ...........
^ - src
^ - dst

ab c ab c ..........
^ - src
^ - dst

abc a bc a .........
^ - src
^ - dst

abca b ca b ........
^ - src
^ - dst

Mit anderen Worten, wir müssen eine sich wiederholende Sequenz erstellen. Die ursprüngliche Implementierung von LZ4 verwendete dazu überraschend seltsamen Code:

 const unsigned dec32table[] = {0, 1, 2, 1, 4, 4, 4, 4}; const int dec64table[] = {0, 0, 0, -1, 0, 1, 2, 3}; const int dec64 = dec64table[offset]; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += dec32table[offset]; memcpy(op+4, match, 4); match -= dec64; 

Es kopiert die ersten 4 Bytes nacheinander, überspringt eine magische Zahl, kopiert die nächsten 4 Bytes vollständig und bewegt den Cursor mit einer anderen magischen Zahl zu einer Übereinstimmung. Der Autor des Codes ( Yan Collet ) hat irgendwie vergessen, einen Kommentar zu hinterlassen, was dies bedeutet. Außerdem sind die Variablennamen verwirrend. Sie heißen beide dec ... table, aber eine wird hinzugefügt und die andere wird subtrahiert. Außerdem ist einer von ihnen nicht signiert und der andere ist int. Der Autor hat diesen Platz im Code jedoch kürzlich verbessert.

So funktioniert es tatsächlich. Wir kopieren die ersten 4 Bytes nacheinander:

abc abca .........
^^^^ - src
^^^^ - dst

Jetzt können wir 4 Bytes gleichzeitig kopieren:

abcabca bcab .....
^^^^ - src
^^^^ - dst

Wir können wie gewohnt fortfahren und 8 Bytes gleichzeitig kopieren:

abcabcabcab cabcabca .....
^^^^^^^^ - src
^^^^^^^^ - dst

Wie wir alle aus Erfahrung wissen, ist es manchmal am besten, Code neu zu schreiben, um ihn zu verstehen. Folgendes haben wir uns ausgedacht:

 inline void copyOverlap8(UInt8 * op, const UInt8 *& match, const size_t offset) {    /// 4 % n.    /// Or if 4 % n is zero, we use n.    /// It gives an equivalent result, but is more CPU friendly for unknown reasons.    static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4 };    /// 8 % n - 4 % n    static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3 };    op[0] = match[0];    op[1] = match[1];    op[2] = match[2];    op[3] = match[3];    match += shift1[offset];    memcpy(op + 4, match, 4);    match += shift2[offset]; } 

Wie erwartet ändert dies nichts an der Leistung. Ich wollte nur unbedingt die Optimierung für das gleichzeitige Kopieren von 16 Bytes ausprobieren.

Dies erschwert jedoch den "Sonderfall" und führt dazu, dass er häufiger aufgerufen wird (die Bedingung " offset < 16 wird mindestens so oft ausgeführt wie der offset < 8 ). Das Kopieren überlappender Bereiche mit 16-Byte-Kopieren sieht folgendermaßen aus (nur der Anfang wird angezeigt):

 inline void copyOverlap16(UInt8 * op, const UInt8 *& match, const size_t offset) {    /// 4 % n.    static constexpr int shift1[]        = { 0, 1, 2, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 };    /// 8 % n - 4 % n    static constexpr int shift2[]        = { 0, 0, 0, 1, 0, -1, -2, -3, -4, 4, 4, 4, 4, 4, 4, 4 };    /// 16 % n - 8 % n    static constexpr int shift3[]        = { 0, 0, 0, -1, 0, -2, 2, 1, 8, -1, -2, -3, -4, -5, -6, -7 };    op[0] = match[0];    op[1] = match[1];    op[2] = match[2];    op[3] = match[3];    match += shift1[offset];    memcpy(op + 4, match, 4);    match += shift2[offset];    memcpy(op + 8, match, 8);    match += shift3[offset]; } 

Kann diese Funktion effektiver implementiert werden? Wir möchten eine magische SIMD-Anweisung für solch komplexen Code finden, da wir nur 16 Bytes schreiben möchten, die vollständig aus einigen Bytes Eingabedaten bestehen (von 1 bis 15). Dann müssen sie nur noch in der richtigen Reihenfolge wiederholt werden.

Es gibt eine pshufb Anweisung namens pshufb (gepackte Shuffle-Bytes), die Teil von SSSE3 (drei S) ist. Es akzeptiert zwei 16-Byte-Register. Eines der Register enthält die Quelldaten. Der andere hat den "Selektor": Jedes Byte enthält eine Zahl von 0 bis 15, abhängig davon, aus welchem ​​Byte des Quellregisters das Ergebnis entnommen werden soll. Wenn der Bytewert des Selektors größer als 127 ist, wird das entsprechende Byte des Ergebnisses mit Null gefüllt.

Hier ist ein Beispiel:

  xmm0: abc .............
 xmm1: 0120120120120120

 pshufb% xmm1,% xmm0

 xmm0: abcabcabcabcabca 

Jedes Byte des Ergebnisses wird mit dem ausgewählten Byte der Quelldaten gefüllt - genau das brauchen wir! So sieht der Code im Ergebnis aus:

 inline void copyOverlap16Shuffle(UInt8 * op, const UInt8 *& match, const size_t offset) { #ifdef __SSSE3__    static constexpr UInt8 __attribute__((__aligned__(16))) masks[] =    {        0, 1, 2, 1, 4, 1, 4, 2, 8, 7, 6, 5, 4, 3, 2, 1, /* offset = 0, not used as mask, but for shift amount instead */        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, /* offset = 1 */        0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1,        0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0,        0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3,        0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0,        0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3,        0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1,        0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7,        0, 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, 2, 3, 4, 5, 6,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 0, 1, 2,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 0, 1,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 0,    };    _mm_storeu_si128(reinterpret_cast<__m128i *>(op),        _mm_shuffle_epi8(            _mm_loadu_si128(reinterpret_cast<const __m128i *>(match)),            _mm_load_si128(reinterpret_cast<const __m128i *>(masks) + offset)));    match += masks[offset]; #else    copyOverlap16(op, match, offset); #endif } 

Hier ist _mm_shuffle_epi8 eine intrinsische Eigenschaft , die mit dem pshufb CPU-Befehl kompiliert wird.

Können wir diesen Vorgang mit neueren Anweisungen für mehrere Bytes gleichzeitig ausführen? Immerhin ist SSSE3 ein sehr alter Befehlssatz, der seit 2006 existiert. AVX2 verfügt über einen Befehl, der dies für 32 Bytes gleichzeitig, jedoch separat für einzelne 16-Byte-Lanes ausführt. Dies wird als vektorpermute Bytes bezeichnet und nicht als gepackte Shuffle-Bytes - die Wörter sind unterschiedlich, aber die Bedeutung ist dieselbe. AVX-512 VBMI verfügt über eine weitere Anweisung, die für 64 Byte gleichzeitig funktioniert. Prozessoren, die dies unterstützen, wurden jedoch erst kürzlich angezeigt. ARM NEON hat ähnliche Anweisungen namens vtbl (Vector Table Lookup), aber sie erlauben nur das Schreiben von 8 Bytes.

Zusätzlich gibt es eine Version des pshufb Befehls mit 64-Bit-MMX-Registern, um 8 Bytes zu bilden. Es ist genau richtig, um die Originalversion des Codes zu ersetzen. Ich habe mich jedoch (aus schwerwiegenden Gründen) für die 16-Byte-Option entschieden.

Auf der Highload ++ Siberia-Konferenz kam nach meiner Präsentation ein Teilnehmer auf mich zu und erwähnte, dass Sie für den 8-Byte-Fall nur die Multiplikation mit einer speziell ausgewählten Konstante verwenden können (Sie benötigen auch einen Offset) - dies war noch nicht einmal geschehen zu mir vor!

So entfernen Sie eine überflüssige if-Anweisung

Angenommen, ich möchte eine Variante verwenden, die 16 Bytes kopiert. Wie kann ich vermeiden, dass eine zusätzliche Überprüfung auf Pufferüberlauf durchgeführt werden muss?

Ich entschied, dass ich diesen Check einfach nicht machen würde. Die Kommentare zur Funktion besagen, dass der Entwickler einen Speicherblock für eine bestimmte Anzahl von Bytes mehr als erforderlich zuweisen sollte, damit wir dort unnötigen Müll lesen und schreiben können. Die Benutzeroberfläche der Funktion ist schwieriger zu verwenden, dies ist jedoch ein anderes Problem.

Tatsächlich könnte es negative Konsequenzen geben. Angenommen, die Daten, die zum Dekomprimieren benötigt werden, wurden aus Blöcken von jeweils 65.536 Byte gebildet. Dann gibt uns der Benutzer ein Stück Speicher, das 65.536 Bytes für die dekomprimierten Daten beträgt. Mit der neuen Funktionsschnittstelle muss der Benutzer jedoch einen Speicherblock zuweisen, der beispielsweise 65.551 Byte umfasst. Dann kann der Allokator gezwungen sein, abhängig von seiner Implementierung tatsächlich 96 oder sogar 128 Kilobyte zuzuweisen. Wenn der Allokator sehr schlecht ist, munmap er möglicherweise plötzlich auf, den Speicher im "Heap" zwischenzuspeichern, und verwendet jedes Mal mmap und munmap für die Speicherzuweisung (oder gibt den Speicher mit madvice ). Dieser Vorgang ist aufgrund von Seitenfehlern extrem langsam. Infolgedessen könnte diese kleine Optimierung alles verlangsamen.

Gibt es eine Beschleunigung?

Also habe ich eine Version des Codes erstellt, die drei Optimierungen verwendet:

1. Kopieren von 16 Bytes anstelle von 8.
2. Verwenden Sie die Shuffle-Anweisungen für den Fall offset < 16 .
3. Ein Extra entfernt, wenn.

Ich habe begonnen, diesen Code an verschiedenen Datensätzen zu testen, und habe unerwartete Ergebnisse erhalten.

Beispiel 1:
Xeon E2650v2, Yandex-Browserdaten, AppVersion-Spalte.
Referenz: 1,67 GB / s.
16 Bytes, Shuffle: 2,94 GB / s (76% schneller).

Beispiel 2:
Xeon E2650v2, Yandex Direct-Daten, Spalte ShowsSumPosition.
Referenz: 2,30 GB / s.
16 Bytes, Shuffle: 1,91 GB / s (20% langsamer).

Ich war zuerst sehr glücklich, als ich sah, dass sich alles um einen so großen Prozentsatz beschleunigt hatte. Dann sah ich, dass mit anderen Dateien nichts schneller war. Für einige von ihnen war es sogar etwas langsamer. Ich kam zu dem Schluss, dass die Ergebnisse vom Kompressionsverhältnis abhängen. Je stärker die Datei komprimiert ist, desto größer ist der Vorteil des Wechsels auf 16 Byte. Dies fühlt sich natürlich an: Je größer das Komprimierungsverhältnis ist, desto länger ist die durchschnittliche Länge der zu kopierenden Fragmente.

Zur Untersuchung habe ich C ++ - Vorlagen verwendet, um Codeoptionen für vier Fälle zu erstellen: Verwenden von 8-Byte- oder 16-Byte-Blöcken und mit oder ohne Shuffle-Anweisung.

 template <size_t copy_amount, bool use_shuffle> void NO_INLINE decompressImpl(    const char * const source,    char * const dest,    size_t dest_size) 

Völlig unterschiedliche Varianten des Codes zeigten bei verschiedenen Dateien eine bessere Leistung, aber beim Testen auf einem Desktop gewann immer die Version mit Shuffle. Das Testen auf einem Desktop ist unpraktisch, da Sie Folgendes tun müssen:

 sudo echo 'performance' | tee /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor kill -STOP $(pidof firefox) $(pidof chromium) 

Dann ging ich auf einen der alten "Entwicklungs" -Server (mit dem Xeon E5645-Prozessor), nahm noch mehr Datensätze und erzielte fast die gegenteiligen Ergebnisse, was mich total verwirrte. Es stellt sich heraus, dass die Wahl des optimalen Algorithmus zusätzlich zum Komprimierungsverhältnis vom Prozessormodell abhängt. Der Prozessor bestimmt, wann es am besten ist, den Shuffle-Befehl zu verwenden, sowie den Schwellenwert für den Beginn des 16-Byte-Kopierens.

Übrigens ist es beim Testen auf unseren Servern sinnvoll, dies zu tun:

 sudo kill -STOP $(pidof python) $(pidof perl) $(pgrep -u skynet) $(pidof cqudp-client) 

Andernfalls sind die Ergebnisse instabil. Achten Sie auch auf thermische Drosselung und Leistungsbegrenzung.

So wählen Sie den besten Algorithmus aus

Wir haben also vier Varianten des Algorithmus und müssen die beste für die Bedingungen auswählen. Wir könnten einen repräsentativen Satz von Daten und Hardware erstellen, dann ernsthafte Lasttests durchführen und die Methode auswählen, die im Durchschnitt am besten ist. Wir haben jedoch keinen repräsentativen Datensatz. Zum Testen habe ich eine Stichprobe von Daten von Yandex Metrica , Yandex Direct, Yandex Browser und Flügen in den USA verwendet . Dies reicht jedoch nicht aus, da ClickHouse von Hunderten von Unternehmen auf der ganzen Welt verwendet wird. Durch eine Überoptimierung eines Datensatzes kann es zu Leistungseinbußen bei anderen Daten kommen, die nicht einmal realisiert werden. Und wenn die Ergebnisse vom Prozessormodell abhängen, müssen wir die Bedingungen explizit in den Code schreiben und auf jedem Modell testen (oder das Referenzhandbuch zu Timing-Anweisungen konsultieren, was denken Sie?). In beiden Fällen ist dies zu zeitaufwändig.

Deshalb habe ich mich für eine andere Methode entschieden, die für Kollegen, die an unserer School of Data Analysis studiert haben, offensichtlich ist: "mehrarmige Banditen" . Der Punkt ist, dass die Variante des Algorithmus zufällig ausgewählt wird und wir dann Statistiken verwenden, um zunehmend häufiger die Optionen auszuwählen, die eine bessere Leistung erzielen.

Wir haben viele Datenblöcke, die dekomprimiert werden müssen, daher benötigen wir unabhängige Funktionsaufrufe zum Dekomprimieren von Daten. Wir könnten einen der vier Algorithmen für jeden Block auswählen und seine Ausführungszeit messen. Ein solcher Vorgang kostet normalerweise nichts im Vergleich zur Verarbeitung eines Datenblocks, und in ClickHouse beträgt ein Block unkomprimierter Daten mindestens 64 KB. (Lesen Sie diesen Artikel über die Zeitmessung.)

Um ein besseres Verständnis für die Funktionsweise des Algorithmus "Mehrarmige Banditen" zu erhalten, schauen wir uns an, woher der Name stammt. Dies ist eine Analogie zu Spielautomaten in einem Casino, die mehrere Hebel haben, die ein Spieler ziehen kann, um einen zufälligen Geldbetrag zu erhalten. Der Spieler kann die Hebel mehrmals in beliebiger Reihenfolge ziehen. Jeder Hebel hat eine feste Wahrscheinlichkeit für den entsprechenden ausgegebenen Geldbetrag, aber der Spieler weiß nicht, wie er funktioniert, und kann ihn nur aus der Erfahrung des Spielens lernen. Sobald sie es herausgefunden haben, können sie ihre Gewinne maximieren.

Ein Ansatz zur Maximierung der Belohnung besteht darin, die Wahrscheinlichkeitsverteilung für jeden Hebel bei jedem Schritt basierend auf den Spielstatistiken aus den vorherigen Schritten zu bewerten. Dann "gewinnen" wir mental eine zufällige Belohnung für jeden Hebel, basierend auf den erhaltenen Verteilungen. Schließlich ziehen wir den Hebel, der das beste Ergebnis in unserem mentalen Spiel erzielt hat. Dieser Ansatz wird als Thompson Sampling bezeichnet.

Wir wählen jedoch einen Dekomprimierungsalgorithmus. Das Ergebnis ist die Ausführungszeit in Pikosekunden pro Byte: Je weniger, desto besser. Wir werden die Ausführungszeit als Zufallsvariable betrachten und ihre Verteilung mithilfe mathematischer Statistiken bewerten. Der Bayes'sche Ansatz wird häufig für solche Aufgaben verwendet, aber es wäre umständlich, komplexe Formeln in C ++ - Code einzufügen. Wir können einen parametrischen Ansatz verwenden und sagen, dass eine Zufallsvariable zu einer parametrischen Familie von Zufallsvariablen gehört, und dann ihre Parameter bewerten.

Wie wählen wir die Familie der Zufallsvariablen aus? Als Beispiel könnten wir annehmen, dass die Ausführungszeit des Codes normal verteilt ist. Das ist aber absolut falsch. Erstens kann die Ausführungszeit nicht negativ sein, und die Normalverteilung nimmt überall auf der Zahlenlinie Werte an. Zweitens gehe ich davon aus, dass die Ausführungszeit am rechten Ende einen schweren "Schwanz" haben wird.

Es gibt jedoch Faktoren, die es zu einer guten Idee machen könnten, die Normalverteilung nur für die Zwecke der Thompson-Stichprobe zu schätzen (trotz der Tatsache, dass die Verteilung der Zielvariablen nicht unbedingt normal ist). Der Grund dafür ist, dass es sehr einfach ist, die mathematische Erwartung und die Varianz zu berechnen, und nach einer ausreichenden Anzahl von Iterationen wird eine Normalverteilung ziemlich eng, nicht viel anders als die Verteilungen, die wir mit anderen Methoden erhalten hätten. Wenn wir uns bei den ersten Schritten nicht zu sehr mit der Konvergenzrate befassen, können diese Details ignoriert werden.

This may seem like a somewhat ignorant approach. Experience has shown us that the average time for query execution, website page loading, and so on is "garbage" that isn't worth calculating. It would be better to calculate the median, which is a robust statistic . But this is a little more difficult, and as I will show later, the described method justifies itself for practical purposes.

At first I implemented calculation of the mathematical expectation and variance, but then I decided that this is too good, and I need to simplify the code to make it "worse":

 /// For better convergence, we don't use proper estimate of stddev. /// We want to eventually separate the two algorithms even in cases /// when there is no statistical significant difference between them. double sigma() const {    return mean() / sqrt(adjustedCount()); } double sample(pcg64 & rng) const {    ...    return std::normal_distribution<>(mean(), sigma())(rng); } 

I wrote it so that the first few iterations were not taken into account, to eliminate the effect of memory latencies.

The result is a test program that can select the best algorithm for the input data, with optional modes that use the reference implementation of LZ4 or a specific version of the algorithm.

So there are six options:
— Reference (baseline): original LZ4 without our modifications.
— Variant 0: copy 8 bytes at a time without shuffle.
— Variant 1: copy 8 bytes at a time with shuffle.
— Variant 2: copy 16 bytes at a time without shuffle.
— Variant 3: copy 16 bytes at a time with shuffle.
— The "bandit" option, which selects the best of the four optimized variants.

Testing on different CPUs

If the result strongly depends on the CPU model, it would be interesting to find out exactly how it is affected. There might be an exceptionally large difference on certain CPUs.

I prepared a set of datasets from different tables in ClickHouse with real data, for a total of 256 different files each with 100 MB of uncompressed data (the number 256 was coincidental). Then I looked at the CPUs of the servers where I can run benchmarks. I found servers with the following CPUs:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz

The most interesting part comes next — the processors provided by the R&D department:
— AMD EPYC 7351 16-Core Processor, a new AMD server processor.
— Cavium ThunderX2, which is AArch64, not x86. For these, my SIMD optimization needed to be reworked a bit. The server has 224 logical and 56 physical cores.

There are 13 servers in total, and each of them runs the test on 256 files in 6 variants (reference, 0, 1, 2, 3, adaptive). The test is run 10 times, alternating between the options in random order. It outputs 199,680 results that we can compare.

For example, we can compare different CPUs with each other. But we shouldn't jump to conclusions from these results, because we are only testing the LZ4 decompression algorithm on a single core (this is a very narrow case, so we only get a micro-benchmark). For example, the Cavium has the lowest performance per single core. But I tested ClickHouse on it myself, and it wins out over Xeon E5-2650 v2 on heavy queries due to the greater number of cores, even though it is missing many optimizations that are made in ClickHouse specifically for the x86.

 ┌─cpu───────────────────┬──ref─┬─adapt─┬──max─┬─best─┬─adapt_boost─┬─max_boost─┬─adapt_over_max─┐
│ E5-2667 v2 @ 3.30GHz │ 2.81 │ 3.19 │ 3.15 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2650 v2 @ 2.60GHz │ 2.5 │ 2.84 │ 2.81 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2683 v4 @ 2.10GHz │ 2.26 │ 2.63 │ 2.59 │ 3 │ 1.16 │ 1.15 │ 1.02 │
│ E5-2660 v4 @ 2.00GHz │ 2.15 │ 2.49 │ 2.46 │ 3 │ 1.16 │ 1.14 │ 1.01 │
│ AMD EPYC 7351 │ 2.03 │ 2.44 │ 2.35 │ 3 │ 1.20 │ 1.16 │ 1.04 │
│ E5-2660 0 @ 2.20GHz │ 2.13 │ 2.39 │ 2.37 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E312xx (Sandy Bridge) │ 1.97 │ 2.2 │ 2.18 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E5530 @ 2.40GHz │ 1.65 │ 1.93 │ 1.94 │ 3 │ 1.17 │ 1.18 │ 0.99 │
│ E5645 @ 2.40GHz │ 1.65 │ 1.92 │ 1.94 │ 3 │ 1.16 │ 1.18 │ 0.99 │
│ AMD Opteron 6380 │ 1.47 │ 1.58 │ 1.56 │ 1 │ 1.07 │ 1.06 │ 1.01 │
│ AMD Opteron 6274 │ 1.15 │ 1.35 │ 1.35 │ 1 │ 1.17 │ 1.17 │ 1 │
│ E5440 @ 2.83GHz │ 1.35 │ 1.33 │ 1.42 │ 1 │ 0.99 │ 1.05 │ 0.94 │
│ Cavium ThunderX2 │ 0.84 │ 0.87 │ 0.87 │ 0 │ 1.04 │ 1.04 │ 1 │
└───────────────────────┴──────┴───────┴──────┴──────┴─────────────┴───────────┴────────────────┘ 

• ref, adapt, max — The speed in gigabytes per second (the value that is the reverse of the arithmetic mean of time for all launches on all datasets).
• best — The number of the best algorithm among the optimized variants, from 0 to 3.
• adapt_boost — The relative advantage of the adaptive algorithm compared to the baseline.
• max_boost — The relative advantage of the best of the non-adaptive variants compared to the baseline.
• adapt_over_max — The relative advantage of the adaptive algorithm over the best non-adaptive one.

The results show that we were able to speed up decompression by 12-20% on modern x86 processors. Even on ARM we saw 4% improvement, despite the fact that we didn't optimize much for this architecture. It is also clear that on average for different datasets, the "bandit" algorithm comes out ahead of the pre-selected best variant on all processors (except for very old Intel CPUs).

Fazit

In practice, the usefulness of this work is dubious. Yes, LZ4 decompression was accelerated on average by 12-20%, and on some datasets the performance more than doubled. But in general, this doesn't have much effect on query execution time. It's difficult to find real queries that gain more than a couple percent in speed.

We decided to use ZStandard level 1 instead of LZ4 on several Yandex Metrica clusters intended for executing long queries, because it is more important to save IO and disk space on cold data. Keep this in mind if you have similar workload.

We observed the greatest benefits from optimizing decompression in highly compressible data, such as columns with mostly duplicate string values. However, we have developed a separate solution specifically for this scenario that allows us to significantly speed up queries over this kind of data.

Another point to remember is that optimization of decompression speed is often limited by the format of the compressed data. LZ4 uses a very good format, but Lizard, Density and LZSSE have other formats that can work faster. Perhaps instead of trying to accelerate LZ4, it would be better to just integrate LZSSE into ClickHouse.

It's unlikely that these optimizations will be implemented in the mainstream LZ4 library: in order to use them, the library interface would have to be modified. In fact, this is often the case with improving algorithms — optimizations don't fit into old abstractions and they have to be revised. However, variable names have already been corrected in the original implementation. For instance, inc and dec tables have been corrected . In addition, about a month ago, the original implementation accelerated decompression by the same 12-15% by copying 32 bytes instead of 16, as discussed above. We tried the 32-byte option ourselves and the results were not that great, but they were still faster .

If you look at the profile at the beginning of the article, you may notice that we could have removed one extra copying operation from the page cache to userspace (either using mmap , or using O_DIRECT and userspace page cache, but both options are problematic). We also could have slightly improved the checksum calculation (CityHash128 is currently used without CRC32-C, but we could use HighwayHash, FARSH or XXH3). Acceleration of these two operations is useful for weakly compressed data, since they are performed on compressed data.

In any case, the changes have already been added to master more than a year ago, and the ideas that resulted from this research have been applied in other tasks. You can also watch the video from HighLoad++ Siberia, or view the presentation (both in Russian).