In diesem Beitrag werde ich erzählen, wie ich das Schreiben eines DDS-Synthesizers auf Verilog verstanden habe. Es wird verwendet, um eine sinusförmige Schwingung zu erzeugen, deren Frequenz und Anfangsphase für die Verwendung mit einem unipolaren 8-Bit-DAC eingestellt und berechnet werden können. Wie der Synthesizer funktioniert, ist in einem Artikel in der Zeitschrift Components and Technologies gut beschrieben . Um die Menge des verwendeten Speichers der Sinustabelle zu reduzieren, wird Symmetrie verwendet.
Für die Kompilierung unter Linux habe ich Iverilog und für die Anzeige von GTKWave verwendet. Der Einfachheit halber wurde ein einfaches Makefile geschrieben, vielleicht ist es für jemanden nützlich. Mit dem iverilog-Compiler erhalten wir zunächst die Datei tb.out und senden sie dann an den vvp-Simulator, der mit iverilog installiert ist. Infolgedessen generiert vvp out.vcd, das alle im Projekt verwendeten Variablen (Signale) enthält. Das Anzeigeziel startet zusätzlich zu den oben genannten GTKWave mit einer variablen Datei und Sie können die Wellenformen der Signale sehen.
SRC = nco.v TB = nco_tb.v all: iverilog -o tb.out $(TB) vvp -lxt tb.out check: iverilog -v $(TB) display: iverilog -o tb.out $(TB) vvp -lxt tb.out gtkwave out.vcd & clean: rm -rf *.out *.vcd *.vvp
Zunächst müssen Sie eine Tabelle des zukünftigen Sinus im Speicher ablegen, da ich ein einfaches Python-Skript geschrieben habe, das ein Viertel der Sinusperiode in 64 Punkte aufteilt und in einem Format generiert, das dann in den Quellcode kopiert werden kann. Da ich die Implementierung von DDS für einen externen unipolaren DAC mit einer Bitkapazität von nicht mehr als 8 Bit konzipiert habe, sollte die Sinusamplitude im Bereich von 0 bis 256 liegen, wobei die negative Halbperiode im Bereich von 0 ... 127 und die positive Hälfte in 128 ... 255 liegt . In dieser Hinsicht werden die erhaltenen Sinuswerte (von 0 bis pi / 4) mit 127 multipliziert und dann mit 127 addiert. Als Ergebnis werden die Werte des ersten Viertels der Periode erhalten, deren Amplitude 128 ... 256 beträgt.
Ich mache darauf aufmerksam, dass bei dieser Formation der Sinus am Ausgang des DAC eine konstante Komponente hat. Um es zu entfernen, muss es durch einen Kondensator geführt werden.
import numpy as np x=np.linspace(0,np.pi/2,64) print(np.sin(x)) y=127*np.sin(x) print(len(y)) print(y) z=[] i = 0 for elem in y: if int(elem)<=16: print("lut[%d] = 7'h0%X;" % (i, int(elem))) else: print("lut[%d] = 7'h%X;" % (i, int(elem))) z.append(hex(int(elem))) i = i + 1
Da die Sinusfunktion symmetrisch (ungerade) ist, können Sie die erste Symmetrie sin (x) = - sin (pi + x) finden. Die zweite Symmetrie ist durch die Tatsache gekennzeichnet, dass mit einer Tabelle für ein Viertel des Zeitraums das zweite Viertel erhalten werden kann, indem die Tabelle in umgekehrter Reihenfolge durchlaufen wird (da der Sinus in der Halbperiode zuerst zunimmt und dann abnimmt).
Der Großteil des DDS-Synthesizers ist eine Phasenbatterie. Im Wesentlichen ist dies der Index eines Elements aus der Nachschlagetabelle (LUT). Für jede Periode des Taktsignals erhöht sich der Wert darin um einen bestimmten Wert, wodurch ein Sinus am Ausgang erhalten wird. Die Frequenz des Ausgangssignals hängt vom Wert des Inkrements des Phasenakkumulators ab - je größer es ist, desto höher ist die Frequenz. Gemäß dem Kotelnikov-Kriterium sollte die Abtastfrequenz jedoch mindestens das Zweifache der Signalfrequenz betragen (um den Effekt der Überlagerung des Spektrums zu vermeiden), daher beträgt die Begrenzung des maximalen Inkrements die Hälfte des Phasenspeichers. Im Allgemeinen ist das technische Kriterium die Abtastfrequenz = 2,2 der Signalfrequenz. Nachdem ich mich entschlossen hatte, sie nicht auf das Äußerste zu bringen, entfernte ich ein weiteres Bit und ließ 6 Bit mit einer 8-Bit-Phasenbatterie inkrementiert (obwohl der Sinus-Jackalit bereits vorhanden ist).
Aufgrund der verwendeten Symmetrie werden nur die unteren 6 Bits von 2 ^ 6 = 64 direkt für die Indexabtastung verwendet. Die hohen 2 Bits werden verwendet, um eine Viertelperiode der Sinuserzeugung zu identifizieren und dementsprechend die Richtung der Tabellenüberquerung zu ändern. Sie sollten etwas Ähnliches bekommen wie:
module nco(clk, rst, out ); input clk, rst; output reg [7:0] out; reg [5:0] phase_inc = 6'h1; reg [7:0] phase_acc = 0; parameter LUT_SIZE = 64; reg [6:0] lut [0:LUT_SIZE-1]; always @(posedge clk) begin if (rst) begin phase_inc = 6'h1; phase_acc = 0; out = 0; lut[0] = 7'h00; // lut[63] = 7'h7F; end else begin // 1 if (phase_acc[7:6] == 2'b00) begin // LUT out <= {1'b1,lut[phase_acc[5:0]]}; end if (phase_acc[7:6] == 2'b01) begin out <= {1'b1,lut[~phase_acc[5:0]]}; end if (phase_acc[7:6] == 2'b10) begin out <= {1'b0,~lut[phase_acc[5:0]]}; end if (phase_acc[7:6] == 2'b11) begin out <= {1'b0,~lut[~phase_acc[5:0]]}; end phase_acc <= phase_acc + {2'b0,phase_inc}; end end endmodule
Beim Zurücksetzen initialisieren wir alles mit Nullen, bis auf den Phaseninkrementwert setzen wir ihn auf Eins. Um die Synthetisierbarkeit des Codes zu erhalten, wird die Tabelle während des Zurücksetzens auch mit Werten gefüllt. In einem realen Projekt ist es ratsam, den im FPGA integrierten Blockspeicher für solche Zwecke zu verwenden, eine separate Konfigurationsdatei dafür zu erstellen und den IP-Core im Projekt selbst zu verwenden.
Eine kleine Erklärung, wie Symmetrie funktioniert. Bei jedem Zyklus wird geprüft (auf den 2 höchstwertigen Bits), in welchem Viertel sich der Phasenspeicher gerade befindet. Wenn der höchste Wert = 00 ist, ist der Ausgang in der höchsten Ziffer 1 (verantwortlich für die positive Halbwelle), in den unteren Ziffern der Wert aus der LUT gemäß dem Index. Nachdem der Wert des Phasenakkumulators 63 überschreitet (das erste Quartal vergeht), erscheint 01 in den hohen Bits und die unteren werden wieder mit Nullen gefüllt.
Um die LUT in umgekehrter Reihenfolge zu übergeben, reicht es aus, die niedrigstwertigen Bits des Phasenakkumulators zu invertieren (sie steigt mit jedem Taktzyklus weiter an und ihr invertierter Wert nimmt ab).
Um eine negative Halbwelle zu bilden, schreiben wir 0. Im oberen Bit der Ausgabe müssen wir nun den Wert selbst aus der Sinustabelle invertieren. Der Punkt hier ist, dass Sie eine Spiegelkopie des Sinusviertels benötigen. Wenn dies nicht erfolgt, erhalten Sie das gleiche Bild wie im ersten Quartal, jedoch um 127 nach unten abgesenkt. Sie können dies überprüfen, indem Sie die Umkehrung im Code entfernen.
Wir ändern die Frequenz und die Anfangsphase
Wie bereits oben beschrieben, ist es zum Ändern der Frequenz erforderlich, den Wert des Phaseninkrements zu ändern. Neue Eingaben werden angezeigt:
input [5:0] freq_res; input [7:0] phase;
Um den Wert des Phaseninkrements zu ändern, fangen wir ihn einfach bei jedem Zyklus ein:
always @(posedge clk) begin if (rst) begin //... end else begin //... phase_inc <= freq_res; end end
In der Anfangsphase ist nicht alles so einfach. Sie müssen es zuerst in das Zwischenregister schreiben und den Phasenakkumulator nur dann mit diesem Wert füllen, wenn der Wert der Anfangsphase am Eingang nicht mit dem zuvor gespeicherten übereinstimmt. Dies wirft einen weiteren wichtigen Punkt in Bezug auf den Stand der Rennen auf. Wir haben bereits eine Stelle, an der wir phase_acc in das Register schreiben. Sie können nicht gleichzeitig an mehreren Stellen aufnehmen, da die zuerst eingehenden Daten aufgezeichnet werden. Daher sieht das Design folgendermaßen aus:
reg change_phase = 0; // // ( ) // : prev_phase <= phase; if (phase != prev_phase) begin // change_phase <= 1'b1; end if (change_phase) begin // phase_acc <= prev_phase; change_phase <= 1'b0; end else begin // phase_acc <= phase_acc + {2'b0,phase_inc}; end
Testbench
Der Testbench-Code für Iverilog und GTKWave enthält einige Designs (mit einem Dollarzeichen), die in der üblichen ISE Design Suite oder Quartus nicht verwendet werden. Ihre Bedeutung besteht darin, überwachte Signale auszuwählen und in eine Datei zu laden, damit sie dann in den Simulator übertragen werden können. Die Arbeit des Prüfstands selbst ist trivial - wir führen einen Reset durch, stellen die Frequenz / Anfangsphase ein und warten eine Weile.
`include "nco.v" `timescale 1ns / 1ps module nco_tb; reg clk = 0, rst = 0; reg [7:0] phase = 0; reg [5:0] freq_res; wire [7:0] out; nco nco_inst ( .clk(clk), .rst(rst), .phase(phase), .freq_res(freq_res), .out(out) ); always #2 clk <= ~clk; initial begin $dumpfile("out.vcd"); $dumpvars(0, nco_tb); //$monitor("time =%4d out=%h",$time,out); rst = 1'b1; freq_res = 1; #8 rst = 1'b0; #300 phase = 8'b00100011; #300 phase = 8'b00001111; #1200 freq_res = 6'b111101; #1200 freq_res = 6'b001111; #1200 freq_res = 6'b011111; #400 phase = 8'b00010011; #1200 $finish; end endmodule
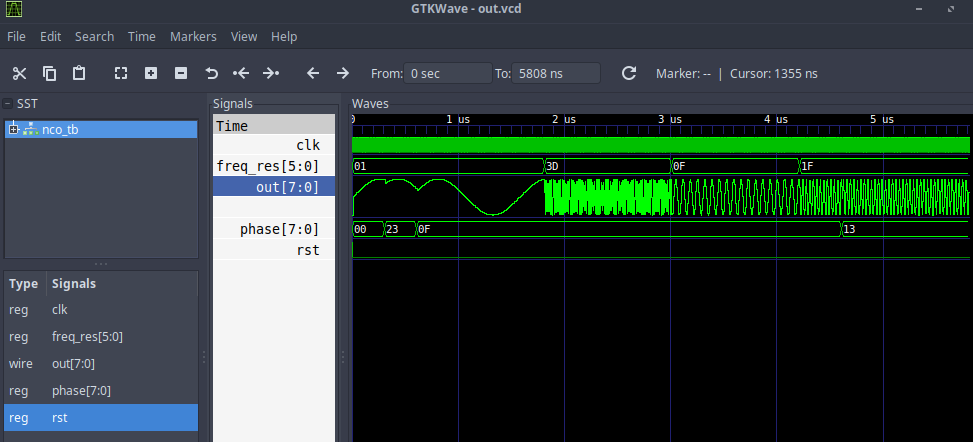
Zeitdiagramme
Am Ausgang erhalten wir etwas Ähnliches wie einen Sinus mit einer sich ändernden Frequenz und Anfangsphase zu den in der Testbench festgelegten Zeitpunkten. Es ist anzumerken, dass mit zunehmender Frequenz die Auflösung entlang (die Anzahl der Abtastwerte pro Periode) abnimmt, die Synthesizer-Taktfrequenz und ihre LUT-Größe eine entscheidende Rolle bei der Reproduktion des reinen Sinus spielen (je mehr sich seine Form dem Ideal nähert, desto weniger Nebenkomponenten im Spektrum des Ergebnisses Signal und die Spitze wird bereits auf der erzeugten Frequenz sein).

Es ist zu erkennen, dass ein Signal mit einer zweiten Frequenz bereits keinen so glatten Sinus aufweist wie die anderen. Schauen wir uns das genauer an.

Es ist zu sehen, dass dies dem Sinus immer noch ein bisschen ähnlich ist. Das Ergebnis wird sogar noch besser, wenn ein solches Signal durch ein Anti-Aliasing-Filter (Tiefpassfilter) geleitet wird.
Projektquellen finden Sie hier .
Quellen