Die Symmetrieeigenschaft der Kointegrationsbeziehung

Der Zweck dieses Artikels ist es, paradoxe Ergebnisse in der Untersuchung der Ko-Integration von Zeitreihen zu teilen: wenn die Zeitreihen $$$A$ zusammen mit in der Nähe integriert $$$B$ Reihe $$$B$ nicht immer zusammen mit einer Nummer integriert $$$A$ .

Wenn wir die Kointegration rein theoretisch untersuchen, ist es leicht zu beweisen, dass die Serie $$$A$ co-integriert mit $$$B$ dann rudern $$$B$ co-integriert mit $$$A$ . Wenn wir jedoch beginnen, die Kointegration empirisch zu untersuchen, stellt sich heraus, dass theoretische Berechnungen nicht immer bestätigt werden. Warum passiert das?

Symmetrie

Haltung $$$A$ symmetrisch genannt, wenn $$$A \ subseteq A ^ {- 1}$ wo $$$A ^ {- 1}$ - das durch die Bedingung definierte inverse Verhältnis: $$$x A ^ {- 1} y$ gleichbedeutend mit $$$yAx$ . Mit anderen Worten, wenn die Beziehung $$$xAy$ dann die Beziehung $$$yAx$ .

Betrachten Sie zwei $$$I (1)$ eine Reihe von $$$x_t$ und $$$y_t$ , $$$t = 0, \ dots, T$ . Die Kointegration ist symmetrisch, wenn $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ beinhaltet $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ das heißt, wenn das Vorhandensein einer direkten Regression zum Vorhandensein des Inversen führt.

Betrachten Sie die Gleichung $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ , $$$\ beta_1 \ neq 0$ . Tauschen Sie die linke und rechte Seite aus und subtrahieren Sie $$$\ varepsilon_ {1t}$ aus beiden Teilen: $$$\ beta_1 x_t = y_t - \ varepsilon_ {1t}$ . Als $$$\ beta_1 \ neq 0$ Teilen Sie per Definition beide Teile in $$$\ beta_1$ ::

$$

$$x_t = \ frac {1} {\ beta_1} y_t - \ frac {\ varepsilon_ {1t}} {\ beta_1}.$$

Ersetzen $$$1 / \ beta_1$ auf $$$\ beta_2$ und $$$- \ varepsilon_ {1t} / \ beta_1$ auf $$$\ varepsilon_ {2t}$ wir bekommen $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ . Daher ist die Kointegrationsbeziehung symmetrisch.

Daraus folgt, wenn die Variable $$$X$ mit variabel integriert $$$Y$ dann die Variable $$$Y$ muss zusammen mit der Variablen integriert werden $$$X$ . Der Angle-Granger-Kointegrationstest bestätigt diese Symmetrieeigenschaft jedoch nicht immer, da es sich manchmal um eine Variable handelt $$$Y$ nicht mit variabel integriert $$$X$ nach diesem Test.

Ich habe die Symmetrieeigenschaft an den Daten 2017 der Börsen in Moskau und New York mit dem Angle-Granger-Test getestet. An der Moskauer Börse befanden sich 7.975 gemeinsam integrierte Aktienpaare. Für 7731 (97%) kointegrierte Paare wurde die Symmetrieeigenschaft bestätigt, für 244 (3%) kointegrierte Paare wurde die Symmetrieeigenschaft nicht bestätigt.

An der New Yorker Börse gab es 140.903 gemeinsam integrierte Aktienpaare. Für 136586 (97%) kointegrierte Paare wurde die Symmetrieeigenschaft bestätigt, für 4317 (3%) kointegrierte Paare wurde die Symmetrieeigenschaft nicht bestätigt.

Interpretation

Dieses Ergebnis kann durch die geringe Leistung und die hohe Fehlerwahrscheinlichkeit der zweiten Art des Dickey-Fuller-Tests interpretiert werden, auf dem der Angle-Granger-Test basiert. Die Wahrscheinlichkeit eines Fehlers der zweiten Art kann mit bezeichnet werden $$$\ beta = P (H_0 | H_1)$ dann der Wert $$$1 - \ beta$ nannte die Kraft des Tests. Leider kann der Dickey-Fuller-Test nicht zwischen instationären und nahezu instationären Zeitreihen unterscheiden.

Was ist eine nahezu instabile Zeitreihe? Betrachten Sie die Zeitreihen $$$x_t = \ phi x_ {t-1} + \ varepsilon_t$ . Eine stationäre Zeitreihe ist eine Reihe, in der $$$0 <\ phi <1$ . Eine instationäre Zeitreihe ist eine Reihe, in der $$$\ phi = 1$ . Eine nahezu instationäre Zeitreihe ist eine Reihe, in der der Wert angegeben wird $$$\ phi$ in der Nähe von einem.

Bei nahezu instationären Zeitreihen können wir die Nullhypothese der instationären Zeitreihen oft nicht ablehnen. Dies bedeutet, dass der Dickey-Fuller-Test ein hohes Risiko für einen Fehler zweiter Art aufweist, dh die Wahrscheinlichkeit, die falsche Nullhypothese nicht abzulehnen.

KPSS-Test

Eine mögliche Antwort auf die Schwäche des Dickey-Fuller-Tests ist der KPSS-Test, der seinen Namen den Initialen der Wissenschaftler von Kvyatkovsky, Phillips, Schmidt und Sheen verdankt. Obwohl sich der methodische Ansatz dieses Tests vollständig vom Dickey-Fuller-Ansatz unterscheidet, sollte der Hauptunterschied in der Permutation der Null- und Alternativhypothesen verstanden werden.

Im KPSS-Test besagt die Nullhypothese, dass die Zeitreihe stationär ist, im Gegensatz zu der Alternative über das Vorhandensein von Nichtstationarität. Nahezu instationäre Zeitreihen, die mit dem Dickey-Fuller-Test häufig als nicht stationär identifiziert wurden, können mit dem KPSS-Test korrekt als stationär identifiziert werden.

Wir müssen uns jedoch bewusst sein, dass die Ergebnisse statistischer Tests lediglich probabilistisch sind und nicht mit einem bestimmten wahren Urteil verwechselt werden dürfen. Es besteht immer eine Wahrscheinlichkeit ungleich Null, dass wir uns irren. Aus diesem Grund wird vorgeschlagen, die Ergebnisse der Dickey-Fuller- und KPSS-Tests als idealen Test für Nichtstationarität zu kombinieren.



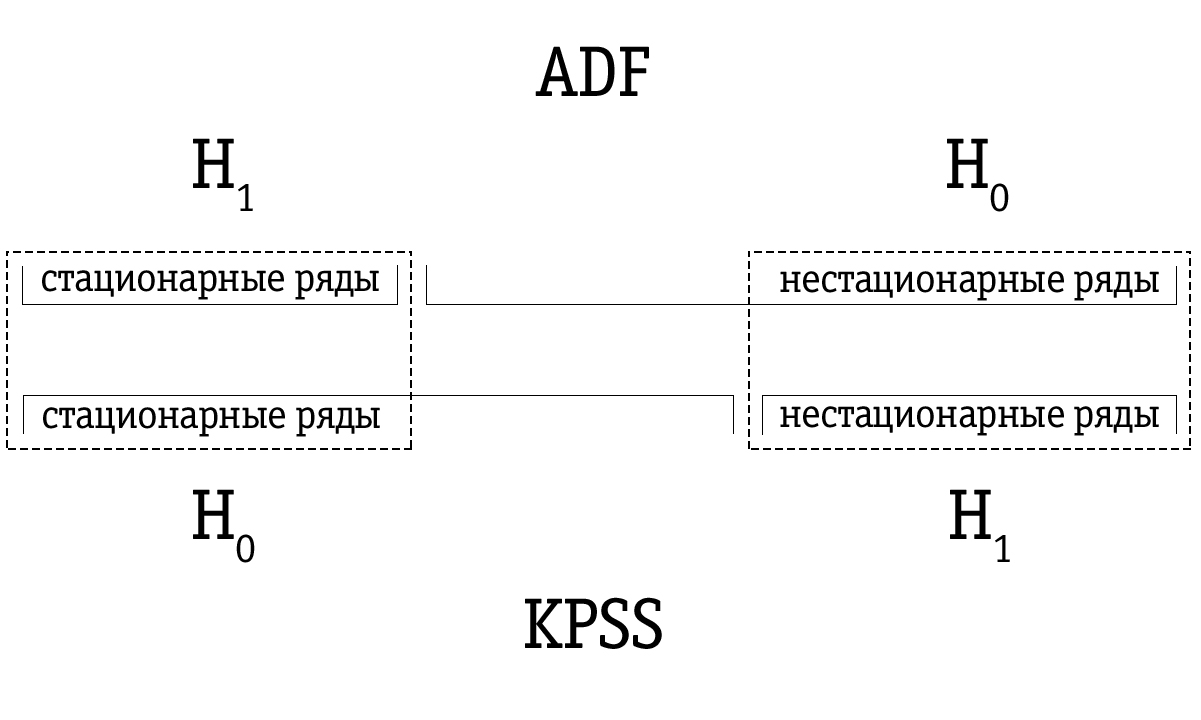
Aufgrund der geringen Leistung identifiziert der Dickey-Fuller-Test eine Serie häufig fälschlicherweise als nicht stationär, sodass sich herausstellt, dass der resultierende Satz von Zeitreihen, der durch den Dickey-Fuller-Test als instabil identifiziert wurde, größer ist als viele Zeitreihen, die mit dem KPSS-Test als nicht stationär identifiziert wurden. Daher ist die Testreihenfolge wichtig.

Wenn die Zeitreihe mit dem Dickey-Fuller-Test als stationär identifiziert wird, wird sie höchstwahrscheinlich auch mit dem KPSS-Test als stationär identifiziert. In diesem Fall können wir davon ausgehen, dass die Serie tatsächlich stationär ist.

Wenn die Zeitreihe mit dem KPSS-Test als instabil identifiziert wurde, wird sie höchstwahrscheinlich auch mit dem Dickey-Fuller-Test als instabil identifiziert. In diesem Fall können wir davon ausgehen, dass die Serie tatsächlich instabil ist.

Es kommt jedoch häufig vor, dass eine Zeitreihe, die mit dem Dickey-Fuller-Test als nicht stationär identifiziert wurde, mit dem KPSS-Test als stationär markiert wird. In diesem Fall müssen wir mit unserer endgültigen Schlussfolgerung sehr vorsichtig sein. Wir können überprüfen, wie stark die Basis für die Stationarität im Fall des KPSS-Tests und für die Unstetigkeit im Fall des Dickey-Fuller-Tests ist, und eine geeignete Entscheidung treffen. Natürlich können wir auch die Frage nach der Stationarität einer solchen Zeitreihe ungelöst lassen.

Der KPSS-Testansatz geht von Zeitreihen aus $$$y_t$ Auf Stationarität relativ zu einem Trend getestet, kann in die Summe eines deterministischen Trends zerlegt werden $$$\ beta t$ zufälliger Spaziergang $$$r_t$ und stationärer Fehler $$$\ varepsilon_t$ ::

$$

$$y_t = \ beta t + r_t + \ varepsilon_t, \\ r_t = r_ {t-1} + u_t,$$

wo $$$u_t$ - normaler iid-Prozess mit Mittelwert Null und Varianz $$$\ sigma ^ 2$ ( $$$u_t \ sim N (0, \ sigma ^ 2)$ ) Anfangswert $$$r_0$ als fest behandelt und spielt die Rolle eines freien Mitglieds. Stationärer Fehler $$$\ varepsilon_t$ kann durch jeden gängigen ARMA-Prozess erzeugt werden, dh er kann eine starke Autokorrelation aufweisen.

Ähnlich wie beim Dickey-Fuller-Test die Fähigkeit, eine beliebige Struktur der Autokorrelation zu berücksichtigen $$$\ varepsilon_t$ Sehr wichtig, da die meisten wirtschaftlichen Zeitreihen stark zeitabhängig sind und daher eine starke Autokorrelation aufweisen. Wenn wir die Stationarität in Bezug auf die horizontale Achse überprüfen wollen, dann der Begriff $$$\ beta t$ gerade aus der obigen Gleichung ausgeschlossen.

Aus der obigen Gleichung folgt die Nullhypothese $$$H_0$ über Stationarität $$$y_t$ äquivalent zur Hypothese $$$\ sigma ^ 2 = 0$ , woraus folgt, dass $$$r_t = r_0$ für alle $$$t$ ( $$$r_0$ Ist eine Konstante). Ebenso eine alternative Hypothese $$$H_1$ Nichtstationarität entspricht der Hypothese $$$\ sigma ^ 2 \ neq 0$ .

Um die Hypothese zu testen $$$H_0$ :: $$$\ sigma ^ 2 = 0$ (stationäre Zeitreihen) versus Alternative $$$H_1$ :: $$$\ sigma ^ 2 \ neq 0$ (instationäre Zeitreihen) Autoren des KPSS-Tests erhalten Einwegstatistiken des Lagrange-Multiplikator-Tests. Sie berechnen auch die asymptotische Verteilung und modellieren die asymptotischen kritischen Werte. Wir betrachten hier keine theoretischen Details, sondern skizzieren nur kurz den Testausführungsalgorithmus.

Bei der Durchführung des KPSS-Tests für eine Zeitreihe $$$y_t$ , $$$t = 1, \ dots, T$ Die Methode der kleinsten Quadrate (kleinste Quadrate) wird verwendet, um eine der folgenden Gleichungen zu schätzen:

$$

$$y_t = a_0 + \ varepsilon_t, \\ y_t = a_0 + \ beta t + \ varepsilon_t.$$

Wenn wir die Stationarität in Bezug auf die horizontale Achse überprüfen wollen, bewerten wir die erste Gleichung. Wenn wir die Stationarität in Bezug auf den Trend überprüfen wollen, wählen wir die zweite Gleichung.

Reste $$$e_t$ Aus der geschätzten Gleichung werden die Statistiken des Tests der Lagrange-Multiplikatoren berechnet. Der Lagrange-Multiplikator-Test basiert auf der Idee, dass bei Erfüllung der Nullhypothese alle Lagrange-Multiplikatoren gleich Null sein müssen.

Lagrange-Multiplikator-Test

Der Lagrange-Multiplikator-Test ist mit einem allgemeineren Ansatz zur Parameterschätzung unter Verwendung der Maximum-Likelihood-Methode (ML) verbunden. Nach diesem Ansatz werden Daten als Hinweise auf Verteilungsparameter angesehen. Der Beweis wird als Funktion unbekannter Parameter ausgedrückt - eine Wahrscheinlichkeitsfunktion:

$$

$$L (X_1, X_2, X_3, \ Punkte, X_n; \ Phi_1, \ Phi_2, \ Punkte, \ Phi_k),$$

wo $$$X_i$ Sind die beobachteten Werte und $$$\ Phi_i$ - Parameter, die wir auswerten möchten.

Die Maximum-Likelihood-Funktion ist die gemeinsame Wahrscheinlichkeit von Probenbeobachtungen.

$$

$$L (X_1, X_2, X_3, \ Punkte, X_n; \ Phi_1, \ Phi_2, \ Punkte, \ Phi_k) = P (X_1 \ Land X_2 \ Land X_3 \ Punkte X_n).$$

Das Ziel der Maximum-Likelihood-Methode besteht darin, die Likelihood-Funktion zu maximieren. Dies wird erreicht, indem die maximale Wahrscheinlichkeitsfunktion für jeden der geschätzten Parameter differenziert und die partiellen Ableitungen mit Null gleichgesetzt werden. Die Werte der Parameter, bei denen der Wert der Funktion maximal ist, sind die gewünschte Schätzung.

Zur Vereinfachung der nachfolgenden Arbeit wird normalerweise zuerst der Logarithmus der Wahrscheinlichkeitsfunktion verwendet.

Betrachten Sie ein verallgemeinertes lineares Modell $$$Y = \ beta X + \ varepsilon$ wo davon ausgegangen wird, dass $$$\ varepsilon$ normal verteilt $$$N (0, \ sigma ^ 2)$ , also $$$Y - \ beta X \ sim N (0, \ sigma ^ 2)$ .

Wir wollen die Hypothese testen, dass das System $$$q$ ( $$$q <k$ ) unabhängige lineare Bedingungen $$$R \ beta = r$ . Hier $$$R$ - berühmt $$$q \ times k$ Rangmatrix $$$q$ und $$$r$ - berühmt $$$q \ times 1$ Vektor.

Für jedes Paar beobachteter Werte $$$X$ und $$$Y$ Unter normalen Bedingungen existiert eine Wahrscheinlichkeitsdichtefunktion der folgenden Form:

$$

$$f (X_i, Y_i) = \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ right) ^ 2}.$$

Vorbehaltlich $$$n$ gemeinsame Beobachtungen $$$X$ und $$$Y$ Die Gesamtwahrscheinlichkeit, alle Werte in der Stichprobe zu beobachten, ist gleich dem Produkt der einzelnen Werte der Wahrscheinlichkeitsdichtefunktion. Somit ist die Wahrscheinlichkeitsfunktion wie folgt definiert:

$$

$$L (\ beta) = \ prod \ limit_ {i = 1} ^ n \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ right) ^ 2}.$$

Da es einfacher ist, die Summe als das Produkt zu unterscheiden, wird normalerweise der Logarithmus der Wahrscheinlichkeitsfunktion verwendet, also:

$$

$$\ ln L (\ beta) = \ sum \ limit_ {i = 1} ^ n \ left (\ ln \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} - \ frac {1} { 2 \ sigma ^ 2} (Y_i - \ beta X_i) ^ 2 \ right).$$

Diese nützliche Konvertierung wirkt sich nicht auf das Endergebnis aus, da $$$\ ln L$ Ist eine zunehmende Funktion $$$L$ . Also dann der Wert $$$\ beta$ was maximiert $$$\ ln L$ wird auch maximieren $$$L$ .

ML Punktzahl für $$$\ beta$ in Regression mit Einschränkung ( $$$R \ beta = r$ ) wird durch Maximieren der Funktion erhalten $$$\ ln L (\ beta)$ vorbehaltlich $$$R \ beta = r$ . Um diese Schätzung zu finden, schreiben wir die Lagrange-Funktion:

$$

$$\ psi (\ beta) = \ ln L (\ beta) - g '(R \ beta - r),$$

wo durch $$$g = \ left (g_1, \ dots, g_q \ right) '$ markierter Vektor $$$q$ Lagrange-Multiplikatoren.

Lagrange-Multiplikator-Teststatistik bezeichnet mit $$$\ eta_ \ mu$ bei Stationarität in Bezug auf die horizontale Achse und durch $$$\ eta_ \ tau$ Bei Stationarität relativ zum Trend wird dies durch den Ausdruck bestimmt

$$

$$\ eta _ {\ mu / \ tau} = T ^ 2 \ frac {1} {s ^ 2 (l)} \ sum \ limit_ {t = 1} ^ T S_t ^ 2,$$

wo

$$

$$S_t = \ sum \ limit_ {i = 1} ^ t e_i$$

und

$$

$$s ^ 2 (l) = T ^ {- 1} \ Summe \ Grenzen_ {t = 1} ^ T e_t ^ 2 + 2 T ^ {- 1} \ Summe \ Grenzen_ {1} ^ lw (s, l) \ sum \ limit_ {t = s + 1} ^ T e_t e_ {ts},$$

wo

$$

$$w (s, l) = 1 - \ frac {s} {l + 1}.$$

In den obigen Gleichungen $$$S_t$ - der Prozess der Teilbilanzen $$$e_t$ aus der geschätzten Gleichung; $$$s ^ 2 (l)$ - Bewertung der langfristigen Verteilung von Rückständen $$$e_t$ ;; aber $$$w (s, l)$ - das sogenannte Bartlett-Spektralfenster, wo $$$l$ - Verzögerungskürzungsparameter.

In dieser Anwendung wird das Spektralfenster verwendet, um die spektrale Fehlerdichte für ein bestimmtes Intervall (Fenster) zu schätzen, das sich über den gesamten Bereich der Reihe bewegt. Daten außerhalb des Intervalls werden ignoriert, da die Fensterfunktion außerhalb eines ausgewählten Intervalls (Fensters) eine Funktion gleich Null ist.

Varianzschätzung $$$s ^ 2 (l)$ hängt vom Parameter ab $$$l$ und seitdem $$$l$ erhöht sich und mehr als 0, Punktzahl $$$s ^ 2 (l)$ beginnt mögliche Autokorrelation in Residuen zu berücksichtigen $$$e_t$ .

Schließlich die Lagrange-Multiplikator-Teststatistik $$$\ eta_ \ mu$ oder $$$\ eta_ \ tau$ vergleicht mit kritischen Werten. Wenn die Statistik des Lagrange-Multiplikator-Tests den entsprechenden kritischen Wert überschreitet, gilt die Nullhypothese $$$H_0$ (stationäre Zeitreihen) weicht zugunsten einer alternativen Hypothese ab $$$H_1$ (instationäre Zeitreihen). Andernfalls können wir die Nullhypothese nicht ablehnen $$$H_0$ über die Stationarität einer Zeitreihe.

Kritische Werte sind asymptotisch und daher am besten für große Stichproben geeignet. In der Praxis werden sie jedoch auch für eine kleine Stichprobe verwendet. Darüber hinaus sind die kritischen Werte unabhängig vom Parameter $$$l$ . Die Statistik des Lagrange-Multiplikator-Tests hängt jedoch vom Parameter ab $$$l$ . Die Autoren des KPSS-Tests bieten keinen allgemeinen Algorithmus zur Auswahl des geeigneten Parameters an. $$$l$ . Der Test wird normalerweise für durchgeführt $$$l$ im Bereich von 0 bis 8.

Mit zunehmender Zunahme $$$l$ Es ist weniger wahrscheinlich, dass wir die Nullhypothese ablehnen $$$H_0$ über Stationarität, was teilweise zu einer Abnahme der Testleistung führt und zu gemischten Ergebnissen führen kann. Im Allgemeinen können wir dies jedoch sagen, wenn die Nullhypothese $$$H_0$ Die Stationarität der Zeitreihen wird auch bei kleinen Werten nicht verworfen $$$l$ (0, 1 oder 2) schließen wir, dass die verifizierten Zeitreihen stationär sind.

Vergleich der Testergebnisse

Die folgende Methodik wurde entwickelt, um die Wahrscheinlichkeit einer Symmetrie zu bewerten.

1. Alle Zeitreihen werden mit dem Dickey-Fuller-Test bei einem Signifikanzniveau von 0,05 auf Integrierbarkeit 1. Ordnung überprüft. Im Folgenden werden nur integrierbare Reihen erster Ordnung betrachtet.
2. Die in Abschnitt 1 erhaltenen integrierbaren Reihen erster Ordnung umfassen Paare durch Kombinieren ohne Wiederholung.
3. Die in Abschnitt 2 erstellten Aktienpaare werden mit dem Angle-Granger-Test auf Kointegration geprüft. Als Ergebnis werden kointegrierte Paare identifiziert.
4. Die Regressionsrückstände, die als Ergebnis der Prüfung in Absatz 3 erhalten wurden, werden unter Verwendung des KPSS-Tests auf Stationarität geprüft. Somit werden die Ergebnisse der beiden Tests kombiniert.
5. Die Zeitreihen in den kointegrierten Paaren aus Abschnitt 2 werden vertauscht und erneut mit dem Angle-Granger-Test auf Kointegration überprüft, dh wir untersuchen, ob die Beziehung zwischen Zeitreihen symmetrisch ist.
6. Die Zeitreihen in den co-integrierten Paaren von Punkt 4 werden vertauscht und die Residuen aus der Regression werden erneut mit dem KPSS-Test auf Stationarität überprüft, dh wir werden untersuchen, ob die Beziehung zwischen den Zeitreihen symmetrisch ist.

Alle Berechnungen werden mit dem MATLAB-Paket durchgeführt. Die Ergebnisse sind in der folgenden Tabelle dargestellt. Für jeden Test haben wir eine Reihe von Beziehungen, die gemäß den Testergebnissen symmetrisch sind (markiert) $$$S$ ); Wir haben eine Reihe von Beziehungen, die gemäß den Testergebnissen nicht symmetrisch sind (markiert) $$$¬S$ ); und wir haben eine empirische Wahrscheinlichkeit, dass das Verhältnis gemäß den Testergebnissen symmetrisch ist ( $$$P (S) = \ frac {S} {S + ¬S}$ )

An der Moskauer Börse:


An der New Yorker Börse:

Vergleich der Backtest-Ergebnisse

Vergleichen wir die Ergebnisse der Handelsstrategie anhand historischer Daten für co-integrierte Paare, die mit dem Angle-Granger-Test ausgewählt wurden, und für co-integrierte Paare, die mit dem KPSS-Test ausgewählt wurden.

Wie aus der Tabelle hervorgeht, konnte dank einer genaueren Identifizierung von gemeinsam integrierten Aktienpaaren die durchschnittliche Jahresrendite beim Handel mit einem separaten gemeinsam integrierten Paar um 9,21% erhöht werden. Somit kann die vorgeschlagene Methodik die Rentabilität des algorithmischen Handels unter Verwendung marktneutraler Strategien erhöhen.

Alternative Interpretation

Wie wir oben gesehen haben, sind die Ergebnisse des Angle-Granger-Tests eine Lotterie. Für einige werden meine Gedanken zu kategorisch erscheinen, aber ich denke, es ist sehr sinnvoll, die durch statistische Analyse bestätigte Nullhypothese nicht auf den Glauben zu übertragen.

Der Konservatismus der wissenschaftlichen Methode zum Testen von Hypothesen besteht darin, dass wir bei der Analyse der Daten nur eine gültige Schlussfolgerung ziehen können: Die Nullhypothese wird auf dem ausgewählten Signifikanzniveau verworfen. Dies bedeutet nicht, dass die Alternative wahr ist. $$$H_1$ - Wir haben gerade indirekte Beweise für ihre Glaubwürdigkeit auf der Grundlage eines typischen "gegenteiligen Beweises" erhalten. In dem Fall, wenn es wahr ist $$$H_0$ Der Forscher wird auch angewiesen, eine vorsichtige Schlussfolgerung zu ziehen: Aufgrund der unter den Versuchsbedingungen erhaltenen Daten war es nicht möglich, genügend Beweise zu finden, um die Nullhypothese abzulehnen.

In Übereinstimmung mit meinen Gedanken im September 2018 wurde ein Artikel von einflussreichen Personen verfasst, die darauf drängten, das Konzept der „statistischen Signifikanz“ und das Paradigma des Testens der Nullhypothese aufzugeben.

Am wichtigsten: „Vorschläge wie die Änderung des Schwellenwerts $$$p$ -die Standardwerte, die Verwendung von Konfidenzintervallen mit Schwerpunkt darauf, ob sie Null enthalten oder nicht, oder die Verwendung des Bayes-Koeffizienten zusammen mit allgemein anerkannten Klassifikationen zur Bewertung der Beweiskraft, die sich aus denselben oder ähnlichen Problemen wie die derzeitige Verwendung ergibt $$$p$ -Werte mit einem Wert von 0,05 ... sind eine Form der statistischen Alchemie, die ein falsches Versprechen abgibt, Zufälligkeit in Zuverlässigkeit umzuwandeln, das sogenannte „Waschen der Unsicherheit“ (Gelman, 2016), das mit Daten beginnt und mit dichotomen Schlussfolgerungen über Wahrheit oder Falschheit endet - binäre Aussagen dass "es gibt eine Wirkung" oder "keine Wirkung" - auf der Grundlage einiger zu erreichen $$$p$ -Werte oder andere Schwellenwerte.

Ein entscheidender Schritt nach vorne wird die Akzeptanz von Unsicherheit und Variabilität der Auswirkungen sein (Carlin, 2016; Gelman, 2016), die Erkenntnis, dass wir mehr (viel mehr) über die Welt lernen können, und das falsche Versprechen der Gewissheit, das eine solche Dichotomisierung bietet, aufgeben. “

Schlussfolgerungen

Wir haben gesehen, dass, obwohl die Symmetrieeigenschaft der Kointegrationsbeziehung theoretisch erfüllt sein sollte, die experimentellen Daten von den theoretischen Berechnungen abweichen. Eine der Interpretationen dieses Paradoxons ist die geringe Leistung des Dickey-Fuller-Tests.

Als neue Methode zur Identifizierung von co-integrierten Asset-Paaren wurde vorgeschlagen, die mit dem Angle-Granger-Test erhaltenen Regressionsrückstände mit dem KPSS-Test auf Stationarität zu testen und die Ergebnisse dieser Tests zu kombinieren. und kombinieren Sie die Ergebnisse des Angle-Granger-Tests und des KPSS-Tests sowohl für die direkte als auch für die umgekehrte Regression.

Backtests wurden mit den Daten der Moskauer Börse für 2017 durchgeführt. Nach den Ergebnissen von Backtests betrug die durchschnittliche jährliche Rendite bei Verwendung der oben vorgeschlagenen Methode zur Identifizierung von integrierten Aktienpaaren 22,72%. Verglichen mit der Identifizierung von co-integrierten Bestandspaaren mit dem Angle-Granger-Test konnte somit die durchschnittliche Jahresrendite um 9,21% gesteigert werden.

Eine alternative Interpretation des Paradoxons besteht darin, die durch statistische Analyse bestätigte Nullhypothese nicht auf den Glauben zu übertragen. Das Nullhypothesen-Testparadigma und die Dichotomie, die ein solches Paradigma bietet, geben uns ein falsches Gefühl für Marktkenntnisse.

Als ich gerade mit meiner Forschung anfing, schien es mir, dass man den Markt nehmen, ihn in den "Fleischwolf" statistischer Tests legen und am Ausgang gefilterte leckere Reihen bekommen kann. Leider sehe ich jetzt, dass dieses Konzept der statistischen Brute Force nicht funktionieren wird.

Ob es eine Integration auf dem Markt gibt oder nicht - für mich bleibt diese Frage offen. Ich habe noch große Fragen an die Begründer dieser Theorie. Ich hatte im Westen einige Angst und jene Wissenschaftler, die Finanzmathematik zu einer Zeit entwickelten, als die Ökonometrie in der Sowjetunion als korrupte Bourgeoisie galt. Es schien mir, dass wir sehr weit hinten waren, und irgendwo in Europa und Amerika saßen die Götter der Finanzen, die den heiligen Gral der Wahrheit kannten.

Jetzt verstehe ich, dass sich europäische und amerikanische Wissenschaftler nicht wesentlich von unseren unterscheiden. Der einzige Unterschied besteht im Ausmaß der Quacksalber. Unsere Wissenschaftler sitzen in einer Elfenbeinburg, schreiben Unsinn und erhalten Zuschüsse in Höhe von 500.000 Rubel. Im Westen sitzen ungefähr dieselben Wissenschaftler in ungefähr derselben Elfenbeinburg, sie schreiben über denselben Unsinn und erhalten "Nobel" und Zuschüsse in Höhe von 500.000 Dollar dafür. Das ist der ganze Unterschied.

Im Moment habe ich keine klare Sicht auf das Thema meiner Forschung. Es ist falsch zu sagen, dass „alle Hedge-Fonds den Paarhandel nutzen“, weil die meisten Hedge-Fonds genauso gut bankrott gehen.

Leider muss man immer mit dem eigenen Kopf denken und Entscheidungen treffen, besonders wenn wir Geld riskieren.