Hallo Habr! Ich präsentiere Ihnen die Übersetzung des Artikels
„ Bildähnlichkeit
mit Deep Ranking“ von Akarsh Zingade.
Deep-Ranking-Algorithmus
Das Konzept der "
Ähnlichkeit der beiden Bilder " wurde nicht eingeführt, daher wollen wir dieses Konzept zumindest im Rahmen des Artikels einführen.
Die Ähnlichkeit zweier Bilder ergibt sich aus dem Vergleich zweier Bilder nach bestimmten Kriterien. Sein quantitatives Maß bestimmt den Ähnlichkeitsgrad zwischen den Intensitätsdiagrammen zweier Bilder. Unter Verwendung eines Ähnlichkeitsmaßes werden einige Merkmale, die die Bilder beschreiben, verglichen. Als Maß für die Ähnlichkeit die Hamming-Distanz, die euklidische Distanz, die Manhattan-Distanz usw.
Deep Ranking - Untersucht die feinkörnige Bildähnlichkeit und charakterisiert das feinteilige Bildähnlichkeitsverhältnis mithilfe eines Satzes von Tripletts.
Was ist ein Triplett?
Das Triplett enthält das Anforderungsbild, das positive und das negative Bild. Wo ein positives Bild eher einem Anforderungsbild als einem negativen ähnelt.
Ein Beispiel für eine Reihe von Drillingen:
Die erste, zweite und dritte Zeile entspricht dem Bild der Anfrage. Die zweite Zeile (positive Bilder) ähnelt eher Anforderungsbildern als die dritte (negative Bilder).
Deep Ranking Netzwerkarchitektur
Das Netzwerk besteht aus 3 Teilen: Triplett-Abtastung, ConvNet und einer Rangfolge.
Das Netzwerk akzeptiert Tripletts von Bildern als Eingabe. Ein Bildtriplett enthält ein Anforderungsbild
$ inline $ p_i $ inline $ positives Bild
$ inline $ p_i ^ + $ inline $ und negatives Bild
$ inline $ p_i ^ - $ inline $ die unabhängig voneinander an drei identische tiefe neuronale Netze übertragen werden.
Die oberste Rangschicht - bewertet die Triplettverlustfunktion. Dieser Fehler wird in den unteren Schichten korrigiert, um die Verlustfunktion zu minimieren.
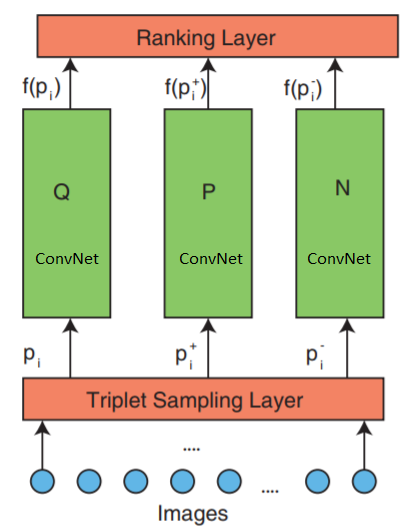
Schauen wir uns nun die mittlere Schicht genauer an:
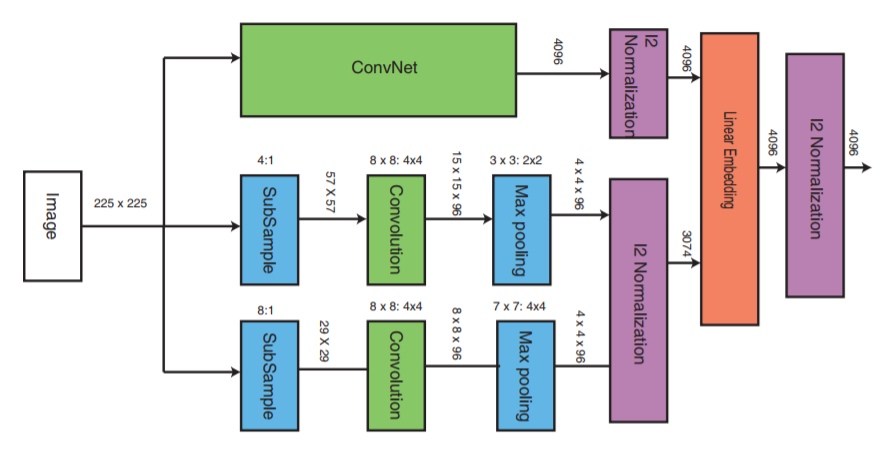
ConvNet kann ein beliebiges tiefes neuronales Netzwerk sein (in diesem Artikel wird eine der Implementierungen des Faltungs-neuronalen Netzwerks VGG16 erläutert). ConvNet enthält Faltungsschichten, eine maximale Poolschicht, lokale Normalisierungsschichten und vollständig verbundene Schichten.
Die anderen beiden Teile empfangen Bilder mit einer reduzierten Abtastrate und führen die Faltungsstufe und das maximale Pooling durch. Dann findet die Normalisierungsstufe der drei Teile statt und am Ende werden sie mit einer linearen Schicht mit anschließender Normalisierung kombiniert.
Triplettbildung
Es gibt verschiedene Möglichkeiten, eine Triplett-Datei zu erstellen, z. B. eine Expertenbewertung. In diesem Artikel wird jedoch der folgende Algorithmus verwendet:
- Jedes Bild in der Klasse bildet ein Anforderungsbild.
- Jedes Bild mit Ausnahme des Anforderungsbildes bildet ein positives Bild. Sie können jedoch die Anzahl der positiven Bilder für jede Bildanforderung begrenzen
- Ein negatives Bild wird zufällig aus einer Klasse ausgewählt, die keine Anforderungsbildklasse ist
Triplettverlustfunktion
Ziel ist es, eine Funktion zu trainieren, die den ähnlichsten Bildern einen kleinen und den verschiedenen Bildern einen großen Abstand zuweist. Dies kann ausgedrückt werden als:
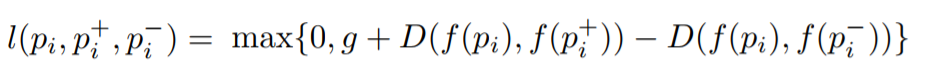
Wobei
l der Verlustkoeffizient für Tripletts ist, ist
g der Spaltkoeffizient zwischen dem Abstand zwischen zwei Bildpaaren:
$ inline $ p_i $ inline $ ,
$ inline $ p_i ^ + $ inline $ ) und (
$ inline $ p_i $ inline $ ,
$ inline $ p_i ^ - $ inline $ ),
f - Einbettungsfunktion, die das Bild in einem Vektor anzeigt,
$ inline $ p_i $ inline $ Ist das Bild der Anfrage,
$ inline $ p_i ^ + $ inline $ Ist ein positives Bild,
$ inline $ p_i ^ - $ inline $ Ist ein negatives Bild und
D ist der euklidische Abstand zwischen zwei euklidischen Punkten.
Implementierung eines Deep Ranking-Algorithmus
Implementierung mit Keras.
Drei parallele Netzwerke werden für Abfragen, positive und negative Bilder verwendet.
Die Implementierung besteht aus drei Hauptteilen:
- Implementierung von drei parallelen mehrskaligen neuronalen Netzen
- Implementierung der Verlustfunktion
- Triplett-Erzeugung
Das Erlernen von drei parallelen tiefen Netzwerken verbraucht viel Speicher. Anstelle von drei parallelen tiefen Netzwerken, die ein Anforderungsbild, ein positives und ein negatives Bild empfangen, werden diese Bilder nacheinander einem tiefen neuronalen Netzwerk am Eingang eines neuronalen Netzwerks zugeführt. Der auf die Verlustschicht übertragene Tensor enthält in jeder Zeile einen Bildanhang. Jede Zeile entspricht jedem Eingabebild in einem Paket. Da das Anforderungsbild, das positive Bild und das negative Bild nacheinander übertragen werden, entspricht die erste Zeile dem Anforderungsbild, die zweite dem positiven Bild und die dritte dem negativen Bild und wird dann bis zum Ende des Pakets wiederholt. Somit erhält die Rangfolge eine Einbettung aller Bilder. Danach wird die Verlustfunktion berechnet.
Um die Rangfolge zu implementieren, müssen wir unsere eigene Verlustfunktion schreiben, die den euklidischen Abstand zwischen dem Anforderungsbild und dem positiven Bild sowie den euklidischen Abstand zwischen dem Anforderungsbild und dem negativen Bild berechnet.
Implementierung der Verlustberechnungsfunktion_EPSILON = K.epsilon() def _loss_tensor(y_true, y_pred): y_pred = K.clip(y_pred, _EPSILON, 1.0-_EPSILON) loss = tf.convert_to_tensor(0,dtype=tf.float32)
Die Paketgröße sollte immer ein Vielfaches von 3 sein. Da ein Triplett 3 Bilder enthält und Triplettbilder nacheinander übertragen werden (wir senden jedes Bild nacheinander an ein tiefes neuronales Netzwerk).
Der Rest des Codes ist hier