Dynamische Programmierung hat einen guten Ruf für die Methode, die Sie an der Universität studieren und an die Sie sich nur in Interviews erinnern. Tatsächlich ist die Methode jedoch in vielen Situationen anwendbar. Tatsächlich ist dies eine Technik zur effektiven Lösung von Problemen, die in viele sich stark wiederholende Unteraufgaben unterteilt werden kann .

In dem Artikel werde ich eine interessante reale Anwendung der dynamischen Programmierung zeigen - die Nahtschnitzaufgabe. Die Aufgabe und Methodik werden in der Arbeit von Avidan und Shamir „Schneiden von Nähten zum Ändern der Größe von Bildern basierend auf Inhalten“ (Artikel im öffentlichen Bereich) ausführlich beschrieben.

Dies ist einer aus einer Reihe von Artikeln zur dynamischen Programmierung. Wenn Sie Methoden auffrischen möchten, lesen Sie die illustrierte Einführung in die dynamische Programmierung .

Ändern Sie die Bildgröße basierend auf dem Inhalt

Um ein echtes Problem mit dynamischer Programmierung zu lösen, müssen Sie es richtig formulieren. In diesem Abschnitt werden die erforderlichen Voreinstellungen für die ausgewählte Aufgabe beschrieben.

Die Autoren des Originalartikels beschreiben die inhaltsorientierte Größenänderung von Bildern, dh das Ändern der Breite oder Höhe des Bildes basierend auf dem Inhalt. Einzelheiten finden Sie in der Originalarbeit, und ich biete einen kurzen Überblick. Angenommen, Sie möchten die Größe eines Fotos eines Surfers ändern:


Draufsicht auf einen Surfer mitten in einem ruhigen Ozean, mit turbulenten Wellen auf der rechten Seite. Foto: Kiril Dobrev auf Pixabay

Wie im Artikel ausführlich beschrieben, gibt es verschiedene Möglichkeiten, die Bildbreite zu verringern: Dies sind Standardbeschneidungen und -skalierungen mit ihren inhärenten Nachteilen sowie das Entfernen von Pixelspalten aus der Mitte. Wie Sie sich vorstellen können, bleibt auf dem Foto eine sichtbare Naht, bei der das Bild links und rechts nicht übereinstimmt. Auf diese Weise können Sie nur eine begrenzte Anzahl von Bildern löschen.


Ein Versuch, die Breite zu reduzieren, indem die linke Seite abgeschnitten und der Block aus der Mitte herausgeschnitten wird. Letzteres hinterlässt eine sichtbare Naht.

Avidan und Shamir beschreiben im Artikel die neue Technik des „Nahtschnitzens“. Es identifiziert zuerst weniger wichtige „energiearme“ Bereiche und berechnet dann die energiearmen „Nähte“, die durch das Bild verlaufen. Beim Verringern der Bildbreite wird eine vertikale Naht von der Oberseite des Bildes nach unten bestimmt, die in jeder Zeile um nicht mehr als ein Pixel nach links oder rechts verschoben wird.

Auf dem Foto des Surfers verläuft die Naht mit der niedrigsten Energie durch die Bildmitte, wo das Wasser am leisesten ist. Dies steht im Einklang mit unserer Intuition.


Die Naht mit der niedrigsten Energie im Bild des Surfers wird zur besseren Sichtbarkeit mit einer fünf Pixel breiten roten Linie angezeigt, obwohl die Naht tatsächlich nur ein Pixel breit ist.

Nachdem wir die Naht mit der geringsten Energie bestimmt und dann entfernt haben, reduzieren wir die Bildbreite um ein Pixel. Durch wiederholtes Wiederholen dieses Vorgangs wird die Breite des gesamten Fotos erheblich verringert.


Surferbild nach Breitenreduzierung um 1024 Pixel

Wiederum entfernte der Algorithmus logischerweise das stille Wasser in der Mitte sowie auf der linken Seite des Fotos. Im Gegensatz zum Zuschneiden bleibt die Textur des Wassers auf der linken Seite erhalten und es gibt keine scharfen Übergänge. Zwar finden Sie in der Mitte einige unvollständige Übergänge, aber im Grunde sieht das Ergebnis natürlich aus.

Bildenergiedefinition

Die Magie besteht darin, die Naht mit der niedrigsten Energie zu finden. Dazu weisen wir zunächst jedem Pixel im Bild Energie zu. Anschließend verwenden wir die dynamische Programmierung, um den Pfad durch das Bild mit der geringsten Energie zu finden. Dieser Algorithmus wird im nächsten Abschnitt ausführlich erläutert. Schauen wir uns zunächst an, wie Pixel-Energiewerte zugewiesen werden.

Der wissenschaftliche Artikel diskutiert verschiedene Energiefunktionen und ihre Unterschiede. Lassen Sie es uns nicht komplizieren und eine Funktion verwenden, die einfach das Ausmaß der Farbänderung um jedes Pixel erfasst. Um das Bild zu vervollständigen, werde ich die Energiefunktion detaillierter beschreiben, falls Sie sie selbst implementieren möchten. Dies ist jedoch nur eine Voreinstellung für nachfolgende dynamische Programmierberechnungen.


Links sind drei Pixel von dunkel nach hell. Der Unterschied zwischen dem ersten und dem letzten ist groß. Rechts drei dunkle Pixel mit leichtem Unterschied in der Farbintensität

Um die Energie eines bestimmten Pixels zu berechnen, betrachten Sie die Pixel links und rechts davon. In Bezug auf die Komponenten berechnen wir das Quadrat des Abstands zwischen ihnen, dh das Quadrat der Differenz zwischen den roten, grünen und blauen Komponenten, und addieren sie dann. Wir machen dasselbe für Pixel oberhalb und unterhalb der Mitte. Addieren Sie abschließend die horizontalen und vertikalen Abstände.

$$

$$| \ Delta x | ^ 2 = (\ Delta r_x) ^ 2 + (\ Delta g_x) ^ 2 + (\ Delta b_x) ^ 2$$

$$

$$| \ Delta y | ^ 2 = (\ Delta r_y) ^ 2 + (\ Delta g_y) ^ 2 + (\ Delta b_y) ^ 2$$

$$

$$e (x, y) = | \ Delta x | ^ 2 + | \ Delta y | ^ 2$$

Die einzige Einschränkung: Wenn sich beispielsweise ein Pixel am linken Rand befindet, befindet sich links kein Nachbar. In diesem Fall vergleichen wir nur mit dem richtigen Pixel. Ähnliche Überprüfungen werden für Pixel am oberen, rechten und unteren Rand durchgeführt.

Die Energiefunktion ist groß, wenn die benachbarten Pixel eine sehr unterschiedliche Farbe haben, und klein, wenn sie ähnlich sind.


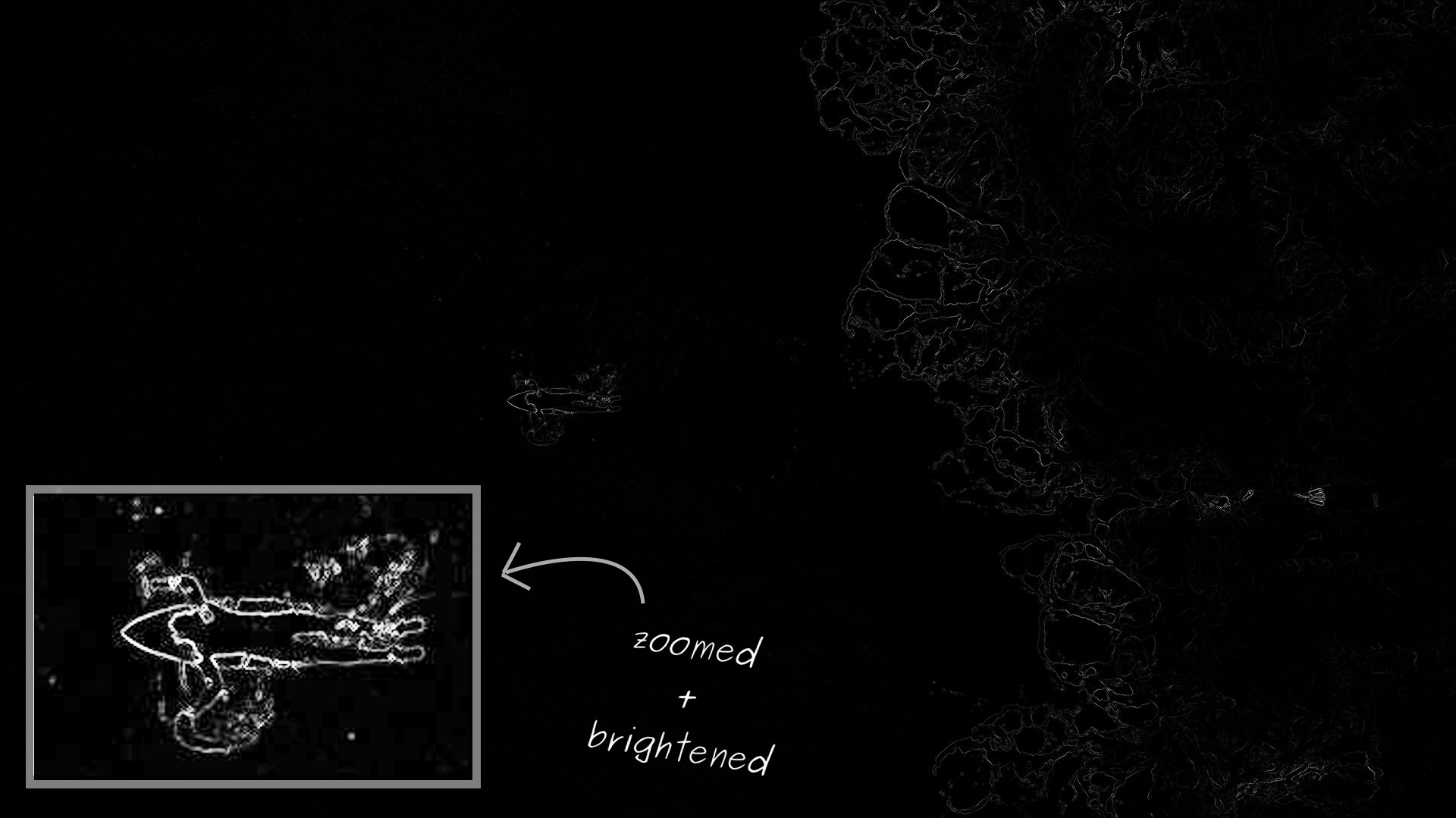Die Energie jedes Pixels auf dem Foto eines Surfers: Je heller - desto höher ist es. Wie erwartet hat der Surfer die höchste Energie in den mittleren und turbulenten Wellen rechts

Die Energiefunktion funktioniert gut auf einem Surferfoto. Es dauert jedoch einen sehr großen Wertebereich. Daher scheint es beim Rendern zu sein, dass Pixel in den meisten Fotos keine Energie haben. Tatsächlich gibt es im Vergleich zu den Regionen mit der höchsten Energie einfach sehr niedrige Werte. Um die Visualisierung zu vereinfachen, habe ich den Surfer vergrößert und diesen Bereich hervorgehoben.

Suche nach energiearmen Nähten mit dynamischer Programmierung

Durch Berechnung der Energie jedes Pixels können wir die Naht mit der niedrigsten Energie von der Oberseite des Bildes bis zur Unterseite finden. Die gleiche Analyse gilt für horizontale Nähte, um die Höhe des Originalbilds zu verringern. Wir werden uns jedoch auf vertikale konzentrieren.

Beginnen wir mit der Definition:

• Eine Naht ist eine Folge von Pixeln, ein Pixel pro Zeile. Voraussetzung ist, dass zwischen zwei aufeinanderfolgenden Linien die Koordinate liegt $$$x$ändert sich um nicht mehr als ein Pixel. Dadurch bleibt die Nahtfolge erhalten.
  
• Die Naht mit der niedrigsten Energie ist diejenige, deren Gesamtenergie über alle Pixel in der Naht minimiert wird.

Es ist wichtig zu beachten, dass die Verbindung mit der niedrigsten Energie nicht unbedingt alle Pixel mit der niedrigsten Energie durchläuft. Die Gesamtenergie aller, nicht einzelner Pixel, wird berücksichtigt.


Der gierige Ansatz funktioniert nicht. Wenn wir frühzeitig ein energiearmes Pixel auswählen, bleiben wir im energiereichen Bereich des Bildes stecken (roter Pfad rechts).

Wie Sie sehen, können Sie nicht nur das Pixel mit der niedrigsten Energie in der nächsten Zeile auswählen.

Wir teilen das Problem in Unteraufgaben auf

Das Problem mit dem gierigen Ansatz ist, dass wir bei der Entscheidung für den nächsten Schritt den Rest der bevorstehenden Naht nicht berücksichtigen. Wir können nicht in die Zukunft schauen, aber wir können alles berücksichtigen, was wir bereits wissen.

Lassen Sie uns die Aufgabe auf den Kopf stellen. Anstatt zwischen mehreren Pixeln zu wählen, um eine Naht fortzusetzen, wählen wir zwischen mehreren Nähten, um zu einem Pixel zu gelangen . Was wir tun müssen, ist, jedes Pixel zu nehmen und zwischen den Pixeln in der obigen Zeile zu wählen, aus denen die Naht kommen kann. Wenn jedes der Pixel in der obigen Zeile den zu diesem Punkt zurückgelegten Pfad codiert, betrachten wir im Wesentlichen den vollständigen Verlauf bis zu diesem Punkt.


Für jedes Pixel untersuchen wir drei Pixel in der obigen Zeile. Grundlegende Wahl - welche der Nähte soll fortgesetzt werden?

Dies setzt eine Unteraufgabe für jedes Pixel im Bild voraus. Die Unteraufgabe sollte den besten Pfad zu einem bestimmten Pixel finden. Daher ist es eine gute Idee, jedem Pixel die Energie der energiearmen Naht zuzuordnen, die in diesem Pixel endet .

Im Gegensatz zum gierigen Ansatz versucht der obige Ansatz im Wesentlichen alle möglichen Pfade durch das Bild. Es ist nur so, dass bei der Überprüfung aller möglichen Pfade immer wieder dieselben Unteraufgaben gelöst werden, was diesen Ansatz zu einer idealen Option für die dynamische Programmierung macht.

Definition einer Wiederholungsbeziehung

Wie üblich müssen wir die Idee jetzt in einer rekursiven Beziehung formalisieren. Es gibt eine Unteraufgabe, die jedem Pixel im Originalbild entspricht, sodass die Eingaben in unsere Wiederholungsbeziehung nur Koordinaten sein können $$$x$und $$$y$dieses Pixels. Dies bietet ganzzahlige Eingaben, die das Organisieren von Unteraufgaben erleichtern, sowie die Möglichkeit, zuvor berechnete Werte in einem zweidimensionalen Array zu speichern.

Definieren Sie eine Funktion $$$M (x, y)$, die die Energie der vertikalen Naht mit der geringsten Energie darstellt. Es beginnt oben im Bild und endet in einem Pixel $$$(x, y)$. Titel $$$M$ausgewählt wie im ursprünglichen wissenschaftlichen Artikel.

Zunächst benötigen Sie eine Basisversion. Alle Nähte, die in der obersten Zeile enden, haben eine Länge von nur einem Pixel. Eine Naht mit minimaler Energie ist also nur ein Pixel mit minimaler Energie:

$$

$$M (x, 0) = e (x, 0)$$

Für Pixel in den verbleibenden Zeilen sehen Sie sich die Pixel oben an. Da die Naht durchgehend sein sollte, berücksichtigen wir nur drei Pixel oben links, oben und oben rechts. Aus diesen wählen wir die Naht mit der niedrigsten Energie aus, die in einem dieser Pixel endet, und addieren die Energie des aktuellen Pixels:

$$

$$M (x, y) = e (x, y) + \ min \ begin {Fälle} M (x - 1, y - 1) \\ M (x, y - 1) \\ M (x + 1, y - 1) \ end {Fälle}$$

Betrachten Sie als Grenzsituation den Fall, in dem sich das aktuelle Pixel am linken oder rechten Bildrand befindet. In diesen Fällen lassen wir weg $$$M (x-1, y-1)$für Pixel am linken Rand oder $$$M (x + 1, y-1)$am rechten Rand.

Schließlich müssen Sie die Energie der energiearmen Naht extrahieren, die die gesamte Höhe des Bildes abdeckt. Dies bedeutet, dass wir uns die untere Zeile des Bildes ansehen und die Naht mit der niedrigsten Energie auswählen, die an einem dieser Pixel endet. Für Foto breit $$$W$und groß $$$H$Pixel:

$$

$$\ min_ {0 \ le x <W} M (x, H - 1)$$

Wir haben also eine Wiederholungsbeziehung mit allen notwendigen Eigenschaften:

• Eine Wiederholungsrelation hat ganzzahlige Eingaben.
  
• Die endgültige Antwort ist leicht aus der Beziehung zu extrahieren.
  
• Das Verhältnis hängt von sich selbst ab.

Überprüfung der DAG-Teilaufgabe (orientierter azyklischer Graph)

Da jede Unteraufgabe $$$M (x, y)$entspricht einem Pixel des Originalbildes, der Abhängigkeitsgraph ist sehr einfach zu visualisieren. Platzieren Sie sie einfach auf einem zweidimensionalen Raster, wie im Originalbild!


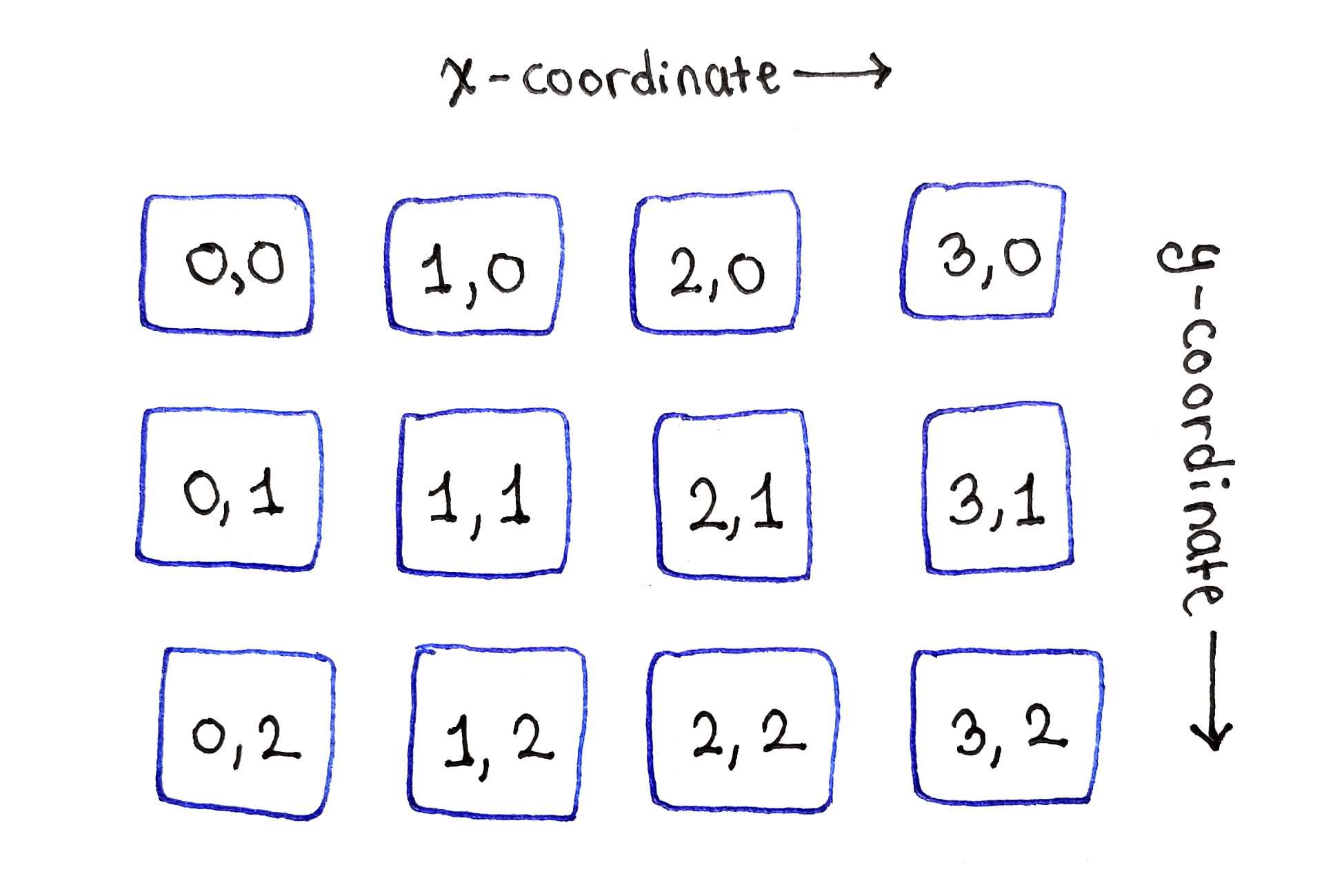Die Unteraufgaben befinden sich wie die Pixel im Originalbild in einem zweidimensionalen Raster

Wie aus dem Basisszenario der Wiederholungsbeziehung folgt, kann die oberste Zeile der Unteraufgaben mit den Energiewerten einzelner Pixel initialisiert werden.


Die oberste Zeile ist unabhängig von anderen Unteraufgaben. Beachten Sie das Fehlen von Pfeilen in der oberen Zellenreihe

In der zweiten Zeile werden Abhängigkeiten angezeigt. Erstens sind wir in der Zelle ganz links in der zweiten Reihe mit einer Grenzsituation konfrontiert. Da es links keine Zellen gibt, die Zelle $$$(1,0)$hängt nur von den Zellen ab, die sich direkt darüber und oben rechts befinden. Das gleiche passiert später mit der Zelle ganz links in der dritten Reihe.


Die Unteraufgaben am linken Rand hängen nur von zwei darüber liegenden Unteraufgaben ab

In der zweiten Zelle der zweiten Reihe (1,1) sehen wir die typischste Manifestation der Wiederholungsbeziehung. Diese Zelle hängt von drei Zellen ab: oben links, rechts darüber und oben rechts. Diese Abhängigkeitsstruktur gilt für alle "mittleren" Zellen in der zweiten und den folgenden Zeilen.


Die Unteraufgaben zwischen dem linken und rechten Rand hängen von den drei oberen Unteraufgaben ab

Schließlich repräsentiert die Zelle am rechten Rand die zweite Grenzsituation. Da rechts keine Zellen mehr vorhanden sind, hängt dies nur von den Zellen direkt oben und oben links ab.


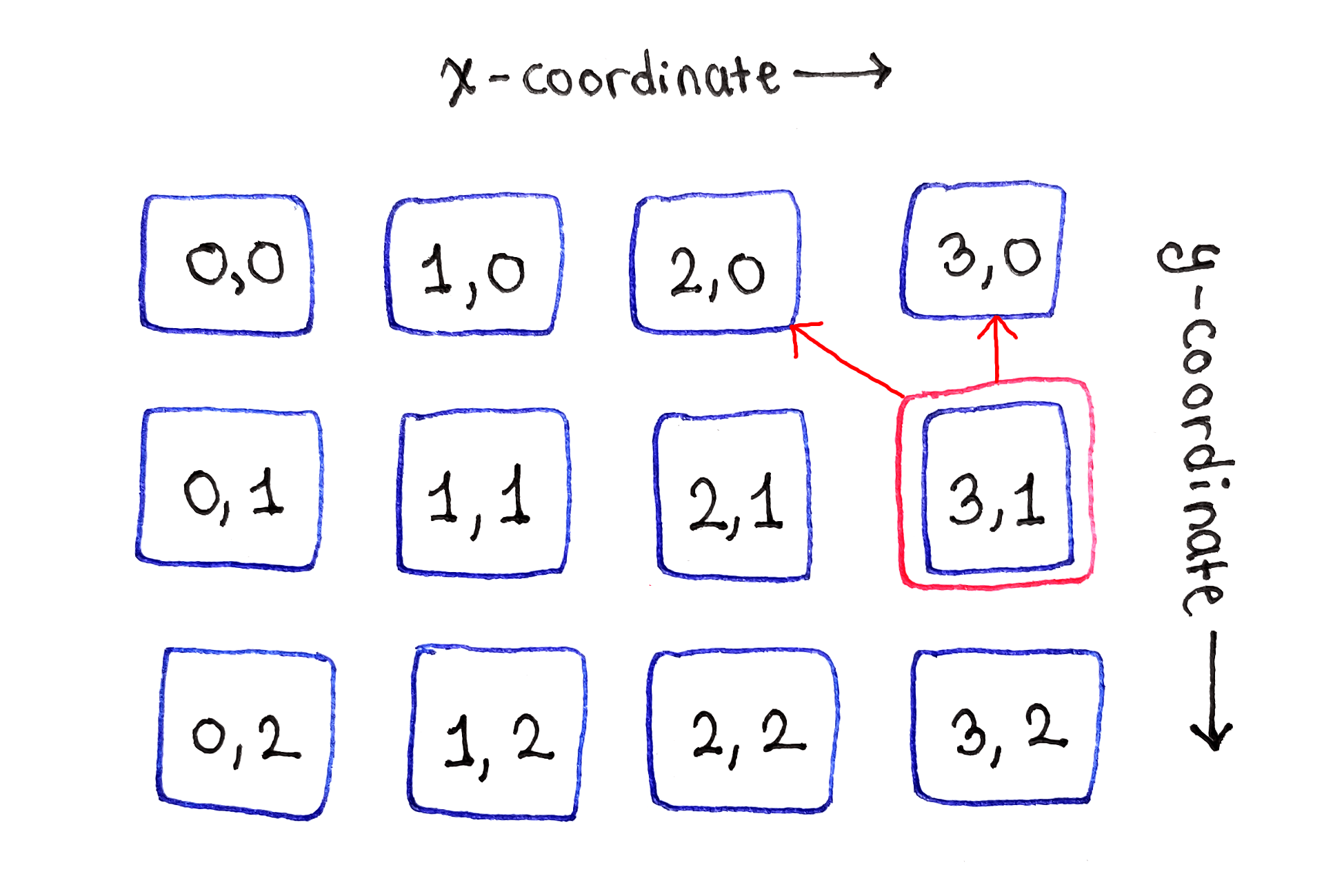Unteraufgaben am rechten Rand hängen von nur zwei Zellen oben ab

Der Vorgang wird für alle nachfolgenden Zeilen wiederholt.


Da das Abhängigkeitsdiagramm viele Pfeile enthält, zeigt diese Animation nacheinander die Abhängigkeiten für jede Unteraufgabe

Ein vollständiges Abhängigkeitsdiagramm macht Ihnen eine große Anzahl von Pfeilen Angst, aber wenn Sie sie einzeln betrachten, können Sie explizite Muster erstellen.

Bottom-up-Implementierung

Nach Durchführung dieser Analyse erhielten wir den Verarbeitungsauftrag:

• Gehen Sie von oben nach unten.
  
• Jede Zeile kann in beliebiger Reihenfolge ausgeführt werden. Die natürliche Wahl ist, von links nach rechts zu gehen.

Da jede Zeile nur von der vorherigen abhängt, müssen Sie nur zwei Datenzeilen speichern: eine für die vorherige Zeile und eine für die aktuelle Zeile. Wenn wir uns von links nach rechts bewegen, können wir sogar einzelne Elemente aus der vorherigen Zeile verwerfen, wenn sie verwendet werden. Dies erschwert jedoch den Algorithmus, da herausgefunden werden muss, welche Teile der vorherigen Zeile verworfen werden können.

Im folgenden Python-Code ist die Eingabe eine Liste von Zeilen, wobei jede Zeile eine Liste von Zahlen enthält, die die einzelnen Pixelnergien in dieser Zeile darstellen. Die Eingabe heißt pixel_energies und pixel_energies[y][x] repräsentiert die pixel_energies[y][x] in Koordinaten $$$(x, y)$.

Beginnen wir mit der Berechnung der Energie der Nähte der oberen Reihe, indem wir einfach die einzelnen Pixelnergien in der oberen Reihe kopieren:

 previous_seam_energies_row = list(pixel_energies[0]) 

Dann durchlaufen wir die verbleibenden Eingabezeilen und berechnen die Nahtenergien für jede Zeile. Der „schwierigste“ Teil besteht darin, zu bestimmen, auf welche Elemente der vorherigen Zeile Bezug genommen werden soll, da links vom linken Rand oder rechts vom rechten Rand keine Pixel vorhanden sind.

Bei jeder Iteration wird eine neue Liste der Nahtenergien für die aktuelle Linie erstellt. Am Ende der Iteration ersetzen wir die Daten der vorherigen Zeile durch die Daten der aktuellen Zeile für die nächste Iteration. So verwerfen wir die vorherige Zeile:

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_seam_energy = pixel_energy + \ min(previous_seam_energies_row[x_i] for x_i in x_range) seam_energies_row.append(min_seam_energy) previous_seam_energies_row = seam_energies_row 

Infolgedessen enthält previous_seam_energies_row die Nahtenergie für das Endergebnis. Wir finden den Mindestwert in dieser Liste - und das ist die Antwort!

 min(seam_energy for seam_energy in previous_seam_energies_row) 

Sie können diese Implementierung testen, indem Sie den Code in eine Funktion einschließen und ihn dann mit dem von Ihnen erstellten zweidimensionalen Array aufrufen. Die folgende Eingabe wurde so gewählt, dass der gierige Ansatz mit einer offensichtlichen Naht mit der niedrigsten Energie fehlschlägt:

 ENERGIES = [ [9, 9, 0, 9, 9], [9, 1, 9, 8, 9], [9, 9, 9, 9, 0], [9, 9, 9, 0, 9], ] print(min_seam_energy(ENERGIES)) 

Räumliche und zeitliche Komplexität

Jedes Pixel im Originalbild entspricht einer Unteraufgabe. Für jede der Unteraufgaben gibt es nicht mehr als drei Abhängigkeiten. Das Lösen jeder dieser Aufgaben erfordert also einen konstanten Arbeitsaufwand. Die letzte Reihe wird zweimal gehalten. Also für bildweit $$$W$und groß $$$H$Pixel Zeitkomplexität ist $$$O (B × H + B)$.

Zu jedem Zeitpunkt haben wir zwei Listen: eine für die vorherige Zeile und eine für die aktuelle. Im ersten $$$W$Elemente, und die zweite steigt allmählich auf $$$W$. Somit ist die räumliche Komplexität gleich $$$O (2W)$das ist einfach $$$O (w)$.

Beachten Sie, dass wir, wenn wir die Datenelemente der vorherigen Zeile tatsächlich verwerfen, die Liste der Elemente der vorherigen Zeile mit ungefähr der gleichen Geschwindigkeit verkürzen würden, mit der die Liste der aktuellen Zeile wächst. Somit bleibt die räumliche Komplexität erhalten $$$O (w)$. Obwohl die Breite variieren kann, ist dies normalerweise nicht so wichtig.

Niedrigenergie-Rückwärtszeiger

Wir haben also die Bedeutung der Niedrigenergienaht gefunden, aber was tun mit diesen Informationen? In der Tat sind wir nicht besorgt über die Bedeutung von Energie, sondern über die Naht selbst! Das Problem ist, dass es vom letzten Pixel keine Möglichkeit gibt, zum Rest der Naht zurückzukehren.

Dies ist, was ich in früheren Artikeln vermisst habe, aber das gleiche gilt für viele dynamische Programmierprobleme. Wenn Sie sich beispielsweise an die Aufgabe eines Hausräubers erinnern, haben wir den Maximalwert für die Anzahl der Raubüberfälle ermittelt, jedoch nicht, welche bestimmten Häuser ausgeraubt werden müssen, um diese Menge zu erhalten.

Darstellung von Rückzeigern

Allgemeine Antwort: Zeiger zurückspeichern . Beim Schneiden von Nähten benötigen wir nicht nur den Wert der Energie der Naht an jedem Pixel. Sie müssen auch wissen, welches der Pixel in der vorherigen Zeile zu dieser Energie geführt hat. Durch Speichern dieser Informationen können wir den umgekehrten Zeigern bis zur obersten Zeile folgen und die Koordinaten aller Pixel ermitteln, aus denen die Verbindung mit der geringsten Energie besteht.

Erstellen Sie zunächst eine Klasse zum Speichern von Energie und Rückzeigern. Energie wird zur Berechnung von Unteraufgaben verwendet. Da der Rückwärtszeiger bestimmt, welches Pixel in der vorherigen Zeile die aktuelle Energie liefert, können wir es uns einfach als x-Koordinate vorstellen.

 class SeamEnergyWithBackPointer(): def __init__(self, energy, x_coordinate_in_previous_row=None): self.energy = energy self.x_coordinate_in_previous_row = x_coordinate_in_previous_row 

Das Berechnungsergebnis für jede Unteraufgabe ist nicht nur eine Zahl, sondern eine Instanz dieser Klasse.

Speicher für Rückwärtszeiger

Am Ende müssen Sie über die gesamte Höhe des Bildes zurückgehen und den umgekehrten Zeichen folgen, um die Naht mit der geringsten Energie wiederherzustellen. Leider bedeutet dies, dass Sie Zeiger für alle Pixel im Bild speichern müssen, nicht nur für die vorherige Zeile.

Dazu speichern wir einfach das vollständige Ergebnis aller Unteraufgaben, obwohl es technisch möglich ist, die numerischen Energien der Naht der vorherigen Zeilen abzulehnen. Die Ergebnisse werden in einem zweidimensionalen Array gespeichert, das dem Eingabearray entspricht.

Beginnen wir mit der ersten Zeile, die nur einzelne Pixelnergien enthält. Da keine vorherige Zeile vorhanden ist, fehlen alle hinteren Zeiger. Aus SeamEnergyWithBackPointers Konsistenz werden jedoch weiterhin Instanzen von SeamEnergyWithBackPointers :

 seam_energies = [] # Initialize the top row of seam energies by copying over the top row of # the pixel energies. There are no back pointers in the top row. seam_energies.append([ SeamEnergyWithBackPointer(pixel_energy) for pixel_energy in pixel_energies[0] ]) 

Die Hauptschleife funktioniert im Wesentlichen genauso wie die vorherige Implementierung, mit den folgenden Unterschieden:

• Die Daten für die vorherige Zeile enthalten Instanzen von SeamEnergyWithBackPointer . Wenn Sie also den Wert des Wiederholungsverhältnisses berechnen, sollten Sie nach der Energie der Naht in diesen Objekten suchen.
  
• Um Daten für das aktuelle Pixel zu speichern, müssen Sie eine neue Instanz von SeamEnergyWithBackPointer . Hier speichern wir die Nahtenergie für das aktuelle Pixel sowie die x-Koordinate aus der vorherigen Zeile, die zur Berechnung der aktuellen Nahtenergie verwendet wird.
  
• Anstatt die Daten der vorherigen Zeile zu verwerfen, fügen wir am Ende jeder Zeile einfach die Daten der aktuellen Zeile zu seam_energies .

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_parent_x = min( x_range, key=lambda x_i: seam_energies[y - 1][x_i].energy ) min_seam_energy = SeamEnergyWithBackPointer( pixel_energy + seam_energies[y - 1][min_parent_x].energy, min_parent_x ) seam_energies_row.append(min_seam_energy) seam_energies.append(seam_energies_row) 

Folgen Sie den Schildern

Jetzt ist die gesamte Tabelle der Unteraufgaben gefüllt und wir können die Naht mit der geringsten Energie wiederherstellen. Wir beginnen mit der Suche nach der x-Koordinate in der unteren Zeile, die der Verbindung mit der geringsten Energie entspricht:

 # Find the x coordinate with minimal seam energy in the bottom row. min_seam_end_x = min( range(len(seam_energies[-1])), key=lambda x: seam_energies[-1][x].energy ) 

Gehen Sie nun von unten nach oben und ändern Sie sich $$$y$von len(seam_energies) - 1 bis null. Fügen Sie bei jeder Iteration das aktuelle Paar hinzu $$$(x, y)$in die Liste, die unsere Naht darstellt, und legen Sie dann den Wert fest $$$x$für das Objekt, auf das SeamEnergyWithBackPointer in der aktuellen Zeile zeigt.

 # Follow the back pointers to form a list of coordinates that form the # lowest-energy seam. seam = [] seam_point_x = min_seam_end_x for y in range(len(seam_energies) - 1, -1, -1): seam.append((seam_point_x, y)) seam_point_x = \ seam_energies[y][seam_point_x].x_coordinate_in_previous_row seam.reverse() 

Damit die Naht nach oben aufgebaut ist, kann die Liste in umgekehrter Reihenfolge gelesen werden, wenn Sie Koordinaten von oben nach unten benötigen.

Räumliche und zeitliche Komplexität

Die zeitliche Komplexität ist ähnlich wie bei der vorherigen, da wir jedes Pixel noch einmal verarbeiten müssen. Nachdem wir uns die letzte Linie angesehen und das Gelenk mit der geringsten Energie gefunden haben, gehen wir die gesamte Höhe des Bildes hinauf, um das Gelenk wiederherzustellen. Also für das Bild $$$B × H$Zeitkomplexität ist gleich $$$O (B × H + B + H)$.

Was das Volumen betrifft, behalten wir immer noch eine konstante Datenmenge für jede Unteraufgabe bei, aber jetzt verwerfen wir keine Daten. Also verwenden wir Volumen $$$O (B × H)$.

Niedrigenergienahtentfernung

Sobald die vertikale Verbindung mit der niedrigsten Energie gefunden wurde, können wir einfach die Pixel aus dem Originalbild in ein neues kopieren. Jede Zeile des neuen Bildes enthält alle Pixel aus der entsprechenden Zeile des Originalbilds, mit Ausnahme des Pixels aus der Naht mit der niedrigsten Energie. Da wir in jeder Zeile ein Pixel löschen, beginnend mit dem Bild $$$B × H$dann bekommen wir das Bild $$$(B - 1) × H$.

Wir können diesen Vorgang wiederholen, indem wir die Energiefunktion im neuen Bild wiedergeben und die Naht mit der niedrigsten Energie darauf finden. Es scheint verlockend, mehr als eine energiearme Naht im Originalbild zu finden und sie dann alle auf einmal zu löschen. Das Problem ist, dass sich die beiden Nähte schneiden können. Wenn das erste gelöscht wird, wird das zweite ungültig, da ein oder mehrere Pixel darin fehlen.


Animation des Nahtentfernungsprozesses. Besser im Vollbildmodus betrachten, um eine klarere Sicht auf die Nähte zu erhalten

Jedes Bild des Videos ist bei jeder Iteration ein Bild mit überlagerter Visualisierung der Naht mit der geringsten Energie.

Ein weiteres Beispiel

Der Artikel hatte viele detaillierte Erklärungen, also lassen Sie uns mit einer Reihe wunderschöner Fotos enden! Das folgende Foto zeigt eine Felsformation im Arches National Park:


Felsformation mit einem Loch im Arches National Park. Foto: Mike Goad auf Flickr

Energiefunktion für dieses Bild:


Die Energie jedes Pixels auf dem Foto: Je heller - desto höher ist es. Achten Sie auf die hohe Energie am Rand des Lochs.

Als Ergebnis der Berechnung wird eine solche Naht mit der niedrigsten Energie erhalten. Beachten Sie, dass es durch den Felsen rechts verläuft und direkt in die Felsformation eintritt, wo der beleuchtete Teil oben auf dem Felsen der Farbe des Himmels entspricht. Vielleicht sollten Sie eine bessere Energiefunktion wählen!


Die Naht mit der niedrigsten Energie im Bild wird zur besseren Sichtbarkeit mit einer fünf Pixel breiten roten Linie angezeigt, obwohl die Naht tatsächlich nur ein Pixel breit ist.

Zum Schluss das Bild des Bogens nach dem Ändern der Größe:


Bogen nach Komprimierung bei 1024 Pixel

Das Ergebnis ist definitiv nicht perfekt: Viele Ränder des Berges vom Originalbild sind verzerrt. Eine der Verbesserungen kann die Implementierung einer der anderen im wissenschaftlichen Artikel aufgeführten Energiefunktionen sein.

---

Obwohl dynamische Programmierung normalerweise theoretisch diskutiert wird, ist sie eine nützliche praktische Methode zur Lösung komplexer Probleme. In diesem Artikel haben wir eine der Anwendungen der dynamischen Programmierung untersucht: die Größenanpassung von Bildern an den Inhalt durch Schneiden von Nähten.

Wir haben die gleichen Prinzipien angewendet, ein Problem in kleinere Unteraufgaben zu unterteilen, die Abhängigkeiten zwischen diesen Unteraufgaben zu analysieren und dann die Unteraufgaben in einer Reihenfolge zu lösen, die die räumliche und zeitliche Komplexität des Algorithmus minimiert. Darüber hinaus haben wir die Verwendung von Umkehrzeigern untersucht, um nicht nur den Energiewert für die optimale Naht zu ermitteln, sondern auch die Koordinaten jedes Pixels zu bestimmen, aus dem dieser Wert besteht. Dann haben wir diese Teile auf ein echtes Problem angewendet, das eine Vor- und Nachbearbeitung erfordert, um den dynamischen Programmieralgorithmus wirklich effektiv nutzen zu können.