Einführung
Eines der ersten Radioteleskope, das 1937 von der amerikanischen Grotte Reber gebaut wurde. Das Radioteleskop war ein Blechspiegel mit einem Durchmesser von 9,5 m, der auf einem Holzrahmen montiert war:

Bis 1944 hatte Reber die erste Karte der Verteilung der Weltraumfunkwellen in der Milchstraße zusammengestellt.
Die Entwicklung der Radioastronomie brachte eine Reihe von Entdeckungen mit sich: 1946 wurde die Radioemission aus dem Sternbild Cygnus entdeckt, 1951 - extragalaktische Strahlung, 1963 - Quasare und 1965 Relikthintergrundstrahlung mit einer Wellenlänge von 7,5 cm.
1963 wurde in Arecibo (Puerto Rico) ein einzigartiges 300-Meter-Radioteleskop gebaut. Dies ist eine bewegungslose Schüssel mit einem beweglichen Bestrahlungsgerät, die in einer natürlichen Spalte des Geländes eingebaut ist.

Einzelne Radioteleskope haben eine kleine Winkelauflösung, die durch die Formel bestimmt wird:
T h e t a = f r a c l a m b d a d wo
l a m b d a - Wellenlänge
d - Durchmesser des Radioteleskops.
Um die Auflösung zu verbessern, ist es natürlich notwendig, den Durchmesser der Antenne zu vergrößern, was physikalisch eine schwierige Aufgabe ist. Es war möglich, es mit dem Aufkommen von Funkinterferometern zu lösen.
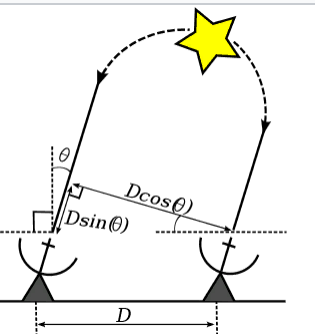
Die Vorderseite einer elektromagnetischen Welle, die von einem entfernten Stern in der Nähe der Erde ausgesendet wird, kann als flach betrachtet werden. Im Fall des einfachsten Interferometers, das aus zwei Antennen besteht, ist die Differenz im Weg der Strahlen, die an diesen beiden Antennen ankommen, gleich:
D e l t a = D c d o t s i n ( T h e t a ) ,
wo:
D e l t a - der Unterschied im Strahlengang;
D. - Abstand zwischen den Antennen;
T h e t a - der Winkel zwischen der Einfallsrichtung der Strahlen und der Normalen zu der Linie, auf der sich die Antennen befinden.
Bei
T h e t a = 0 Wellen, die an beiden Antennen ankommen, werden in Phase summiert. Gegenphasig erscheinen die Wellen zum ersten Mal mit:
Delta= frac lambda2, Theta=arcsin frac lambda2D ,
wo:
lambda - Wellenlänge.
Das nächste Maximum wird bei sein
Delta= lambda, Minimum bei
Delta= frac3 lambda2 usw. Es wird ein mehrblättriges Strahlungsmuster (DN) erhalten, dessen Breite des Hauptlappens bei
lambda<<D ist gleich
lambda/D . Die Breite der Hauptkeule bestimmt die maximale Winkelauflösung des Funkinterferometers, sie entspricht in etwa der Breite der Keule.
Die Ultra-Long-Base-Radiointerferometrie (VLBI) ist eine Art der Interferometrie, die in der Radioastronomie verwendet wird und bei der sich die Empfangselemente des Interferometers (Teleskope) nicht näher als in kontinentalen Abständen voneinander befinden.
Mit der VLBI-Methode können Sie die Beobachtungen mehrerer Teleskope kombinieren und so ein Teleskop simulieren, dessen Abmessungen dem maximalen Abstand zwischen den Originalteleskopen entsprechen. Die Winkelauflösung des VLBI ist zehntausendmal höher als die Auflösung der besten optischen Instrumente.
Der aktuelle Status von VLBI-Netzwerken
Heute hören mehrere VLBI-Netzwerke den Weltraum:
- European-EVN (European VLBI Network), bestehend aus mehr als 20 Radioteleskopen;
- American-VLBA (Very Long Baseline Array) mit zehn Teleskopen mit einem Durchmesser von jeweils 25 Metern;
- Japanisch - JVN (japanisches VLBI-Netzwerk) besteht aus zehn Antennen in Japan, darunter vier astrometrische Antennen (VERA-Projekt - VLBI Exploration of Radio Astrometry);
- Australisch - LBA (Long Baseline Array);
- Chinesisch - CVN (Chinese VLBI Network), bestehend aus vier Antennen;
- Südkorea - KVN (Korean VLBI Network), das drei 21-Meter-Radioteleskope umfasst;
- Der Russe - basierend auf dem permanenten radiointerferometrischen Komplex - „Kvazar-KVO“ mit Radioteleskopen mit einem Durchmesser von 32 m, ausgestattet mit hochempfindlichen Kryoradiometern im Wellenlängenbereich von 1,35 cm bis 21 cm. Die Länge der Basen - der effektive Durchmesser des synthetisierten „Spiegels“ - beträgt in Richtung etwa 4400 km Ost-West (siehe Bild).
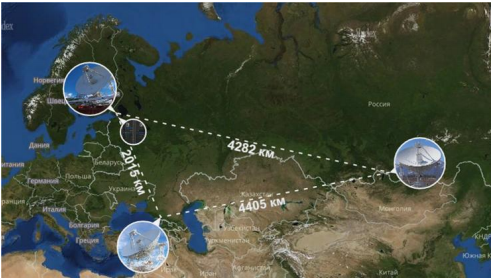
Im VLBI-Komplex „Kvazar-KVO“ werden Wasserstoffstandards als Referenzfrequenzquelle für alle Frequenztransformationen verwendet, die den Übergang zwischen den Ebenen der Hyperfeinstruktur des Grundzustands eines Wasserstoffatoms mit einer Frequenz von 1420,405 MHz verwenden, was 21 cm in der Radioastronomie entspricht.
Mit dem VLBI gelöste Aufgaben
- Astrophysik Radiobilder von natürlichen Weltraumobjekten (Quasare und andere Objekte) werden mit einer Auflösung von Zehntel und Hundertstel Mas (Millisekunden eines Bogens) erstellt.
- Astrometrische Studien. Konstruktion von Koordinaten-Zeit-Systemen. Die Forschungsobjekte sind Radioquellen mit extrem kleinen Winkelgrößen, einschließlich quasistellarer Radioquellen und der Kerne von Radiogalaxien, die aufgrund ihrer großen Entfernung nahezu ideale Objekte für die Schaffung eines Netzwerks unterstützender stationärer Objekte sind.
- Forschung zur Himmelsmechanik und zur Dynamik des Sonnensystems, Weltraumnavigation. Die Installation eines Leuchtfeuers auf den Oberflächen von Planeten und die Verfolgung der Leuchtfeuer interplanetarer automatischer Stationen ermöglicht es, mithilfe der VLBI-Methode Parameter wie die Umlaufbewegung des Planeten, die Richtung der Rotationsachsen und ihre Präzession sowie die Dynamik des Planeten-Satelliten-Systems zu untersuchen. Für den Mond wird auch das sehr wichtige Problem der Bestimmung der physikalischen Libration und der Dynamik der Mond-Erde-Systeme gelöst.
Navigation im Weltraum mit VLBI
- Überwachung der Bewegungen von Astronauten auf der Mondoberfläche im Jahr 1971. Sie bewegten sich mit Hilfe des Mondrovers Rover. Die Genauigkeit der Bestimmung seiner Position relativ zum Mondmodul erreichte 20 cm und hing hauptsächlich von der Libration des Mondes ab (Libration - periodische pendelartige Schwingungen des Mondes relativ zu seinem Massenmittelpunkt);
- Navigationsunterstützung für die Lieferung und Entladung von Aerostat-Sonden von fliegenden Fahrzeugen in die Atmosphäre der Venus (VEGA-Projekt). Die Entfernung zur Venus beträgt mehr als 100 Millionen km, die Sendeleistung beträgt nur 1 Watt. VEGA-1/2-Starts fanden im Dezember 1984 statt. Am 11. und 15. Juni 1985 wurden Ballons in die Atmosphäre der Venus geworfen. Die Beobachtung wurde 46 Stunden lang durchgeführt.
Strukturdiagramm eines vereinfachten VLBI-Netzwerks
Basierend auf einem echten VLBI-Netzwerk modellieren wir mithilfe der Python-Software ein vereinfachtes VLBI-System in Form separater Modelle für jede Einheit oder jeden Prozess. Diese Modelle reichen aus, um die grundlegenden Prozesse zu beobachten. Das Strukturdiagramm eines vereinfachten VLBI-Netzwerks ist in der Abbildung dargestellt:
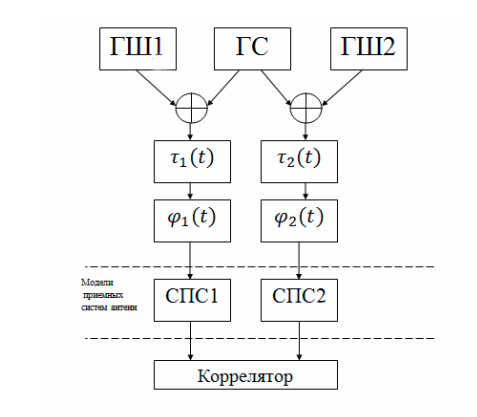
Das System enthält die folgenden Komponenten:
- Generator nützliches phasenmoduliertes Signal (HS);
- Geräuschgeneratoren (GSh1, GSh2). Das System verfügt über zwei Radioteleskope (Empfangsantennen), die ihr eigenes Rauschen haben. Darüber hinaus gibt es Geräusche der Atmosphäre und anderer natürlicher und künstlicher Quellen von Funkemissionen.
- eine Zeitverzögerungseinheit, die eine linear variierende Zeitverzögerung aufgrund der Erdrotation simuliert;
- Phasenschieber, der den Doppler-Effekt simuliert;
- Signalumwandlungssystem (SPS), bestehend aus einem lokalen Oszillator zum Übertragen des Signals in der Frequenz und einem Bandpassfilter;
- FX-Korrelator.
Die Korrelatorschaltung ist in der folgenden Abbildung dargestellt:
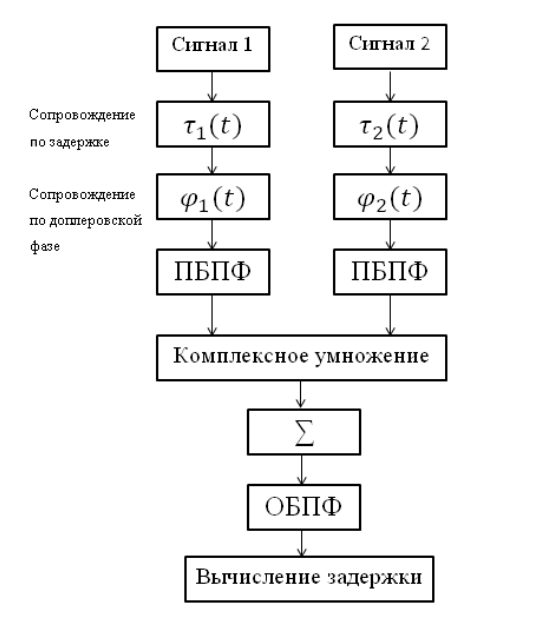
Die gegebene Korrelatorschaltung, die die folgenden Blöcke enthält:
- direkte schnelle Fourier-Transformation (PBPF) und inverse Fourier-Transformation (OBPF);
- Kompensieren der zuvor eingeführten Verzögerung;
- kompensierender Doppler-Effekt;
- komplexe Multiplikation zweier Spektren;
- Summieren akkumulierter Implementierungen.
Navigationssignalmodell
Am bequemsten für VLBI-Messungen sind die Navigationssignale des Raumfahrzeugs von Satellitennavigationssystemen wie GPS und GLONASS. An Navigationssignale werden eine Reihe von Anforderungen gestellt:
- Ermöglichen es Ihnen, Pseudobereiche gut zu definieren.
- Informationen über die Position des Navigationssystems übertragen;
- von Signalen anderer NS unterscheidbar sein;
- Andere Funksysteme nicht stören.
- Zum Empfangen und Senden sind keine komplexen Geräte erforderlich.
In ausreichendem Maße sind sie mit einem Signal mit binärer (Zwei-Positionen-) Phasenmodulation zufrieden - BPSK (Binary Phase Shift Key), das in der russischen Literatur als FM-2 bezeichnet wird. Diese Modulation ändert die Phase der Trägerschwingung um π, was dargestellt werden kann als:
S(t)=A cdotG(t) cdotcos(2 pift),wobei G (t) die Modulationsfunktion ist.
Zur Implementierung der Phasenmodulation können zwei Generatoren verwendet werden, von denen jeder die gleiche Frequenz bildet, jedoch eine andere Anfangsphase aufweist. Mit der Modulationsfunktion können Sie das Spektrum des Signals erweitern und die Pseudobereiche genau messen (die Entfernung zwischen dem Satelliten und dem Empfänger, berechnet durch die Signalausbreitungszeit ohne Korrektur der Differenz zwischen der Uhr des Satelliten und des Empfängers).
Hier ist eine Auflistung, die die Grundprinzipien von BPSK erklärt:
Auflistungfrom scipy import* from pylab import* import numpy as np import scaleogram as scg f = 2;
Wir bekommen:
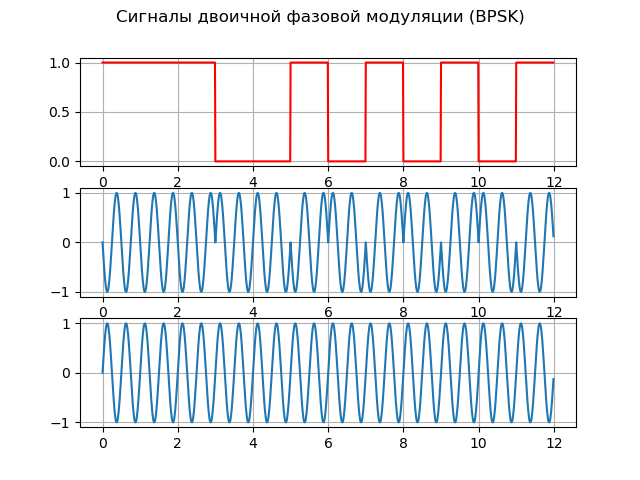
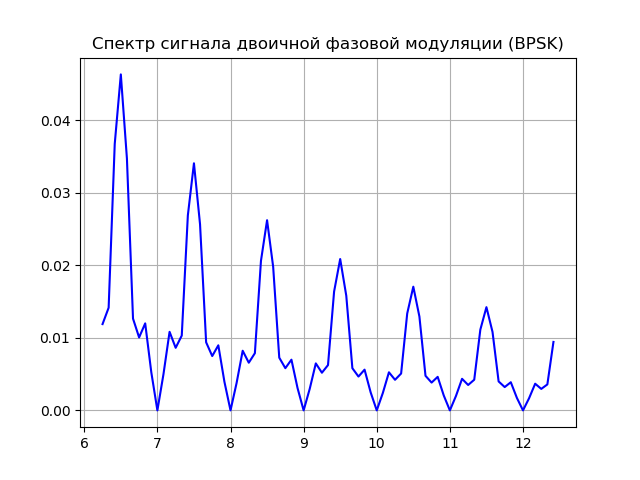
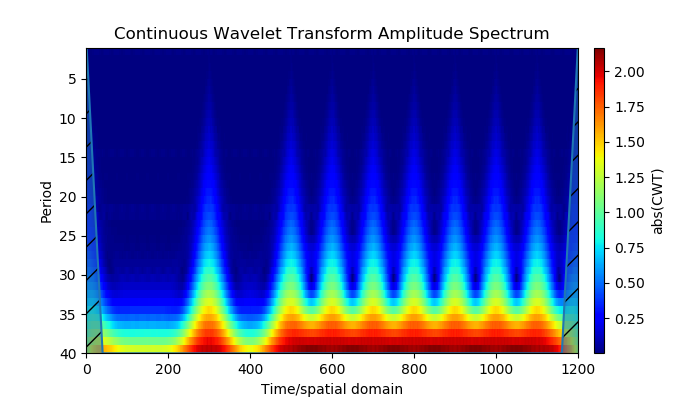
Quellmodell
Das phasenmodulierte harmonische Navigationssignal von einem Satelliten oder Raumfahrzeug hat die Form:
x=a(2 pifct+ sumsncos(2 pifnt)),Wo ist die Trägerfrequenz?
fc=$8. GHz
Das Signal hat mehrere gesteuerte Parameter: die Amplitude der n-ten modulierenden Schwingung
sn, seine Frequenz
fc und die Amplitude der Trägerschwingung a.
Um eine Korrelationsfunktion zu erhalten, bei der die Nebenkeulen so weit wie möglich unterdrückt werden und der engste Korrelationspeak erreicht wird, variieren wir die Frequenzwerte unter Verwendung der Werte von 2, 4, 8 und 16 MHz und des Modulationsindex im Bereich von 0 bis 2π in Schritten von π. Lassen Sie mich Ihnen eine Liste des Programms für eine solche Suche nach Parametern einer phasenmodulierten Funktion für das Endergebnis geben:
Wir bekommen:
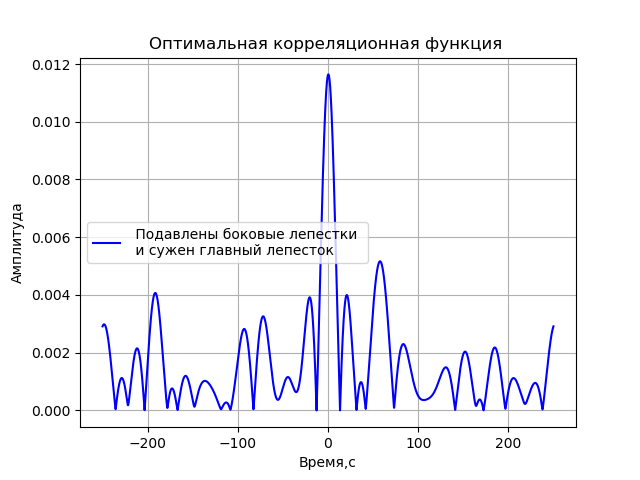
Die resultierende Funktion hat die Form:
x=cos(2 pifct+2 picos(2 pi106t)+2 picos(2 pi108t)+4 picos(2 pi1016t)).(1)Ferner wird diese Funktion verwendet, um VLBI zu simulieren.
Modell eines Rauschgenerators, der Interferenzen simuliert, die zusammen mit einem Signal aus dem Weltraum und der Erdatmosphäre empfangen werden
Die Funktion (1) des phasenmodulierten Navigationssignals kann auf beide Kanäle des Funkinterferometers angewendet werden, es ist jedoch erforderlich, die Signalverzögerung im zweiten Kanal und das Rauschen in beiden Kanälen zu berücksichtigen, wie in der folgenden Auflistung gezeigt:
Wir bekommen:
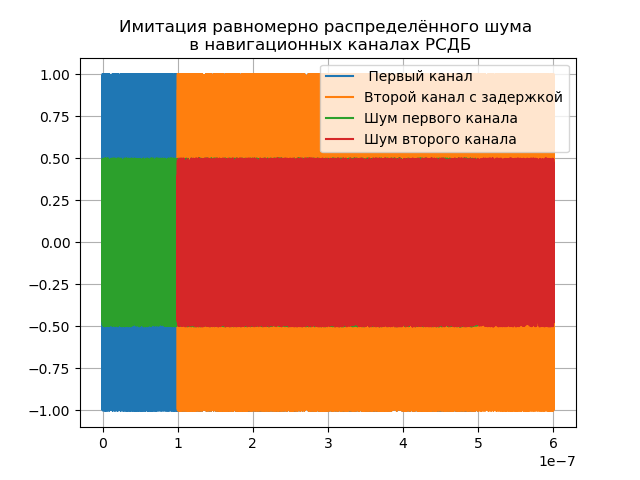
Die Verzögerungsverzögerung = 1e-7 wird zur Demonstration eingestellt. In Wirklichkeit hängt sie von der Basis ab und kann vier oder mehr Einheiten erreichen.
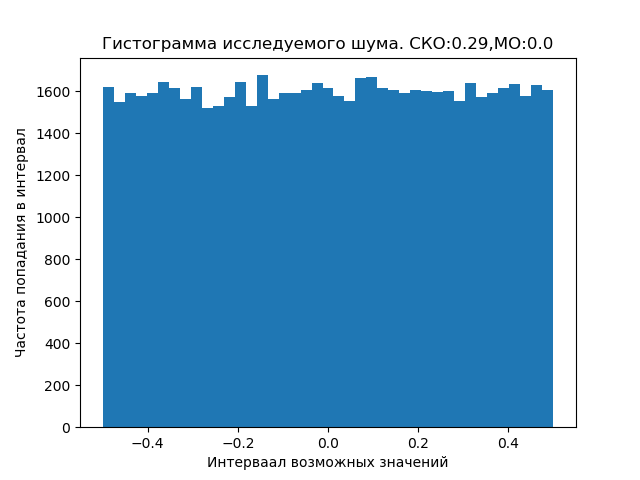
Sowohl kosmische als auch erdnahe Geräusche können nach einem Gesetz verteilt werden, das sich von der gegebenen Uniform unterscheidet und spezielle Studien erfordert.
Modellierung des Doppler-Effekts
Aufgrund der Tatsache, dass die Erde eine abgerundete Form hat und sich um ihre Achse dreht, gelangen Signale aus dem Weltraum mit unterschiedlichen Verzögerungen zu Antennen. Aus diesem Grund ist es notwendig, die Signale zeitlich zu verschieben und die Dopplerfrequenz zu berücksichtigen. Wir werden ungefähr berücksichtigen, dass die Verzögerung gemäß einem linearen Gesetz variiert:
taux(t)=ax+bxt,(2)wo
ax=1..3 cdot10−3 ms und
bx=1..3 cdot10−6 ms Die Doppler-Phase wird als Ableitung der Verzögerung gefunden:
fdx= fracd tau(t)dt=bx,(3)Das empfangene Signal sollte folgendermaßen aussehen:
hatx=x(t− taux)ej2 pifdxt,wobei x (t) das vom Raumfahrzeug abgestrahlte Signal ist.
Eine Demonstration des Doppler-Effekts ist in der folgenden Auflistung dargestellt:
Wir bekommen:
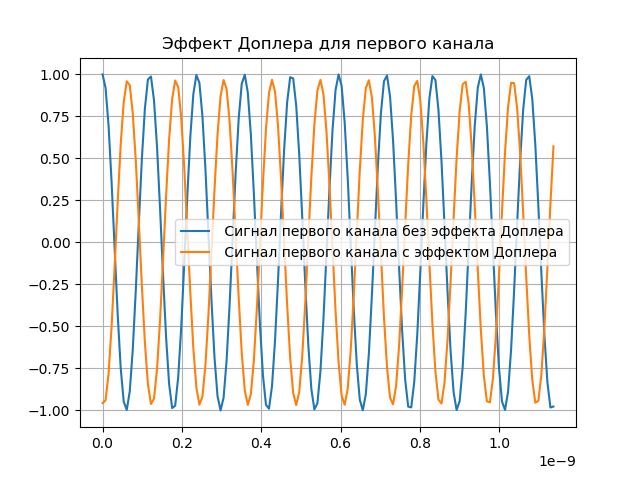
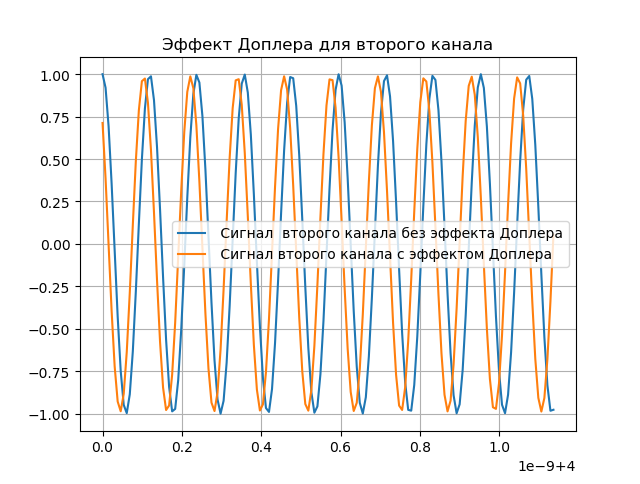
Modellierung der Doppler-Kompensation
Offensichtlich müssen Änderungen am Signal kompensiert werden. Zu diesem Zweck enthält das System Unterstützung für die Verzögerungs- und Doppler-Phase. Nachdem das Signal das Registrierungssystem durchlaufen hat, wird eine Verzögerung eingeführt:
tauex(t)=ax+bext,(4)Es wird berücksichtigt, dass die Verzögerung mit einer bestimmten Genauigkeit berechnet wird, so dass
left|aex−ax right|<30 ns
left|bex−bx right|<10 ns, d.h. Es wird ein wenig anders sein als bei früheren Verzögerungen. Es ist klar, dass die Verzögerung mit dem entgegengesetzten Vorzeichen als zuvor eingeführt wird.
Das empfangene Signal sieht folgendermaßen aus:
hatx= tildex(t+ tauex)e−j2 pifdet.(5)Die Doppler-Effektkompensation ist in der folgenden Auflistung dargestellt:
Wir bekommen:
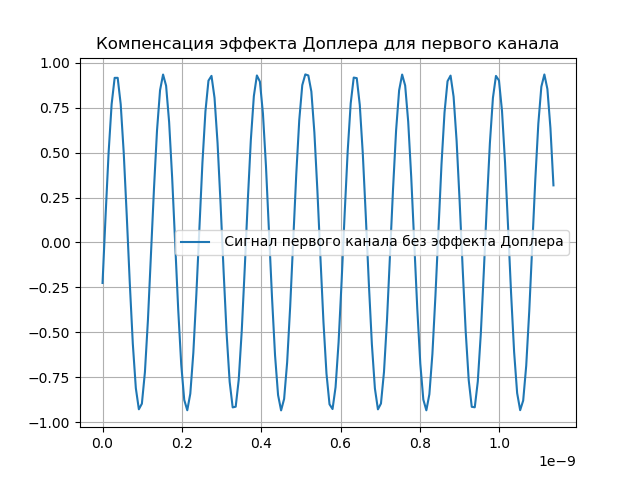
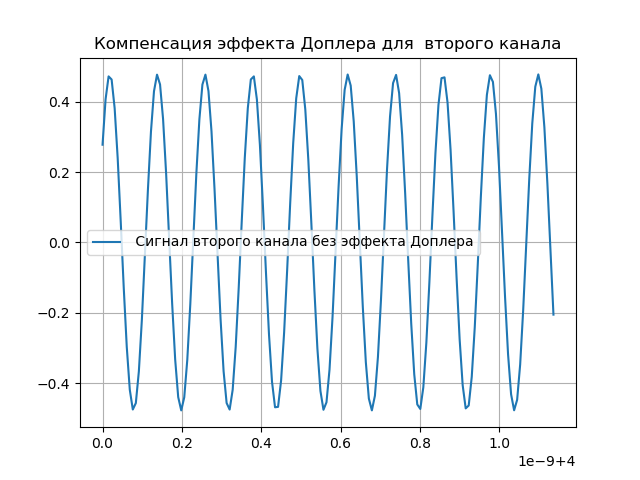
Signalüberlagerungssimulation
Nachdem das Signal in das Registrierungssystem eingetreten ist, erfolgt eine Frequenzumwandlung, die auch als Heterodyning bezeichnet wird. Dies ist eine nichtlineare Transformation, bei der die Signale von zwei verschiedenen Frequenzen
f1 und
f2 das Differenzfrequenzsignal wird hervorgehoben -
f= left|f1−f2 right.| Die Frequenz des lokalen Oszillatorsignals entspricht der Differenz zwischen der Frequenz des untersuchten Signals und der Frequenz, die Sie nach der Übertragung erhalten möchten. Die Überlagerung wird unter Verwendung eines Hilfsgenerators für harmonische Schwingungen durchgeführt - eines lokalen Oszillators und eines nichtlinearen Elements. Heterodyning ist mathematisch gesehen die Multiplikation eines Signals mit einem Exponenten:
xg= hatxej2 pifgt,(6)wo
fg - lokales Oszillatorsignal.
Programm für Heterodyning:
Wir bekommen:
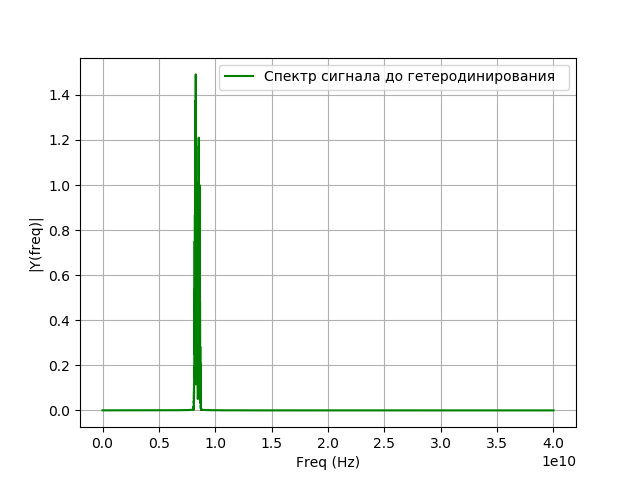
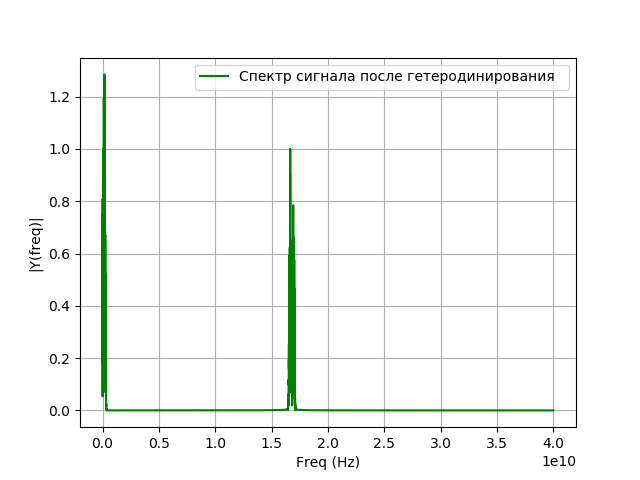
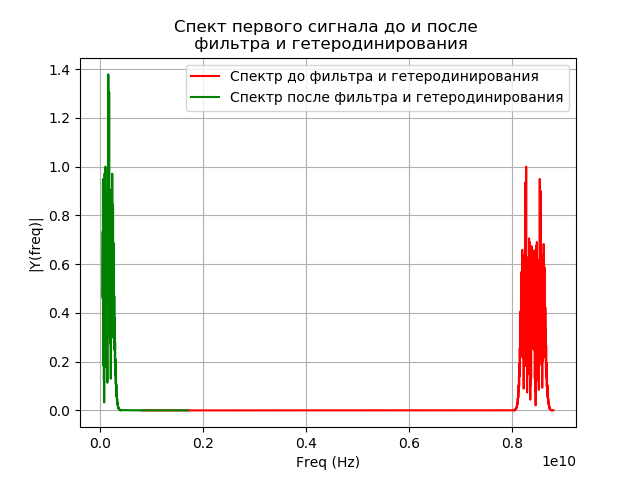
Modellierung der Signalfilterung nach der Überlagerung
Nach der Überlagerung tritt das Signal in das Bandpassfilter ein. Filterpassband (PP)
fpass=32 MHz Die Impulsantwort des Filters wird durch die Fenstermethode unter Verwendung der Bibliotheksfunktion signal.firwin berechnet. Um ein Signal am Ausgang des Filters zu erhalten, wird die Faltung des Filters und des Signals im Zeitbereich durchgeführt. Das Faltungsintegral für unseren Fall hat die Form:
checkx(t)= int+ infty− inftyxg(t)h(t−t′)dt,(7)wobei h (t) die Impulsantwort des Filters ist.
Die Faltung wird mithilfe der Bibliotheksfunktion signal.convolve ermittelt. Das registrierte Signal wird unter Berücksichtigung von Heterodyning und Filterung in Form einer Formel dargestellt
checkx(t)=( hatx(t)e−j2 pifgt)∗hwobei die Faltung durch * angegeben ist.
Programm zur Modellierung der Filtration:
Wir bekommen:
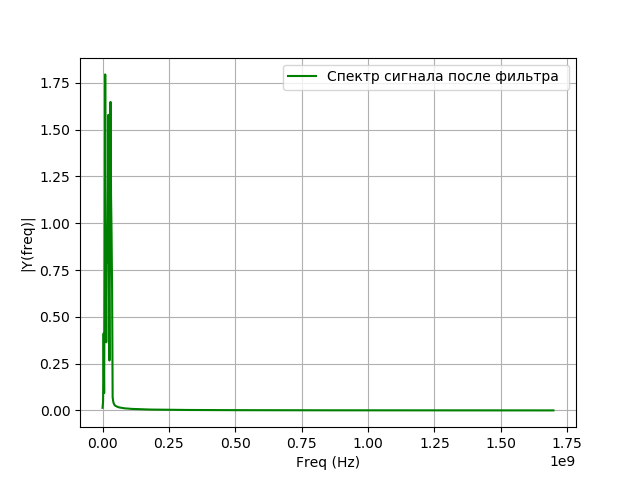
Digitale Signalwandler für VLBI verwenden hauptsächlich Filter mit einer endlichen Impulsantwort (FIR), da sie gegenüber Filtern mit einer unendlichen Impulsantwort (IIR) eine Reihe von Vorteilen haben:
- FIR-Filter können im Fall einer Impulsantwortsymmetrie (IM) eine streng lineare Phasenantwort haben. Dies bedeutet, dass mit einem solchen Filter Phasenverzerrungen vermieden werden können, was für die Funkinterferometrie besonders wichtig ist. Filter mit einer unendlichen Impulsantwort (IIR) haben nicht die Symmetrieeigenschaften von THEM und können keine lineare Phasenantwort haben.
- FIR-Filter sind nicht rekursiv, was bedeutet, dass sie immer stabil sind. Die Stabilität von IIR-Filtern kann nicht immer garantiert werden.
- Die praktischen Konsequenzen der Verwendung einer begrenzten Anzahl von Bits zum Implementieren von Filtern sind für FIR-Filter signifikant weniger bedeutsam.
In der obigen Auflistung wird das Modell des FIR-Bandpassfilters unter Verwendung der Fenstermethode implementiert, wobei die Filterreihenfolge so ausgewählt wurde, dass die Form des Frequenzgangs des Filters nahezu rechteckig war. Die Anzahl der Koeffizienten des simulierten Filters beträgt n = 100001, d. H. Die Reihenfolge des Filters beträgt P = 100000.
Programm zum Aufbau des Frequenzgangs und des Phasengangs des erhaltenen FIR-Filters:
Wir bekommen:

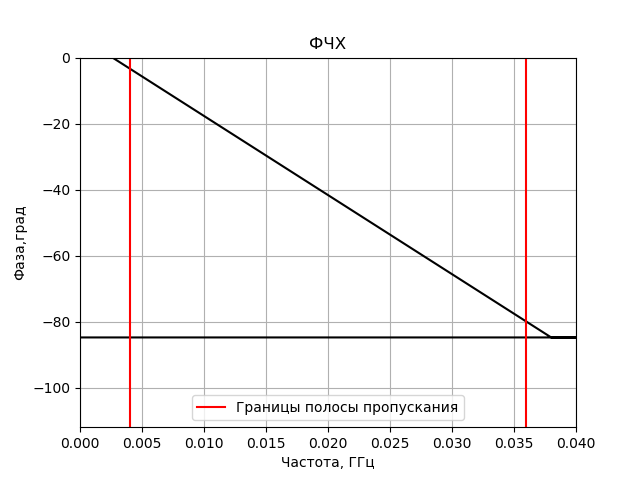
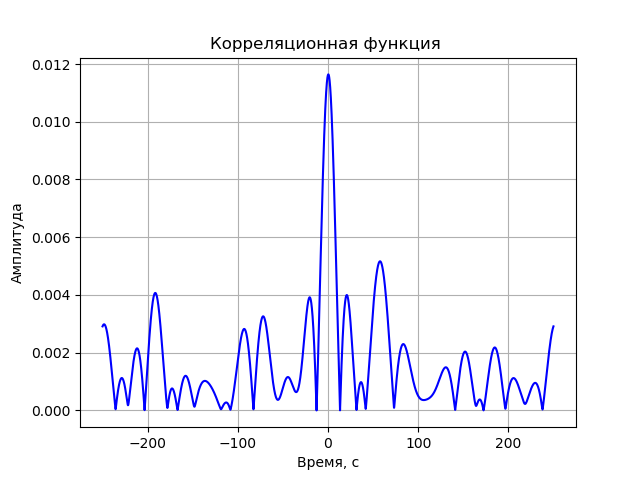
FX-Korrelatormodell
Als nächstes wird jedes Signal einer schnellen Fourier-Transformation (FFT) unterzogen. FFT wird mit der Funktion fft library aus scipy.fftpack implementiert. Die resultierenden Spektren sind komplex konjugiert multipliziert:
S(j omega)=S1(j omega)∗S2(j omega)=(a1+jb1)∗(a2−jb2)=a1a2+b1b2+j( b 1 a 2 - a 1 b 2 )Die letzte Aktion ist die Umkehrung der FFT. Da die Amplitude der Korrelationsfunktion von Interesse ist, muss das resultierende Signal durch die Formel umgewandelt werden:
A = s q r t r e 2 + i m 2 Das Programm für die Korrelationsfunktion ohne Berücksichtigung der Verzerrungen des Registrierungssystems:
Wir bekommen:
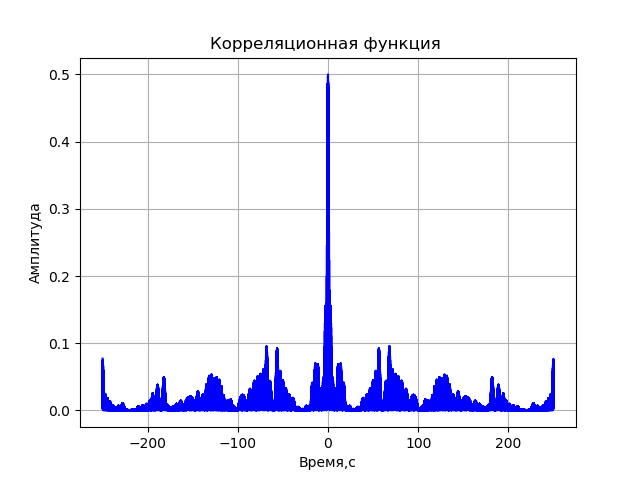
Vollständige Auflistung des Computermodells von VLBI:
Wir bekommen:
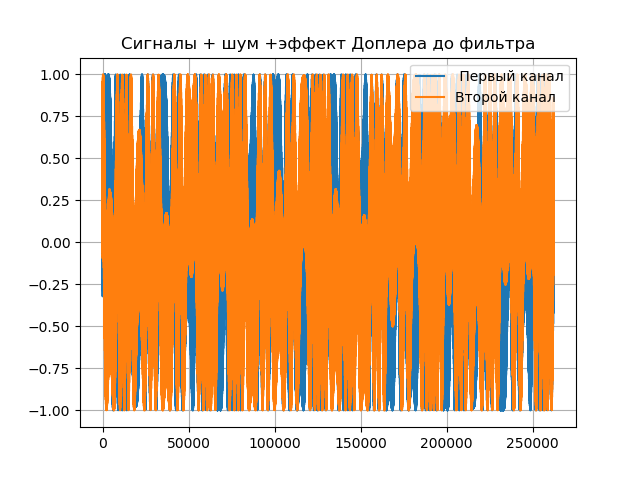

Schlussfolgerungen
- Es wird eine kurze Geschichte der Entwicklung der Radioastronomie gegeben.
- Der aktuelle Status von VLBI-Netzwerken wird analysiert.
- Die mittels VLBI-Netzwerken gelösten Probleme werden berücksichtigt.
- Python-Tools erstellten ein Modell von Navigationssignalen mit binärer Phasenmodulation (mit zwei Positionen) - BPSK (Binary Phase Shift Key). Das Modell verwendet eine Wavelet-Analyse der Phasenmodulation.
- Es wurde ein Modell von Signalquellen erhalten, das es ermöglicht, die Modulationsparameter zu bestimmen, die die optimale Korrelationsfunktion gemäß dem Kriterium zur Unterdrückung von Nebenkeulen und der maximalen Amplitude der zentralen Keule liefern.
- Man erhält ein Modell eines vereinfachten VLBI-Netzwerks unter Berücksichtigung des Rauschens und des Doppler-Effekts. Die Merkmale der Filterung unter Verwendung eines Filters mit einer endlichen Impulsantwort werden berücksichtigt.
- Nach einer kurzen Zusammenfassung der Theorie sind alle Modelle mit Demonstrationsprogrammen ausgestattet, mit denen Sie den Einfluss von Modellparametern verfolgen können.