Wir sprechen weiterhin über die Konferenz zu Statistik und maschinellem Lernen AISTATS 2019. In diesem Beitrag werden wir Artikel über Tiefenmodelle aus Baumensembles analysieren, Regularisierung für sehr spärliche Daten mischen und zeiteffiziente Annäherung an die Kreuzvalidierung.

Deep Forest-Algorithmus: Eine Untersuchung von Nicht-NN-Tiefenmodellen basierend auf nicht differenzierbaren Modulen
Zhi-Hua Zhou (Universität Nanjing)
→ Präsentation
→ Artikel
Implementierungen - unten
Ein Professor aus China sprach über das Baumensemble, das die Autoren als erstes tiefes Training für nicht differenzierbare Module bezeichnen. Dies mag wie eine zu laute Aussage erscheinen, aber dieser Professor und sein H-Index 95 sind eingeladene Redner. Diese Tatsache ermöglicht es uns, die Aussage ernster zu nehmen. Die grundlegende Theorie von Deep Forest wurde für eine lange Zeit entwickelt, der ursprüngliche Artikel ist bereits 2017 (fast 200 Zitate), aber die Autoren schreiben Bibliotheken und jedes Jahr verbessern sie den Algorithmus in der Geschwindigkeit. Und jetzt, so scheint es, haben sie den Punkt erreicht, an dem diese schöne Theorie endlich in die Praxis umgesetzt werden kann.
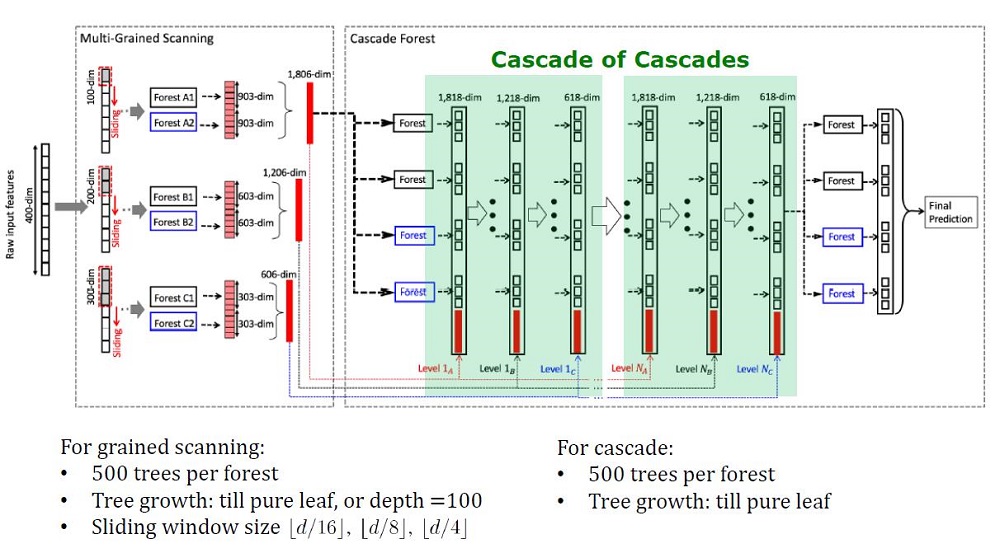
Gesamtansicht der Tiefwaldarchitektur
Hintergrund
Tiefe Modelle, die heute als tiefe neuronale Netze verstanden werden, werden verwendet, um komplexe Datenabhängigkeiten zu erfassen. Darüber hinaus stellte sich heraus, dass das Erhöhen der Anzahl von Schichten effizienter ist als das Erhöhen der Anzahl von Einheiten auf jeder Schicht. Neuronale Netze haben jedoch ihre Nachteile:
- Es braucht viele Daten, um nicht umzuschulen,
- Es erfordert eine Menge Rechenressourcen, um in angemessener Zeit zu lernen.
- Zu viele Hyperparameter, die sich nur schwer optimal konfigurieren lassen
Darüber hinaus sind Elemente tiefer neuronaler Netze differenzierbare Module, die nicht unbedingt für jede Aufgabe wirksam sind. Trotz der Komplexität neuronaler Netze funktionieren konzeptionell einfache Algorithmen wie eine zufällige Gesamtstruktur oft besser oder nicht viel schlechter. Für solche Algorithmen müssen Sie jedoch Features manuell entwerfen, was auch schwierig optimal zu tun ist.
Forscher haben bereits festgestellt, dass die Ensembles auf Kaggle: „sehr perfekt“ sind. Inspiriert von den Worten von Scholl und Hinton, dass Differenzierung die schwächste Seite von Deep Learning ist, haben sie beschlossen, ein Ensemble von Bäumen mit DL-Eigenschaften zu erstellen.
Folie „Wie man ein gutes Ensemble macht“
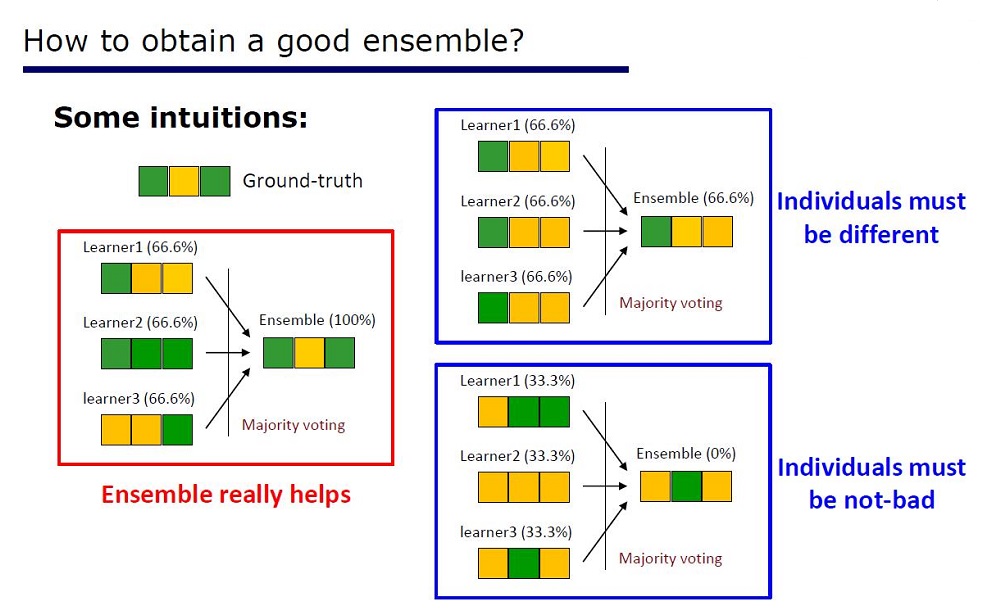
Die Architektur wurde aus den Eigenschaften der Ensembles abgeleitet: Die Elemente der Ensembles sollten nicht von sehr schlechter Qualität sein und sich unterscheiden.
GcForest besteht aus zwei Phasen: Cascade Forest und Multi-Grained Scanning. Damit die Kaskade nicht umgeschult wird, besteht sie außerdem aus zwei Baumarten - von denen eine absolut zufällige Bäume sind, die für nicht zugewiesene Daten verwendet werden können. Die Anzahl der Schichten wird innerhalb des Kreuzvalidierungsalgorithmus bestimmt.
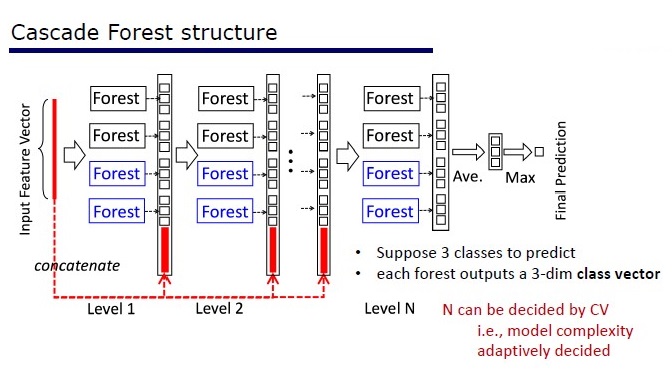
Zwei Arten von Bäumen
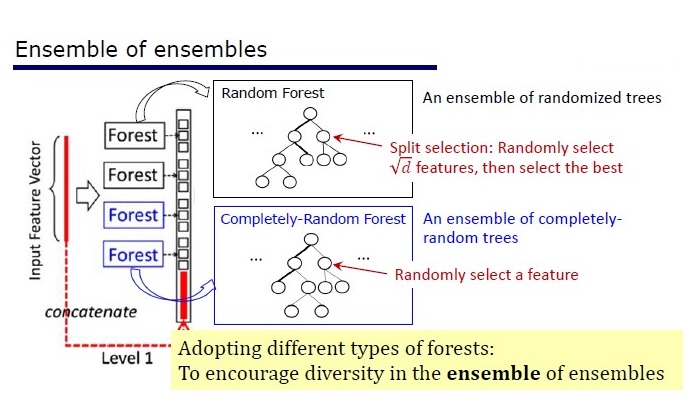
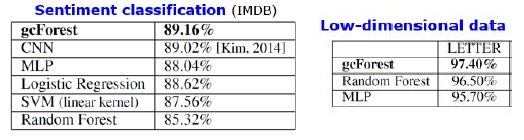
Ergebnisse
Zusätzlich zu den Ergebnissen für Standarddatensätze versuchten die Autoren, gcForest für Transaktionen des chinesischen Zahlungssystems zu verwenden, um nach Betrug zu suchen, und erzielten F1 und AUC viel höher als die von LR und DNN. Diese Ergebnisse sind nur in der Präsentation enthalten, aber der Code, der für einige Standarddatensätze ausgeführt werden soll, befindet sich auf Git.
Ergebnisse der Algorithmusersetzung. mdDF ist die optimale Margin Distribution Deep Forest, eine Variante von gcForest
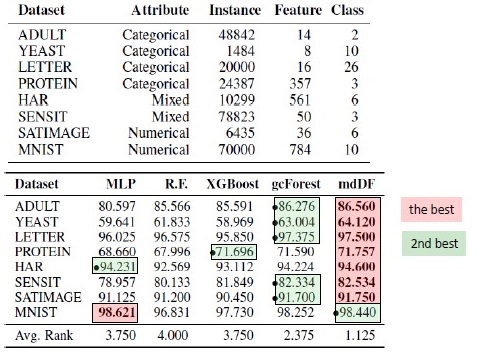
Vorteile:
- Bei wenigen Hyperparametern wird die Anzahl der Ebenen innerhalb des Algorithmus automatisch angepasst
- Die Standardeinstellungen sind so gewählt, dass sie bei vielen Aufgaben gut funktionieren.
- Adaptive Komplexität des Modells für kleine Daten - ein kleines Modell
- Keine Notwendigkeit, Funktionen einzustellen
- Es funktioniert qualitativ vergleichbar mit tiefen neuronalen Netzen und manchmal besser
Nachteile:
- Nicht auf GPU beschleunigt
- In den Bildern verliert DNNs
Neuronale Netze haben ein Problem mit der Gradientendämpfung, während tiefe Wälder ein Problem mit dem Verschwinden der Vielfalt haben. Da es sich um ein Ensemble handelt, ist die Qualität umso höher, je mehr „unterschiedliche“ und „gute“ Elemente verwendet werden. Das Problem ist, dass die Autoren bereits fast alle klassischen Ansätze (Stichproben, Randomisierung) ausprobiert haben. Solange keine neue Grundlagenforschung zum Thema „Unterschiede“ erscheint, wird es schwierig sein, die Qualität tiefer Wälder zu verbessern. Jetzt ist es jedoch möglich, die Rechengeschwindigkeit zu verbessern.
Reproduzierbarkeit der Ergebnisse
Ich war von XGBoost in Bezug auf die Tabellendaten fasziniert und wollte das Ergebnis reproduzieren. Ich nahm das Adults-Dataset und wandte GcForestCS (eine leicht beschleunigte Version von GcForest) mit Parametern der Autoren des Artikels und XGBoost mit Standardparametern an. In dem Beispiel, das die Autoren hatten, wurden kategoriale Merkmale bereits irgendwie vorverarbeitet, aber es wurde nicht angegeben, wie. Als Ergebnis habe ich CatBoostEncoder und eine andere Metrik verwendet - ROC AUC. Die Ergebnisse waren statistisch unterschiedlich - XGBoost gewann. Die Betriebszeit von XGBoost ist vernachlässigbar, während gcForestCS 20 Minuten jeder Kreuzvalidierung mit 5 Falten hat. Andererseits haben die Autoren den Algorithmus an verschiedenen Datensätzen getestet und die Parameter für diesen Datensatz an ihre Feature-Vorverarbeitung angepasst.
Den Code finden Sie hier .
Implementierungen
→ Der offizielle Code der Autoren des Artikels
→ Offizielle verbesserte Änderung, schneller, aber keine Dokumentation
→ Die Implementierung ist einfacher
PcLasso: Das Lasso erfüllt die Regression der Hauptkomponenten
J. Kenneth Tay, Jerome Friedman, Robert Tibshirani (Stanford University)
→ Artikel
→ Präsentation
→ Anwendungsbeispiel
Anfang 2019 schlugen J. Kenneth Tay, Jerome Friedman und Robert Tibshirani von der Stanford University eine neue Unterrichtsmethode mit einem Lehrer vor, die besonders für spärliche Daten geeignet ist.
Die Autoren des Artikels lösten das Problem der Analyse von Daten zu Genexpressionsstudien, die in Zeng & Breesy (2016) beschrieben sind. Ziel ist der Mutationsstatus des p53-Gens, der die Genexpression als Reaktion auf verschiedene Signale von zellulärem Stress reguliert. Ziel der Studie ist es, Prädiktoren zu identifizieren, die mit dem Mutationsstatus von p53 korrelieren. Die Daten bestehen aus 50 Zeilen, von denen 17 als normal klassifiziert sind und die restlichen 33 Mutationen im p53-Gen tragen. Nach einer Analyse von Subramanian et al. (2005) 308 Sätze von Genen zwischen 15 und 500 sind in dieser Analyse enthalten. Diese Gen-Kits enthalten insgesamt 4.301 Gene und sind im Paket grpregOverlap R verfügbar. Beim Erweitern von Daten zur Verarbeitung überlappender Gruppen werden 13.237 Spalten ausgegeben. Die Autoren des Artikels verwendeten die pcLasso-Methode, die zur Verbesserung der Modellergebnisse beitrug.
Im Bild sehen wir einen Anstieg der AUC bei Verwendung von "pcLasso"

Die Essenz der Methode
Methode kombiniert  -regelmäßigkeit mit
-regelmäßigkeit mit  , wodurch der Koeffizientenvektor auf die Hauptkomponenten der Merkmalsmatrix eingegrenzt wird. Sie nannten die vorgeschlagene Methode "Kern-Lasso-Komponenten" ("pcLasso" auf R verfügbar). Die Methode kann besonders leistungsfähig sein, wenn die Variablen zuvor gruppiert wurden (der Benutzer wählt aus, was und wie gruppiert werden soll). In diesem Fall komprimiert pcLasso jede Gruppe und erhält die Lösung in Richtung der Hauptkomponenten dieser Gruppe. Während des Lösungsprozesses wird auch die Auswahl signifikanter Gruppen unter den verfügbaren durchgeführt.
, wodurch der Koeffizientenvektor auf die Hauptkomponenten der Merkmalsmatrix eingegrenzt wird. Sie nannten die vorgeschlagene Methode "Kern-Lasso-Komponenten" ("pcLasso" auf R verfügbar). Die Methode kann besonders leistungsfähig sein, wenn die Variablen zuvor gruppiert wurden (der Benutzer wählt aus, was und wie gruppiert werden soll). In diesem Fall komprimiert pcLasso jede Gruppe und erhält die Lösung in Richtung der Hauptkomponenten dieser Gruppe. Während des Lösungsprozesses wird auch die Auswahl signifikanter Gruppen unter den verfügbaren durchgeführt.
Wir präsentieren die diagonale Matrix der singulären Zerlegung einer zentrierten Matrix von Merkmalen  wie folgt:
wie folgt:
Wir repräsentieren unsere singuläre Zerlegung der zentrierten Matrix X (SVD) als  wo
wo  Ist eine Diagonalmatrix, die aus singulären Werten besteht. In dieser Form
Ist eine Diagonalmatrix, die aus singulären Werten besteht. In dieser Form  - Regularisierung kann dargestellt werden:
- Regularisierung kann dargestellt werden:
 wo
wo  - Diagonalmatrix mit der Funktion von Quadraten singulärer Werte:
- Diagonalmatrix mit der Funktion von Quadraten singulärer Werte: %2C%E2%80%A6%2CZ_%7B22%7D%3Df_2%20(d_1%5E2%2Cd_2%5E2%2C%E2%80%A6%2Cd_m%5E2%20)) .
.
Im Allgemeinen in  -regelmäßigkeit
-regelmäßigkeit  für alle
für alle  das entspricht
das entspricht  . Sie schlagen vor, die folgenden Funktionen zu minimieren:
. Sie schlagen vor, die folgenden Funktionen zu minimieren:
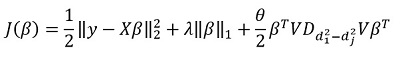
Hier  - Matrix der Unterschiede der diagonalen Elemente
- Matrix der Unterschiede der diagonalen Elemente  . Mit anderen Worten, wir steuern den Vektor
. Mit anderen Worten, wir steuern den Vektor  auch mit Hyperparameter
auch mit Hyperparameter  .
.
Wenn wir diesen Ausdruck transformieren, erhalten wir die Lösung:
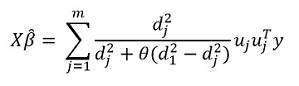
Das Hauptmerkmal der Methode ist natürlich die Fähigkeit, Daten zu gruppieren und auf der Grundlage dieser Gruppen die Hauptkomponenten der Gruppe hervorzuheben. Dann schreiben wir unsere Lösung in der Form um:
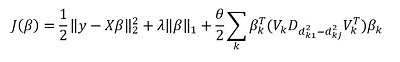
Hier  - Vektorsubvektor
- Vektorsubvektor  entsprechend der Gruppe k,
entsprechend der Gruppe k, ) - singuläre Werte
- singuläre Werte  in absteigender Reihenfolge angeordnet, und
in absteigender Reihenfolge angeordnet, und  - Diagonalmatrix
- Diagonalmatrix 
Einige Hinweise zur Lösung der Zielfunktion:
Die Zielfunktion ist konvex und die nicht glatte Komponente ist trennbar. Daher kann es unter Verwendung eines Gradientenabfalls effektiv optimiert werden.
Der Ansatz besteht darin, mehrere Werte festzuschreiben  (einschließlich Null, um den Standard zu erhalten
(einschließlich Null, um den Standard zu erhalten  -regelmäßigkeit) und dann optimieren:
-regelmäßigkeit) und dann optimieren:  abholen
abholen  . Dementsprechend sind die Parameter
. Dementsprechend sind die Parameter  und
und  werden zur Kreuzvalidierung ausgewählt.
werden zur Kreuzvalidierung ausgewählt.
Parameter  schwer zu interpretieren. In der Software (pcLasso-Paket) legt der Benutzer den Wert dieses Parameters fest, der zum Intervall [0,1] gehört, wobei 1 entspricht
schwer zu interpretieren. In der Software (pcLasso-Paket) legt der Benutzer den Wert dieses Parameters fest, der zum Intervall [0,1] gehört, wobei 1 entspricht  = 0 (Lasso).
= 0 (Lasso).
In der Praxis variieren die Werte  = 0,25, 0,5, 0,75, 0,9, 0,95 und 1 können Sie eine breite Palette von Modellen abdecken.
= 0,25, 0,5, 0,75, 0,9, 0,95 und 1 können Sie eine breite Palette von Modellen abdecken.
Der Algorithmus selbst ist wie folgt

Dieser Algorithmus ist bereits in R geschrieben. Wenn Sie möchten, können Sie ihn bereits verwenden. Die Bibliothek heißt 'pcLasso'.
Ein Infinitesimal Jackjack der Schweizer Armee
Ryan Giordano (UC Berkeley); William Stephenson (MIT); Runjing Liu (UC Berkeley);
Michael Jordan (UC Berkeley); Tamara Broderick (MIT)
→ Artikel
→ Code
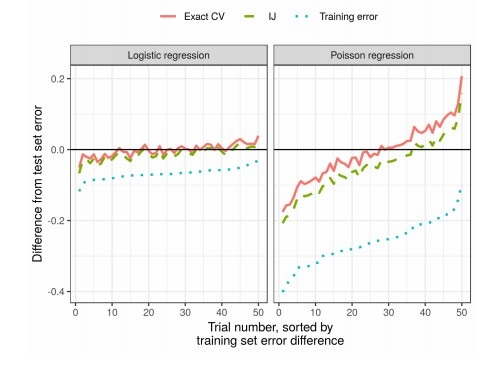
Die Qualität von Algorithmen für maschinelles Lernen wird häufig durch mehrfache Kreuzvalidierung (Kreuzvalidierung oder Bootstrap) gemessen. Diese Methoden sind leistungsstark, bei großen Datenmengen jedoch langsam.
In dieser Arbeit verwenden Kollegen die lineare Approximation von Gewichten, um Ergebnisse zu erzielen, die schneller funktionieren. Diese lineare Näherung ist in der statistischen Literatur als "infinitesimales Klappmesser" bekannt. Es wird hauptsächlich als theoretisches Instrument zum Nachweis asymptotischer Ergebnisse verwendet. Die Ergebnisse des Artikels sind unabhängig davon anwendbar, ob die Gewichte und Daten stochastisch oder deterministisch sind. Infolgedessen schätzt diese Näherung sequentiell die wahre Kreuzvalidierung für jedes feste k.
Verleihung des Paper Award an den Autor des Artikels

Die Essenz der Methode
Betrachten Sie das Problem der Schätzung eines unbekannten Parameters  wo
wo  Ist kompakt und die Größe unseres Datensatzes ist
Ist kompakt und die Größe unseres Datensatzes ist  . Unsere Analyse wird an einem festen Datensatz durchgeführt. Definieren Sie unsere Bewertung
. Unsere Analyse wird an einem festen Datensatz durchgeführt. Definieren Sie unsere Bewertung  wie folgt:
wie folgt:
- Für jeden
 einstellen
einstellen  (
(  ) Ist eine Funktion von
) Ist eine Funktion von 
 Ist eine reelle Zahl und
Ist eine reelle Zahl und  Ist ein Vektor bestehend aus
Ist ein Vektor bestehend aus 
Dann  kann dargestellt werden als:
kann dargestellt werden als:

Wenn wir dieses Optimierungsproblem mit der Gradientenmethode lösen, nehmen wir an, dass die Funktionen differenzierbar sind und wir den Hessischen berechnen können. Das Hauptproblem, das wir lösen, sind die mit der Bewertung verbundenen Rechenkosten ) für alle
für alle  . Der Hauptbeitrag der Autoren des Artikels besteht in der Berechnung der Schätzung
. Der Hauptbeitrag der Autoren des Artikels besteht in der Berechnung der Schätzung ) wo
wo ) . Mit anderen Worten, unsere Optimierung hängt nur von Derivaten ab
. Mit anderen Worten, unsere Optimierung hängt nur von Derivaten ab ) von denen wir annehmen, dass sie existieren und hessisch sind:
von denen wir annehmen, dass sie existieren und hessisch sind:
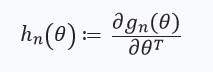
Als nächstes definieren wir eine Gleichung mit einem festen Punkt und seiner Ableitung:
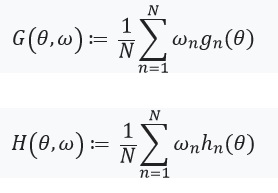
Hier lohnt es sich, darauf zu achten %2Cw)%3D0) , als
, als ) - Lösung für
- Lösung für %3D0) . Wir definieren auch:
. Wir definieren auch: ) und die Matrix der Gewichte als:
und die Matrix der Gewichte als:  . In dem Fall, wenn
. In dem Fall, wenn  hat eine inverse Matrix, können wir den impliziten Funktionssatz und die 'Kettenregel' verwenden:
hat eine inverse Matrix, können wir den impliziten Funktionssatz und die 'Kettenregel' verwenden:
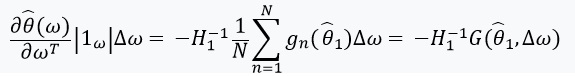
Diese Ableitung ermöglicht es uns, eine lineare Näherung zu bilden ) durch
durch  das sieht so aus:
das sieht so aus:
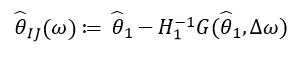
Als  hängt nur ab von
hängt nur ab von  und
und  und nicht aus Lösungen für andere Werte
und nicht aus Lösungen für andere Werte  Dementsprechend besteht keine Notwendigkeit, neue Werte von & ohgr; neu zu berechnen und zu finden. Stattdessen muss man das SLE (System linearer Gleichungen) lösen.
Dementsprechend besteht keine Notwendigkeit, neue Werte von & ohgr; neu zu berechnen und zu finden. Stattdessen muss man das SLE (System linearer Gleichungen) lösen.
Ergebnisse
In der Praxis reduziert dies die Zeit im Vergleich zur Kreuzvalidierung erheblich: