Alexey Savvateev: Modelle des Internets und sozialer Netzwerke

"Der einzige Grund für die Existenz der Wirtschaft besteht darin, Mathematiker zu neuen Heldentaten zu inspirieren."



Im Jahr 2013 hielt Alexey Savvateev mehrere Vorträge über Modelle sozialer Netzwerke und des Internets. Ich fand dieses Thema sehr neugierig und unverdient vergessen. Versuchen wir, das Problem zu verstehen. Mich interessiert auch, wie sich die Situation seitdem geändert hat und welche nützlichen Veröffentlichungen in diesem Bereich vorliegen.

Sowohl im Internet als auch in der Biologie sozialer Netzwerke weisen sie Eigenschaften auf, die individuell durch Modelle beschrieben werden, aber alle zusammen - sie verwirren die moderne Mathematik. Savvateev behauptet, dass "derjenige, der sich damit befasst, den Nobelpreis erhalten wird". Die Zukunft wird von der Fähigkeit abhängen, mit Netzwerken zu arbeiten.

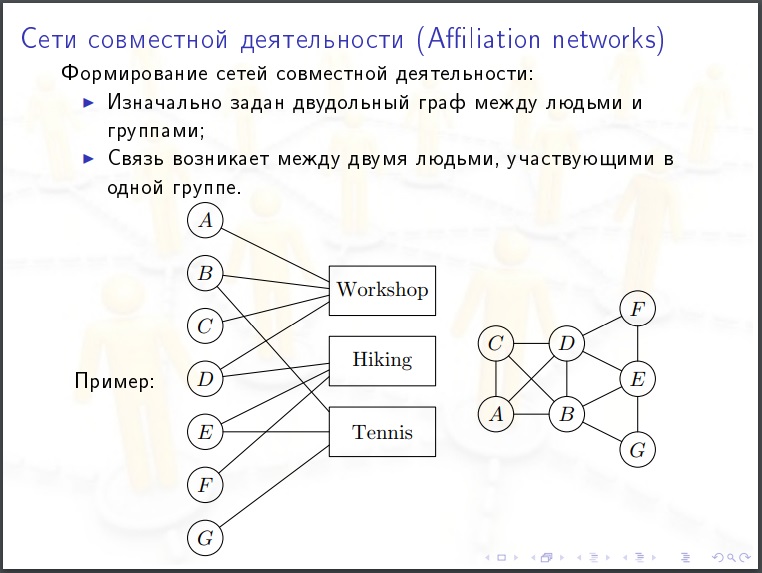
Das Folgende ist eine Zusammenstellung von drei Vorlesungsvideos, das Video selbst ist am Ende. (Der Beitrag sieht aus wie eine Reihe von Folien mit Zitaten von Dozenten, um alles in einen einzigen und schlanken Text zu binden. Mir fehlen die Kenntnisse der russischen Sprache und Mathematik, aber das Thema ist sehr wichtig, deshalb möchte ich es veröffentlichen.)

Das soziale Netzwerk besteht aus:

• Agenten
• Kommunikation zwischen Agenten

Verbindungen können in beide Richtungen (Freunde, Mitautorschaft) und in eine Richtung (Abonnenten) erfolgen. Soziales gab es immer, aber das Studium auf Makroebene wurde erst mit dem Aufkommen von Online-Netzwerken möglich. Die Menschheit hat in den letzten 10 Jahren einen Quantensprung gemacht. Es lernte, sich selbst als Ganzes zu untersuchen. Es kann digitalisieren. Sammeln Sie Informationen über sich.

Es wäre fair, ein Modell gewichteter Graphen zu erstellen, wenn die Koeffizienten der „Bindungsstärke“ angegeben sind. Aber für uns wie zuvor zum Mond.

Galerie

Es ist nützlich, sich die Bilder anzusehen. Die Hypothese, die Sie nach dem Betrachten des Bildes aufstellen könnten, kann offensichtlich absurd sein.

Wer ist nützlich, um soziale Netzwerke zu studieren

Wirtschaft: Es wird davon ausgegangen, dass die Mikro- und Makroebenen in der Wirtschaft über ein „Netzwerk“ verbunden sind.
Politikwissenschaft: Es wird davon ausgegangen, ob das Regime bestehen bleibt oder sich ändert, je nachdem, wer über leistungsfähigere Netzwerkspezialisten verfügt.



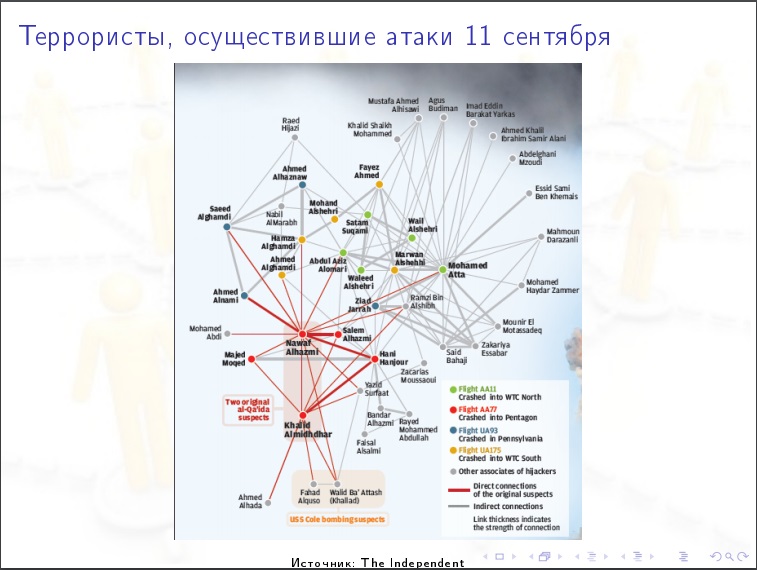Beispiel für eine Analyse in sozialen Medien.

Numerische Merkmale sozialer Netzwerke

• Entfernung
• Durchmesser
• Scheitelpunktgrad
• Scheitelpunktgradverteilung
• Maßnahmen zur Knotenzentralität
• Zentralitätsverteilung
• Clustering-Koeffizient
• Sortimentskoeffizient

Abstand - Wie viele Kanten müssen Sie passieren, um von einem Scheitelpunkt zum anderen zu gelangen?

Der Durchmesser ist der maximale Abstand in der Grafik.

Der Grad eines Scheitelpunkts ist die Anzahl der Kanten am Scheitelpunkt.

Theorie der sechs Handschläge

Jeder soziale Graph hat einen sehr geringen durchschnittlichen Durchmesser ( Theory of Six Handshakes ). Darüber hinaus gibt es einen sehr dichten Kern. Ich bin mit einigen Afrikanern durch meinen Präsidenten "vertraut", der dem afrikanischen Präsidenten die Hand geschüttelt hat.







Lokaler Clusterkoeffizient . Wir betrachten alle Nachbarn einer Person, "k" Stücke. Maximale Rippen - k (k-1) / 2. Wir betrachten die tatsächliche Anzahl der Kanten und dividieren durch dieses Maximum.

Globaler Clustering-Faktor . Wie viele "Dreiecke" im Vergleich zu "Häkchen".





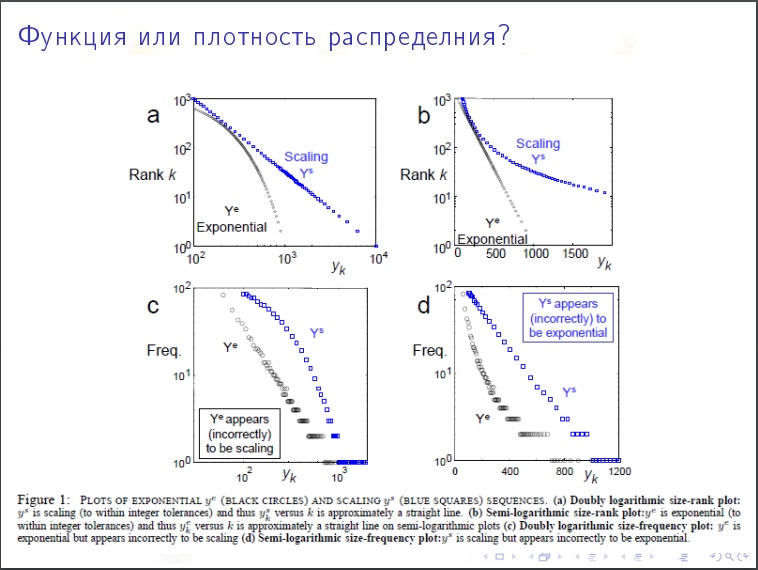
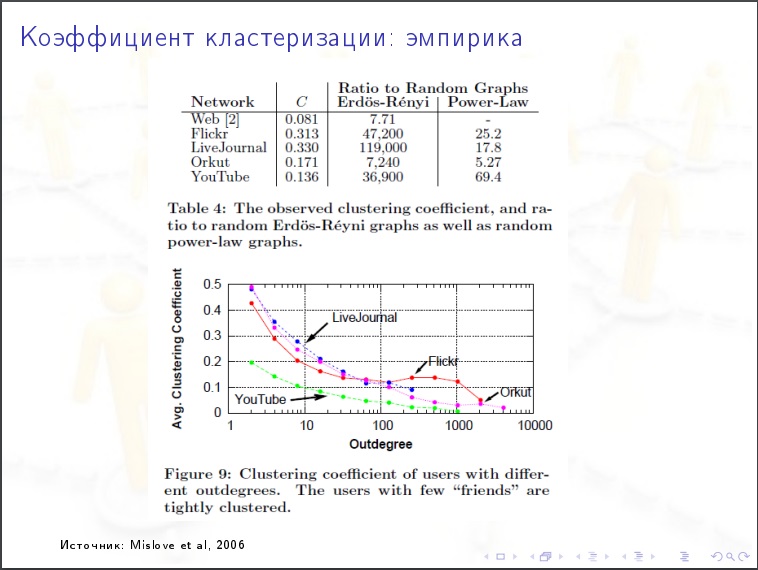Die Gradverteilung des Scheitelpunkts . Wie viel Prozent der Eckpunkte haben Grad unter 1000? Ist die Art der Verteilung exponentiell oder exponentiell? Es stellt sich heraus, dass das Internet einen ruhigen Charakter hat.

Der Koeffizient ist "2". Die Eckpunkte, deren Grad "x" ist, sind N / x ² . Wir überprüfen, dass in LJ eine Milliarde Benutzer Tausendstelstel durch Tausend bis Tausend Quadrat geteilt werden sollten. Tausendtausendstel.

Dies ist eine sehr langsam abnehmende Sache.













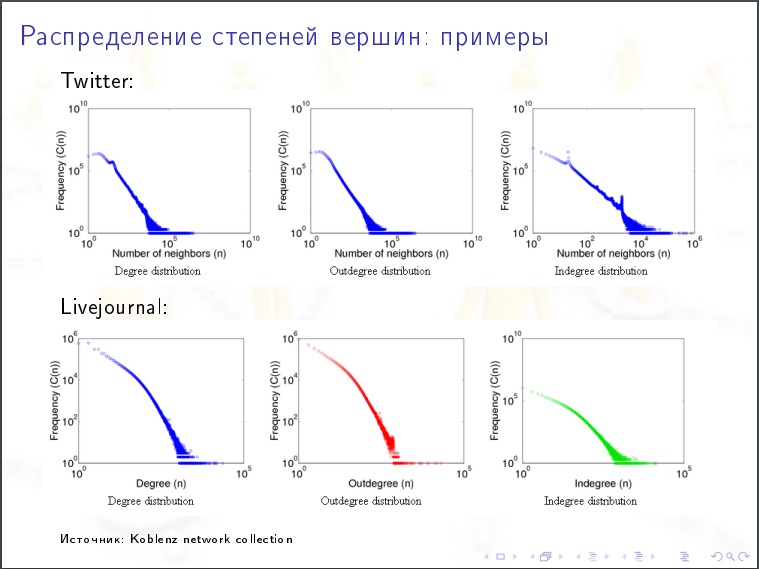
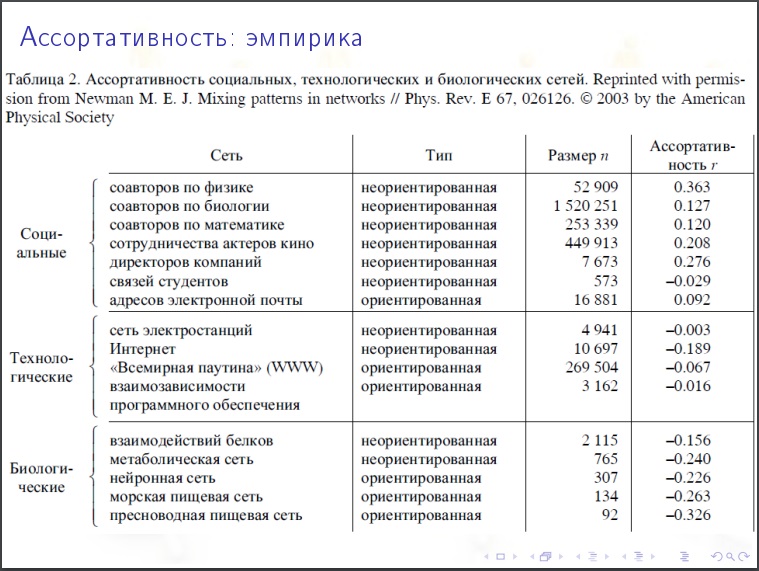
Sortierkoeffizient . grobe Annäherung - wir nehmen Spitzen mit ungefähr der gleichen Anzahl von Graden, sind sie eher miteinander oder mit weniger verbunden? Wenn ja, dann ist es sortiert. Dissortativität - wenn mit einer großen Anzahl von Abschlüssen eher mit weniger verbunden ist. Dies ist ein naiver Ansatz. Ein korrekterer Ansatz ist dies. An jedem Scheitelpunkt gibt es ein anderes Merkmal (Gesamtkapital der Bank), und die Sortierbarkeit dieses Indikators sieht aus.





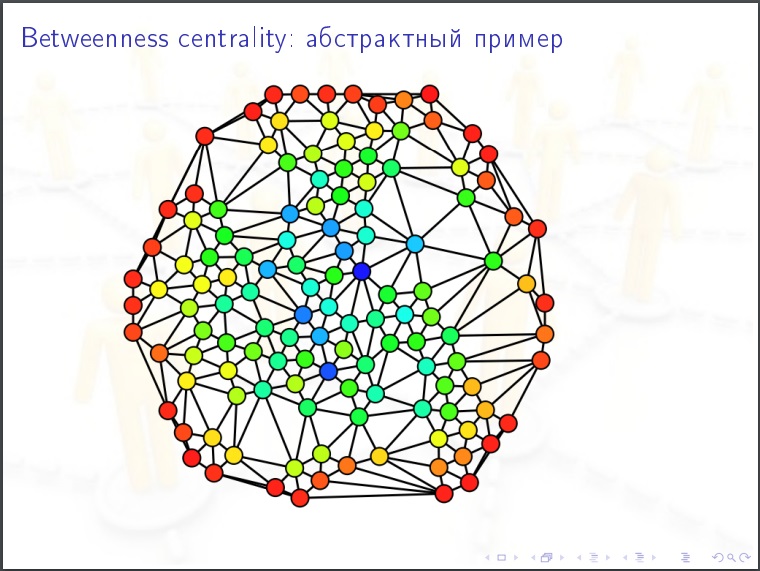
Die Zentralität des Knotens für ein soziales Netzwerk. Wir nehmen eine Person, wir betrachten den folgenden Wert für sie. Wir sortieren alle Paare anderer Personen (N-1) (N-2) / 2 und fragen in jedem Fall nach dem nächsten Datierungspfad in der Grafik, ob er diese Person durchläuft. Es kann mehrere kürzeste Wege geben und einige enthalten unsere Person, dann geben wir ihm%. Dies ist das wichtigste Merkmal in sozialen Netzwerken. Für die Ausbreitung von Epidemien, öffentliche Meinung. Dies muss gemessen werden.









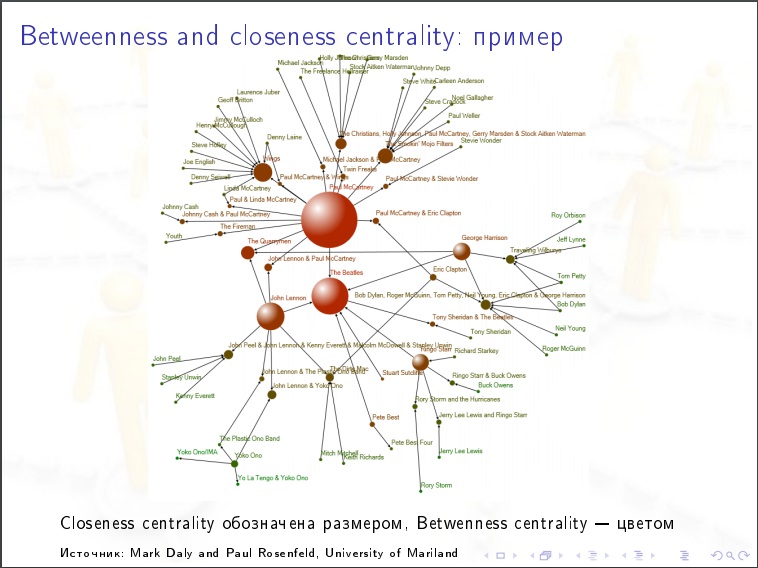
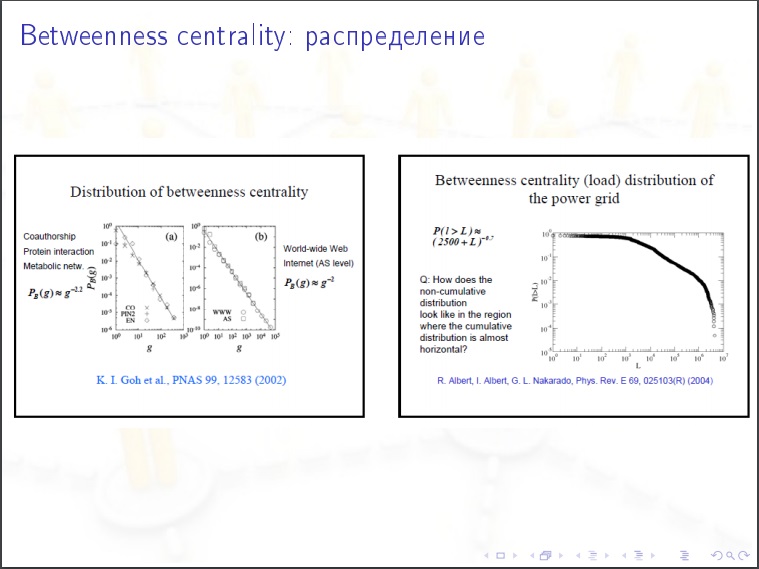
Merkmale sozialer Netzwerke:

• Kleiner Durchmesser und durchschnittlicher Abstand zwischen den Eckpunkten
• Das Potenzgesetz der Verteilung der Eckpunkte und der Zentralität zwischen den Gleichheiten
• Hohes Clustering-Verhältnis
• Sortiment
• Das Vorhandensein eines eng verwandten Kerns

Die Aufgabe besteht darin, ein Modell zu erstellen, das die ersten drei Eigenschaften (und vorzugsweise die letzten beiden) abdeckt. Die ersten drei sind zu diesem Zeitpunkt bereits unüberwindlich komplex. Für 2013 gibt es kein solches Modell.

Wir wenden uns der Beschreibung der existierenden Zufallsgraphenmodelle zu.

Modelle

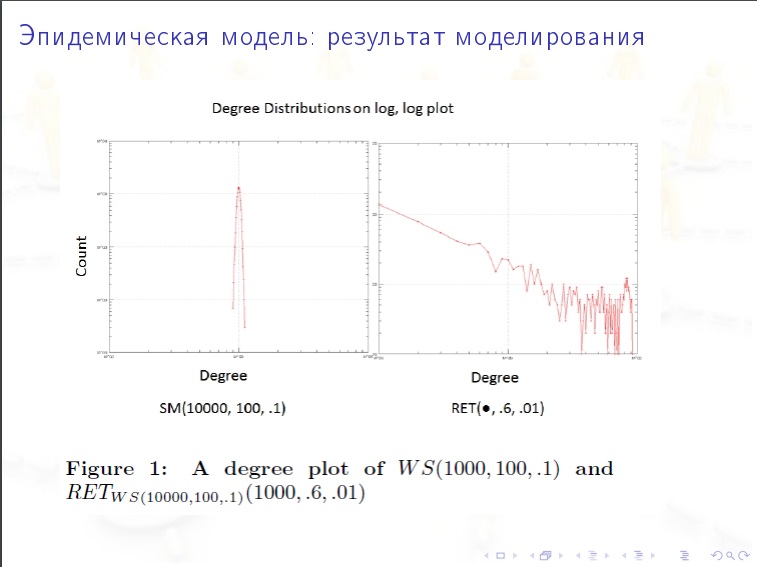
Modelle sind:

• Technisch (Kanten werden zufällig generiert)
• Spieltheoretisch (wenn es für jemanden von Vorteil ist)
• Keine Struktur (nur viele Eckpunkte)
• Strukturell (die Eckpunkte sind Punkte des metrischen Raums oder haben Gewichte; es gibt eine Struktur auf der Menge der Eckpunkte)

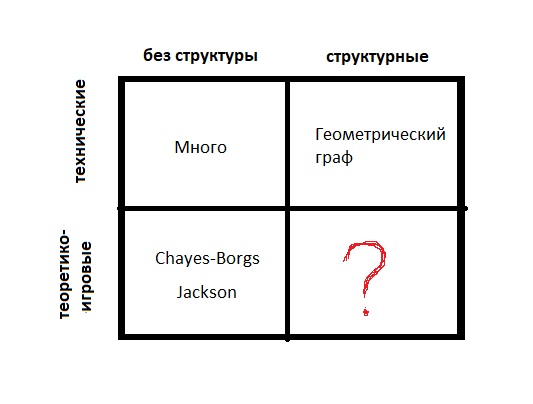
Wenn Sie verstehen, was zugrunde liegt, können Sie sich von einer sehr großen Anzahl von Parametern leiten lassen. Wenn gut gewählte Parameter eine gute Annäherung ergeben, sind Sie gut gemacht. Und selbst wenn die beste Kombination ein schlechtes Ergebnis liefert und nicht mit den beobachteten Fakten übereinstimmt, dann auf Wiedersehen.

All dies geschieht zu einem Zweck - zur Bekämpfung von Spam.

Das Internet kann auf mehreren Ebenen als komplexes Netzwerk vorgestellt werden:

• Technologisches Niveau . Eckpunkte und Kanten sind Knoten und Kommunikationslinien.
• Hypertext-Ebene . Die Scheitelpunkte sind Websites oder Seiten, und die Kanten sind Hyperlinks.
• Soziale Ebene . Die Eckpunkte sind Benutzer, und die Kanten sind diese oder andere Verbindungen zwischen ihnen: Freundschaften in sozialen Netzwerken, Abonnieren von Blogs, Zusammenarbeit in verteilten Projekten (z. B. Wikipedia) usw.

Für komplexe Netzwerke sind viele lokale und globale numerische Merkmale bekannt: die Verteilung der Eckpunkte, der Clusterkoeffizient und der Assortivitätskoeffizient

Es stellt sich heraus, dass eine Reihe von Merkmalen für Internet-Netzwerke charakteristisch sind:

• Paretto-Gradverteilung
• hoher Clusterkoeffizient,
• positive Assortivität
• kleiner Durchmesser.

Das ultimative Ziel der Modellierung von Internet-Netzwerken besteht darin, Modelle mit denselben Funktionen zu erstellen.

Erdos Model - Renyi

Das Erdos-Renyi-Modell ist eines von zwei eng verwandten Modellen zur Erzeugung zufälliger Graphen. Die Modelle sind nach den Mathematikern Pal Erdös und Alfred Renyi benannt, die 1959 als erste eines der Modelle vorstellten. Erkundete das Dating-Diagramm.

Betrachten Sie N Punkte. Mögliche Kanten - N * (N-1) / 2. Für jede Rippe führen wir einen Zufallstest durch. Die Wahrscheinlichkeit, dass die Rippe passiert ist - p. Was nicht passiert ist - (1-p). Lassen Sie uns den "Test" ausführen, wir erhalten eine Grafik. Es gibt jedoch einige Probleme. Damit die Eigenschaft "Spärlichkeit" erscheint, muss p sehr klein sein, in der Größenordnung von 1 / N, und dann wird der Durchmesser sehr groß sein.

Jeder Forscher, der hört, dass das Internet nach dem Erds-Renyi-Modell als Zufallsgraph beschrieben wird, wird lachen.

Ein interessanter Effekt ist, dass der Graph verbunden wird, wenn Sie eine bestimmte Wahrscheinlichkeitsschwelle überschreiten.

Bollobashi-Modell

Dies ist ein dynamisches Modell zum Aufbau des Internets. Wir versuchen zu erraten, wie es sich allmählich gebildet hat. Die Idee ist dies. Wir nehmen ein Diagramm mit einem Scheitelpunkt und einer Kante und spielen dann bei jedem Schritt zufällig. Wir fügen einen Scheitelpunkt hinzu, danach schließt er sich mit einiger Wahrscheinlichkeit von selbst und verbindet sich mit einiger Wahrscheinlichkeit mit dem vorherigen. Der nächste Peak schließt sich mit einiger Wahrscheinlichkeit von selbst und geht mit einigen zu einem der vorherigen. Darüber hinaus ist die Wahrscheinlichkeit, die Oberseite zu treffen, immer proportional zur Anzahl der Kanten, die vorhanden sind. Es wird ein zufälliger Wert ausgespielt, und die nächste Ziehung hängt vom Ergebnis der vorherigen ab. Ein solches Modell ist intuitiv, aber mathematisch schwer zu berechnen. Dieses Modell liefert eine nicht exponentielle Leistungsverteilung. Der Durchmesser ist der gleiche.

Dieses Modell funktioniert jedoch nicht mit Clustering.

Es gibt zwei konkurrierende Ansätze, die mit Clustering arbeiten.

Geometrischer Ansatz

Die Annahme wird von der Decke genommen. Das Internetdiagramm basiert auf dem metrischen Raum. Der Raum der Geschmäcker, Interessen, Vorlieben. Wie interessant Menschen für einander sind. Wie nah im Geist, in der Meinung. Wenn Menschen nahe sind, beziehen sie sich aufeinander.

Wir nehmen und werfen 10 ¹⁰ Punkte in dieses Feld. Hier erscheint eine Vielzahl von Parametern. Riesig

Clustering ist ausgezeichnet, aber die abnehmenden Eckpunkte sind exponentiell. Kontroverse.

Diese Methode ist furchtbar einfach und die Algorithmen werden „zufällig“ ausgeführt.

Game-Borgs spieltheoretischer Ansatz

Wussten Sie, dass in den Tagen von Neumanns angekündigt wurde, dass die Spieltheorie eine Waffe der neuen Generation gegen die Sowjetunion sein würde?

Wir gehen davon aus, dass Menschen Entscheidungen treffen, um miteinander zu kommunizieren oder nicht.

Wir organisieren Meetings / Events. Eine Veranstaltung ist eine Liste der eingeladenen Gäste sowie deren „Intensität“.
Kosten = Intensität * (Konstante + K * (Anzahl der eingeladenen Personen)). Ich muss Ressourcen ausgeben, um die Veranstaltung zu „verkaufen“, und ich muss mehr für jeden Teilnehmer ausgeben. Es gibt Geburtstage und Wanderungen. Es erscheint der Koeffizient "P", der für einen Geburtstag klein und für eine Wanderung groß ist. Intensitätsdatierung.

Eine Person kann mehrere Veranstaltungen mit den Intensitäten P ₁ , P ₂ ... P _{n organisieren} . Andere machen das Gleiche.

Es gibt meine Aktionen zum Aufbau sozialer Bindungen, und es gibt Fremde.

Gewinnfunktion = (die Anzahl der Personen, mit denen Sie vertraut geworden sind) - Kosten

"Vertraut genug" bedeutet, dass die Summe der Intensitäten aller Ereignisse, bei denen Sie zusammen waren, größer als ein bestimmter Schwellenwert ist. Und es spielt keine Rolle, wer die Veranstaltung organisiert hat.

Rippen werden für gut genug Bekannte gehalten.



Es ist bewiesen, dass in diesem Modell viele Eigenschaften eines realen Verschlusses erhalten werden. In allen Nash-Gleichgewichten werden auch reale Schließungseigenschaften und noch stärkere Clustering-Eigenschaften beobachtet, die auch in der Grafik des realen Internets beobachtet werden.



Über die anderen Eigenschaften ist jedoch nichts klar, aber das ist die halbe Miete. Das Problem ist, dass wenn es mindestens ein Nash-Gleichgewicht gibt, in dem sich mindestens zwei Menschen kennen, es ein Nash-Gleichgewicht gibt, in dem jeder mit jedem vertraut ist.





Es gibt eine Idee, die beiden Ansätze zu kombinieren. Um zu berücksichtigen, dass Menschen in einem metrischen Raum leben und wenn sie Veranstaltungen organisieren oder an einer Veranstaltung teilnehmen, hängen Kosten, Intensität und Schwellenwerte von der „Nähe“ ab. Dies ist die fünfte Modellgeneration.

Differenzierte Kosten

Optionen sind differenzierte Kosten und differenzierte Gewinne. Einige sind leichter einzuladen als andere. Die Bekanntschaft mit einem ist rentabler als die Bekanntschaft mit einem anderen.





Nehmen wir an, wir ordnen alle Menschen gleichmäßig um den Umfang. Und es ist billiger, jemanden einzuladen, der näher dran ist. Wie wird die Balance aussehen? Jeder wird eine Nachbarschaft einladen, oder? Nicht wahr. Es gibt kein solches Gleichgewicht.

Beweis. Angenommen, es existiert, dann sind Menschen, die nahe beieinander liegen, bereits zu vielen verschiedenen Treffen eingeladen. Dann muss er diesen geliebten Menschen nicht einladen. Die Existenz dieses Gleichgewichts widerspricht der Existenz dieses Gleichgewichts.



Es besteht ein reines Gleichgewicht, es wird gefunden, es ist das einzige. Jeder lädt eine Nachbarschaft ein, die (oder gegen den Uhrzeigersinn) in einem bestimmten Abstand und einer bestimmten Länge liegt.

(- Dies ist die Bildung von Galaxien!)
(- Dies ist eine spontane Symmetriebrechung!)

Schlussfolgerungen

Pelevin schrieb einmal: "Der Sinn des russischen Lebens liegt in der ruhigen Vergoldung einer immensen Ikonostase." Dies ist die Bedeutung der Mathematik - im selben. Nur die Ikonostase ist wissenschaftlich.



Dies ist eine sehr multidisziplinäre Studie. Höher als du dir vorstellen kannst.

Quellen

PS

„Als ich nach Navalny in den Club gerufen wurde, gibt es einige junge Leute, Enthusiasten, die ihm helfen. Ich warnte sofort, dass ich unangenehme Dinge sagen würde. Eine Revolution ist siegreich, wenn die Mathematiker, die für die Revolution sind, stärker sind als diejenigen, die dagegen sind. Navalnys Jugend wusste nicht, wie sie ihnen solche Modelle erzählen sollte, aber sie verstehen nicht, sie wissen nicht einmal, wie sie sich integrieren sollen - sie rennen einfach und schreien irgendwo. Und gegen sie sitzt ein starkes Institut mit ernsthaften Leuten an der Spitze, die auf Befehl des Kremls sagen, wer genau und wie viel verhaftet werden soll, damit es nichts gibt. Sie sagen: "Wir sind dezentralisiert - speziell Navalny hat nichts zu bedeuten, es gibt mehrere wichtige Führer." Und dann kommt ein Mathematiker und glaubt, dass die Zentralisierung 90% dieses Netzwerks ausmacht. Sie blockieren jemanden, den Sie brauchen, für ein paar Tage - und es gibt keine Revolution. Mathe gewinnt. “
- Alexey Savvateev, "Revolution gewinnt, wenn sie gute Mathematiker hat"

PPS

Wer weiß, welche anderen interessanten Werke (Artikel, Vorträge) es im Bereich der sozialen Netzwerke gibt und welche praktischen Vorteile sie haben, teilen Sie bitte mit.