Neuronale Netze und tiefes Lernen, Kapitel 3, Teil 1: Verbesserung des Trainings neuronaler Netze

Wenn eine Person Golf spielen lernt, verbringt sie normalerweise die meiste Zeit damit, einen einfachen Treffer zu inszenieren. Er nähert sich dann allmählich anderen Schlägen, studiert diese oder jene Tricks, basierend auf dem Grundschlag, und entwickelt ihn weiter. In ähnlicher Weise haben wir uns bisher darauf konzentriert, den Backpropagation-Algorithmus zu verstehen. Dies ist unser „Basisstreik“, die Grundlage für das Training für den größten Teil der Arbeit mit neuronalen Netzen (NS). In diesem Kapitel werde ich über eine Reihe von Techniken sprechen, die verwendet werden können, um unsere einfachere Implementierung von Backpropagation zu verbessern und die Art und Weise, NS zu unterrichten, zu verbessern.

Zu den Techniken, die wir in diesem Kapitel lernen werden, gehören: die beste Option für die Rolle der Kostenfunktion, nämlich die Kostenfunktion mit Kreuzentropie; vier sogenannte Regularisierungsmethoden (Regularisierung von L1 und L2, Ausschluss von Neuronen [Dropout], künstliche Erweiterung von Trainingsdaten), die die Generalisierbarkeit unserer NS über die Grenzen von Trainingsdaten hinaus verbessern; beste Methode zum Initialisieren von Netzwerkgewichten; Eine Reihe heuristischer Methoden, mit denen Sie gute Hyperparameter für das Netzwerk auswählen können. Ich werde auch einige andere Techniken betrachten, etwas oberflächlicher. Diese Diskussionen sind größtenteils unabhängig voneinander, sodass Sie auf Wunsch darüber springen können. Wir implementieren auch viele Technologien in den Arbeitscode und verwenden sie, um die Ergebnisse zu verbessern, die für die in Kapitel 1 untersuchte Aufgabe der Klassifizierung handschriftlicher Zahlen erzielt wurden.

Natürlich betrachten wir nur einen Bruchteil der Vielzahl von Techniken, die für die Verwendung mit neuronalen Netzen entwickelt wurden. Das Fazit ist, dass der beste Weg, in die Welt der Fülle verfügbarer Techniken einzutreten, darin besteht, einige der wichtigsten im Detail zu studieren. Das Beherrschen dieser wichtigen Techniken ist nicht nur an sich nützlich, sondern vertieft auch Ihr Verständnis für die Probleme, die bei der Verwendung neuronaler Netze auftreten können. So sind Sie bereit, neue Techniken bei Bedarf schnell anzupassen.

Cross Entropy Cost Function

Die meisten von uns hassen es, falsch zu liegen. Kurz nachdem ich angefangen hatte Klavier zu lernen, gab ich vor Publikum ein kleines Konzert. Ich war nervös und begann ein Stück eine Oktave tiefer als nötig zu spielen. Ich war verwirrt und konnte nicht weitermachen, bis mich jemand auf einen Fehler aufmerksam machte. Ich schämte mich sehr. Obwohl dies unangenehm ist, lernen wir auch sehr schnell und entscheiden, dass wir falsch lagen. Und natürlich habe ich das nächste Mal, wenn ich mit dem Publikum sprach, in der richtigen Oktave gespielt! Umgekehrt lernen wir langsamer, wenn unsere Fehler nicht genau definiert sind.

Im Idealfall erwarten wir, dass unsere neuronalen Netze schnell aus ihren Fehlern lernen. Kommt das in der Praxis vor? Um diese Frage zu beantworten, schauen wir uns ein weit hergeholtes Beispiel an. Es handelt sich um ein Neuron mit nur einer Eingabe:



Wir bringen diesem Neuron bei, etwas lächerlich Einfaches zu tun: 1 akzeptieren und 0 geben. Natürlich könnten wir eine Lösung für ein so triviales Problem finden, indem wir Gewicht und Versatz manuell auswählen, ohne den Trainingsalgorithmus zu verwenden. Es wird jedoch sehr nützlich sein, den Gradientenabstieg zu verwenden, um Gewicht und Verschiebung als Ergebnis des Trainings zu erhalten. Schauen wir uns an, wie ein Neuron trainiert wird.

Für die Bestimmtheit werde ich ein Anfangsgewicht von 0,6 und einen Anfangsversatz von 0,9 wählen. Dies sind einige allgemeine Werte, die als Ausgangspunkt zugewiesen wurden, und ich habe sie nicht speziell ausgewählt. Anfänglich produziert ein Ausgangsneuron 0,82, daher müssen wir viel lernen, um dem gewünschten Ausgang von 0,0 nahe zu kommen. Der Originalartikel verfügt über ein interaktives Formular, auf dem Sie auf "Ausführen" klicken und den Lernprozess beobachten können. Diese Animation ist nicht voraufgezeichnet, der Browser berechnet den Verlauf tatsächlich und aktualisiert damit das Gewicht und den Versatz und zeigt das Ergebnis an. Die Lerngeschwindigkeit beträgt η = 0,15, langsam genug, um zu sehen, was passiert, aber schnell genug, damit das Lernen in Sekunden stattfinden kann. Die Kostenfunktion C ist quadratisch und wird im ersten Kapitel vorgestellt. Ich werde Sie bald an die genaue Form erinnern, so dass es nicht notwendig ist, zurück zu kommen und dort zu stöbern. Das Training kann mehrmals gestartet werden, indem Sie einfach auf die Schaltfläche „Ausführen“ klicken.

Wie Sie sehen können, lernt das Neuron schnell das Gewicht und die Vorspannung, was die Kosten senkt, und ergibt eine Ausgabe von 0,09. Dies ist nicht ganz das gewünschte Ergebnis von 0,0, aber ziemlich gut. Angenommen, wir wählen stattdessen ein Anfangsgewicht und einen Versatz von 2,0. In diesem Fall beträgt die anfängliche Ausgabe 0,98, was völlig falsch ist. Mal sehen, wie das Neuron in diesem Fall lernt, 0 zu produzieren.

Obwohl dieses Beispiel dieselbe Lernrate verwendet (η = 0,15), sehen wir, dass das Lernen langsamer ist. Etwa 150 der ersten Epochen, Gewichte und Verschiebungen ändern sich kaum. Dann beschleunigt sich das Training und fast wie im ersten Beispiel bewegt sich das Neuron schnell auf 0,0. Dieses Verhalten ist seltsam, nicht wie das Lernen einer Person. Wie ich zu Beginn sagte, lernen wir oft am schnellsten, wenn wir uns sehr irren. Aber wir haben gerade gesehen, wie unser künstliches Neuron mit großen Schwierigkeiten lernt und viele Fehler macht - viel schwieriger als wenn er einen kleinen Fehler gemacht hat. Darüber hinaus stellt sich heraus, dass ein solches Verhalten nicht nur in unserem einfachen Beispiel auftritt, sondern auch in einem allgemeineren NS. Warum lernt man so langsam? Kann ich einen Weg finden, um dieses Problem zu vermeiden?

Um die Ursache des Problems zu verstehen, erinnern wir uns, dass unser Neuron durch Gewichts- und Verschiebungsänderungen mit einer Geschwindigkeit lernt, die durch die partiellen Ableitungen der Kostenfunktion ∂C / ∂w und ∂C / ∂b bestimmt wird. Zu sagen, dass „Lernen langsam ist“, ist dasselbe wie zu sagen, dass diese partiellen Ableitungen klein sind. Das Problem ist zu verstehen, warum sie klein sind. Berechnen wir dazu die partiellen Ableitungen. Denken Sie daran, dass wir die quadratische Kostenfunktion verwenden, die durch Gleichung (6) gegeben ist:

$$

$$C = \ frac {(y-a) ^ 2} {2} \ tag {54}$$

Dabei ist a die Neuronenausgabe, wenn am Eingang x = 1 verwendet wird, und y = 0 ist die gewünschte Ausgabe. Um dies direkt durch Gewicht und Verschiebung zu schreiben, sei daran erinnert, dass a = σ (z) ist, wobei z = wx + b. Unter Verwendung der Kettenregel zur Differenzierung nach Gewicht und Verschiebung erhalten wir:

$$

$$\ frac {\ partielles C} {\ partielles w} = (a-y) \ sigma '(z) x = a \ sigma' (z) \ tag {55}$$

$$

$$\ frac {\ partielles C} {\ partielles b} = (a-y) \ sigma '(z) = a \ sigma' (z) \ tag {56}$$

wo ich x = 1 und y = 0 eingesetzt habe. Um das Verhalten dieser Ausdrücke zu verstehen, schauen wir uns den Term σ '(z) rechts genauer an. Erinnern Sie sich an die Form eines Sigmoid:



Die Grafik zeigt, dass, wenn die Ausgabe des Neurons nahe bei 1 liegt, die Kurve sehr flach wird und σ '(z) klein wird. Die Gleichungen (55) und (56) sagen uns, dass ∂C / ∂w und ∂C / ∂b sehr klein werden. Daher die Verlangsamung des Lernens. Darüber hinaus tritt, wie wir später sehen werden, die Verlangsamung der Ausbildung tatsächlich aus demselben Grund und in der Nationalversammlung allgemeinerer Natur auf, und zwar nicht nur in unserem einfachsten Beispiel.

Einführung der Cross-Entropy-Cost-Funktion

Was machen wir mit der Verlangsamung des Lernens? Es stellt sich heraus, dass wir das Problem lösen können, indem wir die quadratische Wertfunktion durch eine andere Wertfunktion ersetzen, die als Kreuzentropie bekannt ist. Um die Kreuzentropie zu verstehen, entfernen wir uns von unserem einfachsten Modell. Angenommen, wir trainieren ein Neuron mit mehreren Eingabewerten x ₁ , x ₂ , ... entsprechenden Gewichten w ₁ , w ₂ , ... und Offset b:



Die Ausgabe des Neurons ist natürlich a = σ (z), wobei z = ∑ _j w _j x _j + b die gewichtete Summe der Eingaben ist. Wir definieren die Kreuzentropiekostenfunktion für ein gegebenes Neuron als

$$

$$C = - \ frac {1} {n} \ sum_x \ left [y \ ln a + (1-y) \ ln (1-a) \ right] \ tag {57}$$

Dabei ist n die Gesamtzahl der Trainingsdateneinheiten, die Summe geht über alle Trainingsdaten x und y ist die entsprechende gewünschte Ausgabe.

Es ist nicht offensichtlich, dass Gleichung (57) das Problem der Verlangsamung des Lernens löst. Ehrlich gesagt ist es nicht einmal offensichtlich, dass es sinnvoll ist, es eine Wertfunktion zu nennen! Bevor wir uns der Verlangsamung des Lernens zuwenden, wollen wir sehen, in welchem ​​Sinne Kreuzentropie als Funktion des Wertes interpretiert werden kann.

Insbesondere zwei Eigenschaften machen es sinnvoll, die Kreuzentropie als Funktion des Wertes zu interpretieren. Erstens ist es größer als Null, dh C> 0. Um dies zu sehen, ist zu beachten, dass (a) alle einzelnen Mitglieder der Summe in (57) negativ sind, da beide Logarithmen aus Zahlen im Bereich von 0 bis 1 entnommen werden und (b) das Minuszeichen vor der Summe steht.

Zweitens, wenn die reale Ausgabe des Neurons für alle Trainingseingaben x nahe an der gewünschten Ausgabe liegt, ist die Kreuzentropie nahe Null. Um dies zu beweisen, müssen wir annehmen, dass die gewünschten Ausgaben y entweder 0 oder 1 sind. Normalerweise geschieht dies, wenn Klassifizierungsprobleme gelöst oder Boolesche Funktionen berechnet werden. Um zu verstehen, was passiert, wenn Sie eine solche Annahme nicht treffen, lesen Sie die Übungen am Ende des Abschnitts.

Um dies zu beweisen, stellen Sie sich vor, dass y = 0 und a≈0 für eine Eingabe x ist. So wird es sein, wenn das Neuron eine solche Eingabe gut handhabt. Wir sehen, dass der erste Ausdrucksausdruck (57) für den Wert verschwindet, da y = 0 ist und der zweite −ln (1 - a) ≈0 ist. Gleiches gilt, wenn y = 1 und a≈1. Daher ist der Wertbeitrag gering, wenn die tatsächliche Leistung nahe an der gewünschten liegt.

Zusammenfassend ergibt sich, dass die Kreuzentropie positiv ist und gegen Null tendiert, wenn das Neuron die gewünschte Ausgabe y für alle Trainingseingaben x besser berechnet. Wir erwarten das Vorhandensein beider Objekte in der Kostenfunktion. Und tatsächlich werden diese beiden Eigenschaften durch den quadratischen Wert erfüllt. Daher ist Cross-Entropie eine gute Nachricht. Die Cross-Entropy-Kostenfunktion hat jedoch einen Vorteil, da sie im Gegensatz zum quadratischen Wert das Problem der Verlangsamung des Lernens vermeidet. Um dies zu sehen, berechnen wir die partielle Ableitung des Wertes mit Kreuzentropie nach Gewicht. Ersetzen Sie a = σ (z) in (57), wenden Sie die Kettenregel zweimal an und erhalten Sie

$$

$$\ frac {\ partielles C} {\ partielles w_j} = - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ right) \ frac {\ partielles \ sigma} {\ partielles w_j} \ tag {58}$$

$$

$$= - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ right) \ sigma '(z) x_j \ tag {59}$$

Wenn wir uns auf einen gemeinsamen Nenner reduzieren und vereinfachen, erhalten wir:

$$

$$\ frac {\ partielles C} {\ partielles w_j} = \ frac {1} {n} \ sum_x \ frac {\ sigma '(z) x_j} {\ sigma (z) (1- \ sigma (z)) } (\ sigma (z) -y). \ tag {60}$$

Mit der Definition von Sigmoid, σ (z) = 1 / (1 + e - z) und etwas Algebra können wir zeigen, dass σ ′ (z) = σ (z) (1 - σ (z)). Ich werde Sie bitten, dies in der Übung weiter zu überprüfen, aber akzeptieren Sie es vorerst als die Wahrheit. Die Terme σ (z) und σ (z) (1 - σ (z)) werden aufgehoben, und dies führt zu

$$

$$\ frac {\ partielles C} {\ partielles w_j} = \ frac {1} {n} \ sum_x x_j (\ sigma (z) -y). \ tag {61}$$

Toller Ausdruck. Daraus folgt, dass die Geschwindigkeit, mit der Gewichte trainiert werden, durch σ (z) - y gesteuert wird, d. H. Durch einen Fehler am Ausgang. Je größer der Fehler ist, desto schneller lernt das Neuron. Dies ist intuitiv zu erwarten. Diese Option vermeidet die durch den Term σ '(z) in einer ähnlichen quadratischen Kostengleichung (55) verursachte Verlangsamung des Lernens. Wenn wir Kreuzentropie verwenden, wird der Term σ '(z) reduziert und wir müssen uns nicht mehr um seine Kleinheit kümmern. Diese Reduzierung ist ein besonderes Wunder, das durch die Kreuzentropiekostenfunktion garantiert wird. In der Tat ist dies natürlich kein Wunder. Wie wir später sehen werden, wurde die Kreuzentropie speziell für diese Eigenschaft ausgewählt.

In ähnlicher Weise kann die partielle Ableitung für die Vorspannung berechnet werden. Ich werde nicht noch einmal alle Details angeben, aber Sie können das leicht überprüfen

$$

$$\ frac {\ partielles C} {\ partielles b} = \ frac {1} {n} \ sum_x (\ sigma (z) -y). \ tag {62}$$

Dies hilft wiederum, eine Lernverzögerung aufgrund des Terms σ '(z) in einer ähnlichen Gleichung für den quadratischen Wert (56) zu vermeiden.

Übung

• Überprüfen Sie, ob σ ′ (z) = σ (z) (1 - σ (z)) ist.

Kehren wir zu unserem weit hergeholten Beispiel zurück, mit dem wir zuvor gespielt haben, und sehen, was passiert, wenn wir anstelle des quadratischen Werts die Kreuzentropie verwenden. Zum Einstellen beginnen wir mit dem Fall, in dem die quadratischen Kosten perfekt funktionierten, wenn das Anfangsgewicht 0,6 und der Versatz 0,9 betrug. Der Originalartikel verfügt über eine interaktive Form, in der Sie auf die Schaltfläche Ausführen klicken und sehen können, was passiert, wenn Sie den quadratischen Wert durch Kreuzentropie ersetzen.

Es überrascht nicht, dass das Neuron in diesem Fall wie zuvor perfekt trainiert ist. Schauen wir uns nun den Fall an, in dem das Neuron stecken geblieben ist , wobei Gewicht und Verschiebung bei 2,0 beginnen.



Erfolg! Diesmal lernte das Neuron schnell, wie wir wollten. Wenn Sie genau hinschauen, können Sie feststellen, dass die Steigung der Kostenkurve im Vergleich zum flachen Bereich der entsprechenden quadratischen Wertekurve zunächst steiler ist. Diese Cross-Country-Entropie verleiht uns diese Coolness und lässt uns nicht dort hängen bleiben, wo wir das schnellste Training eines Neurons erwarten, wenn es mit sehr großen Fehlern beginnt.

Ich habe nicht gesagt, welche Trainingsgeschwindigkeit in den letzten Beispielen verwendet wurde. Früher haben wir mit einem quadratischen Wert η = 0,15 verwendet. Sollten wir in den neuen Beispielen die gleiche Geschwindigkeit verwenden? Tatsächlich ist es bei einer Änderung der Kostenfunktion unmöglich, genau zu sagen, was es bedeutet, die „gleiche“ Lerngeschwindigkeit zu verwenden. Es wird ein Vergleich von Äpfeln mit Orangen sein. Für beide Kostenfunktionen habe ich experimentiert, indem ich nach einer Lerngeschwindigkeit gesucht habe, mit der ich sehen kann, was passiert. Wenn Sie immer noch interessiert sind, dann ist in den neuesten Beispielen η = 0,005.

Sie können argumentieren, dass das Ändern der Lerngeschwindigkeit die Grafiken bedeutungslos macht. Wen interessiert es, wie schnell ein Neuron lernt, wenn wir willkürlich eine Lerngeschwindigkeit wählen können? Dieser Einwand berücksichtigt jedoch nicht den Hauptpunkt. Die Bedeutung der Diagramme liegt nicht in der absoluten Lerngeschwindigkeit, sondern darin, wie sich diese Geschwindigkeit ändert. Bei Verwendung der quadratischen Funktion ist das Training langsamer, wenn das Neuron sehr falsch ist, und es geht schneller, wenn sich das Neuron der gewünschten Antwort nähert. Mit Cross-Entropy ist das Lernen schneller, wenn ein Neuron einen großen Fehler macht. Und diese Aussagen hängen nicht von einer bestimmten Lerngeschwindigkeit ab.

Wir untersuchten die Kreuzentropie für ein Neuron. Dies lässt sich jedoch leicht auf Netzwerke mit vielen Schichten und vielen Neuronen verallgemeinern. Angenommen, y = y ₁ , y ₂ , ... sind die gewünschten Werte der Ausgangsneuronen, dh der Neuronen in der letzten Schicht, und ein ^L ₁ , ein ^L ₂ , ... sind die Ausgangswerte selbst. Dann kann die Kreuzentropie definiert werden als:

$$

$$C = - \ frac {1} {n} \ sum_x \ sum_j \ left [y_j \ ln a ^ L_j + (1-y_j) \ ln (1-a ^ L_j) \ right] \ tag {63}$$

Dies ist dasselbe wie in Gleichung (57), nur dass jetzt unser ∑ _j über alle Ausgangsneuronen summiert. Ich werde die Ableitung nicht im Detail analysieren, aber es ist vernünftig anzunehmen, dass wir mit Ausdruck (63) eine Verlangsamung in Netzwerken mit vielen Neuronen vermeiden können. Bei Interesse können Sie die Ableitung im folgenden Problem nehmen.

Übrigens verwirrte der Begriff „Kreuzentropie“, den ich verwende, einige frühe Leser des Buches, weil er anderen Quellen widerspricht. Insbesondere wird häufig die Kreuzentropie für zwei Wahrscheinlichkeitsverteilungen pj bestimmt
und qj als ∑ _j p _j lnq _j . Diese Definition kann mit (57) assoziiert werden, wenn angenommen wird, dass ein Sigmoidneuron eine Wahrscheinlichkeitsverteilung ergibt, die aus der Aktivierung des Neurons a und des dazu komplementären 1-a-Werts besteht.

Wenn wir jedoch viele Sigmoidneuronen in der letzten Schicht haben, gibt der Vektor a ^L _j normalerweise keine Wahrscheinlichkeitsverteilung. Infolgedessen ist die Definition des Typs ∑ _j p _j lnq _j bedeutungslos, da wir nicht mit Wahrscheinlichkeitsverteilungen arbeiten. Stattdessen (63) kann man sich vorstellen, wie eine summierte Menge von Kreuzentropien jedes Neurons zusammengefasst wird, wobei die Aktivierung jedes Neurons als Teil einer Zwei-Elemente-Wahrscheinlichkeitsverteilung interpretiert wird (natürlich gibt es in unseren Netzwerken keine probabilistischen Elemente, also sind dies eigentlich keine Wahrscheinlichkeiten). In diesem Sinne wird (63) eine Verallgemeinerung der Kreuzentropie für Wahrscheinlichkeitsverteilungen sein.

Wann sollte die Kreuzentropie anstelle des quadratischen Werts verwendet werden? In der Tat wird Kreuzentropie fast immer besser verwendet, wenn Sie Sigmoid-Ausgangsneuronen haben. Um dies zu verstehen, denken Sie daran, dass beim Einrichten eines Netzwerks Gewichte und Offsets normalerweise nach einem zufälligen Verfahren initialisiert werden. Es kann vorkommen, dass diese Auswahl dazu führt, dass das Netzwerk einige Trainingseingabedaten vollständig falsch interpretiert - beispielsweise tendiert das Ausgangsneuron zu 1, wenn es zu 0 gehen sollte, oder umgekehrt. Wenn wir einen quadratischen Wert verwenden, der das Training verlangsamt, wird das Training überhaupt nicht gestoppt, da die Gewichte weiterhin an anderen Trainingsbeispielen trainiert werden, aber diese Situation ist offensichtlich unerwünscht.

Übungen

• Ein Haken der Kreuzentropie ist, dass es zunächst schwierig sein kann, sich an die entsprechenden Rollen von y und a zu erinnern. Es ist leicht zu verwirren, wie es richtig sein wird, - [ylna + (1 - y) ln (1 - a)] oder - [alny + (1 - a) ln (1 - y)]. Was passiert mit dem zweiten Ausdruck, wenn y = 0 oder 1 ist? Betrifft dieses Problem den ersten Ausdruck? Warum?
• In der Diskussion eines einzelnen Neurons am Anfang des Abschnitts sagte ich, dass die Kreuzentropie klein ist, wenn σ (z) ≈y für alle Trainingseingabedaten gilt. , y 0 1. , (, ) y 0 1. , , σ(z)=y . ,

  $$

  $$C = -\frac{1}{n} \sum_x [y \ln y+(1-y) \ln(1-y)] \tag{64}$$
  . −[ylny+(1−y)ln(1−y)] .

• . ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \sigma'(z^L_j) \tag{65}$$
  σ'(z ^L _j ) , . , δ ^L x

  $$

  $$\delta^L = a^L-y \tag{66}$$
  , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{67}$$
  σ'(z ^L _j ) , , , . . , .
• . , . , , , , a ^L _j = z ^L _j . , δL x

  $$

  $$\delta^L = a^L-y \tag{68}$$
  , , , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{69}$$

  $$

  $$\frac{\partial C}{\partial b^L_{j}} = \frac{1}{n} \sum_x (a^L_j-y_j) \tag{70}$$
  , , . .

MNIST

Die Kreuzentropie ist einfach als Teil eines Programms zu implementieren, das das Netzwerk mithilfe von Gradientenabstieg und Rückausbreitung unterrichtet. Wir werden dies später tun, indem wir eine verbesserte Version unseres frühen handgeschriebenen numerischen Klassifizierungsprogramms von MNIST, network.py, entwickeln. Das neue Programm heißt network2.py und enthält nicht nur Kreuzentropie, sondern auch mehrere andere in diesem Kapitel entwickelte Techniken. In der Zwischenzeit wollen wir sehen, wie gut unser neues Programm die MNIST-Ziffern klassifiziert. Wie in Kapitel 1 werden wir ein Netzwerk mit 30 versteckten Neuronen und einem Minipaket der Größe 10 verwenden. Wir werden die Lerngeschwindigkeit η = 0,5 einstellen und 30 Epochen lernen.

Wie ich bereits sagte, ist es unmöglich, genau zu sagen, welche Trainingsgeschwindigkeit in welchem ​​Fall geeignet ist, also habe ich mit der Auswahl experimentiert. Es stimmt, es gibt eine Möglichkeit, die Lernrate sehr grob heuristisch mit Kreuzentropie und quadratischem Wert in Beziehung zu setzen. Wir haben früher gesehen, dass es in Bezug auf den Gradienten für den quadratischen Wert einen zusätzlichen Term σ '= σ (1-σ) gibt. Angenommen, wir mitteln diese Werte für σ, ∫ ¹ ₀ dσ σ (1 - σ) = 1/6. Es ist ersichtlich, dass die (sehr ungefähr) quadratischen Kosten bei gleicher Lernrate im Durchschnitt sechsmal langsamer lernen. Dies legt nahe, dass ein guter Ausgangspunkt darin besteht, die Lerngeschwindigkeit für eine quadratische Funktion durch 6 zu teilen. Dies ist natürlich kein striktes Argument, und Sie sollten es nicht zu ernst nehmen. Aber es kann manchmal als Ausgangspunkt nützlich sein.

Die Schnittstelle für network2.py unterscheidet sich geringfügig von network.py, es sollte jedoch klar sein, was gerade passiert. Die Dokumentation zu network2.py kann mit dem Hilfebefehl (network2.Network.SGD) in der Python-Shell abgerufen werden.

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True) 

Beachten Sie übrigens, dass der Befehl net.large_weight_initializer () verwendet wird, um Gewichte und Offsets auf die gleiche Weise wie in Kapitel 1 beschrieben zu initialisieren. Wir müssen ihn ausführen, da wir später die Initialisierung von Gewichten standardmäßig ändern werden. Als Ergebnis erhalten wir nach dem Starten aller oben genannten Befehle ein Netzwerk, das mit einer Genauigkeit von 95,49% arbeitet. Dies kommt dem Ergebnis aus dem ersten Kapitel (95,42%) unter Verwendung des quadratischen Werts sehr nahe.

Schauen wir uns auch den Fall an, in dem wir 100 versteckte Neuronen und Kreuzentropie verwenden, und lassen den Rest gleich. In diesem Fall beträgt die Genauigkeit 96,82%. Dies ist eine wesentliche Verbesserung gegenüber den Ergebnissen aus dem ersten Kapitel, in dem wir mit dem quadratischen Wert eine Genauigkeit von 96,59% erreicht haben. Die Änderung mag gering erscheinen, aber ich denke, dass der Fehler von 3,41% auf 3,18% gesunken ist. Das heißt, wir haben ungefähr 1/14 Fehler beseitigt. Das ist ziemlich gut.

Es ist ziemlich schön, dass die Kreuzentropiekostenfunktion im Vergleich zum quadratischen Wert ähnliche oder bessere Ergebnisse liefert. Sie beweisen jedoch nicht eindeutig, dass Kreuzentropie die beste Wahl ist. Tatsache ist, dass ich überhaupt nicht versucht habe, Hyperparameter zu wählen - die Geschwindigkeit des Trainings, die Größe des Minipakets usw. Um die Verbesserung überzeugender zu machen, müssen wir ihre Optimierung richtig angehen. Die Ergebnisse sind jedoch immer noch inspirierend, und unsere theoretischen Berechnungen bestätigen, dass die Kreuzentropie eine bessere Wahl ist als die quadratische Kostenfunktion.

In diesem Sinne wird das gesamte Kapitel und im Prinzip der Rest des Buches durchlaufen. Wir werden neue Technologien entwickeln, testen und "verbesserte Ergebnisse" erzielen. Natürlich ist es gut, dass wir diese Verbesserungen sehen. Aber sie zu interpretieren ist immer schwierig. Es wird nur überzeugend sein, wenn wir nach ernsthafter Arbeit an der Optimierung aller anderen Hyperparameter Verbesserungen sehen. Und dies ist eine ziemlich komplizierte Aufgabe, die große Rechenressourcen erfordert, und normalerweise werden wir uns nicht mit einer so gründlichen Untersuchung befassen. Stattdessen werden wir auf der Grundlage informeller Tests wie den oben aufgeführten weiter gehen. Sie müssen jedoch berücksichtigen, dass solche Tests keine eindeutigen Beweise sind, und diese Fälle sorgfältig überwachen, wenn die Argumente zu scheitern beginnen.

Bisher haben wir die Kreuzentropie ausführlich diskutiert. Warum so viel Aufwand verschwenden, wenn sich dadurch unsere MNIST-Ergebnisse so geringfügig verbessern? Später in diesem Kapitel werden wir andere Techniken - insbesondere die Regularisierung - sehen, die viel stärkere Verbesserungen bringen. Warum konzentrieren wir uns also auf Kreuzentropie? Insbesondere weil die Kreuzentropie eine häufig verwendete Wertfunktion ist, lohnt es sich, sie gut zu verstehen. Der wichtigere Grund ist jedoch, dass die Sättigung von Neuronen ein wichtiges Problem im Bereich der neuronalen Netze ist, auf das wir im gesamten Buch ständig zurückkommen werden. Daher habe ich die Kreuzentropie so ausführlich diskutiert, da es ein gutes Labor ist, um die Sättigung von Neuronen zu verstehen und Ansätze für dieses Problem zu finden.

Was bedeutet Kreuzentropie? Woher kommt es?

Unsere Diskussion über Kreuzentropie drehte sich um algebraische Analyse und praktische Implementierung. Dies ist nützlich, aber infolgedessen bleiben umfassendere konzeptionelle Fragen unbeantwortet, zum Beispiel: Was bedeutet Kreuzentropie? Gibt es eine intuitive Möglichkeit, es zu präsentieren? Wie könnten Menschen überhaupt auf Kreuzentropie kommen?

Beginnen wir mit dem letzten: Was könnte uns dazu bringen, über Kreuzentropie nachzudenken? Angenommen, wir haben eine zuvor beschriebene Lernverlangsamung entdeckt und festgestellt, dass sie durch die Terme σ '(z) in den Gleichungen (55) und (56) verursacht wurde. Wenn wir einen kleinen Blick auf diese Gleichungen werfen, könnten wir darüber nachdenken, ob es möglich ist, eine solche Kostenfunktion so zu wählen, dass der Term σ '(z) verschwindet. Dann würden die Kosten C = C _x eines Trainingsbeispiels die Gleichungen erfüllen:

$$

$$\ frac {\ partielles C} {\ partielles w_j} = x_j (a-y) \ tag {71}$$

$$

$$\ frac {\ partielles C} {\ partielles b} = (a-y) \ tag {72}$$

Wenn wir eine Wertefunktion wählen, die sie wahr macht, dann beschreiben sie lieber einfach ein intuitives Verständnis, dass das Neuron umso schneller lernt, je größer der anfängliche Fehler ist. Sie würden auch das Verlangsamungsproblem beheben. Ausgehend von diesen Gleichungen würden wir zeigen, dass es möglich ist, die Form der Kreuzentropie abzuleiten, indem man einfach einem mathematischen Instinkt folgt. Um dies zu sehen, stellen wir fest, dass wir basierend auf der Kettenregel Folgendes erhalten:

$$

$$\ frac {\ partielles C} {\ partielles b} = \ frac {\ partielles C} {\ partielles a} \ sigma '(z) \ tag {73}$$

Unter Verwendung der letzten Gleichung σ '(z) = σ (z) (1 - σ (z)) = a (1 - a) erhalten wir:

$$

$$\ frac {\ partielles C} {\ partielles b} = \ frac {\ partielles C} {\ partielles a} a (1-a) \ tag {74}$$

Im Vergleich zu Gleichung (72) erhalten wir:

$$

$$\ frac {\ partielles C} {\ partielles a} = \ frac {a-y} {a (1-a)} \ tag {75}$$

Wenn wir diesen Ausdruck über a integrieren, erhalten wir:

$$

$$C = - [y \ ln a + (1-y) \ ln (1-a)] + {\ rm Konstante} \ tag {76}$$

Dies ist der Beitrag eines separaten Trainingsbeispiels x zur Kostenfunktion. Um die volle Kostenfunktion zu erhalten, müssen wir alle Trainingsbeispiele mitteln und kommen zu:

$$

$$C = - \ frac {1} {n} \ sum_x [y \ ln a + (1-y) \ ln (1-a)] + {\ rm Konstante} \ tag {77}$$

Die Konstante ist hier der Durchschnitt der einzelnen Konstanten jedes Trainingsbeispiels. Wie Sie sehen können, bestimmen die Gleichungen (71) und (72) eindeutig die Form der Kreuzentropie, Fleisch bis zu einer gemeinsamen Konstante. Die Kreuzentropie wurde nicht magisch aus der Luft genommen. Sie konnte auf einfache und natürliche Weise gefunden werden.

Was ist mit der intuitiven Idee der Kreuzentropie? Wie stellen wir uns das vor? Eine ausführliche Erklärung würde dazu führen, dass wir unseren Trainingskurs überholen. Wir können jedoch die Existenz einer Standardmethode zur Interpretation der Kreuzentropie erwähnen, die aus dem Bereich der Informationstheorie stammt. Grob gesagt ist die Kreuzentropie ein Maß für die Überraschung. Zum Beispiel versucht unser Neuron, die Funktion x → y = y (x) zu berechnen. Stattdessen zählt die Funktion x → a = a (x). Angenommen, wir stellen uns a als Neuronschätzung der Wahrscheinlichkeit vor, dass y = 1 ist, und 1-a ist die Wahrscheinlichkeit, dass der korrekte Wert für y 0 ist. Dann misst die Kreuzentropie, wie sehr wir im Durchschnitt „überrascht“ sind, wenn finde den wahren Wert von y. Wir sind nicht sehr überrascht, wenn wir einen Ausweg erwarten, und wir sind sehr überrascht, wenn der Ausweg unerwartet ist. Natürlich habe ich keine strenge Definition von "Überraschung" gegeben, daher kann dies alles wie ein leerer Scherz erscheinen. Tatsächlich gibt es in der Informationstheorie einen genauen Weg, um Unerwartetheit zu bestimmen. Leider sind mir keine Beispiele für eine gute, kurze und autarke Diskussion dieses Punktes im Internet bekannt. Wenn Sie jedoch ein wenig tiefer graben möchten, enthält der Wikipedia-Artikel gute allgemeine Informationen, die Sie in die richtige Richtung lenken. Details finden Sie in Kapitel 5 zur Kraft-Ungleichung in einem Buch zur Informationstheorie .

Herausforderung

• Wir haben die Verlangsamung des Lernens, die auftreten kann, wenn Neuronen in Netzwerken gesättigt sind, unter Verwendung der quadratischen Kostenfunktion beim Lernen ausführlich erörtert. Ein weiterer Faktor, der das Lernen hemmen kann, ist das Vorhandensein des Ausdrucks x _j in Gleichung (61). Aus diesem Grund wird das entsprechende Gewicht w _j langsam trainiert, wenn sich der Ausgang x _j Null nähert. Erklären Sie, warum es unmöglich ist, den Term x _{j durch} Auswahl einer ausgeklügelten Kostenfunktion zu eliminieren.

Softmax (weiche Maximalfunktion)

In diesem Kapitel werden wir hauptsächlich die entropieübergreifende Kostenfunktion verwenden, um die Probleme der Verlangsamung des Lernens zu lösen. Ich möchte jedoch kurz einen anderen Ansatz für dieses Problem diskutieren, der auf dem sogenannten basiert Softmax-Schichten von Neuronen. Für den Rest dieses Kapitels werden keine Softmax-Ebenen verwendet. Wenn Sie es also eilig haben, können Sie diesen Abschnitt überspringen. Softmax ist jedoch immer noch verständlich, insbesondere weil es an sich interessant ist und insbesondere, weil wir in Kapitel 6 Softmax-Schichten in unserer Diskussion über tiefe neuronale Netze verwenden werden.

Die Idee von Softmax ist es, einen neuen Typ von Ausgabeschicht für HC zu definieren. Es beginnt auf die gleiche Weise wie die Sigmoidschicht mit der Bildung gewichteter Eingaben $$$z ^ L_j = \ sum_ {k} w ^ L_ {jk} a ^ {L-1} _k + b ^ L_j$ . Wir verwenden jedoch kein Sigmoid, um eine Antwort zu erhalten. In der Softmax-Ebene wenden wir die Softmax-Funktion auf z ^L _{j an} . Ihrer Meinung nach ist die Aktivierung a ^L _{j des} Ausgangsneurons Nr. J gleich:

$$

$$a ^ L_j = \ frac {e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} \ tag {78}$$

wo im Nenner summieren wir über alle Ausgangsneuronen.

Wenn Ihnen die Softmax-Funktion nicht vertraut ist, erscheint Ihnen Gleichung (78) mysteriös. Es ist überhaupt nicht offensichtlich, warum wir eine solche Funktion verwenden sollten. Es ist auch nicht offensichtlich, dass es uns helfen wird, das Problem der Verlangsamung des Lernens zu lösen. Um Gleichung (78) besser zu verstehen, nehmen wir an, wir haben ein Netzwerk mit vier Ausgangsneuronen und vier entsprechenden gewichteten Eingängen, die wir als z ^L ₁ , z ^L ₂ , z ^L ₃ und z ^L _{4 bezeichnen werden} . Der Originalartikel enthält interaktive Anpassungsregler, denen die möglichen Werte der gewichteten Eingaben und der Zeitplan der entsprechenden Ausgabeaktivierungen zugewiesen sind. Ein guter Ausgangspunkt, um sie zu untersuchen, wäre die Verwendung des unteren Schiebereglers, um z ^L ₄ zu erhöhen.





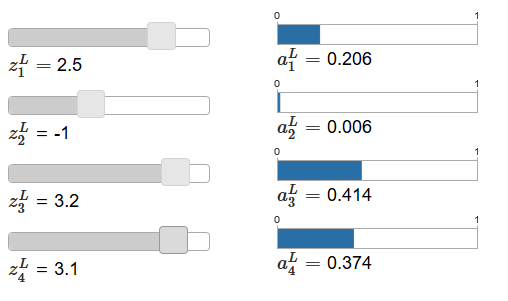
Durch Erhöhen von z ^L ₄ kann man eine Zunahme der entsprechenden Ausgangsaktivierung, a ^L ₄ und eine Abnahme anderer Ausgangsaktivierungen beobachten. Mit abnehmendem z ^L _{4 nimmt} a ^L ₄ ab und alle anderen Ausgangsaktivierungen nehmen zu. Bei genauerem Hinsehen werden Sie feststellen, dass in beiden Fällen die allgemeine Änderung anderer Aktivierungen die Änderung, die in einem ^L ₄ auftritt, genau kompensiert. Der Grund dafür ist die Garantie, dass alle Ausgangsaktivierungen insgesamt 1 ergeben, was wir mit Gleichung (78) und etwas Algebra beweisen können:

$$

$$\ sum_j a ^ L_j = \ frac {\ sum_j e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} = 1 \ tag {79}$$

Infolgedessen müssen mit einer Erhöhung von ^L _{4 die} verbleibenden Ausgangsaktivierungen insgesamt um denselben Wert verringert werden, um sicherzustellen, dass die Summe aller Ausgangsaktivierungen gleich 1 ist. Und natürlich gelten ähnliche Aussagen für alle anderen Aktivierungen.

Aus Gleichung (78) folgt auch, dass alle Ausgangsaktivierungen positiv sind, da die Exponentialfunktion positiv ist. Wenn wir dies mit der Beobachtung aus dem vorherigen Absatz kombinieren, stellen wir fest, dass die Ausgabe der Softmax-Schicht eine Menge positiver Zahlen ist, die insgesamt 1 ergeben. Mit anderen Worten, die Ausgabe der Softmax-Schicht kann als Wahrscheinlichkeitsverteilung dargestellt werden.

Die Tatsache, dass die Ausgabe der Softmax-Schicht eine Wahrscheinlichkeitsverteilung ist, ist sehr angenehm. Bei vielen Problemen ist es zweckmäßig, die Ausgangsaktivierungen a ^L _j als eine Schätzung des Netzwerks der Wahrscheinlichkeit interpretieren zu können, dass Bulet j die richtige Option ist. So können wir beispielsweise im Klassifizierungsproblem MNIST ein ^L _j als die Schätzung des Netzwerks für die Wahrscheinlichkeit interpretieren, dass j die korrekte Klassifizierung der Zahlen ist.

Wenn umgekehrt die Ausgabeschicht Sigmoid war, können wir definitiv nicht davon ausgehen, dass Aktivierungen eine Wahrscheinlichkeitsverteilung bilden. Ich werde dies nicht streng beweisen, aber es ist vernünftig anzunehmen, dass Aktivierungen der Sigmoidschicht im allgemeinen Fall keine Wahrscheinlichkeitsverteilung bilden. Daher erhalten wir unter Verwendung einer Sigmoid-Ausgabeschicht keine so einfache Interpretation der Ausgabeaktivierungen.

Übung

• Machen Sie ein Beispiel, das zeigt, dass in einem Netzwerk mit einer Sigmoid-Ausgabeschicht die Ausgabeaktivierungen a ^L _j nicht immer 1 ergeben.

Wir beginnen ein wenig über Softmax-Funktionen und das Verhalten von Softmax-Ebenen zu verstehen. Um es zusammenzufassen: Die Exponenten in Gleichung (78) stellen sicher, dass alle Ausgangsaktivierungen positiv sind. Die Summe im Nenner von Gleichung (78) stellt sicher, dass Softmax insgesamt 1 ergibt. Daher erscheint diese Art von Gleichung nicht mehr mysteriös: Dies ist ein natürlicher Weg, um sicherzustellen, dass die Ausgabeaktivierungen eine Wahrscheinlichkeitsverteilung bilden. Softmax kann als eine Möglichkeit vorgestellt werden, z ^L _j zu skalieren und sie dann zusammen zu komprimieren, um eine Wahrscheinlichkeitsverteilung zu bilden.

Übungen

• Die Monotonie von Softmax. Zeigen Sie, dass ∂a ^L _j / ∂z ^L _k positiv ist, wenn j = k, und negativ, wenn j ≠ k ist. Infolgedessen _wird garantiert, dass eine Erhöhung von z ^L _j die entsprechende Ausgangsaktivierung a ^L _j erhöht und alle anderen Ausgangsaktivierungen verringert. Wir haben dies bereits empirisch am Beispiel von Schiebereglern gesehen, aber dieser Beweis wird streng sein.
• Nichtlokalität Softmax. Ein schönes Merkmal von Sigmoidschichten ist, dass die Ausgabe a ^L _j eine Funktion der entsprechenden gewichteten Eingabe a ^L _j = σ (z ^L _j ) ist. Erklären Sie, warum dies bei der Softmax-Schicht nicht der Fall ist: Jede Ausgangsaktivierung a ^L _j hängt von allen gewichteten Eingängen ab.

Herausforderung

• Softmax-Ebene umkehren. Angenommen, wir haben einen NS mit einer ausgegebenen Softmax-Schicht und die Aktivierungen a ^L _{j sind} bekannt. Zeigen Sie, dass die entsprechenden gewichteten Eingaben die Form z ^L _j = ln a ^L _j + C haben, wobei C eine von j unabhängige Konstante ist.

Problem mit der Verlangsamung des Lernens

Wir sind bereits mit Softmax-Schichten von Neuronen vertraut geworden. Bisher haben wir jedoch noch nicht gesehen, wie Softmax-Ebenen es uns ermöglichen, das Problem der Verlangsamung des Lernens zu lösen. Um dies zu verstehen, definieren wir eine Kostenfunktion basierend auf der „Log-Wahrscheinlichkeit“. Wir werden x verwenden, um die Trainingseingabe des Netzwerks zu bezeichnen, und y für die entsprechende gewünschte Ausgabe. Dann ist das mit dieser Trainingseingabe verknüpfte LPS:

$$

$$C \ equiv - \ ln a ^ L_y \ tag {80}$$

Wenn wir zum Beispiel MNIST-Bilder untersuchen und Bild 7 in die Eingabe eingeht, ist das LPS −ln a ^L ₇ . Um dies intuitiv zu verstehen, betrachten wir den Fall, in dem das Netzwerk mit der Erkennung gut zurechtkommt, das heißt, es ist sicher, dass es sich am Eingang 7 befindet. In diesem Fall wird der Wert der entsprechenden Wahrscheinlichkeit a ^L ₇ nahe 1 bewertet, daher sind die Kosten in einem ^L ₇ gering . Wenn umgekehrt das Netzwerk nicht gut funktioniert, ist die Wahrscheinlichkeit eines ^L ₇ geringer und die Kosten in einem ^L ₇ sind höher. Daher verhält sich LPS wie von einer Kostenfunktion erwartet.

Was ist mit dem Problem der Verlangsamung? Um es zu analysieren, erinnern wir uns, dass die Hauptsache bei der Verzögerung das Verhalten von ∂C / ∂w ^L _jk und ∂C / ∂b ^L _{j ist} . Ich werde die Erfassung der Ableitung nicht im Detail beschreiben - ich werde Sie bitten, dies in Aufgaben zu tun, aber mit etwas Algebra können Sie Folgendes zeigen:

$$

$$\ frac {\ partielles C} {\ partielles b ^ L_j} = a ^ L_j-y_j \ tag {81}$$

$$

$$\ frac {\ partielles C} {\ partielles w ^ L_ {jk}} = a ^ {L-1} _k (a ^ L_j-y_j) \ tag {82}$$

Ich habe hier ein wenig mit der Notation gespielt und verwende „y“ etwas anders als im letzten Absatz. Dort bezeichnet y die gewünschte Netzwerkausgabe - das heißt, wenn die Ausgabe "7" ist, dann war die Eingabe Bild 7. Und in diesen Gleichungen bezeichnet y den Ausgabeaktivierungsvektor, der 7 entspricht, dh einen Vektor mit allen Nullen außer Eins in 7 th Position.

Diese Gleichungen sind dieselben wie ähnliche Ausdrücke, die wir in einer früheren Analyse der Kreuzentropie erhalten haben. Vergleiche zum Beispiel die Gleichungen (82) und (67). Dies ist die gleiche Gleichung, obwohl letztere über Trainingsbeispiele gemittelt wird. Und wie im ersten Fall garantieren diese Ausdrücke, dass das Lernen nicht verlangsamt wird. Es ist nützlich sich vorzustellen, dass die Softmax-Ausgangsschicht mit LPS der Schicht mit Sigmoid-Ausgabe und Kosten basierend auf der Kreuzentropie ziemlich ähnlich ist.

Was sollte angesichts ihrer Ähnlichkeit verwendet werden - Sigmoid-Ausgabe und Kreuzentropie oder Softmax-Ausgabe und LPS? In vielen Fällen funktionieren beide Ansätze sogar gut. Obwohl wir später in diesem Kapitel eine Sigmoid-Ausgabeschicht verwenden werden, deren Kosten auf der Kreuzentropie basieren. Später, in Kapitel 6, werden wir manchmal Softmax-Ausgang und LPS verwenden. Der Grund für die Änderungen besteht darin, einige der folgenden Netzwerke den Netzwerken einiger einflussreicher Forschungsarbeiten ähnlicher zu machen. Aus einer allgemeineren Sicht sollten Softmax und LPS verwendet werden, wenn Sie Ausgabeaktivierungen als Wahrscheinlichkeiten interpretieren müssen. Dies ist nicht immer erforderlich, kann jedoch bei Klassifizierungsproblemen (z. B. MNIST) hilfreich sein, zu denen sich nicht überschneidende Klassen gehören.

Die Aufgaben

• Leiten Sie die Gleichungen (81) und (82) her.
• Woher kommt der Name Softmax? Angenommen, wir ändern die Softmax-Funktion so, dass die Ausgangsaktivierungen durch die Gleichung gegeben sind

  $$

  $$a ^ L_j = \ frac {e ^ {c z ^ L_j}} {\ sum_k e ^ {c z ^ L_k}} \ tag {83}$$
  wobei c eine positive Konstante ist. Beachten Sie, dass c = 1 der Standard-Softmax-Funktion entspricht. Wenn wir jedoch einen anderen Wert von c verwenden, erhalten wir eine andere Funktion, die Softmax qualitativ noch ähnlich ist. Zeigen Sie, dass die Ausgabeaktivierungen eine Wahrscheinlichkeitsverteilung bilden, wie dies bei regulärem Softmax der Fall ist. Angenommen, wir machen c sehr groß, dh c → & inf; Was ist der Grenzwert der Ausgangsaktivierungen a ^L _j ? Nach der Lösung dieses Problems sollte klar sein, warum eine Funktion mit c = 1 als "erweichte Version" der Maximalfunktion betrachtet wird. Hier kommt der Begriff Softmax her.
• Rückausbreitung mit Softmax und LPS. Im letzten Kapitel haben wir den Backpropagation-Algorithmus für ein Netzwerk abgeleitet, das Sigmoid-Schichten enthält. Um diesen Algorithmus auf die Netzwerk- und Softmax-Schichten anzuwenden, müssen wir den Ausdruck für den Fehler δLj ≡ ∂C / ∂zLj ableiten. Zeigen Sie, dass ein geeigneter Ausdruck wäre

  $$

  $$\ delta ^ L_j = a ^ L_j -y_j \ tag {84}$$
  Mit diesem Ausdruck können wir den Backpropagation-Algorithmus mithilfe der Ausgabe-Softmax-Schicht und des LPS auf das Netzwerk anwenden.

Umschulung und Regularisierung

Der Nobelpreisträger Enrico Fermi wurde einmal um eine Stellungnahme zu dem von mehreren Kollegen vorgeschlagenen mathematischen Modell gebeten, um ein wichtiges ungelöstes physikalisches Problem zu lösen. Das Modell entsprach perfekt dem Experiment, aber Fermi war skeptisch. Er fragte, wie viele freie Parameter darin geändert werden können. "Vier", sagten sie ihm. Fermi antwortete: "Ich erinnere mich, wie mein Freund Johnny von Neumann gern sagte, dass man mit vier Parametern einen Elefanten dorthin schieben und mit fünf ihn seinen Rüssel winken lassen kann."

Die Bedeutung der Geschichte ist natürlich, dass Modelle mit einer großen Anzahl freier Parameter eine überraschend breite Palette von Phänomenen beschreiben können.Selbst wenn ein solches Modell mit verfügbaren Daten gut funktioniert, ist es nicht automatisch ein gutes Modell. Dies könnte bedeuten, dass das Modell genügend Freiheit hat, um fast jeden Datensatz einer bestimmten Größe zu beschreiben, ohne die Hauptidee des Phänomens preiszugeben. In diesem Fall funktioniert das Modell gut mit vorhandenen Daten, kann jedoch die neue Situation nicht verallgemeinern. Ein echter Test eines Modells ist seine Fähigkeit, Vorhersagen in Situationen zu treffen, denen es zuvor noch nicht begegnet ist.

Fermi und von Neumann standen Modellen mit vier Parametern misstrauisch gegenüber. Unser NS mit 30 versteckten Neuronen zur Klassifizierung von MNIST-Ziffern hat fast 24.000 Parameter! Dies sind einige Parameter. Unsere NS mit 100 versteckten Neuronen hat fast 80.000 Parameter, und fortgeschrittene tiefe NS dieser Parameter haben manchmal Millionen oder sogar Milliarden. Können wir den Ergebnissen ihrer Arbeit vertrauen?

Lassen Sie uns dieses Problem komplizieren, indem wir eine Situation schaffen, in der unser Netzwerk eine neue Situation für dieses Problem schlecht verallgemeinert. Wir werden NS mit 30 versteckten Neuronen und 23.860 Parametern verwenden. Wir werden das Netzwerk jedoch nicht mit allen 50.000 MNIST-Bildern trainieren. Stattdessen verwenden wir nur die ersten 1000. Die Verwendung eines begrenzten Satzes macht das Generalisierungsproblem offensichtlicher. Wir werden wie zuvor unter Verwendung der auf Kreuzentropie basierenden Kostenfunktion mit einer Lerngeschwindigkeit von η = 0,5 und einer Minipaketgröße von 10 untersuchen. Wir werden jedoch 400 Epochen untersuchen, was etwas mehr als zuvor ist, da es Trainingsbeispiele gibt Wir haben nicht viel. Lassen Sie uns mit network2 untersuchen, wie sich die Kostenfunktion ändert:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True, monitor_training_cost=True) 

Anhand der Ergebnisse können wir ein Diagramm der Kostenänderungen beim Training des Netzwerks erstellen (Diagramme wurden mit dem Programm overfitting.py erstellt):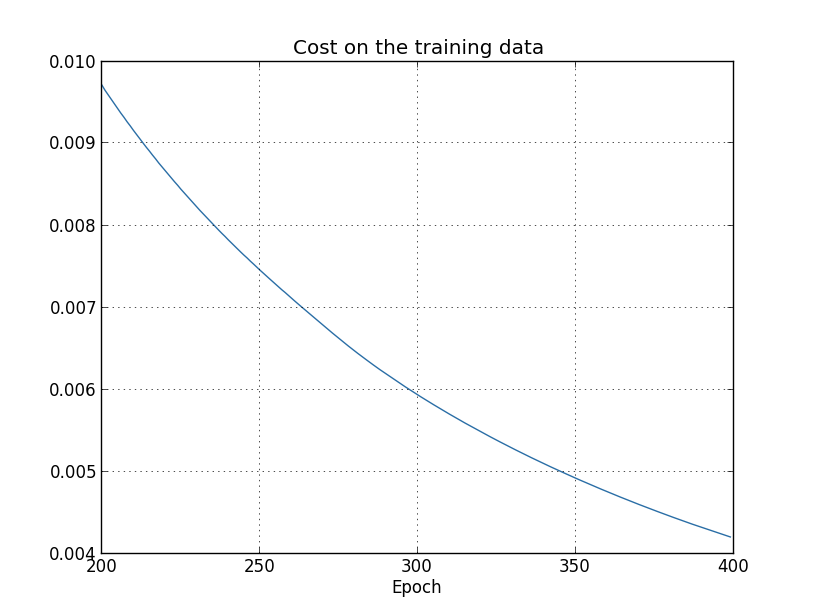



Es sieht ermutigend aus, dass die Kosten erwartungsgemäß reibungslos sinken. Denken Sie daran, dass ich nur die Epochen von 200 bis 399 gezeigt habe. Infolgedessen sehen wir in vergrößertem Maßstab die späten Phasen des Trainings, in denen, wie wir später sehen werden, das Interessanteste passiert.

Lassen Sie uns nun sehen, wie sich die Klassifizierungsgenauigkeit der Verifizierungsdaten im Laufe der Zeit ändert:



Dann habe ich den Zeitplan noch einmal erhöht. In den ersten 200 Epochen, die hier nicht sichtbar sind, steigt die Genauigkeit auf fast 82%. Dann verlangsamt sich das Training allmählich. Um die 280. Ära schließlich verbessert sich die Klassifizierungsgenauigkeit nicht mehr. In späteren Epochen werden nur geringe stochastische Schwankungen um den in der 280. Epoche erreichten Genauigkeitswert beobachtet. Vergleichen Sie dies mit dem vorherigen Diagramm, in dem die mit Trainingsdaten verbundenen Kosten allmählich sinken. Wenn Sie nur diese Kosten untersuchen, scheint sich das Modell zu verbessern. Die Ergebnisse der Arbeit mit Testdaten zeigen jedoch, dass diese Verbesserung nur eine Illusion ist. Wie in dem Modell, das Fermi nicht gefiel, wird das, was unser Netzwerk nach der 280. Ära untersucht, nicht mehr auf Verifizierungsdaten verallgemeinert. Daher ist dieses Training nicht mehr nützlich. Wir sagen, dass das Netzwerk nach der 280. Ära umgeschult wird,oder Überanpassung.

Sie fragen sich vielleicht, ob es kein Problem ist, dass ich die Kosten anhand von Trainingsdaten und nicht anhand der Genauigkeit der Klassifizierung von Verifizierungsdaten untersuche. Mit anderen Worten, vielleicht liegt das Problem darin, dass wir Äpfel mit Orangen vergleichen. Was passiert, wenn wir die Kosten für Schulungsdaten mit den Kosten für die Überprüfung vergleichen, dh vergleichbare Maßnahmen vergleichen? Oder könnten wir vielleicht die Klassifizierungsgenauigkeit von Trainings- und Testdaten vergleichen? Tatsächlich tritt das gleiche Phänomen auf, unabhängig davon, wie der Vergleich durchgeführt wird. Aber die Details ändern sich. Sehen wir uns zum Beispiel den Wert der Verifizierungsdaten an:



Es ist ersichtlich, dass sich die Kosten für Verifizierungsdaten bis etwa zur 15. Ära verbessern und sich dann insgesamt zu verschlechtern beginnen, obwohl sich die Kosten für Trainingsdaten weiter verbessern. Dies ist ein weiteres Zeichen für ein umgeschultes Modell. Es stellt sich jedoch die Frage, in welcher Ära wir den Punkt berücksichtigen sollten, an dem die Umschulung die Ausbildung überwiegt - 15 oder 280? Aus praktischer Sicht sind wir dennoch daran interessiert, die Genauigkeit der Klassifizierung von Verifizierungsdaten zu verbessern, und die Kosten sind nur ein Mediator für die Genauigkeit der Klassifizierung. Daher ist es sinnvoll, die Ära von 280 als einen Punkt zu betrachten, nach dem die Umschulung die Ausbildung unserer Nationalversammlung überwiegt.

Ein weiteres Zeichen für eine Umschulung ist die Genauigkeit der Klassifizierung der Trainingsdaten:



Die Genauigkeit wächst und erreicht 100%. Das heißt, unser Netzwerk klassifiziert alle 1000 Trainingsbilder korrekt! In der Zwischenzeit steigt die Überprüfungsgenauigkeit auf nur 82,27%. Das heißt, unser Netzwerk untersucht nur die Merkmale des Trainingssatzes und lernt überhaupt nicht, Zahlen zu erkennen. Es scheint, dass sich das Netzwerk einfach an den Trainingssatz erinnert und die Zahlen nicht gut genug versteht, um dies auf den Testsatz zu verallgemeinern.

Die Umschulung ist ein ernstes Problem der Nationalversammlung. Dies gilt insbesondere für moderne NS, die normalerweise eine große Menge an Gewichten und Verschiebungen aufweisen. Für ein effektives Training müssen wir feststellen können, wann eine Umschulung stattfindet, um nicht umzuschulen. Und wir möchten auch die Auswirkungen der Umschulung reduzieren können.

Eine naheliegende Möglichkeit, eine Umschulung zu erkennen, besteht darin, den oben beschriebenen Ansatz zu verwenden und die Genauigkeit der Arbeit mit Verifizierungsdaten während des Netzwerktrainings zu überwachen. Wenn wir feststellen, dass sich die Genauigkeit der Verifizierungsdaten nicht mehr verbessert, müssen wir das Training beenden. Genau genommen wird dies natürlich nicht unbedingt ein Zeichen für eine Umschulung sein. Möglicherweise verbessert sich gleichzeitig die Genauigkeit der Arbeit mit Test- und Trainingsdaten nicht mehr. Die Anwendung einer solchen Strategie verhindert jedoch eine Umschulung.

Und wir werden eine kleine Variation dieser Strategie verwenden. Denken Sie daran, dass wir Daten beim Laden in MNIST in drei Gruppen aufteilen:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Bisher haben wir training_data und test_data verwendet und validation_data [bestätigend] ignoriert. Validation_data enthält 10.000 Bilder, die sich sowohl von 50.000 Bildern des MNIST-Trainingssatzes als auch von 10.000 Bildern des Validierungssatzes unterscheiden. Anstatt test_data zu verwenden, um eine Überanpassung zu verhindern, verwenden wir validation_data. Dazu verwenden wir fast dieselbe Strategie, die oben für test_data beschrieben wurde. Das heißt, wir werden die Klassifizierungsgenauigkeit von validation_data am Ende jeder Ära berechnen. Sobald die Klassifizierungsgenauigkeit von validation_data vollständig ist, hören wir auf zu lernen. Diese Strategie wird als vorzeitiger Stopp bezeichnet. In der Praxis werden wir natürlich nicht sofort feststellen können, dass die Genauigkeit zufriedenstellend ist. Stattdessen werden wir weiter trainieren, bis wir dies sicherstellen (und entscheidenWenn Sie aufhören müssen, ist dies nicht immer einfach und Sie können hierfür mehr oder weniger aggressive Ansätze verwenden.

Warum sollten Sie validation_data verwenden, um eine Umschulung zu verhindern, anstatt test_data? Es ist Teil einer allgemeineren Strategie, validation_data zu verwenden, um verschiedene Auswahlmöglichkeiten für Hyperparameter zu bewerten - die Anzahl der zu lernenden Epochen, die Lerngeschwindigkeit, die beste Netzwerkarchitektur usw. Wir verwenden diese Schätzungen, um Hyperparameter zu finden und ihnen gute Werte zuzuweisen. Und obwohl ich dies noch nicht erwähnt habe, habe ich teilweise aus diesem Grund in den früheren Beispielen des Buches die Wahl der Hyperparameter getroffen.

Natürlich beantwortet diese Bemerkung nicht die Frage, warum wir Validierungsdaten und nicht Testdaten verwenden, um eine Überanpassung zu verhindern. Es ersetzt einfach die Antwort auf eine allgemeinere Frage: Warum verwenden wir Validierungsdaten und nicht Testdaten, um Hyperparameter auszuwählen? Um dies zu verstehen, denken Sie daran, dass wir bei der Auswahl von Hyperparametern höchstwahrscheinlich aus einer Vielzahl ihrer Optionen auswählen müssen. Wenn wir Hyperparameter basierend auf den Bewertungen von test_data zuweisen, werden wir diese Daten wahrscheinlich zu sehr speziell für test_data anpassen. Das heißt, wir finden möglicherweise Hyperparameter, die für die spezifischen Merkmale bestimmter Daten aus test_data gut geeignet sind. Der Betrieb unseres Netzwerks wird jedoch nicht auf andere Datensätze verallgemeinert. Wir vermeiden dies, indem wir Hyperparameter mit validation_data auswählen. Und dann, nachdem wir den GP erhalten haben, den wir brauchen,Wir führen eine endgültige Genauigkeitsbewertung mit test_data durch. Dies gibt uns die Gewissheit, dass unsere Ergebnisse mit test_data ein echtes Maß für den Grad der Verallgemeinerung des NS sind. Mit anderen Worten, unterstützende Daten sind solche speziellen Trainingsdaten, die uns helfen, einen guten Hausarzt zu lernen. Dieser Ansatz zum Auffinden von Hausärzten wird manchmal als Aufbewahrungsmethode bezeichnet, da Validierungsdaten getrennt von Trainingsdaten "gehalten" werden.

In der Praxis werden wir auch nach der Bewertung der Qualität der Arbeit an test_data unsere Meinung ändern und einen anderen Ansatz - möglicherweise eine andere Netzwerkarchitektur - ausprobieren wollen, der die Suche nach einer neuen Gruppe von Hausärzten umfasst. Besteht in diesem Fall die Gefahr, dass wir uns unnötig an test_data anpassen? Benötigen wir eine möglicherweise unendliche Anzahl von Datensätzen, damit wir sicher sein können, dass unsere Ergebnisse gut verallgemeinert sind? Im Allgemeinen ist dies ein tiefes und komplexes Problem. Aber für unsere praktischen Zwecke werden wir uns darüber keine allzu großen Sorgen machen. Wir tauchen einfach kopfüber in die weitere Forschung ein, indem wir eine einfache Aufbewahrungsmethode verwenden, die auf Trainingsdaten, Validierungsdaten und Testdaten basiert, wie oben beschrieben.

Bisher haben wir über eine Umschulung mit 1000 Trainingsbildern nachgedacht. Was passiert, wenn wir einen vollständigen Trainingssatz von 50.000 Bildern verwenden? Wir werden alle anderen Parameter unverändert lassen (30 versteckte Neuronen, Lerngeschwindigkeit 0,5, Minipaketgröße 10), aber wir werden 30 Epochen mit allen 50.000 Bildern untersuchen. Hier ist eine Grafik, die die Genauigkeit der Klassifizierung anhand von Trainingsdaten und Testdaten zeigt. Beachten Sie, dass ich hier Validierungsdaten anstelle von Validierungsdaten verwendet habe, um den Vergleich der Ergebnisse mit früheren Diagrammen zu vereinfachen.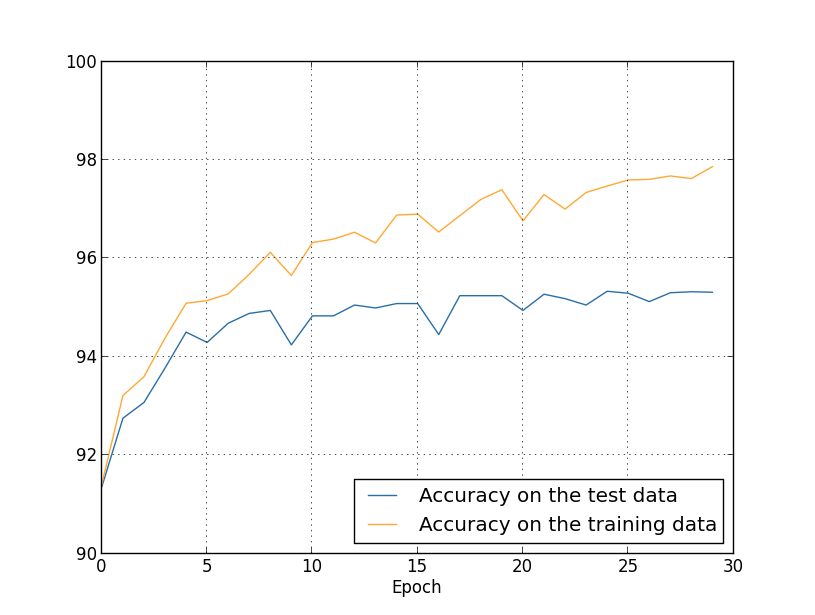



Es ist ersichtlich, dass die Genauigkeitsindikatoren auf den Test- und Trainingsdaten näher beieinander bleiben als bei Verwendung von 1000 Trainingsbeispielen. Insbesondere ist die beste Klassifizierungsgenauigkeit von 97,86% nur 2,53% höher als 95,33% der Verifizierungsdaten. Vergleichen Sie mit einer frühen Pause von 17,73%! Die Umschulung findet statt, ist aber stark reduziert. Unser Netzwerk sammelt Informationen viel besser und wechselt vom Training zu den Testdaten. Im Allgemeinen besteht eine der besten Möglichkeiten zur Reduzierung der Umschulung darin, die Menge der Trainingsdaten zu erhöhen. Mit genügend Trainingsdaten ist es schwierig, selbst ein sehr großes Netzwerk neu zu trainieren. Leider ist das Abrufen von Trainingsdaten teuer und / oder schwierig, sodass diese Option nicht immer praktikabel ist.

Regularisierung

Das Erhöhen der Trainingsdatenmenge ist eine Möglichkeit, die Umschulung zu reduzieren. Gibt es andere Möglichkeiten, die Umschulung zu reduzieren? Ein möglicher Ansatz besteht darin, die Netzwerkgröße zu reduzieren. Zwar haben große Netzwerke mehr Potenzial als kleine, daher zögern wir, auf diese Option zurückzugreifen.

Glücklicherweise gibt es andere Techniken, die die Umschulung reduzieren können, selbst wenn wir die Größe des Netzwerks und die Trainingsdaten festgelegt haben. Sie sind als Regularisierungstechniken bekannt. In diesem Kapitel werde ich eine der beliebtesten Techniken beschreiben, die manchmal als Schwächung von Gewichten oder Regularisierung von L2 bezeichnet werden. Ihre Idee ist es, der Kostenfunktion ein zusätzliches Mitglied hinzuzufügen, das als Regularisierungsmitglied bezeichnet wird. Hier ist Kreuzentropie mit Regularisierung:

$$

$$C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2 \tag{85}$$

Der erste Begriff ist ein gebräuchlicher Ausdruck für Kreuzentropie. Aber wir haben eine Sekunde hinzugefügt, nämlich die Summe der Quadrate aller Netzwerkgewichte. Sie wird mit dem Faktor λ / 2n skaliert, wobei λ> 0 der Regularisierungsparameter ist und n wie üblich die Größe des Trainingssatzes ist. Wir werden diskutieren, wie man λ wählt. Es ist auch erwähnenswert, dass Verzerrungen nicht im Regularisierungsbegriff enthalten sind. Darüber unten.

Natürlich ist es möglich, andere Kostenfunktionen zu regulieren, beispielsweise quadratisch. Dies kann auf ähnliche Weise erfolgen:

$$

$$C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2 \tag{86}$$

In beiden Fällen können wir die regulierte Kostenfunktion als schreiben

$$

$$C = C_0 + \frac{\lambda}{2n} \sum_w w^2 \tag{87}$$

wobei C ₀ die ursprüngliche Kostenfunktion ohne Regularisierung ist.

Es ist intuitiv klar, dass der Punkt der Regularisierung darin besteht, das Netzwerk davon zu überzeugen, kleinere Gewichte zu bevorzugen, wobei alle anderen Dinge gleich sind. Große Gewichte sind nur möglich, wenn sie den ersten Teil der Kostenfunktion erheblich verbessern. Mit anderen Worten, Regularisierung ist eine Möglichkeit, einen Kompromiss zwischen dem Finden kleiner Gewichte und dem Minimieren der anfänglichen Kostenfunktion zu wählen. Es ist wichtig, dass diese beiden Elemente des Kompromisses vom Wert von λ abhängen: Wenn λ klein ist, bevorzugen wir es, die ursprüngliche Kostenfunktion zu minimieren, und wenn λ groß ist, bevorzugen wir kleine Gewichte.

Es ist überhaupt nicht offensichtlich, warum die Wahl eines solchen Kompromisses dazu beitragen sollte, die Umschulung zu reduzieren! Aber es stellt sich heraus, dass es hilft. Wir werden im nächsten Abschnitt herausfinden, warum es hilft. Aber zuerst arbeiten wir mit einem Beispiel, das zeigt, dass Regularisierung die Umschulung reduziert.

Um ein Beispiel zu konstruieren, müssen wir zunächst verstehen, wie der Trainingsalgorithmus mit stochastischem Gradientenabstieg auf eine regulierte NS angewendet wird. Insbesondere müssen wir wissen, wie die partiellen Ableitungen ∂C / ∂w und ∂C / ∂b für alle Gewichte und Offsets im Netzwerk berechnet werden. Nach den partiellen Ableitungen in Gleichung (87) erhalten wir:

$$

$$\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{88}$$

$$

$$\frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b} \tag{89}$$

Die Terme ∂C ₀ / ∂w und ∂C ₀ / ∂w können über das OP berechnet werden, wie im vorherigen Kapitel beschrieben. Wir sehen, dass es einfach ist, den Gradienten der regulierten Kostenfunktion zu berechnen: Sie müssen nur das OP wie gewohnt verwenden und dann λ / nw zur partiellen Ableitung aller Gewichtsterme hinzufügen. Die partiellen Ableitungen in Bezug auf Verschiebungen ändern sich nicht, daher unterscheidet sich die Regel des Lernens durch Gradientenabstieg für Verschiebungen nicht von der üblichen:

$$

$$b \rightarrow b -\eta \frac{\partial C_0}{\partial b} \tag{90}$$

Die Trainingsregel für Gewichte lautet:

$$

$$w \rightarrow w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{91}$$

$$

$$= \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w} \tag{92}$$

Alles ist das gleiche wie in der üblichen Gradientenabstiegsregel, außer dass wir zuerst das Gewicht w um einen Faktor von 1 - ηλ / n skalieren. Diese Skalierung wird manchmal als Gewichtsverlust bezeichnet, da sie das Gewicht reduziert. Auf den ersten Blick scheinen die Gewichte unwiderstehlich gegen Null zu tendieren. Dies ist jedoch nicht der Fall, da der andere Begriff zu einer Gewichtszunahme führen kann, wenn dies zu einer Abnahme der unregelmäßigen Kostenfunktion führt.

Ok, lass den Gradientenabstieg so funktionieren. Was ist mit stochastischem Gefälle? Nun, wie in der unregelmäßigen Version des stochastischen Gradientenabfalls können wir ∂C ₀ / ∂w durch Mittelung über das Minipaket von m Trainingsbeispielen schätzen . Daher wird die regulierte Lernregel für den stochastischen Gradientenabstieg zu (siehe Gleichung (20)):

$$

$$w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w} \tag{93}$$

wobei die Summe für Trainingsbeispiele x im Minipaket gilt und C _x die unregelmäßigen Kosten für jedes Trainingsbeispiel sind. Alles ist das gleiche wie in der üblichen Regel des stochastischen Gradientenabfalls, mit Ausnahme von 1 - ηλ / n, dem Gewichtsverlustfaktor. Lassen Sie mich zum Abschluss des Bildes eine regulierte Regel für Offsets aufschreiben. Natürlich ist es genau das gleiche wie im unregelmäßigen Fall (siehe Gleichung (21)):

$$

$$b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b} \tag{94}$$

wo der Betrag für Trainingsbeispiele x im Minipaket geht.

Mal sehen, wie die Regularisierung die Wirksamkeit unserer Nationalversammlung verändert. Wir werden ein Netzwerk mit 30 versteckten Neuronen, einem Minipaket der Größe 10, einer Lerngeschwindigkeit von 0,5 und einer Kostenfunktion mit Kreuzentropie verwenden. Diesmal verwenden wir jedoch den Regularisierungsparameter λ = 0,1. Im Code habe ich diese Variable lmbda genannt, da das Wort Lambda in Python für Dinge reserviert ist, die nicht mit unserem Thema zusammenhängen. Ich habe auch wieder test_data anstelle von validation_data verwendet. Ich habe mich jedoch für test_data entschieden, da die Ergebnisse direkt mit unseren frühen, unregelmäßigen Ergebnissen verglichen werden können. Sie können den Code einfach so ändern, dass er validationsdaten verwendet, und sicherstellen, dass die Ergebnisse ähnlich sind.

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, ... evaluation_data=test_data, lmbda = 0.1, ... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True, ... monitor_training_cost=True, monitor_training_accuracy=True) 

Die Kosten für Trainingsdaten sinken wie im frühen Fall ohne Regularisierung ständig:



Diesmal steigt jedoch die Genauigkeit von test_data in allen 400 Epochen weiter an: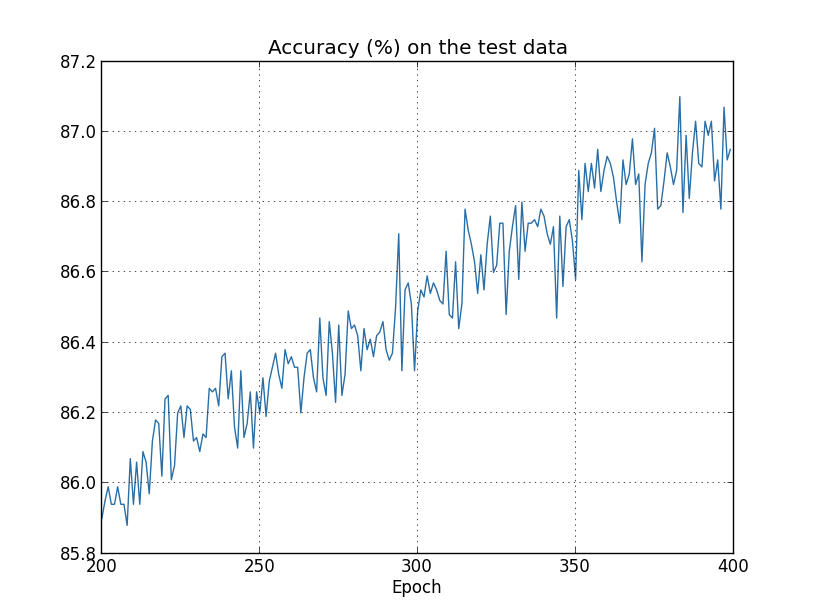



Offensichtlich hat die Regularisierung die Umschulung unterdrückt. Darüber hinaus hat sich die Genauigkeit erheblich erhöht, und die Genauigkeit der Peakklassifizierung erreicht 87,1%, verglichen mit dem Peak von 82,27%, der im Fall ohne Regularisierung erreicht wurde. Im Allgemeinen erzielen wir mit ziemlicher Sicherheit bessere Ergebnisse, wenn wir nach 400 Epochen weiter studieren. Empirisch scheint die Regularisierung unser Netzwerk besser zu verallgemeinern und die Auswirkungen der Umschulung erheblich zu verringern.

Was passiert, wenn wir unsere künstliche Umgebung verlassen, in der nur 1.000 Lehrbilder verwendet werden, und zum vollständigen Satz von 50.000 Bildern zurückkehren? Natürlich haben wir bereits gesehen, dass die Umschulung bei einem vollständigen Satz von 50.000 Bildern ein viel kleineres Problem darstellt. Hilft die Regularisierung, das Ergebnis zu verbessern? Behalten wir die vorherigen Werte der Hyperparameter bei - 30 Epochen, Geschwindigkeit 0,5, Minipaketgröße 10. Wir müssen jedoch den Regularisierungsparameter ändern. Tatsache ist, dass die Größe n des Trainingssatzes von 1000 auf 50 000 sprang, und dies ändert den Schwächungsfaktor der Gewichte 1 - ηλ / n. Wenn wir weiterhin λ = 0,1 verwenden, würde dies bedeuten, dass die Gewichte viel weniger geschwächt werden und infolgedessen der Effekt der Regularisierung abnimmt. Wir kompensieren dies, indem wir λ = 5,0 akzeptieren.

Ok, lassen Sie uns unser Netzwerk trainieren, indem wir zuerst die Gewichte neu initialisieren:

 >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, ... evaluation_data=test_data, lmbda = 5.0, ... monitor_evaluation_accuracy=True, monitor_training_accuracy=True) 

Wir bekommen die Ergebnisse: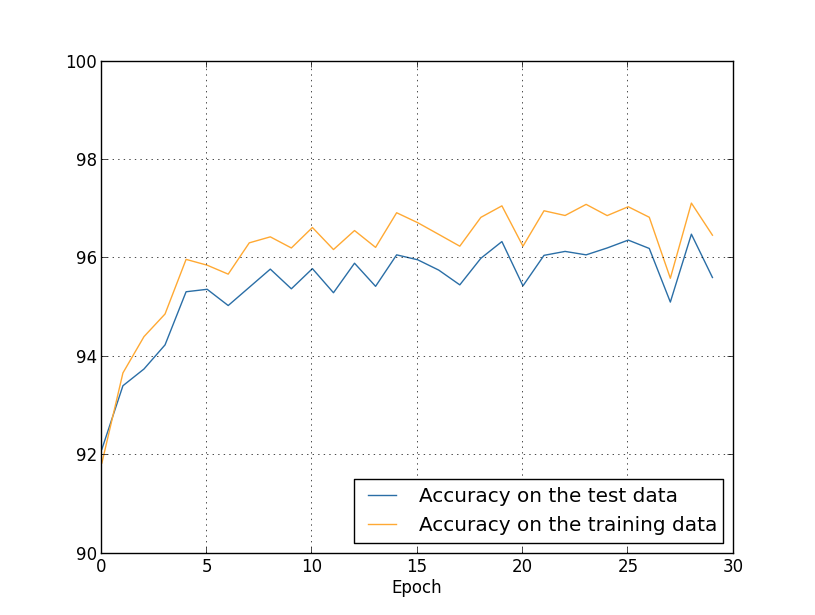



Viele aller angenehmen Dinge. Erstens ist unsere Klassifizierungsgenauigkeit für Verifizierungsdaten von 95,49% ohne Regularisierung auf 96,49% mit Regularisierung gestiegen. Dies ist eine wesentliche Verbesserung. Zweitens ist ersichtlich, dass die Lücke zwischen den Ergebnissen der Arbeit an den Trainings- und Testsätzen viel geringer ist als zuvor und weniger als 1% beträgt. Die Lücke ist immer noch anständig, aber wir haben offensichtlich erhebliche Fortschritte bei der Reduzierung der Umschulung erzielt.

Sehen Sie abschließend, welche Klassifizierungsgenauigkeit wir erhalten, wenn 100 versteckte Neuronen und der Regularisierungsparameter & lambda = 5.0 verwendet werden. Ich werde keine detaillierte Analyse der Umschulung geben, dies ist nur zum Spaß, um zu sehen, wie viel Genauigkeit mit unseren neuen Tricks erreicht werden kann: eine Kostenfunktion mit Kreuzentropie und Regularisierung von L2.

 >>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

Das Endergebnis ist eine Klassifizierungsgenauigkeit von 97,92% für unterstützende Daten. Ein großer Sprung im Vergleich zu 30 versteckten Neuronen. Sie können eine Feinabstimmung vornehmen, den Prozess für 60 Epochen mit η = 0,1 und λ = 5,0 starten und die Barriere von 98% überwinden, um eine Genauigkeit von 98,04 für die unterstützenden Daten zu erreichen. Nicht schlecht für 152 Codezeilen!

Ich habe die Regularisierung als einen Weg beschrieben, die Umschulung zu reduzieren und die Klassifizierungsgenauigkeit zu erhöhen. Dies sind jedoch nicht die einzigen Vorteile. Empirisch gesehen, nachdem ich viele Starts unseres Netzwerk-MNIST ausprobiert und jedes Mal die Gewichte geändert hatte, stellte ich fest, dass Starts ohne Regularisierung manchmal „stecken blieben“ und offensichtlich in das lokale Minimum der Kostenfunktion fielen. Infolgedessen führten unterschiedliche Starts manchmal zu sehr unterschiedlichen Ergebnissen. Im Gegensatz dazu können Sie durch Regularisierung viel einfacher reproduzierbare Ergebnisse erzielen.

Warum ist das so? Heuristisch gesehen wird die Länge des Gewichtsvektors höchstwahrscheinlich zunehmen, wenn die Kostenfunktion keine Regularisierung aufweist, wobei alle anderen Dinge gleich sind. Dies kann im Laufe der Zeit zu einem sehr großen Gewichtsvektor führen. Und aus diesem Grund kann der Vektor der Skalen stecken bleiben und ungefähr in die gleiche Richtung zeigen, da Änderungen aufgrund des Gradientenabfalls nur winzige Richtungsänderungen mit einer großen Länge des Vektors bewirken. Ich glaube, dass es aufgrund dieses Phänomens für unseren Trainingsalgorithmus sehr schwierig ist, den Raum der Gewichte richtig zu untersuchen, und daher ist es schwierig, ein gutes Minimum der Kostenfunktion zu finden.