Rauschen in Big Data. Entropieanalyse

Ich bin auf eine Aufgabe namens Enscombe Quartet ( Anscombe ) gestoßen “( englische Version ).

Abbildung 1 zeigt eine tabellarische Verteilung von 4 Zufallsfunktionen (aus Wikipedia).


Abb. 1. Tabellenverteilung von vier Zufallsfunktionen

Abbildung 2 zeigt die Verteilungsparameter dieser Zufallsfunktionen


Abb. 2. Verteilungsparameter von vier Zufallsfunktionen

Und ihre Grafiken in Abbildung 3.


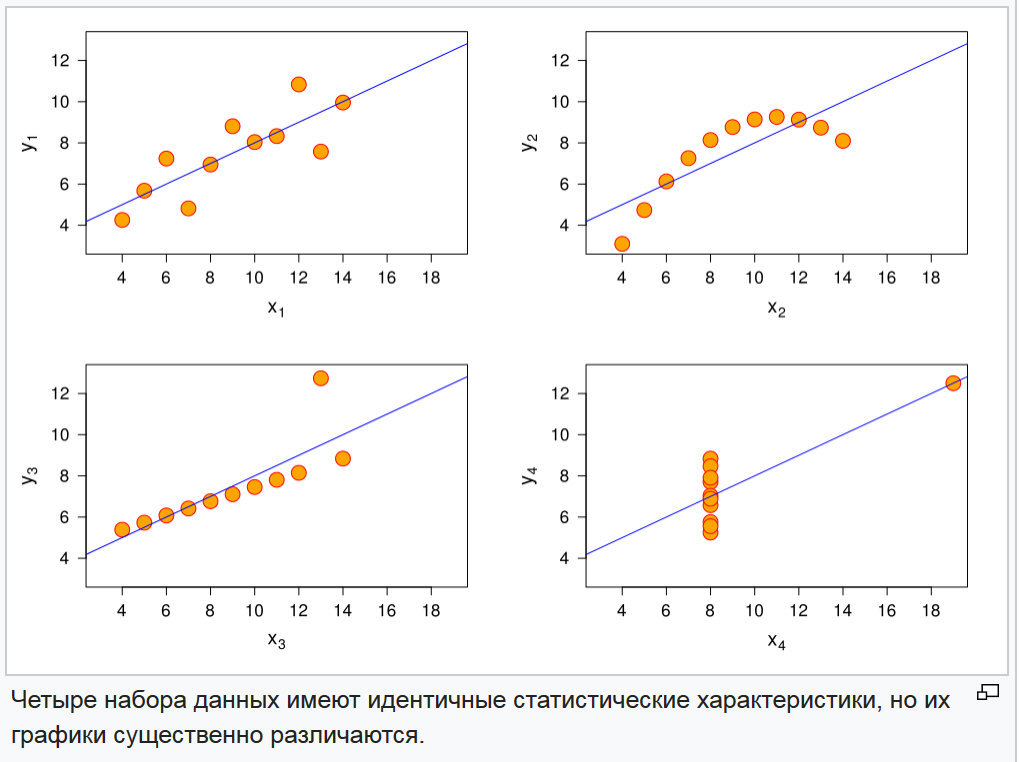Abb. 3. Diagramme von vier Zufallsfunktionen

Das Problem der Unterscheidung dieser Funktionen wird ganz einfach gelöst, indem die Momente höherer Ordnung und ihre normalisierten Indikatoren verglichen werden: Asymmetriekoeffizient und Überschusskoeffizient . Diese Indikatoren sind in Abbildung 4 dargestellt.


Abb. 4. Indikatoren für Momente dritter und vierter Ordnung sowie für die Asymmetrie und die Überschusskoeffizienten von vier Zufallsfunktionen

Wie aus der Tabelle in Abbildung 4 ersichtlich ist, ist die Kombination dieser Indikatoren für alle Funktionen unterschiedlich.
Die erste Schlussfolgerung, die natürlich darauf hindeutet, dass die Informationen über die relativen Positionen der Punkte in den Verteilungsparametern auf einer höheren Ebene als die Varianz der Zufallsverteilung gespeichert sind.

Viele Analysten versuchen, bestimmte Regressionsgleichungen in Big Data zu isolieren. Bisher ist dies eine Methode zur Auswahl der Gleichung mit der geringsten Restdispersion. Es gab nicht viel hinzuzufügen. Aber ich habe darauf hingewiesen, dass dies alles Informationen sind und Informationen einen Indikator für Entropie haben . Und es, Entropie, hat seine Grenzen von 0, wenn die Information vollständig zu weißem Rauschen bestimmt ist. Und das weiße Rauschen im Übertragungskanal ist gleichmäßig verteilt.

Wenn die Daten analysiert werden müssen, wird zunächst davon ausgegangen, dass sie verwandte Daten enthalten, die als Beziehung formalisiert werden müssen. Und dies deutet darauf hin, dass die Daten kein weißes Rauschen sind. Das heißt, die erste Stufe ist die Auswahl der Regressionsgleichung und die Bestimmung der Restvarianz. Wenn die Regression richtig gewählt wird, folgt die Restvarianz dem Gesetz der Normalverteilung. Lassen Sie uns sehen und in den Abbildungen 5-7 sind die Entropieformeln für eine gleichmäßig verteilte und normalverteilte Zufallsvariable dargestellt.



Abb. 5. Die Formel der Differentialentropie für eine normalverteilte Größe (VV Afanasyev, Wahrscheinlichkeitstheorie in Fragen und Aufgaben . Ministerium für Bildung und Wissenschaft der Russischen Föderation, Staatliche Pädagogische Universität Jaroslawl, benannt nach KD Ushinsky)


Abb. 6. Die Formel der Differentialentropie für eine normalverteilte Größe (Pugachev VS Die Theorie der Zufallsfunktionen und ihre Anwendung auf automatische Steuerungsprobleme . Hrsg. 2., überarbeitet und ergänzt. - M .: Fizmatlit, 1960. - 883 S.)


Abb. 7. Die Formel der Differentialentropie für eine gleichmäßig verteilte Größe (Pugachev VS Die Theorie der Zufallsfunktionen und ihre Anwendung auf Probleme der automatischen Steuerung . Ed. 2., überarbeitet und ergänzt. - M .: Fizmatlit, 1960. - 883 S.)

Als nächstes zeigen wir ein Beispiel. Aber zuerst nehmen wir die Bedingungen an, dass jede der vier Funktionen die Koordinate der Hyperebene ist, das heißt, wir überprüfen gleichzeitig die Funktionsweise des Modells im mehrdimensionalen Raum. Zeichnen Sie eine Faltung eines Hyperwürfels in eine Ebene. Der Mechanismus ist in Abbildung 8 dargestellt.




Abb. 8. Anfangsdaten mit dem Faltungsmechanismus


Abb. 9. Aggregierte Gruppierung in der Abbildung.


Abb. 10. Verteilungsparameter von vier Zufallsfunktionen und eine zusammenfassende Gruppierung.

Berücksichtigen Sie den Mechanismus zur Auswahl der Größe des Partitionsintervalls. Die Anfangsbedingungen sind in Abbildung 11 dargestellt.


Abb. 11. Die Anfangsbedingungen für die Aufteilung in Intervalle.

Bedingung 1. Sie muss im Variationsbereich mit einer Wahrscheinlichkeit ungleich Null vorliegen, da ansonsten die Entropie gleich unendlich ist. Sowohl für die Erstprobe als auch für den Rest.

Bedingung 2. Da es unmöglich ist, die Möglichkeit eines Ausreißers in neuen Daten usw. für die extremen Intervalle zu ignorieren, ist es notwendig, die Wahrscheinlichkeit nach dem normalen oder einem anderen allgemein anerkannten theoretischen Gesetz der Wahrscheinlichkeitsverteilung nach dem Prinzip der Wahrscheinlichkeit von Schwänzen zu bestimmen.

Bedingung 3. Der Intervallschritt sollte die minimal erforderliche Anzahl von Intervallen für die Verteilung der Restprobe bereitstellen.

Bedingung 4. Die Anzahl der Intervalle muss ungerade sein.

Bedingung 5. Die Anzahl der Intervalle muss eine zuverlässige Übereinstimmung mit dem für die Studie ausgewählten theoretischen Verteilungsgesetz gewährleisten.


Abb. 12. Der Rest der Verteilung

Definieren Sie den Intervallauswahlmechanismus in Abbildung 13.


Abb. 13. Der Intervallauswahlalgorithmus

Das Hauptproblem war meiner Meinung nach die Entscheidung, ob Schwanzintervalle eingeführt werden sollten oder nicht. Wenn es für die Restdispersion ganz natürlich aussah, dann ist es für die Hauptserie ziemlich angespannt.


Abb. 14. Die Ergebnisse der Verarbeitung von Datenwerten bei der Bestimmung der Informationsentropie

Schlussfolgerungen Wo kann dieses Tool angewendet werden?

Beim Vergleich der resultierenden Indikatoren der Tabelle in Abbildung 14 ist zu erkennen, dass sie auf die Änderung der Datenstruktur reagiert haben. Dies bedeutet, dass das Tool eine Empfindlichkeit aufweist und es Ihnen ermöglicht, Probleme zu lösen, die der Aufgabe des Enskomb-Quartetts ähneln.

Ohne Zweifel können diese Probleme mit Hilfe von Momenten höherer Ordnung gelöst werden. Im Kern hängt die Informationsentropie jedoch von der Varianz einer Zufallsvariablen ab, dh sie ist ein Varianzmerkmal eines Dritten. Wir können also die Intervalle angeben, in denen die Verwendung der Varianzanalyse zu einem bestimmten Ergebnis führen kann.

Die numerische Eigenschaft der Entropie ermöglicht die Durchführung einer Korrelationsanalyse mit unabhängigen Variablen. Als ein Beispiel für die Manifestation einer möglichen Verbindung gilt Folgendes: Angenommen, über den Zeitraum von a bis b stieg der Rauschpegel einer Reihe von Daten an, und beim Vergleich der Werte unabhängiger Variablen wurde festgestellt, dass die Variable xn danach in den Bereich von mehr als 5 Einheiten eintrat variabel, unter +5 gesunken, Rauschen verringert. Ferner kann eine zusätzliche Überprüfung durchgeführt werden, und wenn diese Hypothese bestätigt wird, verbieten Sie in weiteren Studien, dass die Variable xn über +5 steigt. Da in diesem Fall die Daten unbrauchbar werden.

Ich gehe davon aus, dass es andere Möglichkeiten gibt, dieses Tool zu verwenden.

Wie man es benutzt

In diesem Aspekt wird der natürliche Mechanismus des „gleitenden Durchschnitts“ untersucht. Ich nehme an, dass die Stichprobengröße, die durch die Stichprobengrößenformel aus der statistischen Analyse erhalten wird, ein angemessenes Volumen der Gleitfläche ergibt. Nach der aktuellen Analyse wurde der Schluss gezogen, dass die Stichprobengröße aus dem Mindestanteil bestimmt werden sollte, der auf die geringste Wahrscheinlichkeit fällt. In unserem Beispiel beträgt für die Restvarianz der minimale Bruchteil des empirischen Intervalls 0,15909. Dies muss getan werden, denn wenn sich herausstellt, dass ein Intervall im Schlupfvolumen leer ist, ist in diesem Fall die Rauschzahl empörend oder die Regel funktioniert, dass der Logarithmus von 0 gleich minus unendlich ist. Bei einer korrekt ausgewählten Stichprobengröße zeigen die transzendentalen Werte dieses Indikators eine grundlegende Änderung der Informationsstruktur an.