Stichproben- und Berechnungsgenauigkeit

Einige meiner Kollegen haben das Problem, dass Sie zur Berechnung einer Metrik, z. B. der Conversion-Rate, die gesamte Datenbank quadrieren müssen. Oder Sie müssen für jeden Kunden, bei dem es Millionen von Kunden gibt, eine detaillierte Studie durchführen. Diese Art von Kerry kann einige Zeit funktionieren, selbst in speziell angefertigten Repositories. Es macht keinen großen Spaß, 5-15-40 Minuten zu warten, bis eine einfache Metrik berücksichtigt wird, um herauszufinden, dass Sie etwas anderes berechnen oder etwas anderes hinzufügen müssen.

Eine Lösung für dieses Problem ist die Stichprobe: Wir versuchen nicht, unsere Metrik für das gesamte Datenarray zu berechnen, sondern nehmen eine Teilmenge, die die benötigten Metriken repräsentativ darstellt. Dieses Beispiel kann 1000-mal kleiner sein als unser Datenarray, aber es ist gut genug, um die benötigten Zahlen anzuzeigen.

In diesem Artikel habe ich beschlossen zu demonstrieren, wie sich Stichprobengrößen auf den endgültigen Metrikfehler auswirken.

Das Problem

Die Schlüsselfrage lautet: Wie gut beschreibt die Stichprobe die „Bevölkerung“? Da wir eine Stichprobe aus einem gemeinsamen Array entnehmen, stellen sich die Metriken, die wir erhalten, als Zufallsvariablen heraus. Unterschiedliche Stichproben führen zu unterschiedlichen metrischen Ergebnissen. Anders, bedeutet keine. Die Wahrscheinlichkeitstheorie besagt, dass die durch die Stichprobe erhaltenen Metrikwerte mit einer bestimmten Fehlerstufe um den wahren Metrikwert (über die gesamte Stichprobe hinweg) gruppiert werden sollten. Darüber hinaus haben wir häufig Probleme, bei denen auf eine andere Fehlerstufe verzichtet werden kann. Es ist eine Sache herauszufinden, ob wir eine Conversion von 50% oder 10% erhalten, und es ist eine andere Sache, ein Ergebnis mit einer Genauigkeit von 50,01% gegenüber 50,02% zu erhalten.

Es ist interessant, dass aus theoretischer Sicht der von uns über die gesamte Stichprobe beobachtete Umrechnungskoeffizient ebenfalls eine Zufallsvariable ist, weil Die „theoretische“ Umrechnungsrate kann nur für eine Stichprobe unendlicher Größe berechnet werden. Dies bedeutet, dass sogar alle unsere Beobachtungen in der Datenbank tatsächlich eine Umrechnungsschätzung mit ihrer Genauigkeit liefern, obwohl es uns scheint, dass diese berechneten Zahlen absolut genau sind. Dies führt auch zu dem Schluss, dass selbst wenn sich die Conversion-Rate heute von gestern unterscheidet, dies nicht bedeutet, dass sich etwas geändert hat, sondern nur, dass die aktuelle Stichprobe (alle Beobachtungen in der Datenbank) aus der allgemeinen Bevölkerung stammt (alle möglich) Beobachtungen für diesen Tag, die auftraten und nicht auftraten, ergaben ein etwas anderes Ergebnis als gestern. In jedem Fall sollte dies für ein ehrliches Produkt oder einen ehrlichen Analysten eine grundlegende Hypothese sein.

Aufgabenstellung

Angenommen, wir haben 1.000.000 Datensätze in einer Datenbank vom Typ 0/1, die uns mitteilen, ob bei einem Ereignis eine Konvertierung stattgefunden hat. Dann ist der Umrechnungskurs einfach die Summe von 1 geteilt durch 1 Million.

Frage: Wenn wir eine Stichprobe der Größe N nehmen, wie viel und mit welcher Wahrscheinlichkeit unterscheidet sich die Conversion-Rate von der über die gesamte Stichprobe berechneten?

Theoretische Überlegungen

Die Aufgabe reduziert sich auf die Berechnung des Konfidenzintervalls des Umrechnungskoeffizienten für eine Stichprobe einer bestimmten Größe für eine Binomialverteilung.

Aus der Theorie ist die Standardabweichung für die Binomialverteilung:
S = sqrt (p * (1 - p) / N)

Wo
p - Umrechnungskurs
N - Probengröße
S - Standardabweichung

Ich werde das direkte Konfidenzintervall aus der Theorie nicht berücksichtigen. Es gibt eine ziemlich komplexe und verwirrende Matan, die letztendlich die Standardabweichung und die endgültige Schätzung des Konfidenzintervalls in Beziehung setzt.

Lassen Sie uns eine "Intuition" über die Standardabweichungsformel entwickeln:

1. Je größer die Stichprobe ist, desto kleiner ist der Fehler. In diesem Fall fällt der Fehler in die inverse quadratische Abhängigkeit, d.h. Durch Erhöhen der Probe um das Vierfache wird die Genauigkeit nur um das Zweifache erhöht. Dies bedeutet, dass zu einem bestimmten Zeitpunkt eine Erhöhung der Probengröße keine besonderen Vorteile bringt und dass mit einer relativ kleinen Probe eine ziemlich hohe Genauigkeit erzielt werden kann.

1. Es besteht eine Abhängigkeit des Fehlers vom Wert der Umrechnungsrate. Der relative Fehler (dh das Verhältnis des Fehlers zum Wert der Umrechnungsrate) hat eine "abscheuliche" Tendenz, umso größer zu sein, je niedriger die Umrechnungsrate ist:

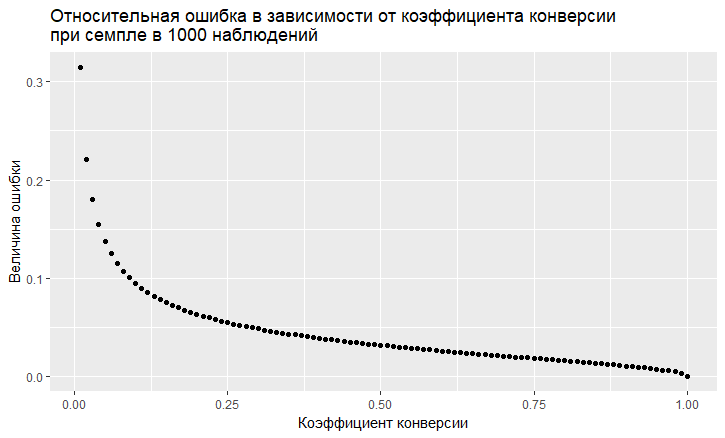
1. Wie wir sehen, "fliegt" der Fehler mit einer geringen Conversion-Rate in den Himmel. Dies bedeutet, dass Sie bei Stichproben seltener Ereignisse große Stichproben benötigen. Andernfalls erhalten Sie eine Conversion-Schätzung mit einem sehr großen Fehler.

Modellierung

Wir können uns vollständig von der theoretischen Lösung entfernen und das Problem "frontal" lösen. Dank der R-Sprache ist dies jetzt sehr einfach. Um die Frage zu beantworten, welchen Fehler wir beim Sampling bekommen, können Sie einfach tausend Samples machen und sehen, welchen Fehler wir bekommen.

Der Ansatz ist folgender:

1. Wir nehmen unterschiedliche Conversion-Raten an (von 0,01% bis 50%).
2. Wir nehmen 1000 Proben von 10, 100, 1000, 10000, 50.000, 100.000, 250.000, 500.000 Elementen in die Probe
3. Wir berechnen die Umrechnungsrate für jede Gruppe von Stichproben (1000 Koeffizienten)
4. Wir erstellen für jede Probengruppe ein Histogramm und bestimmen, inwieweit 60%, 80% und 90% der beobachteten Umwandlungsraten liegen.

Daten zur Erzeugung von R-Code:

sample.size <- c(10, 100, 1000, 10000, 50000, 100000, 250000, 500000) bootstrap = 1000 Error <- NULL len = 1000000 for (prob in c(0.0001, 0.001, 0.01, 0.1, 0.5)){ CRsub <- data.table(sample_size = 0, CR = 0) v1 = seq(1,len) v2 = rbinom(len, 1, prob) set = data.table(index = v1, conv = v2) print(paste('probability is: ', prob)) for (j in 1:length(sample.size)){ for(i in 1:bootstrap){ ss <- sample.size[j] subset <- set[round(runif(ss, min = 1, max = len),0),] CRsample <- sum(subset$conv)/dim(subset)[1] CRsub <- rbind(CRsub, data.table(sample_size = ss, CR = CRsample)) } print(paste('sample size is:', sample.size[j])) q <- quantile(CRsub[sample_size == ss, CR], probs = c(0.05,0.1, 0.2, 0.8, 0.9, 0.95)) Error <- rbind(Error, cbind(prob,ss,t(q))) } 

Als Ergebnis erhalten wir die folgende Tabelle (es werden später Diagramme angezeigt, aber die Details sind in der Tabelle besser sichtbar).

Lassen Sie uns die Fälle mit 10% Umsatz und mit einem niedrigen 0,01% Umsatz sehen, weil Alle Merkmale der Arbeit mit Stichproben sind auf ihnen deutlich sichtbar.

Bei 10% Conversion sieht das Bild ziemlich einfach aus:

Punkte sind die Kanten des 5-95% -Konfidenzintervalls, d.h. Bei der Erstellung einer Stichprobe erhalten wir in 90% der Fälle innerhalb dieses Intervalls CR für die Stichprobe. Vertikale Skala - Stichprobengröße (logarithmische Skala), horizontal - Wert der Conversion-Rate. Der vertikale Balken ist ein "wahrer" CR.

Wir sehen dasselbe, was wir aus dem theoretischen Modell gesehen haben: Die Genauigkeit nimmt mit zunehmender Größe der Stichprobe zu, und man konvergiert ziemlich schnell und die Stichprobe erhält ein Ergebnis nahe "wahr". Insgesamt haben wir für 1000 Proben 8,6% - 11,7%, was für eine Reihe von Aufgaben ausreicht. Und in 10 Tausend schon 9,5% - 10,55%.

Bei seltenen Ereignissen ist es schlimmer und dies steht im Einklang mit der Theorie:

Bei einer niedrigen Conversion-Rate von 0,01% liegt das Problem bei Statistiken zu 1 Million Beobachtungen, und bei Stichproben ist die Situation noch schlimmer. Der Fehler ist einfach gigantisch. Bei Stichproben bis zu 10.000 ist die Metrik grundsätzlich nicht gültig. Bei einer Stichprobe von 10 Beobachtungen hat mein Generator beispielsweise 1000-mal nur 0 Umrechnungen erhalten, sodass es nur 1 Punkt gibt. Bei 100.000 haben wir eine Streuung von 0,005% bis 0,0016%, d. H. Wir können mit einer solchen Abtastung fast die Hälfte des Koeffizienten machen.

Es ist auch erwähnenswert, dass Sie, wenn Sie eine Umwandlung eines so kleinen Maßstabs in 1 Million Versuche beobachten, einfach einen großen natürlichen Fehler haben. Daraus folgt, dass Rückschlüsse auf die Dynamik derart seltener Ereignisse an wirklich großen Stichproben gezogen werden müssen, andernfalls jagen Sie einfach nach Geistern, zufälligen Schwankungen in den Daten.

Schlussfolgerungen:

1. Stichprobe einer Arbeitsmethode, um Schätzungen zu erhalten
2. Die Probengenauigkeit nimmt mit zunehmender Probengröße zu und mit abnehmender Conversion-Rate ab.
3. Die Genauigkeit der Schätzungen kann für Ihre Aufgabe modelliert werden und Sie können die optimale Stichprobe für sich selbst auswählen.
4. Es ist wichtig, sich daran zu erinnern, dass seltene Ereignisse nicht gut ablaufen
5. Im Allgemeinen sind seltene Ereignisse schwer zu analysieren, da sie große Datenproben ohne Proben erfordern.