Hallo Habr.
In einer kürzlich hier auf der Website veröffentlichten Veröffentlichung wurde ein Gerät beschrieben, mit dem Blinde ein Bild „sehen“ und mithilfe von Schallwellen transformieren können. Aus technischer Sicht gab es in diesem Artikel keinerlei Details (
was wäre, wenn die Idee für eine Million gestohlen würde ), aber das Konzept selbst schien interessant zu sein. Nachdem ich einige Erfahrungen mit der Signalverarbeitung gesammelt hatte, beschloss ich, selbst zu experimentieren.
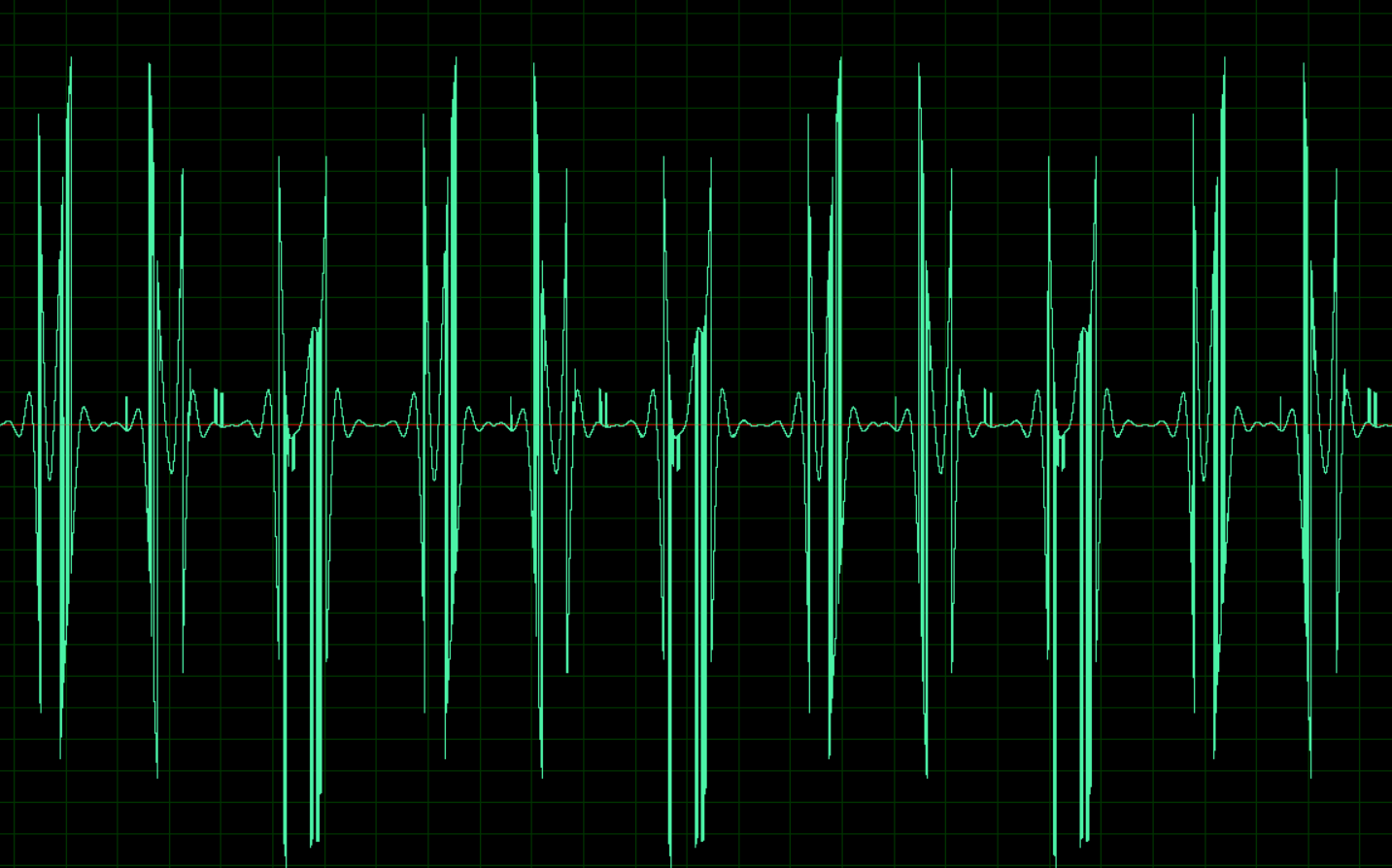
Was dabei herauskam, Details und Beispiele von Akten unter der Katze.
Konvertieren Sie 2D in 1D
Die erste offensichtliche Aufgabe, die uns erwartet, besteht darin, ein zweidimensionales „flaches“ Bild in eine „eindimensionale“ Schallwelle umzuwandeln. Wie in den Kommentaren zu diesem Artikel vorgeschlagen, ist es zweckmäßig, hierfür
die Hilbert-Kurve zu verwenden.

Es ähnelt im Wesentlichen einem Fraktal, und die Idee ist, dass sich mit zunehmender Bildauflösung die relative Position der Objekte nicht ändert (wenn sich das Objekt in der oberen linken Ecke des Bildes befindet,
bleibt es dort ). Unterschiedliche Abmessungen von Hilbert-Kurven können zu unterschiedlichen Bildern führen: 32 x 32 für N = 5, 64 x 64 für N = 6 usw. Wenn wir das Bild entlang dieser Kurve „herumlaufen“, erhalten wir eine Linie, ein eindimensionales Objekt.
Die nächste Frage ist die Größe des Bildes. Ich möchte intuitiv ein größeres Bild aufnehmen, aber es gibt ein großes „Aber“: Selbst das Bild ist 512 x 512, es ist 262144 Pixel. Wenn wir jeden Punkt in einen Tonimpuls umwandeln, erhalten wir bei einer Abtastfrequenz von 44100 eine Sequenz von bis zu 6 Sekunden, und dies ist zu lang - die Bilder müssen schnell aktualisiert werden, beispielsweise mit einer Webkamera. Es macht keinen Sinn, die Abtastrate zu erhöhen. Wir erhalten Ultraschallfrequenzen, die vom Ohr nicht gehört werden können (obwohl dies für eine Eule oder eine Fledermaus funktionieren könnte). Infolgedessen wurde eine Auflösung
von 128 x 128
nach der Methode des wissenschaftlichen Stocherns gewählt , die Impulse mit einer Länge von 0,37 c liefert. Zum einen ist es schnell genug, um in Echtzeit zu navigieren, zum anderen reicht es aus, Änderungen in der Form des Signals mit dem Ohr zu erfassen.
Bildverarbeitung
Der erste Schritt besteht darin, das Bild herunterzuladen, in Schwarzweiß umzuwandeln und auf die gewünschte Größe zu skalieren. Die Bildgröße hängt von der Abmessung der Hilbert-Kurve ab.
from PIL import Image from hilbertcurve.hilbertcurve import HilbertCurve import numpy as np from scipy.signal import butter, filtfilt
Der nächste Schritt ist die Bildung einer Schallwelle. Hier kann es natürlich sehr viele Algorithmen und Know-how geben, für den Test habe ich gerade die Helligkeitskomponente genommen. Natürlich gibt es wahrscheinlich bessere Möglichkeiten.
width, height = img_grayscale.size sound_data = np.zeros(width*height) for ii in range(width*height): coord_x, coord_y = hilbert_curve.coordinates_from_distance(ii) pixel_l = img_data[coord_x][coord_y]
Aus dem Code hoffe ich, dass alles klar ist. Die Funktion koordinates_from_distance erledigt die gesamte Arbeit für uns, um die Koordinaten (x, y) in einen Abstand auf einer Hilbert-Kurve umzuwandeln. Wir invertieren und konvertieren den Helligkeitswert L in Farbe.
Das ist noch nicht alles. Weil Das Bild enthält möglicherweise große Blöcke derselben Farbe. Dies kann zum Auftreten einer „Gleichstromkomponente“ im Ton führen - eine lange Reihe von Werten ungleich Null, z. B. [100, 100, 100, ...]. Um sie zu entfernen, wenden wir ein Hochpassfilter (
Butterworth-Filter ) auf unser Array mit einer Grenzfrequenz von 50 Hz an (die Übereinstimmung mit der Netzwerkfrequenz ist zufällig). In der Scipy-Bibliothek gibt es eine Synthese von Filtern, die wir verwenden werden.
def butter_highpass(cutoff, fs, order=5): nyq = 0.5 * fs normal_cutoff = cutoff / nyq b, a = butter(order, normal_cutoff, btype='high', analog=False) return b, a def butter_highpass_filter(data, cutoff, fs, order=5): b, a = butter_highpass(cutoff, fs, order) y = filtfilt(b, a, data) return y
Der letzte Schritt ist das Speichern des Bildes. Weil Die Länge eines Impulses ist kurz. Wir wiederholen ihn zehnmal. Er ist näher an einem sich wirklich wiederholenden Bild, beispielsweise von einer Webkamera, hörbarer.
Ergebnisse
Der obige Algorithmus ist natürlich ziemlich primitiv. Ich wollte drei Punkte überprüfen - wie viel Sie zwischen verschiedenen einfachen Formen unterscheiden können und wie viel Sie den Abstand zu den Formen schätzen können.
Test 1
Das Bild entspricht folgendem Tonsignal:
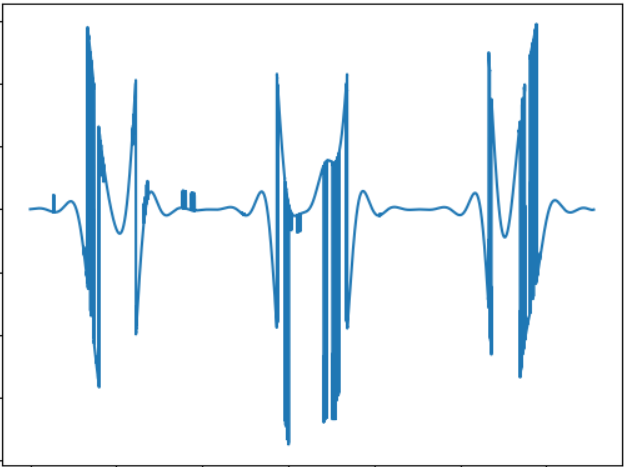
WAV:
cloud.mail.ru/public/nt2R/2kwBvyRupTest 2
Die Idee dieses Tests ist es, den „Klang“ eines Objekts einer anderen Form zu vergleichen. Tonsignal:
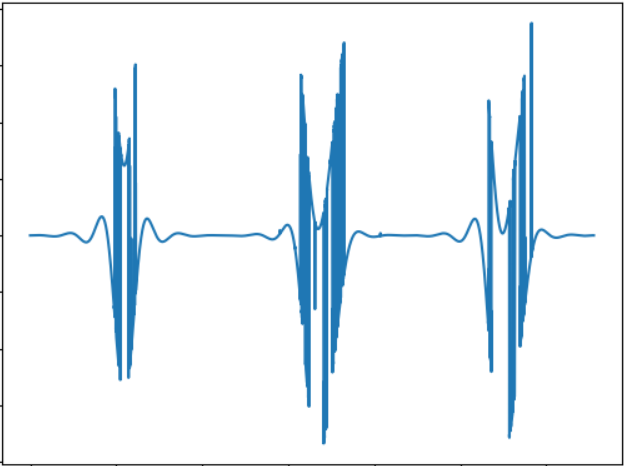
WAV:
cloud.mail.ru/public/2rLu/4fCNRxCG2Möglicherweise stellen Sie fest, dass der Klang wirklich anders ist und es einen Unterschied nach Gehör gibt.
Test 3
Die Idee des Tests ist es, ein kleineres Objekt zu testen. Tonsignal:
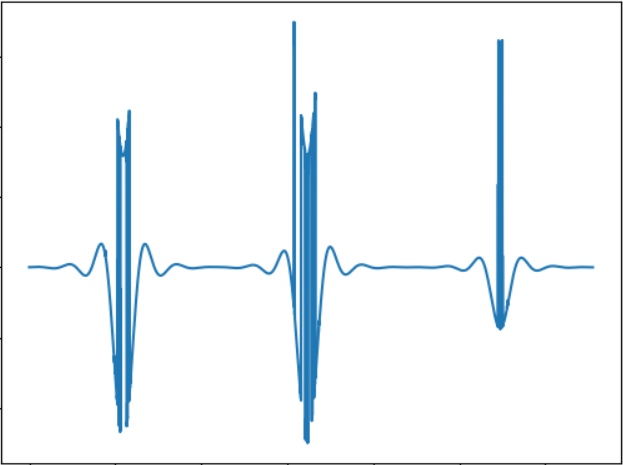
WAV:
cloud.mail.ru/public/5GLV/2HoCHvoaYGrundsätzlich gilt: Je kleiner das Objekt ist, desto weniger „Bursts“ treten im Klang auf, sodass die Abhängigkeit hier ziemlich direkt ist.
Bearbeiten:Wie in den Kommentaren vorgeschlagen, können Sie die Fourier-Transformation verwenden, um Bilder direkt in Ton umzuwandeln. Ein schneller Test zeigt die folgenden Ergebnisse (die Bilder sind die gleichen):
Test 1:
cloud.mail.ru/public/2C5Z/5MEQ8SwjoTest 2:
cloud.mail.ru/public/2dxp/3sz8mjAibTest 3:
cloud.mail.ru/public/3NjJ/ZYrfdTYrkTests klingen interessant, zumindest für kleine und große Quadrate (Dateien 1 und 3), der Unterschied im Hören ist spürbar. Die Form der Figuren (1 und 2) unterscheidet sich jedoch praktisch nicht, so dass es auch etwas zu überlegen gibt. Aber im Allgemeinen gefällt mir der mit FFT erhaltene Klang nach Gehör besser.
Fazit
Dieser Test ist natürlich keine Dissertation, sondern lediglich ein Proof of Concept, der in wenigen Stunden Freizeit erstellt wurde. Aber trotzdem funktioniert es im Grunde und es ist durchaus möglich, den Unterschied nach Gehör zu spüren. Ich weiß nicht, ob es möglich ist, durch solche Geräusche hypothetisch, wahrscheinlich nach etwas Training, das Navigieren im Raum zu lernen. Obwohl es ein großes Feld für Verbesserungen und Experimente gibt, können Sie beispielsweise Stereoton verwenden, mit dem Sie Objekte besser von verschiedenen Seiten trennen können. Sie können auch mit anderen Methoden experimentieren, um Bilder in Ton umzuwandeln, z. B. Farben mit unterschiedlichen Frequenzen codieren usw. Schließlich ist es vielversprechend die Verwendung von 3D-Kameras, die in der Lage sind, Tiefen wahrzunehmen (leider ist eine solche Kamera nicht verfügbar). Übrigens kann mit Hilfe eines einfachen OpenCV-Codes der obige Algorithmus für die Verwendung einer Webkamera angepasst werden, mit der Sie mit dynamischen Bildern experimentieren können.
Nun, wie immer alle erfolgreichen Experimente.