Grasshopper kryptografischer Algorithmus: fast der Komplex

In diesem Artikel wird der in GOST R 34.12-2015 als Grasshopper definierte Blockverschlüsselungsalgorithmus detailliert beschrieben. Worauf basiert es, was ist die Mathematik von blockkryptografischen Algorithmen und wie ist dieser Algorithmus in Java implementiert.

Wer, wie, wann und warum dieser Algorithmus entwickelt wurde, bleibt außerhalb des Geltungsbereichs des Artikels, da wir in diesem Fall von geringem Interesse sind, außer:

Heuschrecke = Kuznetsov, Nechaev AND Company.



Da die Kryptographie in erster Linie auf Mathematik basiert, sodass eine weitere Erklärung nicht viele Fragen aufwirft, sollten Sie zunächst die grundlegenden Konzepte und mathematischen Funktionen analysieren, auf denen dieser Algorithmus basiert.

Felder Galois

Die Arithmetik von Galois-Feldern ist eine Polynomarithmetik, dh jedes Element dieses Feldes ist ein Polynom. Das Ergebnis einer Operation ist ebenfalls ein Element dieses Feldes. Ein bestimmtes Galois-Feld besteht aus einem festen Zahlenbereich. Die Feldcharakteristik wird als Primzahl p bezeichnet. Feldreihenfolge, d.h. Die Menge seiner Elemente ist ein gewisser natürlicher Grad an Charakteristik $$$p ^ m$ , wobei m ϵ N ist. Für m = 1 heißt das Feld einfach. In Fällen, in denen m> 1 ist, ist für die Bildung eines Feldes auch ein erzeugendes Polynom vom Grad m erforderlich, ein solches Feld wird als erweitert bezeichnet. $$$Gf (p ^ m)$ - Bezeichnung des Galois-Feldes. Das erzeugende Polynom ist irreduzibel, das heißt einfach (analog zu Primzahlen ist es durch 1 und für sich ohne Rest teilbar). Da das Arbeiten mit Informationen mit Bytes arbeitet und ein Byte 8 Bit umfasst, nehmen Sie es als Feld $$$Gf (2 ^ 8)$ und das erzeugende Polynom:

$$

$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1.$$

Zunächst werden wir jedoch die grundlegenden Operationen in einem einfacheren Bereich analysieren $$$Gf (2 ^ 3)$ mit Polynom erzeugen $$$f (x) = x ^ 3 + x + 1$ .

Additionsoperation

Am einfachsten ist die Additionsoperation, die in der Galois-Feldarithmetik ein einfaches bitweises Additionsmodulo 2 (R) ist.

Ich mache sofort darauf aufmerksam, dass sich das "+" - Zeichen hier und im Folgenden auf die Operation von bitweisem XOR bezieht und nicht auf die Addition in der üblichen Form.

Die Wahrheitstabelle der HOR-Funktion



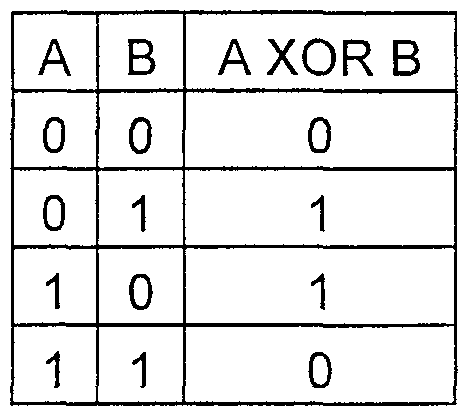
Ein Beispiel: $$$5 + 3 = 101 + 011 = 110_2 = 6_ {10}$

In Polynomform sieht diese Operation so aus

$$

$$(x ^ 2 + 1) + (x + 1) = x ^ 2 + x = 110_2 = 6_ {10}$$

Multiplikationsoperation

Um die Multiplikationsoperation auszuführen, müssen die Zahlen in Polynomform umgewandelt werden:

$$

$$5 = 101_2 = 1 * x ^ 2 + 0 * x ^ 1 + 1 * x ^ 0 = x ^ 2 + 1$$

Wie Sie sehen können, ist die Zahl in Polynomform ein Polynom, dessen Koeffizienten die Werte der Bits in der binären Darstellung der Zahl sind.

Multiplizieren Sie zwei Zahlen in Polynomform:

$$

$$5 * 7 = (x ^ 2 + 1) * (x ^ 2 + x + 1) = x ^ 4 + x ^ 3 + x ^ 2 + x ^ 2 + x + 1 =$$

$$

$$= x ^ 4 + x ^ 3 + x + 1 = 11011_2 = 27_ {10}$$

Das Multiplikationsergebnis 27 befindet sich nicht im verwendeten Feld. $$$Gf (2 ^ 3)$ (Es besteht aus Zahlen von 0 bis 7, wie oben erwähnt). Um dieses Problem zu bekämpfen, muss ein generierendes Polynom verwendet werden.

Es wird auch angenommen, dass x die Gleichung erfüllt $$$f (x) = x ^ 3 + x + 1 = 0$ dann



Lassen Sie uns eine Multiplikationstabelle erstellen:



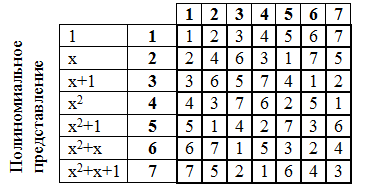
Von großer Bedeutung ist die Gradtabelle der Elemente des Galois-Feldes. Das Erhöhen auf eine Potenz erfolgt ebenfalls in Polynomform, ähnlich wie bei der Multiplikation.

Ein Beispiel:

$$

$$5 ^ 2 = (x ^ 2 + 1) ^ 2 = x ^ 4 + x ^ 2 + x ^ 2 + 1 = x ^ 4 + x ^ 2 + x + x ^ 2 + x + 1 =$$

$$

$$= x (x ^ 3 + x + 1) + x ^ 2 + x + 1 = x ^ 2 + x + 1 = 111_2 = 7_ {10}$$

So stellen wir eine Gradtabelle zusammen:



Die Grad-Tabelle ist zyklisch: Der siebte Grad entspricht Null, der achte entspricht dem ersten usw. Sie können dies überprüfen, wenn Sie möchten.

In Galois-Feldern gibt es das Konzept eines primitiven Begriffs - eines Elements eines Feldes, dessen Grad alle Nicht-Null-Elemente des Feldes enthält. Es ist ersichtlich, dass alle Elemente dieser Bedingung entsprechen (naja, außer natürlich 1). Dies ist jedoch nicht immer der Fall.

Wählen Sie für die Felder, die wir betrachten, dh mit Merkmal 2, immer 2. Als primitives Element kann aufgrund seiner Eigenschaft jedes Element des Feldes als Grad des primitiven Elements ausgedrückt werden.



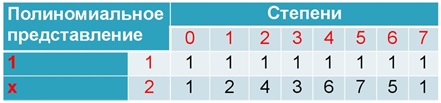
Ein Beispiel: $$$5 = 2 ^ 6,7 = 2 ^ 5$

Mit dieser Eigenschaft und unter Berücksichtigung der Zyklizität der Grad-Tabelle werden wir versuchen, die Zahlen erneut zu multiplizieren:

$$

$$5 * 7 = 2 ^ 6 * 2 ^ 5 = 2 ^ {(6 + 5)} = 2 ^ {(11mod7)} = 2 ^ 4 = 6$$

Das Ergebnis stimmte mit dem überein, was wir zuvor berechnet hatten.

Nun machen wir die Teilung:

$$

$$6/5 = 2 ^ 4/2 ^ 6 = 2 ^ {(4-6)} = 2 ^ {((- 2) mod7)} = 2 ^ 5 = 7$$

Das erhaltene Ergebnis ist auch wahr.

Schauen wir uns der Vollständigkeit halber an, wie wir uns zu einer Macht erheben:

$$

$$5 ^ 2 = (2 ^ 6) ^ 2 = 2 ^ {(6 * 2)} = 2 ^ {(12mod7)} = 2 ^ 5 = 7$$

Ein solcher Ansatz zur Multiplikation und Division ist viel einfacher als reale Operationen unter Verwendung von Polynomen, und für sie besteht keine Notwendigkeit, eine große Multiplikationstabelle zu speichern, sondern nur eine Gradreihe eines primitiven Feldelements.

Nun zurück zu unserem Feld $$$Gf (2 ^ 8)$

Das Nullelement des Feldes ist Eins, das 1. Element ist eine Zwei, jedes nachfolgende Element vom 2. bis zum 254. Element wird als das vorherige Element multipliziert mit 2 berechnet, und wenn sich das Element außerhalb des Feldes befindet, ist sein Wert größer als $$$(2 ^ 8-1)$ dann ist XOR mit der Nummer fertig $$$195_ {10}$ Diese Zahl repräsentiert das irreduzible Polynom des Feldes $$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1 = 2 ^ 8 + 2 ^ 7 ++ 2 ^ 6 + 2 + 1 = 451$ bringen wir diese Nummer ins Feld $$$451-256 = $ 19$ . Und das 255. Element ist wieder 1. Wir haben also ein Feld mit 256 Elementen, dh einen vollständigen Satz von Bytes, und wir haben die grundlegenden Operationen analysiert, die in diesem Feld ausgeführt werden.



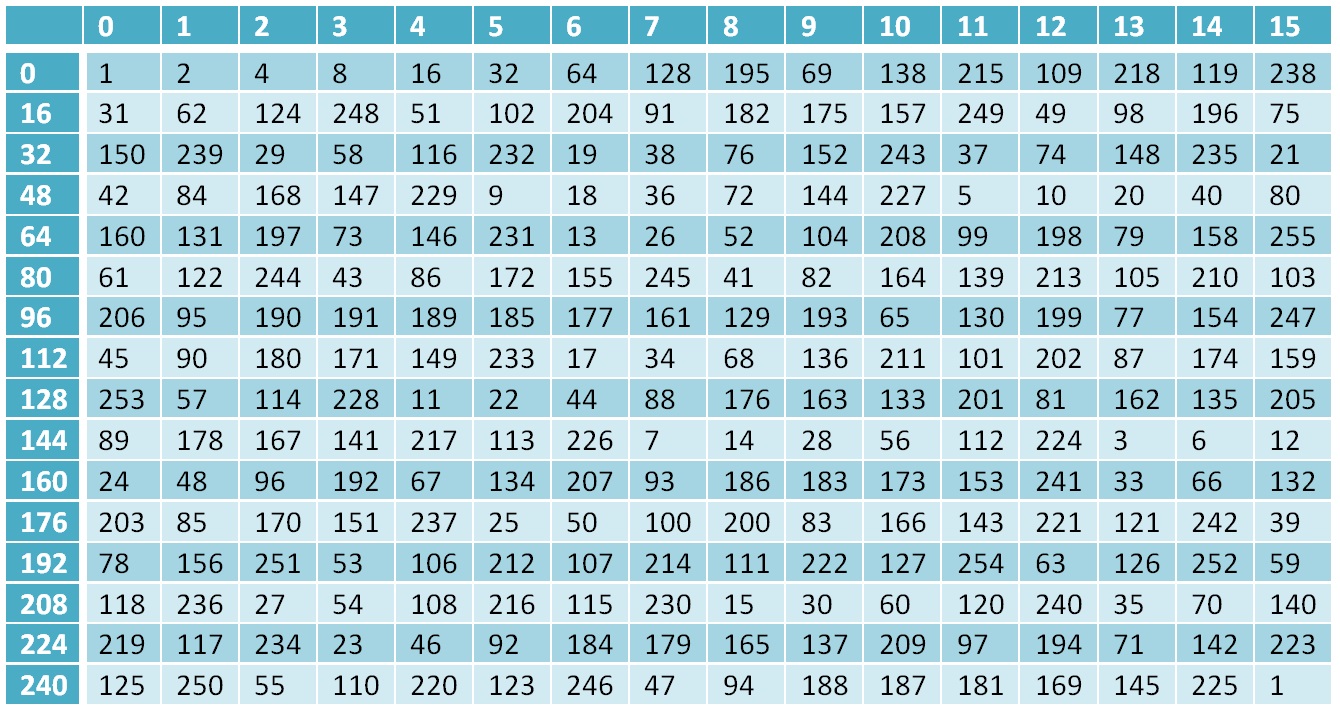
Tabelle der Zweierpotenzen für das Feld $$$Gf (2 ^ 8)$

Warum es benötigt wurde - Ein Teil der Berechnungen im Grasshopper-Algorithmus wird im Galois-Feld durchgeführt, und die Ergebnisse der Berechnungen sind Elemente dieses Feldes.

Feistel Network

Feistel Network ist eine Blockverschlüsselungsmethode, die 1971 von Horst Feistel bei IBM entwickelt wurde. Das Netzwerk von Feistel ist heute die Grundlage einer Vielzahl kryptografischer Protokolle.

Das Feistel-Netzwerk arbeitet mit Klartextblöcken:

1. Der Block ist in zwei gleiche Teile unterteilt - links L und rechts R.
2. Der linke Unterblock L wird durch die Funktion f mit der Taste K geändert: X = f (L, K). Als Funktion kann es jede Transformation geben.
3. Der resultierende Unterblock X wird Modulo 2 mit dem rechten Unterblock R hinzugefügt, der unverändert bleibt: X = X + R.
4. Die resultierenden Teile werden ausgetauscht und geklebt.

Diese Abfolge von Aktionen wird als Feistel-Zelle bezeichnet.


Abbildung 1. Feistelzelle

Das Feistel-Netzwerk besteht aus mehreren Zellen. Die am Ausgang der ersten Zelle erhaltenen Unterblöcke gehen zum Eingang der zweiten Zelle, die resultierenden Unterblöcke aus der zweiten Zelle gehen zum Eingang der dritten Zelle und so weiter.

Verschlüsselungsalgorithmus

Jetzt haben wir uns mit den verwendeten Operationen vertraut gemacht und können zum Hauptthema übergehen - dem Grasshopper-Kryptoalgorithmus.

Grundlage des Algorithmus ist das sogenannte SP-Netzwerk - Substitution-Permutation-Netzwerk. Die auf dem SP-Netzwerk basierende Verschlüsselung empfängt einen Block und einen Schlüssel am Eingang und führt mehrere abwechselnde Runden aus, die aus Substitutionsstufen und Permutationsstufen bestehen. Grasshopper führt neun vollständige Runden durch, von denen jede drei aufeinanderfolgende Operationen umfasst:

1. Die Operation zum Anwenden eines runden Schlüssels oder eines bitweisen XOR eines Schlüssels und eines Eingabedatenblocks;
2. Nichtlineare Konvertierung, bei der ein Byte gemäß der Tabelle einfach durch ein anderes ersetzt wird;
3. Lineare Transformation. Jedes Byte aus dem Block wird im Galois-Feld mit einem der Koeffizienten der Reihe (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1) in Abhängigkeit von der Ordnungszahl multipliziert Bytenummern (eine Reihe wird für Seriennummern vom 15. bis zum 0. dargestellt, wie in der Abbildung gezeigt). Bytes werden zu Modulo 2 addiert, und alle 16 Bytes des Blocks werden in Richtung der niedrigen Ordnung verschoben, und die resultierende Zahl wird anstelle des gelesenen Bytes geschrieben.

Die letzte zehnte Runde ist nicht abgeschlossen, sondern enthält nur die erste XOR-Operation.

Grasshopper ist ein Blockalgorithmus, der mit Datenblöcken von 128 Bit oder 16 Byte Länge arbeitet. Die Schlüssellänge beträgt 256 Bit (32 Byte).


Abbildung 2. Das Ver- und Entschlüsselungsschema des Datenblocks

Das Diagramm zeigt die Abfolge von Operationen, wobei S eine nichtlineare Transformation ist, L eine lineare Transformation ist, Ki runde Schlüssel sind. Es stellt sich sofort die Frage, woher die runden Schlüssel kommen.

Runde Schlüsselbildung

Iterative (oder runde) Schlüssel werden durch bestimmte Transformationen erhalten, die auf einem Hauptschlüssel basieren, dessen Länge, wie wir bereits wissen, 256 Bit beträgt. Dieser Vorgang beginnt mit der Aufteilung des Hauptschlüssels in zwei Hälften, sodass das erste Paar runder Schlüssel erhalten wird. Acht Iterationen des Feistel-Netzwerks werden verwendet, um jedes nachfolgende Paar von runden Schlüsseln zu erzeugen. In jeder Iteration wird eine Konstante verwendet, die durch Anwenden einer linearen Transformation des Algorithmus auf den Wert der Iterationszahl berechnet wird.


Das Schema zum Erhalten iterativer (runder) Schlüssel

Wenn wir uns an 1 erinnern, dann ist der linke Unterblock L die linke Hälfte des ursprünglichen Schlüssels, der rechte Unterblock R ist die rechte Hälfte des ursprünglichen Schlüssels, K ist die Konstante Ci, die Funktion f ist die Folge von Operationen R XOR Ci, nichtlineare Transformation, lineare Transformation.

Die Iterationskonstanten Ci werden unter Verwendung der L-Transformation der Iterationssequenznummer erhalten.

Um einen Textblock zu verschlüsseln, müssen wir zuerst 32 iterative Konstanten berechnen, dann 10 runde Schlüssel basierend auf dem Schlüssel berechnen und dann die in Abbildung 2 gezeigte Abfolge von Operationen ausführen.

Beginnen wir mit der Berechnung der Konstanten:
Erste const $$$C_1 = 1_ {10} = 00000001_2 = 01_ {16}$ Alle Transformationen in unserem Algorithmus werden jedoch mit Blöcken von 16 Bytes Länge ausgeführt. Daher ist es notwendig, die Konstante durch die Länge des Blocks zu ergänzen, dh 15 Null-Bytes nach rechts zu addieren

$$

$$C_1 = 01000000000000000000000000000000$$

Multiplizieren Sie es mit einer Reihe (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) wie folgt:

$$

$$a_ {15} = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 +$$

$$

$$+ a_5 * 194 + a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

(Diese Gleichheit ist in den Operationen der Galois-Felder gegeben)
Da alles außer dem Null-Byte gleich 0 ist und das Null-Byte mit 1 multipliziert wird, erhalten wir 1 und schreiben es in die hohe Ordnung der Zahl, wobei wir alle Bytes in die niedrige Ordnung verschieben, erhalten wir:

$$

$$C_1 = 00000000000000000000000000000001$$

Wiederholen Sie die gleichen Vorgänge. Diesmal $$$a_ {15} = 1$ sind alle anderen Bytes 0, daher bleibt nur das erste von den Begriffen übrig $$$a_ {15} * 148 = 1 * 148 = 148_ {10} = 94_ {16}$ wir bekommen:

$$

$$C_1 = 00000000000000000000000000000194$$

Wir machen die dritte Iteration, hier sind zwei Begriffe ungleich Null:

$$

$$a_ {15} * 148 + a_ {14} * 32 = 148 * 148 + 1 * 32 =$$

$$

$$= 10010100 * 10010100 + 00000001 * 00100000 =$$

$$

$$= (x ^ 7 + x ^ 4 + x ^ 2) * (x ^ 7 + x ^ 4 + x ^ 2) + 1 * x ^ 5 = x ^ {14} + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 6 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {13} + x ^ {12} + x ^ 7 + x ^ 6 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 5 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {11} + x ^ 5 + x ^ 7 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 3 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {10} + x ^ 9 + x ^ 3 + x ^ 8 + x ^ 7 =$$

$$

$$= x ^ 2 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ 2 + x ^ 7 = x ^ 7 + x ^ 2 = 132_ {10}$$

$$

$$132_ {10} = 84_ {16}$$

Laut der Tabelle der Abschlüsse könnte es viel einfacher gelöst werden:

$$

$$148 * 148 + 1 * 32 = 2 ^ {45} * 2 ^ {45} + 2 ^ 5 = 2 ^ {90} + 2 ^ 5 = 164 + 32 = 132$$

$$

$$C_1 = 00000000000000000000000000019484$$

Außerdem ist alles genau gleich, nur 16 Iterationen für jede Konstante

$$

$$C_1 = 000000000000000000000000019484DD$$

$$

$$C_1 = 0000000000000000000000019484DD10$$

$$

$$C_1 = 00000000000000000000019484DD10BD$$

$$

$$C_1 = 000000000000000000019484DD10BD27$$

$$

$$C_1 = 0000000000000000019484DD10BD275D$$

$$

$$C_1 = 00000000000000019484DD10BD275DB8$$

$$

$$C_1 = 000000000000019484DD10BD275DB87A$$

$$

$$C_1 = 0000000000019484DD10BD275DB87A48$$

$$

$$C_1 = 00000000019484DD10BD275DB87A486C$$

$$

$$C_1 = 000000019484DD10BD275DB87A486C72$$

$$

$$C_1 = 0000019484DD10BD275DB87A486C727$$

$$

$$C_1 = 00019484DD10BD275DB87A486C7276A2$$

Und die letzte Konstante:

$$

$$C_1 = 019484DD10BD275DB87A486C7276A2E6$$

Andere Konstanten:

$$

$$C_2 = 02EBCB7920B94EBAB3F490D8E4EC87DC$$

$$

$$C_3 = 037F4FA4300469E70B8ED8B4969A25B2$$

$$

$$C_4 = 041555F240B19CB7A52BE3730B1BCD7B$$

$$

$$C_5 = 0581D12F500CBBEA1D51AB1F796D6F15$$

$$

$$C_6 = 06FE9E8B6008D20D16DF73ABEFF74AA7$$

$$

$$C_7 = 076A1A5670B5F550AEA53BC79D81E8C9$$

$$

$$C_8 = 082AAA2780A1FBAD895605E6163659F6$$

$$

$$C_9 = 09BE2EFA901CDCF0312C4D8A6440FB98$$

$$

$$C_ {10} = 0AC1615EA018B5173AA2953EF2DADE2A$$

$$

$$C_ {11} = 0B55E583B0A5924A82D8DD5280AC7C44$$

$$

$$C_ {12} = 0C3FFFD5C010671A2C7DE6951D2D948D$$

$$

$$C_ {13} = 0DAB7B08D0AD40479407AEF96F5B36E3$$

$$

$$C_ {14} = 0ED434ACE0A929A09F89764DF9C11351$$

$$

$$C_ {15} = 0F40B071F0140EFD27F33E218BB7B13F$$

$$

$$C_ {16} = 1054974EC3813599D1AC0A0F2C6CB22F$$

$$

$$C_ {17} = 11C01393D33C12C469D642635E1A1041$$

$$

$$C_ {18} = 12BF5C37E3387B2362589AD7C88035F3$$

$$

$$C_ {19} = 132BD8EAF3855C7EDA22D2BBBAF6979D$$

$$

$$C_ {20} = 1441C2BC8330A92E7487E97C27777F54$$

$$

$$C_ {21} = 15D54661938D8E73CCFDA1105501DD3A$$

$$

$$C_ {22} = 16AA09C5A389E794C77379A4C39BF888$$

$$

$$C_ {23} = 173E8D18B334C0C97F0931C8B1ED5AE6$$

$$

$$C_ {24} = 187E3D694320CE3458FA0FE93A5AEBD9$$

$$

$$C_ {25} = 19EAB9B4539DE969E0804785482C49B7$$

$$

$$C_ {26} = 1A95F6106399808EEB0E9F31DEB66C05$$

$$

$$C_ {27} = 1B0172CD7324A7D35374D75DACC0CE6B$$

$$

$$C_ {28} = 1C6B689B03915283FDD1EC9A314126A2$$

$$

$$C_ {29} = 1DFFEC46132C75DE45ABA4F6433784CC$$

$$

$$C_ {30} = 1E80A3E223281C394E257C42D5ADA17E$$

$$

$$C_ {31} = 1F14273F33953B64F65F342EA7DB0310$$

$$

$$C_ {32} = 20A8ED9C45C16AF1619B141E58D8A75E$$

Jetzt berechnen wir die runden Schlüssel gemäß dem oben dargestellten Schema. Nehmen Sie den Verschlüsselungsschlüssel:

$$

$$K = 7766554433221100FFEEDDCCBBAA9988$$

$$

$$EFCDAB89674523011032547698BADCFE$$

Dann

$$

$$K_1 = 7766554433221100FFEEDDCCBBAA9988$$

$$

$$K_2 = EFCDAB89674523011032547698BADCFE$$

$$$K_1$ wird der linke Unterblock des Feistel-Netzwerks sein, und $$$K_2$ - Richtig.
Lassen Sie uns die Operation durchführen $$$K_1 + C_1$
Erstes Byte $$$K_1$ ist gleich $$$77_ {16} = 01110111_2$
Erstes Byte $$$C_1$ ist gleich $$$01_ {16} = 00000001_2$

$$

$$01110111_2 + 00000001_2 = 01110110_2 = 76_ {16}$$

Die verbleibenden Bytes werden daher auf die gleiche Weise konvertiert $$$X (K_1, C_1) = K_1 + C_1$ ::

$$

$$X (K_1, C_1) = 76F2D199239F365D479495A0C9DC3BE6$$

Als nächstes führen wir eine nichtlineare Transformation durch $$$S (X (K_1, C_1))$ . Es wird gemäß der Tabelle durchgeführt:


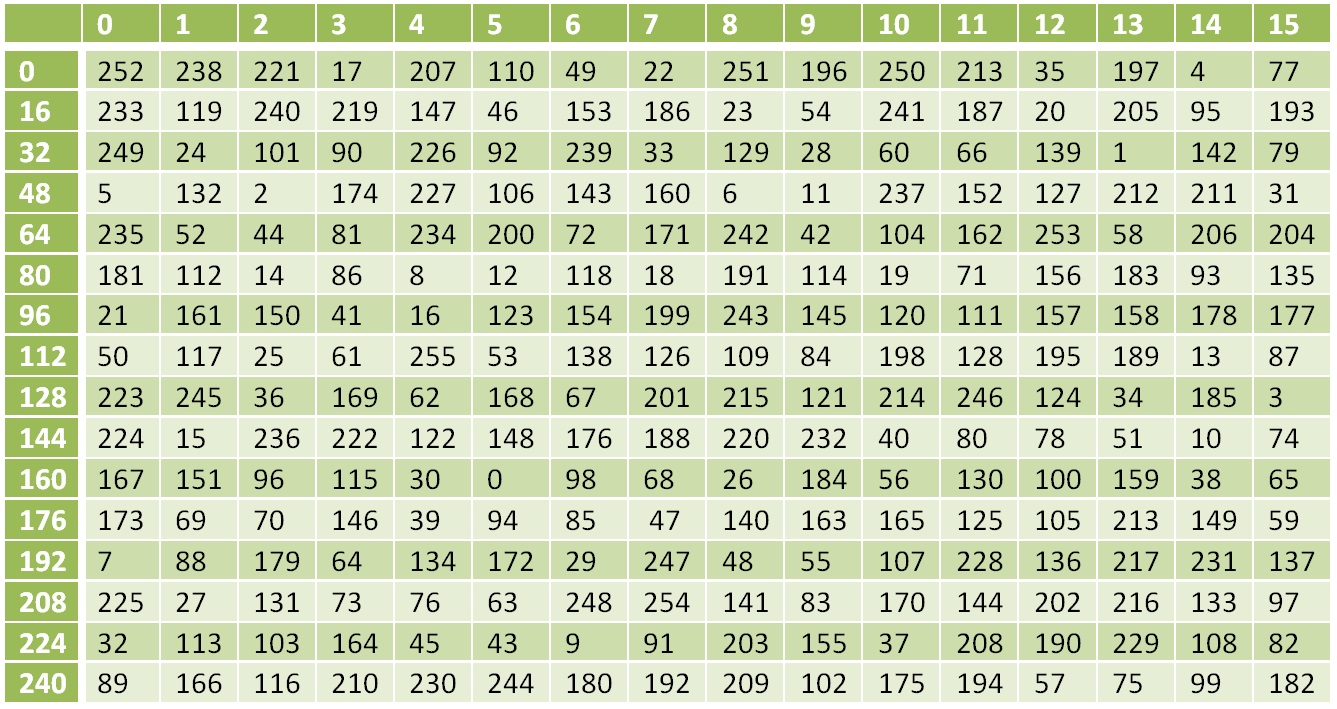Nichtlineare Umrechnungstabelle

Die Zahl 0 wird durch 252, 1 durch 238, 17 durch 119 usw. ersetzt.

$$

$$76_ {16} = 118_ {10}$$

$$

$$S (118) = 138_ {10} = 8A_ {16}$$

$$

$$S (X (K_1, C_1)) = 8A741BE85A4A8FB7AB7A94A737CA9809$$

Führen Sie nun eine lineare Transformation durch $$$L (S (X (K_1, C_1)))$ wurde es bei der Berechnung iterativer Konstanten im Detail berücksichtigt, daher geben wir hier nur das Endergebnis an:

$$

$$L (S (X (K_1, C_1))) = A644615E1D0757926A5DB79D9940093D$$

Gemäß dem Schema der Feistel-Zelle führen wir XOR mit dem rechten Unterblock durch, d. H. Mit $$$K_2$ ::

$$

$$X (L (S (X (K_1, C_1))), K_2) = 4989CAD77A4274937A6FE3EB01FAD5C3$$

Und das Ergebnis am Ausgang der ersten Feistel-Zelle:

$$

$$EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3$$

Dieser Wert wird halbiert und geht zum Eingang der zweiten Feistel-Zelle, wo die zweite Konstante bereits verwendet wird $$$C_2$ . Nachdem wir acht Zellen durchlaufen haben, erhalten wir die folgenden 2 Schlüssel $$$K_3$ und $$$K_4$ . Wir werden acht Iterationen des Feistel-Netzwerks mit ihnen durchführen, das nächste Schlüsselpaar erhalten und so weiter. Acht Iterationen pro Schlüsselpaar, da wir zunächst das erste Paar haben, werden insgesamt 32 Iterationen durchgeführt, jede mit ihrer eigenen Konstante.

Verbleibende Schlüssel:

$$

$$K_3 = 448CC78CEF6A8D2243436915534831DB$$

$$

$$K_4 = 04FD9F0AC4ADEB1568ECCFE9D853453D$$

$$

$$K_5 = ACF129F44692E5D3285E4AC468646457$$

$$

$$K_6 = 1B58DA3428E832B532645C16359407BD$$

$$

$$K_7 = B198005A26275770DE45877E7540E651$$

$$

$$K_8 = 84F98622A2912AD73EDD9F7B0125795A$$

$$

$$K_9 = 17E5B6CD732FF3A52331C77853E244BB$$

$$

$$K_ {10} = 43404A8EA8BA5D755BF4BC1674DDE972$$

Blockverschlüsselung

Wir haben alle Schlüssel berechnet und können nun endlich direkt zur Verschlüsselung des Textblocks übergehen. Wenn Sie alles, was oben geschrieben wurde, sorgfältig lesen, ist die Verschlüsselung des Textes nicht schwierig, da alle in diesem Prozess verwendeten Vorgänge und ihre Reihenfolge im Detail untersucht wurden.

Nehmen Sie den Klartextblock:

$$

$$T = 8899AABBCCDDEEFF0077665544332211$$

Führen Sie die Abfolge der Operationen X, S, L aus

$$

$$X (T, K_1) = FFFFFFFFFFFFFFFFFFFF99BB99FF99BB99$$

$$

$$S (X (T, K_1)) = B6B6B6B6B6B6B6B6B6E87DE8B6E87DE8$$

$$

$$L (S (X (T, K_1))) = 30081449922F4ACFA1B055E386B697E2$$

$$

$$T_1 = 30081449922F4ACFA1B055E386B697E2$$

$$

$$X (T_1, K_2) = DFC5BFC0F56A69CEB18201951E0C4B1C$$

$$

$$S (X (T_1, K_2)) = 61AC3B07F47891E74524EE945F23A214$$

$$

$$L (S (X (T_1, K_2))) = 7290C6A158426FB396D562087A495E28$$

$$

$$T_2 = 7290C6A158426FB396D562087A495E28$$

und so weiter, das Endergebnis sieht folgendermaßen aus:

$$

$$T_ {10} = CDEDD4B9428D465A3024BCBE909D677F$$

Blockentschlüsselung

Um den Text zu entschlüsseln, müssen Sie die inversen Operationen in umgekehrter Reihenfolge verwenden (siehe Abb. 2).

Die XOR-Operation ist zu sich selbst invers, die Umkehrung zur Operation S ist die Substitution gemäß der folgenden Tabelle:


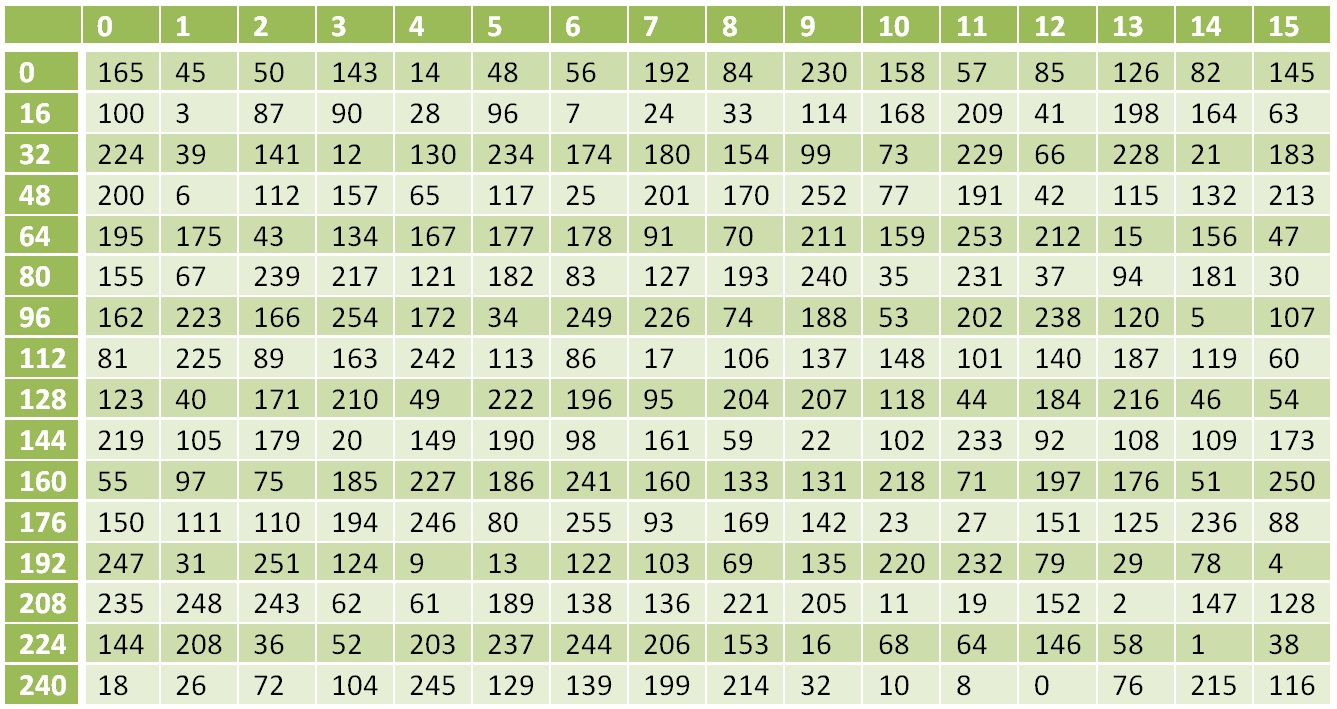Inverse nichtlineare Transformationstabelle

Die inverse Transformation zur Funktion L ist:

$$

$$a_0 = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 + a_5 * 194 +$$

$$

$$+ a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

und eine Verschiebung in Richtung der höheren Ebene. (Vorgang 16 Mal wiederholen)

Java-Implementierung

Zunächst definieren wir die notwendigen Konstanten

static final int BLOCK_SIZE = 16; //   //     static final byte[] Pi = { (byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16, (byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D, (byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA, 0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1, (byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21, (byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F, 0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0, 0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F, (byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB, (byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC, (byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, (byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87, 0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7, (byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1, 0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E, 0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57, (byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9, (byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03, (byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC, (byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A, (byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41, (byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F, (byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B, 0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7, 0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89, (byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE, (byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61, 0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B, (byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52, 0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0, (byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6 }; //     static final byte[] reverse_Pi = { (byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0, 0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91, 0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F, (byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4, (byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7, (byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9, (byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5, (byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B, 0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F, (byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F, (byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E, (byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2, 0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B, 0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11, 0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C, 0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F, (byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36, (byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1, 0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD, 0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0, (byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA, (byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D, (byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58, (byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04, (byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88, (byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80, (byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE, (byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26, 0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7, (byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74 }; //    static final byte[] l_vec = { 1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1, (byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148 }; //     static byte[][] iter_C = new byte[32][16]; //     static byte[][] iter_key = new byte[10][64]; 

Lassen Sie uns alle Hauptfunktionen erstellen:

 //  X static private byte[] GOST_Kuz_X(byte[] a, byte[] b) { int i; byte[] c = new byte[BLOCK_SIZE]; for (i = 0; i < BLOCK_SIZE; i++) c[i] = (byte) (a[i] ^ b[i]); return c; } //  S static private byte[] GOST_Kuz_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = Pi[data]; } return out_data; } 

Um die Funktion L zu implementieren, benötigen wir mehrere Hilfsfunktionen, eine zur Berechnung der Multiplikation von Zahlen im Galois-Feld und eine für die Verschiebung.

 //     static private byte GOST_Kuz_GF_mul(byte a, byte b) { byte c = 0; byte hi_bit; int i; for (i = 0; i < 8; i++) { if ((b & 1) == 1) c ^= a; hi_bit = (byte) (a & 0x80); a <<= 1; if (hi_bit < 0) a ^= 0xc3; // x^8+x^7+x^6+x+1 b >>= 1; } return c; } //  R     ,    L- static private byte[] GOST_Kuz_R(byte[] state) { int i; byte a_15 = 0; byte[] internal = new byte[16]; for (i = 15; i >= 0; i--) { if(i == 0) internal[15] = state[i]; else internal[i - 1] = state[i]; a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]); } internal[15] = a_15; return internal; } static private byte[] GOST_Kuz_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal = in_data; for (i = 0; i < 16; i++) { internal = GOST_Kuz_R(internal); } out_data = internal; return out_data; } 

Inverse Funktionen:

 //  S^(-1) static private byte[] GOST_Kuz_reverse_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = reverse_Pi[data]; } return out_data; } static private byte[] GOST_Kuz_reverse_R(byte[] state) { int i; byte a_0; a_0 = state[15]; byte[] internal = new byte[16]; for (i = 1; i < 16; i++) { internal[i] = state[i - 1]; a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]); } internal[0] = a_0; return internal; } static private byte[] GOST_Kuz_reverse_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal; internal = in_data; for (i = 0; i < 16; i++) internal = GOST_Kuz_reverse_R(internal); out_data = internal; return out_data; } //    static private void GOST_Kuz_Get_C() { int i; byte[][] iter_num = new byte[32][16]; for (i = 0; i < 32; i++) { for(int j = 0; j < BLOCK_SIZE; j++) iter_num[i][j] = 0; iter_num[i][0] = (byte) (i+1); } for (i = 0; i < 32; i++) { iter_C[i] = GOST_Kuz_L(iter_num[i]); } } // ,     static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const) { byte[] internal; byte[] out_key_2 = in_key_1; internal = GOST_Kuz_X(in_key_1, iter_const); internal = GOST_Kuz_S(internal); internal = GOST_Kuz_L(internal); byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2); byte key[][] = new byte[2][]; key[0] = out_key_1; key[1] = out_key_2; return key; } //     public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2) { int i; byte[][] iter12 = new byte[2][]; byte[][] iter34 = new byte[2][]; GOST_Kuz_Get_C(); iter_key[0] = key_1; iter_key[1] = key_2; iter12[0] = key_1; iter12[1] = key_2; for (i = 0; i < 4; i++) { iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]); iter_key[2 * i + 2] = iter12[0]; iter_key[2 * i + 3] = iter12[1]; } } //    public byte[] GOST_Kuz_Encript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; for(i = 0; i < 9; i++) { out_blk = GOST_Kuz_X(iter_key[i], out_blk); out_blk = GOST_Kuz_S(out_blk); out_blk = GOST_Kuz_L(out_blk); } out_blk = GOST_Kuz_X(out_blk, iter_key[9]); return out_blk; } //   public byte[] GOST_Kuz_Decript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; out_blk = GOST_Kuz_X(out_blk, iter_key[9]); for(i = 8; i >= 0; i--) { out_blk = GOST_Kuz_reverse_L(out_blk); out_blk = GOST_Kuz_reverse_S(out_blk); out_blk = GOST_Kuz_X(iter_key[i], out_blk); } return out_blk; } 

Nun, und die Hauptfunktion

 static byte[] key_1 = {0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee, (byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88}; static byte[] key_2 = {(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01, 0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe}; static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211"); public static void main(String[] args) { GOST_Kuz_Expand_Key(key_1, key_2); byte[] encriptBlok = GOST_Kuz_Encript(blk); System.out.println(DatatypeConverter.printHexBinary(encriptBlok)); byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok); System.out.println(DatatypeConverter.printHexBinary(decriptBlok)); } 

Wir haben gelernt, einen Datenblock zu verschlüsseln, um Text zu verschlüsseln, dessen Länge länger als die Länge des Blocks ist. Im Standard sind mehrere Modi beschrieben - GOST 34.13-2015:

• einfacher Austauschmodus (elektronisches Codebuch, EZB);
• Gammamodus (Zähler, CTR);
• Gammamodus mit Ausgangsrückkopplung (Ausgangsrückkopplung, OFB);
• einfacher Ersatzgetriebemodus (Cipher Block Chaining, CBC);
• Gammamodus mit Rückmeldung im Chiffretext (Cipher Feedback, CFB);
• MAC-Modus (Message Authentication Code).

In allen Modi sollte die Textlänge immer ein Vielfaches der Länge des Blocks sein, sodass der Text immer rechts mit einem einzelnen Bit und Nullen zur Länge des Blocks aufgefüllt wird.

Der einfachste Modus ist der einfache Ersatzmodus. In diesem Modus wird der Text in Blöcke unterteilt, dann wird jeder Block separat vom Rest verschlüsselt, dann werden die Blöcke des Chiffretextes zusammengeklebt und wir erhalten eine verschlüsselte Nachricht. Dieser Modus ist sowohl der einfachste als auch der anfälligste und wird in der Praxis fast nie angewendet.

Andere Modi können später im Detail betrachtet werden.