B-Baum-Datenstruktur

Hallo allerseits! Wir haben ein neues Set für den Kurs "Algorithmen für Entwickler" gestartet und möchten heute eine interessante Übersetzung für Studenten dieses Kurses veröffentlichen.



In Suchbäumen wie binärem Suchbaum, AVL-Baum, rot-schwarzem Baum usw. Jeder Knoten enthält nur einen Wert (Schlüssel) und maximal zwei Nachkommen. Es gibt jedoch eine spezielle Art von Suchbaum, den B-Baum (ausgesprochen Bi-Baum). Darin enthält der Knoten mehr als einen Wert (Schlüssel) und mehr als zwei Nachkommen. Der B-Baum wurde 1972 von Bayer und McCrate entwickelt und als höhenausgeglichener M-Way -Suchbaum bezeichnet. Sein moderner Name B-Baum erhielt später.

Ein B-Baum kann wie folgt definiert werden:
Ein B-Baum ist ein ausgeglichener Suchbaum, in dem jeder Knoten viele Schlüssel enthält und mehr als zwei untergeordnete Knoten hat.

Hier hängt die Anzahl der Schlüssel im Knoten und die Anzahl seiner Nachkommen von der Reihenfolge des B-Baums ab. Jeder B-Baum hat eine Reihenfolge.

Ein B-Baum der Ordnung m hat folgende Eigenschaften:

Eigenschaft 1: Die Tiefe aller Blätter ist gleich.
Eigenschaft 2: Alle Knoten außer der Wurzel müssen mindestens (m / 2) - 1 Schlüssel und maximal m - 1 Schlüssel haben.
Eigenschaft 3: Alle Knoten ohne Blätter mit Ausnahme der Wurzel (d. H. Alle internen Knoten) müssen mindestens m / 2 Nachkommen haben.
Eigenschaft 4: Wenn die Wurzel ein blattloser Knoten ist, muss sie mindestens 2 Nachkommen haben.
Eigenschaft 5: Ein Knoten ohne Blätter mit n-1 Schlüsseln muss n Kinder haben.
Eigenschaft 6: Alle Schlüssel im Knoten sollten in aufsteigender Reihenfolge ihrer Werte angeordnet sein.

Beispielsweise enthält ein B-Baum 4-Ordnung maximal 3 Schlüsselwerte und maximal 4 Kinder für jeden Knoten.


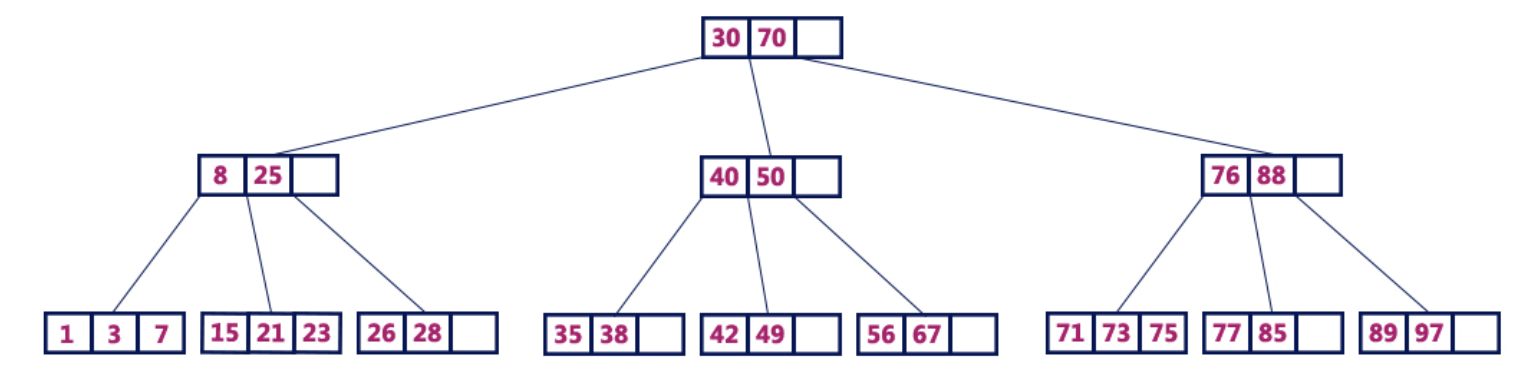B-Baum 4 Bestellungen

B-Baum-Operationen

Die folgenden Operationen können am B-Baum ausgeführt werden:

1. Suche
2. Einfügen
3. Löschen

Suche B-Baum

B-Baum-Suchen ähneln Binärbaum-Suchen. Im binären Suchbaum beginnt die Suche an der Wurzel und jedes Mal, wenn eine Zwei-Wege-Entscheidung getroffen wird (entlang des linken Teilbaums oder rechts). Im B-Baum beginnt die Suche ebenfalls am Wurzelknoten, aber bei jedem Schritt wird eine n-seitige Entscheidung getroffen, wobei n die Gesamtzahl der Nachkommen des betreffenden Knotens ist. Im B-Baum ist die Suchkomplexität O (log n) . Die Suche ist wie folgt:

Schritt 1: Lesen Sie den zu suchenden Artikel.
Schritt 2: Vergleichen Sie das gesuchte Element mit dem ersten Schlüsselwert im Stammknoten des Baums.
Schritt 3: Wenn sie übereinstimmen, drucken Sie: "Der gefundene Knoten!" und schließen Sie die Suche ab.
Schritt 4: Wenn sie nicht übereinstimmen, überprüfen Sie, ob der Artikelwert mehr oder weniger als der aktuelle Schlüsselwert beträgt.
Schritt 5: Wenn das gesuchte Element kleiner ist, suchen Sie weiter im linken Teilbaum.
Schritt 6: Wenn das gewünschte Element größer ist, vergleichen Sie das Element mit dem nächsten Schlüsselwert im Knoten und wiederholen Sie die Schritte 3, 4, 5 und 6, bis eine Übereinstimmung gefunden wird oder bis das gesuchte Element mit dem letzten Schlüsselwert im Blattknoten verglichen wird.
Schritt 7: Wenn der letzte Schlüsselwert im Listenknoten nicht mit der Suche übereinstimmt, drucken Sie "Element nicht gefunden!". und schließen Sie die Suche ab.

B-Baum-Einfügeoperation

Im B-Baum kann ein neues Element nur einem Blattknoten hinzugefügt werden. Dies bedeutet, dass ein neues Schlüssel-Wert-Paar immer nur dem Blattknoten hinzugefügt wird. Die Beilage lautet wie folgt:

Schritt 1: Überprüfen Sie, ob der Baum leer ist.
Schritt 2: Wenn der Baum leer ist, erstellen Sie einen neuen Knoten mit einem neuen Schlüsselwert und nehmen Sie ihn als Stammknoten.
Schritt 3: Wenn der Baum nicht leer ist, suchen Sie einen geeigneten Blattknoten, zu dem mithilfe der Logik des binären Suchbaums ein neuer Wert hinzugefügt wird.
Schritt 4: Wenn der aktuelle Blattknoten eine leere Zelle enthält, fügen Sie dem aktuellen Blattknoten einen neuen Schlüsselwert hinzu, und folgen Sie dabei der aufsteigenden Reihenfolge der Schlüsselwerte innerhalb des Knotens.
Schritt 5: Wenn der aktuelle Knoten voll ist und keine freien Zellen hat, teilen Sie den Blattknoten auf, indem Sie den Durchschnittswert an den übergeordneten Knoten senden. Wiederholen Sie den Schritt, bis der zu sendende Wert an den Knoten übergeben wird.
Schritt 6: Wenn die Trennung mit der Wurzel des Baumes erfolgt, wird der Durchschnitt zur neuen Wurzel des Baumes und die Höhe des Baumes erhöht sich um eins.

Ein Beispiel:

Erstellen wir einen B-Baum der Ordnung 3, indem wir Zahlen von 1 bis 10 hinzufügen.

Einfügen (1):
Da "1" das erste Element des Baums ist, wird es in einen neuen Knoten eingefügt und dieser Knoten wird zur Wurzel des Baums.



Einfügen (2):
Element 2 wird einem vorhandenen Blattknoten hinzugefügt. Jetzt haben wir nur noch einen Knoten, daher ist es gleichzeitig die Wurzel und das Blatt. Dieses Blatt hat eine leere Zelle. Dann kommt "2" in diese leere Zelle.



Einfügen (3):
Element 3 wird einem vorhandenen Blattknoten hinzugefügt. Jetzt haben wir nur einen Knoten, der sowohl die Wurzel als auch das Blatt ist. Dieses Blatt enthält keine leere Zelle. Daher trennen wir diesen Knoten, indem wir den Durchschnittswert (2) an den übergeordneten Knoten senden. Der aktuelle Knoten hat jedoch keinen übergeordneten Knoten. Daher wird der Durchschnittswert zum Wurzelknoten des Baums.



Einfügen (4):
Das Element „4“ ist größer als der Wurzelknoten mit dem Wert „2“, während der Wurzelknoten kein Blatt ist. Daher bewegen wir uns entlang des rechten Teilbaums von "2". Wir kommen zum Blattknoten mit dem Wert „3“, der eine leere Zelle hat. Somit können wir das "4" -Element in diese leere Zelle einfügen.



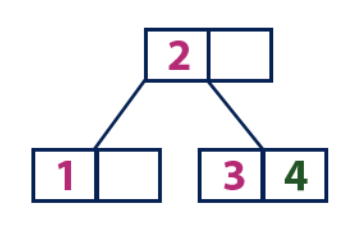Einfügen (5):
Das Element „5“ ist größer als der Wurzelknoten mit dem Wert „2“, während der Wurzelknoten kein Blatt ist. Daher bewegen wir uns entlang des rechten Teilbaums von "2". Wir kommen zum Blattknoten und stellen fest, dass er bereits voll ist und keine leeren Zellen hat. Dann teilen wir diesen Knoten, indem wir den Durchschnittswert (4) an den übergeordneten Knoten (2) senden. Der übergeordnete Knoten hat eine leere Zelle, daher wird der Wert "4" zu dem Knoten hinzugefügt, der bereits den Wert "2" hat, und das neue Element "5" wird als neues Blatt hinzugefügt.



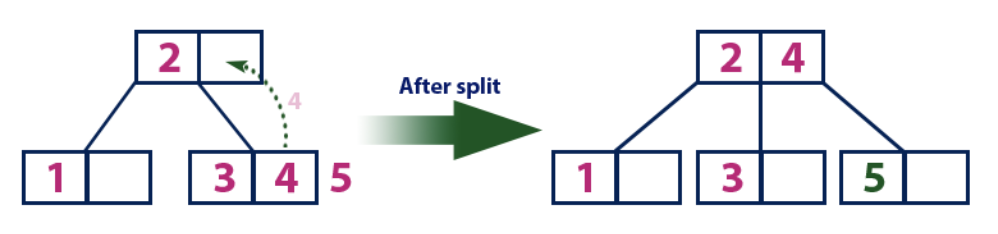Einfügen (6):
Das Element "6" ist größer als die Elemente der Wurzel "2" und "4", die kein Blatt ist. Wir bewegen uns entlang des rechten Teilbaums des Elements "4". Wir erreichen ein Blatt mit dem Wert "5", das eine leere Zelle enthält, sodass das Element "6" genau darin platziert wird.



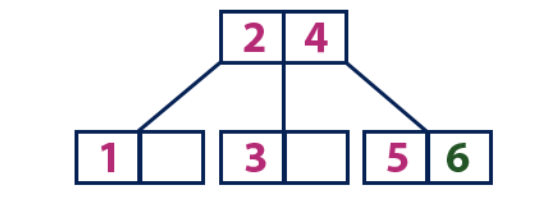Einfügen (7):
Das Element "7" ist größer als die Elemente der Wurzel "2" und "4", die kein Blatt ist. Wir bewegen uns entlang des rechten Teilbaums des Elements "4". Wir erreichen den Blattknoten und sehen, dass er voll ist. Wir teilen diesen Knoten, indem wir den Durchschnittswert von „6“ mit den Elementen „2“ und „4“ an den übergeordneten Knoten senden. Der übergeordnete Knoten ist jedoch auch voll, sodass wir den Knoten mit den Elementen „2“ und „4“ teilen und den Wert „4“ an den übergeordneten Knoten senden. Nur dieser Knoten ist noch nicht da. In diesem Fall wird der Knoten mit dem Element „4“ zur neuen Wurzel des Baums.



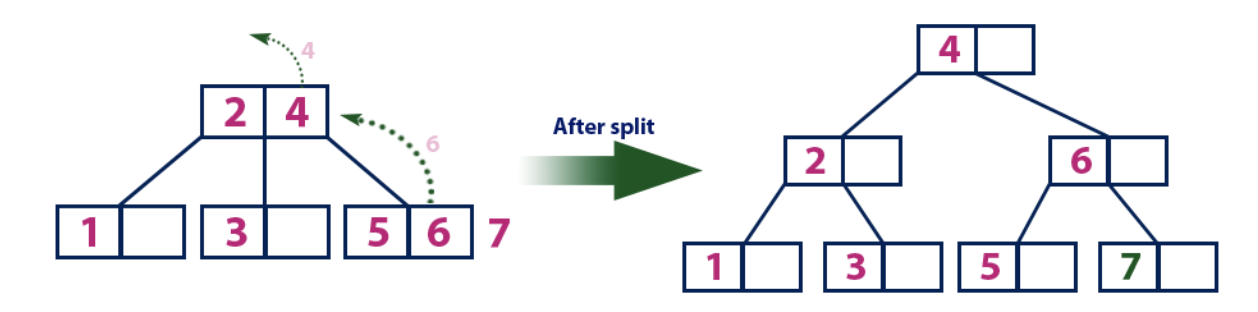Einfügen (8):
Element 8 ist größer als der Wurzelknoten mit einem Wert von 4, und der Wurzelknoten ist kein Blatt. Wir bewegen uns vom Element „4“ entlang des rechten Teilbaums und kommen zum Knoten mit dem Wert „6“. "8" ist größer als "6" und der Knoten mit dem Element "6" ist kein Blatt, also bewegen wir uns entlang des rechten Teilbaums von "6". Wir erreichen den Blattknoten mit "7", der eine leere Zelle hat, also setzen wir "8" ein.



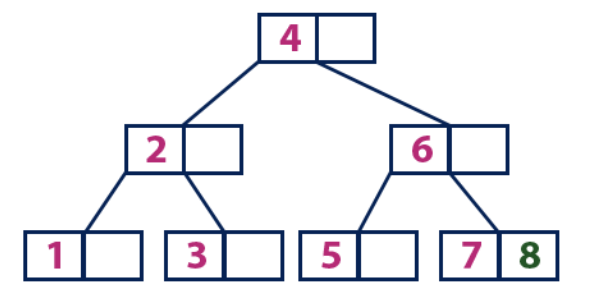Einfügen (9):
Element 9 ist größer als der Wurzelknoten mit einem Wert von 4, und der Wurzelknoten ist kein Blatt. Wir bewegen uns vom Element „4“ entlang des rechten Teilbaums und kommen zum Knoten mit dem Wert „6“. "9" ist größer als "6" und der Knoten mit dem Element "6" ist kein Blatt, also bewegen wir uns entlang des rechten Teilbaums von "6". Wir erreichen den Blattknoten mit den Werten "7" und "8". Er ist voll. Wir teilen diesen Knoten, indem wir den Durchschnittswert (8) an den übergeordneten Knoten senden. Der übergeordnete Knoten "6" hat eine leere Zelle, daher setzen wir "8" ein. In diesem Fall wird der Knotenliste ein neues Element "9" hinzugefügt.



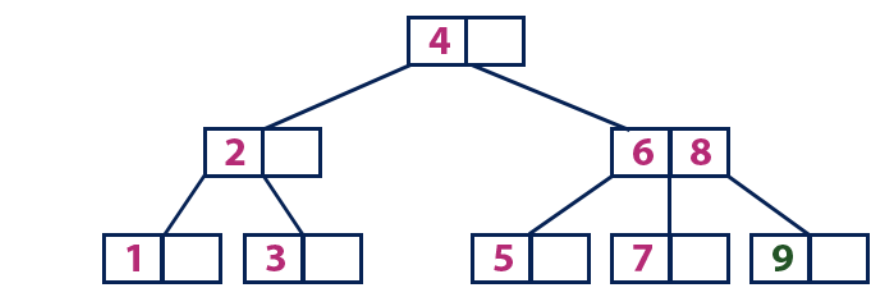
Einfügen (10):
Das Element "10" ist größer als der Wurzelknoten mit dem Wert "4", während der Wurzelknoten kein Blatt ist. Wir bewegen uns vom Element „4“ entlang des rechten Teilbaums und kommen zum Knoten mit den Werten „6“ und „8“. "10" ist größer als "6" und "8" und der Knoten mit diesen Elementen ist kein Blatt, also bewegen wir uns entlang des rechten Teilbaums von "8". Wir erreichen den Blattknoten mit einem Wert von "9". Er hat eine leere Zelle, also setzen wir dort "10".



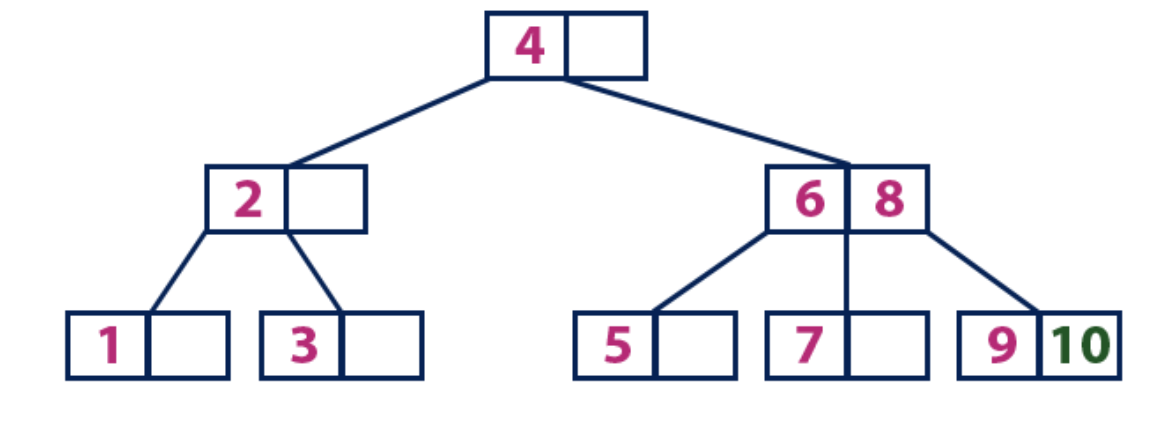
Wir empfehlen Ihnen, in der Praxis unabhängig zu verstehen, wie B-Bäume mithilfe dieser Visualisierung angeordnet werden.

Wir warten auf alle bei einer kostenlosen offenen Lektion , die am 12. Juli stattfinden wird. Bis dann!