Ein Modell einer natürlichen Zahlenreihe und ihrer Elemente. Rauten

   

In dieser Arbeit wird das grundlegende G ^{2 ±} -Modell beibehalten, aber eine andere Organisation seiner Zellen wird akzeptiert (eine andere Abbildung). Auf dem Primärgitter mit 1 × 1- Zellen wird ein größeres Gitter dargestellt - ein Gitter von Rauten und auch ein Gitter von Zentren von Rauten wird betrachtet (SCR). Das letzte Gitter ist nicht dargestellt, um die Linien mit dem Muster nicht mit Rauten zu überladen. Wir werden die Definitionen und Konzepte, die in früheren Arbeiten ausführlich beschrieben wurden, nicht wiederholen, sondern Links zu diesen Arbeiten geben.

Konstruktive Modellbeschreibung

Durch die Zellen G ^{2 ±} -Modelle, die in selbst langen D _{i -} und kurzen K _i -Diagonalen mit Zahlen enthalten sind, die mit Nullen innerhalb des G ^{2 -} - Submodells enden, werden Linien gezogen, die ein großes Netzwerk von Rauten in der Ebene bilden. Die rhombischen Regionen für Zellen bedecken gemeinsam die gesamte Ebene ohne Lücken. Jede Raute enthält 41 Zellen, von denen nur 16 von Interesse sind, und bei der Untersuchung einer Raute werden nur 4 Zellen mit fester Flexion verwendet.

Die Eigenschaften von Rauten umfassen:

• die Anzahl der Zellen in der Raute;
• der Wert der Zahl in der zentralen Zelle;
• die Zahlen seiner horizontalen ( N _i ) und vertikalen ( V _i );
• Identifizieren von Zellen für Zahlen mit Beugungen 1, 3, 7, 9;
• die Koordinaten dieser Zellen im Koordinatensystem der Raute mit dem Ursprung in der zentralen Zelle der Raute.

Ein Gitter von Rautenzentren wird auch durch die Zellen der Rautenzentren konstruiert, deren Knoten sich in den Zellen am Schnittpunkt langer und kurzer Diagonalen mit Zahlen befinden, die Vielfache der Zahl 5 sind.
Aus der Figur mit Rauten ist ersichtlich, um welche Art von Gitter es sich handelt. Zur Veranschaulichung der Merkmale von Rauten werden Bilder eines Rautenpaares in jeder Halbebene gegeben. Diese Rauten sind mit einer identifizierenden Anzahl von Zellen in der unteren Hälfte und einem weiteren Paar solcher Rauten in der oberen Halbebene markiert. Die Markierung von Rauten in der Halbebene unterhalb der Diagonale D ₀ unterscheidet sich von der Markierung von Rauten in der Halbebene darüber, aber innerhalb derselben Halbebene ist die Markierung aller Rauten sowohl für die untere als auch für die obere Halbebene identisch. Das Wesentliche beim Markieren ist die Lokalisierung von Zellen mit Zahlen mit gleichen Beugungen (markiert durch Füllen von Zellen mit derselben Farbe), wobei ihre Koordinaten x ₁ , x _{0 festgelegt werden} . Die bezeichneten Rauten werden als grundlegend bezeichnet, aus denen andere Rauten mit Vergrößerung gebildet werden können.

Die Zentren der Rauten der unteren Halbebene sind Zellen mit zweistelligen Zahlen, entweder 25 mit der horizontalen Zahl mit Flexion 5 und mit der vertikalen Nummer mit Flexion 0 oder 75 mit der horizontalen Nummer mit Flexion 0 und mit der vertikalen Nummer mit Flexion 5. In der oberen Halbebene ^{2 +} - Untermodelle aller Zahlen in den zentralen Zellen aller Rauten enden mit zwei Ziffern 25. Ferner beschränken wir die Betrachtung auf die Halbebene ^{2 -} .


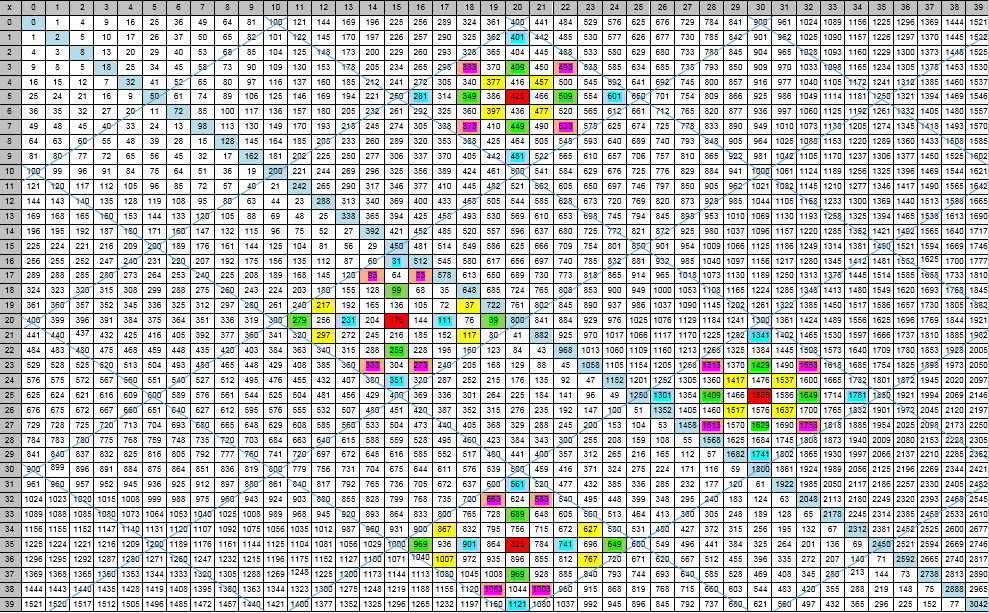_{Abbildung 1 - Visuelle Darstellung eines Diamantmodells}

Definition 1. Die fundamentale Raute ist die Struktur des ^{2 ±} -Modells, das durch zwei kurze und zwei lange Diagonalen dieser Ebene mit durch die Zahl 10 teilbaren Zahlen begrenzt ist. Das Hauptelement, das die Raute charakterisiert, ist die Zelle ( x _1c , x _0c ) ihres Zentrums. Das Zentrum enthält einen numerischen Wert von N, ein Vielfaches von 5.

Definition 2. Die Menge der Zentren grundlegender Rauten sind die Knoten (Zellen) des Netzwerks der Zentren von Rauten (SCR) sich kreuzender kurzer und langer Diagonalen mit Zahlen, die ein Vielfaches von 5 sind. Die Rauten selbst decken die Ebene ^{2 ±} - Modelle vollständig ab (Parkettprinzip).

Alle Rauten sind auf die gleiche Weise angeordnet, und die Zahlen in ihren Zellen mit festen Enden werden an festen Positionen (Zellen) platziert. Auf diese Weise können Sie diese Zahl leicht faktorisieren, wenn Sie das Problem der Lokalisierung der Zahl N in einer bestimmten Raute lösen. Zehn Horizontale, deren Zellen eine Raute bilden, und benachbarte Rauten (mit anderen Koordinaten) werden als Rautenstreifen bezeichnet. Horizontale Bänder werden berücksichtigt: West-Ost (); vertikal: Nord-Süd (NW), entlang kurzer Diagonalen: Nordosten (NE) und entlang langer Diagonalen: Nordwesten (NW). Der Versatz von einer Raute zur anderen kann zusätzlich zur Anzeige des Streifens durch eine Anzeige (auf und ab) entlang der angegebenen Bänder ergänzt werden.

Da aus Definition 2 folgt, dass die Menge der Zellen aller Rauten alle Zellen des G ^{2 ±} -Modells ist, ist in einer der Zellen (x _1p , x _0p ), die zu einer bestimmten Raute gehören, eine vorbestimmte zusammengesetzte ungerade natürliche Zahl (ELF) N ( x _1p , x _0p ) = N (x ₁ , x ₀ ) . Gleichzeitig glauben wir, dass es möglich ist, eine solche Raute (durch Bestimmen der Koordinaten ihrer zentralen Zelle) (x _1c , x _0c ) _anzuzeigen, als alle Zellen zu untersuchen und sich sogar darauf zu beschränken, nur ungerade Diagonalen zu untersuchen.

Die Angabe einer solchen Raute und der gewünschten Zelle darin ist eine Lösung für das Lokalisierungsproblem für eine gegebene Zahl N (x ₁ , x ₀ ) . Dieses Problem und seine Lösung gehen dem Eingang der Entscheidung des WFCH voraus. Die Bedeutung und das endgültige Ziel des Lokalisierungsproblems besteht darin, in einer bestimmten Raute für einen gegebenen ELF N (x ₁ , x ₀ ) die Werte der Koordinaten der Zelle (x _1p , x _0p ) im G ^{2 ±} -Modell _anzugeben , in dem eine Zahl mit N übereinstimmt (x ₁ , x ₀ ) .

In diesem Artikel verwenden wir den Mechanismus, um die Zugehörigkeit einer bestimmten Zahl N zu einer bestimmten Raute und einer Zelle darin festzustellen. Dieser Mechanismus ist bei weitem nicht der beste, aber in den vorgeschlagenen Beispielen wird er mit der Aufgabe fertig. Die Leser werden gebeten, entweder ihr Original anzubieten oder diesen Mechanismus zu verbessern.

Unser Mechanismus basiert auf der bemerkenswerten Regelmäßigkeit des vom Autor entdeckten G ^{2 ±} -Modells: das Vorhandensein in den horizontalen Linien mit Zahlen, die Vielfache von fünf (und einigen anderen) sind, Zellen mit Quadraten der Elemente der pythagoreischen Tripel (PFT) < g, k ₁ , k ₂ > = <Hypotenuse , Bein ₁ , Bein ₂ >. Die CFT wird in einer anderen Arbeit diskutiert.

Um die Schlussfolgerungen und Berechnungen zu vereinfachen, benötigen wir drei Koordinatensysteme: planar, das bereits eingeführt wurde , Netzwerk mit einer anderen Anzahl von Diagonalen für den SCR (Abb. 2) und rhombisch (Tabelle 1), wobei der Anfang mit der Zelle des Zentrums der Raute assoziiert ist.


<sub>Abbildung 2. Nummerierung (doppelt) der kurzen Diagonalen und
Verteilung der Diamantzentren auf kurzen Diagonalen

Tabelle 1. Bestimmen der Koordinaten eines Suchpunkts innerhalb einer festen Raute</sub>



Im SCR-System wird Folgendes angegeben: Die Nummer der kurzen Diagonale n _p , c ist die Seriennummer des Zentrums darauf sowie die netzwerkweite C- Nummer des Zentrums, seine eigene Nummerierung der kurzen Diagonalen ab n _p = 1 (im planaren System ist die 5. kurze Diagonale). dann ist die Zahl n _p = 2 (dies ist die um 10 erhöhte Zahl, d. h. die 15. Ebene K _i ) und dann mit dem Schritt 10 alle anderen. Die Position aller Zellen der Rhombuszentren in jedem K _{i des} SCR ist ebenfalls von c = 1 bis c = 2n _{p der} doppelten Netzwerknummer der kurzen Diagonale nummeriert.

Beispiel 1 Es sei erforderlich, die netzwerkweite Nummer C des Zentrums einer der Rauten und die Nummer N in dieser Zelle für eine gegebene kurze Diagonale zu finden, die durch die Zentren der Rauten verläuft, ihre Netzwerknummer n _p = 5 und die Seriennummer des Zentrums c = 3 einer der Rauten darauf. Ganz einfach, die Netzwerkkoordinaten der zentralen Zelle dieser Raute werden in der Form (n _p , q) = (5, 3) dargestellt .

1. Finden Sie die Ebene x ₁ Koordinate der Zelle am Anfang der angegebenen Diagonale (nd):
   x ₁ = x _nd = 10n _p - 5 = 50 - 5 = 45.
   Für unseren Fall haben wir x ₁ = x _nd = 45 .
   
2. Jetzt können wir sofort mit der Suche nach den Ebenenkoordinaten der Zelle ( x _1c , x _sc ) des gewünschten Zentrums fortfahren: x ₁ = x _nd - 5 (c - 1) = 45 - 5 (3 - 1) = 35, x ₀ = 0 + 5 ( μ - 1) = 2 ∙ 5 = 10.
   
3. Finden Sie die Netzwerknummer des Zentrums der Raute ( C ).
   
   Bemerkung. Es ist bekannt, dass für die Zahl x die Formel 2C _{x + 1} ² = x (x + 1) die doppelte Anzahl von Kombinationen von x + 1 in zwei ist.
   Die Anzahl der Zentren vor der kurzen Diagonale n _p = 5 beträgt 2n _p (n _p - 1) . Dann wird die Seriennummer C des Netzwerkzentrums durch die Formel angegeben
   C = np (np -1) + c = 2Cnp2 + 3 = 5 ≤ 4 + 3 = 23 .
   
4. Finden Sie den Wert der Zahl N (x _1c , x _sc ) in der Zelle des Zentrums der Raute N = x ₁ ² - x ₀ ² - das Vorzeichen in der Formel wird abhängig von der Position des Zentrums relativ zur Hauptdiagonale genommen.
   N = 35 ² - 10 ² = 1125 - für unseren Fall.
   

Wenn also nur die Netzwerknummer n _{p der} kurzen Diagonale, die durch die Zellen der Zentren verläuft, und die aktuelle Zentrumsnummer der Raute c auf dieser Diagonale vorliegen, können wir alle anderen Informationen über das Zentrum der Raute erhalten.

Alle ungeraden positiven ganzen Zahlen von Interesse N gehören zu Diamantzellen. Das Konzept der Flexion, die letzte Ziffer einer Zahl, ermöglicht es, ihre Position innerhalb der Rauten zu lokalisieren. Für die Faktorisierung sind die Zahlen N von Interesse, die mit den Zahlen 1, 3, 7, 9 enden.

Gerade Zahlen werden nicht als N betrachtet , da sie einen Primteiler 2 haben. Zahlen, die mit einer Fünf enden, haben einen Primteiler 5, was auch für N nicht akzeptabel ist . Es ist ratsam, ein spezifisches N durch Beugung innerhalb der Raute relativ zum Zentrum der Raute zu lokalisieren, da das Zentrum das wichtigste Merkmal der Raute ist. Aufgrund der Tatsache, dass alle Rauten die gleiche Struktur haben, besteht eine klare Beziehung zwischen der für die Faktorisierung angegebenen Zahl N und den Zahlen in Rautenzellen mit bestimmten Beugungen und in der Zelle des Rautenzentrums. Daten zu solchen Beziehungsnummern sind in der Tabelle angegeben. 1.

Das Aussortieren aller Rauten in einer Ebene, um die gewünschte Raute zu finden, ist jedoch weder zeitlich noch rechenintensiv. Somit ergab sich das Problem der Lokalisierung der zu faktorisierenden Regionen ^{2 -} - Submodelle (Halbebenen), einschließlich solcher Rauten, die die Anfangszahl N enthalten würden.

Pythagoreische Tripel . Zur Lösung des formulierten Problems werden verwendet
Pythagoreische Tripel sind Tripel von Zahlen, die den Satz von Pythagoras erfüllen: Pythagoreische Tripel, die die Regel des sogenannten ägyptischen Dreiecks erfüllen, d. H. Ein Dreieck mit Seiten, die Vielfache von 3, 4, 5 sind.
In jeder horizontalen x _1, die die Zentren der Rauten enthält, gibt es ein oder mehrere solcher pythagoreischen Tripel.

Die erste Raute im Lokalisierungsproblem wird ungefähr angezeigt, und im Falle eines „Fehlschlags“ sollten die folgenden Rauten ausgewählt werden. Dazu ist es notwendig, die Bewegungsrichtung entlang des SCR zu bestimmen, um sich dem Endziel allmählich zu nähern. Wenn zum Beispiel die kleinere der 4 in der aktuellen Zahlenraute kleiner als das gegebene N ist, dann enthalten die Nordost- und Ost-Rauten davon sogar weniger als 4 Zahlen, das heißt, solche Rauten sollten nicht untersucht werden. Die Bewegung zur westlichen Raute führt zu einem solchen Wertanstieg in allen vier Zellen, dass sich herausstellt, dass sogar eine kleinere Anzahl der westlichen Raute größer ist als die größere Anzahl der vorherigen Raute und daher größer als N. Daher die Lösung: Bewegen Sie sich von der Raute zur Raute in nordwestlicher Richtung.

Wenn eine Raute gefunden wird, die eine Zelle mit einer Zahl von N (x _1p , x _0p ) = N enthält , und die Koordinaten der Zelle (x _1p , x _0p ) bestimmt werden, wird die Lösung des FBCH durch die Grundrelation ^{2 ±} - des Modells bestimmt
N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q

Ein weiteres Teilproblem ist die Auswahl und Implementierung der Zellbypass-Sequenz der für die Untersuchung ausgewählten Raute. Hier wird die Traversalreihenfolge gegen den Uhrzeigersinn übernommen, beginnend mit der oberen linken Zelle, die die Nummer mit der erforderlichen Beugung enthält. In einer Situation des Zusammentreffens der Werte in der Diamantzelle N (x _1p , x _0p ) und einer gegebenen Zahl N (x ₁ , x ₀ ) stellt sich heraus, dass die Differenz zwischen ihnen Null ist.

ZFBCH-Lösungsalgorithmus unter Verwendung grundlegender Rauten und PFT

1. Wir extrahieren die Wurzel aus der Zahl N. Runden Sie ab.
   
2. Wir prüfen, ob √N durch 3 teilbar ist. Wenn teilbar, weisen Sie diesen Wert dem ersten Abschnitt k1 zu. Andernfalls subtrahieren Sie 1 oder 2 vom Ergebnis und speichern Sie ihn als k1, um die Teilbarkeitseigenschaft durch 3 zu erfüllen. Das Ergebnis der Division des vollständig ausgewählten Werts durch drei M = √N / 3 - Denken Sie an den skalierenden PFT-Koeffizienten.
   
3. Wir erhalten den Wert für das Rückspiel k ₂ nach der Regel des ägyptischen Dreiecks k ₂ = 4 ∙ M.
   
4. Wir finden den Wert der Hypotenuse g = 5 ∙ M , und der Wert x ₁ = g sollte durch die Zahl fünf geteilt werden. Wie Sie sehen können, ist der Wert der Hypotenuse bei PFT immer gleich der horizontalen Zahl.
   
5. Finden Sie die Koordinate x ₁ = g .
   
6. Danach bestimmen wir die Beugung (letzte Ziffer) der Zahl N , φ = N (mod10) .
   
7. Wir finden das Zentrum der Raute, das k1 am nächsten liegt, und untersuchen dann benachbarte Rauten in einem der Rautenbänder (es gibt 4 Richtungen), um eine Lösung zu finden.
   
8. Abhängig davon, welche Art von Beugung wir in Absatz 6 erhalten, verwenden wir die gewünschte Spalte (Maske) aus den in der Tabelle angegebenen. 1, um die Koordinaten des _Suchpunkts ( x _1p , x _0p ) zu _bestimmen und den Wert der Zahl in dieser Zelle N _{p zu finden} . In jeder Raute werden nur 4 Zellen aus der 41. Zelle überprüft.
   
9. Nachdem festgestellt wurde, dass die Zahl N zu einer bestimmten Raute und einer Zelle darin gehört, basierend auf derselben Tabelle. 1 erhalten wir die Ebenenkoordinaten N: (x _1p , x _0p ) .
   
10. Verwenden der Eigenschaften des ausgewählten mathematischen Modells
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q
    Wir erhalten die multiplikative Darstellung von N aus dem Additiv.
    
11. Am Ausgang des Algorithmus haben wir also: N = p ∙ q . Abhängig vom Wert der Beugung f gemäß den Formeln in der Tabelle. In 1 werden die Koordinaten des Punktes (x _1p , x _0p ) _bestimmt und die Differenz ∆ = N (x _1p , x _0p ) - N (x ₁ , x ₀ ) berechnet. Wenn ∆ ∆ 0 , dann gehe zu einer anderen Zelle, wenn alle Zellen der Raute überprüft sind, dann zu einer anderen Raute.
    Wenn Δ = 0 ist , dann ist x ₁ = x _1p , x ₀ = x _0p und p = (x ₁ - x ₀ ) , q = N / p = (x ₁ + x ₀ ) .
    

Beispiel 2. Gegeben: N = 1037 , eine Zahl mit einer Kapazität von 4. Es ist erforderlich, sie zu faktorisieren. Wir handeln nach dem vorgegebenen Algorithmus.

1. Wir extrahieren die Wurzel aus N : √N = 32.202 . Wir runden ab: √N = 32 .
2. Wir prüfen, ob 32 durch 3 teilbar ist. Da 32 nicht durch 3 teilbar ist, subtrahieren wir 2. Wir nehmen also an, dass der erste Abschnitt k ₁ = 3 ∙ 10 = 30 ist , hier ist M = 10 = 30/3 der PFT- Skalierungsfaktor.
3. Wir erhalten den Wert für das Rückspiel k ₂ = 4 ∙ 10 = 40 .
4. Wir finden den Hypotenusenwert g = (k ² ₁ + k ² ₂ ) ^0,5 , vorausgesetzt, er wird durch 5 geteilt, (30 ² + 40 ² ) ^0,5 = 50.
5. Somit ist x1 = k1 = 50 und die PFT transformiert sich in die Form g = 50 , k ₁ = 30, k ₂ = 40 .
6. Wir finden die Beugung der Zahl N : φ (1037) = 1037 (mod10) = 7 .
7. Wir finden das Zentrum der Raute, das N = 1037 am nächsten liegt.
   Es hat die Koordinaten der zentralen Zelle der Raute: x ₁ = 50, x ₀ = 35 . Die erste Koordinate ist die Zeilennummer, die die CFT enthält. Das Quadrat des kleineren Beins ist 900, es ist in der Vertikalen mit der Nummer 40 enthalten. Die Zelle mit der Nummer 957, die mit den sieben am nächsten an 900 endet, liegt in der vorherigen Horizontalen mit der Nummer 49 und in der Vertikalen mit der Nummer 38. Dies ist die kleinste Nummer von 4 in der Raute und mit Flexion 7. Hier verwenden wir die Daten von Tabelle 1. Das nächste Zentrum der Raute sollte drei Zellen links sein, dh es gehört zur Vertikalen 38 - 3 = 35, dies ist die zweite Koordinate des Zentrums der Raute. Der Wert der Zahl in der Zelle des Zentrums der Raute ist N (50, 35) = 1275
   
   Dies ist eine Raute mit Quadraten der Beine k ₁ und k ₂ an ihren Rändern. Innerhalb dieser Raute ist min eine Zahl, die in einer Zelle mit sieben 957 endet ( x ₁ = 49, x ₀ = 38 ), und eine andere Zahl in dieser Vertikalen, die mit 7. 1157 endet, liegen links von der zentralen Zelle große Zahlen 1377 und 1577 , die mit der Zahl übereinstimmen N = 1037 nein, daher ist es notwendig, mit dem Wert in der zentralen Zelle 1125 und mit den Koordinaten der zentralen Zelle ( x ₁ = 50 - 5 = 45, x ₀ = 35 - 5 = 30 ) zur Raute nach links und höher zu steigen. Überprüfen Sie die vier Zahlen auf Flexion 7 Dies sind 847, 1027, 1207 und 1387, und es gibt keine Übereinstimmungen mit N = 1037 in dieser Raute. Wir werden entlang des NW-Bandes der Rauten in derselben Richtung noch höher steigen. Die mittlere Zelle der neuen Raute hat einen Wert von 975 und Koordinaten ( x ₁ = 45 - 5 = 40, x ₀ = 35 - 5 = 25 ). Wir überprüfen in dieser Raute die vier Zahlen für die Flexion 7. Dies ist 737, 897, 1197 und schließlich erhalten wir 1037 in der Zelle ( x _1p = 39, x _0p = 22 ), wir haben eine vollständige Übereinstimmung mit dem angegebenen N.
   
   Im Detail werden diese Aktionen durch die folgenden Berechnungen dargestellt: Gemäß Tabelle 1 berechnen wir die Koordinaten der Zellen und die Zahlenwerte in ihnen. Danach finden wir die Unterschiede zwischen den berechneten und gegebenen Werten von N. In der ersten Raute werden alle 4 Zellen berechnet.
   
   ∆ = N (x _1c -1, x _0c -3) - N (x ₁ , x ₀ ) = N (49,32) - 1037 = 1377 - 1037 = 340 ≠ 0,
   ∆ = N (x _1c + 1, x _0c -3) - N (x ₁ , x ₀ ) = N (51,32) - 1037 = 1577 - 1037 = 540 ≠ 0,
   ∆ = N (x _1c + 1, x _0c + 3) - N (x ₁ , x ₀ ) = N (51,38) - 1037 = 1157 - 1037 = 120 ≠ 0,
   ∆ = N (x _1c -1, x _0c + 3) - N (x ₁ , x ₀ ) = N (49,38) - 1037 = 957 - 1037 = - 80 ≠ 0.
   In dieser Raute gibt es keine Übereinstimmung der Zahl N mit den Zahlen in den Zellen.
   
   Wir gehen zur nächsten Raute mit dem Zentrum in der Zelle (x _1c -5, x _0c -5) = (45, 30) und dem Wert darin N (x _1c -5, x _0c -5) = N (45, 30) = 1125 .
   ∆ = N (x _1ts -1, x _0ts -3) - N (x ₁ , x ₀ ) = N (44,27) - 1037 = 1207 - 1037 = 170 ≠ 0,
   ∆ = N (x _1c + 1, x _0c -3) - N (x ₁ , x ₀ ) = N (46,27) - 1037 = 1387 - 1037 = 350 ≠ 0,
   ∆ = N (x _1c + 1, x _0c + 3) - N (x ₁ , x ₀ ) = N (46,33) - 1037 = 1027 - 1037 = - 10 ≠ 0,
   ∆ = N (x _1c -1, x _0c + 3) - N (x ₁ , x ₀ ) = N (44,33) - 1037 = 847 - 1037 = - 190 ≠ 0.
   In dieser Raute gibt es auch keine Übereinstimmung der Zahl N mit den Zahlen in den Zellen.
   
   Wir gehen zur nächsten Raute mit dem Zentrum in der Zelle (x _1c -5, x _0c -5) = (40, 25) und dem Wert darin N (x _1c -5, x _0c -5) = N (40, 25) = 975
   ∆ = N (x _1c -1, x _0c -3) - N (x ₁ , x ₀ ) = N (39,22) - 1037 = 1037 - 1037 = 0.
   Ich habe eine Wertedifferenz von Null. Es ist ein völliger Zufall. Daraus folgt, dass die gegebene Zahl N (x ₁ , x ₀ ) = 1037 in der Zelle mit den Koordinaten (x ₁ , x ₀ ) = (39, 22) enthalten ist. Schließlich wird die Lösung des HFBC durch die Grundrelation ^{2 ±} - des Modells bestimmt
   N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = (39 - 22) (39 + 22) = p ≤ q = 17 ≤ 61 .
   
8. Sie können anders handeln. Beginnen Sie mit der in Absatz 6 angegebenen Raute anhand der Tabelle. In 1 finden wir heraus, ob die Zahl N zu einer bestimmten Raute gehört, indem wir uns zwischen den Zentren der Rauten zuerst horizontal in Richtung der Hauptdiagonale bewegen, dann zum nächsten Rhombusstreifen hinuntergehen und alles erneut wiederholen.
9. Nachdem festgestellt wurde, dass die Zahl N zu einer bestimmten Raute gehört (in unserem Fall hat die Raute Koordinaten ( x ₁ = 40, x ₀ = 25 )), die auf derselben Tabelle basieren. 1 erhalten wir die Koordinaten N : x _1p = 39 , x _2p = 22 (9 Rauten betrachtet).
10. Verwenden der Eigenschaften des ausgewählten mathematischen Modells der Zahl
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q
    Wir erhalten die multiplikative Darstellung von N aus dem Additiv:
    N = (39 - 22) (39 + 22) = 17 ≤ 61 = 1037 .

Somit haben wir am Ausgang N = p · q = 17 · 61 = 1037 , d. H. Die Lösung des Problems wurde erfolgreich erhalten.

Wir erhalten auch das Ergebnis einer Softwarelösung für das Problem in Beispiel 3.

Beispiel 3 Gegeben: N = 3808572773, eine Zahl mit einer Auflösung von 10.

1. Wir extrahieren die Wurzel aus N: √N = 61713 , 64 = 61713 .
2. Überprüfen Sie, ob 61713 durch 3 teilbar ist. Da 61713 durch 3 teilbar ist,
   6 + 1 + 7 + 1 + 3 = 18 wird durch 3 geteilt, dann ist das erste Bein k ₁ gleich k ₁ = 61713 .
3. Wir erhalten das Rückspiel k ₂ = 4k 1/3 => 4k 2/3 = 82284 .
4. Wir finden die Hypotenuse g = √k ₁₂ + k ₂₂ , vorausgesetzt, sie wird geteilt durch
   5 g = 617132 + 822842 = 102855 .
5. Somit ist x ₁ = k ₁ = 61713 und das pythagoreische Tripel transformiert sich jeweils in die Form k ₁ = 61713, k ₂ = 82284, g = 102855 .
6. N: (3808572773) = 3808572773(mod10) = 3 .
7. . x ₁ = 61715; x ₉ = 0 .
8. , 7, . 1, N , , , , .
9. N ( x ₁ = 62015 , x ₀ = 6085 ) N :
   x _1p = 62013; x _0p = 6086 ; ( 60 ).
10. 
    N = x ² ₁ — x ² ₀ = (x ₁ — x ₀ )(x ₁ + x ₀ ) =p ·q N :
    N = (62013 — 6086) · (62013 + 62086) = 55927 · 68099 = 3808572773 ;
11. , N = p · q = 55927 · 68099 = 3808572773 , . . .