Stellen Sie sich vor, Sie müssen eine gleichmäßig verteilte Zufallszahl von 1 bis 10 generieren. Das heißt, eine Ganzzahl von 1 bis einschließlich 10 mit einer gleichen Wahrscheinlichkeit (10%) für jedes Vorkommen. Aber zum Beispiel ohne Zugang zu Münzen, Computern, radioaktivem Material oder anderen ähnlichen Quellen von (Pseudo-) Zufallszahlen. Sie haben nur ein Zimmer mit Menschen.

Angenommen, in diesem Raum befinden sich etwas mehr als 8500 Studenten.

Am einfachsten ist es, jemanden zu fragen: „Hey, wähle eine Zufallszahl von eins bis zehn!“. Der Mann antwortet: "Sieben!". Großartig! Jetzt hast du eine Nummer. Sie fragen sich jedoch, ob es gleichmäßig verteilt ist.

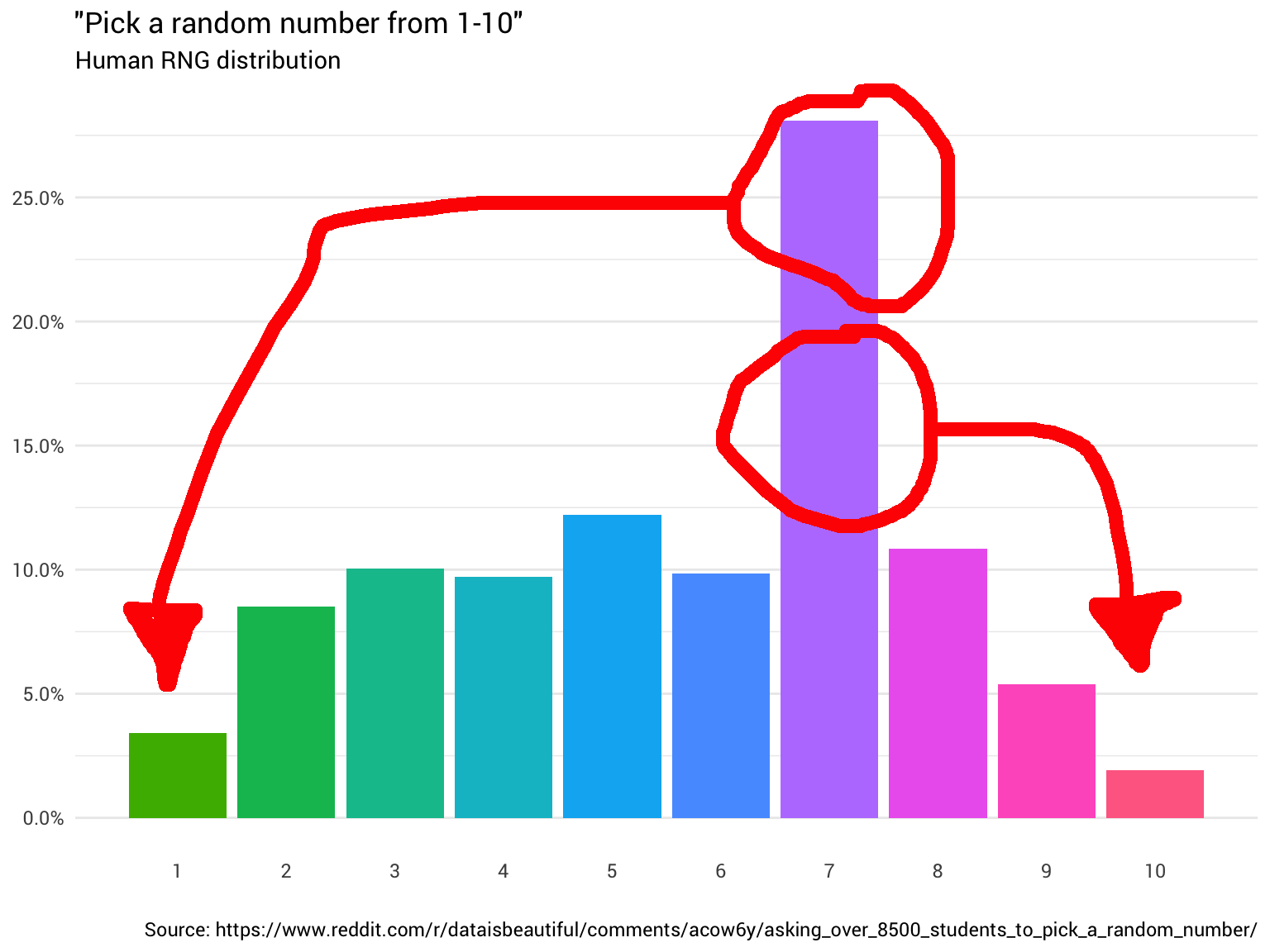
Also hast du beschlossen, noch ein paar Leute zu fragen. Sie fragen sie immer wieder und zählen ihre Antworten, runden die Bruchzahlen ab und ignorieren diejenigen, die glauben, dass der Bereich von 1 bis 10 0 umfasst. Am Ende stellen Sie fest, dass die Verteilung überhaupt nicht gleichmäßig ist:

library(tidyverse) probabilities <- read_csv("https://git.io/fjoZ2") %>% count(outcome = round(pick_a_random_number_from_1_10)) %>% filter(!is.na(outcome), outcome != 0) %>% mutate(p = n / sum(n)) probabilities %>% ggplot(aes(x = outcome, y = p)) + geom_col(aes(fill = as.factor(outcome))) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = '"Pick a random number from 1-10"', subtitle = "Human RNG distribution", x = "", y = NULL, caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/") 

Daten von Reddit

Sie schlagen sich auf die Stirn. Nun, natürlich wird es nicht zufällig sein. Schließlich kann man Menschen nicht vertrauen .

Was tun?

Ich wünschte, ich könnte eine Funktion finden, die die Verteilung des „menschlichen RNG“ in eine gleichmäßige Verteilung umwandelt ...

Die Intuition ist hier relativ einfach. Sie müssen nur die Verteilungsmasse von über 10% nehmen und auf weniger als 10% verschieben. Damit sich alle Spalten im Diagramm auf derselben Ebene befinden:



Theoretisch sollte eine solche Funktion existieren. Tatsächlich muss es viele verschiedene Funktionen geben (für die Permutation). Im Extremfall können Sie jede Spalte in unendlich kleine Blöcke „schneiden“ und eine Verteilung beliebiger Form erstellen (z. B. Legosteine).

Ein solch extremes Beispiel ist natürlich etwas umständlich. Idealerweise möchten wir so viel wie möglich von der anfänglichen Verteilung behalten (d. H. So wenig Fetzen und Bewegungen wie möglich machen).

Wie finde ich eine solche Funktion?

Nun, unsere obige Erklärung klingt sehr nach linearer Programmierung . Aus Wikipedia:

Die lineare Programmierung (LP, auch lineare Optimierung genannt) ist eine Methode, um das beste Ergebnis zu erzielen ... in einem mathematischen Modell, dessen Anforderungen durch lineare Beziehungen dargestellt werden ... Die Standardform ist die übliche und intuitivste Form zur Beschreibung eines linearen Programmierproblems. Es besteht aus drei Teilen:

• Zu maximierende lineare Funktion
  
• Problembeschränkungen der folgenden Form
  
• Nicht negative Variablen

Ebenso kann das Problem der Umverteilung formuliert werden.

Darstellung des Problems

Wir haben eine Reihe von Variablen $$$(x_ {i, j}$ , von denen jeder einen Bruchteil der Wahrscheinlichkeit codiert, die von einer ganzen Zahl umverteilt wird $$$i$ (1 bis 10) zu einer ganzen Zahl $$$j$ (von 1 bis 10). Deshalb, wenn $$$(x_ {7,1} = 0,2$ Dann müssen wir 20% der Antworten von sieben auf eins übertragen.

 variables <- crossing(from = probabilities$outcome, to = probabilities$outcome) %>% mutate(name = glue::glue("x({from},{to})"), ix = row_number()) variables 

  ## # Ein Tibble: 100 x 4
 ## von bis ix benennen
 ## <dbl> <dbl> <kleber> <int>
 ## 1 1 1 x (1,1) 1
 2 1 2 x (1,2) 2
 ## 3 1 3 x (1,3) 3
 ## 4 1 4 x (1,4) 4
 ## 5 1 5 x (1,5) 5
 6 1 6 x (1,6) 6
 7 1 7 x (1,7) 7
 8 1 8 x (1,8) 8
 9 1 9 x (1,9) 9
 ## 10 1 10 x (1,10) 10
 ## # ... mit 90 weiteren Zeilen 

Wir möchten diese Variablen so begrenzen, dass sich alle umverteilten Wahrscheinlichkeiten auf 10% summieren. Mit anderen Worten, für jeden $$$j$ von 1 bis 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0,1$$

Wir können diese Einschränkungen als Liste von Arrays in R darstellen. Später binden wir sie in eine Matrix.

 fill_array <- function(indices, weights, dimensions = c(1, max(variables$ix))) { init <- array(0, dim = dimensions) if (length(weights) == 1) { weights <- rep_len(1, length(indices)) } reduce2(indices, weights, function(a, i, v) { a[1, i] <- v a }, .init = init) } constrain_uniform_output <- probabilities %>% pmap(function(outcome, p, ...) { x <- variables %>% filter(to == outcome) %>% left_join(probabilities, by = c("from" = "outcome")) fill_array(x$ix, x$p) }) 

Wir müssen auch sicherstellen, dass die gesamte Masse der Wahrscheinlichkeiten aus der anfänglichen Verteilung erhalten bleibt. Also für alle $$$j$ im Bereich von 1 bis 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0,1$$

 one_hot <- partial(fill_array, weights = 1) constrain_original_conserved <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome) %>% pull(ix) %>% one_hot() }) 

Wie bereits erwähnt, möchten wir die Erhaltung der ursprünglichen Distribution maximieren. Das ist unser Ziel :

$$

$$maximiere (x_ {1, 1} + x_ {2, 2} + \ ldots \ x_ {10, 10})$$

 maximise_original_distribution_reuse <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome, to == outcome) %>% pull(ix) %>% one_hot() }) objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums() 

Dann übergeben wir das Problem an den Löser, zum Beispiel das lpSolve Paket in R, und kombinieren die erstellten Einschränkungen in einer Matrix:

 # Make results reproducible... set.seed(23756434) solved <- lpSolve::lp( direction = "max", objective.in = objective, const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)), const.dir = c(rep_len("==", length(constrain_original_conserved)), rep_len("==", length(constrain_uniform_output))), const.rhs = c(rep_len(1, length(constrain_original_conserved)), rep_len(1 / nrow(probabilities), length(constrain_uniform_output))) ) balanced_probabilities <- variables %>% mutate(p = solved$solution) %>% left_join(probabilities, by = c("from" = "outcome"), suffix = c("_redistributed", "_original")) 

Die folgende Umverteilung wird zurückgegeben:

 library(gganimate) redistribute_anim <- bind_rows(balanced_probabilities %>% mutate(key = from, state = "Before"), balanced_probabilities %>% mutate(key = to, state = "After")) %>% ggplot(aes(x = key, y = p_redistributed * p_original)) + geom_col(aes(fill = as.factor(from)), position = position_stack()) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = 'Balancing the "Human RNG distribution"', subtitle = "{closest_state}", x = "", y = NULL) + transition_states( state, transition_length = 4, state_length = 3 ) + ease_aes('cubic-in-out') animate( redistribute_anim, start_pause = 8, end_pause = 8 ) 

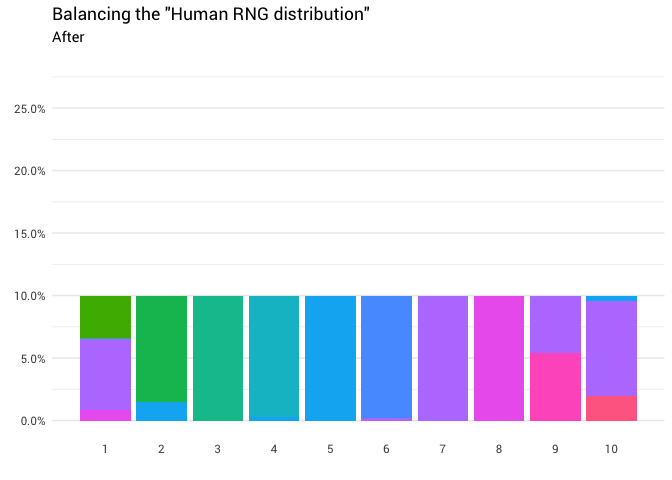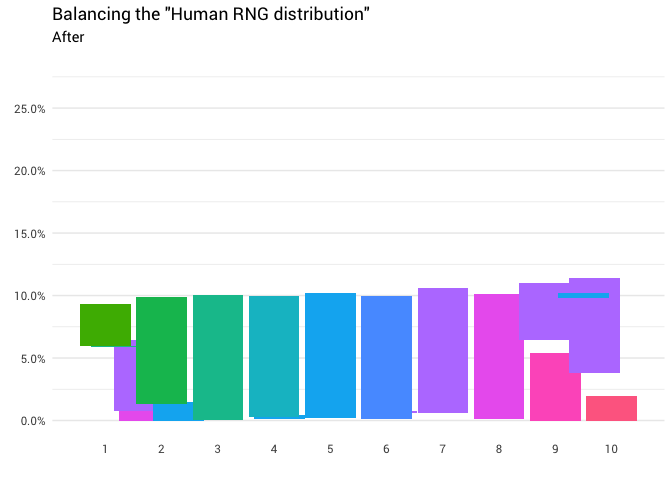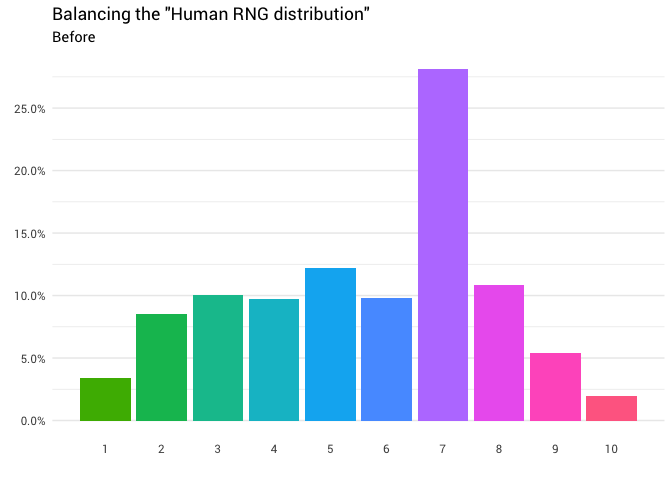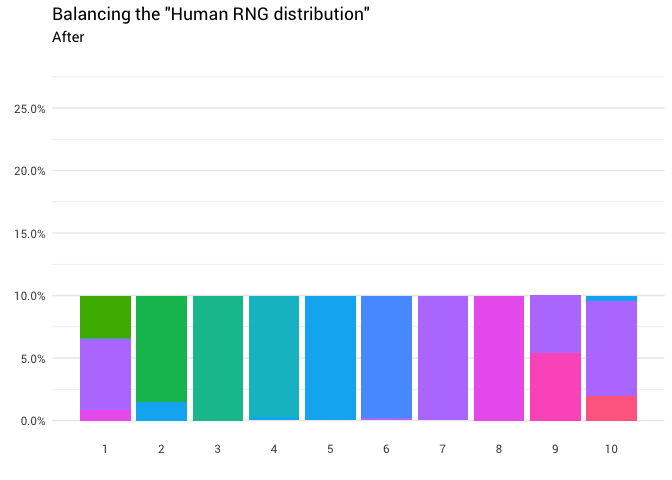
Großartig! Jetzt haben wir eine Umverteilungsfunktion. Schauen wir uns genau an, wie sich die Masse bewegt:

 balanced_probabilities %>% ggplot(aes(x = from, y = to)) + geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) + geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) + scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) + scale_fill_discrete(h = c(120, 360)) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(breaks = 1:10) + theme_minimal(base_family = "Roboto") + theme(panel.grid.minor = element_blank(), panel.grid.major = element_line(linetype = "dotted"), legend.position = "none") + labs(title = "Probability mass redistribution", x = "Original number", y = "Redistributed number") 

Diese Tabelle besagt, dass in etwa 8% der Fälle, in denen jemand acht als Zufallszahl anruft, Sie die Antwort als Einheit nehmen müssen. In den restlichen 92% der Fälle bleibt er der Acht.

Es wäre ziemlich einfach, das Problem zu lösen, wenn wir Zugang zu einem Generator mit gleichmäßig verteilten Zufallszahlen (von 0 bis 1) hätten. Aber wir haben nur einen Raum voller Menschen. Glücklicherweise können Sie, wenn Sie bereit sind, sich mit ein paar kleinen Ungenauigkeiten abzufinden, aus Menschen ein ziemlich gutes RNG machen, ohne mehr als zweimal zu fragen.

Zurück zu unserer ursprünglichen Verteilung haben wir die folgenden Wahrscheinlichkeiten für jede Zahl, die verwendet werden können, um bei Bedarf jede Wahrscheinlichkeit neu zuzuweisen.

 probabilities %>% transmute(number = outcome, probability = scales::percent(p)) 

  ## # Ein Tibble: 10 x 2
 ## Zahlenwahrscheinlichkeit
 ## <dbl> <chr>
 ## 1 1 3,4%
 2 2 8,5%
 ## 3 3 10,0%
 ## 4 4 9,7%
 ## 5 5 12,2%
 ## 6 6 9,8%
 7 7 28,1%
 ## 8 8 10,9%
 ## 9 9 5,4%
 ## 10 10 1,9% 

Wenn uns zum Beispiel jemand acht als Zufallszahl gibt, müssen wir bestimmen, ob diese acht eine Einheit werden sollen oder nicht (Wahrscheinlichkeit 8%). Wenn wir eine andere Person nach einer Zufallszahl fragen, antwortet sie mit einer Wahrscheinlichkeit von 8,5% mit „zwei“. Wenn diese zweite Zahl also 2 ist, wissen wir, dass wir 1 als gleichmäßig verteilte Zufallszahl zurückgeben müssen.

Wenn wir diese Logik auf alle Zahlen erweitern, erhalten wir den folgenden Algorithmus:

• Fragen Sie eine Person nach einer Zufallszahl, $$$n_1$ .
• $$$n_1 = 1, 2, 3, 4, 6, 9,$ oder $$$10$ ::
  
  • Deine Zufallszahl $$$n_1$
• Wenn $$$n_1 = 5$ ::
  
  • Fragen Sie eine andere Person nach einer Zufallszahl ( $$$n_2$ )
  • Wenn $$$n_2 = 5$ (12,2%):
    
    • Deine Zufallszahl 2
  • Wenn $$$n_2 = 10$ (1,9%):
    
    • Deine Zufallszahl 4
  • Ansonsten ist Ihre Zufallszahl 5
• Wenn $$$n_1 = 7$ ::
  
  • Fragen Sie eine andere Person nach einer Zufallszahl ( $$$n_2$ )
  • Wenn $$$n_2 = 2$ oder $$$5$ (20,7%):
    
    • Deine Zufallszahl 1
  • Wenn $$$n_2 = 8$ oder $$$9$ (16,2%):
    
    • Ihre Zufallszahl ist 9
  • Wenn $$$n_2 = 7$ (28,1%):
    
    • Ihre Zufallszahl ist 10
  • Ansonsten ist Ihre Zufallszahl 7
• Wenn $$$n_1 = 8$ ::
  
  • Fragen Sie eine andere Person nach einer Zufallszahl ( $$$n_2$ )
  • Wenn $$$n_2 = 2$ (8,5%):
    
    • Deine Zufallszahl 1
  • Ansonsten ist Ihre Zufallszahl 8

Mit diesem Algorithmus können Sie eine Gruppe von Personen verwenden, um einem Generator gleichmäßig verteilter Zufallszahlen von 1 bis 10 nahe zu kommen!