Neuronale Netze und tiefes Lernen, Kapitel 3, Teil 2: Warum trägt Regularisierung dazu bei, die Umschulung zu reduzieren?

Empirisch haben wir gesehen, dass Regularisierung dazu beiträgt, die Umschulung zu reduzieren. Das ist inspirierend - aber leider ist nicht klar, warum Regularisierung hilft. Normalerweise erklären die Leute es auf irgendeine Weise: In gewissem Sinne sind kleinere Gewichte weniger komplex, was eine einfachere und effizientere Erklärung der Daten ermöglicht, weshalb sie bevorzugt werden sollten. Dies ist jedoch eine zu kurze Erklärung, und einige Teile davon mögen zweifelhaft oder mysteriös erscheinen. Lassen Sie uns diese Geschichte entfalten und mit kritischem Blick untersuchen. Nehmen wir dazu an, wir haben einen einfachen Datensatz, für den wir ein Modell erstellen möchten:


In Bezug auf die Bedeutung untersuchen wir hier das Phänomen der realen Welt, und x und y bezeichnen reale Daten. Unser Ziel ist es, ein Modell zu erstellen, mit dem wir y als Funktion von x vorhersagen können. Wir könnten versuchen, ein neuronales Netzwerk zu verwenden, um ein solches Modell zu erstellen, aber ich schlage etwas Einfacheres vor: Ich werde versuchen, y als Polynom in x zu modellieren. Ich werde dies anstelle von neuronalen Netzen tun, da die Verwendung von Polynomen die Erklärung besonders deutlich macht. Sobald wir uns mit dem Fall des Polynoms befassen, werden wir zur Nationalversammlung übergehen. In der obigen Grafik gibt es zehn Punkte, was bedeutet, dass wir ein eindeutiges Polynom 9. Ordnung y = a ₀ x ⁹ + a ₁ x ⁸ + ... + a _{9 finden können} , das genau zu den Daten passt. Und hier ist der Graph dieses Polynoms.


Perfekter Hit. Mit dem linearen Modell y = 2x können wir jedoch eine gute Annäherung erhalten


Welches ist besser? Welches ist wahrscheinlicher wahr? Was lässt sich besser auf andere Beispiele des gleichen Phänomens der realen Welt verallgemeinern?

Schwierige Fragen. Und sie können ohne zusätzliche Informationen über das zugrunde liegende Phänomen der realen Welt nicht genau beantwortet werden. Schauen wir uns jedoch zwei Möglichkeiten an: (1) Ein Modell mit einem Polynom 9. Ordnung beschreibt das Phänomen der realen Welt wirklich und verallgemeinert sich daher perfekt; (2) Das richtige Modell ist y = 2x, aber mit dem Messfehler ist zusätzliches Rauschen verbunden, sodass das Modell nicht perfekt passt.

A priori kann man nicht sagen, welche der beiden Möglichkeiten richtig ist (oder dass es keine dritte gibt). Logischerweise kann sich jeder von ihnen als wahr herausstellen. Und der Unterschied zwischen ihnen ist nicht trivial. Ja, basierend auf den verfügbaren Daten kann gesagt werden, dass es nur einen geringen Unterschied zwischen den Modellen gibt. Angenommen, wir möchten den Wert von y vorhersagen, der einem großen Wert von x entspricht, der viel größer ist als der in der Grafik gezeigte. Wenn wir dies versuchen, wird ein großer Unterschied zwischen den Vorhersagen der beiden Modelle auftreten, da der Term x ⁹ im Polynom 9. Ordnung dominiert und das lineare Modell linear bleibt.

Ein Gesichtspunkt in Bezug auf das Geschehen ist die Feststellung, dass eine einfachere Erklärung in der Wissenschaft verwendet werden sollte, wenn dies möglich ist. Wenn wir ein einfaches Modell finden, das viele Bezugspunkte erklärt, wollen wir nur rufen: "Eureka!" Schließlich ist es unwahrscheinlich, dass eine einfache Erklärung rein zufällig erscheint. Wir vermuten, dass das Modell eine mit dem Phänomen verbundene Wahrheit hervorbringen sollte. In diesem Fall scheint das Modell y = 2x + Rauschen viel einfacher zu sein als y = a ₀ x ⁹ + a ₁ x ⁸ + ... Es wäre überraschend, wenn die Einfachheit zufällig entstanden wäre, sodass wir vermuten, dass y = 2x + Rauschen etwas ausdrückt zugrunde liegende Wahrheit. Unter diesem Gesichtspunkt untersucht das Modell 9. Ordnung lediglich die Wirkung von lokalem Rauschen. Obwohl das Modell 9. Ordnung für diese spezifischen Referenzpunkte perfekt funktioniert, kann es nicht auf andere Punkte verallgemeinert werden, wodurch das lineare Modell mit Rauschen bessere Vorhersagefähigkeiten aufweist.

Mal sehen, was dieser Standpunkt für neuronale Netze bedeutet. Angenommen, in unserem Netzwerk gibt es hauptsächlich geringe Gewichte, wie dies normalerweise in regulierten Netzwerken der Fall ist. Aufgrund seines geringen Gewichts ändert sich das Netzwerkverhalten nicht wesentlich, wenn hier und da mehrere zufällige Eingaben geändert werden. Infolgedessen ist es für das regulierte Netzwerk schwierig, die Auswirkungen des in den Daten vorhandenen lokalen Rauschens zu lernen. Dies ähnelt dem Wunsch, sicherzustellen, dass einzelne Beweise die Leistung des gesamten Netzwerks nicht stark beeinflussen. Stattdessen wird das regulierte Netzwerk geschult, um auf Beweise zu reagieren, die häufig in Trainingsdaten enthalten sind. Umgekehrt kann ein Netzwerk mit großen Gewichten sein Verhalten als Reaktion auf kleine Änderungen der Eingabedaten ziemlich stark ändern. Daher kann ein unregelmäßiges Netzwerk große Gewichte verwenden, um ein komplexes Modell zu trainieren, das viele Rauschinformationen in Trainingsdaten enthält. Kurz gesagt, die Einschränkungen regulierter Netzwerke ermöglichen es ihnen, relativ einfache Modelle auf der Grundlage von Mustern zu erstellen, die häufig in Trainingsdaten zu finden sind, und sie sind resistent gegen Abweichungen, die durch Rauschen in Trainingsdaten verursacht werden. Es besteht die Hoffnung, dass unsere Netzwerke dadurch das Phänomen selbst untersuchen und das gewonnene Wissen besser verallgemeinern können.

Nach alledem sollte die Idee, einfacheren Erklärungen den Vorzug zu geben, Sie nervös machen. Manchmal nennen die Leute diese Idee „Occams Rasiermesser“ und wenden sie eifrig an, als hätte sie den Status eines allgemeinen wissenschaftlichen Prinzips. Dies ist natürlich kein allgemeines wissenschaftliches Prinzip. Es gibt keinen a priori logischen Grund, einfache Erklärungen komplexen vorzuziehen. Manchmal ist eine kompliziertere Erklärung richtig.

Lassen Sie mich zwei Beispiele beschreiben, wie sich eine komplexere Erklärung als richtig herausstellte. In den 1940er Jahren kündigte der Physiker Marcel Shane die Entdeckung eines neuen Teilchens an. Das Unternehmen, für das er arbeitete, General Electric, war begeistert und verbreitete die Veröffentlichung dieser Veranstaltung in großem Umfang. Der Physiker Hans Bethe war jedoch skeptisch. Bethe besuchte Shane und studierte die Platten mit Spuren von Shane's neuem Partikel. Shane zeigte Beta Platte für Platte, aber Bete fand bei jedem von ihnen ein Problem, das darauf hinwies, dass diese Daten abgelehnt werden mussten. Schließlich zeigte Shane Beta einen Rekord, der fit aussah. Bethe sagte, es sei wahrscheinlich nur eine statistische Abweichung. Shane: Ja, aber die Wahrscheinlichkeit, dass dies auf Statistiken zurückzuführen ist, selbst nach Ihrer eigenen Formel, ist eins zu fünf. Bethe: "Ich habe mir aber schon fünf Platten angesehen." Schließlich sagte Shane: "Aber Sie haben jede meiner Aufzeichnungen, jedes gute Bild mit einer anderen Theorie erklärt, und ich habe eine Hypothese, die alle Aufzeichnungen auf einmal erklärt, woraus folgt, dass wir über ein neues Teilchen sprechen." Bethe antwortete: „Der einzige Unterschied zwischen meinen und Ihren Erklärungen besteht darin, dass Ihre falsch und meine richtig sind. Deine einzige Erklärung ist falsch und alle meine Erklärungen sind richtig. “ Anschließend stellte sich heraus, dass die Natur mit Bethe übereinstimmte und Shane's Partikel verdampften.

Im zweiten Beispiel entdeckte der Astronom Urbain Jean Joseph Le Verrier 1859, dass die Form der Merkurbahn nicht Newtons Theorie der universellen Gravitation entspricht. Es gab eine winzige Abweichung von dieser Theorie, und dann wurden mehrere Optionen zur Lösung des Problems vorgeschlagen, die darauf hinausliefen, dass Newtons Theorie insgesamt korrekt ist und nur eine geringfügige Änderung erfordert. Und 1916 zeigte Einstein, dass diese Abweichung mit seiner allgemeinen Relativitätstheorie, die sich radikal von der Newtonschen Schwerkraft unterscheidet und auf einer viel komplexeren Mathematik basiert, gut erklärt werden kann. Trotz dieser zusätzlichen Komplexität wird heute allgemein angenommen, dass Einsteins Erklärung richtig ist und die Newtonsche Schwerkraft selbst in modifizierter Form falsch ist. Dies geschieht insbesondere, weil wir heute wissen, dass Einsteins Theorie viele andere Phänomene erklärt, mit denen Newtons Theorie Schwierigkeiten hatte. Noch erstaunlicher ist, dass Einsteins Theorie einige Phänomene genau vorhersagt, die die Newtonsche Schwerkraft überhaupt nicht vorhergesagt hat. Diese beeindruckenden Eigenschaften waren jedoch in der Vergangenheit nicht offensichtlich. Auf der Grundlage der Einfachheit zu urteilen, hätte eine modifizierte Form der Newtonschen Theorie attraktiver ausgesehen.

Aus diesen Geschichten lassen sich drei Moralitäten ableiten. Erstens ist es manchmal ziemlich schwierig zu entscheiden, welche der beiden Erklärungen „einfacher“ sein wird. Zweitens muss die Einfachheit, selbst wenn wir eine solche Entscheidung getroffen haben, äußerst sorgfältig geführt werden! Drittens ist der wahre Test des Modells nicht die Einfachheit, sondern wie gut es neue Phänomene unter neuen Verhaltensbedingungen vorhersagt.

In Anbetracht all dessen und Vorsicht werden wir eine empirische Tatsache akzeptieren - regulierte NS sind normalerweise besser verallgemeinert als irreguläre. Daher werden wir später in diesem Buch häufig die Regularisierung verwenden. Die erwähnten Geschichten werden nur benötigt, um zu erklären, warum noch niemand eine völlig überzeugende theoretische Erklärung dafür entwickelt hat, warum Regularisierung Netzwerken bei der Verallgemeinerung hilft. Die Forscher veröffentlichen weiterhin Arbeiten, in denen sie versuchen, verschiedene Ansätze zur Regularisierung auszuprobieren, sie zu vergleichen, herauszufinden, was am besten funktioniert, und zu verstehen, warum verschiedene Ansätze schlechter oder besser funktionieren. Regularisierung kann also wie eine Wolke behandelt werden. Wenn es ziemlich oft hilft, haben wir kein völlig zufriedenstellendes systemisches Verständnis dessen, was passiert - nur unvollständige heuristische und praktische Regeln.

Hier liegt eine tiefere Reihe von Problemen, die das Herz der Wissenschaft betreffen. Dies ist ein Verallgemeinerungsproblem. Durch die Regularisierung erhalten wir einen rechnergestützten Zauberstab, mit dem unsere Netzwerke Daten besser verallgemeinern können. Sie vermittelt jedoch kein grundlegendes Verständnis dafür, wie die Generalisierung funktioniert und wie sie am besten angegangen werden kann.

Diese Probleme gehen auf das Problem der Induktion zurück , dessen bekannte Interpretation vom schottischen Philosophen David Hume in dem Buch " A Study on Human Cognition " (1748) durchgeführt wurde. Das Induktionsproblem ist Gegenstand des " Theorems über das Fehlen freier Mahlzeiten " von David Walpert und William Macredie (1977).

Und das ist besonders ärgerlich, weil Menschen im normalen Leben phänomenal gut in der Lage sind, Daten zu verallgemeinern. Zeigen Sie dem Kind einige Bilder des Elefanten, und es wird schnell lernen, andere Elefanten zu erkennen. Natürlich kann er manchmal einen Fehler machen, zum Beispiel ein Nashorn mit einem Elefanten verwechseln, aber im Allgemeinen funktioniert dieser Prozess überraschend genau. Jetzt haben wir ein System - das menschliche Gehirn - mit einer großen Menge freier Parameter. Und nachdem ihm ein oder mehrere Trainingsbilder gezeigt wurden, lernt das System, sie auf andere Bilder zu verallgemeinern. In gewisser Weise kann unser Gehirn erstaunlich gut regulieren! Aber wie machen wir das? Dies ist uns derzeit nicht bekannt. Ich denke, dass wir in Zukunft leistungsfähigere Regularisierungstechnologien in künstlichen neuronalen Netzen entwickeln werden, Techniken, die es der Nationalversammlung letztendlich ermöglichen, Daten auf der Grundlage noch kleinerer Datensätze zu verallgemeinern.

Tatsächlich verallgemeinern sich unsere Netzwerke bereits viel besser als a priori zu erwarten wäre. Ein Netzwerk mit 100 versteckten Neuronen hat fast 80.000 Parameter. Wir haben nur 50.000 Bilder in Trainingsdaten. Dies ist dasselbe wie der Versuch, ein Polynom von 80.000 Ordnung über 50.000 Referenzpunkte zu strecken. Nach allen Angaben muss unser Netzwerk furchtbar umgeschult werden. Und doch, wie wir gesehen haben, verallgemeinert sich ein solches Netzwerk tatsächlich ziemlich gut. Warum passiert das? Dies ist nicht ganz klar. Es wurde die Hypothese aufgestellt, dass "die Dynamik des Lernens durch Gradientenabstieg in mehrschichtigen Netzwerken der Selbstregulierung unterliegt". Dies ist ein extremes Vermögen, aber auch eine ziemlich beunruhigende Tatsache, da wir nicht verstehen, warum dies geschieht. In der Zwischenzeit werden wir einen pragmatischen Ansatz verfolgen und, wo immer möglich, die Regularisierung anwenden. Dies wird für unsere Nationalversammlung von Vorteil sein.

Lassen Sie mich diesen Abschnitt beenden, indem ich zu dem zurückkehre, was ich zuvor nicht erklärt habe: Die Regularisierung von L2 begrenzt die Verschiebungen nicht. Natürlich wäre es einfach, das Regularisierungsverfahren so zu ändern, dass Verschiebungen reguliert werden. Empirisch ändert dies jedoch häufig nichts an den Ergebnissen, weshalb es in gewissem Maße eine Frage der Übereinstimmung ist, sich mit der Regularisierung von Verzerrungen zu befassen oder nicht. Es ist jedoch erwähnenswert, dass eine große Verschiebung ein Neuron nicht für Eingaben wie große Gewichte empfindlich macht. Daher müssen wir uns keine Gedanken über große Offsets machen, die es unseren Netzwerken ermöglichen, das Rauschen in den Trainingsdaten zu lernen. Gleichzeitig machen wir unsere Netzwerke flexibler in ihrem Verhalten, indem wir große Verschiebungen zulassen - insbesondere erleichtern große Verschiebungen die Sättigung von Neuronen, die wir möchten. Aus diesem Grund berücksichtigen wir normalerweise keine Offsets in der Regularisierung.

Andere Regularisierungstechniken

Neben L2 gibt es viele Regularisierungstechniken. Tatsächlich wurden bereits so viele Techniken entwickelt, dass ich bei allem Wunsch nicht alle kurz beschreiben konnte. In diesem Abschnitt werde ich kurz drei weitere Ansätze zur Reduzierung der Umschulung beschreiben: Regularisierung von L1, Abbruch und künstliche Erhöhung des Trainingssatzes. Wir werden sie nicht so gründlich studieren wie die vorherigen Themen. Stattdessen lernen wir sie nur kennen und schätzen gleichzeitig die Vielfalt der vorhandenen Regularisierungstechniken.

Regularisierung L1

Bei diesem Ansatz modifizieren wir die unregelmäßige Kostenfunktion, indem wir die Summe der absoluten Werte der Gewichte addieren:

$$

$$C = C_0 + \ frac {\ lambda} {n} \ sum_w | w | \ tag {95}$$

Intuitiv ähnelt dies der Regularisierung von L2, die für große Gewichte Geldstrafen berechnet und das Netzwerk dazu veranlasst, niedrige Gewichte zu bevorzugen. Natürlich ist der Regularisierungsterm L1 nicht wie der Regularisierungsterm L2, daher sollten Sie nicht genau dasselbe Verhalten erwarten. Versuchen wir zu verstehen, wie sich das Verhalten eines mit Regularisierung L1 trainierten Netzwerks von einem mit Regularisierung L2 trainierten Netzwerk unterscheidet.

Schauen Sie sich dazu die partiellen Ableitungen der Kostenfunktion an. Durch Differenzieren (95) erhalten wir:

$$

$$\ frac {\ partielles C} {\ partielles w} = \ frac {\ partielles C_0} {\ partielles w} + \ frac {\ lambda} {n} \, {\ rm sgn} (w) \ tag {96 }$$

wobei sgn (w) das Vorzeichen von w ist, dh +1, wenn w positiv ist, und -1, wenn w negativ ist. Mit diesem Ausdruck modifizieren wir die Rückausbreitung geringfügig, so dass ein stochastischer Gradientenabstieg unter Verwendung der Regularisierung L1 durchgeführt wird. Die endgültige Aktualisierungsregel für das L1-regulierte Netzwerk:

$$

$$w \ rightarrow w '= w- \ frac {\ eta \ lambda} {n} \ mbox {sgn} (w) - \ eta \ frac {\ partielle C_0} {\ partielle w} \ tag {97}$$

wobei wie üblich ∂C / ∂w optional unter Verwendung des Durchschnittswerts des Minipakets geschätzt werden kann. Vergleichen Sie dies mit der Regularisierungsaktualisierungsregel L2 (93):

$$

$$w \ rightarrow w '= w \ left (1 - \ frac {\ eta \ lambda} {n} \ right) - \ eta \ frac {\ partielle C_0} {\ partielle w} \ tag {98}$$

In beiden Ausdrücken bewirkt die Regularisierung eine Gewichtsreduzierung. Dies stimmt mit der intuitiven Vorstellung überein, dass beide Arten der Regularisierung große Gewichte benachteiligen. Gewichte werden jedoch auf unterschiedliche Weise reduziert. Bei der Regularisierung von L1 nehmen die Gewichte um einen konstanten Wert ab, der gegen 0 tendiert. Bei der Regularisierung von L2 nehmen die Gewichte um einen Wert proportional zu w ab. Wenn daher ein gewisses Gewicht einen großen Wert | w | hat, verringert die Regularisierung von L1 das Gewicht nicht so sehr wie L2. Und umgekehrt, wenn | w | klein, Regularisierung von L1 reduziert das Gewicht viel mehr als Regularisierung von L2. Infolgedessen tendiert die Regularisierung von L1 dazu, die Netzwerkgewichte auf eine relativ kleine Anzahl von Bindungen von hoher Bedeutung zu konzentrieren, während andere Gewichte gegen Null tendieren.

Ich habe ein Problem in der vorherigen Diskussion leicht geglättet - die partielle Ableitung ∂C / ∂w ist nicht definiert, wenn w = 0 ist. Dies liegt daran, dass die Funktion | w | es gibt einen akuten "Knick" am Punkt w = 0, daher kann er dort nicht unterschieden werden. Das ist aber nicht beängstigend. Wir wenden nur die übliche unregelmäßige Regel für den stochastischen Gradientenabstieg an, wenn w = 0 ist. Intuitiv ist daran nichts auszusetzen - Regularisierung sollte Gewichte reduzieren, und offensichtlich kann sie Gewichte, die bereits gleich 0 sind, nicht reduzieren. Genauer gesagt werden wir die Gleichungen (96) und (97) mit der Bedingung verwenden, dass sgn (0) = 0. Dies gibt uns eine bequeme und kompakte Regel für den stochastischen Gradientenabstieg mit der Regularisierung L1.

Ausnahme [Aussetzer]

Eine Ausnahme bildet eine völlig andere Regularisierungstechnik. Im Gegensatz zur Regularisierung von L1 und L2 betrifft die Ausnahme keine Änderung der Kostenfunktion. Stattdessen ändern wir das Netzwerk selbst. Lassen Sie mich die grundlegenden Mechanismen der Funktionsweise einer Ausnahme erläutern, bevor ich mich mit dem Thema befasse, warum sie funktioniert und mit welchen Ergebnissen.

Angenommen, wir versuchen, ein Netzwerk zu trainieren:


Nehmen wir insbesondere an, wir haben die Trainingseingabe x und die entsprechende gewünschte Ausgabe y. Normalerweise trainieren wir es, indem wir x direkt über das Netzwerk verteilen und uns dann zurück ausbreiten, um den Beitrag des Gradienten zu bestimmen. Eine Ausnahme ändert diesen Prozess. Wir beginnen damit, zufällig und vorübergehend die Hälfte der versteckten Neuronen im Netzwerk zu entfernen, wobei die Eingabe- und Ausgabe-Neuronen unverändert bleiben. Danach werden wir ungefähr ein solches Netzwerk haben. Beachten Sie, dass ausgeschlossene Neuronen, die vorübergehend entfernt werden, weiterhin im Diagramm markiert sind:


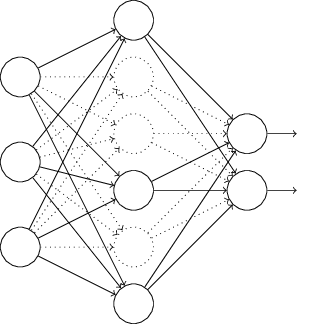
Wir übergeben x durch direkte Verteilung über das geänderte Netzwerk und verteilen das Ergebnis dann auch über das geänderte Netzwerk zurück. Nachdem wir dies mit einem Mini-Paket von Beispielen getan haben, aktualisieren wir die entsprechenden Gewichte und Offsets. Dann wiederholen wir diesen Vorgang, indem wir zuerst die ausgeschlossenen Neuronen wiederherstellen, dann eine neue zufällige Teilmenge versteckter Neuronen zum Entfernen auswählen, den Gradienten für ein anderes Minipaket auswerten und die Netzwerkgewichte und -versätze aktualisieren.

Wenn wir diesen Vorgang immer wieder wiederholen, erhalten wir ein Netzwerk, das einige Gewichte und Verschiebungen gelernt hat. Natürlich wurden diese Gewichte und Verschiebungen unter Bedingungen gelernt, bei denen die Hälfte der verborgenen Neuronen ausgeschlossen war.Und wenn wir das Netzwerk vollständig starten, werden wir doppelt so viele aktive versteckte Neuronen haben. Um dies zu kompensieren, halbieren wir die Gewichte, die von versteckten Neuronen kommen.

Das Ausschlussverfahren mag seltsam und willkürlich erscheinen. Warum sollte sie bei der Regularisierung helfen? Um zu erklären, was passiert, möchte ich, dass Sie die Ausnahme für eine Weile vergessen und die Ausbildung der Nationalversammlung auf übliche Weise präsentieren. Stellen Sie sich insbesondere vor, wir trainieren mehrere verschiedene NS mit denselben Trainingsdaten. Natürlich können Netzwerke zunächst variieren, und manchmal kann Training zu unterschiedlichen Ergebnissen führen. In solchen Fällen könnten wir eine Art Mittelungs- oder Abstimmungsschema anwenden, um zu entscheiden, welche der Ergebnisse akzeptiert werden sollen. Wenn wir beispielsweise fünf Netzwerke trainiert haben und drei von ihnen die Zahl als „3“ klassifizieren, ist dies wahrscheinlich die wahre Drei. Und die anderen beiden Netzwerke sind wahrscheinlich einfach falsch. Ein solches Mittelungsschema ist oft ein nützlicher (wenn auch teurer) Weg, um die Umschulung zu reduzieren. Der Grund istdass verschiedene Netzwerke auf unterschiedliche Weise umgeschult werden können und die Mittelwertbildung dazu beitragen kann, eine solche Umschulung zu vermeiden.

Wie hängt das alles mit Ausnahmen zusammen? Heuristisch gesehen ist es so, als würden wir verschiedene NS trainieren, wenn wir verschiedene Neutronensätze ausschließen. Daher ähnelt das Ausschlussverfahren den Mittelungseffekten über eine sehr große Anzahl verschiedener Netzwerke. Verschiedene Netzwerke werden auf unterschiedliche Weise umgeschult, so dass gehofft wird, dass der durchschnittliche Effekt des Ausschlusses die Umschulung verringert.

Eine verwandte heuristische Erklärung der Vorteile des Ausschlusses findet sich in einem der frühesten Werkemit dieser Technik: „Diese Technik reduziert die komplexe Gelenkanpassung von Neuronen, da sich das Neuron nicht auf die Anwesenheit bestimmter Nachbarn verlassen kann. Am Ende muss er zuverlässigere Eigenschaften lernen, die bei der Zusammenarbeit mit vielen verschiedenen zufälligen Untergruppen von Neuronen nützlich sein können. “ Mit anderen Worten, wenn wir uns unsere Nationalversammlung als ein Modell vorstellen, das Vorhersagen macht, wird eine Ausnahme eine Möglichkeit sein, die Stabilität des Modells gegenüber dem Verlust einzelner Beweismittelteile zu gewährleisten. In diesem Sinne ähnelt die Technik den Regularisierungen von L1 und L2, die darauf abzielen, die Gewichte zu reduzieren und auf diese Weise das Netzwerk widerstandsfähiger gegen den Verlust einzelner Verbindungen im Netzwerk zu machen.

Das wahre Maß für die Nützlichkeit des Ausschlusses ist natürlich sein enormer Erfolg bei der Verbesserung der Effizienz neuronaler Netze. In der OriginalarbeitWo diese Methode eingeführt wurde, wurde sie auf viele verschiedene Aufgaben angewendet. Wir sind besonders daran interessiert, dass die Autoren die Ausnahme auf die Klassifizierung von Zahlen aus MNIST angewendet haben, indem sie ein einfaches direktes Vertriebsnetz verwendet haben, das dem von uns untersuchten ähnlich ist. Das Papier stellt fest, dass bis dahin das beste Ergebnis für eine solche Architektur eine Genauigkeit von 98,4% war. Sie verbesserten es auf 98,7% unter Verwendung einer Kombination aus Ausschluss und einer modifizierten Form der Regularisierung L2. Ebenso beeindruckende Ergebnisse wurden für viele andere Aufgaben erzielt, einschließlich Muster- und Spracherkennung sowie Verarbeitung natürlicher Sprache. Die Ausnahme war besonders nützlich beim Training großer tiefer Netzwerke, bei denen häufig das Problem der Umschulung auftritt.

Trainingsdatensatz künstlich erweitern

Wir haben zuvor gesehen, dass unsere MNIST-Klassifizierungsgenauigkeit auf 80 Prozent gesunken ist, als wir nur 1.000 Trainingsbilder verwendet haben. Kein Wunder, dass unser Netzwerk mit weniger Daten weniger Möglichkeiten zum Schreiben von Zahlen durch Personen bietet. Versuchen wir, unser Netzwerk aus 30 versteckten Neuronen zu trainieren, indem wir verschiedene Volumina des Trainingssatzes verwenden, um die Änderung der Effizienz zu untersuchen. Wir trainieren mit der Minipaketgröße 10, der Lerngeschwindigkeit η = 0,5, dem Regularisierungsparameter λ = 5,0 und der Kostenfunktion mit Kreuzentropie. Wir werden ein Netzwerk von 30 Epochen mit einem vollständigen Datensatz trainieren und die Anzahl der Epochen proportional zur Verringerung des Volumens der Trainingsdaten erhöhen. Um den gleichen Gewichtsreduktionsfaktor für verschiedene Sätze von Trainingsdaten zu gewährleisten, verwenden wir den Regularisierungsparameter λ = 5,0 mit einem vollständigen Trainingssatz und reduzieren Sie ihn proportional mit einer Verringerung des Datenvolumens.


Es ist ersichtlich, dass die Klassifizierungsgenauigkeit mit der Zunahme der Trainingsdaten signifikant zunimmt. Dieses Wachstum dürfte sich mit einem weiteren Mengenanstieg fortsetzen. Nach der obigen Grafik zu urteilen, nähern wir uns natürlich der Sättigung. Angenommen, wir wiederholen dieses Diagramm in einer logarithmischen Abhängigkeit von der Menge der Trainingsdaten:


Es ist zu sehen, dass das Diagramm am Ende immer noch tendenziell steigt. Dies deutet darauf hin, dass wir wahrscheinlich ein viel besser funktionierendes Netzwerk erhalten werden, selbst wenn wir eine viel größere Datenmenge verwenden - zum Beispiel Millionen oder sogar Milliarden handgeschriebener Beispiele anstelle von 50.000.

Es ist eine gute Idee, mehr Trainingsdaten zu erhalten. Leider kann dies teuer sein, so dass es in der Praxis nicht immer möglich ist. Es gibt jedoch eine andere Idee, die fast genauso gut funktionieren kann - den Datensatz künstlich zu vergrößern. Nehmen wir zum Beispiel an, wir nehmen ein Bild einer Fünf von MNIST und drehen es ein wenig, Grad um 15:



Dies ist eindeutig die gleiche Zahl. Auf Pixelebene unterscheidet es sich jedoch stark von den in der MNIST-Datenbank verfügbaren Bildern. Es ist anzunehmen, dass das Hinzufügen dieses Bildes zum Trainingsdatensatz unserem Netzwerk helfen kann, mehr über die Bildklassifizierung zu erfahren. Darüber hinaus sind wir natürlich nicht auf die Möglichkeit beschränkt, nur ein Bild hinzuzufügen. Wir können unsere Trainingsdaten erweitern, indem wir alle Trainingsbilder von MNIST ein paar kleine Umdrehungen machen und dann den erweiterten Satz von Trainingsdaten verwenden, um die Effizienz des Netzwerks zu steigern.

Diese Idee ist sehr mächtig und weit verbreitet. Schauen wir uns die Ergebnisse der wissenschaftlichen Arbeit ander verschiedene Variationen dieser Idee auf MNIST anwendete. Eine der Architekturen der von ihnen betrachteten Netzwerke ähnelte der von uns verwendeten - ein direktes Verteilungsnetzwerk mit 800 versteckten Neuronen, das die Kostenfunktion mit Kreuzentropie verwendet. Durch den Start dieses Netzwerks mit dem Standard-MNIST-Trainingssatz wurde eine Klassifizierungsgenauigkeit von 98,4% erreicht. Aber dann erweiterten sie die Trainingsdaten und verwendeten nicht nur die oben beschriebene Drehung, sondern auch die Übertragung und Verzerrung von Bildern. Nachdem sie das Netzwerk auf fortgeschrittene Daten geschult hatten, erhöhten sie die Genauigkeit auf 98,9%. Sie experimentierten auch mit den sogenannten "Elastische Verzerrung", eine spezielle Art der Bildverzerrung, um die zufälligen Vibrationen der Handmuskeln zu beseitigen. Mit elastischen Verzerrungen zur Erweiterung der Daten erreichten sie eine Genauigkeit von 99,3%. Im Wesentlichen erweiterten sie ihre Netzwerkerfahrung,Geben Sie ihr verschiedene handschriftliche Variationen, die in echter Handschrift zu finden sind.

Varianten dieser Idee können verwendet werden, um die Leistung vieler Lernaufgaben zu verbessern, nicht nur zur Handschrifterkennung. Das allgemeine Prinzip besteht darin, die Trainingsdaten zu erweitern, indem Operationen auf sie angewendet werden, die die in der Realität auftretenden Abweichungen widerspiegeln. Solche Variationen sind leicht zu finden. Angenommen, wir erstellen NS für die Spracherkennung. Menschen können Sprache auch bei Verzerrungen wie Hintergrundgeräuschen erkennen. Daher können Sie die Daten durch Hinzufügen von Hintergrundgeräuschen erweitern. Wir können auch beschleunigte und langsame Sprache erkennen. Dies ist eine weitere Möglichkeit, Trainingsdaten zu erweitern. Diese Techniken werden nicht immer verwendet. Anstatt beispielsweise den Trainingssatz durch Hinzufügen von Rauschen zu erweitern, kann es effizienter sein, die Eingabe durch Anwenden eines Rauschfilters zu bereinigen. Es lohnt sich jedoch, die Idee zu berücksichtigen, das Trainingsset zu erweitern.und suchen Sie nach Möglichkeiten, es zu verwenden.

Übung

• Wie oben erläutert, besteht eine Möglichkeit, die Trainingsdaten von MNIST zu erweitern, darin, kleine Rotationen der Trainingsbilder zu verwenden. Welches Problem kann auftreten, wenn wir die Drehung der Bilder in beliebigen Winkeln zulassen?

Big-Data-Exkurs und die Bedeutung des Vergleichs der Klassifizierungsgenauigkeit

Lassen Sie uns noch einmal einen Blick darauf werfen, wie sich die Genauigkeit unserer NS in Abhängigkeit von der Größe des Trainingssatzes ändert:


Angenommen, wir würden anstelle von NS eine andere Technologie für maschinelles Lernen verwenden, um Zahlen zu klassifizieren. Wir werden beispielsweise versuchen, die SVM-Methode (Support Vector Machine) zu verwenden, die wir in Kapitel 1 kurz kennengelernt haben. Machen Sie sich also keine Sorgen, wenn Sie mit SVM nicht vertraut sind. Wir müssen die Details nicht verstehen. Wir werden SVM über die Scikit-Learn-Bibliothek verwenden. So variiert die Effektivität von SVM mit der Größe des Trainingssatzes. Zum Vergleich habe ich den Zeitplan und die Ergebnisse der Nationalversammlung aufgestellt.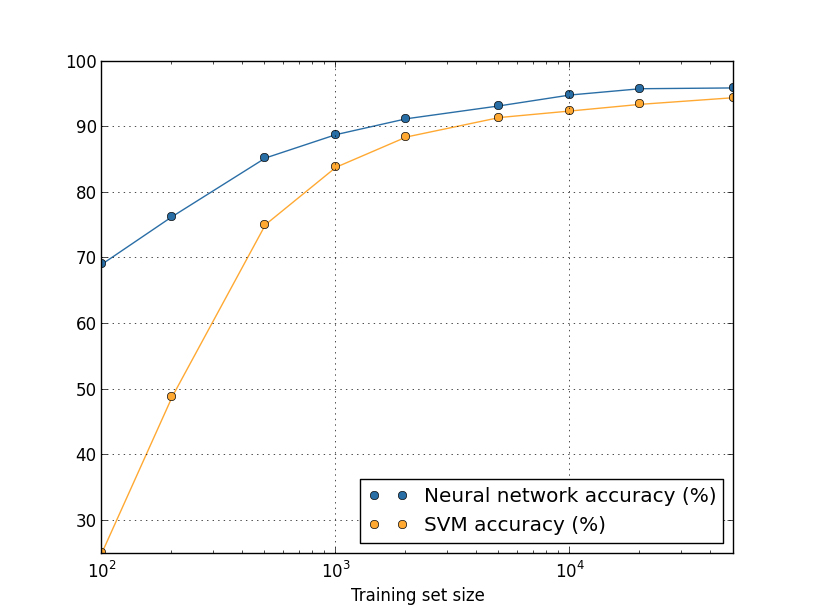


Wahrscheinlich das erste, was auffällt - NS übertrifft SVM in jeder Größe des Trainingssatzes. Das ist gut, obwohl es sich nicht lohnt, daraus weitreichende Schlussfolgerungen zu ziehen, da ich die vordefinierten Einstellungen für das Scikit-Lernen verwendet habe und wir ziemlich ernsthaft an unserem NS gearbeitet haben. Eine weniger anschauliche, aber interessantere Tatsache, die sich aus der Grafik ergibt, ist, dass wenn wir unsere SVM mit 50.000 Bildern trainieren, sie besser funktioniert (94,48% Genauigkeit) als unsere mit 5000 Bildern trainierte NS ( 93,24%). Mit anderen Worten, eine Zunahme des Trainingsdatenvolumens gleicht manchmal den Unterschied in den MO-Algorithmen aus.

Es kann etwas Interessanteres passieren. Angenommen, wir versuchen, ein Problem mit zwei Algorithmen MO, A und B zu lösen. Manchmal kommt es vor, dass Algorithmus A bei einem Satz von Trainingsdaten vor Algorithmus B und Algorithmus B bei einem anderen Satz von Trainingsdaten vor Algorithmus A liegt. Wir haben das oben nicht gesehen - dann würden sich die Graphen schneiden - aber das passiert . Die richtige Antwort auf die Frage: "Ist Algorithmus A Algorithmus B überlegen?" in der Tat: "Welchen Trainingsdatensatz verwenden Sie?"

All dies muss sowohl bei der Entwicklung als auch beim Lesen wissenschaftlicher Arbeiten berücksichtigt werden. Viele Arbeiten konzentrieren sich darauf, neue Tricks zu finden, um bessere Ergebnisse mit Standardmessdatensätzen zu erzielen. „Mit unserer Superfood-Technologie konnten wir den Standard-Vergleichssatz Y um X% verbessern“ - das kanonische Antragsformular in einer solchen Studie. Manchmal sind solche Aussagen tatsächlich interessant, aber es lohnt sich zu verstehen, dass sie nur im Kontext eines bestimmten Trainingssatzes anwendbar sind. Stellen Sie sich eine alternative Geschichte vor, in der Personen, die ursprünglich ein Vergleichsset erstellt haben, ein größeres Forschungsstipendium erhalten haben. Sie könnten zusätzliches Geld verwenden, um zusätzliche Daten zu sammeln. Es ist möglich, dass die „Verbesserung“ der Super-Duper-Technologie in einem größeren Datensatz verschwindet. Mit anderen Worten,Das Wesentliche der Verbesserung kann nur ein Unfall sein. Daraus sollte die folgende Moral in den Bereich der praktischen Anwendung aufgenommen werden: Wir brauchen sowohl verbesserte Algorithmen als auch verbesserte Trainingsdaten. Es ist nichts Falsches daran, nach verbesserten Algorithmen zu suchen, aber stellen Sie sicher, dass Sie sich nicht darauf konzentrieren und den einfacheren Weg zum Gewinnen ignorieren, indem Sie das Volumen oder die Qualität der Trainingsdaten erhöhen.

Herausforderung

• . ? . – , , , . , . - ? , .

Zusammenfassung

Wir haben unser Eintauchen in Umschulung und Regularisierung abgeschlossen. Natürlich werden wir auf diese Probleme zurückkommen. Wie ich bereits mehrfach erwähnt habe, ist die Umschulung im Bereich der NS ein großes Problem, insbesondere wenn Computer leistungsfähiger werden und wir größere Netzwerke trainieren können. Infolgedessen ist es dringend erforderlich, wirksame Regularisierungstechniken zu entwickeln, um die Umschulung zu verringern. Daher ist dieser Bereich heute sehr aktiv.

Gewichtsinitialisierung

Wenn wir unsere NS erstellen, müssen wir die Anfangswerte von Gewichten und Offsets auswählen. Bisher haben wir sie gemäß den in Kapitel 1 kurz beschriebenen Richtlinien ausgewählt. Ich möchte Sie daran erinnern, dass wir Gewichte und Offsets basierend auf einer unabhängigen Gaußschen Verteilung mit einer mathematischen Erwartung von 0 und einer Standardabweichung von 1 ausgewählt haben. Dieser Ansatz hat gut funktioniert, scheint aber ziemlich willkürlich zu sein, also lohnt es sich Überarbeiten Sie es und überlegen Sie, ob es möglich ist, die anfänglichen Gewichte und Verschiebungen besser zuzuweisen und unseren NSs möglicherweise dabei zu helfen, schneller zu lernen.

Es stellt sich heraus, dass der Initialisierungsprozess im Vergleich zur normalisierten Gaußschen Verteilung erheblich verbessert werden kann. Um dies zu verstehen, nehmen wir an, wir arbeiten mit einem Netzwerk mit einer großen Anzahl von Eingangsneuronen, beispielsweise mit 1000. Nehmen wir an, wir haben die normalisierte Gaußsche Verteilung verwendet, um Gewichte zu initialisieren, die mit der ersten verborgenen Schicht verbunden sind. Bisher werde ich mich nur auf die Skalen konzentrieren, die die Eingangsneuronen mit dem ersten Neuron in der verborgenen Schicht verbinden, und den Rest des Netzwerks ignorieren:


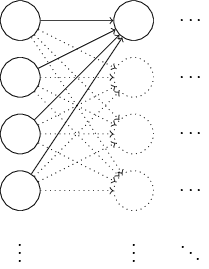
Stellen wir uns der Einfachheit halber vor, wir versuchen, das Netzwerk mit Eingang x zu trainieren, in dem die Hälfte der Eingangsneuronen eingeschaltet ist, dh einen Wert von 1 hat und die Hälfte ausgeschaltet ist, dh einen Wert von 0. Das nächste Argument funktioniert in einem allgemeineren Fall, aber es ist einfacher für Sie werde ihn an diesem speziellen Beispiel verstehen. Betrachten Sie die gewichtete Summe z = ∑ _j w _j x _j + b der Eingaben für ein verstecktes Neuron. 500 Mitglieder der Summe verschwinden, weil die entsprechenden x _j 0 sind. Daher ist z die Summe von 501 normalisierten Gaußschen Zufallsvariablen, 500 Gewichten und 1 zusätzlichen Versatz. Daher hat der z-Wert selbst eine Gaußsche Verteilung mit einer mathematischen Erwartung von 0 und einer Standardabweichung von √501 ≈ 22,4. Das heißt, z hat eine ziemlich breite Gaußsche Verteilung ohne scharfe Spitzen:


Insbesondere zeigt dieser Graph, dass | z | wahrscheinlich ziemlich groß ist, dh z ≤ 1 oder z ≤ -1. In diesem Fall liegt die Ausgabe der versteckten Neuronen σ (z) sehr nahe bei 1 oder 0. Dies bedeutet, dass unser verstecktes Neuron gesättigt ist. Und wenn dies geschieht, führen kleine Gewichtsänderungen, wie wir bereits wissen, zu geringfügigen Änderungen der Aktivierung eines verborgenen Neurons. Diese winzigen Änderungen wirken sich wiederum praktisch nicht auf die verbleibenden Neutronen im Netzwerk aus, und wir werden die entsprechenden winzigen Änderungen in der Kostenfunktion sehen. Infolgedessen werden diese Gewichte sehr langsam trainiert, wenn wir den Gradientenabstiegsalgorithmus verwenden. Dies ähnelt der Aufgabe, die wir bereits in diesem Kapitel besprochen haben, bei der mit falschen Werten gesättigte Ausgangsneuronen das Lernen verlangsamen. Früher haben wir dieses Problem gelöst, indem wir eine Kostenfunktion geschickt ausgewählt haben. Obwohl dies bei gesättigten Ausgangsneuronen hilfreich war, hilft es leider überhaupt nicht bei der Sättigung versteckter Neuronen.

Jetzt sprach ich über die eingehenden Skalen der ersten verborgenen Schicht. Die gleichen Argumente gelten natürlich für die folgenden verborgenen Ebenen: Wenn die Gewichte in den späteren verborgenen Ebenen mit normalisierten Gaußschen Verteilungen initialisiert werden, liegt ihre Aktivierung häufig nahe bei 0 oder 1, und das Training verläuft sehr langsam.

Gibt es eine Möglichkeit, die besten Initialisierungsoptionen für Gewichte und Offsets auszuwählen, damit wir keine solche Sättigung erhalten und Lernverzögerungen vermeiden können? Angenommen, wir haben ein Neuron mit der Anzahl der eingehenden Gewichte n _in . Dann müssen wir diese Gewichte mit zufälligen Gaußschen Verteilungen mit einer mathematischen Erwartung von 0 und einer Standardabweichung von 1 / √n _in initialisieren. Das heißt, wir komprimieren die Gaußschen und verringern die Wahrscheinlichkeit einer Sättigung des Neurons. Dann wählen wir eine Gaußsche Verteilung für Verschiebungen mit einer mathematischen Erwartung von 0 und einer Standardabweichung von 1 aus Gründen, auf die ich etwas später zurückkommen werde. Nachdem wir diese Wahl getroffen haben, stellen wir erneut fest, dass z = ∑ _j w _j x _j + b eine Zufallsvariable mit einer Gaußschen Verteilung mit einer mathematischen Erwartung von 0, aber mit einem viel ausgeprägteren Peak als zuvor ist. Nehmen wir nach wie vor an, dass 500 Eingaben 0 und 500 1 sind. Dann ist es einfach zu zeigen (siehe Übung unten), dass z eine Gaußsche Verteilung mit einer mathematischen Erwartung von 0 und einer Standardabweichung von √ (3/2) = 1,22 hat ... Dieses Diagramm hat einen viel schärferen Peak, so dass selbst im Bild unten die Situation etwas untertrieben ist, da ich den Maßstab der vertikalen Achse im Vergleich zum vorherigen Diagramm ändern musste:


Ein solches Neuron wird mit einer viel geringeren Wahrscheinlichkeit gesättigt sein und dementsprechend mit einer geringeren Wahrscheinlichkeit auf eine Verlangsamung des Lernens stoßen.

Übung

• Bestätigen Sie, dass die Standardabweichung von z = ∑ _j w _j x _j + b vom vorherigen Absatz √ (3/2) ist. Überlegungen dazu: Die Varianz der Summe der unabhängigen Zufallsvariablen ist gleich der Summe der Varianzen der einzelnen Zufallsvariablen; Die Varianz entspricht dem Quadrat der Standardabweichung.

Ich habe oben erwähnt, dass wir weiterhin Verschiebungen initialisieren werden, basierend auf einer unabhängigen Gaußschen Verteilung mit einer mathematischen Erwartung von 0 und einer Standardabweichung von 1. Und dies ist normal, da dies die Wahrscheinlichkeit der Sättigung unserer Neuronen nicht stark erhöht. Tatsächlich spielt die Initialisierung von Offsets keine große Rolle, wenn es uns gelingt, das Sättigungsproblem zu vermeiden. Einige versuchen sogar, alle Offsets auf Null zu initialisieren, und verlassen sich auf die Tatsache, dass der Gradientenabstieg die entsprechenden Offsets lernen kann. Da die Wahrscheinlichkeit, dass sich dies auf etwas auswirkt, gering ist, werden wir weiterhin das gleiche Initialisierungsverfahren wie zuvor verwenden.

Vergleichen wir die Ergebnisse des alten und des neuen Ansatzes zur Initialisierung von Gewichten mithilfe der Aufgabe, Zahlen aus MNIST zu klassifizieren. Nach wie vor werden wir 30 versteckte Neuronen, ein Minipaket der Größe 10, einen Regularisierungsparameter & lambda = 5,0 und eine Kostenfunktion mit Kreuzentropie verwenden. Wir werden die Lerngeschwindigkeit schrittweise von η = 0,5 auf 0,1 reduzieren, da auf diese Weise die Ergebnisse in den Diagrammen etwas besser sichtbar sind. Sie können mit der alten Gewichtsinitialisierungsmethode lernen:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

Sie können auch lernen, wie Sie mit dem neuen Ansatz Gewichte initialisieren. Dies ist noch einfacher, da network2 standardmäßig Gewichte mit einem neuen Ansatz initialisiert. Dies bedeutet, dass wir den Aufruf net.large_weight_initializer () früher weglassen können:

 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

Wir zeichnen (mit dem Programm weight_initialization.py):


In beiden Fällen wird eine Klassifizierungsgenauigkeit von 96% erhalten. Die resultierende Genauigkeit ist in beiden Fällen nahezu gleich. Aber die neue Initialisierungstechnik erreicht diesen Punkt viel, viel schneller. Am Ende der letzten Ära des Trainings erreicht der alte Ansatz zur Initialisierung von Gewichten eine Genauigkeit von 87%, und der neue Ansatz nähert sich bereits 93%. Anscheinend beginnt ein neuer Ansatz zum Initialisieren von Gewichten an einer viel besseren Position, sodass wir viel schneller gute Ergebnisse erzielen. Das gleiche Phänomen wird beobachtet, wenn wir die Ergebnisse für ein Netzwerk mit 100 Neuronen konstruieren:


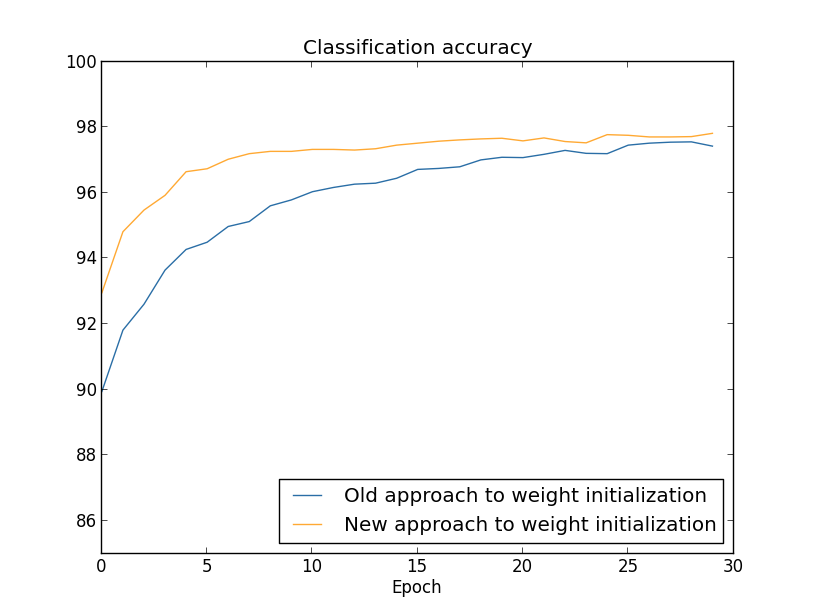
In diesem Fall treten zwei Kurven nicht auf. Meine Experimente besagen jedoch, dass die Genauigkeit fast zusammenfällt, wenn Sie etwas mehr Epochen hinzufügen. Auf der Grundlage dieser Experimente können wir daher sagen, dass die Verbesserung der Initialisierung von Gewichten das Training nur beschleunigt, aber die gesamte Netzwerkeffizienz nicht verändert. In Kapitel 4 werden wir jedoch Beispiele für NSs sehen, bei denen die langfristige Effizienz infolge der Initialisierung von Gewichten durch 1 / √n _in erheblich verbessert wird. Daher verbessert es nicht nur die Lerngeschwindigkeit, sondern manchmal auch die daraus resultierende Effektivität.

Der Ansatz zum Initialisieren von Gewichten durch 1 / √n _in hilft, das Training neuronaler Netze zu verbessern. Es wurden andere Techniken zum Initialisieren von Gewichten vorgeschlagen, von denen viele auf dieser Grundidee basieren. Ich werde sie hier nicht berücksichtigen, da 1 / √n _in für unsere Zwecke gut funktioniert. Wenn Sie interessiert sind, empfehle ich, die Diskussion auf den Seiten 14 und 15 in einem Artikel von Yoshua Benggio aus dem Jahr 2012 zu lesen.

Herausforderung

• Die Kombination aus Regularisierung und einer verbesserten Gewichtsinitialisierungsmethode. Manchmal liefert die Regularisierung von L2 automatisch Ergebnisse, die einer neuen Methode zum Initialisieren von Gewichten ähneln. Angenommen, wir verwenden den alten Ansatz zum Initialisieren von Gewichten. Skizzieren Sie ein heuristisches Argument, das beweist, dass: (1) wenn λ nicht zu klein ist, in den ersten Trainingsepochen die Schwächung der Gewichte fast vollständig dominiert; (2) wenn ηλ ≪ n ist, werden die Gewichte in der Epoche e ^{−ηλ / m-} mal schwächer; (3) Wenn λ nicht zu groß ist, verlangsamt sich die Schwächung der Gewichte, wenn die Gewichte auf etwa 1 / √n abnehmen, wobei n die Gesamtzahl der Gewichte im Netzwerk ist. Beweisen Sie, dass diese Bedingungen in den Beispielen erfüllt sind, für die in diesem Abschnitt Diagramme erstellt wurden.

Zurück zur Handschrifterkennung: Code

Lassen Sie uns die in diesem Kapitel beschriebenen Ideen umsetzen. Wir werden ein neues Programm entwickeln, network2.py, eine verbesserte Version des Programms network.py, das wir in Kapitel 1 erstellt haben. Wenn Sie den Code lange nicht gesehen haben, müssen Sie ihn möglicherweise schnell durchgehen. Dies sind nur 74 Codezeilen, und es ist leicht zu verstehen.

Wie bei network.py ist der Star von network2.py die Network-Klasse, mit der wir unsere NSs darstellen. Wir initialisieren die Klasseninstanz mit einer Liste der Größen der entsprechenden Netzwerkschichten, und bei Auswahl der Kostenfunktion handelt es sich standardmäßig um eine Kreuzentropie:

 class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost 

Die ersten Zeilen der __init__ -Methode sind mit network.py identisch und werden von sich aus verstanden. Die nächsten beiden Zeilen sind neu und wir müssen im Detail verstehen, was sie tun.

Beginnen wir mit der Methode default_weight_initializer. Er verwendet einen neuen, verbesserten Ansatz zum Initialisieren von Gewichten. Wie wir gesehen haben, werden bei diesem Ansatz die in das Neuron eintretenden Gewichte auf der Grundlage einer unabhängigen Gaußschen Verteilung mit einer mathematischen Erwartung von 0 und einer Standardabweichung von 1 geteilt durch die Quadratwurzel der Anzahl der eingehenden Verbindungen zum Neuron initialisiert. Außerdem initialisiert diese Methode die Offsets unter Verwendung der Gaußschen Verteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1. Hier ist der Code:

  def default_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] 

Um es zu verstehen, müssen Sie sich daran erinnern, dass np eine Numpy-Bibliothek ist, die sich mit linearer Algebra befasst. Wir haben es zu Beginn des Programms importiert. Beachten Sie auch, dass wir keine Verschiebungen in der ersten Schicht von Neuronen initialisieren. Die erste Schicht ist eingehend, daher werden keine Offsets verwendet. Das gleiche war network.py.

Zusätzlich zur default_weight_initializer-Methode erstellen wir eine large_weight_initializer-Methode. Es initialisiert Gewichte und Offsets nach dem alten Ansatz aus Kapitel 1, bei dem Gewichte und Offsets basierend auf einer unabhängigen Gaußschen Verteilung mit einer mathematischen Erwartung von 0 und einer Standardabweichung von 1 initialisiert werden. Dieser Code unterscheidet sich natürlich nicht wesentlich von default_weight_initializer:

  def large_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] 

Ich habe diese Methode hauptsächlich aufgenommen, weil es für uns bequemer war, die Ergebnisse dieses Kapitels und von Kapitel 1 zu vergleichen. Ich kann mir keine wirklichen Optionen vorstellen, bei denen ich die Verwendung empfehlen würde!

Die zweite Neuheit der __init__ -Methode ist die Initialisierung des Kostenattributs. Um zu verstehen, wie dies funktioniert, schauen wir uns die Klasse an, die wir zur Darstellung der entropieübergreifenden Kostenfunktion verwenden (die Direktive @staticmethod teilt dem Interpreter mit, dass diese Methode unabhängig vom Objekt ist, sodass der Parameter self nicht an die Methoden fn und delta übergeben wird).

 class CrossEntropyCost(object): @staticmethod def fn(a, y): return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): return (ay) 

Lass es uns herausfinden. Das erste, was hier zu sehen ist, ist, dass Kreuzentropie zwar eine Funktion aus mathematischer Sicht ist, wir sie jedoch als Python-Klasse implementieren, nicht als Python-Funktion. Warum habe ich mich dazu entschieden? In unserem Netzwerk spielt Wert zwei verschiedene Rollen. Offensichtlich - es ist ein Maß dafür, wie gut die Ausgangsaktivierung a dem gewünschten Ausgang y entspricht. Diese Rolle wird von der CrossEntropyCost.fn-Methode bereitgestellt. (Beachten Sie übrigens, dass der Aufruf von np.nan_to_num in CrossEntropyCost.fn sicherstellt, dass Numpy den Logarithmus von Zahlen nahe Null korrekt verarbeitet.) Die Kostenfunktion wird in unserem Netzwerk jedoch auf die zweite Weise verwendet. Wir erinnern uns aus Kapitel 2 daran, dass wir beim Starten des Backpropagation-Algorithmus den Ausgabefehler des Netzwerks δ ^L berücksichtigen müssen ^. Die Form des Ausgabefehlers hängt von der Kostenfunktion ab: Unterschiedliche Kostenfunktionen haben unterschiedliche Formen des Ausgabefehlers. Für die Kreuzentropie ist der Ausgabefehler wie folgt aus Gleichung (66) gleich:

$$

$$\ delta ^ L = a ^ L-y \ tag {99}$$

Daher definiere ich eine zweite Methode, CrossEntropyCost.delta, deren Ziel es ist, dem Netzwerk zu erklären, wie der Ausgabefehler berechnet wird. Und dann kombinieren wir diese beiden Methoden zu einer Klasse, die alles enthält, was unser Netzwerk über die Kostenfunktion wissen muss.

Aus einem ähnlichen Grund enthält network2.py eine Klasse, die eine quadratische Kostenfunktion darstellt. Einschließlich dieser zum Vergleich mit den Ergebnissen von Kapitel 1, da wir in Zukunft hauptsächlich Kreuzentropie verwenden werden. Der Code ist unten. Die QuadraticCost.fn-Methode ist eine einfache Berechnung der quadratischen Kosten, die mit der Ausgabe a und der gewünschten Ausgabe y verbunden sind. Der von QuadraticCost.delta zurückgegebene Wert basiert auf dem Ausdruck (30) für den Ausgabefehler des quadratischen Werts, den wir in Kapitel 2 abgeleitet haben.

 class QuadraticCost(object): @staticmethod def fn(a, y): return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): return (ay) * sigmoid_prime(z) 

Jetzt haben wir die Hauptunterschiede zwischen network2.py und network2.py herausgefunden. Alles ist sehr einfach. Es gibt andere kleine Änderungen, die ich unten beschreiben werde, einschließlich der Implementierung der Regularisierung von L2. Schauen wir uns vorher den vollständigen network2.py-Code an. Es ist nicht notwendig, es im Detail zu studieren, aber Sie sollten die Grundstruktur verstehen, insbesondere die Kommentare lesen, um zu verstehen, was die einzelnen Teile des Programms tun. Natürlich verbiete ich nicht, mich so oft mit dieser Frage zu beschäftigen, wie Sie möchten! Wenn Sie sich verlaufen haben, lesen Sie den Text nach dem Programm und kehren Sie erneut zum Code zurück. Im Allgemeinen ist es hier:

 """network2.py ~~~~~~~~~~~~~~   network.py,            .   –      , ,   .     ,    .   ,       . """ ####  #  import json import random import sys #  import numpy as np ####   ,      class QuadraticCost(object): @staticmethod def fn(a, y): """ ,    ``a``    ``y``. """ return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): """  delta   .""" return (ay) * sigmoid_prime(z) class CrossEntropyCost(object): @staticmethod def fn(a, y): """ ,    ``a``    ``y``. np.nan_to_num    .  ,   ``a``  ``y``      1.0,   (1-y)*np.log(1-a)  nan. np.nan_to_num ,       (0.0). """ return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): """  delta   .  ``z``    ,          delta     . """ return (ay) ####   Network class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].       ,   ``self.default_weight_initializer`` (.  ). """ self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost def default_weight_initializer(self): """            0    1,       ,       .          0    1.    ,         ,           . """ self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def large_weight_initializer(self): """          0    1.          0    1.    ,         ,           .         1,    .       . """ self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def feedforward(self, a): """  ,  ``a``  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, lmbda = 0.0, evaluation_data=None, monitor_evaluation_cost=False, monitor_evaluation_accuracy=False, monitor_training_cost=False, monitor_training_accuracy=False): """     -    . ``training_data`` –   ``(x, y)``,       .       ,    ``lmbda``.    ``evaluation_data``,     ,   .         ,     ,   .      :   ,    ,   ,              .  ,      30 ,        30 ,        .     ,   . """ if evaluation_data: n_data = len(evaluation_data) n = len(training_data) evaluation_cost, evaluation_accuracy = [], [] training_cost, training_accuracy = [], [] for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch( mini_batch, eta, lmbda, len(training_data)) print "Epoch %s training complete" % j if monitor_training_cost: cost = self.total_cost(training_data, lmbda) training_cost.append(cost) print "Cost on training data: {}".format(cost) if monitor_training_accuracy: accuracy = self.accuracy(training_data, convert=True) training_accuracy.append(accuracy) print "Accuracy on training data: {} / {}".format( accuracy, n) if monitor_evaluation_cost: cost = self.total_cost(evaluation_data, lmbda, convert=True) evaluation_cost.append(cost) print "Cost on evaluation data: {}".format(cost) if monitor_evaluation_accuracy: accuracy = self.accuracy(evaluation_data) evaluation_accuracy.append(accuracy) print "Accuracy on evaluation data: {} / {}".format( self.accuracy(evaluation_data), n_data) print return evaluation_cost, evaluation_accuracy, \ training_cost, training_accuracy def update_mini_batch(self, mini_batch, eta, lmbda, n): """    ,          -. ``mini_batch`` –    ``(x, y)``, ``eta`` –  , ``lmbda`` -  , ``n`` -     .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) # backward pass delta = (self.cost).delta(zs[-1], activations[-1], y) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """  l      ,      . l = 1    , l = 2 – ,   .    ,   python      . """ for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def accuracy(self, data, convert=False): """    ``data``,      .   –        .  ``convert``  False,    –    ( )  True,   .    - ,  ``y`` -     .  ,       .           .          ?     –       ,      .   ,      .       mnist_loader.load_data_wrapper. """ if convert: results = [(np.argmax(self.feedforward(x)), np.argmax(y)) for (x, y) in data] else: results = [(np.argmax(self.feedforward(x)), y) for (x, y) in data] return sum(int(x == y) for (x, y) in results) def total_cost(self, data, lmbda, convert=False): """      ``data``.  ``convert``   False,   –  (),   True,   –   . .    ,      ``accuracy``, . """ cost = 0.0 for x, y in data: a = self.feedforward(x) if convert: y = vectorized_result(y) cost += self.cost.fn(a, y)/len(data) cost += 0.5*(lmbda/len(data))*sum( np.linalg.norm(w)**2 for w in self.weights) return cost def save(self, filename): """    ``filename``.""" data = {"sizes": self.sizes, "weights": [w.tolist() for w in self.weights], "biases": [b.tolist() for b in self.biases], "cost": str(self.cost.__name__)} f = open(filename, "w") json.dump(data, f) f.close() ####  Network def load(filename): """    ``filename``.    Network. """ f = open(filename, "r") data = json.load(f) f.close() cost = getattr(sys.modules[__name__], data["cost"]) net = Network(data["sizes"], cost=cost) net.weights = [np.array(w) for w in data["weights"]] net.biases = [np.array(b) for b in data["biases"]] return net ####   def vectorized_result(j): """  10-    1.0   j     .      (0..9)     . """ e = np.zeros((10, 1)) e[j] = 1.0 return e def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

Zu den interessanteren Änderungen gehört die Einbeziehung der L2-Regularisierung. Obwohl dies eine große konzeptionelle Änderung ist, ist sie so einfach zu implementieren, dass Sie sie im Code möglicherweise nicht bemerken. In den meisten Fällen wird der Parameter lmbda einfach an verschiedene Methoden übergeben, insbesondere an Network.SGD. Alle Arbeiten werden in einer Programmzeile ausgeführt, die vierte vom Ende der Methode Network.update_mini_batch. Dort ändern wir die Aktualisierungsregel für den Gradientenabstieg, um die Gewichtsreduzierung einzuschließen. Die Änderung ist winzig, wirkt sich aber ernsthaft auf die Ergebnisse aus!

Dies geschieht übrigens häufig bei der Implementierung neuer Techniken in neuronalen Netzen. Wir haben Tausende von Wörtern damit verbracht, über Regularisierung zu diskutieren. Konzeptionell ist dies eine ziemlich subtile und schwer zu verstehende Sache. Es kann jedoch trivial zum Programm hinzugefügt werden! Unerwarteterweise können komplexe Techniken mit geringfügigen Codeänderungen implementiert werden.

Eine weitere kleine, aber wichtige Änderung im Code ist das Hinzufügen mehrerer optionaler Flags zur stochastischen Gradientenabstiegsmethode Network.SGD.Diese Flags ermöglichen es, Kosten und Genauigkeit entweder anhand von Trainingsdaten oder Auswertungsdaten zu verfolgen, die an Network.SGD übertragen werden können. Zu Beginn des Kapitels haben wir diese Flags häufig verwendet, aber lassen Sie mich zur Erinnerung ein Beispiel für ihre Verwendung geben:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True) 

Wir setzen Evaluierungsdaten durch Validierungsdaten. Wir können jedoch die Leistung von test_data und anderen Datensätzen verfolgen. Wir haben auch vier Flags, die die Notwendigkeit angeben, Kosten und Genauigkeit sowohl für Evaluierungsdaten als auch für Trainingsdaten zu verfolgen. Diese Flags sind standardmäßig auf False gesetzt. Sie sind jedoch hier enthalten, um die Effektivität des Netzwerks zu verfolgen. Darüber hinaus gibt die Network.SGD-Methode von network2.py ein Tupel mit vier Elementen zurück, das die Verfolgungsergebnisse darstellt. Sie können es so verwenden:

 >>> evaluation_cost, evaluation_accuracy, ... training_cost, training_accuracy = net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True) 

So ist evaluation_cost beispielsweise eine Liste von 30 Elementen, die die Kosten der geschätzten Daten am Ende jeder Ära enthalten. Solche Informationen sind äußerst nützlich, um das Verhalten eines neuronalen Netzwerks zu verstehen. Solche Informationen sind äußerst nützlich, um das Netzwerkverhalten zu verstehen. Es kann zum Beispiel verwendet werden, um Diagramme des Netzwerklernens über die Zeit zu zeichnen. So habe ich alle Grafiken aus diesem Kapitel erstellt. Wenn jedoch eines der Flags nicht gesetzt ist, ist das entsprechende Tupelelement eine leere Liste.

Weitere Code-Ergänzungen sind die Network.save-Methode, mit der das Network-Objekt auf der Festplatte gespeichert wird, und die Funktion zum Laden in den Speicher. Das Speichern und Laden erfolgt über JSON, nicht über die Python-Pickle- oder cPickle-Module, die üblicherweise zum Speichern auf der Festplatte und zum Laden in Python verwendet werden. Die Verwendung von JSON erfordert mehr Code als für pickle oder cPickle erforderlich wäre. Um zu verstehen, warum ich mich für JSON entschieden habe, stellen Sie sich vor, dass wir uns irgendwann in der Zukunft entschlossen haben, unsere Netzwerkklasse so zu ändern, dass es mehr als nur Sigmoid-Neuronen gibt. Um diese Änderung zu implementieren, würden wir höchstwahrscheinlich die in der Methode Network .__ init__ definierten Attribute ändern. Und wenn wir nur Gurke zum Speichern verwenden würden, würde unsere Ladefunktion nicht funktionieren. Die Verwendung von JSON mit expliziter Serialisierung erleichtert uns die Garantiedass ältere Versionen des Netzwerkobjekts heruntergeladen werden können.

Es gibt viele kleine Änderungen im Code, aber dies sind nur kleine Variationen von network.py. Das Endergebnis ist eine Erweiterung unseres Programms mit 74 Zeilen auf ein viel funktionaleres Programm mit 152 Zeilen.

Herausforderung

• Ändern Sie den folgenden Code, indem Sie die Regularisierung L1 einführen, und klassifizieren Sie damit MNIST-Ziffern nach einem Netzwerk mit 30 versteckten Neuronen. Können Sie einen Regularisierungsparameter auswählen, mit dem Sie das Ergebnis im Vergleich zu einem Netzwerk ohne Regularisierung verbessern können?
• Network.cost_derivative method network.py. . ? , ? network2.py Network.cost_derivative, CrossEntropyCost.delta. ?