Heute schauen wir uns ein Grafikpaket für die Julia-Sprache namens Luxor an . Dies ist eines dieser Werkzeuge, die den Prozess der Erstellung von Vektorbildern in die Lösung logischer Probleme mit einem begleitenden Sturm von Emotionen verwandeln.
Achtung Unter dem Schnitt 8,5 MB leichte Bilder und Gifs mit psychedelischen Eiern und vierdimensionalen Objekten, deren Betrachtung zu einer leichten Trübung des Geistes führen kann!
Installation
https://julialang.org - Laden Sie die Julia-Distribution von der offiziellen Website herunter. Dann starten wir den Interpreter und steuern die Befehle in seine Konsole:
using Pkg Pkg.add("Colors") Pkg.add("ColorSchemes") Pkg.add("Luxor")
Dadurch werden Pakete für fortgeschrittene Arbeiten mit Farben und Luxor selbst installiert.
Mögliche Probleme
Das Hauptproblem sowohl der modernen Programmierung im Allgemeinen als auch von Open Source im Besonderen besteht darin, dass einige Projekte auf anderen aufbauen, alle Fehler erben und aufgrund von Inkompatibilitäten sogar neue generieren. Wie viele andere Pakete verwendet Luxor für seine Arbeit andere Julia-Pakete, die wiederum Schalen bestehender Lösungen sind.
ImageMagick.jl wollte also keine Dateien herunterladen und speichern. Die Lösung wurde auf der Originalseite gefunden - es stellte sich heraus, dass er das kyrillische Alphabet in keiner Weise mag.
Problem Nummer zwei trat mit dem Low-Level-Grafikpaket von Cairo unter Windows 7 auf. Ich werde die Lösung hier verstecken:
Tanzen mit einem Tamburin- Wir geben den Interpreter ein
]add Gtk - das Paket für die Arbeit mit GUI wird installiert und fällt höchstwahrscheinlich während des Baus - Laden Sie als Nächstes gtk + -bundle_3.6.4-20130513_win64 herunter
- Während der Installation war alles in dem Ordner mit Julias Paketen erforderlich, aber gtk war während der Ausführung des Elements nicht fertig. Deshalb haben wir die fertige Version für unseren Computer heruntergeladen. Wir werfen den Inhalt des heruntergeladenen Archivs in das Verzeichnis C: \ Users \ User.julia \ packages \ WinRPM \ Y9QdZ \ deps \ usr \ x86_64-w64-mingw32 \ sys-root \ mingw (Ihr Pfad kann variieren)
- Starten Sie Julia und fahren Sie in
]build Gtk Nach dem ]build Gtk wir Luxor neu auf: ]build Luxor - Wir starten Julia neu und können sicher alles verwenden, was wir brauchen:
using Luxor
Bei anderen Problemen versuchen wir , unseren eigenen Fall zu finden.
Wenn Sie Animation ausprobieren möchten
Das Luxor-Paket erstellt Animationen mit ffmpeg , sofern diese auf Ihrem Computer vorhanden sind. ffmpeg ist eine plattformübergreifende Open-Source-Bibliothek für die Verarbeitung von Video- und Audiodateien, eine sehr nützliche Sache (es gibt einen guten Ausflug auf dem Hub ). Installieren Sie es:
- Laden Sie ffmpeg offsite herunter. In meinem Fall ist dies ein Download für Windows
- Entpacken Sie den Pfad zu ffmpeg.exe und schreiben Sie ihn in die Variable Path .
Weitere Informationen zum Verstopfen im Pfad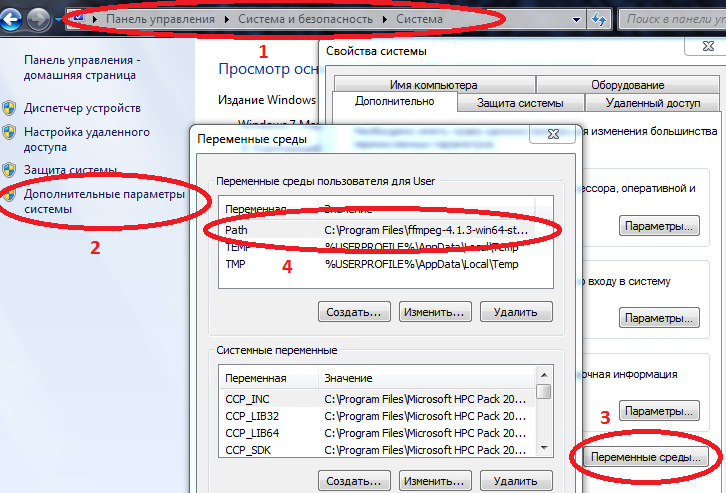
Computer / Systemeigenschaften / Erweiterte Systemparameter / Umgebungsvariablen / Pfad (Erstellen, falls nicht) und fügen Sie dort den Pfad zu Ihrer ffmpeg.exe hinzu
Beispiel C: \ Programme \ ffmpeg-4.1.3-win64-static \ bin
Wenn Path bereits Werte hat, trennen Sie diese mit einem Semikolon.
Wenn Sie nun ffmpeg mit den erforderlichen Parametern in die Befehlskonsole ( cmd ) fahren, wird es gestartet und funktioniert, und Julia kommuniziert nur mit ihm.
Hallo Welt
Beginnen wir mit einer kleinen Gefahr: Beim Erstellen eines Bildes wird eine Grafikdatei erstellt und im Arbeitsverzeichnis gespeichert. Das heißt, wenn Sie in REPL arbeiten, wird der Julia-Stammordner mit Bildern verstopft. Wenn Sie in Jupyter zeichnen, sammeln sich die Bilder neben dem Projektnotizbuch an. Daher ist es eine gute Angewohnheit, das Arbeitsverzeichnis vor Beginn der Arbeit an einem separaten Ort festzulegen:
using Luxor cd("C:\\Users\\User\\Desktop\\mycop")
Erstellen Sie die erste Zeichnung
Drawing(220, 220, "hw.png") origin() background("white") sethue("black") text("Hello world") circle(Point(0, 0), 100, :stroke) finish() preview()

Drawing() erstellt eine Zeichnung. Standardmäßig im PNG-Format lautet der Standarddateiname 'luxor-draw.png', die Standardgröße ist 800x800, für alle Formate außer png können Sie nicht ganzzahlige Größen angeben und Sie können auch Papierformate ("A0" verwenden "," A1 "," A2 "," A3 "," A4 "...)
finish() - Beendet das Zeichnen und schließt die Datei. Sie können es in einer externen Anzeigeanwendung mit preview() öffnen. Bei der Arbeit in Jupyter (IJulia) wird eine PNG- oder SVG-Datei im Editor angezeigt. Wenn Sie in Juno arbeiten, wird eine PNG- oder SVG-Datei im Grafikfenster angezeigt. In Repl wird das Tool zum Arbeiten mit Bildern aufgerufen, das Sie in Ihrem Betriebssystem für dieses Format festgelegt haben.
Das gleiche kann in Kurzform mit Makros geschrieben werden
@png begin text("Hello world") circle(Point(0, 0), 100, :stroke) end
Bei den Vektorformaten EPS, SVG, PDF funktioniert alles auf die gleiche Weise.
Euklidisches Ei

Dies ist eine ziemlich interessante Art, ein Ei zu zeichnen, und wenn Sie die Schlüsselpunkte verbinden und entlang der erhaltenen Linien schneiden, wird ein ausgezeichnetes Tangram herauskommen
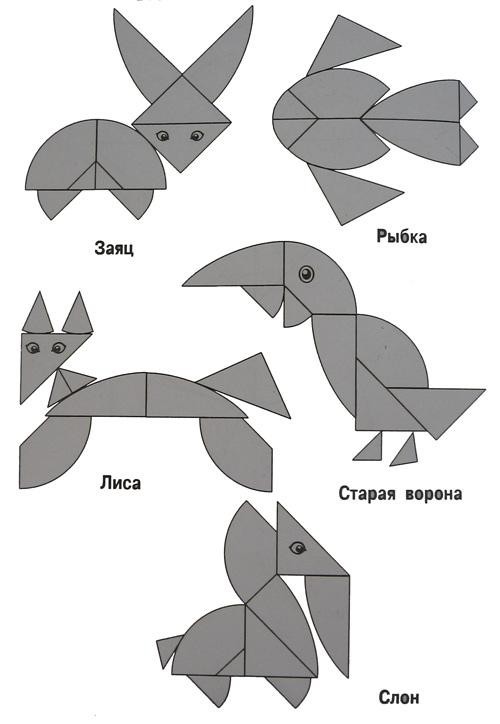
Beginnen wir mit dem Kreis:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) end 200 200 "egg0"

Alles ist sehr einfach: setdash("dot") - mit Punkten zeichnen, sethue("gray30") - Linienfarbe: sethue("gray30") kleiner, sethue("gray30") dunkler, sethue("gray30") näher an 100 sethue("gray30") weißer. Die Punktklasse wird ohne uns definiert und der Koordinatenmittelpunkt (0,0) kann durch den Buchstaben O angegeben werden O Fügen Sie zwei Kreise hinzu und unterschreiben Sie die Punkte:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke) end 600 400 "egg2"
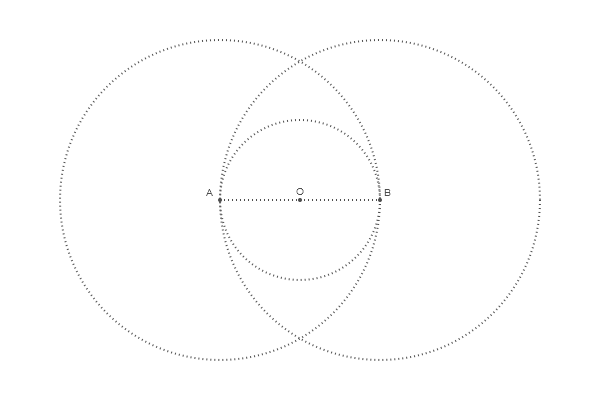
Um nach Schnittpunkten zu suchen, gibt es eine Funktion namens intersectionlinecircle() , die den Punkt oder die Punkte findet, an denen die Linie den Kreis schneidet. Somit können wir zwei Punkte finden, an denen einer der Kreise eine imaginäre vertikale Linie schneidet, die durch O gezogen wird. Aufgrund der Symmetrie können wir nur den Kreis A verarbeiten.
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
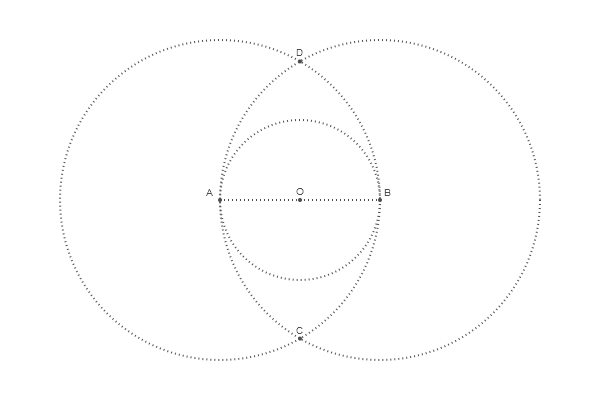
Um den Mittelpunkt des oberen Kreises zu bestimmen, finden wir den Schnittpunkt OD
Code @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

Der Radius des untergeordneten Kreises wird durch die Beschränkung auf zwei große Kreise bestimmt:
Code @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

Das Ei ist fertig! Es bleibt, es aus vier durch die Funktion arc2r() angegebenen Bögen zusammenzusetzen und den Bereich auszufüllen:
Code @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
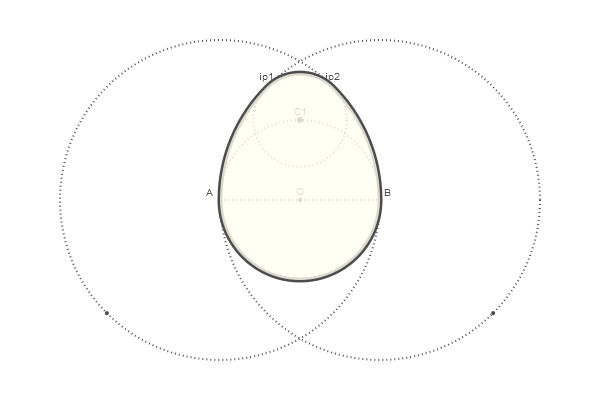
Und jetzt, um uns richtig zu verwöhnen, bringen wir unsere Erfolge ein
die Funktion function egg(radius, action=:none) A, B = [Point(x, 0) for x in [-radius, radius]] nints, C, D = intersectionlinecircle(Point(0, -2radius), Point(0, 2radius), A, 2radius) flag, C1 = intersectionlinecircle(C, D, O, radius) nints, I3, I4 = intersectionlinecircle(A, C1, A, 2radius) nints, I1, I2 = intersectionlinecircle(B, C1, B, 2radius) if distance(C1, I1) < distance(C1, I2) ip1 = I1 else ip1 = I2 end if distance(C1, I3) < distance(C1, I4) ip2 = I3 else ip2 = I4 end newpath() arc2r(B, A, ip1, :path) arc2r(C1, ip1, ip2, :path) arc2r(A, ip2, B, :path) arc2r(O, B, A, :path) closepath() do_action(action) end
Wir verwenden zufällige Farben, Ebenenmalerei und verschiedene Anfangsbedingungen:
@png begin setopacity(0.7) for θ in range(0, step=π/6, length=12) @layer begin rotate(θ) translate(100, 50)


Zusätzlich zu Strich und Füllung können Sie den Umriss als Beschneidungsbereich (Zuschneiden eines anderen Bildes in Form eines Eies) oder als Grundlage für verschiedene Designer verwenden. Die Funktiongg () erstellt einen Umriss und ermöglicht es Ihnen, eine Aktion darauf anzuwenden. Es ist auch möglich, unsere Kreation in ein Polygon (ein Array von Punkten) umzuwandeln. Der folgende Code konvertiert den Umriss eines Eies in ein Polygon und verschiebt dann den anderen Punkt des Polygons auf halber Strecke zum Schwerpunkt.
@png begin egg(160, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) circle(pc, 5, :fill) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.5) end poly(pgon, :stroke) end 350 500 "polyegg"

Das ungleichmäßige Erscheinungsbild der internen Punkte ergibt sich aus den Standardeinstellungen für die Leitungsverbindung. Experimentieren Sie mit setlinejoin("round") , um setlinejoin("round") , ob sich dadurch die Geometrie ändert. Nun versuchen offsetpoly() , offsetpoly() erstellen, um eine polygonale Kontur außerhalb oder innerhalb eines vorhandenen Polygons zu erstellen.
@png begin egg(80, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.9) end for i in 30:-3:-8 randomhue() op = offsetpoly(pgon, i) poly(op, :stroke, close=true) end end 350 500 "polyeggs"

Kleine Änderungen in der Regelmäßigkeit von Punkten, die durch Konvertieren des Pfads in ein Polygon erstellt wurden, und die unterschiedliche Anzahl von Abtastwerten werden in aufeinanderfolgenden Konturen ständig verstärkt.
Animation
Definieren wir zunächst die Funktionen, die den Hintergrund und das Rendern des Eies in Abhängigkeit von der Frame-Nummer implementieren:
Code using Colors demo = Movie(400, 400, "test") function backdrop(scene, framenumber) background("black") end function frame(scene, framenumber) setopacity(0.7) θ = framenumber * π/6 @layer begin rotate(θ) translate(100, 50) egg(50, :path) setline(10) randomhue() fillpreserve() randomhue() strokepath() end end
Die Animation wird durch einen einfachen Befehlssatz implementiert:
animate(demo, [ Scene(demo, backdrop, 0:12), Scene(demo, frame, 0:12, easingfunction=easeinoutcubic, optarg="made with Julia") ], framerate=10, tempdirectory="C:\\Users\\User\\Desktop\\mycop", creategif=true)
Was verursacht eigentlich unser ffmpeg
run(`ffmpeg -f image2 -i $(tempdirectory)/%10d.png -vf palettegen -y $(seq.stitle)-palette.png`) run(`ffmpeg -framerate 30 -f image2 -i $(tempdirectory)/%10d.png -i $(seq.stitle)-palette.png -lavfi paletteuse -y /tmp/$(seq.stitle).gif`)
Das heißt, eine Reihe von Bildern wird erstellt, und dann wird aus diesen Frames ein GIF zusammengestellt:

Pentahore
Er ist ein Fünfkern - der richtige vierdimensionale Simplex. Um 4-dimensionale Objekte auf zweidimensionalen Bildern zu zeichnen und zu bearbeiten, definieren wir zunächst
Klasse 4-dimensionaler Punkt struct Point4D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 w::Float64 end Point4D(a::Array{Float64, 1}) = Point4D(a...) Base.size(pt::Point4D) = (4, ) Base.getindex(pt::Point4D, i) = [pt.x, pt.y, pt.z, pt.w][i] struct Point3D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 end Base.size(pt::Point3D) = (3, )
Anstatt viele Operationen manuell zu definieren, können wir unsere Struktur als Subtyp von AbstractArray definieren ( Weitere Informationen zu Klassen als Schnittstellen ).
Die Hauptaufgabe, die wir lösen müssen, ist das Konvertieren eines 4D-Punkts in einen 2D-Punkt. Beginnen wir mit einer einfacheren Aufgabe: Wie konvertiere ich einen 3D-Punkt in einen 2D-Punkt, d. H. Wie können wir eine 3D-Figur auf einer ebenen Fläche zeichnen? Betrachten Sie einen einfachen Würfel. Die Vorder- und Rückseite können die gleichen X- und Y-Koordinaten haben und variieren nur in ihren Z-Werten.
Code @png begin fontface("Menlo") fontsize(8) setblend(blend( boxtopcenter(BoundingBox()), boxmiddlecenter(BoundingBox()), "skyblue", "white")) box(boxtopleft(BoundingBox()), boxmiddleright(BoundingBox()), :fill) setblend(blend( boxmiddlecenter(BoundingBox()), boxbottomcenter(BoundingBox()), "grey95", "grey45" )) box(boxmiddleleft(BoundingBox()), boxbottomright(BoundingBox()), :fill) sethue("black") setline(2) bx1 = box(O, 250, 250, vertices=true) poly(bx1, :stroke, close=true) label.(["-1 1 1", "-1 -1 1", "1 -1 1", "1 1 1"], slope.(O, bx1), bx1) setline(1) bx2 = box(O, 150, 150, vertices=true) poly(bx2, :stroke, close=true) label.(["-1 1 0", "-1 -1 0", "1 -1 0", "1 1 0"], slope.(O, bx2), bx2, offset=-45) map((x, y) -> line(x, y, :stroke), bx1, bx2) end 400 400 "cube.png"

Daher besteht die Idee darin, einen Würfel von 3D in 2D zu projizieren, die ersten beiden Werte zu speichern und sie mit dem dritten Wert zu multiplizieren oder zu ändern. Überprüfen Sie
Wie funktioniert es? const K = 4.0 function convert(Point, pt3::Point3D) k = 1/(K - pt3.z) return Point(pt3.x * k, pt3.y * k) end @png begin cube = Point3D[ Point3D(-1, -1, 1), Point3D(-1, 1, 1), Point3D( 1, -1, 1), Point3D( 1, 1, 1), Point3D(-1, -1, -1), Point3D(-1, 1, -1), Point3D( 1, -1, -1), Point3D( 1, 1, -1), ] circle.(convert.(Point, cube) * 300, 5, :fill) end 220 220 "points"

Erstellen wir nach demselben Prinzip eine Methode zum Konvertieren von 4D-Punkten und eine Funktion, die eine Liste von vierdimensionalen Punkten verwendet und diese zweimal einer Liste von zweidimensionalen Punkten zuordnet, die zum Zeichnen geeignet sind.
function convert(Point3D, pt4::Point4D) k = 1/(K - pt4.w) return Point3D(pt4.x * k, pt4.y * k, pt4.z * k) end function flatten(shape4) return map(pt3 -> convert(Point, pt3), map(pt4 -> convert(Point3D, pt4), shape4)) end
Als nächstes legen Sie die Eckpunkte und Flächen fest und überprüfen Sie, wie es in Farbe funktioniert
Tyk! const n = -1/√5 const pentachoron = [Point4D(vertex...) for vertex in [ [ 1.0, 1.0, 1.0, n], [ 1.0, -1.0, -1.0, n], [-1.0, 1.0, -1.0, n], [-1.0, -1.0, 1.0, n], [ 0.0, 0.0, 0.0, n + √5]]]; const pentachoronfaces = [ [1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]]; @png begin setopacity(0.2) pentachoron2D = flatten(pentachoron) for (n, face) in enumerate(pentachoronfaces) randomhue() poly(1500 * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end 300 250 "5ceil"

Jeder sich selbst respektierende Spieleentwickler sollte die mathematischen Grundlagen der Maschinengrafik kennen . Wenn Sie nie versucht haben, Teekannen in OpenGL zu komprimieren, zu drehen oder zu reflektieren - seien Sie nicht beunruhigt, alles ist ganz einfach. Um einen Punkt relativ zu einer geraden Linie zu reflektieren oder eine Ebene um eine bestimmte Achse zu drehen, müssen Sie die Koordinaten mit einer speziellen Matrix multiplizieren. Tatsächlich werden wir die Transformationsmatrizen, die wir benötigen, weiter bestimmen
nimm mehr auf function XY(θ) [cos(θ) -sin(θ) 0 0; sin(θ) cos(θ) 0 0; 0 0 1 0; 0 0 0 1] end function XW(θ) [cos(θ) 0 0 -sin(θ); 0 1 0 0; 0 0 1 0; sin(θ) 0 0 cos(θ)] end function XZ(θ) [cos(θ) 0 -sin(θ) 0; 0 1 0 0; sin(θ) 0 cos(θ) 0; 0 0 0 1] end function YZ(θ) [1 0 0 0; 0 cos(θ) -sin(θ) 0; 0 sin(θ) cos(θ) 0; 0 0 0 1] end function YW(θ) [1 0 0 0; 0 cos(θ) 0 -sin(θ); 0 0 1 0; 0 sin(θ) 0 cos(θ)] end function ZW(θ) [1 0 0 0; 0 1 0 0; 0 0 cos(θ) -sin(θ); 0 0 sin(θ) cos(θ)]; end function rotate4(A, matrixfunction) return map(A) do pt4 Point4D(matrixfunction * pt4) end end
Normalerweise drehen Sie Punkte auf einer Ebene relativ zu einem eindimensionalen Objekt. 3D-Punkte liegen um eine 2D-Linie (häufig ist dies eine der XYZ-Achsen). Daher ist es logisch, dass sich 4D-Punkte relativ zur 3D-Ebene drehen. Wir haben Matrizen identifiziert, die eine vierdimensionale Drehung um eine Ebene ausführen, die durch zwei Achsen X, Y, Z und W definiert ist. Die XY-Ebene ist normalerweise die Ebene der Zeichenfläche. Wenn Sie die XY-Ebene als Computerbildschirm wahrnehmen, verläuft die XZ-Ebene parallel zu Ihrem Tisch oder Boden, und die YZ-Ebene ist die Wand neben Ihrem Tisch rechts oder links. Aber was ist mit XW, YW und ZW? Dies ist das Geheimnis vierdimensionaler Figuren: Wir können diese Ebenen nicht sehen, wir können uns ihre Existenz nur vorstellen, indem wir beobachten, wie sich Formen durch sie und um sie herum bewegen.
Jetzt stellen wir die Funktionen für die Frames ein und nähen die Animation:
Spoiler using ColorSchemes function frame(scene, framenumber, scalefactor=1000) background("white")

Nun, und noch ein Winkel:
Code function frame(scene, framenumber, scalefactor=1000) background("antiquewhite") setlinejoin("bevel") setline(1.0) setopacity(0.2) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) pentachoron2D = flatten( rotate4( pentachoron, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(pentachoronfaces) sethue(get(ColorSchemes.diverging_rainbow_bgymr_45_85_c67_n256, n/length(pentachoronfaces))) poly(scalefactor * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end makemovie(500, 500, "pentachoron-xz-yw.gif", scalefactor=2000)
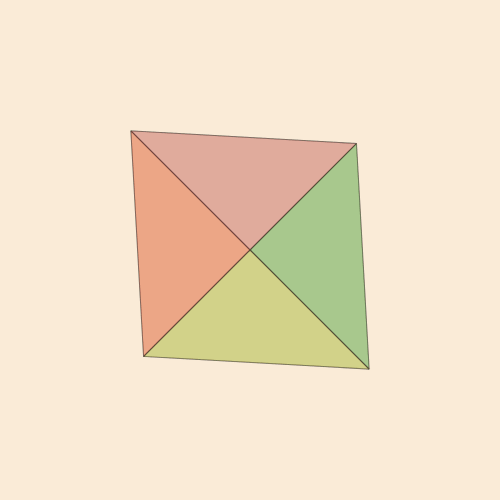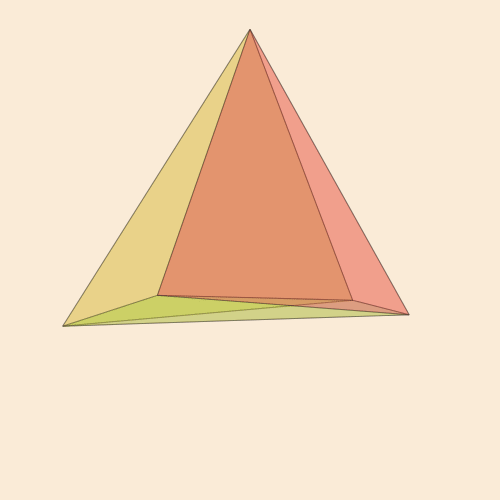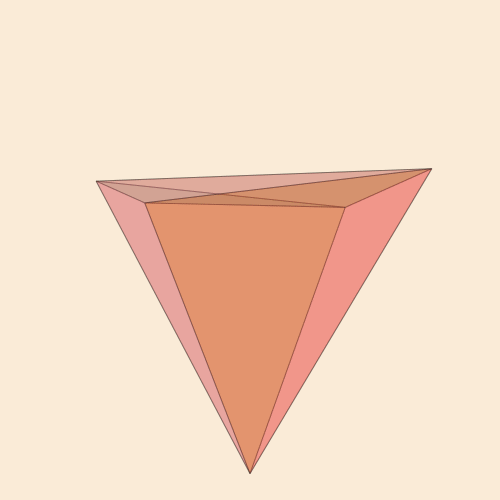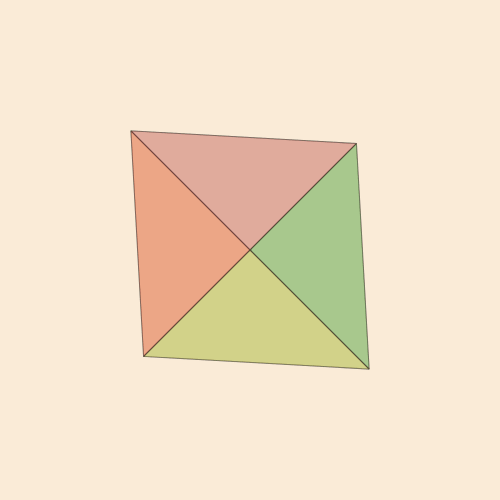
Der Wunsch, ein beliebteres vierdimensionales Objekt, den Tesseract, zu realisieren , ist völlig natürlich.
Tops und Gesichter const tesseract = [Point4D(vertex...) for vertex in [ [-1, -1, -1, 1], [ 1, -1, -1, 1], [ 1, 1, -1, 1], [-1, 1, -1, 1], [-1, -1, 1, 1], [ 1, -1, 1, 1], [ 1, 1, 1, 1], [-1, 1, 1, 1], [-1, -1, -1, -1], [ 1, -1, -1, -1], [ 1, 1, -1, -1], [-1, 1, -1, -1], [-1, -1, 1, -1], [ 1, -1, 1, -1], [ 1, 1, 1, -1], [-1, 1, 1, -1]]] const tesseractfaces = [ [1, 2, 3, 4], [1, 2, 10, 9], [1, 4, 8, 5], [1, 5, 6, 2], [1, 9, 12, 4], [2, 3, 11, 10], [2, 3, 7, 6], [3, 4, 8, 7], [5, 6, 14, 13], [5, 6, 7, 8], [5, 8, 16, 13], [6, 7, 15, 14], [7, 8, 16, 15], [9, 10, 11, 12], [9, 10, 14, 13], [9, 13, 16, 12], [10, 11, 15, 14], [13, 14, 15, 16]];
Animation erstellen function frame(scene, framenumber, scalefactor=1000) background("black") setlinejoin("bevel") setline(10.0) setopacity(0.7) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) tesseract2D = flatten( rotate4( tesseract, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(tesseractfaces) sethue([Luxor.lighter_blue, Luxor.lighter_green, Luxor.lighter_purple, Luxor.lighter_red][mod1(n, 4)]...) poly(scalefactor * tesseract2D[face], :fillpreserve, close=true) sethue([Luxor.darker_blue, Luxor.darker_green, Luxor.darker_purple, Luxor.darker_red][mod1(n, 4)]...) strokepath() end end makemovie(500, 500, "tesseract-xz-yw.gif", scalefactor=1000)

Hausaufgabe: Automatisieren Sie die Erstellung von Arrays von Koordinaten und Scheitelpunktnummern ( Permutationen mit Wiederholungen bzw. ohne Wiederholungen ). Außerdem haben wir nicht alle Übersetzungsmatrizen verwendet. Jede neue Perspektive bringt ein neues „Wow!“, Aber ich habe beschlossen, die Seite nicht zu überladen. Nun, Sie können mit vielen Gesichtern und Dimensionen experimentieren.
Referenzen