Entfernen von hochfrequenten Geräuschen aus den Signalen von Schwingungssensoren während der Schwingungsdiagnose von Lagern

Foto aus der Veröffentlichung genommen

Einführung

Eine der dringendsten Aufgaben der digitalen Signalverarbeitung ist die Reinigung des Signals von Rauschen. Jedes praktische Signal enthält nicht nur nützliche Informationen, sondern auch Spuren einiger Nebeneffekte von Interferenzen oder Rauschen. Zusätzlich haben während der Schwingungsdiagnose Signale von Schwingungssensoren ein instationäres Frequenzspektrum, was die Filteraufgabe erschwert.

Es gibt viele verschiedene Möglichkeiten, um hochfrequentes Rauschen aus einem Signal zu entfernen. Beispielsweise enthält die Scipy-Bibliothek Filter, die auf verschiedenen Filtermethoden basieren: Kalman; Glätten des Signals durch Mitteln entlang der Zeitachse und anderer.

Der Vorteil des DWT-Verfahrens (Discrete Wavelet Transform) ist jedoch die Vielzahl der Wavelet-Formen. Sie können ein Wavelet auswählen, das eine für die erwarteten Phänomene charakteristische Form aufweist. Sie können beispielsweise ein Signal in einem bestimmten Frequenzbereich auswählen, dessen Form für das Auftreten eines Defekts verantwortlich ist.

Der Zweck dieser Veröffentlichung ist die Analyse der Methoden zum Filtern der Signale von Schwingungssensoren unter Verwendung der DWT-Signalumwandlung, des Kalman-Filters und der Methode des gleitenden Durchschnitts.

Quelldaten zur Analyse

In der Veröffentlichung wird der Betrieb von Filtern basierend auf verschiedenen Filtermethoden anhand eines NASA-Datensatzes analysiert. Auf der Versuchsplattform PRONOSTIA erhaltene Daten:



Das Kit enthält Daten zu Vibrationssensorsignalen für den Verschleiß verschiedener Lagertypen. Der Zweck der Ordner mit den Signaldateien ist in der Tabelle angegeben :



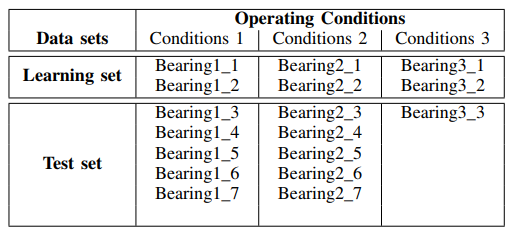
Die Überwachung des Lagerzustands erfolgt durch die Signale von Schwingungssensoren (horizontale und vertikale Beschleunigungsmesser), Kraft und Temperatur.



Empfangene Signale für drei verschiedene Lasten:

• Erste Arbeitsbedingungen: 1800 U / min und 4000 N;
• Zweite Arbeitsbedingungen: 1650 U / min und 4200 N;
• Dritte Betriebsbedingungen: 1500 U / min und 5000 N.

Für diese Bedingungen erstellen wir unter Verwendung einer kontinuierlichen Wavelet-Signalumwandlung die Spektroleistungsskalogramme für die Daten aus dem Testsatz - eine Datei (für einen Lagertyp) aus den Ordnern: ['Test_set / Bearing1_3 / acc_00001.csv', 'Test_set / Bearing2_3 / acc_00001. csv ',' Test_set / Bearing3_3 / acc_00001.csv '] (siehe Tabelle 1).






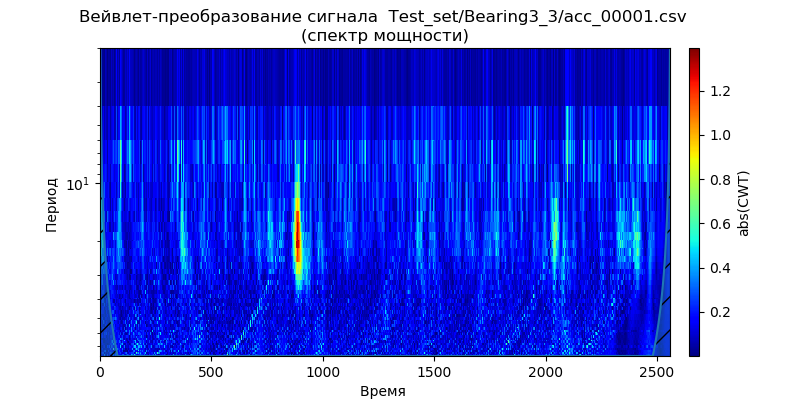
Aus den gegebenen Skalogrammen folgt, dass die Momente der Erhöhung der Leistung des Spektrums früher auftreten und eine Periodizität für die Betriebsbedingungen zeigen: 1650 U / min und 4200 N, was auf eine beschleunigte Verschlechterung der Lager in diesem Frequenzband für die verringerte Kraft hinweist. Wir werden dieses Signal ('Test_set / Bearing2_3 / acc_00001.csv') verwenden, um Rauschunterdrückungsmethoden zu analysieren.

Signaldekonstruktion mit DWT

In der Veröffentlichung haben wir gesehen, wie eine Filterbank auf dem DWT implementiert ist, die ein Signal in seine Frequenzteilbänder zerlegen kann. Die Approximationskoeffizienten (cA) repräsentieren den niederfrequenten Teil des Signals (Mittelungsfilter). Detailkoeffizienten (cD) repräsentieren den Hochfrequenzanteil des Signals. Als nächstes werden wir untersuchen, wie DWT verwendet werden kann, um ein Signal in seine Frequenzteilbänder zu zerlegen und das ursprüngliche Signal wiederherzustellen.

Es gibt zwei Möglichkeiten, um das Problem der Signaldekonstruktion mit PyWavelets-Tools zu lösen:

Der erste Weg besteht darin, pywt.dwt () auf das Signal anzuwenden, um die Approximations- und Detailkoeffizienten (cA1, cD1) zu extrahieren. Um das Signal wiederherzustellen, verwenden wir dann pywt.idwt ():




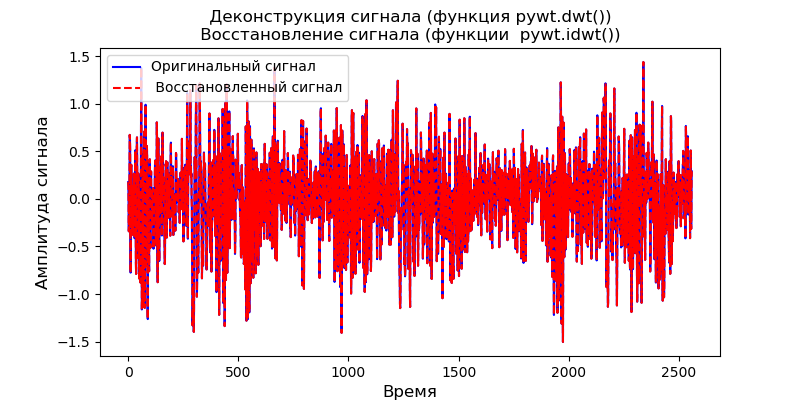
Die zweite Möglichkeit, die Funktion pywt.wavedec () auf das Signal anzuwenden, besteht darin, alle Approximations- und Detailkoeffizienten auf ein bestimmtes Niveau zurückzusetzen. Diese Funktion nimmt das Eingangssignal und den Pegel als Eingang und gibt einen Satz von Approximationskoeffizienten (n-ten Pegel) und n Sätze von Detailkoeffizienten (von 1 bis n-ten Pegel) zurück. Wenden Sie für die Dekonstruktion pywt.waverec () an:



Die zweite Möglichkeit, das Signal zu dekonstruieren und wiederherzustellen, ist bequemer. Sie können sofort den gewünschten Dekonstruktionsgrad einstellen.

Entfernen von hochfrequentem Rauschen durch Eliminieren einiger Detailkoeffizienten während der Signaldekonstruktion

Wir werden das Signal wiederherstellen, indem wir einige der Detailkoeffizienten löschen. Da die Detailkoeffizienten den hochfrequenten Teil des Signals darstellen, filtern wir diesen Teil des Frequenzspektrums einfach. Wenn das Signal hochfrequentes Rauschen enthält, können Sie es auf diese Weise filtern.

In der PyWavelets-Bibliothek kann dies mit der Schwellenwertverarbeitungsfunktion pywt.threshol () erfolgen:

pywt.threshold (Daten, Wert, Modus = 'weich', Ersatz = 0) ¶
Daten: array_like
Numerische Daten.
Wert: Skalar
Schwellenwert.
Modus: {'weich', 'hart', 'garrote', 'größer', 'kleiner'}
Definiert den Typ des Schwellenwerts, der auf die Eingabe angewendet wird. Der Standardwert ist "weich".
Ersatz: float, optional
Substitutionswert (Standard: 0).
Ausgabe: Array
Schwellenwertarray.

Die Anwendung der Schwellenwertverarbeitungsfunktion für einen bestimmten Schwellenwert wird am besten anhand des folgenden Beispiels betrachtet:

 >>>> from scipy import* >>> import pywt >>> data =linspace(1, 4, 7) >>> data array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'soft') array([0. , 0. , 0. , 0.5, 1. , 1.5, 2. ]) >>> pywt.threshold(data, 2, 'hard') array([0. , 0. , 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'garrote') array([0. , 0. , 0., 0.9,1.66666667, 2.35714286, 3.]) 

Wir zeichnen den Schwellenwertfunktionsgraphen anhand der folgenden Auflistung:



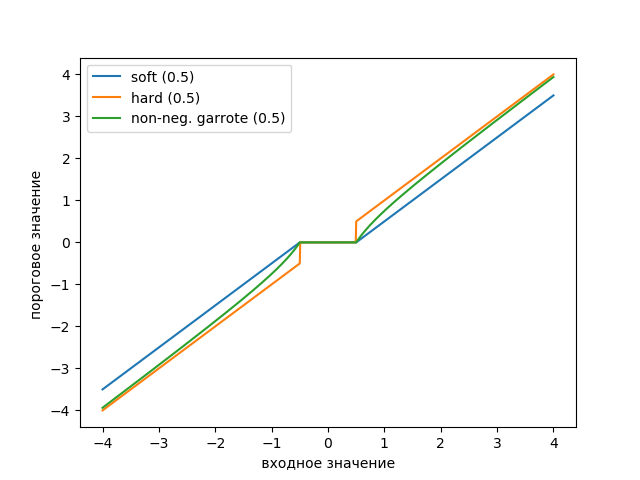
Die Grafik zeigt, dass die nicht negative Garott-Schwelle zwischen der weichen und der harten Schwelle liegt. Es sind zwei Schwellenwerte erforderlich, die die Breite des Übergangsbereichs definieren.

Der Einfluss der Schwellenwertfunktion auf die Filtereigenschaften

Wie aus der obigen Grafik hervorgeht, sind für uns nur zwei Schwellenwertfunktionen "weich" und "Garrote" geeignet. Um ihren Einfluss auf die Filtereigenschaften zu untersuchen, schreiben wir die Liste auf:





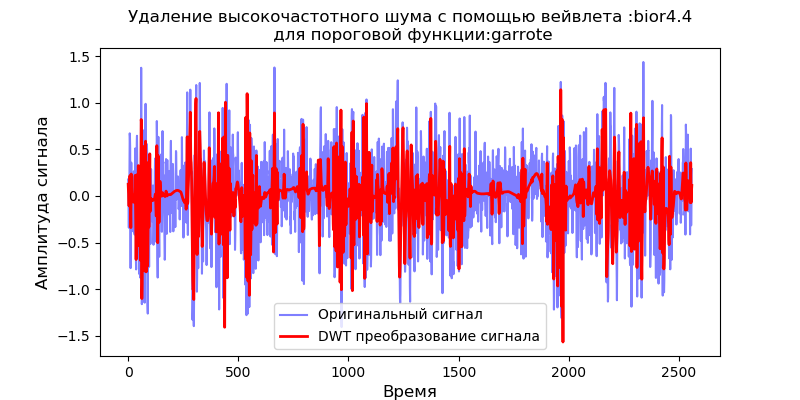
Wie aus den Diagrammen hervorgeht, bietet die Soft-Funktion eine bessere Glättung als die Garrote-Funktion, daher werden wir die Soft-Funktion in Zukunft verwenden.

Der Einfluss der Detailschwelle auf die Filtereigenschaften

Für den betrachteten Filtertyp ist der Schwellenwert für die Änderung der Detailkoeffizienten ein wichtiges Merkmal. Daher untersuchen wir seine Wirkung anhand der folgenden Auflistung:






Wie aus den erhaltenen Diagrammen hervorgeht, beeinflusst der Detaillierungsgradschwellenwert den Maßstab der gesiebten Teile. Mit einer Erhöhung des Schwellenwerts subtrahiert das Wavelet das Rauschen eines immer höheren Pegels, bis eine übermäßige Vergrößerung der Detailskala auftritt und die Transformation beginnt, die Form des ursprünglichen Signals zu verzerren. Für unser Signal sollte der Schwellenwert nicht höher als 0,63 sein.

Die Wirkung von Wavelet auf die Filtereigenschaften

Die PyWavelets-Bibliothek verfügt über eine ausreichende Anzahl von Wavelets für die DWT-Konvertierung, die wie folgt abgerufen werden können:

 >>> import pywt >>> print(pywt.wavelist(kind= 'discrete')) ['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20'] 

Der Einfluss des Wavelets auf die Filtercharakteristik hängt von seiner primitiven Funktion ab. Um diese Abhängigkeit zu demonstrieren, wählen wir zwei Wavelets aus der Dobeshi-Familie aus - db1 und db38 - und betrachten diese Familien:




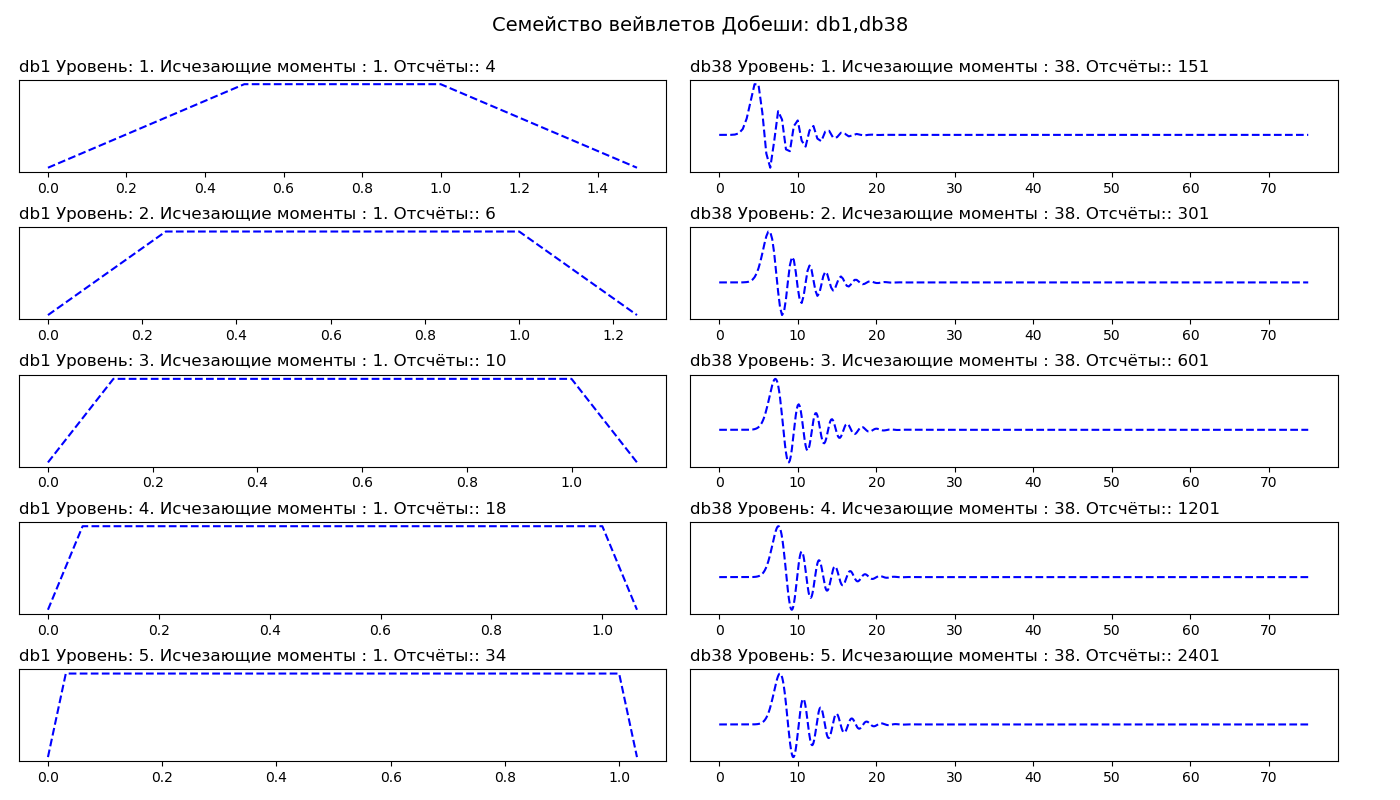
In der ersten Spalte sehen wir Daubeshi-Wavelets erster Ordnung (db1), in der zweiten Spalte achtunddreißigster Ordnung (db38). Somit hat db1 einen Moment des Aussterbens und db38 hat 38 Momente des Aussterbens. Die Anzahl der Momente des Verschwindens hängt mit der Reihenfolge der Approximation und der Glätte des Wavelets zusammen. Wenn ein Wavelet P Verschwindungspunkte hat, kann es Polynome vom Grad P - 1 approximieren.

Glattere Wavelets erzeugen eine glattere Signalannäherung, und umgekehrt - „kurze“ Wavelets verfolgen die Spitzen der angenäherten Funktion besser. Bei der Auswahl eines Wavelets können wir auch den Zersetzungsgrad angeben. Standardmäßig wählt PyWavelets den maximal möglichen Zerlegungspegel für das Eingangssignal aus. Der maximale Zerlegungspegel hängt von der Länge des Eingangssignals und des Wavelets ab:


Für db1 Wavelet maximales Zerlegungsniveau: 11
Für db38 Wavelet maximales Zerlegungsniveau: 5

Für die erhaltenen Werte der maximalen Wavelet-Zerlegungspegel betrachten wir den Betrieb des Filters, um hochfrequentes Rauschen zu entfernen:









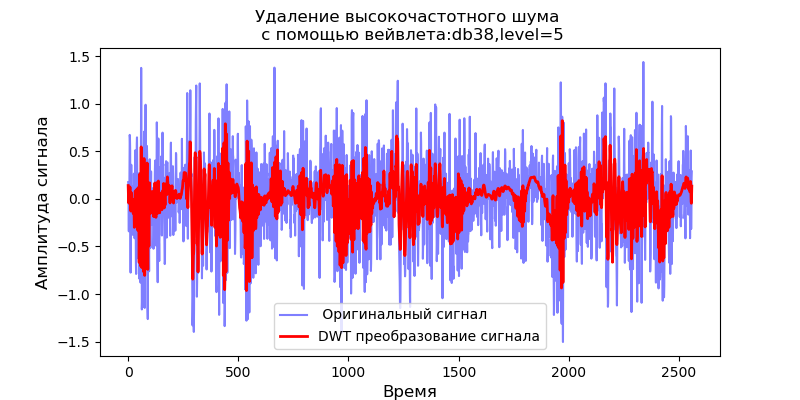
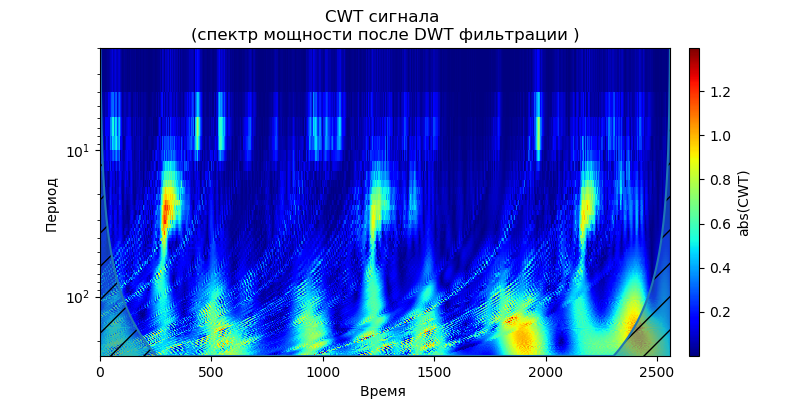
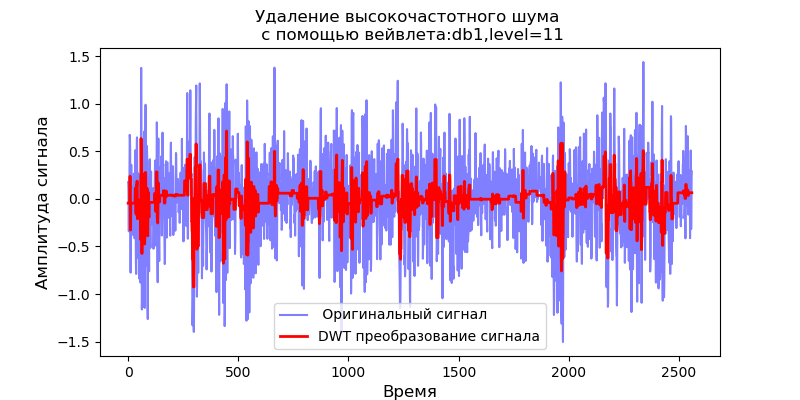
Aus den zitierten Wellenformen der Signale am Filterausgang folgt, dass für das db38-Wavelet auf die Spitzenleistung des Spektrums lokalisierte Bereiche folgen, für das db1-Wavelet verschwinden diese Bereiche. Es ist anzumerken, dass beispielsweise das db38-Wavelet ein Signal mit einem Polynom vom Grad 37 approximieren kann. Dies erweitert die Klassifizierung von Signalen, um beispielsweise Fehlfunktionen von Geräten anhand der Signale von Vibrationssensoren zu identifizieren.

Da das Signal nach dem Filter mit dem Daubechies-Wavelet eine Zeitreihe unter Verwendung von Approximations- und Zerlegungskoeffizienten als Eigenschaften der Reihe bildet, kann man den Grad der Nähe solcher Reihen bestimmen, was ihre Suche und Klassifizierung stark vereinfacht

Kalman-Filter zur Entfernung von hochfrequentem Rauschen

Das Kalman-Filter wird häufig zum Filtern von Rauschen in verschiedenen dynamischen Systemen verwendet. Betrachten Sie ein dynamisches System mit einem Zustandsvektor x.

$$$x = F \ cdot x + w (Q)$

wobei F die Übergangsmatrix ist
w (Q) ist ein zufälliger Prozess (Rauschen) mit einer mathematischen Erwartung von Null und einer Kovarianzmatrix Q.

Wir werden zu jedem Zeitpunkt Zustandsübergänge des Systems mit einem bekannten Messfehler beobachten. Das Entfernen von Rauschen mit der Kalman-Methode besteht aus zwei Schritten: Extrapolation und Korrektur.

Stellen Sie die Systemparameter ein:

Q-Matrix der Rauschkovarianz (Prozessrauschkovarianz).
H ist die Beobachtungsmatrix (Messung).
R - Kovarianz des Beobachtungsrauschens (Messrauschkovarianz).
P = Q ist der Anfangswert der Kovarianzmatrix für den Zustandsvektor.
z (t) ist der beobachtete Zustand des Systems.
x = z (0) ist der Anfangswert der Bewertung des Zustands des Systems.

Für jede Beobachtung z berechnen wir den gefilterten Zustand x
und dazu führen wir die folgenden schritte aus.

• Schritt 1: Extrapolation
1. Extrapolation (Vorhersage) des Zustands des Systems
$$$x = F \ cdot x$
2. Berechnen Sie die Kovarianzmatrix für den extrapolierten Zustandsvektor
$$$F = F \ cdot P \ cdot F ^ {T} + Q$

• Schritt 2: Korrektur
1. Berechnen Sie den Fehlervektor, die Abweichung der Beobachtung vom erwarteten Zustand
$$$y = z-H \ cdot x$
2. Berechnen Sie die Kovarianzmatrix für den Abweichungsvektor (Fehlervektor)
$$$S = H \ cdot P \ cdot H ^ {T} + R$
3. Berechnen Sie die Kalman-Gewinne
$$$K = P \ cdot H \ cdot H ^ {T} \ cdot S ^ {- 1}$
4. Korrektur der Zustandsvektorschätzung
$$$x = x + K \ cdot y$
5. Wir korrigieren die Kovarianzmatrix zur Schätzung des Systemzustandsvektors
$$$P = (I-K \ cdot H) \ cdot P$




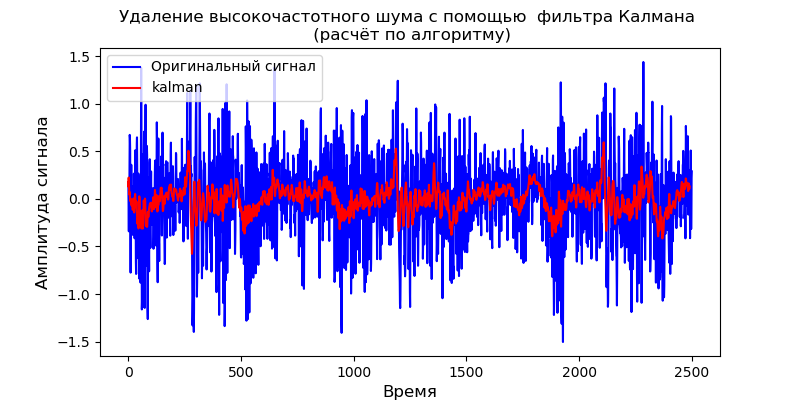
Für das angegebene dynamische Modell können Sie die pyKalman-Bibliothek verwenden:






Das Kalman-Filter entfernt hochfrequentes Rauschen, erlaubt jedoch keine Änderung der Form des Ausgangssignals.

Methode des gleitenden Durchschnitts

Bei der Bestimmung der Hauptrichtung von Änderungen in einer stark oszillierenden Sequenz tritt das Problem auf, sie unter Verwendung der Methode des gleitenden Durchschnitts zu glätten. Dies können die Messwerte des Kraftstoffstandsensors im Auto oder, wie in unserem Fall, die Daten von Hochfrequenzsensoren bezüglich des beschleunigten Abbaus von Lagern sein. Das Problem kann als Wiederherstellung einer Sequenz r betrachtet werden, der Rauschen überlagert wurde.

Kurzer einfacher gleitender Durchschnitt - SMA (Simple Moving Average). Berechnung des aktuellen Filterwerts $$$r_ {i}$Wir mitteln nur die vorherigen n Elemente der Sequenz, sodass der Filter mit dem Element der Sequenz n arbeitet.

$$$r_ {i} = \ frac {1} {n} \ cdot \ sum_ {j = 1} ^ {n} y _ {(i-j)}; i> n$






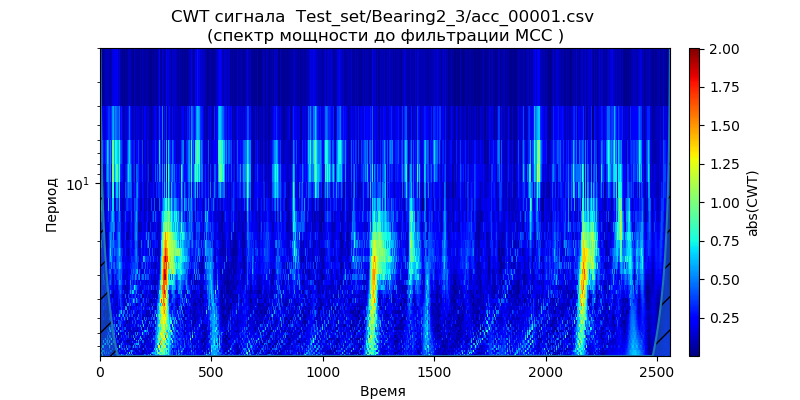
Wie aus dem Skalogramm folgt, reinigt das SMA-Verfahren das Signal schlecht von hochfrequentem Rauschen und
wie oben erwähnt wird zum Glätten verwendet.

Schlussfolgerungen:

1. Unter Verwendung des Skalogrammmoduls wurden CWT-Wavelet-Skalogramme von drei Testvibrationssensorsignalen für verschiedene Testbedingungen für Lager des gleichen Typs erhalten. Gemäß den Skalogrammdaten wurde ein Signal mit deutlich zum Ausdruck gebrachten Anzeichen einer späten Verschlechterung ausgewählt. Dieses Signal wurde verwendet, um die Funktionsweise von Filtern in allen angegebenen Beispielen zu demonstrieren.
2. Die Methoden der PyWavelets-Bibliothek zur DWT-Dekonstruktion und Wiederherstellung des Schwingungssensorsignals unter Verwendung der Module pywt.dwt (), pywt.idwt () und des Moduls pywt.wavedec () für einen bestimmten Wavelet-Pegel werden berücksichtigt.
3. Die Beispiele veranschaulichen die Anwendungsmerkmale des Moduls pywt.threshol () zum Filtern von DWT-Detailkoeffizienten, die für den hochfrequenten Teil des Spektrums unter Verwendung von Schwellenwertfunktionen für einen bestimmten Schwellenwert verantwortlich sind.
4. Die Auswirkungen des antiderivativen DWT-Wavelets auf die Form eines vom Rauschen befreiten Signals werden berücksichtigt.
5. Man erhält ein Kalman-Filtermodell für ein dynamisches Medium, das Modell wird am Testsignal des Schwingungssensors getestet. Das Rauschunterdrückungsdiagramm ist das gleiche wie das, das mit dem pyKalman-Modul erhalten wurde. Die Art des Diagramms stimmt mit dem Skalogramm überein.
6. .