Die Übersetzung des Artikels wurde speziell für Studenten des Kurses "Algorithmen für Entwickler" vorbereitet.

Die Pyramidensortierung (oder Heap-Sortierung, HeapSort) ist eine Vergleichssortierungsmethode, die auf einer Datenstruktur wie einem binären Heap basiert. Es ähnelt der Sortierung nach Auswahl, bei der wir zuerst nach dem maximalen Element suchen und es am Ende platzieren. Als nächstes wiederholen wir den gleichen Vorgang für die verbleibenden Elemente.

Was ist ein binärer Haufen ?

Definieren wir zunächst einen vollständigen Binärbaum. Ein fertiger Binärbaum ist ein Binärbaum, in dem jede Ebene, mit der möglichen Ausnahme der letzten, einen vollständigen Satz von Knoten aufweist und sich alle Blätter links befinden (Quelle Wikipedia ).

Ein binärer Heap ist ein vollständiger binärer Baum, in dem Elemente in einer speziellen Reihenfolge gespeichert werden: Der Wert im übergeordneten Knoten ist größer (oder kleiner als) die Werte in seinen beiden untergeordneten Knoten. Die erste Option heißt max-heap und die zweite ist min-heap. Ein Heap kann durch einen Binärbaum oder ein Array dargestellt werden.

Warum wird eine Array-basierte Darstellung für einen binären Heap verwendet?

Da der binäre Heap ein vollständiger binärer Baum ist, kann er leicht als Array dargestellt werden, und die Array-basierte Darstellung ist hinsichtlich des Speicherverbrauchs effizient. Wenn der übergeordnete Knoten in Index I gespeichert ist, kann das linke Kind als 2 I + 1 und das rechte Kind als 2 I + 2 berechnet werden (vorausgesetzt, die Indizierung beginnt bei 0).

Pyramidaler Sortieralgorithmus in aufsteigender Reihenfolge:

1. Erstellen Sie max-heap aus der Eingabe.
2. Zu diesem Zeitpunkt wird das größte Element im Stammverzeichnis des Heaps gespeichert. Ersetzen Sie es durch das letzte Element des Heaps und reduzieren Sie seine Größe um 1. Konvertieren Sie schließlich den resultierenden Baum in max-heap mit einem neuen Stamm.
3. Wiederholen Sie die obigen Schritte, bis der Heap größer als 1 ist.

Wie baue ich einen Haufen?

Die Heap-Konvertierungsprozedur (im Folgenden als Heapify-Prozedur bezeichnet) kann nur dann auf einen Knoten angewendet werden, wenn seine untergeordneten Knoten bereits konvertiert sind. Daher muss die Konvertierung von unten nach oben durchgeführt werden. Lassen Sie es uns anhand eines Beispiels herausfinden:

 : 4, 10, 3, 5, 1 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4)           .   heapify   1: 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4)   heapify   0: 10(0) / \ 5(1) 3(2) / \ 4(3) 1(4)  heapify        . 

Empfehlung: Bitte lösen Sie das Problem zuerst unter „PRAXIS“, bevor Sie mit der Lösung fortfahren .

C ++

 //     C++ #include <iostream> using namespace std; //           i,   //   arr[]. n -   void heapify(int arr[], int n, int i) { int largest = i; //      int l = 2*i + 1; //  = 2*i + 1 int r = 2*i + 2; //  = 2*i + 2 //       if (l < n && arr[l] > arr[largest]) largest = l; //     ,        if (r < n && arr[r] > arr[largest]) largest = r; //       if (largest != i) { swap(arr[i], arr[largest]); //        heapify(arr, n, largest); } } //  ,    void heapSort(int arr[], int n) { //   ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); //        for (int i=n-1; i>=0; i--) { //      swap(arr[0], arr[i]); //   heapify    heapify(arr, i, 0); } } /*         n*/ void printArray(int arr[], int n) { for (int i=0; i<n; ++i) cout << arr[i] << " "; cout << "\n"; } //   int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr)/sizeof(arr[0]); heapSort(arr, n); cout << "Sorted array is \n"; printArray(arr, n); } 

Java

 //     Java public class HeapSort { public void sort(int arr[]) { int n = arr.length; //   ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); //        for (int i=n-1; i>=0; i--) { //      int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; //   heapify    heapify(arr, i, 0); } } //           i,   //   arr[]. n -   void heapify(int arr[], int n, int i) { int largest = i; //      int l = 2*i + 1; //  = 2*i + 1 int r = 2*i + 2; //  = 2*i + 2 //       if (l < n && arr[l] > arr[largest]) largest = l; //     ,        if (r < n && arr[r] > arr[largest]) largest = r; //       if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; //        heapify(arr, n, largest); } } /*         n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } //   public static void main(String args[]) { int arr[] = {12, 11, 13, 5, 6, 7}; int n = arr.length; HeapSort ob = new HeapSort(); ob.sort(arr); System.out.println("Sorted array is"); printArray(arr); } } 

Python

 #     Python #           i,     arr[]. n -   def heapify(arr, n, i): largest = i # Initialize largest as root l = 2 * i + 1 # left = 2*i + 1 r = 2 * i + 2 # right = 2*i + 2 #       ,   if l < n and arr[i] < arr[l]: largest = l #       ,   if r < n and arr[largest] < arr[r]: largest = r #  ,   if largest != i: arr[i],arr[largest] = arr[largest],arr[i] #  #  heapify  . heapify(arr, n, largest) #        def heapSort(arr): n = len(arr) #  max-heap. for i in range(n, -1, -1): heapify(arr, n, i) #      for i in range(n-1, 0, -1): arr[i], arr[0] = arr[0], arr[i] #  heapify(arr, i, 0) #     arr = [ 12, 11, 13, 5, 6, 7] heapSort(arr) n = len(arr) print ("Sorted array is") for i in range(n): print ("%d" %arr[i]), #    Mohit Kumra 

Cis

 //     C# using System; public class HeapSort { public void sort(int[] arr) { int n = arr.Length; //   ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); //        for (int i=n-1; i>=0; i--) { //      int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; //   heapify    heapify(arr, i, 0); } } //           i,   //   arr[]. n -   void heapify(int[] arr, int n, int i) { int largest = i; //      int l = 2*i + 1; // left = 2*i + 1 int r = 2*i + 2; // right = 2*i + 2 //       if (l < n && arr[l] > arr[largest]) largest = l; //     ,        if (r < n && arr[r] > arr[largest]) largest = r; //       if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; //        heapify(arr, n, largest); } } /*         n */ static void printArray(int[] arr) { int n = arr.Length; for (int i=0; i<n; ++i) Console.Write(arr[i]+" "); Console.Read(); } //  public static void Main() { int[] arr = {12, 11, 13, 5, 6, 7}; int n = arr.Length; HeapSort ob = new HeapSort(); ob.sort(arr); Console.WriteLine("Sorted array is"); printArray(arr); } } //   // Akanksha Ra (Abby_akku) 

Php

 <?php //     Php //           i,   //   arr[]. n -   function heapify(&$arr, $n, $i) { $largest = $i; //      $l = 2*$i + 1; //  = 2*i + 1 $r = 2*$i + 2; //  = 2*i + 2 //       if ($l < $n && $arr[$l] > $arr[$largest]) $largest = $l; //    ,        if ($r < $n && $arr[$r] > $arr[$largest]) $largest = $r; //       if ($largest != $i) { $swap = $arr[$i]; $arr[$i] = $arr[$largest]; $arr[$largest] = $swap; //        heapify($arr, $n, $largest); } } // ,    function heapSort(&$arr, $n) { //   ( ) for ($i = $n / 2 - 1; $i >= 0; $i--) heapify($arr, $n, $i); //       for ($i = $n-1; $i >= 0; $i--) { //      $temp = $arr[0]; $arr[0] = $arr[$i]; $arr[$i] = $temp; //   heapify    heapify($arr, $i, 0); } } /*         n */ function printArray(&$arr, $n) { for ($i = 0; $i < $n; ++$i) echo ($arr[$i]." ") ; } //   $arr = array(12, 11, 13, 5, 6, 7); $n = sizeof($arr)/sizeof($arr[0]); heapSort($arr, $n); echo 'Sorted array is ' . "\n"; printArray($arr , $n); //    Shivi_Aggarwal ?> 

Fazit:

  : 5 6 7 11 12 13 

Hier ist der vorherige C-Code als Referenz.

Anmerkungen:
Pyramidensortierung ist ein perfekt geeigneter Algorithmus. Die typische Implementierung ist nicht stabil, kann aber als solche durchgeführt werden (siehe hier ).

Zeitkomplexität: Die Zeitkomplexität von Heapify ist O (Logn). Die zeitliche Komplexität von createAndBuildHeap () beträgt O (n), und die Gesamtlaufzeit der Pyramidensortierung beträgt O (nLogn).

Pyramidale Sortieranwendungen:

1. Sortieren Sie ein fast sortiertes (oder nach K Positionen sortiertes) Array .
2. k größte (oder kleinste) Elemente im Array .

Der pyramidenförmige Sortieralgorithmus wird nur begrenzt verwendet, da Quicksort und Mergesort in der Praxis besser sind. Die Heap-Datenstruktur selbst wird jedoch häufig verwendet. Siehe Heap-Datenstrukturanwendungen

Screenshots:

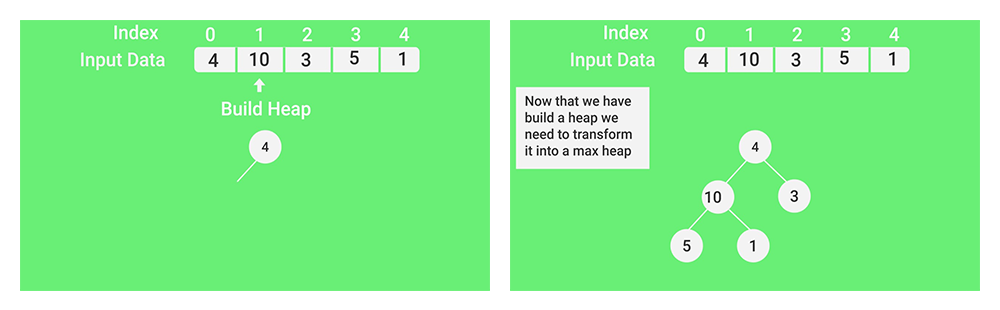
- (Nachdem wir den Heap erstellt haben, müssen wir ihn in max-heap konvertieren.)

- (In max-heap ist der übergeordnete Knoten immer größer oder gleich den untergeordneten Knoten
10 mehr als 4. Deshalb tauschen wir 4 und 10)
- (In max-heap ist der übergeordnete Knoten immer größer oder gleich den untergeordneten Knoten
5 weitere 4. Deshalb tauschen wir die Plätze 5 und 4)

- (Tauschen Sie den ersten und den letzten Knoten aus und löschen Sie den letzten vom Heap.)

Pyramidentest

Andere Sortieralgorithmen in GeeksforGeeks / GeeksQuiz:
Schnelle Sortierung , Sortieren nach Auswahl , Blasensortieren , Einfügen Sortieren , Zusammenführen Sortieren , Pyramidensortieren , Bitsortieren , Zählsortieren , Blocksortieren , Shell- Sortieren, Kammsortieren, Zählen Sortieren mit Liste .

Sortierwerkstatt

Bitte hinterlassen Sie Kommentare, wenn Sie etwas falsch finden oder zusätzliche Informationen zu dem oben diskutierten Thema teilen möchten.