Buch "Maschinelles Lernen für Wirtschaft und Marketing"

Die Datenwissenschaft wird zu einem integralen Bestandteil jeder Marketingaktivität, und dieses Buch ist ein lebendiges Porträt der digitalen Transformation im Marketing. Datenanalyse und intelligente Algorithmen automatisieren zeitaufwändige Marketingaufgaben. Der Entscheidungsprozess wird nicht nur perfekter, sondern auch schneller, was in einem sich ständig beschleunigenden Wettbewerbsumfeld von großer Bedeutung ist.

„Dieses Buch ist ein lebendiges Porträt der digitalen Transformation im Marketing. Es zeigt, wie Data Science zu einem integralen Bestandteil jeder Marketingaktivität wird. Es wird detailliert beschrieben, wie auf Datenanalyse und intelligenten Algorithmen basierende Ansätze zur tiefgreifenden Automatisierung traditionell arbeitsintensiver Marketingaufgaben beitragen. Der Entscheidungsprozess wird nicht nur fortschrittlicher, sondern auch schneller, was in unserem sich ständig beschleunigenden Wettbewerbsumfeld wichtig ist. Dieses Buch muss von Datenverarbeitungs- und Marketingfachleuten gelesen werden, und es ist besser, wenn sie es gemeinsam lesen. “ Andrey Sebrant, Direktor für strategisches Marketing, Yandex.

Auszug. 5.8.3. Modelle mit versteckten Faktoren

In den bisher diskutierten gemeinsamen Filteralgorithmen basieren die meisten Berechnungen auf den einzelnen Elementen der Bewertungsmatrix. Proximity-basierte Methoden bewerten fehlende Bewertungen direkt anhand bekannter Werte in der Bewertungsmatrix. Modellbasierte Methoden fügen der Bewertungsmatrix eine Abstraktionsschicht hinzu und erstellen ein Vorhersagemodell, das bestimmte Beziehungsmuster zwischen Benutzern und Elementen erfasst. Das Modelltraining hängt jedoch weiterhin stark von den Eigenschaften der Bewertungsmatrix ab. Infolgedessen sind diese kollaborativen Filtertechniken normalerweise mit den folgenden Problemen konfrontiert:

Die Bewertungsmatrix kann Millionen von Benutzern, Millionen von Elementen und Milliarden bekannter Bewertungen enthalten, was zu ernsthaften Problemen hinsichtlich der Komplexität und Skalierbarkeit der Berechnungen führt.

Die Bewertungsmatrix ist normalerweise sehr spärlich (in der Praxis fehlen möglicherweise 99% der Bewertungen). Dies wirkt sich auf die Rechenstabilität der Empfehlungsalgorithmen aus und führt zu unzuverlässigen Schätzungen, wenn der Benutzer oder das Element keine wirklich ähnlichen Nachbarn hat. Dieses Problem wird häufig durch die Tatsache verschärft, dass die meisten grundlegenden Algorithmen entweder benutzer- oder elementorientiert sind, was ihre Fähigkeit einschränkt, alle Arten von Ähnlichkeiten und Beziehungen aufzuzeichnen, die in der Bewertungsmatrix verfügbar sind.

Die Daten in der Bewertungsmatrix sind aufgrund von Ähnlichkeiten zwischen Benutzern und Elementen normalerweise stark korreliert. Dies bedeutet, dass die in der Bewertungsmatrix verfügbaren Signale nicht nur spärlich, sondern auch redundant sind, was zur Verschärfung des Skalierbarkeitsproblems beiträgt.

Die obigen Überlegungen weisen darauf hin, dass die ursprüngliche Bewertungsmatrix möglicherweise nicht die optimalste Darstellung von Signalen ist, und andere alternative Darstellungen, die für die gemeinsame Filterung besser geeignet sind, sollten in Betracht gezogen werden. Um diese Idee zu untersuchen, kehren wir zum Ausgangspunkt zurück und denken ein wenig über die Art der Empfehlungsdienste nach. Tatsächlich kann der Empfehlungsdienst als ein Algorithmus betrachtet werden, der Bewertungen basierend auf einem gewissen Maß an Ähnlichkeit zwischen dem Benutzer und dem Element vorhersagt:


Eine Möglichkeit, dieses Ähnlichkeitsmaß zu bestimmen, besteht darin, den Hidden-Factor-Ansatz zu verwenden und Benutzer und Elemente auf Punkte in einem k-dimensionalen Raum abzubilden, sodass jeder Benutzer und jedes Element durch einen k-dimensionalen Vektor dargestellt wird:


Vektoren müssen so konstruiert sein, dass die entsprechenden Dimensionen p und q miteinander vergleichbar sind. Mit anderen Worten kann jede Dimension als Zeichen oder Konzept betrachtet werden, dh puj ist ein Maß für die Nähe von Benutzer u und Konzept j, und qij ist ein Maß für Element i und Konzept j. In der Praxis werden diese Dimensionen häufig als Genres, Stile und andere Attribute interpretiert, die gleichzeitig für Benutzer und Elemente gelten. Die Ähnlichkeit zwischen dem Benutzer und dem Element und dementsprechend die Bewertung kann als das Produkt der entsprechenden Vektoren definiert werden:


Da jede Bewertung in ein Produkt aus zwei Vektoren zerlegt werden kann, die zu einem Konzeptraum gehören, der in der ursprünglichen Bewertungsmatrix nicht direkt beobachtet wird, werden p und q als versteckte Faktoren bezeichnet. Der Erfolg dieses abstrakten Ansatzes hängt natürlich ganz davon ab, wie die verborgenen Faktoren bestimmt und konstruiert werden. Um diese Frage zu beantworten, stellen wir fest, dass der Ausdruck 5.92 wie folgt in Matrixform umgeschrieben werden kann:


wobei P die aus den Vektoren p zusammengesetzte n × k-Matrix ist und Q die aus den Vektoren q zusammengesetzte m × k-Matrix ist, wie in Fig. 1 gezeigt. 5.13. Das Hauptziel eines gemeinsamen Filtersystems besteht normalerweise darin, die Vorhersagefehler der Bewertung zu minimieren, wodurch Sie das Optimierungsproblem in Bezug auf die Matrix der verborgenen Faktoren direkt bestimmen können:



Unter der Annahme, dass die Anzahl der verborgenen Dimensionen k fest ist und k ≤ n und k ≤ m ist, reduziert sich das Optimierungsproblem 5.94 auf das in Kapitel 2 berücksichtigte niedrigrangige Approximationsproblem. Um den Lösungsansatz zu demonstrieren, nehmen wir für einen Moment an, dass die Bewertungsmatrix vollständig ist. In diesem Fall hat das Optimierungsproblem eine analytische Lösung hinsichtlich der Singular Value Decomposition (SVD) der Bewertungsmatrix. Insbesondere kann unter Verwendung des Standard-SVD-Algorithmus die Matrix in das Produkt von drei Matrizen zerlegt werden:


wobei U die durch Spalten orthonormalisierte n × n-Matrix ist, Σ die n × m-Diagonalmatrix ist und V die durch Spalten orthonormalisierte m × m-Matrix ist. Eine optimale Lösung für Problem 5.94 kann in Bezug auf diese Faktoren erhalten werden, abgeschnitten auf die k wichtigsten Dimensionen:


Folglich können versteckte Faktoren, die hinsichtlich der Vorhersagegenauigkeit optimal sind, durch singuläre Zerlegung erhalten werden, wie unten gezeigt:


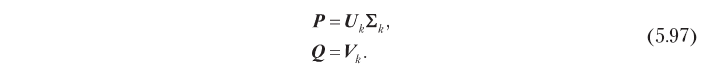
Dieses SVD-basierte Hidden-Factor-Modell hilft bei der Lösung der am Anfang dieses Abschnitts beschriebenen Co-Filtering-Probleme. Erstens ersetzt es die große n × m-Bewertungsmatrix durch n × k- und m × k-Faktormatrizen, die normalerweise viel kleiner sind, da in der Praxis die optimale Anzahl versteckter Dimensionen k häufig klein ist. Es gibt zum Beispiel einen Fall, in dem die Bewertungsmatrix mit 500.000 Benutzern und 17.000 Elementen mit 40 Messungen ziemlich gut angenähert werden konnte [Funk, 2016]. Ferner eliminiert SVD die Korrelation in der Bewertungsmatrix: Die durch 5,97 definierten Latentfaktormatrizen sind in Spalten orthonormal, d. H. Versteckte Dimensionen sind nicht korreliert. Wenn SVD, was in der Praxis normalerweise der Fall ist, auch das Problem der Spärlichkeit löst, weil das in der ursprünglichen Bewertungsmatrix vorhandene Signal effektiv konzentriert ist (denken Sie daran, dass wir k Dimensionen mit der höchsten Signalenergie auswählen) und die Matrix der verborgenen Faktoren nicht dünn ist. Abbildung 5.14 zeigt diese Eigenschaft. Der benutzerbasierte Näherungsalgorithmus (5.14, a) reduziert spärliche Bewertungsvektoren für ein bestimmtes Element und einen bestimmten Benutzer, um eine Bewertungsbewertung zu erhalten. Das Hidden-Factor-Modell (5.14, b) schätzt dagegen die Bewertung durch Faltung zweier Vektoren mit reduzierter Dimension und höherer Energiedichte.


Der soeben beschriebene Ansatz scheint eine kohärente Lösung für das Problem der versteckten Faktoren zu sein, hat jedoch aufgrund der Annahme, dass die Ratingmatrix vollständig ist, einen schwerwiegenden Nachteil. Wenn die Bewertungsmatrix dünn ist, was fast immer der Fall ist, kann der Standard-SVD-Algorithmus nicht direkt angewendet werden, da er fehlende (undefinierte) Elemente nicht verarbeiten kann. Die einfachste Lösung in diesem Fall besteht darin, die fehlenden Bewertungen mit einem Standardwert zu füllen. Dies kann jedoch zu einer ernsthaften Verzerrung der Prognose führen. Darüber hinaus ist es rechnerisch ineffizient, da die rechnerische Komplexität einer solchen Lösung gleich der SVD-Komplexität für die vollständige n × m-Matrix ist, während es wünschenswert ist, ein Verfahren mit einer Komplexität zu haben, die proportional zur Anzahl bekannter Bewertungen ist. Diese Probleme können mit den in den folgenden Abschnitten beschriebenen alternativen Zerlegungsmethoden gelöst werden.

5.8.3.1. Unbegrenzte Zersetzung

Der Standard-SVD-Algorithmus ist eine analytische Lösung für das niedrigrangige Approximationsproblem. Dieses Problem kann jedoch als Optimierungsproblem betrachtet werden, und es können auch universelle Optimierungsmethoden darauf angewendet werden. Einer der einfachsten Ansätze besteht darin, die Gradientenabstiegsmethode zu verwenden, um die Werte versteckter Faktoren iterativ zu verfeinern. Ausgangspunkt ist die Definition der Kostenfunktion J als verbleibender Prognosefehler:


Bitte beachten Sie, dass wir diesmal der Matrix der versteckten Faktoren keine Einschränkungen wie Orthogonalität auferlegen. Wenn wir den Gradienten der Kostenfunktion in Bezug auf versteckte Faktoren berechnen, erhalten wir das folgende Ergebnis:


wobei E die Restfehlermatrix ist:


Der Gradientenabstiegsalgorithmus minimiert die Kostenfunktion, indem er sich bei jedem Schritt in die negative Richtung des Gradienten bewegt. Daher können Sie versteckte Faktoren finden, die den quadratischen Fehler der Bewertungsvorhersage minimieren, indem Sie die Matrizen P und Q iterativ ändern, um gemäß den folgenden Ausdrücken zu konvergieren:


wobei α die Lerngeschwindigkeit ist. Der Nachteil der Gradientenabstiegsmethode ist die Notwendigkeit, die gesamte Matrix der Restfehler zu berechnen und gleichzeitig alle Werte der verborgenen Faktoren in jeder Iteration zu ändern. Ein alternativer Ansatz, der möglicherweise besser für große Matrizen geeignet ist, ist der stochastische Gradientenabstieg [Funk, 2016]. Der stochastische Gradientenabstiegsalgorithmus verwendet die Tatsache, dass der Gesamtprognosefehler J die Summe der Fehler für einzelne Elemente der Bewertungsmatrix ist, daher kann der allgemeine Gradient J durch einen Gradienten an einem Datenpunkt angenähert werden und die verborgenen Faktoren können elementweise geändert werden. Die vollständige Umsetzung dieser Idee ist in Algorithmus 5.1 dargestellt.


Die erste Stufe des Algorithmus ist die Initialisierung der Matrix versteckter Faktoren. Die Wahl dieser Anfangswerte ist nicht sehr wichtig, aber in diesem Fall wird eine gleichmäßige Verteilung der Energie bekannter Bewertungen unter zufällig erzeugten versteckten Faktoren gewählt. Dann optimiert der Algorithmus nacheinander die Dimensionen des Konzepts. Bei jeder Messung werden alle Bewertungen im Trainingssatz wiederholt umgangen, jede Bewertung anhand der aktuellen Werte der verborgenen Faktoren vorhergesagt, der Fehler geschätzt und die Werte der Faktoren gemäß den Ausdrücken 5.101 korrigiert. Die Messoptimierung ist abgeschlossen, wenn die Konvergenzbedingung erfüllt ist, wonach der Algorithmus mit der nächsten Messung fortfährt.

Algorithmus 5.1 hilft, die Einschränkungen der Standard-SVD-Methode zu überwinden. Es optimiert versteckte Faktoren durch Durchlaufen einzelner Datenpunkte und vermeidet so Probleme mit fehlenden Bewertungen und algebraischen Operationen mit riesigen Matrizen. Der iterative Ansatz macht den stochastischen Gradientenabstieg für praktische Anwendungen auch bequemer als den Gradientenabstieg, bei dem ganze Matrizen unter Verwendung der Ausdrücke 5.101 modifiziert werden.

BEISPIEL 5.6

Tatsächlich ist ein Ansatz, der auf verborgenen Faktoren basiert, eine ganze Gruppe von Methoden zum Unterrichten von Darstellungen, mit denen Muster, die in der Bewertungsmatrix enthalten sind, identifiziert und explizit in Form von Konzepten dargestellt werden können. Manchmal haben Konzepte eine völlig bedeutungsvolle Interpretation, insbesondere solche mit hoher Energie, obwohl dies nicht bedeutet, dass alle Konzepte immer eine bedeutungsvolle Bedeutung haben. Wenn Sie beispielsweise den Matrixzerlegungsalgorithmus auf eine Filmbewertungsdatenbank anwenden, können Faktoren erzeugt werden, die ungefähr den psychografischen Dimensionen entsprechen, z. B. Melodram, Komödie, Horror usw. Lassen Sie uns dieses Phänomen anhand eines kleinen numerischen Beispiels veranschaulichen, das die Bewertungsmatrix aus Tabelle verwendet. 5.3:


Subtrahieren Sie zuerst den globalen Durchschnitt μ = 2,82 von allen Elementen, um die Matrix zu zentrieren, und führen Sie dann den Algorithmus 5.1 mit k = 3 versteckten Messungen und der Lernrate α = 0,01 aus, um die folgenden zwei Faktorenmatrix zu erhalten:


Jede Zeile in diesen Matrizen entspricht einem Benutzer oder einem Film, und alle 12 Zeilenvektoren sind in Fig. 4 gezeigt. 5.15. Bitte beachten Sie, dass die Elemente in der ersten Spalte (der erste Vektor von Konzepten) die größten Werte haben und die Werte in den nachfolgenden Spalten allmählich abnehmen. Dies wird durch die Tatsache erklärt, dass der erste Konzeptvektor so viel Signalenergie erfasst, wie mit einer Messung erfasst werden kann, der zweite Konzeptvektor nur einen Teil der Restenergie erfasst usw. Beachten Sie ferner, dass das erste Konzept semantisch als Dramaachse interpretiert werden kann - Actionfilm, wobei die positive Richtung dem Actionfilm-Genre und die negative - dem Drama-Genre entspricht. Die Bewertungen in diesem Beispiel sind stark korreliert, so dass deutlich zu sehen ist, dass die ersten drei Benutzer und die ersten drei Filme im ersten Vektorkonzept (Dramafilme und Benutzer, die solche Filme mögen) große negative Werte aufweisen, während die letzten drei Benutzer und die letzten drei Filme haben in derselben Spalte große positive Bedeutungen (Actionfilme und Benutzer, die dieses Genre bevorzugen). Die zweite Dimension in diesem speziellen Fall entspricht hauptsächlich der Tendenz des Benutzers oder Elements, die als psychografisches Attribut interpretiert werden kann (Kritikalität der Urteile des Benutzers? Filmpopularität?). Andere Konzepte können als Rauschen betrachtet werden.


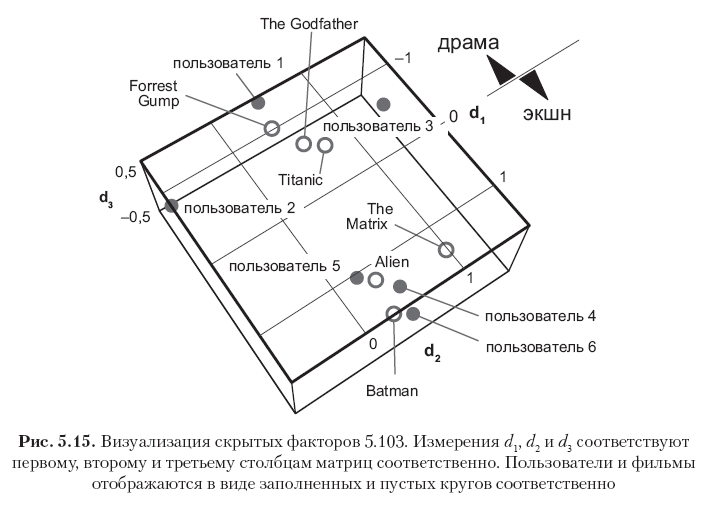
Die resultierende Matrix von Faktoren ist in den Spalten nicht vollständig orthogonal, sondern tendenziell orthogonal, da dies aus der Optimalität der SVD-Lösung folgt. Dies lässt sich anhand der Produkte von PTP und QTQ erkennen, die nahe an den Diagonalmatrizen liegen:


Die Matrizen 5.103 sind im Wesentlichen ein Vorhersagemodell, mit dem sowohl bekannte als auch fehlende Bewertungen bewertet werden können. Schätzungen können erhalten werden, indem zwei Faktoren multipliziert und der globale Durchschnitt addiert werden:


Die Ergebnisse geben die bekannten genau wieder und prognostizieren die fehlenden Bewertungen gemäß den intuitiven Erwartungen. Die Genauigkeit der Schätzungen kann durch Ändern der Anzahl der Messungen erhöht oder verringert werden, und die optimale Anzahl von Messungen kann in der Praxis durch Gegenprüfung und Auswahl eines angemessenen Kompromisses zwischen Rechenkomplexität und Genauigkeit bestimmt werden.

»Weitere Informationen zum Buch finden Sie auf der Website des Herausgebers
» Inhalt
» Auszug

25% Rabatt-Gutschein für Straßenhändler - Maschinelles Lernen

Nach Bezahlung der Papierversion des Buches wird ein elektronisches Buch per E-Mail verschickt.