Hallo allerseits!
Oft wenden sich Leute mit Fragen zu Aufgaben aus dem Bereich der digitalen Signalverarbeitung (DSP) an mich. Ich erzähle im Detail die Nuancen, schlage die notwendigen Informationsquellen vor. Aber allen Zuhörern fehlen, wie die Zeit gezeigt hat, praktische Aufgaben und Beispiele beim Erlernen dieses Bereichs. In diesem Zusammenhang habe ich beschlossen, einen kurzen interaktiven Kurs über die digitale Signalverarbeitung zu schreiben und ihn
öffentlich zugänglich zu machen .
Der größte Teil des Schulungsmaterials für visuelle und interaktive Präsentationen wird mit dem
Jupyter-Notizbuch implementiert. Es wird davon ausgegangen, dass der Leser Grundkenntnisse auf dem Gebiet der höheren Mathematik sowie ein wenig Beherrschung der Programmiersprache Python besitzt.

Vorlesungsliste
Dieser Kurs enthält Materialien in Form von fertigen Vorlesungen zu verschiedenen Themen aus dem Bereich der digitalen Signalverarbeitung. Die Materialien werden mithilfe von Python-Bibliotheken (numpy, scipy, matplotlib-Pakete usw.) präsentiert. Die grundlegenden Informationen für diesen Kurs stammen aus meinen Vorlesungen, die ich als Doktorand an Studenten des Moskauer Energieinstituts (NRU MEI) gegeben habe. Ein Teil der Informationen aus diesen Vorlesungen wurde bei Schulungsseminaren im
Zentrum für zeitgenössische Elektronik verwendet , wo ich als Dozent tätig war. Darüber hinaus umfasst dieses Material die Übersetzung verschiedener wissenschaftlicher Artikel, die Zusammenstellung von Informationen aus zuverlässigen Quellen und Literatur zur digitalen Signalverarbeitung sowie die offizielle Dokumentation zu Anwendungspaketen und integrierten Funktionen der Scipy- und Numpy-Bibliotheken von Python.
Für Benutzer von MATLAB (GNU Octave) ist es nicht schwierig, das Material unter dem Gesichtspunkt des Programmcodes zu beherrschen, da die Hauptfunktionen und ihre Attribute weitgehend identisch und den Methoden aus den Python-Bibliotheken ähnlich sind.
Alle Materialien sind nach den Hauptthemen der digitalen Signalverarbeitung gruppiert:
- Signale: analog, diskret, digital. Z-Umwandlung
- Fourier-Transformation: Amplituden- und Phasensignal, DFT und FFT,
- Faltung und Korrelation. Lineare und zyklische Faltung. Schnelle Faltung
- Zufällige Prozesse. Weißes Rauschen. Wahrscheinlichkeitsdichtefunktion
- Deterministische Signale. Modulation: AM, FM, FM, LFM. Manipulation
- Signalfilterung: IIR-, FIR-Filter
- Fensterfunktionen beim Filtern von Aufgaben. Erkennung schwacher Signale.
- Resampling: Dezimierung und Interpolation. CIC-Filter, gleitende Durchschnittsfilter
Die Liste der Vorlesungen ist ausreichend,
aber natürlich unvollständig für eine einführende Einführung in das Gebiet der DSP. In meiner Freizeit plane ich, dieses Projekt zu unterstützen und weiterzuentwickeln.
Wo zu finden?
Alle Materialien sind
absolut kostenlos und als offenes Repository auf
meinem Github als OpenSource-Projekt verfügbar. Die Materialien werden in zwei Formaten präsentiert - in Form von Jupyter-Notizbüchern zum interaktiven Arbeiten, Lernen und Bearbeiten sowie in Form von HTML-Dateien, die aus diesen Notizbüchern zusammengestellt wurden (nach dem Herunterladen vom Github haben sie ein durchaus geeignetes Format zum Lesen und Drucken).
Das Folgende ist eine sehr
kurze Beschreibung der Abschnitte des Kurses mit kurzen Erklärungen, Begriffen und Definitionen. Grundlegende Informationen finden Sie in den ersten Vorlesungen, hier nur eine kurze Übersicht!
Signale. Z-Umwandlung
Einführungsabschnitt, der grundlegende Informationen zu den Signaltypen enthält. Das Konzept einer diskreten Sequenz, einer Delta-Funktion und einer Heaviside-Funktion (Einheitssprung) wird vorgestellt.
Alle Signale gemäß der Darstellungsmethode am Set können in vier Gruppen unterteilt werden:
- analog - werden durch zeitkontinuierliche Funktionen beschrieben,
- diskret - werden zeitlich mit einem durch Abtastung festgelegten Schritt unterbrochen,
- quantisiert - haben eine Reihe von endlichen Pegeln (normalerweise in der Amplitude),
- digital - eine Kombination der Eigenschaften diskreter und quantisierter Signale.
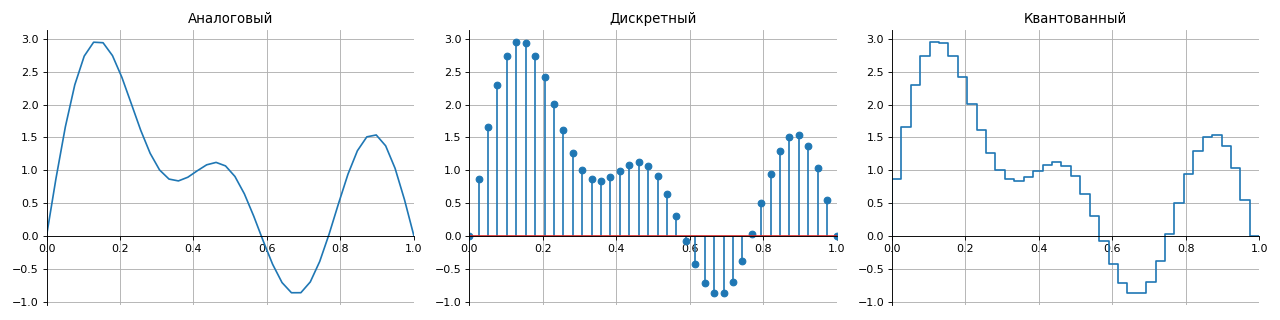
Für die korrekte Rekonstruktion eines analogen Signals aus einem digitalen Signal ohne Verzerrung und Verlust wird der als
Kotelnikov (Nyquist-Shannon) -Satz bekannte
Abtastsatz verwendet.
Jedes kontinuierliche Signal mit einem begrenzten Spektrum kann eindeutig und ohne Verlust aus seinen diskreten Abtastwerten wiederhergestellt werden, die mit einer Frequenz entnommen wurden, die streng größer als das Doppelte der oberen Frequenz des Spektrums eines kontinuierlichen Signals ist.
Eine solche Interpretation ist gültig, sofern die kontinuierliche Funktion der Zeit ein Frequenzband von 0 bis zum Wert der oberen Frequenz einnimmt. Wenn die Quantisierungs- und Diskretisierungsschritte falsch gewählt werden, wird das Signal von analog zu diskret verzerrt.
Auch in diesem Abschnitt werden die
Z-Transformation und ihre Eigenschaften beschrieben und die Darstellung diskreter Sequenzen in der Z-Form gezeigt.
Beispiel einer endlichen diskreten Folge:
x(nT) = {2, 1, -2, 0, 2, 3, 1, 0}
.
Ein Beispiel für dieselbe Sequenz in Z-Form:
X (z) = 2 + z
-1 - 2z
-2 + 2z
-4 + 3z
-5 + 1z
-6Fourier-Transformation. Eigenschaften DFT und FFT
Dieser Abschnitt beschreibt das Konzept des Zeit- und Frequenzbereichs eines Signals. Die Definition der diskreten Fourier-Transformation (DFT) wird eingeführt. Die direkten und inversen DFTs und ihre Haupteigenschaften werden berücksichtigt. Dargestellt ist der Übergang von der DFT zum FFT-Algorithmus (Fast Fourier Transform) in Basis 2 (Dezimierungsalgorithmen in Frequenz und Zeit). Reflektierte die Wirksamkeit von FFT im Vergleich zu DFT.
In diesem Abschnitt wird insbesondere das Python-Paket scipy.ffpack zur Berechnung verschiedener Fourier-Transformationen (Sinus, Cosinus, direkt, invers, mehrdimensional, real) beschrieben.
Mit der Fourier-Transformation können Sie jede Funktion als Satz harmonischer Signale darstellen! Die Fourier-Transformation ist die Grundlage für Faltungsmethoden und das Design digitaler Korrelatoren, wird aktiv in der Spektralanalyse verwendet und wird bei der Arbeit mit langen Zahlen verwendet.
Merkmale der Spektren diskreter Signale:
1. Die spektrale Dichte eines diskreten Signals ist eine periodische Funktion mit einer Periode gleich der Abtastfrequenz.
2. Wenn die diskrete Sequenz
real ist , ist der Spektraldichtemodul einer solchen Sequenz eine
gerade Funktion, und das Argument ist
eine ungerade Frequenzfunktion.
Harmonisches Signalspektrum:
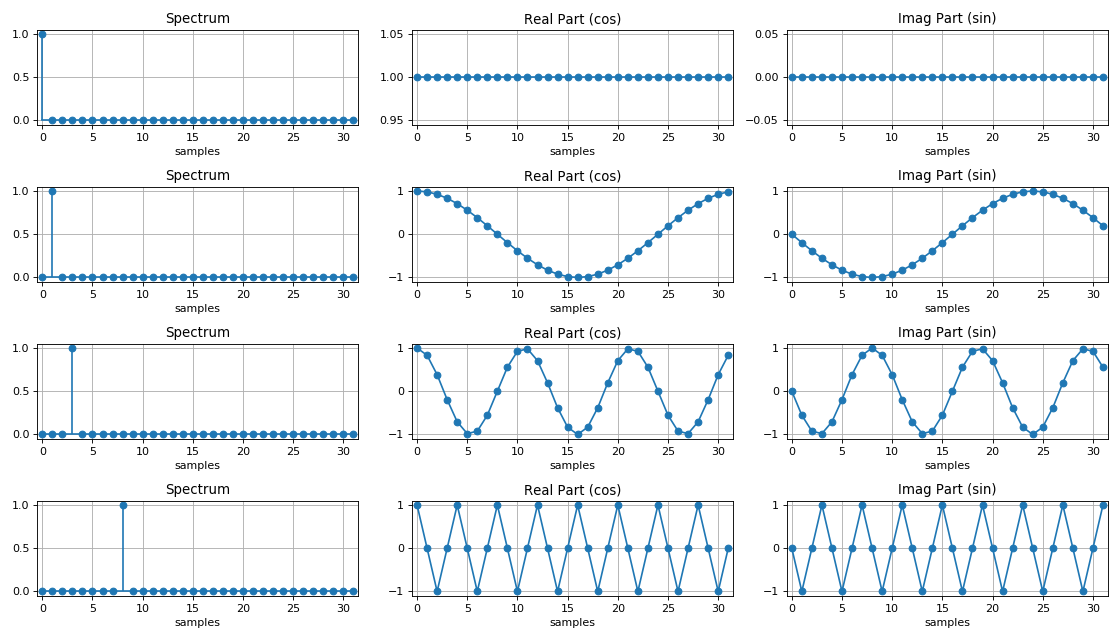
Vergleich der Wirksamkeit von DFT und FFT
Die Effizienz des FFT-Algorithmus und die Anzahl der linear ausgeführten Operationen hängen von der Sequenzlänge N ab:
Wie Sie sehen, sind die Einsparungen bei den Rechenressourcen (in Bezug auf die Verarbeitungsgeschwindigkeit oder die Anzahl der Hardwareeinheiten) umso größer, je länger die Konvertierungslänge ist!
Jede beliebige Wellenform kann als Satz von harmonischen Signalen mit unterschiedlichen Frequenzen dargestellt werden. Mit anderen Worten, ein Signal mit komplexer Form im Zeitbereich weist eine Reihe komplexer Abtastwerte im Frequenzbereich auf, die als * Harmonische * bezeichnet werden. Diese Abtastwerte drücken die Amplitude und Phase des harmonischen Effekts bei einer bestimmten Frequenz aus. Je größer der Satz von Harmonischen im Frequenzbereich ist, desto genauer erscheint die komplexe Wellenform.

Faltung und Korrelation
In diesem Abschnitt wird das Konzept der Korrelation und Faltung für diskrete zufällige und deterministische Sequenzen vorgestellt. Die Beziehung zwischen Autokorrelations- und Kreuzkorrelationsfunktionen mit der Faltung wird gezeigt. Die Eigenschaften der Faltung werden beschrieben, insbesondere werden die Verfahren der linearen und zyklischen Faltung eines diskreten Signals mit detaillierter Analyse am Beispiel einer diskreten Sequenz betrachtet. Zusätzlich wird ein Verfahren zur Berechnung der "schnellen" Faltung unter Verwendung von FFT-Algorithmen gezeigt.
Bei realen Problemen wird häufig die Frage nach dem Grad der Ähnlichkeit eines Prozesses mit einem anderen oder nach der Unabhängigkeit eines Prozesses von einem anderen aufgeworfen. Mit anderen Worten ist es erforderlich, die Beziehung zwischen den Signalen zu bestimmen, dh eine
Korrelation zu finden. Korrelationsmethoden werden in einer Vielzahl von Aufgaben eingesetzt: Signalsuche, Bildverarbeitung und Bildverarbeitung, bei Radarproblemen zur Bestimmung der Eigenschaften von Zielen und zur Bestimmung der Entfernung zu einem Objekt. Zusätzlich wird die Korrelation verwendet, um nach schwachen Signalen im Rauschen zu suchen.
Die Faltung beschreibt die Wechselwirkung von Signalen miteinander. Wenn eines der Signale die Impulsantwort des Filters ist, ist die Faltung der Eingangssequenz mit der Impulsantwort nichts anderes als eine Reaktion der Schaltung auf die Eingangsaktion. Mit anderen Worten spiegelt das resultierende Signal den Durchgang des Signals durch das Filter wider.
Die Autokorrelationsfunktion (ACF) wird zum Codieren von Informationen verwendet. Die Wahl der Codierungssequenz gemäß den Parametern Länge, Frequenz und Form ist weitgehend auf die Korrelationseigenschaften dieser Sequenz zurückzuführen. Die beste Codesequenz weist die geringste Wahrscheinlichkeit einer falschen Erkennung oder Operation (zum Erkennen von Signalen, für Schwellenwertgeräte) oder einer falschen Synchronisation (zum Senden und Empfangen von Codesequenzen) auf.
Dieser Abschnitt enthält eine Tabelle zum Vergleich der Wirksamkeit der schnellen Faltung und der Faltung, berechnet nach der direkten Formel (anhand der Anzahl der reellen Multiplikationen).
Wie Sie sehen können,
verliert die schnelle Faltung bei FFT-Längen bis zu 64 an die direkte Methode. Mit zunehmender FFT-Länge ändern sich die Ergebnisse jedoch in die entgegengesetzte Richtung - eine schnelle Faltung beginnt, die direkte Methode zu übertreffen. Je länger die FFT ist, desto besser ist natürlich die Verstärkung bei der Frequenzmethode.
Zufällige Signale und Rauschen
In diesem Abschnitt wird das Konzept der Zufallssignale, der Wahrscheinlichkeitsdichte und des Zufallsverteilungsgesetzes vorgestellt. Mathematische Momente werden berücksichtigt - Mittelwert (mathematische Erwartung) und Varianz (oder die Wurzel dieser Größe ist die Standardabweichung). Auch in diesem Abschnitt werden die Normalverteilung und das damit verbundene Konzept des
weißen Rauschens als Hauptquelle für Rauschen (Interferenz) während der Signalverarbeitung betrachtet.
Ein Zufallssignal ist eine Funktion der Zeit, deren Werte nicht im Voraus bekannt sind und nur mit einer gewissen
Wahrscheinlichkeit vorhergesagt
werden können . Die Hauptmerkmale von Zufallssignalen umfassen:
- Verteilungsgesetz (relative Verweilzeit eines Signalwerts in einem bestimmten Intervall),
- spektrale Verteilung der Signalleistung.
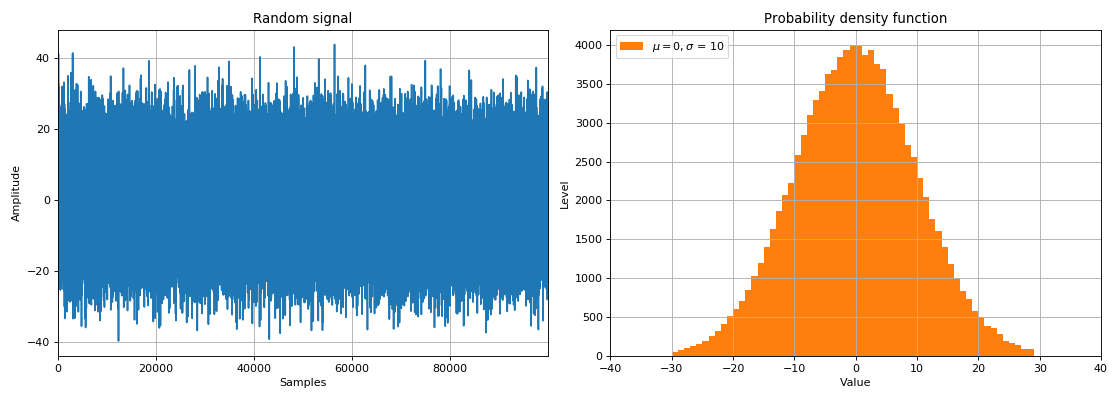
Bei DSP-Aufgaben werden zufällige Signale in zwei Klassen unterteilt:
- Rauschen - zufällige Schwankungen, die aus einer Reihe unterschiedlicher Frequenzen und Amplituden bestehen,
- Signale, die Informationen tragen, für deren Verarbeitung auf probabilistische Methoden zurückgegriffen werden muss.
Mithilfe von Zufallsvariablen können wir die Auswirkung eines realen Mediums auf den Durchgang eines Signals von einer Quelle zu einem Datenempfänger simulieren. Wenn ein Signal eine verrauschte Verbindung durchläuft, wird dem Signal das sogenannte weiße Rauschen hinzugefügt. In der Regel ist die spektrale Dichte eines solchen Rauschens bei allen Frequenzen gleichmäßig (gleichmäßig) verteilt, und die Rauschwerte im Zeitbereich sind normalverteilt (Gaußsches Verteilungsgesetz). Da den Signalamplituden in den ausgewählten Zeitabtastwerten physikalisch weißes Rauschen hinzugefügt wird, wird es als additives weißes Gaußsches Rauschen (AWGN) bezeichnet.
Signale, Modulation und Manipulation
Dieser Abschnitt zeigt die grundlegenden Methoden zum Ändern eines oder mehrerer Parameter eines harmonischen Signals. Die Konzepte der Amplituden-, Frequenz- und Phasenmodulation werden vorgestellt. Insbesondere wird die bei Radarproblemen verwendete lineare Frequenzmodulation hervorgehoben. Dargestellt sind die Hauptmerkmale der Signale, die Spektren der modulierten Signale in Abhängigkeit von den Modulationsparametern.

Der Einfachheit halber wurde in Python eine Reihe von Funktionen erstellt, die die oben genannten Modulationstypen implementieren. Beispiel für die Implementierung eines Chirpsignals:
def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs): """ Create Chirp signal Parameters ---------- amp : float Signal magnitude beta : float Modulation bandwidth: beta < N for complex, beta < 0.5N for real freq : float or int Linear frequency of signal period : integer Number of points for signal (same as period) kwargs : bool Complex signal if is_complex = True Modulated by half-sine wave if is_modsine = True """ is_complex = kwargs.get('is_complex', False) is_modsine = kwargs.get('is_modsine', False) t = np.linspace(0, 1, period) tt = np.pi * (freq * t + beta * t ** 2) if is_complex is True: res = amp * (np.cos(tt) + 1j * np.sin(tt)) else: res = amp * np.cos(tt) if is_modsine is True: return res * np.sin(np.pi * t) return res
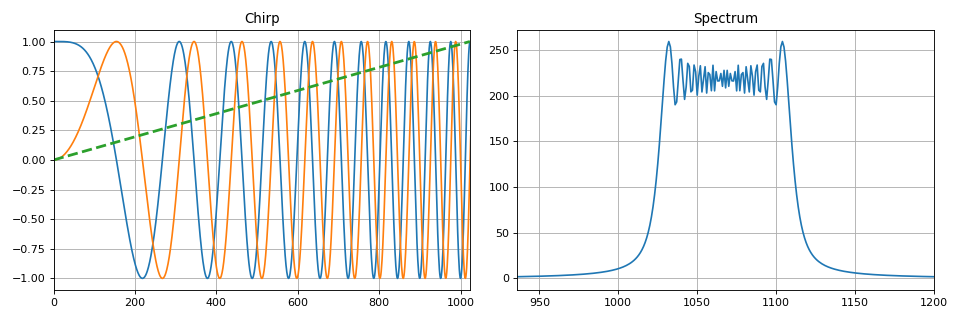
Auch in diesem Abschnitt aus der Theorie der Übertragung diskreter Nachrichten werden Arten der digitalen Modulation - Manipulationen beschrieben. Wie bei analogen Signalen können digitale harmonische Sequenzen in Amplitude, Phase und Frequenz (oder mehreren Parametern gleichzeitig) manipuliert werden.

Digitale Filter - IIR und FIR
Ein ausreichend großer Abschnitt, der der digitalen Filterung diskreter Sequenzen gewidmet ist. Bei digitalen Signalverarbeitungsaufgaben fließen Daten durch Schaltkreise, die als
Filter bezeichnet werden . Digitale Filter haben wie analoge unterschiedliche Eigenschaften - Frequenz: Frequenzgang, Phasengang, Zeit: Impulsgang sowie die Übertragungscharakteristik des Filters. Digitale Filter werden hauptsächlich verwendet, um die Signalqualität zu verbessern - um ein Signal von einer Datensequenz zu isolieren oder um unerwünschte Signale zu verschlechtern - um bestimmte Signale in eingehenden Abtastsequenzen zu unterdrücken.

In diesem Abschnitt werden die wichtigsten Vor- und Nachteile digitaler Filter (im Vergleich zu analogen) aufgeführt. Das Konzept der Impuls- und Übertragungseigenschaften des Filters wird vorgestellt. Es werden zwei Klassen von Filtern betrachtet - mit einer unendlichen Impulsantwort (IIR) und einer endlichen Impulsantwort (FIR). Es wird eine Methode zum Entwerfen von Filtern in
kanonischer und
direkter Form gezeigt. Bei FIR-Filtern wird die Frage berücksichtigt, wie zu einer rekursiven Form gewechselt werden kann.
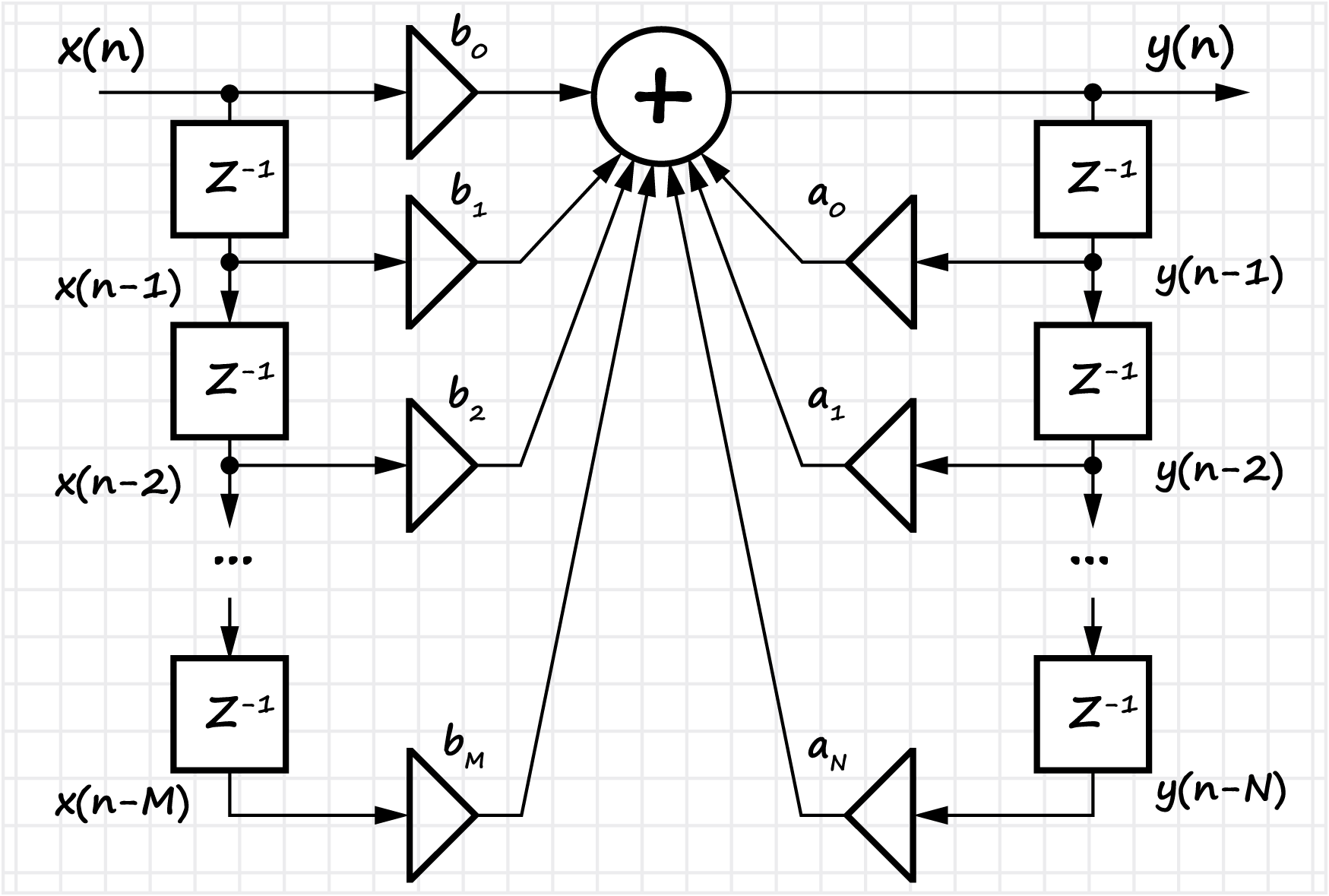
Bei FIR-Filtern wird der Filterentwurfsprozess von der Entwicklung der technischen Spezifikationen (mit den angegebenen Hauptparametern) bis zur Software- und Hardwareimplementierung - Suche nach Filterkoeffizienten (unter Berücksichtigung der Darstellungsform von Anzahl, Bittiefe usw.) gezeigt. Die Definitionen von symmetrischen FIR-Filtern, die lineare Phasenantwort und ihre Beziehung zum Konzept der Gruppenverzögerung werden vorgestellt.

Fensterfunktionen beim Filtern von Aufgaben
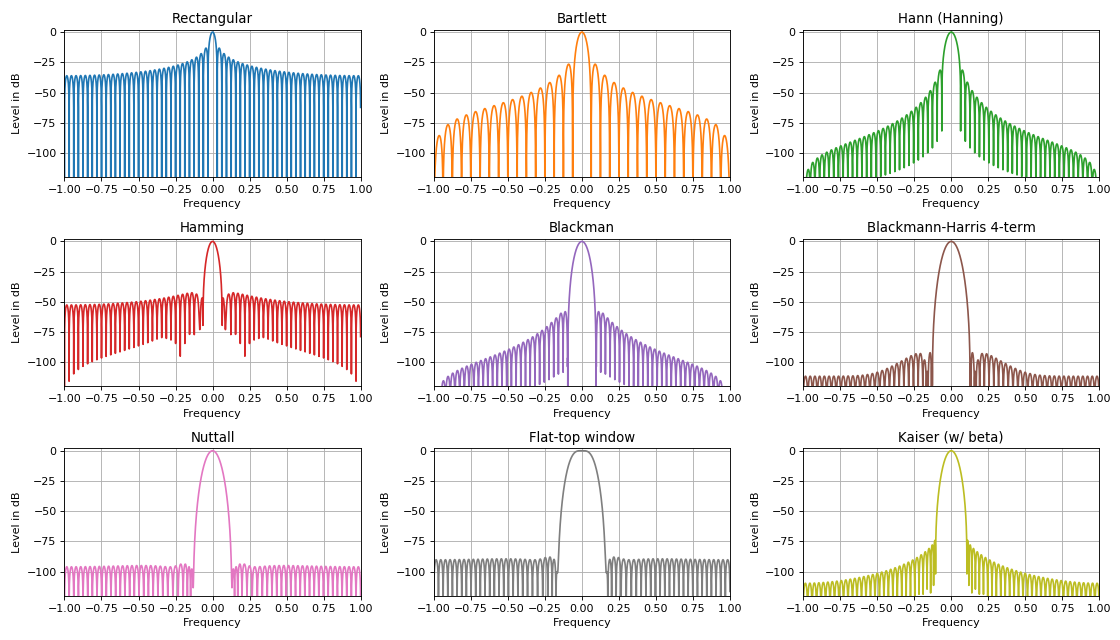
Bei den Aufgaben der digitalen Signalverarbeitung werden Fensterfunktionen verschiedener Formen verwendet, die, wenn sie einem Signal im Zeitbereich überlagert werden, dessen spektrale Eigenschaften qualitativ verbessern können. Eine große Anzahl verschiedener Fenster ist hauptsächlich auf eines der Hauptmerkmale einer Fensterüberlagerung zurückzuführen. Dieses Merkmal drückt sich in der Beziehung zwischen der Höhe der Nebenkeulen und der Breite der Mittellappen aus. Regel:
Je stärker die Unterdrückung der Nebenkeulen des Spektrums ist, desto breiter ist die Hauptkeule des Spektrums und umgekehrt.

Eine der Anwendungen von Fensterfunktionen: Erkennung schwacher Signale vor dem Hintergrund stärkerer Signale durch Unterdrückung des Niveaus von Nebenkeulen. Die Hauptfensterfunktionen in DSP-Aufgaben sind ** dreieckig, sinusförmig, Lanczos, Hann, Hamming, Blackman, Harris, Blackman-Harris-Fenster, Flat-Top-Fenster, Natall, Gauss, Kaiser-Fenster ** und viele andere. Die meisten von ihnen werden durch eine endliche Reihe ausgedrückt, indem harmonische Signale mit bestimmten Gewichten summiert werden. Solche Signale sind in der Praxis auf allen Hardwaregeräten (programmierbaren Logikschaltungen oder Signalprozessoren) perfekt implementiert.
Resampling. Dezimierung und Interpolation
In diesem Abschnitt werden die Probleme der Signalverarbeitung mit mehreren Geschwindigkeiten erläutert - Änderungen der Abtastfrequenz. Die Mehrgeschwindigkeitsverarbeitung von Signalen (Mehrratenverarbeitung) legt nahe, dass es bei der linearen Umwandlung digitaler Signale möglich ist, die Abtastfrequenz in Richtung abnehmend oder ansteigend oder in Bruchteilen von Malen zu ändern. Dies führt zu einer effizienteren Signalverarbeitung, da die Möglichkeit eröffnet wird, die minimal zulässigen Abtastfrequenzen zu verwenden, und infolgedessen die erforderliche Rechenleistung des entworfenen digitalen Systems erheblich verringert wird.
Dezimierung (Dezimierung) - Downsampling.
Interpolation - Erhöhung der Abtastrate.
In diesem Abschnitt wird auch die Klasse der homogenen FIR-Filter betrachtet, die als Integralkammfilter (CIC, Cascaded Integrator - Comb) bezeichnet werden. Die Implementierung, die grundlegenden Eigenschaften und Funktionen von CIC-Filtern werden gezeigt. Aufgrund der Linearität der mathematischen Operationen, die im CIC-Filter auftreten, ist es möglich, mehrere Filter hintereinander zu kaskadieren, was zu einer proportionalen Abnahme des Niveaus der Nebenkeulen führt, aber auch die "Blockierung" der Hauptkeule der Amplituden-Frequenz-Charakteristik erhöht.
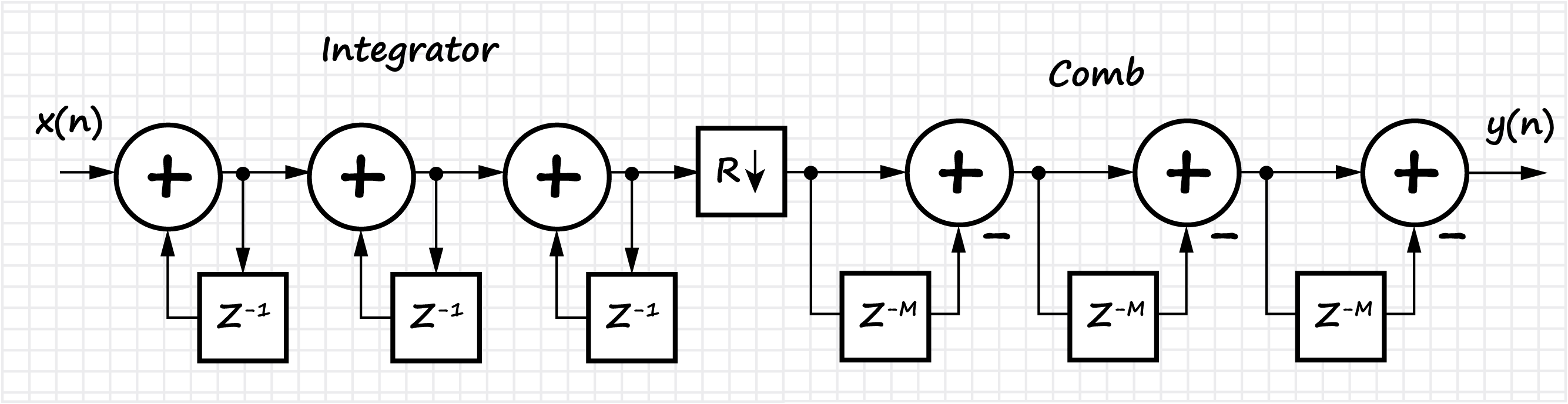
Diagramm des Frequenzgangs des Filters in Abhängigkeit vom Dezimierungskoeffizienten:
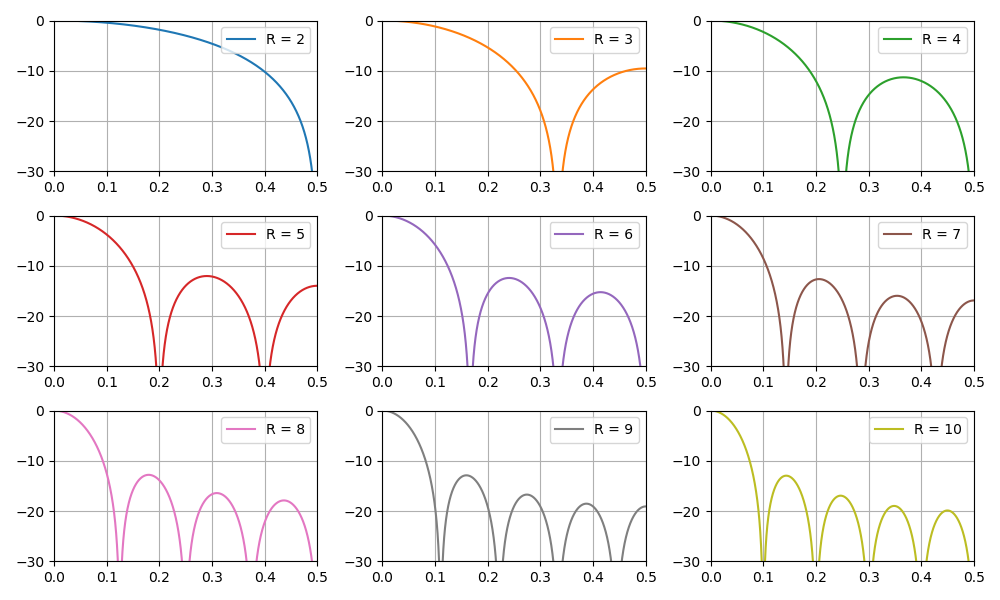
In diesem Abschnitt wird auch das Problem der Erhöhung der Bittiefe der Daten am Ausgang des CIC-Filters in Abhängigkeit von seinen Parametern erörtert. Dies ist besonders wichtig bei Software-Implementierungsaufgaben, insbesondere bei FPGAs.
Für die praktische Implementierung von CIC-Filtern in Python wurde ein separater
CicFilter der Klasse
entwickelt , der Dezimierungs- und Interpolationsmethoden implementiert. Außerdem werden Änderungen der Abtastrate mithilfe der integrierten Methoden aus dem scipy Python-Paket angezeigt.
Python CicFilter-Klasse für die digitale Signalverarbeitung class CicFilter: """ Cascaded Integrator-Comb (CIC) filter is an optimized class of finite impulse response (FIR) filter. CIC filter combines an interpolator or decimator, so it has some parameters: R - decimation or interpolation ratio, N - number of stages in filter (or filter order) M - number of samples per stage (1 or 2)* * for this realisation of CIC filter just leave M = 1. CIC filter is used in multi-rate processing. In hardware applications CIC filter doesn't need multipliers, just only adders / subtractors and delay lines. Equation for 1st order CIC filter: y[n] = x[n] - x[n-RM] + y[n-1]. Parameters ---------- x : np.array input signal """ def __init__(self, x): self.x = x def decimator(self, r, n): """ CIC decimator: Integrator + Decimator + Comb Parameters ---------- r : int decimation rate n : int filter order """
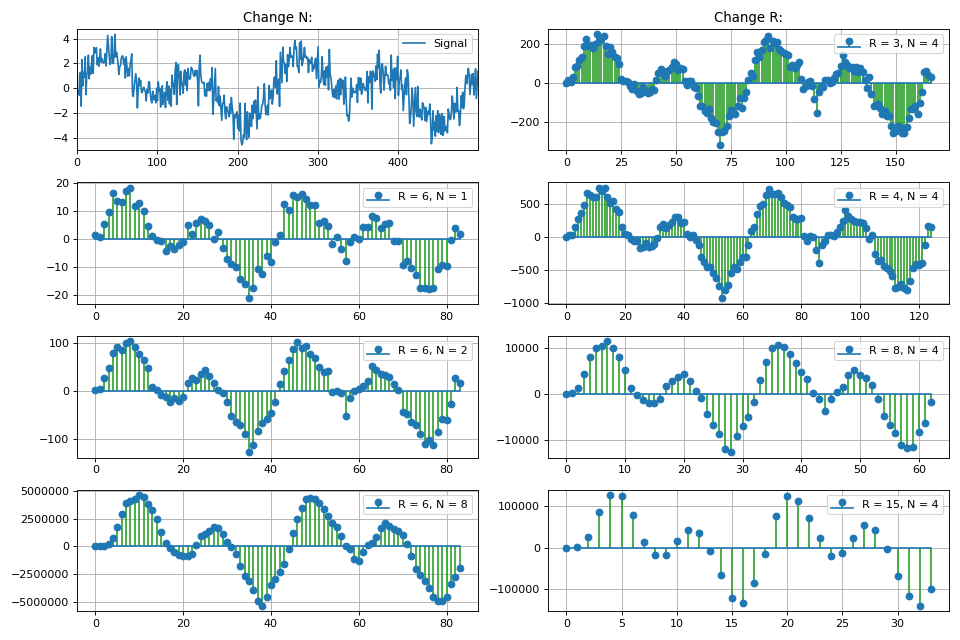
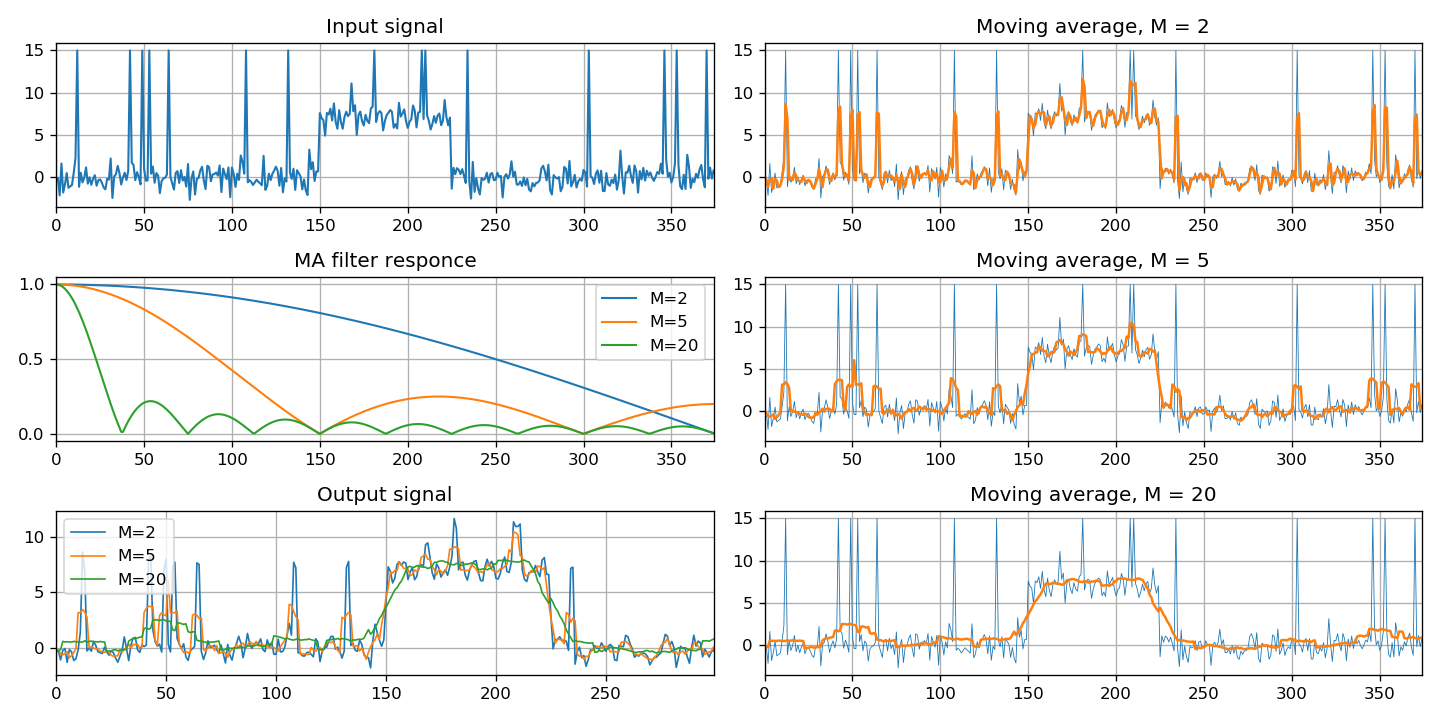
Schließlich enthält dieser Abschnitt eine spezielle Klasse von Filtern - den gleitenden Durchschnitt. Es werden drei Implementierungsmethoden gezeigt: durch Faltung von Signalen unter Verwendung eines FIR-Filters und eines IIR-Filters.
Fazit
Ich hoffe, dass dieser Vorlesungskurs in Verbindung mit meinen vorherigen Artikeln zur digitalen FPGA-Signalverarbeitung praktische Vorteile bringt und dem Leser hilft, die Grundlagen der digitalen Signalverarbeitung besser zu verstehen. Dieses Projekt wird verbessert und durch neues nützliches und nicht weniger interessantes Material ergänzt. Verfolgen Sie die Entwicklung!
Zusätzlich zu diesem Material unterstütze und entwickle
ich mein Projekt auf den wichtigsten DSP-Modulen (in Python). Es enthält ein Paket zum Erzeugen verschiedener Signale, eine Klasse von CIC-Filtern für Dezimierungs- und Interpolationsprobleme, einen Algorithmus zum Berechnen der Koeffizienten eines korrigierenden FIR-Filters, einen Filter für den gleitenden Durchschnitt und einen Algorithmus zum Berechnen einer ultralangen FFT durch zweidimensionale Konvertierungsmethoden (letzteres war sehr nützlich bei der Arbeit mit der Hardware-Implementierung auf FPGAs). .
Vielen Dank für Ihre Aufmerksamkeit!