In der Schule hatte ich einen Klassenkameraden, der hören konnte, wie das Auto auf dem Hof ​​funktioniert, und mit ernstem Gesicht ein Urteil fällen konnte: Alles ist in Ordnung oder etwas ist kaputt, und ich muss dringend nach neuen Teilen / Öl / Werkzeugen suchen! Ich, wie eine absolute Teekanne im Automobilgeschäft, hörte immer das übliche Rasseln des nächsten Dvenashka, bemerkte keine Unterschiede und staunte nur schweigend über sein Gehör und seine Fähigkeiten.

Jetzt habe ich die Innenseiten des Autos nicht besser verstanden, aber ich habe angefangen, mit der Verarbeitung von Tonsignalen und maschinellem Lernen zu arbeiten. Hier werden wir versuchen zu verstehen, ob es möglich ist, einem Computer beizubringen, Anomalien im Geräusch eines Motors zu erkennen.

Zumindest ist es nur interessant zu überprüfen, und in Zukunft könnte eine solche Technologie den Autobesitzern viel Geld sparen. Zumindest meiner Meinung nach treten kritische Fehler allmählich unter der Haube auf, und in den frühen Stadien sind viele von ihnen schnell und kostengünstig zu hören, was Zeit, Geld und bereits wackelige Nerven spart.

Nun, vielleicht ist es Zeit, von Worten zu Taten überzugehen. Lass uns gehen!

Ich möchte gleich sagen, dass ich in allem, was Mathematik und Algorithmen betrifft, mehr Wert auf Bedeutung und Verständnis legen werde. Hier wird es keine Formeln und mathematischen Berechnungen geben. Ich habe hier keine neuen Algorithmen entwickelt. Wenn Sie möchten, ist es für Formeln besser, Google und Wikipedia zu verwenden und die Links zu verwenden, die ich im gesamten Artikel hinterlassen werde.

Ich werde alle Erklärungen am Beispiel des Geräusches eines defekten Motors aus diesem Video auf YouTube geben .

Die von YouTube heruntergeladene Datei (Sie können sie mit Browsererweiterungen oder einfach durch Ändern des YouTube-Links zu ssyoutube herunterladen) konvertieren wir mit ffmpeg in das WAV-Format:

ffmpeg -i input_video.mp4 -c:a pcm_s16le -ar 16000 -ac 1 engine_sound.wav 

Bevor ich mit der Verarbeitung dieser Datei beginne, möchte ich einige Worte darüber sagen, was ein Spektrogramm ist und wie es uns bei der Lösung dieses Problems helfen wird. Sicherlich haben viele von Ihnen ein ähnliches Bild gesehen - dies ist die amplitudenzeitliche Darstellung von Ton oder ein Oszillogramm.

Wenn in einfachen Worten, dann ist Schall eine Welle, und die Amplitudenwerte dieser Welle werden zu bestimmten Zeiten auf dem Oszillogramm beobachtet.

Um aus einer solchen Darstellung ein Spektrogramm zu erhalten, benötigen wir die Fourier-Transformation. Mit seiner Hilfe können Sie die Amplituden-Frequenz-Darstellung des Klangs oder des Amplitudenspektrums erhalten. Ein solches Spektrum zeigt, bei welcher Frequenz und mit welcher Amplitude das untersuchte Signal ausgedrückt wird.

Tatsächlich ist ein Spektrogramm ein Satz von Spektren kurzer aufeinanderfolgender Teile eines Signals. Vielleicht reicht eine solche "Definition" aus, um nicht stark von der Aufgabe abgelenkt zu werden. Alles wird klarer, wenn Sie sich die Visualisierung des Spektrogramms ansehen (das Bild wurde mit WaveAssistant aufgenommen ). Die Zeit ist auf der X-Achse aufgetragen, die Frequenz auf der Y-Achse, dh jede Spalte in dieser Matrix ist der Spektrummodul zu einem bestimmten Zeitpunkt.

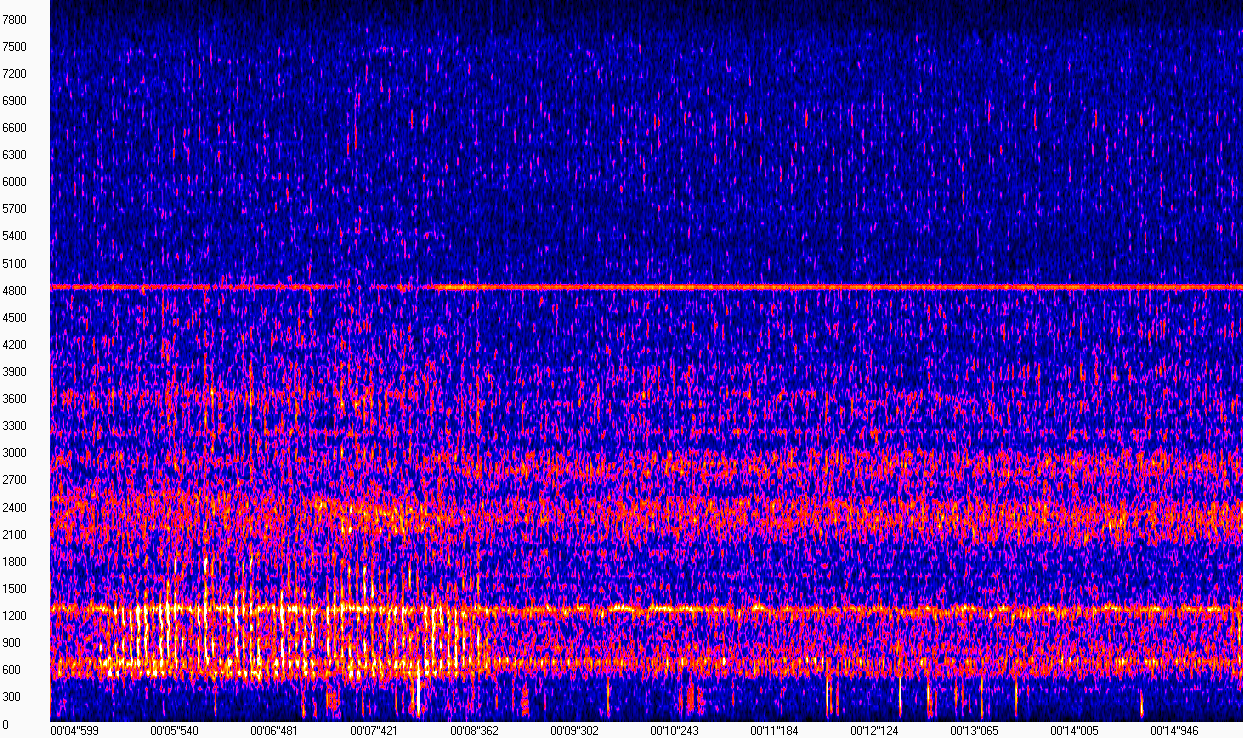
Dieses Spektrogramm zeigt, dass das Geräusch des Motors ohne Klopfen ungefähr gleich aussieht und bei Frequenzen in der Nähe von 600, 1200, 2400 und 4800 Hz ausgedrückt wird. Das Geräusch eines Klopfens, das den Besitzer stört, ist im Frequenzbereich von 600 bis 1200 Hz von 5 bis 8 Sekunden sehr deutlich. Da die Aufnahme unter ziemlich lauten Bedingungen auf der Straße gemacht wurde, sind diese Geräusche auch im Spektrogramm vorhanden, was unsere Aufgabe etwas erschwert.

Wenn wir uns ein solches Spektrogramm ansehen, können wir dennoch sicher sagen, wo das Klopfen war und wo nicht. Der Computer hat keine Augen, daher müssen wir einen Algorithmus auswählen, der in der Lage ist, zwischen einer solchen Abweichung (und vorzugsweise nicht nur dieser) zu unterscheiden, sofern in der Aufzeichnung Rauschen vorhanden ist.

Spektrogramme können mit der librosa-Bibliothek wie folgt berechnet werden:

 from librosa.util import buf_to_float from librosa.core import stft #     import numpy as np from scipy.io import wavfile #    wav- def cut_wav(path_to_wav, start_time, end_time): sr, wav_data = wavfile.read(path_to_wav) return wav_data[int(sr * start_time): int(sr * end_time)] def get_stft(wav_data): feat = np.abs(stft(buf_to_float(wav_data), n_fft=fft_size, hop_length=fft_step)) #  -       return feat.T wav_path = './engine_sound.wav' train_features = [] #    , time_list -    for [ts, te] in time_list: wav_part = cut_wav(wav_path, ts, te) spec = get_stft(wav_part) train_features.append(spec) X_train = np.vstack(train_features) #     full_wav_data = wavfile.read(wav_path)[1] X_test = get_stft(full_wav_data) 

Lösung

Genau genommen müssen wir das Problem der binären Klassifizierung lösen, bei dem wir feststellen müssen, ob der Motor defekt ist oder normal funktioniert. Mein Kollege und ich haben bereits in unserem vorherigen Artikel ähnliche Aufgaben beschrieben , bei denen wir ein Faltungs-Neuronales Netzwerk zur Klassifizierung akustischer Ereignisse verwendet haben. Eine solche Lösung ist hier kaum möglich: Neuronen lieben es sehr, wenn sie große Datenmengen erhalten. Wir haben es mit einer einzelnen Einrückung zu tun, die etwas länger als eine Minute dauert und offensichtlich nicht als großer Datensatz bezeichnet werden kann.

Die Auswahl wurde beim Gaußschen Mischungsmodell (Modell der Gaußschen Mischungen) gestoppt. Ein guter Artikel, der das Funktionsprinzip und das Training dieses Modells beschreibt, ist hier zu finden . Die allgemeine Idee dieses Modells besteht darin, die Daten unter Verwendung einer komplexen Verteilung in Form einer linearen Kombination mehrerer mehrdimensionaler Normalverteilungen zu beschreiben (mehr über die mehrdimensionale Normalverteilung hier ).

Da der Motor während seines Betriebs ungefähr "gleich" klingt, kann das Geräusch seines Betriebs als stationär angesehen werden, und die Idee, dieses Geräusch unter Verwendung einer solchen Verteilung zu beschreiben, scheint ziemlich sinnvoll. Um die Essenz von GMM zu verstehen, empfehle ich dringend, sich ein Beispiel für das Training anzusehen und hier die Anzahl der Gaussoiden zu wählen.

Unser Fall unterscheidet sich von den obigen Beispielen darin, dass anstelle von Punkten auf einer zweidimensionalen Ebene die aus dem Signalspektrogramm entnommenen Spektrumswerte verwendet werden. Sie können Verteilungsparameter wie den Typ der Kovarianzmatrix mithilfe des BIC-Kriteriums ( Beispiel , Beschreibung ) auswählen. In meinem Fall zeigten sich jedoch die optimalen Parameter aus Sicht dieses Kriteriums schlechter als die im folgenden Code gezeigten:

 from sklearn.mixture import GaussianMixture n_components = 3 gmm_clf = GaussianMixture(n_components) gmm_clf.fit(X_train) 

Unter der Annahme, dass das Geräusch des normalen Betriebs durch eine Verteilung beschrieben wird, deren Parameter während des Trainingsprozesses ausgewählt wurden, ist es möglich zu messen, wie nahe ein Geräusch an dieser Verteilung liegt.

Dazu können Sie die durchschnittliche Wahrscheinlichkeit der Spalten des Spektrogramms des untersuchten Signals berechnen und dann einen Schwellenwert auswählen, der die Wahrscheinlichkeit von Geräuschen guter Arbeit von allen anderen trennt. Die Glaubwürdigkeit für jede Sekunde ist wie folgt:

 n_seconds = len(full_wav_data) // sr gmm_scores = [] #     for i in range(n_seconds - 1): test_sec = X_test[(i * sr) // fft_step: ((i + 1) * sr) // fft_step, :] sc = gmm_clf.score(test_sec) gmm_scores.append(sc) 

Wenn Sie die erhaltene Wahrscheinlichkeit in der Tabelle anzeigen, erhalten wir das folgende Bild.
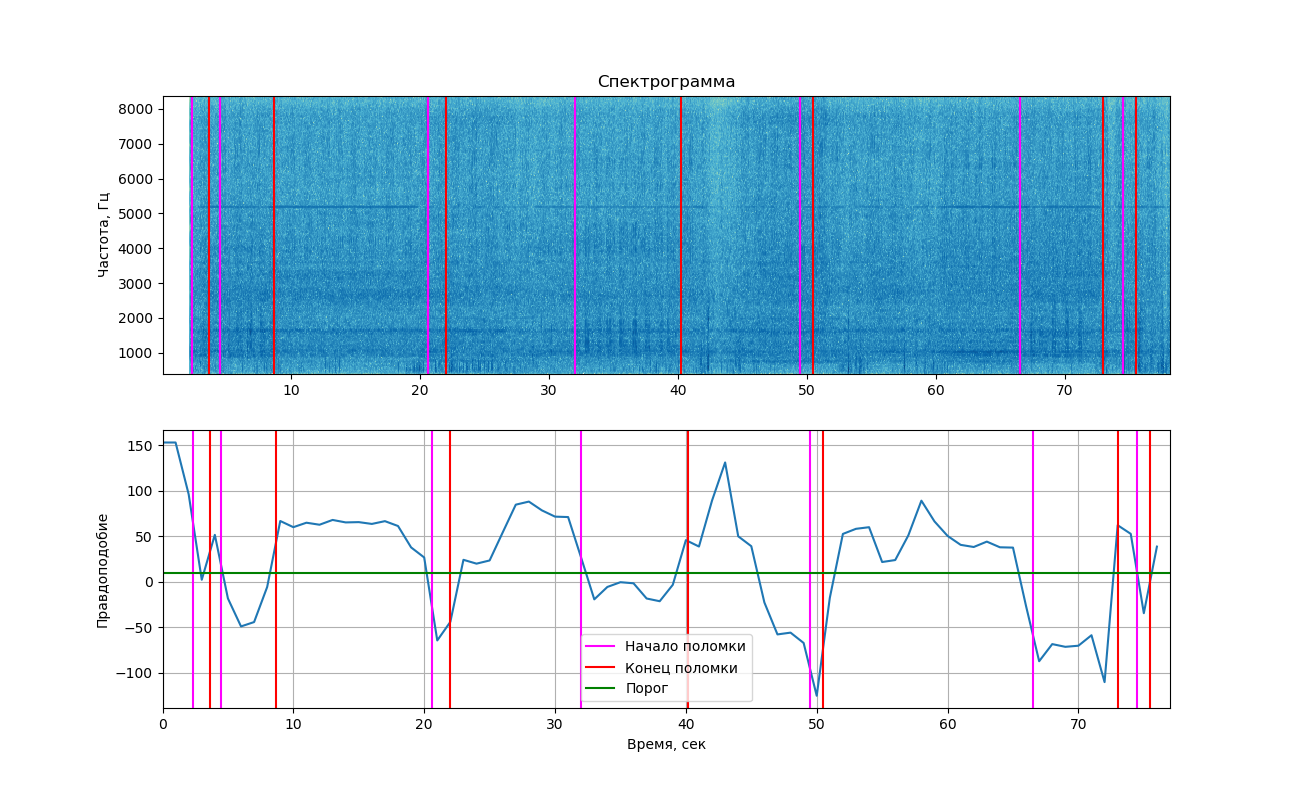
Der obere Teil zeigt das Spektrogramm des Signals, das mit der Matplotlib-Bibliothek angezeigt wird. Durch Klopfen verursachte Änderungen sind nicht so stark erkennbar wie im obigen Beispiel (weshalb Sie hier 2 Bilder gesehen haben). Wenn Sie genau hinschauen, sind sie dennoch sichtbar. Vertikale Linien markieren die Start- und Endzeiten des Klopfens.

Schlussfolgerungen

Wie Sie der Grafik entnehmen können, ist die Wahrscheinlichkeit zum Zeitpunkt des Klopfens tatsächlich unter den Schwellenwert gefallen, was bedeutet, dass wir diese beiden Klassen (Arbeiten mit und ohne Klopfen) trennen können. Aber ich muss sagen, dass dieser Wert nahe genug an der Schwelle und in Bereichen liegt, in denen das Klopfen nicht zu hören ist. Dies liegt daran, dass in der Aufzeichnung häufig Fremdgeräusche auftreten, die sich auch auf die Wahrscheinlichkeit auswirken.

Wir fügen hier Training in nur wenigen Sekunden Sound und schlechten Aufnahmebedingungen hinzu, und Sie können bereits überrascht sein, dass das Experiment irgendwie erfolgreich war!

Um diese Methode in die Praxis umzusetzen und sich ihrer Zuverlässigkeit sicher zu sein, müssen Sie höchstwahrscheinlich viel mehr Ton aufnehmen und das Mikrofon gut platzieren, um das Rauschen beim Eintritt in die Aufnahmen zu minimieren.

Dieser Artikel ist nur ein Versuch, ein ähnliches Problem zu lösen, ohne absolute Korrektheit zu beanspruchen. Wenn Sie Ideen und Vorschläge oder Fragen haben, lassen Sie uns diese gemeinsam in den Kommentaren oder persönlich diskutieren.

Der vollständige Github-Code ist hier