Die Übersetzung des Artikels wurde für Studenten des Kurses "Mathematik für Datenwissenschaften" vorbereitet.

Anmerkung

Dieser Artikel beschreibt die Aufgabe, Gesichtskonturen für ein einzelnes Bild zu finden. Wir zeigen, wie das Ensemble von Regressionsbäumen verwendet werden kann, um die Position von Gesichtskonturen direkt aus einer verstreuten Teilmenge von Pixelintensitäten vorherzusagen und mit hochqualitativen Vorhersagen in Echtzeit eine Superleistung zu erzielen. Wir präsentieren eine allgemeine Struktur, die auf Gradientenverstärkung basiert, um ein Ensemble von Regressionsbäumen zu untersuchen, das die Summe der quadratischen Verluste optimiert und natürlich fehlende oder teilweise markierte Daten verarbeitet. Wir werden zeigen, wie die Verwendung geeigneter Verteilungen, die die Struktur von Bilddaten berücksichtigen, bei der effizienten Auswahl von Konturen hilft. Verschiedene Regularisierungsstrategien und ihre Bedeutung im Kampf gegen Umschulungen werden ebenfalls untersucht. Darüber hinaus analysieren wir die Auswirkung der Menge an Trainingsdaten auf die Genauigkeit von Vorhersagen und untersuchen die Auswirkung der Datenerhöhung anhand synthetisierter Daten.

1. Einleitung

In diesem Artikel stellen wir einen neuen Algorithmus vor, der in Millisekunden nach Gesichtskonturen sucht und eine Genauigkeit erzielt, die modernen Methoden für Standarddatensätze überlegen oder mit diesen vergleichbar ist. Die Erhöhung der Geschwindigkeit im Vergleich zu den vorherigen Methoden ist eine Folge der Identifizierung der Hauptkomponenten der vorherigen Algorithmen für die Suche nach Gesichtskonturen und ihrer anschließenden Aufnahme in eine optimierte Form in die Kaskade von Regressionsmodellen mit hohem Durchsatz, die mithilfe der Gradientenverstärkung konfiguriert wurden.

Wir zeigen, wie bereits zuvor [8, 2], dass die Suche nach Gesichtskonturen mit einer Kaskade von Regressionsmodellen durchgeführt werden kann. In unserem Fall sagt jedes Regressionsmodell in der Kaskade die Form des Gesichts basierend auf der anfänglichen Vorhersage und der Intensität des spärlichen Satzes von Pixeln, die relativ zu dieser anfänglichen Vorhersage indiziert sind, effektiv voraus. Unsere Arbeit basiert auf einer Vielzahl von Studien, die im letzten Jahrzehnt durchgeführt wurden und zu erheblichen Fortschritten bei der Suche nach Gesichtskonturen geführt haben [9, 4, 13, 7, 15, 1, 16, 18, 3, 6, 19]. Insbesondere haben wir in unsere abgestimmten Regressionsmodelle zwei Schlüsselelemente aufgenommen, die in mehreren der folgenden erfolgreichen Algorithmen vorhanden sind, und jetzt werden diese Elemente detailliert beschrieben.

Abbildung 1. Ausgewählte Ergebnisse im HELEN-Datensatz. Um 194 wichtige Punkte (Landmarken) auf dem Gesicht in einem Bild in einer Millisekunde zu erkennen, wird ein Ensemble randomisierter Regressionsbäume verwendet.

Die erste dreht sich um die Indexierung der Pixelintensität relativ zur aktuellen Vorhersage der Gesichtsform. Die unterscheidbaren Merkmale in der Vektordarstellung des Gesichtsbildes können aufgrund der Verformung der Form und aufgrund von Störfaktoren wie Änderungen der Lichtverhältnisse stark variieren. Dies macht es schwierig, die Form unter Verwendung dieser Funktionen genau vorherzusagen. Das Dilemma besteht darin, dass wir zuverlässige Zeichen benötigen, um die Form genau vorherzusagen, und andererseits benötigen wir eine genaue Vorhersage der Form, um zuverlässige Zeichen zu extrahieren. In der vorherigen Arbeit [4, 9, 5, 8] sowie in dieser Arbeit wird ein iterativer Ansatz (Kaskade) verwendet, um dieses Problem zu lösen. Anstatt die Formparameter basierend auf den im globalen Bildkoordinatensystem extrahierten Merkmalen zu regressieren, wird das Bild basierend auf der aktuellen Formvorhersage in ein normalisiertes Koordinatensystem konvertiert, und dann werden Zeichen extrahiert, um den Aktualisierungsvektor für die Formparameter vorherzusagen. Dieser Vorgang wird normalerweise mehrmals bis zur Konvergenz wiederholt.

Im zweiten Teil wird untersucht, wie mit der Komplexität des Erklärungs- / Vorhersageproblems umgegangen werden soll. Während des Tests sollte der Kontursuchalgorithmus die Form des Gesichts vorhersagen - ein hochdimensionaler Vektor, der am besten mit den Bilddaten und unserem Formmodell übereinstimmt. Das Problem ist bei vielen lokalen Optima nicht konvex. Erfolgreiche Algorithmen [4, 9] lösen dieses Problem unter der Annahme, dass die vorhergesagte Form in einem linearen Unterraum liegen sollte, der beispielsweise durch Auffinden der Hauptkomponenten der Trainingsformen erkannt werden kann. Diese Annahme reduziert die Anzahl potenzieller Formen, die bei der Erklärung berücksichtigt werden, erheblich und kann dazu beitragen, lokale Optima zu vermeiden.

Eine kürzlich erschienene Arbeit [8, 11, 2] nutzt die Tatsache aus, dass eine bestimmte Klasse von Regressoren garantiert Vorhersagen erstellt, die in dem durch Lernformen definierten linearen Unterraum liegen, und dass keine zusätzlichen Einschränkungen erforderlich sind. Es ist wichtig, dass unsere Regressionsmodelle diese beiden Elemente aufweisen.
Diese beiden Faktoren hängen mit unserem effektiven Training im Regressionsmodell zusammen. Wir optimieren die entsprechende Verlustfunktion und führen die Merkmalsauswahl anhand von Daten durch. Insbesondere trainieren wir jeden Regressor mit Gradientenverstärkung [10] unter Verwendung der quadratischen Verlustfunktion, der gleichen Verlustfunktion, die wir während des Tests minimieren möchten. Der Satz von spärlichen Pixeln, der als Eingabe in den Regressor verwendet wird, wird unter Verwendung einer Kombination des Gradientenverstärkungsalgorithmus und der a priori-Wahrscheinlichkeit der Abstände zwischen Paaren von Eingabepixeln ausgewählt. Eine A-priori-Verteilung ermöglicht es dem Boosting-Algorithmus, eine große Anzahl relevanter Merkmale effizient zu untersuchen. Das Ergebnis ist eine Kaskade von Regressoren, die Gesichtsmarkierungen lokalisieren können, wenn sie von vorne initialisiert werden.

Die Hauptbeiträge dieses Artikels sind:

1. Eine neue Methode zum Finden von Gesichtskonturen, basierend auf einem Ensemble von Regressionsbäumen (Entscheidungsbäumen), die die Auswahl invarianter Merkmale des Formulars durchführt und gleichzeitig die gleiche Verlustfunktion während des Trainings minimiert, die wir während des Tests minimieren möchten.
2. Wir präsentieren eine natürliche Erweiterung unserer Methode, die fehlende oder undefinierte Labels verarbeitet.
3. Es werden quantitative und qualitative Ergebnisse präsentiert, die bestätigen, dass unsere Methode qualitativ hochwertige Prognosen liefert und viel effektiver ist als die beste vorherige Methode (Abbildung 1).
4. Der Einfluss der Menge an Trainingsdaten, der Verwendung von teilweise gekennzeichneten Daten und verallgemeinerten Daten auf die Qualität von Prognosen wird analysiert.

2. Methode

In diesem Artikel wird ein Algorithmus zur genauen Beurteilung der Position von Gesichtspunkten (Schlüsselpunkten) im Hinblick auf die Recheneffizienz vorgestellt. Wie in früheren Arbeiten [8, 2] wird in unserer Methode die Kaskade der Regressoren verwendet. Im Rest dieses Abschnitts beschreiben wir die Details der Form der einzelnen Komponenten der Kaskade und wie wir das Training durchführen.

2.1. Regressionskaskade

Zuerst führen wir eine Notation ein. Lass , y-Koordinaten des i-ten Orientierungspunkts des Gesichts im Bild I. Dann der Vektor bezeichnet die Koordinaten aller p Flächen in I. Oft nennen wir in diesem Artikel den Vektor S eine Form. Wir benutzen um unsere aktuelle Bewertung S anzuzeigen. Jeder Regressor (·, ·) In der Kaskade sagt der Aktualisierungsvektor aus dem Bild und voraus Dies wird zur aktuellen Formularbewertung hinzugefügt So verbessern Sie die Bewertung:

) (1)

Der entscheidende Punkt der Kaskade ist, dass der Regressor Die Prognosen basieren auf Attributen wie Pixelintensitäten, die von I berechnet und relativ zur aktuellen Formschätzung indiziert werden . Dies führt eine Art geometrische Invarianz in den Prozess ein, und während Sie die Kaskade durchlaufen, können Sie sicherer sein, dass die genaue semantische Position auf dem Gesicht indiziert ist. Wir werden später beschreiben, wie diese Indizierung durchgeführt wird.

Bitte beachten Sie, dass der vom Ensemble erweiterte Ausgabebereich bei der anfänglichen Schätzung garantiert im linearen Unterraum der Trainingsdaten liegt gehört zu diesem Raum. Daher müssen wir keine zusätzlichen Einschränkungen für die Vorhersagen einführen, was unsere Methode erheblich vereinfacht. Die Anfangsform kann einfach als mittlere Form von Trainingsdaten ausgewählt, zentriert und entsprechend der Ausgabe des Begrenzungsrahmens des allgemeinen Gesichtsdetektors skaliert werden.

Alle erziehen Wir verwenden den Gradientenverstärkungsalgorithmus für Bäume mit der Summe der quadratischen Verluste, wie in [10] beschrieben. Jetzt werden wir detaillierte Details dieses Prozesses geben.

2.2. Trainiere jeden Regressor in einer Kaskade

Angenommen, wir haben Trainingsdaten wo alle ist ein Gesichtsbild und sein Formvektor. Um die erste Regressionsfunktion herauszufinden In der Kaskade erstellen wir aus unseren Trainingsdaten Tripletts des Gesichtsbildes, der anfänglichen Formvorhersage und des Zielaktualisierungsschritts, d.h. ) wo

(2)

(3) und

(4)

für i = 1, ..., N.

Wir setzen die Gesamtzahl dieser Tripletts auf N = nR, wobei R die Anzahl der auf Bild Ii verwendeten Initialisierungen ist. Jede anfängliche Formvorhersage für das Bild wird gleichmäßig aus ausgewählt ohne Ersatz.

Anhand dieser Daten trainieren wir die Regressionsfunktion (siehe Algorithmus 1) Verwenden der Gradientenverstärkung von Bäumen mit der Summe der quadratischen Verluste. Der Trainings-Triplett-Satz wird dann aktualisiert, um Trainingsdaten bereitzustellen. % 20) für den nächsten Regressor in der Kaskade durch Setzen (mit t = 0).

% 20) (5)

(6)

Dieser Vorgang wird wiederholt, bis eine Kaskade von T-Regressoren trainiert ist. die in Kombination ein ausreichendes Maß an Genauigkeit bieten.

Wie angegeben, jeder Regressor lernt mit dem Gradientenbaum-Boosting-Algorithmus. Es ist zu beachten, dass die quadratische Verlustfunktion verwendet wird und die in der inneren Schleife berechneten Residuen dem Gradienten dieser Verlustfunktion entsprechen, der in jeder Trainingsprobe geschätzt wird. Die Formulierung des Algorithmus enthält den Lernratenparameter 0 <ν ≤ 1, auch als Regularisierungskoeffizient bekannt. Das Setzen von ν <1 hilft bei der Bekämpfung der Rekonfiguration und führt normalerweise zu Regressoren, die viel besser verallgemeinern als diejenigen, die mit ν = 1 trainiert wurden [10].

Lernalgorithmus 1 in Kaskade

Wir haben Trainingsdaten und Lernrate (Regularisierungskoeffizient) 0 <ν <1

1. Initialisieren
   
2. für k = 1, ..., K:
   a) wir setzen auf i = 1, ...,
   
   b) Wir passen den Regressionsbaum an das Ziel an mit schwacher Regressionsfunktion .
   c) Aktualisieren
3. Fazit
   

2.3. Baumregressor

Im Zentrum jeder RT-Regressionsfunktion stehen baumartige Regressoren, die für Restziele während des Gradientenverstärkungsalgorithmus geeignet sind. Jetzt werden wir uns die wichtigsten Implementierungsdetails für das Training jedes Regressionsbaums ansehen.

2.3.1 Invariante Split-Form-Tests

An jedem Trennknoten im Regressionsbaum treffen wir eine Entscheidung basierend auf dem Schwellenwert der Differenz zwischen den Intensitäten von zwei Pixeln. Die im Test verwendeten Pixel befinden sich an den Positionen u und v, wenn sie im Koordinatensystem der mittleren Form definiert sind. Für ein Bild eines Gesichts mit einer beliebigen Form möchten wir Punkte indizieren, die relativ zu ihrer Form dieselbe Position wie u und v haben, für die durchschnittliche Form. Zu diesem Zweck kann das Bild vor dem Extrahieren der Elemente basierend auf der aktuellen Formschätzung in die mittlere Form deformiert werden. Da wir nur eine sehr spärliche Darstellung des Bildes verwenden, ist es viel effizienter, die Anordnung der Punkte zu verformen als das gesamte Bild. Darüber hinaus kann eine grobe Annäherung an die Verformung vorgenommen werden, indem zusätzlich zu den in [2] vorgeschlagenen globalen Verschiebungen nur die globale Ähnlichkeitstransformation verwendet wird.

Die genauen Details sind wie folgt. Lass Ist der Index des Orientierungspunkts auf dem Gesicht in der mittleren Form am nächsten an u und definiert seine Verschiebung von u als .

Dann für die im Bild definierte Form Si Position in , das u im Bild einer mittleren Form qualitativ ähnlich ist, ist definiert als
(7)

wo und - Skalierungs- und Rotationsmatrix der Ähnlichkeitstransformation, die transformiert in mittlere Form.

Skalierung und Rotation minimieren

(8)

die Summe der Quadrate zwischen den Orientierungspunkten der mittleren Form, und Point Warp. ähnlich definiert.

Formal ist jede Division eine Lösung, die 3 Parameter θ = (τ, u, v) enthält und auf jedes Trainings- und Testbeispiel als angewendet wird

(9)

wo und werden unter Verwendung der Skala und der Rotationsmatrix bestimmt, die sich am besten verformen in gemäß Gleichung (7). In der Praxis werden Aufgaben und lokale Verschiebungen in der Trainingsphase festgelegt. Die Berechnung der Ähnlichkeitstransformation während des Testens des teuersten Teils dieses Prozesses wird auf jeder Ebene der Kaskade nur einmal durchgeführt.

2.3.2 Auswahl der Knotenpartitionen

Für jeden Regressionsbaum approximieren wir die Grundfunktion durch eine stückweise lineare Funktion, wobei ein konstanter Vektor für jeden endlichen Knoten geeignet ist. Um den Regressionsbaum zu trainieren, erzeugen wir zufällig einen Satz geeigneter Partitionen, dh θ, in jedem Knoten. Dann wählen wir eifrig θ * aus diesen Kandidaten aus, was die Summe des quadratischen Fehlers minimiert. Wenn Q ein Satz von Indizes von Trainingsbeispielen in einem Knoten ist, entspricht dies einer Minimierung

(10)

wo - Indizes von Beispielen, die aufgrund der Entscheidung θ an den linken Knoten gesendet werden, Ist der Vektor aller Residuen, die für das Bild i im Gradientenverstärkungsalgorithmus berechnet wurden, und

für (11)

Die optimale Partition kann sehr effizient gefunden werden, denn wenn wir Gleichung (10) transformieren und von θ unabhängige Faktoren weglassen, können wir das sehen

Hier müssen wir nur berechnen bei der Auswertung verschiedener θs, da kann aus den durchschnittlichen Zielen im Elternknoten µ und berechnet werden wie folgt:

2.3.3 Auswahl der Merkmale

Die Lösung an jedem Knoten basiert auf einem Schwellenwert der Differenz der Intensitätswerte in einem Pixelpaar. Dies ist ein ziemlich einfacher Test, der jedoch aufgrund seiner relativen Unempfindlichkeit gegenüber Änderungen der globalen Beleuchtung viel effektiver ist als ein Schwellenwert mit einer einzelnen Intensität. Leider besteht der Nachteil der Verwendung von Pixeldifferenzen darin, dass die Anzahl potenzieller Trennungskandidaten (Merkmal) in Bezug auf die Anzahl von Pixeln im Durchschnittsbild quadratisch ist. Dies macht es schwierig, gute θs zu finden, ohne nach einer sehr großen Anzahl von ihnen zu suchen. Dieser begrenzende Faktor kann jedoch unter Berücksichtigung der Struktur der Bilddaten etwas abgeschwächt werden.

Wir führen die Exponentialverteilung ein

(12)

durch den Abstand zwischen den Pixeln, die bei der Aufteilung verwendet werden, um die Auswahl engerer Pixelpaare zu fördern.

Wir haben festgestellt, dass die Verwendung dieser einfachen Verteilung den Vorhersagefehler für eine Reihe von Gesichtsdatensätzen reduziert. In Abbildung 4 werden die mit und ohne Features ausgewählten Features verglichen, wobei die Größe des Objektpools in beiden Fällen auf 20 festgelegt ist.

2.4. Umgang mit fehlenden Tags

Das Problem von Gleichung (10) kann leicht erweitert werden, um den Fall zu behandeln, in dem einige Orientierungspunkte auf einigen Trainingsbildern nicht markiert sind (oder wir haben ein Maß für die Unsicherheit für jeden Orientierungspunkt). Variable eingeben [0, 1] für jedes Trainingsbild i und jeden Orientierungspunkt j . Installation Ein Wert von 0 zeigt an, dass der Orientierungspunkt j im i- ten Bild nicht markiert ist, und eine Einstellung von 1 zeigt an, dass er markiert ist. Dann kann Gleichung (10) wie folgt dargestellt werden

wo - Diagonalmatrix mit Vektor auf ihrer Diagonale und

für (13)

Der Gradientenverstärkungsalgorithmus muss ebenfalls modifiziert werden, um diese Gewichte zu berücksichtigen. Dies kann erreicht werden, indem einfach das Ensemble-Modell mit dem gewichteten Durchschnittswert der Ziele initialisiert und die Regressionsbäume wie folgt an die gewichteten Residuen in Algorithmus 1 angepasst werden

(14)

3. Experimente

Grundlagen: Um die Leistung unserer vorgeschlagenen Methode, dem Ensemble von Regressionsbäumen (ERT), genau zu bewerten, haben wir zwei weitere Grundlagen erstellt. Der erste basiert auf zufälligen Farnen (zufälligen Farnen) mit einer zufälligen Auswahl von Merkmalen (EF), und der andere ist eine fortgeschrittenere Version dieses Ansatzes mit der Auswahl von Merkmalen basierend auf Korrelation (EF + CB), was unsere neue Implementierung ist [2]. Alle Parameter sind für alle drei Ansätze festgelegt.

EF nutzt die direkte Implementierung von zufälligen Farnen als schwache Regressoren im Ensemble und ist die schnellste für das Training. Wir verwenden dieselbe Regularisierungsmethode wie in [2] für die Regularisierung von Farnen vorgeschlagen.

EF + CB verwendet eine korrelationsbasierte Objektauswahlmethode, die Ausgabewerte projiziert. 's in eine zufällige Richtung w und wählt Zeichenpaare (u, v) aus, für die .

, . rt T = 10, K = 500 . ( ), , F = 5. P = 400 . , P , (9). S = 20 , . , R = 20 .

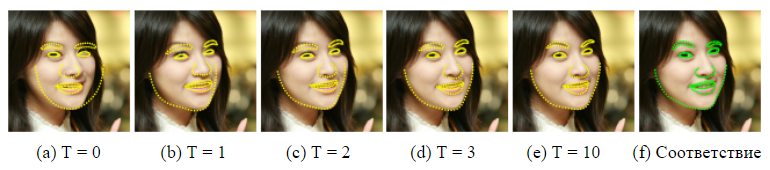
2. , Viola & Jones [17]. .

O (TKF). O (NDTKF S), N — , D — . HELEN [12], .

, , HELEN [12], , , . 2330 , 194 . 2000 , .

LFPW [1], 1432 . , 778 216 , , .

Vergleich
1 . (Active Shape Models) — STASM [14] CompASM [12].

1. HELEN. — . . , . , . .

, , . 3 , , ERT , . , EF + CB . , EF + CB , .

LFPW [1] ( 2). EF + CB , [2]. ( , .) , , .

2. LFPW. 1.

4 (12) , , . λ 0,1 . . 4 .

3. . , , . (12).

, . , . — . ν 1 ( ν = 0.1). . , , , ν = 1. (10 ) . ( .)

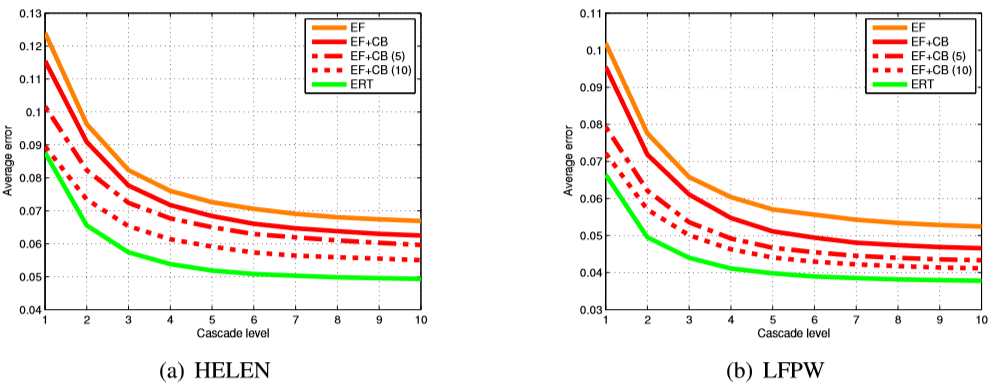
3. HELEN (a) LFPW (b). EF — , EF + CB — , . (5 10), [2]. , (ERT), , , .

4. , . , .

, . , .

4. HELEN . .

, . , , , , .

. . 5 . , , [8, 2] ( 10 × 400 .)

5. .

Trainingsdaten
Um die Wirksamkeit unserer Methode in Bezug auf die Anzahl der Trainingsbilder zu testen, haben wir verschiedene Modelle aus verschiedenen Teilmengen von Trainingsdaten trainiert. Tabelle 6 fasst die Endergebnisse zusammen, und Abbildung 5 zeigt eine grafische Darstellung der Fehler auf jeder Ebene der Kaskade. Die Verwendung vieler Ebenen von Regressoren ist am nützlichsten, wenn wir eine große Anzahl von Trainingsbeispielen haben.

Wir wiederholten dieselben Experimente mit einer festen Gesamtzahl erweiterter Beispiele, änderten jedoch die Kombination der Anfangsformen, die zur Erstellung des Trainingsbeispiels verwendet wurden, aus einem markierten Beispiel des Gesichts und einer Reihe kommentierter Bilder, die zur Untersuchung der Kaskade verwendet wurden (Tabelle 7).

Tabelle 6. Die endgültige Fehlerrate für die Anzahl der Trainingsbeispiele. Bei der Erstellung von Trainingsdaten für das Studium kaskadierender Regressoren wurden aus jedem markierten Gesichtsbild 20 Trainingsbeispiele generiert, wobei 20 verschiedene markierte Gesichter als erste Annahme über die Gesichtsform verwendet wurden.

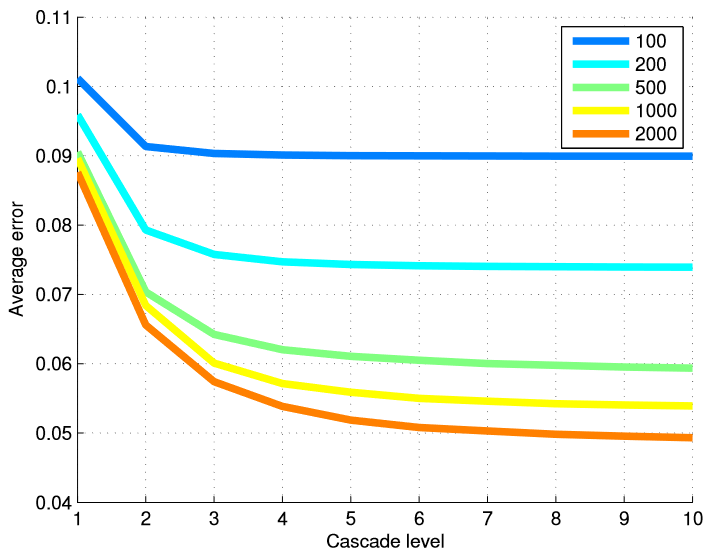
Abbildung 5. Der durchschnittliche Fehler auf jeder Ebene der Kaskade wird in Abhängigkeit von der Anzahl der verwendeten Trainingsbeispiele dargestellt. Die Verwendung vieler Ebenen von Regressoren ist am nützlichsten, wenn die Anzahl der Trainingsbeispiele groß ist.

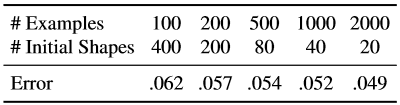
Tabelle 7. Hier ist die effektive Anzahl von Trainingsbeispielen festgelegt, wir verwenden jedoch verschiedene Kombinationen aus der Anzahl von Trainingsbildern und der Anzahl von Anfangsformen, die für jedes markierte Gesichtsbild verwendet werden.

Durch das Erhöhen der Trainingsdaten mithilfe einer Vielzahl von Anfangsformularen wird der Datensatz in Bezug auf die Form erweitert. Unsere Ergebnisse zeigen, dass diese Art der Ergänzung das Fehlen kommentierter Trainingsbilder nicht vollständig kompensiert. Obwohl die Verbesserungsrate, die durch Erhöhen der Anzahl von Trainingsbildern erhalten wird, nach den ersten paar hundert Bildern schnell abnimmt.

Teilanmerkungen
Tabelle 8 zeigt die Ergebnisse der Verwendung von teilweise kommentierten Daten. 200 Fallstudien sind vollständig und der Rest nur teilweise kommentiert.

Tabelle 8. Ergebnisse unter Verwendung teilweise beschrifteter Daten. 200 Beispiele sind immer vollständig kommentiert. Die Werte in Klammern geben den Prozentsatz der beobachteten Orientierungspunkte an.

Die Ergebnisse zeigen, dass wir mit teilweise gekennzeichneten Daten eine signifikante Verbesserung erzielen können. Die angezeigte Verbesserung ist jedoch möglicherweise nicht gesättigt, da wir wissen, dass die Basisgröße der Formparameter viel geringer ist als die Größe der Orientierungspunkte (194 × 2). Folglich besteht das Potenzial für eine signifikantere Verbesserung bei Teilmarkierungen, wenn Sie die Korrelation zwischen der Position der Landmarken explizit verwenden. Bitte beachten Sie, dass das in diesem Artikel beschriebene Verfahren zur Erhöhung des Gradienten keine Korrelation zwischen Orientierungspunkten verwendet. Dieses Problem kann in zukünftigen Arbeiten gelöst werden.

4. Fazit

Wir haben beschrieben, wie ein Ensemble von Regressionsbäumen verwendet werden kann, um die Position von Gesichtsmarkierungen aus einer gestreuten Teilmenge von Intensitätswerten, die aus dem Eingabebild extrahiert wurden, zu regressieren. Die dargestellte Struktur reduziert Fehler schneller als die vorherige Arbeit und kann auch teilweise oder undefinierte Markierungen verarbeiten. Während die Hauptkomponenten unseres Algorithmus verschiedene Zielmessungen als unabhängige Variablen betrachten, wird die natürliche Fortsetzung dieser Arbeit die Verwendung der Korrelation von Formularparametern für ein effektiveres Training und eine bessere Verwendung von Teilbeschriftungen sein.

Abbildung 6. Endergebnisse in der HELEN-Datenbank.

Danksagung
Diese Arbeit wurde von der schwedischen Stiftung für strategische Forschung im Rahmen des VINST-Projekts finanziert.

Gebrauchte Literatur

[1] PN Belhumeur, DW Jacobs, DJ Kriegman und N. Kumar. Lokalisierung von Gesichtsteilen anhand eines Konsenses von Exemplaren. In CVPR, Seiten 545–552, 2011. 1, 5
[2] X. Cao, Y. Wei, F. Wen und J. Sun. Gesichtsausrichtung durch explizite Formregression. In CVPR, Seiten 2887–2894, 2012. 1, 2, 3, 4, 5, 6
[3] TF Cootes, M. Ionita, C. Lindner und P. Sauer. Robuste und genaue Anpassung des Formmodells durch zufällige Waldregressionsabstimmung. In ECCV, 2012.1
[4] TF Cootes, CJ Taylor, DH Cooper und J. Graham. Aktive Formmodelle - ihre Ausbildung und Anwendung. Computer Vision and Image Understanding, 61 (1): 38–59, 1995.1, 2
[5] D. Cristinacce und TF Cootes. Modelle für aktive Regressionsformen. In BMVC, Seiten 79.1–79.10, 2007.1
[6] M. Dantone, J. Gall, G. Fanelli und LV Gool. Erkennung von Gesichtsmerkmalen in Echtzeit mithilfe von bedingten Regressionswäldern. In CVPR, 2012.1
[7] L. Ding und AM Mart´ınez. Präzise detaillierte Erkennung von Gesichtern und Gesichtszügen. In CVPR, 2008.1
[8] P. Dollar, P. Welinder und P. Perona. Kaskadierte Posenregression. In CVPR, Seiten 1078–1085, 2010. 1, 2, 6
[9] GJ Edwards, TF Cootes und CJ Taylor. Fortschritte bei aktiven Erscheinungsmodellen. In ICCV, Seiten 137–142, 1999. 1, 2
[10] T. Hastie, R. Tibshirani und JH Friedman. Die Elemente des statistischen Lernens: Data Mining, Inferenz und Vorhersage. New York: Springer-Verlag, 2001.2.3
[11] V. Kazemi und J. Sullivan. Gesichtsausrichtung mit teilbasierter Modellierung. In BMVC, Seiten 27.1–27.10, 2011.2
[12] V. Le, J. Brandt, Z. Lin, LD Bourdev und TS Huang. Interaktive Lokalisierung von Gesichtsmerkmalen. In [13] L. Liang, R. Xiao, F. Wen und J. Sun. Gesichtsausrichtung über komponentenbasierte diskriminative Suche. In ECCV, Seiten 72–85, 2008. 1ECCV, Seiten 679–692, 2012.5
[14] S. Milborrow und F. Nicolls. Lokalisieren von Gesichtsmerkmalen mit einem erweiterten aktiven Formmodell. In ECCV, Seiten 504–513, 2008.5
[15] J. Saragih, S. Lucey und J. Cohn. Verformbare Modellanpassung durch regulierte Mittelwertverschiebungen. Internation Journal of Computer Vision, 91: 200–215, 2010.1
[16] BM Smith und L. Zhang. Ausrichtung der Gelenkfläche mit nichtparametrischen Formmodellen. In ECCV, Seiten 43–56, 2012.1
[17] PA Viola und MJ Jones. Robuste Gesichtserkennung in Echtzeit. In ICCV, Seite 747, 2001.5
[18] X. Zhao, X. Chai und S. Shan. Gelenkgesichtsausrichtung: Retten Sie schlechte Ausrichtungen durch gute durch regelmäßige Neuanpassung. In ECCV, 2012.1
[19] X. Zhu und D. Ramanan. Gesichtserkennung, Posenschätzung und Lokalisierung von Orientierungspunkten in freier Wildbahn. In CVPR, Seiten 2879–2886, 2012.1