Warum der nächste Artikel darüber, wie man neuronale Netze von Grund auf neu schreibt? Leider konnte ich keine Artikel finden, in denen Theorie und Code von Grund auf zu einem voll funktionsfähigen Modell beschrieben wurden. Ich warne sofort, dass es viel Mathematik geben wird. Ich gehe davon aus, dass der Leser mit den Grundlagen der linearen Algebra, partiellen Ableitungen und zumindest teilweise mit der Wahrscheinlichkeitstheorie sowie Python und Numpy vertraut ist. Wir werden uns mit einem vollständig verbundenen neuronalen Netzwerk und MNIST befassen.
Mathe Teil 1 (einfach)
Was ist eine vollständig verbundene Schicht (FC-Schicht)? Normalerweise sagen sie etwas wie "Eine vollständig verbundene Schicht ist eine Schicht, von der jedes Neuron mit allen Neuronen der vorherigen Schicht verbunden ist". Es ist einfach nicht klar, was Neuronen sind, wie sie verbunden sind, insbesondere im Code. Jetzt werde ich versuchen, dies anhand eines Beispiels zu analysieren. Es gebe eine Schicht von 100 Neuronen. Ich weiß, dass ich noch nicht erklärt habe, was es ist, aber stellen wir uns vor, dass es 100 Neuronen gibt, die eine Eingabe haben, von der die Daten gesendet werden, und eine Ausgabe, von der sie die Daten geben. Der Eingabe wird ein Schwarzweißbild mit 28 x 28 Pixel zugeführt - nur 784 Werte, wenn Sie es in einen Vektor strecken. Ein Bild kann als Eingabeebene bezeichnet werden. Damit sich jedes der 100 Neuronen mit jedem "Neuron" oder, wenn Sie möchten, dem Wert der vorherigen Schicht (dh dem Bild) verbindet, muss jedes der 100 Neuronen 784 Werte des Originalbilds akzeptieren. Zum Beispiel reicht es für jedes der 100 Neuronen aus, 784 Werte des Bildes mit 784 Zahlen zu multiplizieren und diese zu addieren, wodurch eine Zahl herauskommt. Das heißt, dies ist ein Neuron:
$$ display $$ \ text {Neuronenausgabe} = \ text {eine Zahl} _ {1} \ cdot \ text {Bildwert} _1 ~ + \\ + ~ ... ~ + ~ \ text {some- diese Zahl} _ {784} \ cdot \ text {Bildwert} _ {784} $$ display $$
Dann stellt sich heraus, dass jedes Neuron 784 Zahlen hat und alle diese Zahlen: (Anzahl der Neuronen auf dieser Schicht) x (Anzahl der Neuronen auf der vorherigen Schicht) =
$ inline $ 100 \ times784 $ inline $ = 78.400 Stellen. Diese Zahlen werden üblicherweise als Schichtgewichte bezeichnet. Jedes Neuron gibt seine Nummer aus und als Ergebnis erhalten wir einen 100-dimensionalen Vektor. Tatsächlich können wir schreiben, dass dieser 100-dimensionale Vektor erhalten wird, indem der 784-dimensionale Vektor (unser Originalbild) mit einer Gewichtsmatrix der Größe multipliziert wird
$ inline $ 100 \ times784 $ inline $ ::
$$ display $$ \ boldsymbol {x} ^ {100} = W_ {100 \ times784} \ cdot \ boldsymbol {x} ^ {784} $$ display $$
Ferner werden die resultierenden 100 Zahlen an die Aktivierungsfunktion weitergegeben - einige nichtlineare Funktionen - die jede Zahl separat beeinflusst. Zum Beispiel Sigmoid, hyperbolische Tangente, ReLU und andere. Die Aktivierungsfunktion ist notwendigerweise nichtlinear, andernfalls lernt das neuronale Netzwerk nur einfache Transformationen.
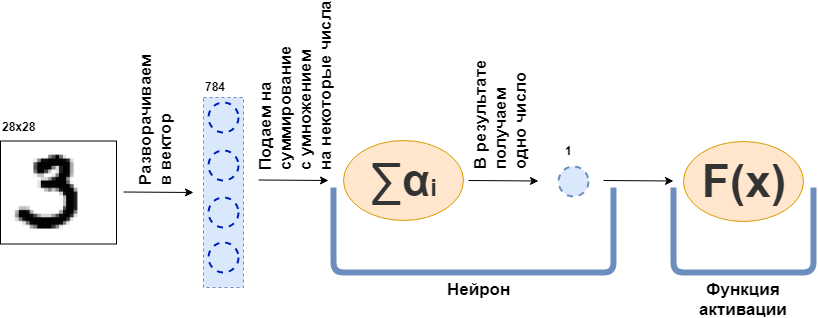
Dann werden die resultierenden Daten erneut einer vollständig verbundenen Schicht, jedoch mit einer anderen Anzahl von Neuronen, und erneut der Aktivierungsfunktion zugeführt. Dies passiert mehrmals. Die letzte Schicht des Netzwerks ist die Schicht, die die Antwort erzeugt. In diesem Fall ist die Antwort eine Information über die Nummer auf dem Bild.
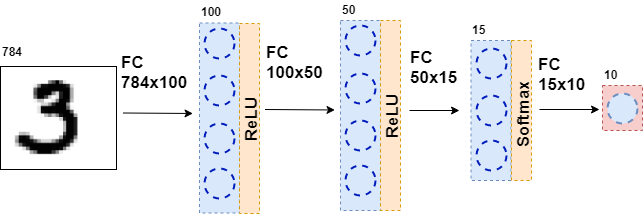
Während des Trainings des Netzwerks ist es notwendig, dass wir wissen, welche Abbildung auf dem Bild gezeigt wird. Das heißt, dass der Datensatz markiert ist. Dann können Sie ein anderes Element verwenden - die Fehlerfunktion. Sie betrachtet die Antwort des neuronalen Netzwerks und vergleicht sie mit der tatsächlichen Antwort. Dank dessen lernt das neuronale Netzwerk.
Allgemeine Erklärung des Problems
Der gesamte Datensatz ist ein großer Tensor (wir werden ein mehrdimensionales Datenarray als Tensor bezeichnen).
$ inline $ \ boldsymbol {X} = \ left [\ boldsymbol {x} _1, \ boldsymbol {x} _2, \ ldots, \ boldsymbol {x} _n \ right] $ inline $ wo
$ inline $ \ boldsymbol {x} _i $ inline $ - i-te Objekt, zum Beispiel ein Bild, das auch ein Tensor ist. Für jedes Objekt gibt es
$ inline $ y_i $ inline $ - die richtige Antwort auf das i-te Objekt. In diesem Fall kann ein neuronales Netzwerk als eine Funktion dargestellt werden, die ein Objekt als Eingabe verwendet und eine Antwort darauf gibt:
$$ display $$ F (\ boldsymbol {x} _i) = \ hat {y} _i $$ display $$
Schauen wir uns nun die Funktion genauer an
$ inline $ F (\ boldsymbol {x} _i) $ inline $ . Da das neuronale Netzwerk aus Schichten besteht, ist jede einzelne Schicht eine Funktion. Und das heißt
$$ display $$ F (\ boldsymbol {x} _i) = f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i))) = \ hat {y} _i $$ display $ $
Das heißt, in der allerersten Funktion - der ersten Schicht - wird ein Bild in Form eines Tensors dargestellt. Funktion
$ inline $ f_1 $ inline $ gibt eine Antwort - auch ein Tensor, aber von einer anderen Dimension. Dieser Tensor wird als interne Darstellung bezeichnet. Diese interne Darstellung wird nun dem Eingang der Funktion zugeführt
$ inline $ f_2 $ inline $ , die seine interne Darstellung gibt. Und so weiter bis zur Funktion
$ inline $ f_k $ inline $ - letzte Schicht - gibt keine Antwort
$ inline $ \ hat {y} _i $ inline $ .
Jetzt besteht die Aufgabe darin, das Netzwerk zu trainieren, damit die Netzwerkantwort mit der richtigen Antwort übereinstimmt. Zuerst müssen Sie messen, wie falsch das neuronale Netzwerk ist. Dies zu messen ist eine Fehlerfunktion.
$ inline $ L (\ hat {y} _i, y_i) $ inline $ . Und wir legen Beschränkungen fest:
1.
$ inline $ \ hat {y} _i \ xrightarrow {} y_i \ Rightarrow L (\ hat {y} _i, y_i) \ xrightarrow {} 0 $ inline $
2.
$ inline $ \ existiert ~ dL (\ hat {y} _i, y_i) $ inline $
3.
$ inline $ L (\ hat {y} _i, y_i) \ geq 0 $ inline $
Die Einschränkung 2 gilt für alle Funktionen der Schichten
$ inline $ f_j $ inline $ - Lassen Sie sie alle differenzierbar sein.
Darüber hinaus (einige davon habe ich nicht erwähnt) hängen einige dieser Funktionen von den Parametern ab - den Gewichten des neuronalen Netzwerks -
$ inline $ f_j (\ boldsymbol {x} _i | \ boldsymbol {\ omega} _j) $ inline $ . Und die ganze Idee ist, solche Gewichte so aufzunehmen, dass
$ inline $ \ hat {y} _i $ inline $ fiel mit zusammen
$ inline $ y_i $ inline $ auf allen Objekten eines Datensatzes. Ich stelle fest, dass nicht alle Funktionen Gewichte haben.
Wo haben wir aufgehört? Alle Funktionen des neuronalen Netzes sind differenzierbar, die Fehlerfunktion ist ebenfalls differenzierbar. Erinnern Sie sich an eine der Eigenschaften des Gradienten - zeigen Sie die Wachstumsrichtung der Funktion. Wir nutzen dies, Einschränkungen 1 und 3, die Tatsache, dass
$$ display $$ L (F (\ boldsymbol {x} _i)) = L (f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i)))) = L (\ hat {y} _i) $$ display $$
und die Tatsache, dass ich partielle Ableitungen und Ableitungen einer komplexen Funktion betrachten kann. Jetzt gibt es alles, was Sie zum Berechnen benötigen
$$ display $$ \ frac {\ partielles L (F (\ boldsymbol {x} _i))} {\ partielles \ boldsymbol {\ omega_j}} $$ display $$
für jedes i und j. Diese partielle Ableitung zeigt die Richtung, in die geändert werden soll
$ inline $ \ boldsymbol {\ omega_j} $ inline $ zu vergrößern
$ inline $ L $ inline $ . Um zu reduzieren, müssen Sie einen Schritt zur Seite machen
$ inline $ - \ frac {\ partielles L (F (\ boldsymbol {x} _i))} {\ partielles \ boldsymbol {\ omega_j}} $ inline $ nichts kompliziertes.
Der Prozess des Trainings des Netzwerks ist also wie folgt aufgebaut: Mehrmals in einem Zyklus durchlaufen wir für jedes betrachtete Datensatzobjekt den gesamten Datensatz (dies wird als Ära bezeichnet)
$ inline $ L (\ hat {y} _i, y_i) $ inline $ (dies wird als Vorwärtsdurchlauf bezeichnet) und berücksichtigen Sie die partielle Ableitung
$ inline $ \ partielle L $ inline $ für alle Gewichte
$ inline $ \ boldsymbol {\ omega_j} $ inline $ Aktualisieren Sie dann die Gewichte (dies wird als Rückwärtsdurchlauf bezeichnet).
Ich stelle fest, dass ich noch keine spezifischen Funktionen und Ebenen eingeführt habe. Wenn zu diesem Zeitpunkt nicht klar ist, was mit all dem zu tun ist, schlage ich vor, weiterzulesen - es wird mehr Mathematik geben, aber jetzt wird es mit Beispielen gehen.
Mathe Teil 2 (schwierig)
Fehlerfunktion
Ich werde am Ende beginnen und die Fehlerfunktion für das Klassifizierungsproblem ableiten. Für das Regressionsproblem ist die Ableitung der Fehlerfunktion im Buch „Deep Learning. Eintauchen in die Welt der neuronalen Netze. "
Der Einfachheit halber gibt es ein neuronales Netzwerk (NN), das Katzenfotos von Hundefotos trennt, und es gibt eine Reihe von Fotos von Katzen und Hunden, auf die es eine richtige Antwort gibt
$ inline $ y_ {true} $ inline $ .
$$ display $$ NN (Bild | \ Omega) = y_ {pred} $$ display $$
Alles, was ich als nächstes tun werde, ist der Maximum-Likelihood-Methode sehr ähnlich. Daher besteht die Hauptaufgabe darin, die Wahrscheinlichkeitsfunktion zu finden. Wenn wir die Details weglassen, ergibt eine solche Funktion, die die Vorhersage des neuronalen Netzwerks und die richtige Antwort vergleicht und wenn sie zusammenfallen, einen großen Wert, wenn nicht, umgekehrt. Die Wahrscheinlichkeit einer korrekten Antwort ergibt sich aus den angegebenen Parametern:
$$ display $$ p (y_ {pred} = y_ {true} | \ Omega) $$ display $$
Und jetzt machen wir eine Finte, die anscheinend nicht von irgendwoher folgt. Lassen Sie das neuronale Netzwerk eine Antwort in Form eines zweidimensionalen Vektors geben, dessen Summe 1 ist. Das erste Element dieses Vektors kann als Konfidenzmaß bezeichnet werden, dass sich die Katze auf dem Foto befindet, und das zweite Element als Konfidenzmaß, dass sich der Hund auf dem Foto befindet. Ja, das ist fast wahrscheinlich!
$$ display $$ NN (Bild | \ Omega) = \ left [\ begin {matrix} p_0 \\ p_1 \\\ end {matrix} \ right] $$ display $$
Jetzt kann die Wahrscheinlichkeitsfunktion wie folgt umgeschrieben werden:
$$ display $$ p (y_ {pred} = y_ {true} | \ Omega) = p_ \ Omega (y_ {pred}) ^ t_ {0} * (1 - p_ \ Omega (y_ {pred})) ^ t_ {1} = \\ p_0 ^ {t_0} * p_1 ^ {t_1} $$ display $$
Wo
$ inline $ t_0, t_1 $ inline $ Beschriftungen der richtigen Klasse, zum Beispiel, wenn
$ inline $ y_ {true} = cat $ inline $ dann
$ inline $ t_0 == 1, t_1 == 0 $ inline $ wenn
$ inline $ y_ {true} = Hund $ inline $ dann
$ inline $ t_0 == 0, t_1 == 1 $ inline $ . Daher wird immer die Wahrscheinlichkeit einer Klasse berücksichtigt, die von einem neuronalen Netzwerk vorhergesagt werden sollte (aber nicht unbedingt von diesem vorhergesagt wird). Dies kann nun auf eine beliebige Anzahl von Klassen verallgemeinert werden (z. B. m Klassen):
$$ display $$ p (y_ {pred} = y_ {true} | \ Omega) = \ prod_0 ^ m p_i ^ {t_i} $$ display $$
In jedem Datensatz gibt es jedoch viele Objekte (z. B. N Objekte). Ich möchte, dass das neuronale Netzwerk auf jedes oder die meisten Objekte die richtige Antwort gibt. Dazu müssen Sie die Ergebnisse der obigen Formel für jedes Objekt aus dem Datensatz multiplizieren.
$$ display $$ MaximumLikelyhood = \ prod_ {j = 0} ^ N \ prod_ {i = 0} ^ m p_ {i, j} ^ {t_ {i, j}} $$ display $$
Um gute Ergebnisse zu erzielen, muss diese Funktion maximiert werden. Aber erstens ist es steiler zu minimieren, weil wir einen stochastischen Gradientenabstieg und alle Brötchen dafür haben - weisen Sie einfach ein Minus zu, und zweitens ist es schwierig, mit einer großen Arbeit zu arbeiten - es ist Logarithmus.
$$ display $$ CrossEntropyLoss = - \ sum \ limit_ {j = 0} ^ {N} \ sum \ limit_ {i = 0} ^ {m} t_ {i, j} \ cdot \ log (p_ {i, j }) $$ display $$
Großartig! Das Ergebnis war Kreuzentropie oder im binären Fall Logloss. Diese Funktion ist einfach zu zählen und noch einfacher zu unterscheiden:
$$ display $$ \ frac {\ partielle CrossEntropyLoss} {\ partielle p_j} = - \ frac {\ boldsymbol {t_j}} {\ boldsymbol {p_ {j}}} $$ display $$
Sie müssen für den Backpropagation-Algorithmus differenzieren. Ich stelle fest, dass die Fehlerfunktion die Dimension des Vektors nicht ändert. Wenn die Ausgabe wie im Fall von MNIST ein 10-dimensionaler Vektor von Antworten ist, erhalten wir bei der Berechnung der Ableitung einen 10-dimensionalen Vektor von Ableitungen. Eine andere interessante Sache ist, dass nur ein Element der Ableitung nicht Null sein wird, bei dem
$ inline $ t_ {i, j} \ neq 0 $ inline $ das heißt, mit der richtigen Antwort. Und je geringer die Wahrscheinlichkeit einer korrekten Antwort ist, die von einem neuronalen Netzwerk an einem bestimmten Objekt vorhergesagt wird, desto größer ist die Fehlerfunktion.
Aktivierungsfunktionen
Am Ausgang jeder vollständig verbundenen Schicht eines neuronalen Netzwerks muss eine nichtlineare Aktivierungsfunktion vorhanden sein. Ohne sie ist es unmöglich, ein sinnvolles neuronales Netzwerk zu trainieren. Mit Blick auf die Zukunft ist eine vollständig verbundene Schicht eines neuronalen Netzwerks einfach eine Multiplikation der Eingabedaten mit einer Gewichtsmatrix. In der linearen Algebra wird dies als lineare Karte bezeichnet - eine lineare Funktion. Die Kombination von linearen Funktionen ist auch eine lineare Funktion. Dies bedeutet jedoch, dass eine solche Funktion nur lineare Funktionen approximieren kann. Leider werden aus diesem Grund keine neuronalen Netze benötigt.
Softmax
Normalerweise wird diese Funktion auf der letzten Schicht des Netzwerks verwendet, da sie den Vektor aus der letzten Schicht in einen Vektor von „Wahrscheinlichkeiten“ verwandelt: Jedes Element des Vektors liegt zwischen 0 und 1 und ihre Summe ist 1. Sie ändert die Dimension des Vektors nicht.
$$ display $$ Softmax_i = \ frac {e ^ {x_i}} {\ sum \ limit_ {j} e ^ {x_j}} $$ display $$
Fahren wir nun mit der abgeleiteten Suche fort. Als
$ inline $ \ boldsymbol {x} $ inline $ Ist ein Vektor und alle seine Elemente sind immer im Nenner vorhanden, dann erhalten wir bei der Ableitung den Jacobi:
$$ Anzeige $$ J_ {Softmax} = \ begin {Fälle} x_i - x_i \ cdot x_j, i = j \\ - x_i \ cdot x_j, i \ neq j \ Ende {Fälle} $$ Anzeige $$
Nun zur Backpropagation. Der Vektor der Ableitungen stammt aus der vorherigen Schicht (normalerweise ist dies eine Fehlerfunktion).
$ inline $ \ boldsymbol {dz} $ inline $ . Für den Fall
$ inline $ \ boldsymbol {dz} $ inline $ kam von einer Fehlerfunktion auf mnist,
$ inline $ \ boldsymbol {dz} $ inline $ - 10-dimensionaler Vektor. Dann hat der Jacobianer eine Dimension von 10x10. Um zu bekommen
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ , die weiter zur vorherigen Schicht geht (vergessen Sie nicht, dass wir vom Ende zum Anfang des Netzwerks gehen, wenn sich der Fehler zurück ausbreitet), müssen wir multiplizieren
$ inline $ \ boldsymbol {dz} $ inline $ auf
$ inline $ J_ {Softmax} $ inline $ (Zeile pro Spalte):
$$ display $$ dz_ {new} = \ boldsymbol {dz} \ times J_ {Softmax} $$ display $$
Am Ausgang erhalten wir einen 10-dimensionalen Vektor von Ableitungen
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ .
Relu
$$ Anzeige $$ ReLU (x) = \ begin {Fälle} x, x> 0 \\ 0, x <0 \ Ende {Fälle} $$ Anzeige $$
ReLU wurde nach 2011 massiv eingesetzt, als der Artikel „Deep Sparse Rectifier Neural Networks“ veröffentlicht wurde. Eine solche Funktion war jedoch zuvor bekannt. Das Konzept der „Aktivierungskraft“ gilt für ReLU (weitere Einzelheiten finden Sie im Buch „Deep Learning. Eintauchen in die Welt der neuronalen Netze“). Das Hauptmerkmal, das ReLU attraktiver macht als andere Aktivierungsfunktionen, ist die einfache Ableitungsberechnung:
$$ Anzeige $$ d (ReLU (x)) = \ begin {Fälle} 1, x> 0 \\ 0, x <0 \ Ende {Fälle} $$ Anzeige $$
Somit ist ReLU rechnerisch effizienter als andere Aktivierungsfunktionen (Sigmoid, hyperbolische Tangente usw.).
Vollständig verbundene Schicht
Jetzt ist es an der Zeit, eine vollständig verbundene Schicht zu diskutieren. Das wichtigste von allen anderen, denn in dieser Schicht befinden sich alle Gewichte, die angepasst werden müssen, damit das neuronale Netzwerk gut funktioniert. Eine vollständig verbundene Schicht ist einfach eine Gewichtsmatrix:
$$ display $$ W = | w_ {i, j} | $$ display $$
Eine neue interne Darstellung wird erhalten, wenn die Gewichtsmatrix mit der Eingabespalte multipliziert wird:
$$ display $$ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $$ display $$
Wo
$ inline $ \ boldsymbol {x} $ inline $ hat Größe
$ inline $ input \ _shape $ inline $ und
$ inline $ x_ {new} $ inline $ - -
$ inline $ output \ _shape $ inline $ . Zum Beispiel
$ inline $ \ boldsymbol {x} $ inline $ - 784-dimensionaler Vektor und
$ inline $ \ boldsymbol {x} _ {new} $ inline $ Ist ein 100-dimensionaler Vektor, dann hat die Matrix W eine Größe von 100x784. Es stellt sich heraus, dass auf dieser Ebene 100x784 = 78.400 Gewichte sind.
Mit der Rückausbreitung des Fehlers muss man die Ableitung in Bezug auf jedes Gewicht dieser Matrix nehmen. Vereinfachen Sie das Problem und nehmen Sie nur die Ableitung in Bezug auf
$ inline $ w_ {1,1} $ inline $ . Beim Multiplizieren der Matrix und des Vektors das erste Element des neuen Vektors
$ inline $ \ boldsymbol {x} _ {new} $ inline $ ist gleich
$ inline $ x_ {new ~ 1} = w_ {1,1} \ cdot x_1 + ... + w_ {1,784} \ cdot x_ {784} $ inline $ und die Ableitung
$ inline $ x_ {new ~ 1} $ inline $ von
$ inline $ w_ {1,1} $ inline $ wird einfach sein
$ inline $ x_1 $ inline $ , müssen Sie nur die Ableitung des oben genannten Betrags nehmen. Ähnliches gilt für alle anderen Gewichte. Dies ist jedoch kein Algorithmus zur Fehlerrückübertragung, solange es sich nur um eine Matrix von Ableitungen handelt. Sie müssen sich daran erinnern, dass von der nächsten Ebene zu dieser (der Fehler geht von Ende zu Anfang) ein 100-dimensionaler Gradientenvektor kommt
$ inline $ d \ boldsymbol {z} $ inline $ . Erstes Element dieses Vektors
$ inline $ dz_1 $ inline $ wird mit allen Elementen der Matrix von Derivaten multipliziert, die an der Erstellung "teilgenommen" haben
$ inline $ x_ {new ~ 1} $ inline $ d.h.
$ inline $ x_1, x_2, ..., x_ {784} $ inline $ . Ebenso der Rest der Elemente. Wenn Sie dies in die Sprache der linearen Algebra übersetzen, dann ist es so geschrieben:
$$ display $$ \ frac {\ partielles L} {\ partielles W} = (d \ boldsymbol {z}, ~ dW) = \ left (\ begin {matrix} dz_ {1} \ cdot \ boldsymbol {x} \ \ ... \\ dz_ {100} \ cdot \ boldsymbol {x} \ end {matrix} \ right) _ {100} $$ display $$
Die Ausgabe ist eine 100x784-Matrix.
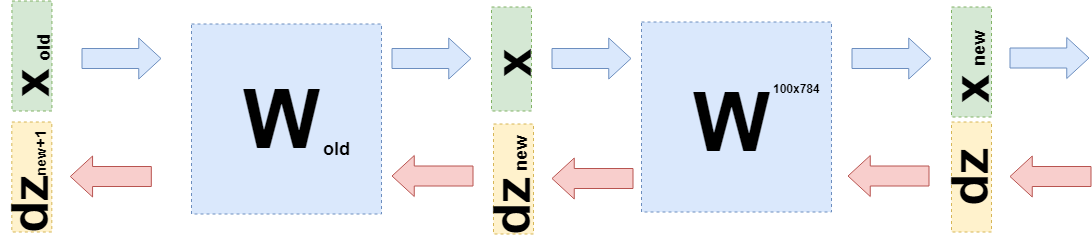
Jetzt müssen Sie verstehen, was auf die vorherige Ebene übertragen werden soll. Aus diesem Grund und um besser zu verstehen, was jetzt passiert ist, möchte ich aufschreiben, was passiert ist, wenn Ableitungen auf dieser Ebene in einer etwas anderen Sprache verwendet werden, um von den Besonderheiten von „was multipliziert wird“ zu Funktionen (wieder) zu gelangen.
Als ich die Gewichte anpassen wollte, wollte ich die Ableitung der Fehlerfunktion für diese Gewichte nehmen:
$ inline $ \ frac {\ partielles L} {\ partielles W} $ inline $ . Es wurde oben gezeigt, wie Ableitungen von Fehlerfunktionen und Aktivierungsfunktionen verwendet werden. Daher können wir einen solchen Fall betrachten (in
$ inline $ d \ boldsymbol {z} $ inline $ Alle Ableitungen der Fehlerfunktion und der Aktivierungsfunktionen sitzen bereits):
$$ display $$ \ frac {\ partielles L} {\ partielles W} = d \ boldsymbol {z} \ cdot \ frac {\ partielles \ boldsymbol {x} _ {new} (W)} {\ partielles W} $ $ display $$
Dies kann getan werden, weil Sie überlegen können
$ inline $ \ boldsymbol {x} _ {new} $ inline $ als Funktion von W:
$ inline $ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $ inline $ .
Sie können dies in die obige Formel einsetzen:
$$ Anzeige $$ \ frac {\ partielles L} {\ partielles W} = d \ Boldsymbol {z} \ cdot \ frac {\ partielles W \ cdot \ Boldsymbol {x}} {\ partielles W} = d \ Boldsymbol { z} \ cdot E \ cdot \ boldsymbol {x} $$ display $$
Wobei E eine aus Einheiten bestehende Matrix ist (KEINE Einheitsmatrix).
Wenn Sie nun die Ableitung der vorherigen Ebene verwenden müssen (auch wenn es sich zur Vereinfachung der Berechnungen um eine vollständig verbundene Ebene handelt, die jedoch im Allgemeinen nichts ändert), müssen Sie dies berücksichtigen
$ inline $ \ boldsymbol {x} $ inline $ als Funktion der vorherigen Schicht
$ inline $ \ boldsymbol {x} (W_ {old}) $ inline $ ::
$$ Anzeige $$ \ begin {gesammelt} \ frac {\ partiell L} {\ partiell W_ {alt}} = d \ boldsymbol {z} \ cdot \ frac {\ partiell \ boldsymbol {x} _ {neu} (W. )} {\ partielles W_ {alt}} = d \ boldsymbol {z} \ cdot \ frac {\ partielles W \ cdot \ boldsymbol {x} (W_ {alt})} {\ partielles W_ {alt}} = \\ = d \ boldsymbol {z} \ cdot \ frac {\ partielles W \ cdot W_ {alt} \ cdot \ boldsymbol {x} _ {alt}} {\ partielles W_ {alt}} = d \ boldsymbol {z} \ cdot W \ cdot E \ cdot \ boldsymbol {x} _ {alt} = \\ = d \ boldsymbol {z} _ {neu} \ cdot E \ cdot \ boldsymbol {x} _ {alt} \ end {gesammelt} $$ $$ anzeigen
Genau
$ inline $ d \ boldsymbol {z} _ {new} = d \ boldsymbol {z} \ cdot W $ inline $ und Sie müssen zur vorherigen Ebene senden.
Code
Dieser Artikel zielt hauptsächlich darauf ab, die Mathematik neuronaler Netze zu erklären. Ich werde dem Code sehr wenig Zeit widmen.
Dies ist eine Beispielimplementierung der Fehlerfunktion:
class CrossEntropy: def forward(self, y_true, y_hat): self.y_hat = y_hat self.y_true = y_true self.loss = -np.sum(self.y_true * np.log(y_hat)) return self.loss def backward(self): dz = -self.y_true / self.y_hat return dz
Die Klasse verfügt über Methoden für den direkten und den umgekehrten Durchlauf. Zum Zeitpunkt des direkten Durchlaufs speichert die Klasseninstanz die Daten in der Ebene und verwendet sie zum Zeitpunkt des Rücklaufs zur Berechnung des Gradienten. Die restlichen Schichten sind auf die gleiche Weise aufgebaut. Dank dessen wird es möglich, ein vollständig verbundenes Neuronales in diesem Stil zu schreiben:
class MnistNet: def __init__(self): self.d1_layer = Dense(784, 100) self.a1_layer = ReLu() self.drop1_layer = Dropout(0.5) self.d2_layer = Dense(100, 50) self.a2_layer = ReLu() self.drop2_layer = Dropout(0.25) self.d3_layer = Dense(50, 10) self.a3_layer = Softmax() def forward(self, x, train=True): ... def backward(self, dz, learning_rate=0.01, mini_batch=True, update=False, len_mini_batch=None): ...
Den vollständigen Code finden Sie
hier .
Ich rate auch, diesen
Artikel über Habré zu studieren.
Fazit
Ich hoffe, dass ich erklären und zeigen konnte, dass hinter neuronalen Netzen eine recht einfache Mathematik steckt und dass dies überhaupt nicht beängstigend ist. Für ein tieferes Verständnis lohnt es sich jedoch, ein eigenes „Fahrrad“ zu schreiben. Korrekturen und Vorschläge lesen Sie gerne in den Kommentaren.