Jeder Android-Entwickler verwendete RecyclerView , um Listen anzuzeigen, und jeder hatte das Problem, die Daten in der Liste zu aktualisieren, bis die magische Klasse DiffUtil im Jahr 2016 erschien. Ich werde an den Fingern erklären, wie es tatsächlich funktioniert, und versuchen, seine Magie zu zerstreuen.
Ein bisschen Geschichte
Eines der häufigsten Elemente in mobilen Anwendungen ist die Liste, in unserem Fall RecyclerView . Dies können Listen von allem sein: Büroadressen, Listen von Freunden in sozialen Netzwerken. Netzwerke, Bestellverlauf in Taxi-Anwendungen usw. All diese Fälle werden durch die Notwendigkeit vereint, die Daten in der Liste ständig in neue zu ändern, wenn der Benutzer beispielsweise zum Aktualisieren über die Liste wischte, die Liste filterte oder auf andere Weise ein Paket neuer Daten von hinten erhielt.
Um dieses Verhalten zu implementieren, hat der Vorfahr des modernen Android-Entwicklers manuell ausgewählt, welche Daten und wie geändert wurden, und die entsprechenden Methoden von RecyclerView aufgerufen. Als Google die Support Library Version 25.1.0 veröffentlichte und dort DiffUtil hinzufügte, änderte sich jedoch alles, DiffUtil Sie die alte Liste auf magische Weise in eine neue umwandeln konnten, ohne RecyclerView vollständig neu zu RecyclerView . In diesem Artikel werde ich die Magie von DiffUtil zerstreuen und erklären, wie es funktioniert.
Wie arbeite ich mit DiffUtil?
Um mit DiffUtil müssen Sie DiffUtil.Callback implementieren, die calculateDiff(@NonNull Callback cb) Methode calculateDiff(@NonNull Callback cb) und das empfangene DiffResult mit der dispatchUpdatesTo() -Methode auf RecyclerView anwenden. Was passiert, wenn die Methode calucalteDiff(@NonNull Callback cd) aufgerufen wird? Diese Methode gibt ein DiffResult , das eine Reihe von Operationen zum Konvertieren der ursprünglichen Liste in eine neue enthält. Aktualisierungen werden durch Aufrufe der notifyItemRangeInserted , notifyItemRangeRemoved , notifyItemMoved und notifyItemRangeChanged . Die ersten drei Methoden ändern die Struktur der Liste, nämlich die Positionen der Elemente, ohne die Elemente selbst zu ändern und nicht onBindViewHolder() (mit Ausnahme des hinzugefügten Elements). Letzterer ändert das Element selbst und ruft onBindViewHolder() auf, um die Ansicht des Elements zu ändern.
DiffUtil überprüft die beiden Listen mithilfe des Myers-Algorithmus auf Unterschiede. Dieser ermittelt nur das Vorhandensein / Fehlen von Änderungen, weiß jedoch nicht, wie die Bewegung von Elementen ermittelt werden kann. Zu diesem DiffUtil geht DiffUtil durch die vom Myers-Algorithmus erstellten DiffUtil (dazu später mehr) und sucht dann nach Bewegungen. DiffResult wird für gebildet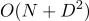 
wenn der Algorithmus die Bewegung von Elementen und nicht überprüft 
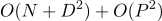Dabei ist P die Anzahl der hinzugefügten und gelöschten Elemente.
Myers-Algorithmus
Als nächstes wird eine Erklärung des Myers-Algorithmus an den Fingern betrachtet. Links zu mathematischen Erklärungen des Algorithmus (sowie anderen coolen Artikeln zum Thema) finden Sie am Ende des Artikels. Betrachten Sie zwei Sequenzen: BACAAC und CBCBAB. Es ist notwendig, eine Folge von Transformationen über die erste Folge zu schreiben, wonach wir die zweite erhalten. Wir schreiben die Sequenzen in der Tabelle wie folgt aus: Die alte Liste bezeichnet die ersten Elemente der Spalten, und die neue Liste ist das erste Element der Zeilen.
Kreuzen Sie die Zellen an, in denen sich identische Elemente beider Sequenzen schneiden:
Eine weitere Aufgabe besteht darin, in der geringsten Anzahl von Schritten von der oberen linken Ecke der Matrix zur unteren rechten Ecke zu gelangen. Sie können sich entlang horizontaler und vertikaler Flächen bewegen. Wenn Sie den Punkt erreichen, an dem die diagonale Linie beginnt, müssen Sie sich entlang dieser bewegen, aber die Kosten für einen solchen Schritt betragen 0. Dementsprechend betragen die Kosten für einen Schritt entlang der Kanten 1.
Ab dem Punkt (0; 0) können wir uns nach rechts und unten bewegen. Wenn Sie sich nach unten bewegen, müssen Sie zusätzlich diagonal gehen. Die in einem Schritt ausgeführte Bewegung wird als Schlange bezeichnet. In diesem Fall werden 2 Schlangen empfangen: (0; 0) -> (0; 1) und (0; 0) -> (1; 2). Der Pfeil zeigt das Ende der Schlange an, d.h. Wenn nach dem vertikalen / horizontalen Schritt ein obligatorischer Schritt entlang der Diagonale vorhanden ist, befindet sich der Pfeil auf dem Schritt entlang der Diagonale. Die vollständige Konstruktion der Schlangen vom Startpunkt bis zum Finale ist unten dargestellt. Einige Pfade im Video wurden da weggelassen waren offensichtlich nicht die kürzesten.
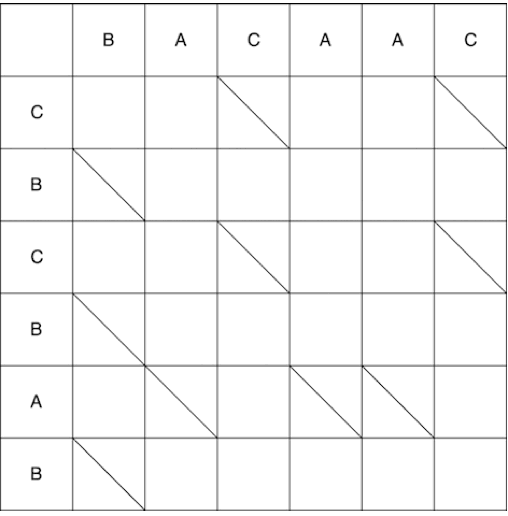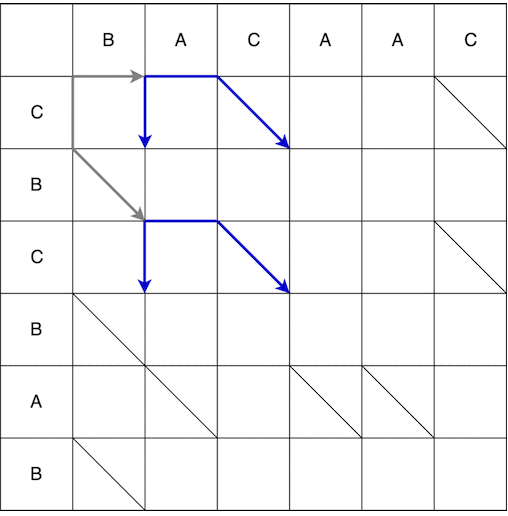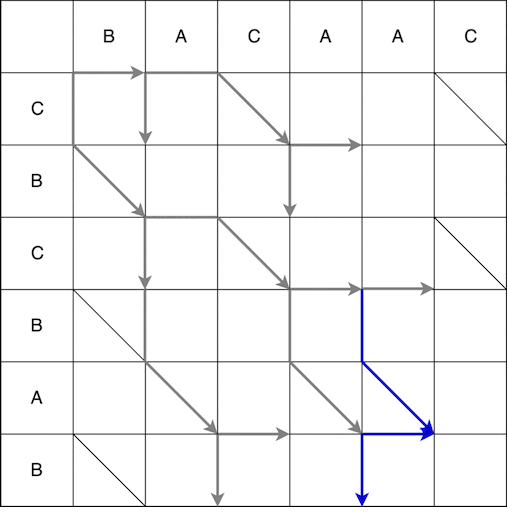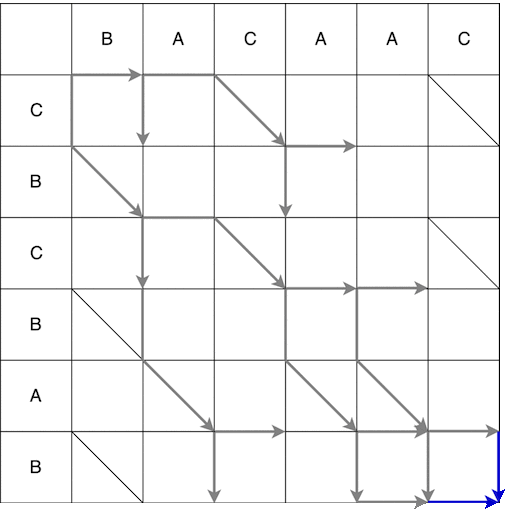
Als Ergebnis erhalten wir mehrere mögliche kürzeste Pfade, von denen einige unten angezeigt werden.
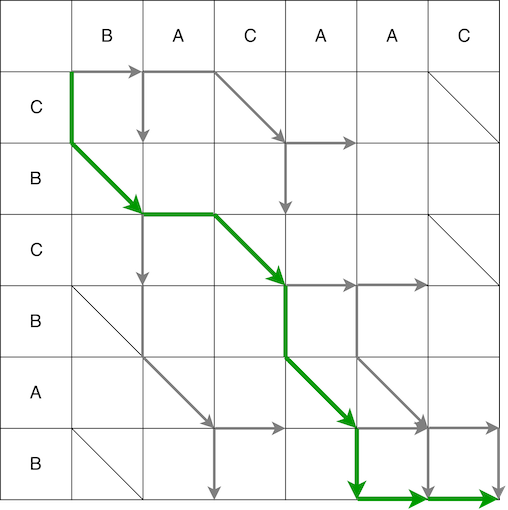
Wie kann das Übergeben einer Matrix von ganz links nach ganz rechts dazu beitragen, die Reihenfolge der Aktionen (Skript) für die Konvertierung einer Sequenz in eine andere zu bestimmen? Was bedeuten horizontale, vertikale und diagonale Schritte? Ein Schritt entlang der Matrix in eine der möglichen Richtungen sind Aktionen auf der alten Linie:
- Horizontaler Schritt - Aus alter Zeile löschen
- Vertikaler Schritt - Zur alten Linie hinzufügen
- Diagonale Stufe - keine Änderung
Am Beispiel des zweiten Pfads vergleichen wir den Pfad und das resultierende Skript. Der erste Schritt ist vertikal, was bedeutet, dass wir das Zeichen "C" an die 0-Position in der alten Zeile hinzufügen.
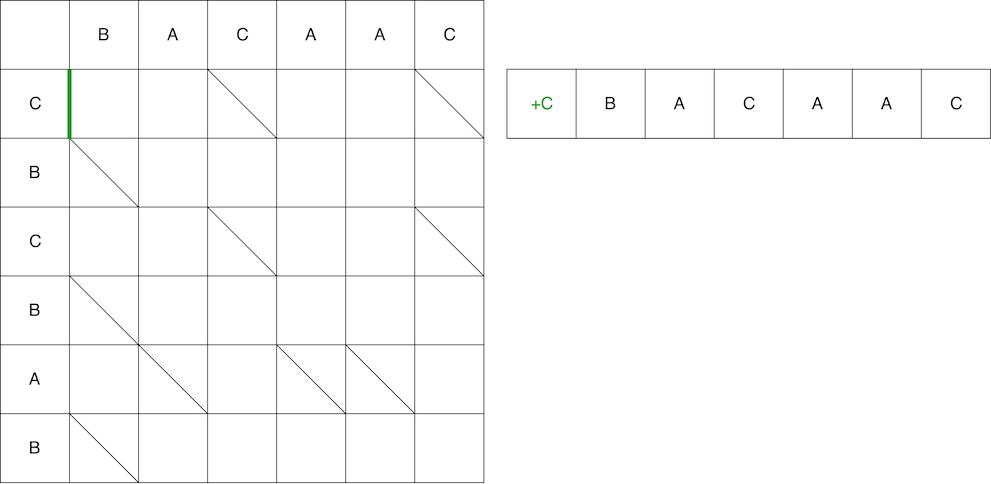
Dies ist jedoch nicht die ganze Schlange. Als nächstes müssen wir uns diagonal bewegen. Bei diagonaler Bewegung bleibt Element B unverändert. Infolgedessen besteht die Schlange aus vertikaler Bewegung + diagonaler Bewegung.
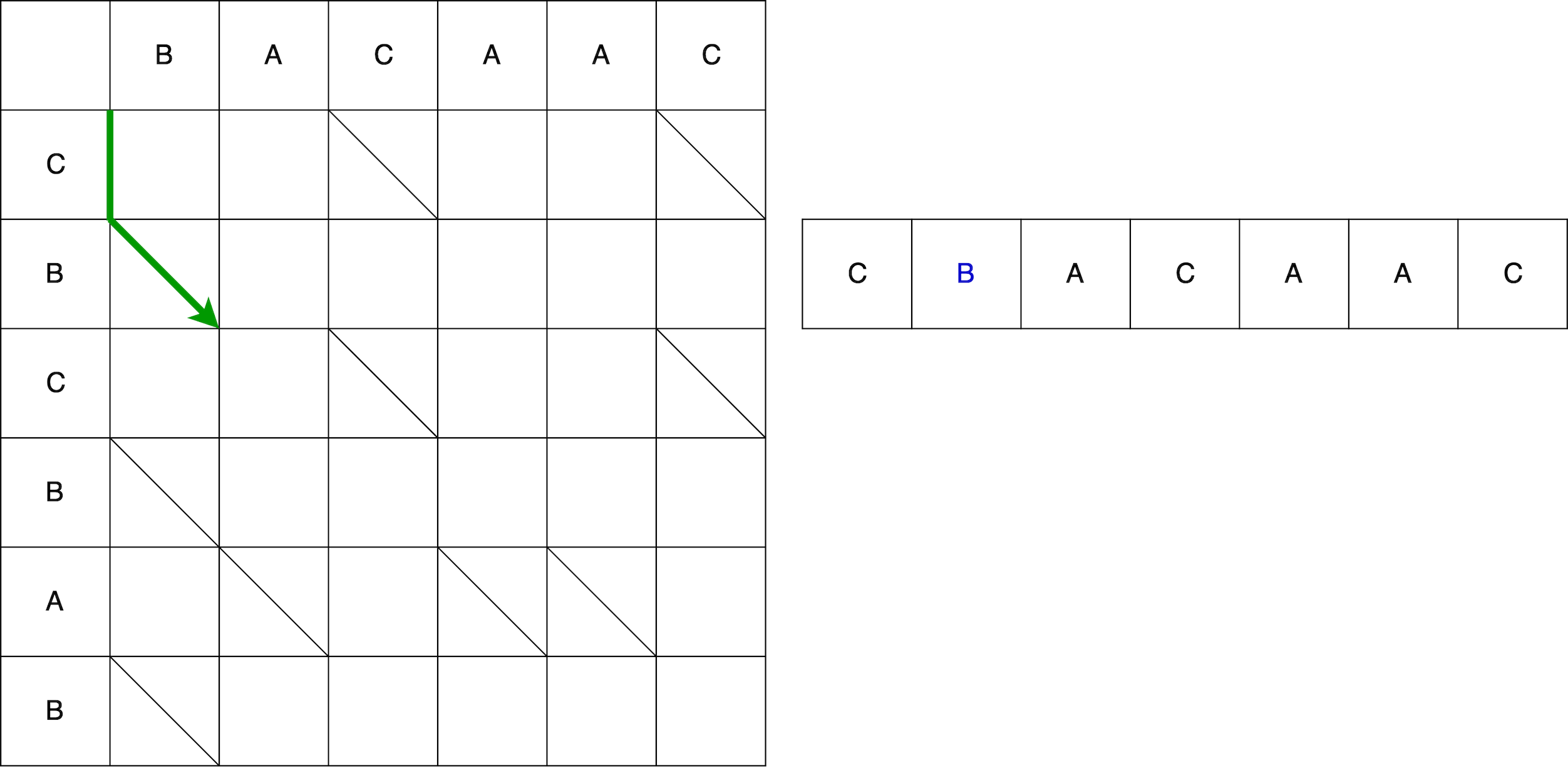
Als nächstes die Schlange horizontal - entfernen Sie Element A. aus der alten Linie
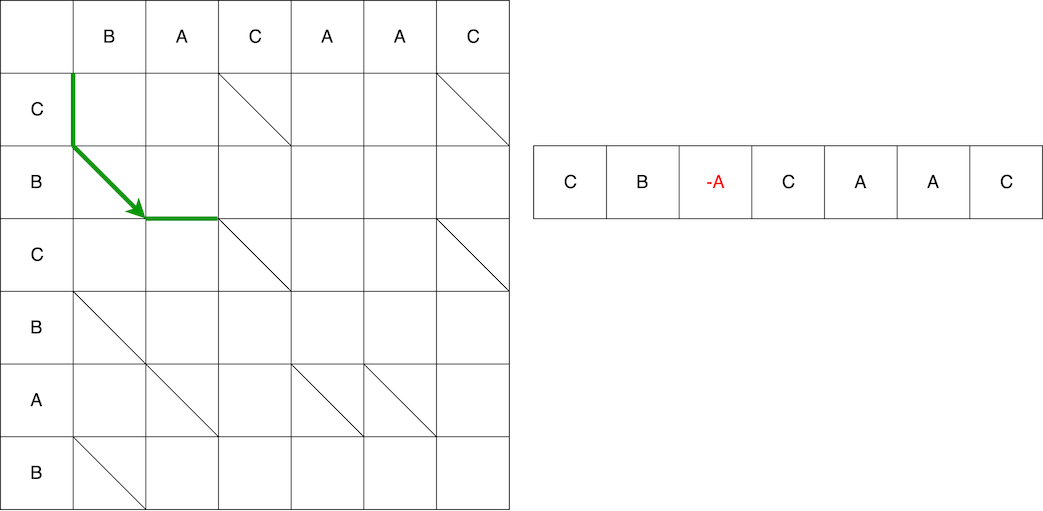
Das Video zeigt den gesamten Pfad von Anfang bis Ende mit einer Änderung der Quellzeichenfolge, bis sie in die endgültige konvertiert wird.
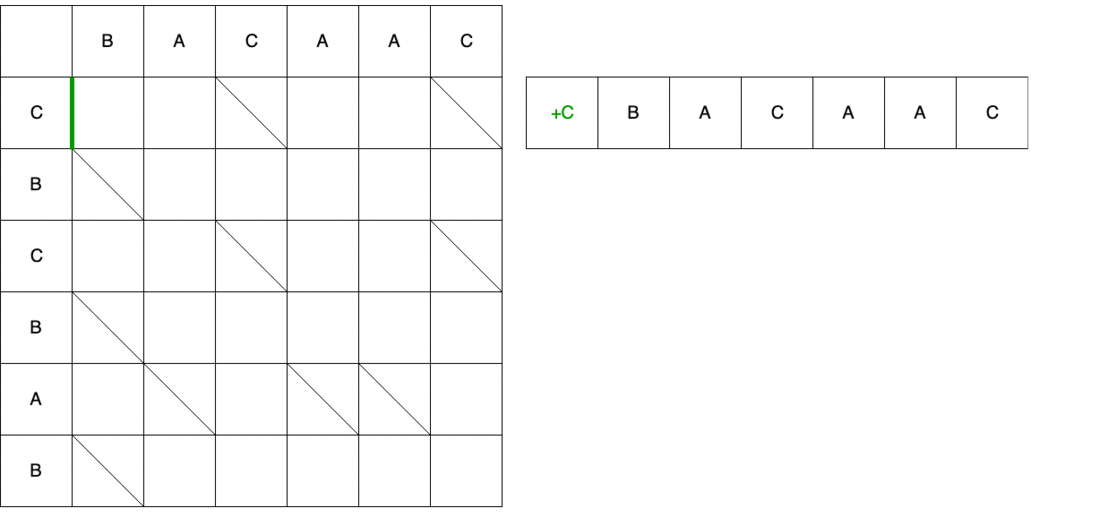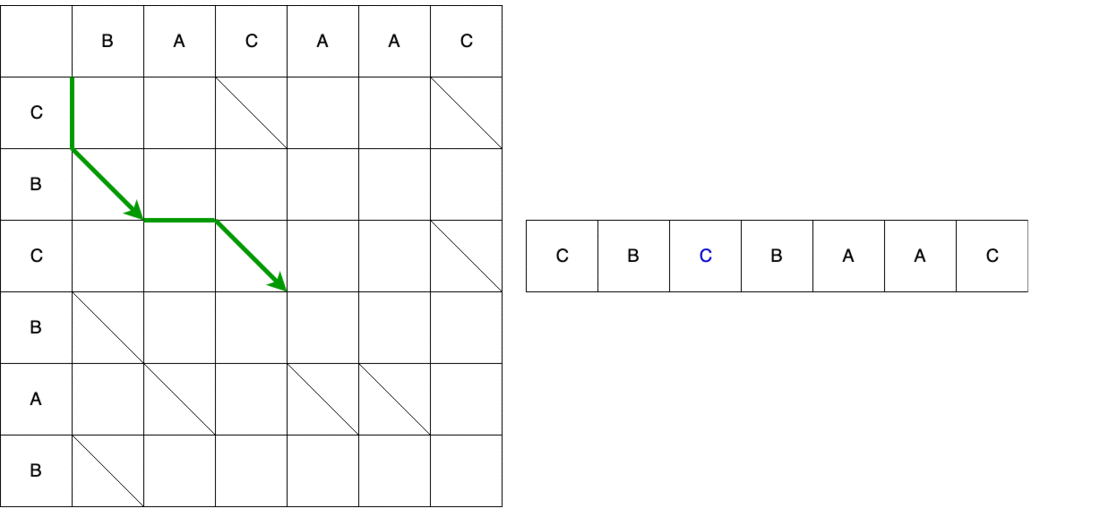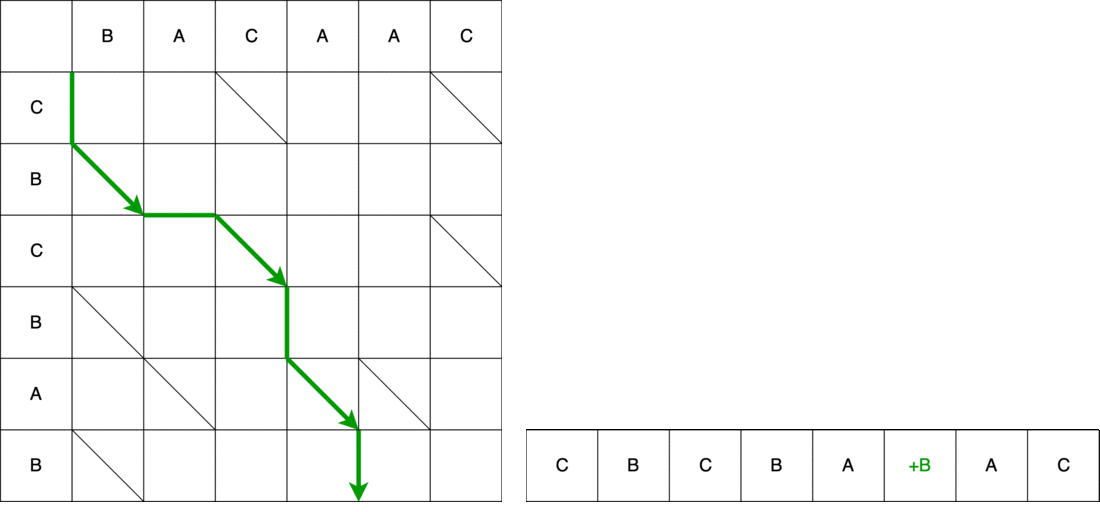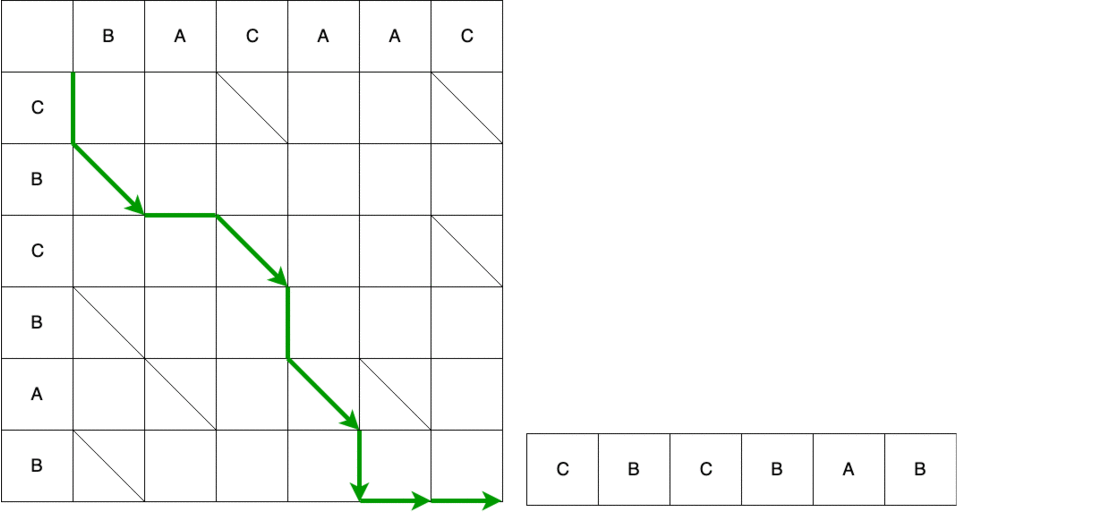
Das Ergebnis des Myers-Algorithmus ist ein Skript mit einer Reihe von Mindestaktionen, die ausgeführt werden müssen, um eine Sequenz in eine andere zu konvertieren. In DiffUtil der Myers-Algorithmus verwendet, um nach verschiedenen Elementen zu suchen, die von der areItemsTheSame() -Methode bestimmt werden. Der Myers-Algorithmus erstellt nicht nur eine Liste von Schlangen, sondern erstellt beim Durchlaufen von Listen auch Listen mit Status der Elemente der alten und neuen Listen. Alle diese Daten sowie das detectMoves Flag und der vom Benutzer implementierte Rückruf werden an den DiffResult(Callback callback, List<Snake> snakes, int[] oldItemStatuses, int[] newItemStatuses, boolean detectMoves) Konstruktor übergeben DiffResult(Callback callback, List<Snake> snakes, int[] oldItemStatuses, int[] newItemStatuses, boolean detectMoves) .
Während ich diesen Artikel schrieb, konnte ich herausfinden, was genau in DiffResult passiert: Der Algorithmus geht durch die Schlangen und setzt Flags auf die Elemente (in den DiffResult ), um zu bestimmen, was genau mit dem Element passiert ist. Mithilfe dieser Flags wird beim Anwenden von Änderungen an RecyclerView festgelegt, auf welche Methode Aktualisierungen notifyItemRangeInserted, notifyItemRangeRemoved, notifyItemMoved notifyItemRangeChanged : notifyItemRangeInserted, notifyItemRangeRemoved, notifyItemMoved notifyItemRangeChanged . Im Detail werde ich das nächste Mal darüber sprechen.
Referenzen