Neuronale Netze und tiefes Lernen, Kapitel 3, Teil 3: Wie werden Hyperparameter für neuronale Netze ausgewählt?

Bisher habe ich nicht erklärt, wie ich die Werte von Hyperparametern wähle - die Lerngeschwindigkeit η, den Regularisierungsparameter λ und so weiter. Ich habe nur schöne Arbeitswerte gegeben. In der Praxis kann es schwierig sein, gute Hyperparameter zu finden, wenn Sie ein neuronales Netzwerk verwenden, um ein Problem anzugreifen. Stellen Sie sich zum Beispiel vor, wir hätten gerade etwas über das MNIST-Problem erfahren und damit begonnen, ohne etwas über die Werte geeigneter Hyperparameter zu wissen. Nehmen wir an, wir hatten zufällig Glück und haben in den ersten Experimenten viele Hyperparameter ausgewählt, wie wir es bereits in diesem Kapitel getan haben: 30 versteckte Neuronen, eine Mini-Paketgröße von 10, Training für 30 Epochen und die Verwendung von Kreuzentropie. Wir haben jedoch die Lernrate η = 10,0 und den Regularisierungsparameter λ = 1000,0 gewählt. Und hier ist, was ich bei einem solchen Lauf gesehen habe:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 1030 / 10000 Epoch 1 training complete Accuracy on evaluation data: 990 / 10000 Epoch 2 training complete Accuracy on evaluation data: 1009 / 10000 ... Epoch 27 training complete Accuracy on evaluation data: 1009 / 10000 Epoch 28 training complete Accuracy on evaluation data: 983 / 10000 Epoch 29 training complete Accuracy on evaluation data: 967 / 10000 

Unsere Klassifizierung funktioniert nicht besser als Stichproben! Unser Netzwerk arbeitet als Zufallsrauschgenerator!

"Nun, das ist einfach zu beheben", könnte man sagen, "reduzieren Sie einfach Hyperparameter wie Lerngeschwindigkeit und Regularisierung." Leider haben Sie a priori keine Informationen darüber, welche genauen Hyperparameter Sie anpassen müssen. Vielleicht ist das Hauptproblem, dass unsere 30 versteckten Neuronen niemals funktionieren, unabhängig davon, wie die anderen Hyperparameter ausgewählt werden? Vielleicht brauchen wir mindestens 100 versteckte Neuronen? Oder 300? Oder viele versteckte Schichten? Oder ein anderer Ansatz zur Ausgabecodierung? Vielleicht lernt unser Netzwerk, aber wir müssen es mehr Epochen trainieren? Vielleicht ist die Größe der Minipakete zu klein? Vielleicht hätten wir es besser gemacht, wenn wir zur quadratischen Funktion des Wertes zurückgekehrt wären? Vielleicht müssen wir einen anderen Ansatz zum Initialisieren von Gewichten ausprobieren? Und so weiter und so fort. Im Raum der Hyperparameter kann man sich leicht verlaufen. Dies kann sehr unangenehm sein, wenn Ihr Netzwerk sehr groß ist oder große Mengen an Trainingsdaten verwendet und Sie sie stunden-, tag- oder wochenlang trainieren können, ohne Ergebnisse zu erhalten. In einer solchen Situation beginnt Ihr Vertrauen zu vergehen. Vielleicht waren neuronale Netze der falsche Ansatz, um Ihr Problem zu lösen? Vielleicht kündigst du und machst Imkerei?

In diesem Abschnitt werde ich einige heuristische Ansätze erläutern, mit denen Sie Hyperparameter in einem neuronalen Netzwerk konfigurieren können. Ziel ist es, Ihnen bei der Ausarbeitung eines Workflows zu helfen, mit dem Sie Hyperparameter recht gut konfigurieren können. Natürlich kann ich nicht das gesamte Thema der Hyperparameteroptimierung behandeln. Dies ist ein riesiger Bereich, und dies ist kein Problem, das vollständig oder nach den richtigen Lösungsstrategien gelöst werden kann, bei denen eine allgemeine Übereinstimmung besteht. Es besteht immer die Möglichkeit, einen anderen Trick auszuprobieren, um zusätzliche Ergebnisse aus Ihrem neuronalen Netzwerk herauszuholen. Die Heuristik in diesem Abschnitt sollte Ihnen jedoch einen Ausgangspunkt geben.

Allgemeine Strategie

Wenn ein neuronales Netzwerk verwendet wird, um ein neues Problem anzugreifen, besteht die erste Schwierigkeit darin, nicht triviale Ergebnisse aus dem Netzwerk zu erhalten, dh eine zufällige Wahrscheinlichkeit zu überschreiten. Dies kann überraschend schwierig sein, insbesondere wenn Sie mit einer neuen Klasse von Aufgaben konfrontiert sind. Schauen wir uns einige Strategien an, die für diese Art von Schwierigkeit verwendet werden können.

Angenommen, Sie sind der erste, der die MNIST-Aufgabe angreift. Sie beginnen mit großer Begeisterung, aber der vollständige Ausfall Ihres ersten Netzwerks ist ein wenig entmutigend, wie im obigen Beispiel beschrieben. Dann müssen Sie das Problem in Teile zerlegen. Sie müssen alle Trainings- und Unterstützungsbilder entfernen, mit Ausnahme von Bildern mit Nullen und Einsen. Versuchen Sie dann, das Netzwerk so zu trainieren, dass 0 von 1 unterschieden wird. Diese Aufgabe ist nicht nur wesentlich einfacher als das Unterscheiden aller zehn Ziffern, sondern reduziert auch die Menge der Trainingsdaten um 80% und beschleunigt das Lernen um das Fünffache. Auf diese Weise können Sie Experimente viel schneller durchführen und schnell verstehen, wie Sie ein gutes Netzwerk erstellen.

Experimente können weiter beschleunigt werden, indem das Netzwerk auf eine Mindestgröße reduziert wird, die wahrscheinlich sinnvoll trainiert wird. Wenn Sie der Meinung sind, dass das Netzwerk [784, 10] MNIST-Ziffern sehr wahrscheinlich besser klassifizieren kann als eine Zufallsstichprobe, experimentieren Sie damit. Es ist viel schneller als das Training [784, 30, 10], und Sie können bereits später darauf aufbauen.

Eine weitere Beschleunigung der Experimente kann durch Erhöhen der Verfolgungsfrequenz erhalten werden. Im Programm network2.py überwachen wir die Qualität der Arbeit am Ende jeder Ära. Bei der Verarbeitung von 50.000 Bildern pro Ära müssen wir ziemlich lange warten - etwa 10 Sekunden pro Ära auf meinem Laptop, wenn ich das Netzwerk lerne [784, 30, 10] -, bevor wir Feedback zur Qualität des Netzwerklernens erhalten. Natürlich sind zehn Sekunden nicht so lang, aber wenn Sie mehrere Dutzend verschiedener Hyperparameter ausprobieren möchten, wird es ärgerlich, und wenn Sie Hunderte oder Tausende von Optionen ausprobieren möchten, ist dies nur verheerend. Feedback kann viel schneller empfangen werden, indem die Bestätigungsgenauigkeit häufiger verfolgt wird, z. B. alle 1000 Trainingsbilder. Anstatt den vollständigen Satz von 10.000 Bestätigungsbildern zu verwenden, können wir mit nur 100 Bestätigungsbildern eine viel schnellere Schätzung erhalten. Die Hauptsache ist, dass das Netzwerk genügend Bilder sieht, um wirklich zu lernen und eine ausreichend gute Einschätzung der Effektivität zu erhalten. Natürlich bietet unser network2.py ein solches Tracking noch nicht an. Um diesen Effekt zur Veranschaulichung zu erzielen, beschneiden wir unsere Trainingsdaten auf die ersten 1000 MNIST-Bilder. Lassen Sie uns versuchen zu sehen, was passiert (der Einfachheit halber habe ich nicht die Idee verwendet, nur die Bilder 0 und 1 zu belassen - dies kann auch mit etwas mehr Aufwand realisiert werden).

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 ... 

Wir bekommen immer noch reines Rauschen, aber wir haben einen großen Vorteil: Das Feedback wird in Sekundenbruchteilen und nicht alle zehn Sekunden aktualisiert. Dies bedeutet, dass Sie mit der Auswahl von Hyperparametern viel schneller experimentieren oder sogar fast gleichzeitig mit vielen verschiedenen Hyperparametern experimentieren können.

Im obigen Beispiel habe ich den Wert von λ wie zuvor gleich 1000,0 belassen. Da wir jedoch die Anzahl der Trainingsbeispiele geändert haben, müssen wir λ ändern, damit die Schwächung der Gewichte gleich ist. Dies bedeutet, dass wir λ um 20,0 ändern. In diesem Fall stellt sich Folgendes heraus:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 12 / 100 Epoch 1 training complete Accuracy on evaluation data: 14 / 100 Epoch 2 training complete Accuracy on evaluation data: 25 / 100 Epoch 3 training complete Accuracy on evaluation data: 18 / 100 ... 

Ja! Wir haben ein Signal. Nicht besonders gut, aber es gibt. Dies kann bereits als Ausgangspunkt genommen werden und die Hyperparameter ändern, um weitere Verbesserungen zu erzielen. Angenommen, wir entscheiden, dass wir die Lerngeschwindigkeit erhöhen müssen (wie Sie wahrscheinlich verstanden haben, haben wir uns aus dem Grund, den wir später diskutieren werden, falsch entschieden, aber versuchen wir dies zunächst). Um unsere Vermutung zu testen, drehen wir η auf 100,0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 Epoch 3 training complete Accuracy on evaluation data: 10 / 100 ... 

Alles ist schlecht! Anscheinend war unsere Vermutung falsch und das Problem lag nicht im sehr niedrigen Wert der Lerngeschwindigkeit. Wir versuchen, η auf einen kleinen Wert von 1,0 festzuziehen:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 62 / 100 Epoch 1 training complete Accuracy on evaluation data: 42 / 100 Epoch 2 training complete Accuracy on evaluation data: 43 / 100 Epoch 3 training complete Accuracy on evaluation data: 61 / 100 ... 

Das ist besser! Und so können wir weiter machen, jeden Hyperparameter verdrehen und die Effizienz schrittweise verbessern. Nachdem wir die Situation untersucht und einen verbesserten Wert für η gefunden haben, suchen wir nach einem guten Wert für λ. Dann werden wir ein Experiment mit einer komplexeren Architektur durchführen, zum Beispiel mit einem Netzwerk von 10 versteckten Neuronen. Dann optimieren wir erneut die Parameter für η und λ. Dann werden wir das Netzwerk auf 20 versteckte Neuronen erhöhen. Ein wenig an den Hyperparametern anpassen. Und so weiter, indem Sie die Wirksamkeit bei jedem Schritt anhand eines Teils unserer unterstützenden Daten bewerten und anhand dieser Schätzungen die besten Hyperparameter auswählen. Im Zuge von Verbesserungen dauert es immer länger, den Effekt der Optimierung von Hyperparametern zu erkennen, sodass wir die Tracking-Frequenz schrittweise reduzieren können.

Als Gesamtstrategie sieht dieser Ansatz vielversprechend aus. Ich möchte jedoch zu diesem ersten Schritt bei der Suche nach Hyperparametern zurückkehren, die es dem Netzwerk ermöglichen, zumindest irgendwie zu lernen. Selbst im obigen Beispiel war die Situation zu optimistisch. Die Arbeit mit einem Netzwerk, das nichts lernt, kann äußerst ärgerlich sein. Sie können Hyperparameter für mehrere Tage anpassen und erhalten keine aussagekräftigen Antworten. Daher möchte ich noch einmal betonen, dass Sie in einem frühen Stadium sicherstellen müssen, dass Sie schnelles Feedback von Experimenten erhalten. Intuitiv scheint es, dass die Vereinfachung des Problems und der Architektur Sie nur verlangsamen wird. Dies beschleunigt den Prozess, da Sie ein Netzwerk mit einem aussagekräftigen Signal viel schneller finden können. Wenn Sie ein solches Signal empfangen haben, können Sie beim Einstellen von Hyperparametern häufig schnelle Verbesserungen erzielen. Wie in vielen Lebenssituationen ist es am schwierigsten, den Prozess zu starten.

Okay, das ist eine allgemeine Strategie. Schauen wir uns nun die spezifischen Empfehlungen für die Verschreibung von Hyperparametern an. Ich werde mich auf die Lerngeschwindigkeit η, den Regularisierungsparameter L2 λ und die Größe des Minipakets konzentrieren. Viele Kommentare werden jedoch auf andere Hyperparameter anwendbar sein, einschließlich solcher, die sich auf die Netzwerkarchitektur, andere Formen der Regularisierung und einige Hyperparameter beziehen, die wir später in diesem Buch erfahren werden, beispielsweise den Impulskoeffizienten.

Lerngeschwindigkeit

Angenommen, wir haben drei MNIST-Netzwerke mit drei unterschiedlichen Lerngeschwindigkeiten gestartet: η = 0,025, η = 0,25 bzw. η = 2,5. Wir werden den Rest der Hyperparameter so lassen, wie sie in den vorherigen Abschnitten waren - 30 Epochen, die Größe des Minipakets beträgt 10, λ = 5,0. Wir werden auch wieder alle 50.000 Trainingsbilder verwenden. Hier ist eine Grafik, die das Verhalten der Schulungskosten zeigt (erstellt vom Programm multiple_eta.py):



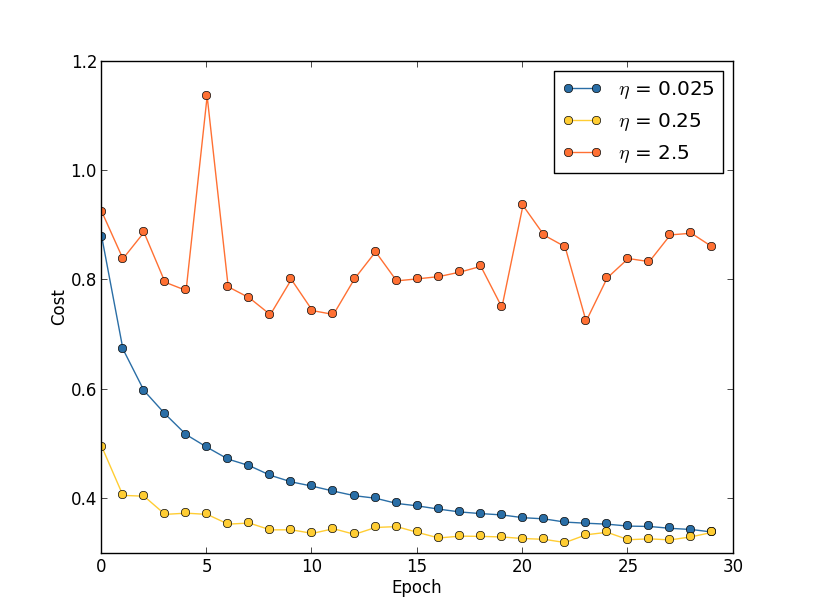
Bei η = 0,025 sinken die Kosten reibungslos bis zur letzten Ära. Mit η = 0,25 sinken die Kosten zunächst, aber nach 20 Epochen sind sie gesättigt, sodass sich die meisten Änderungen als kleine und offensichtlich zufällige Schwankungen herausstellen. Mit η = 2,5 variieren die Kosten von Anfang an stark. Um den Grund für diese Schwankungen zu verstehen, erinnern wir uns, dass der stochastische Gradientenabstieg uns allmählich in das Tal der Kostenfunktion senken sollte:



Dieses Bild hilft, sich intuitiv vorzustellen, was passiert, ist jedoch keine vollständige und umfassende Erklärung. Genauer gesagt, aber kurz, verwendet der Gradientenabstieg eine Näherung erster Ordnung für die Kostenfunktion, um zu verstehen, wie die Kosten gesenkt werden können. Für größere η werden Mitglieder einer Kostenfunktion höherer Ordnung wichtiger, und sie können das Verhalten dominieren, indem sie den Gradientenabstieg unterbrechen. Dies ist besonders wahrscheinlich, wenn Sie sich den Minima und lokalen Minima der Kostenfunktion nähern, da neben solchen Punkten der Gradient klein wird, was es Mitgliedern höherer Ordnung erleichtert, zu dominieren.

Wenn jedoch η zu groß ist, sind die Stufen so groß, dass sie ein Minimum überspringen können, wodurch der Algorithmus aus dem Tal aufsteigt. Wahrscheinlich ist dies der Grund, warum der Preis bei η = 2,5 schwankt. Die Wahl von η = 0,25 führt dazu, dass die ersten Schritte uns wirklich zu einem Minimum der Kostenfunktion führen, und erst wenn wir dazu kommen, treten Schwierigkeiten beim Springen auf. Und wenn wir η = 0,025 wählen, haben wir in den ersten 30 Epochen keine derartigen Schwierigkeiten. Die Wahl eines so kleinen Wertes von η schafft natürlich eine weitere Schwierigkeit - nämlich die Verlangsamung des stochastischen Gradientenabfalls. Der beste Ansatz wäre, mit η = 0,25 zu beginnen, 20 Epochen zu lernen und dann zu η = 0,025 zu gehen. Später werden wir eine solche variable Lernrate diskutieren. Lassen Sie uns in der Zwischenzeit auf die Frage eingehen, einen geeigneten Wert für die Lerngeschwindigkeit η zu finden.

In diesem Sinne können wir η wie folgt wählen. Zunächst bewerten wir den Schwellenwert η, bei dem die Kosten für Trainingsdaten sofort zu sinken beginnen, aber nicht schwanken und nicht zunehmen. Diese Schätzung muss nicht genau sein. Die Reihenfolge kann geschätzt werden, indem mit η = 0,01 begonnen wird. Wenn die Kosten in den ersten Epochen sinken, lohnt es sich, η = 0,1, dann 1,0 usw. zu versuchen, bis Sie einen Wert finden, bei dem der Wert in den ersten Epochen schwankt oder steigt. Und umgekehrt, wenn der Wert in den ersten Epochen mit η = 0,01 schwankt oder zunimmt, versuchen Sie es mit η = 0,001, η = 0,0001, bis Sie den Wert finden, bei dem die Kosten in den ersten Epochen sinken. Diese Prozedur gibt Ihnen die Reihenfolge des Schwellenwerts η. Wenn Sie möchten, können Sie Ihre Bewertung verfeinern, indem Sie den höchsten Wert für η auswählen, bei dem die Kosten in den ersten Epochen sinken, z. B. η = 0,5 oder η = 0,2 (Supergenauigkeit ist hier nicht erforderlich). Dies gibt uns eine Schätzung des Schwellenwerts η.

Der reale Wert von η sollte offensichtlich den ausgewählten Schwellenwert nicht überschreiten. Damit der η-Wert für viele Epochen nützlich bleibt, sollten Sie einen Wert verwenden, der zweimal kleiner als der Schwellenwert ist. Eine solche Wahl ermöglicht es Ihnen normalerweise, aus vielen Epochen zu lernen, ohne Ihr Lernen stark zu verlangsamen.

Im Fall von MNIST-Daten führt das Befolgen dieser Strategie zu einer Schätzung der Schwellenordnung von η bei 0,1. Nach einiger Verfeinerung erhalten wir den Wert η = 0,5. Nach dem obigen Rezept sollten wir η = 0,25 für unsere Lerngeschwindigkeit verwenden. Tatsächlich stellte ich jedoch fest, dass η = 0,5 für 30 Epochen gut funktionierte, sodass ich mir keine Sorgen darüber machte, es zu verringern.

Das alles sieht ziemlich einfach aus. Die Verwendung der Trainingskosten zur Auswahl von η scheint jedoch im Widerspruch zu dem zu stehen, was ich zuvor gesagt habe: Wir wählen Hyperparameter und bewerten die Effektivität des Netzwerks anhand ausgewählter Bestätigungsdaten. Tatsächlich werden wir die Genauigkeit der Bestätigung verwenden, um die Regularisierungshyperparameter, die Größe des Minipakets und Netzwerkparameter wie die Anzahl der Schichten und versteckten Neuronen usw. auszuwählen. Warum machen wir es mit Lerngeschwindigkeit anders? Ehrlich gesagt ist diese Wahl auf meine persönlichen ästhetischen Vorlieben zurückzuführen und wahrscheinlich voreingenommen. Das Argument ist, dass andere Hyperparameter die endgültige Klassifizierungsgenauigkeit des Testsatzes verbessern sollten. Daher ist es sinnvoll, sie basierend auf der Genauigkeit der Bestätigung auszuwählen. Die Lernrate wirkt sich jedoch nur indirekt auf die endgültige Klassifizierungsgenauigkeit aus. Das Hauptziel besteht darin, die Schrittgröße des Gradientenabstiegs zu steuern und die Trainingskosten bestmöglich zu verfolgen, um eine zu große Schrittgröße zu erkennen. Dies ist jedoch eine persönliche ästhetische Präferenz. In den frühen Phasen des Trainings sinken die Trainingskosten normalerweise nur, wenn die Genauigkeit der Bestätigung zunimmt. In der Praxis sollte es daher keine Rolle spielen, welche Kriterien verwendet werden sollen.

Verwenden Sie einen frühen Stopp, um die Anzahl der Trainingszeiten zu bestimmen

Wie wir in diesem Kapitel erwähnt haben, bedeutet ein früher Stopp, dass wir am Ende jeder Ära die Genauigkeit der Klassifizierung anhand der unterstützenden Daten berechnen müssen. Wenn es sich nicht mehr verbessert, hören wir auf zu arbeiten. Infolgedessen wird das Festlegen der Anzahl der Epochen zu einer einfachen Angelegenheit. Dies bedeutet insbesondere, dass wir nicht genau herausfinden müssen, wie die Anzahl der Epochen von anderen Hyperparametern abhängt. Dies geschieht automatisch. Darüber hinaus verhindert ein früher Stopp automatisch eine Umschulung. Dies ist natürlich gut, obwohl es nützlich sein kann, den frühen Stopp in den frühen Phasen der Experimente auszuschalten, damit Sie Anzeichen einer Umschulung erkennen und sie zur Feinabstimmung des Regularisierungsansatzes verwenden können.

Um den RO zu implementieren, müssen wir genauer beschreiben, was es bedeutet, die Verbesserung der Klassifizierungsgenauigkeit zu stoppen. Wie wir gesehen haben, kann die Genauigkeit sehr weit hin und her springen, selbst wenn sich der Gesamttrend verbessert. Wenn wir zum ersten Mal anhalten und die Genauigkeit abnimmt, werden wir mit ziemlicher Sicherheit keine weiteren Verbesserungen erzielen. Der beste Ansatz besteht darin, das Lernen zu beenden, wenn sich die beste Klassifizierungsgenauigkeit über einen längeren Zeitraum nicht verbessert. Nehmen wir zum Beispiel an, wir beschäftigen uns mit MNIST. Dann können wir entscheiden, den Prozess zu stoppen, wenn sich die Genauigkeit der Klassifizierung in den letzten zehn Epochen nicht verbessert hat. Dies stellt sicher, dass wir nicht zu früh aufhören, weil das Training fehlgeschlagen ist, aber wir werden nicht ewig auf Verbesserungen warten, die nicht eintreten werden.

Diese Regel „Keine Verbesserung gegenüber zehn Epochen“ eignet sich gut für die erste MNIST-Studie. Netzwerke können jedoch manchmal ein Plateau nahe einer bestimmten Klassifizierungsgenauigkeit erreichen, dort einige Zeit bleiben und sich dann wieder verbessern. Wenn Sie eine sehr gute Leistung erzielen möchten, ist die Regel „Keine Verbesserung über zehn Epochen“ möglicherweise zu aggressiv. Daher empfehle ich, für primäre Experimente die Regel "Keine Verbesserung über zehn Epochen" zu verwenden und nach und nach weichere Regeln anzuwenden, wenn Sie das Verhalten Ihres Netzwerks besser verstehen: "Keine Verbesserung über zwanzig Epochen", "Keine Verbesserung über fünfzig Epochen" usw. weiter. Dies gibt uns natürlich einen weiteren Hyperparameter für die Optimierung! In der Praxis ist dieser Hyperparameter jedoch normalerweise leicht auf gute Ergebnisse abzustimmen. Und für andere Aufgaben als MNIST kann die Regel „Keine Verbesserung über zehn Epochen“ zu aggressiv oder nicht aggressiv genug sein, abhängig von den Einzelheiten einer bestimmten Aufgabe.Nach einigem Experimentieren ist es jedoch normalerweise recht einfach, eine geeignete Early-Stop-Strategie zu finden.

Wir haben in unseren Experimenten mit MNIST noch keinen frühen Stopp verwendet. Dies liegt an der Tatsache, dass wir viele Vergleiche verschiedener Lernansätze durchgeführt haben. Für solche Vergleiche ist es sinnvoll, in allen Fällen die gleiche Anzahl von Epochen zu verwenden. Es lohnt sich jedoch, network2.py zu ändern, indem Sie den RO in das Programm einführen.

Die Aufgaben

• Ändern Sie network2.py so, dass die Bestellung dort gemäß der Regel "Keine Änderung für n Epochen" angezeigt wird, wobei n ein konfigurierbarer Parameter ist.
• Stellen Sie sich eine andere Regel für den frühen Stopp vor als „in n Epochen unverändert“. Im Idealfall sollte die Regel einen Kompromiss zwischen der Erzielung einer Genauigkeit mit hoher Bestätigung und einer relativ kurzen Schulungszeit suchen. Fügen Sie network2.py eine Regel hinzu, und führen Sie drei Experimente durch, in denen die Validierungsgenauigkeit und die Anzahl der Trainingsperioden mit der Regel "Keine Änderung über 10 Epochen" verglichen werden.

Plan zur Änderung der Lerngeschwindigkeit

Während wir die Lerngeschwindigkeit η konstant hielten. Es ist jedoch oft nützlich, es zu ändern. In den frühen Phasen des Trainingsprozesses werden Gewichte höchstwahrscheinlich völlig falsch zugewiesen. Daher ist es besser, eine hohe Trainingsrate zu verwenden, da sich die Gewichte schneller ändern. Dann können Sie die Trainingsgeschwindigkeit reduzieren, um die Waage feiner einzustellen.

Wie skizzieren wir einen Plan zur Änderung der Lerngeschwindigkeit? Hier können Sie viele Ansätze anwenden. Eine natürliche Option besteht darin, dieselbe Grundidee wie in RO zu verwenden. Wir halten die Lerngeschwindigkeit konstant, bis sich die Genauigkeit der Bestätigung zu verschlechtern beginnt. Dann reduzieren wir den CO um einen bestimmten Betrag, beispielsweise zwei- oder zehnmal. Wir wiederholen dies viele Male, bis der CO 1024 (oder 1000) Mal weniger als der ursprüngliche ist. Und beende das Training.

Ein Plan zur Änderung der Lerngeschwindigkeit kann die Effizienz verbessern und bietet enorme Möglichkeiten für die Auswahl eines Plans. Und das kann Kopfschmerzen bereiten - Sie können den Plan für immer optimieren. Für die ersten Experimente würde ich vorschlagen, einen einzelnen konstanten CO-Wert zu verwenden. Dies gibt Ihnen eine gute erste Annäherung. Wenn Sie später die beste Effizienz aus dem Netzwerk herausholen möchten, sollten Sie mit dem Plan experimentieren, um die Lerngeschwindigkeit so zu ändern, wie ich es beschrieben habe. Eine ziemlich einfach zu lesende wissenschaftliche Arbeit von 2010 zeigt die Vorteile variabler Lerngeschwindigkeiten beim Angriff auf MNIST.

Übung

• Ändern Sie network2.py so, dass der folgende Plan zum Ändern der Lerngeschwindigkeit implementiert wird: Halbieren Sie die CR jedes Mal, wenn die Genauigkeit der Bestätigung der Regel „Keine Änderung in 10 Epochen“ entspricht, und beenden Sie das Lernen, wenn die Lerngeschwindigkeit von der ursprünglichen auf 1/128 abfällt.

Der Regularisierungsparameter λ

Ich empfehle, überhaupt ohne Regularisierung zu beginnen (λ = 0,0) und den Wert von η wie oben angegeben zu bestimmen. Unter Verwendung des ausgewählten Wertes von η können wir dann die unterstützenden Daten verwenden, um einen guten Wert von λ auszuwählen. Beginnen Sie mit λ = 1,0 (ich habe kein gutes Argument für eine solche Wahl) und erhöhen oder verringern Sie sie dann um das Zehnfache, um die Effizienz bei der Arbeit mit bestätigenden Daten zu erhöhen. Nachdem wir die richtige Größenordnung gefunden haben, können wir den Wert von λ genauer einstellen. Danach ist es notwendig, wieder zur Optimierung η zurückzukehren.

Übung

• , , λ η. , λ? , η?

Wenn Sie die Empfehlungen aus diesem Abschnitt verwenden, werden Sie feststellen, dass die ausgewählten Werte von η und λ nicht immer genau denen entsprechen, die ich zuvor verwendet habe. Es ist nur so, dass das Buch Textbeschränkungen aufweist, was es manchmal unpraktisch machte, Hyperparameter zu optimieren. Erinnern Sie sich an alle Vergleiche der verschiedenen Trainingsansätze, an denen wir gearbeitet haben - Vergleichen der quadratischen Kostenfunktion und der Kreuzentropie, alter und neuer Methoden zum Initialisieren von Gewichten, beginnend mit und ohne Regularisierung usw. Um diese Vergleiche aussagekräftig zu machen, habe ich versucht, die Hyperparameter zwischen den verglichenen Ansätzen nicht zu ändern (oder sie richtig zu skalieren). Natürlich gibt es keinen Grund dafür, dass dieselben Hyperparameter für alle unterschiedlichen Lernansätze optimal sind. Die von mir verwendeten Hyperparameter waren daher das Ergebnis eines Kompromisses.

Alternativ könnte ich versuchen, alle Hyperparameter für jeden Lernansatz maximal zu optimieren. Es wäre ein besserer und ehrlicherer Ansatz, da wir von jedem Lernansatz das Beste nehmen würden. Wir haben jedoch Dutzende von Vergleichen durchgeführt, und in der Praxis wäre dies zu rechenintensiv. Daher habe ich mich entschlossen, Kompromisse einzugehen, um ausreichend (aber nicht unbedingt optimale) Hyperparameteroptionen zu verwenden.

Mini Pack Größe

Wie wähle ich die Größe des Mini-Pakets? Um diese Frage zu beantworten, nehmen wir zunächst an, dass wir an Online-Schulungen teilnehmen, dh wir verwenden ein Minipaket der Größe 1.

Das offensichtliche Problem beim Online-Lernen besteht darin, dass die Verwendung von Minipaketen, die aus einem einzelnen Trainingsbeispiel bestehen, zu schwerwiegenden Fehlern bei der Schätzung des Gradienten führt. Tatsächlich stellen diese Fehler jedoch kein so ernstes Problem dar. Der Grund ist, dass einzelne Gradientenschätzungen nicht sehr genau sein müssen. Wir brauchen nur eine ausreichend genaue Schätzung, damit unsere Kostenfunktion abnimmt. Es ist, als würden Sie versuchen, zum Nordmagnetpol zu gelangen, aber Sie hätten einen unzuverlässigen Kompass, bei dem jede Messung um 10 bis 20 Grad falsch ist. Wenn Sie den Kompass ziemlich oft überprüfen und im Durchschnitt die richtige Richtung anzeigen, können Sie schließlich zum Nordmagnetpol gelangen.

Angesichts dieses Arguments sollten wir das Online-Lernen nutzen. In Wirklichkeit ist die Situation jedoch etwas komplizierter. In der Aufgabe zum letzten Kapitel habe ich darauf hingewiesen, dass Sie zur Berechnung der Gradientenaktualisierung für alle Beispiele im Minipaket Matrixtechniken gleichzeitig anstelle einer Schleife verwenden können. Abhängig von den Details Ihrer Hardware und der linearen Algebra-Bibliothek kann es sich als viel schneller herausstellen, eine Schätzung für ein Minipaket von beispielsweise 100 zu berechnen, als eine Gradientenschätzung für ein Minipaket in einem Zyklus für 100 Trainingsbeispiele zu berechnen. Dies kann sich beispielsweise als nur 50-mal langsamer und nicht als 100 herausstellen.

Auf den ersten Blick scheint uns dies nicht viel zu helfen. Bei einer Mini-Paketgröße von 100 sieht die Trainingsregel für Gewichte folgendermaßen aus:

$$

$$w \rightarrow w' = w-\eta \frac{1}{100} \sum_x \nabla C_x \tag{100}$$

Hier geht die Summe über die Trainingsbeispiele im Minipaket. Vergleiche mit

$$

$$w \rightarrow w' = w-\eta \nabla C_x \tag{101}$$

für das Online-Lernen. Selbst wenn die Aktualisierung des Mini-Pakets 50-mal länger dauert, scheint Online-Training die beste Option zu sein, da wir häufiger aktualisiert werden. Nehmen wir jedoch an, dass wir im Fall des Mini-Pakets die Lerngeschwindigkeit um das 100-fache erhöht haben, dann wird die Aktualisierungsregel zu:

$$

$$w \rightarrow w' = w-\eta \sum_x \nabla C_x \tag{102}$$

Dies ähnelt 100 separaten Stufen des Online-Lernens mit einer Lerngeschwindigkeit von η. Ein Schritt beim Online-Lernen dauert jedoch nur 50-mal so lange. In der Realität sind dies natürlich nicht genau 100 Ebenen des Online-Lernens, da im Minipaket alle ∇C _x im Gegensatz zum kumulativen Lernen im Online-Fall für denselben Satz von Gewichten bewertet werden. Und doch scheint die Verwendung größerer Minipakete den Prozess zu beschleunigen.

Angesichts all dieser Faktoren ist die Auswahl der besten Mini-Pack-Größe ein Kompromiss. Wählen Sie zu klein und profitieren Sie nicht von guten Matrixbibliotheken, die für schnelle Hardware optimiert sind. Wählen Sie zu groß und aktualisieren Sie das Gewicht nicht oft genug. Sie müssen einen Kompromisswert auswählen, der die Lerngeschwindigkeit maximiert. Glücklicherweise ist die Wahl der Minipaketgröße, bei der die Geschwindigkeit maximiert wird, relativ unabhängig von anderen Hyperparametern (mit Ausnahme der allgemeinen Architektur). Um eine gute Minipaketgröße zu finden, ist es daher nicht erforderlich, diese zu optimieren. Daher ist es ausreichend, akzeptable (nicht unbedingt optimale) Werte für andere Hyperparameter zu verwenden und dann mehrere verschiedene Größen von Minipaketen zu versuchen, wobei η skaliert wird, wie oben angegeben.Erstellen Sie ein Diagramm der Genauigkeit der Bestätigung im Verhältnis zur Zeit (tatsächlich verstrichene Zeit, keine Epochen!) Und wählen Sie eine Minipaketgröße, die die schnellste Leistungsverbesserung bietet. Mit der ausgewählten Minipaketgröße können Sie andere Hyperparameter optimieren.

Wie Sie zweifellos bereits verstanden haben, habe ich in unserer Arbeit natürlich keine solche Optimierung durchgeführt. Bei unserer Umsetzung der Nationalversammlung wird ein schneller Ansatz zur Aktualisierung von Minipaketen überhaupt nicht verwendet. In fast allen Beispielen habe ich einfach die Mini-Paketgröße 10 verwendet, ohne sie zu kommentieren oder zu erklären. Im Allgemeinen könnten wir das Lernen beschleunigen, indem wir die Größe des Minipakets reduzieren. Ich habe dies insbesondere nicht getan, weil meine vorläufigen Experimente darauf hindeuteten, dass die Beschleunigung eher bescheiden sein würde. In praktischen Implementierungen möchten wir jedoch auf jeden Fall den schnellsten Ansatz zur Aktualisierung von Minipaketen implementieren und versuchen, deren Größe zu optimieren, um die Gesamtgeschwindigkeit zu maximieren.

Automatisierte Techniken

Ich habe diese heuristischen Ansätze als etwas beschrieben, das von Hand optimiert werden muss. Manuelle Optimierung ist ein guter Weg, um eine Vorstellung davon zu bekommen, wie NS funktioniert. Übrigens ist es nicht verwunderlich, dass bereits viel an der Automatisierung dieses Projekts gearbeitet wurde. Eine übliche Technik ist eine Rastersuche, bei der ein Raster systematisch im Raum der Hyperparameter gesiebt wird. Eine Übersicht über die Erfolge und Grenzen dieser Technik (sowie Empfehlungen zu einfach zu implementierenden Alternativen) finden Sie 2012 . Viele ausgefeilte Techniken wurden vorgeschlagen. Ich werde nicht alle überprüfen, aber ich möchte die vielversprechende Arbeit von 2012 zur Bayes'schen Optimierung von Hyperparametern erwähnen . Der Code von der Arbeit steht allen offen und mit einigem Erfolg wurde von anderen Forschern verwendet.

Fassen Sie zusammen

Mit den von mir beschriebenen Übungsregeln erzielen Sie mit Ihrem PS nicht die bestmöglichen Ergebnisse. Aber sie bieten Ihnen wahrscheinlich einen guten Ausgangspunkt und eine Grundlage für weitere Verbesserungen. Insbesondere habe ich Hyperparameter grundsätzlich unabhängig beschrieben. In der Praxis besteht eine Verbindung zwischen ihnen. Sie können mit η experimentieren, entscheiden, dass Sie den richtigen Wert gefunden haben, dann mit der Optimierung von λ beginnen und feststellen, dass dies Ihre η-Optimierung verletzt. In der Praxis ist es nützlich, sich in verschiedene Richtungen zu bewegen und sich allmählich guten Werten anzunähern. Denken Sie vor allem daran, dass die von mir beschriebenen heuristischen Ansätze einfache Übungsregeln sind, aber keine in Stein gemeißelten. Sie müssen nach Anzeichen dafür suchen, dass etwas nicht funktioniert, und Sie möchten experimentieren. Insbesondere,Überwachen Sie sorgfältig das Verhalten Ihres neuronalen Netzwerks, insbesondere die Genauigkeit der Bestätigung.

Die Komplexität der Auswahl von Hyperparametern wird durch die Tatsache verstärkt, dass das praktische Wissen über ihre Wahl über viele Forschungsarbeiten und -programme verteilt ist und häufig nur in den Köpfen einzelner Praktiker liegt. Es gibt eine Menge Arbeit mit Beschreibungen, was zu tun ist (oft im Widerspruch zueinander). Es gibt jedoch einige besonders nützliche Arbeiten, die einen großen Teil dieses Wissens zusammenfassen und hervorheben. In dem Joshua Benji von 2012 gibt praktische Ratschläge für die Verwendung von Backpropagation-Gradientenabfallsaktualisierung und Ausbildung für die Nationalversammlung, einschließlich der Nationalversammlung und tief. Benjio beschreibt viele Details viel detaillierter. Als ich, einschließlich einer systematischen Suche nach Hyperparametern. Ein weiterer guter Job ist die Arbeit.1998 Yanna Lekuna und andere. Beide Werke erscheinen in dem äußerst nützlichen Buch von 2012, das viele Tricks enthält, die in der Nationalversammlung häufig verwendet werden: " Neuronale Netze: Handwerkstricks ". Das Buch ist teuer, aber viele seiner Artikel wurden von ihren Autoren im Internet veröffentlicht und sind in Suchmaschinen zu finden.

Aus diesen Artikeln und insbesondere aus unseren eigenen Experimenten wird eines klar: Das Problem der Optimierung von Hyperparametern kann nicht als vollständig gelöst bezeichnet werden. Es gibt immer einen anderen Trick, mit dem Sie versuchen können, die Effizienz zu verbessern. Autoren haben das Sprichwort, dass ein Buch nicht fertiggestellt, sondern nur fallen gelassen werden kann. Gleiches gilt für die NS-Optimierung: Der Raum der Hyperparameter ist so groß, dass die Optimierung nicht abgeschlossen, sondern nur gestoppt werden kann und die NS den Nachkommen überlassen bleibt. Ihr Ziel ist es daher, einen Workflow zu entwickeln, mit dem Sie schnell eine gute Optimierung durchführen können und bei Bedarf detailliertere Optimierungsoptionen ausprobieren können.

Schwierigkeiten bei der Auswahl von Hyperparametern lassen einige Leute darüber klagen, dass NS im Vergleich zu anderen MO-Techniken zu viel Aufwand erfordern. Ich habe viele Varianten von Beschwerden gehört wie: „Ja, ein gut abgestimmter NS kann bei der Lösung eines Problems die beste Effizienz erzielen. Auf der anderen Seite kann ich eine zufällige Gesamtstruktur [oder SVM oder eine andere Ihrer Lieblingstechnologien] ausprobieren, und es funktioniert einfach. Ich habe keine Zeit herauszufinden, welche NA für mich richtig ist. " Aus praktischer Sicht ist es natürlich gut, einfach zu verwendende Techniken unter einem Freund zu haben. Dies ist besonders gut, wenn Sie gerade erst anfangen, mit einer Aufgabe zu arbeiten, und es ist immer noch unklar, ob das MO überhaupt helfen kann, sie zu lösen. Wenn es für Sie wichtig ist, optimale Ergebnisse zu erzielen, müssen Sie möglicherweise mehrere Ansätze ausprobieren, die spezialisierteres Wissen erfordern. Es wäre toll,Wenn MO immer einfach wäre, aber es gibt keine Gründe, warum es a priori trivial sein sollte.

Andere Techniken

Jede der in diesem Kapitel entwickelten Techniken ist für sich wertvoll, aber dies ist nicht der einzige Grund, warum ich sie beschrieben habe. Es ist wichtiger, sich mit einigen der Probleme vertraut zu machen, die im Bereich der NA auftreten können, und mit einem Analysestil, der helfen kann, diese zu überwinden. In gewisser Weise lernen wir, über die NS nachzudenken. Im Rest dieses Kapitels werde ich kurz eine Reihe anderer Techniken beschreiben. Ihre Beschreibungen werden nicht so tief sein wie in den vorherigen, aber sie sollten einige Empfindungen hinsichtlich der Vielfalt der Techniken vermitteln, die auf dem Gebiet der NA anzutreffen sind.

Variationen des stochastischen Gradientenabfalls

Der stochastische Gradientenabstieg durch Backpropagation hat uns beim Angriff auf das Problem der Klassifizierung handgeschriebener Zahlen von MNIST gute Dienste geleistet. Es gibt jedoch viele andere Ansätze zur Optimierung der Kostenfunktion, und manchmal zeigen sie eine Effizienz, die der des stochastischen Gradientenabfalls mit Minipaketen überlegen ist. In diesem Abschnitt beschreibe ich kurz zwei solche Ansätze, Hessisch und Momentum.

Hessisch

Lassen Sie uns zunächst die Nationalversammlung beiseite legen. Stattdessen betrachten wir einfach das abstrakte Problem der Minimierung der Kostenfunktion C vieler Variablen, w = w1, w2, ..., dh C = C (w). Nach dem Taylorschen Theorem kann die Kostenfunktion am Punkt w angenähert werden:

$$

$$C(w+\Delta w) = C(w) + \sum_j \frac{\partial C}{\partial w_j} \Delta w_j \nonumber \\ + \frac{1}{2} \sum_{jk} \Delta w_j \frac{\partial^2 C}{\partial w_j \partial w_k} \Delta w_k + \ldots \tag{103}$$

Wir können es kompakter umschreiben als

$$

$$C(w+\Delta w) = C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w + \ldots \tag{104}$$

wobei ∇C der gewöhnliche Gradientenvektor ist und H die als hessische Matrix bekannte Matrix anstelle von jk ist, in der ∂ ² C / ∂w _j ∂w _{k ist} . Angenommen, wir approximieren C, indem wir Terme höherer Ordnung aufgeben, die sich in der Formel hinter den Auslassungspunkten verstecken:

$$

$$C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w \tag{105}$$

Mit Algebra kann gezeigt werden, dass der Ausdruck auf der rechten Seite minimiert werden kann, indem Folgendes ausgewählt wird:

$$

$$\Delta w = -H^{-1} \nabla C \tag{106}$$

Streng genommen müssen wir davon ausgehen, dass die hessische Matrix eindeutig positiver ist, damit dies nur ein Minimum und nicht nur ein Extrem ist. Intuitiv bedeutet dies, dass Funktion C wie ein Tal ist, nicht wie ein Berg oder ein Sattel.

Wenn (105) eine gute Annäherung an die Kostenfunktion ist, sollten wir erwarten, dass der Übergang vom Punkt w zum Punkt w + Δw = w - H - 1∇C die Kostenfunktion signifikant reduzieren sollte. Dies bietet einen möglichen Algorithmus zur Kostenminimierung:

• Startpunkt w auswählen.
• Aktualisiere w auf einen neuen Punkt, w ′ = w - H ⁻¹ ∇C, wobei das Hessische H und ∇C in w berechnet werden.
• w' , w′′=w′−H′ ⁻¹ ∇′C, H ∇C w'.
• ...

In der Praxis ist (105) nur eine Annäherung, und es ist besser, kleinere Schritte zu unternehmen. Wir werden dies tun, indem wir w ständig um Δw = −ηH - 1∇C aktualisieren, wobei η die Lerngeschwindigkeit ist.

Dieser Ansatz zur Minimierung der Kostenfunktion wird als hessische Optimierung bezeichnet. Es gibt theoretische und empirische Ergebnisse, die zeigen, dass die hessischen Methoden in weniger Schritten auf ein Minimum konvergieren als ein Standardgradientenabstieg. Insbesondere durch die Einbeziehung von Informationen über Änderungen zweiter Ordnung in die Kostenfunktion ist es möglich, viele Pathologien zu vermeiden, die beim Gradientenabstieg im hessischen Ansatz auftreten. Darüber hinaus gibt es Versionen des Backpropagation-Algorithmus, mit denen der Hessische berechnet werden kann.

Wenn die hessische Optimierung so cool ist, warum verwenden wir sie dann nicht in unserer NS? Obwohl es viele wünschenswerte Eigenschaften hat, ist leider eines sehr unerwünscht: Es ist sehr schwierig, es in die Praxis umzusetzen. Ein Teil des Problems ist die enorme Größe der hessischen Matrix. Angenommen, wir haben eine NS mit 10 ⁷ Gewichten und Offsets. Dann gibt es in der entsprechenden hessischen Matrix 10 ⁷ × 10 ⁷ = 10 ¹⁴ Elemente. Zu viel! Infolgedessen stellt sich heraus, dass es in der Praxis sehr schwierig ist, H ⁻¹ ∇C zu berechnen . Das heißt aber nicht, dass es sinnlos ist, über sie Bescheid zu wissen. Viele Gradientenabstiegsoptionen sind von der hessischen Optimierung inspiriert, sie vermeiden einfach das Problem übermäßig großer Matrizen. Schauen wir uns eine solche Technik an, den Impulsgradientenabstieg.

Impulsbasierter Gradientenabstieg

Intuitiv besteht der Vorteil der hessischen Optimierung darin, dass sie nicht nur Informationen über den Gradienten enthält, sondern auch Informationen über seine Änderung. Der impulsbasierte Gradientenabstieg basiert auf einer ähnlichen Intuition, vermeidet jedoch große Matrizen aus zweiten Ableitungen. Um die Impulstechnik zu verstehen, erinnern wir uns an unser erstes Bild mit Gefälle, in dem wir einen Ball untersucht haben, der ein Tal hinunter rollt. Dann haben wir gesehen, dass der Gefälleabstieg entgegen seinem Namen nur geringfügig einer auf den Boden fallenden Kugel ähnelt. Die Impulstechnik ändert den Gradientenabstieg an zwei Stellen, wodurch er eher einem physischen Bild ähnelt. Zunächst führt sie das Konzept der „Geschwindigkeit“ für die Parameter ein, die wir optimieren möchten. Der Gradient versucht, die Geschwindigkeit zu ändern, nicht den "Ort" direkt, ähnlich wie physikalische Kräfte die Geschwindigkeit ändern.und nur indirekt den Standort beeinflussen. Zweitens ist die Impulsmethode eine Art Reibungsterm, der die Geschwindigkeit allmählich verringert.

Geben wir eine mathematisch genauere Definition. Wir führen die Geschwindigkeitsvariablen v = v1, v2, ... ein, eine für jede entsprechende Variable w _j (im neuronalen Netzwerk enthalten diese Variablen natürlich alle Gewichte und Verschiebungen). Dann ändern wir die Gradientenabstiegsaktualisierungsregel w → w ′ = w - η∇C auf

$$

$$v \rightarrow v' = \mu v - \eta \nabla C \tag{107}$$

$$

$$w \rightarrow w' = w+v' \tag{108}$$

In Gleichungen ist μ ein Hyperparameter, der das Ausmaß der Bremsung oder Reibung des Systems steuert. Um die Bedeutung der Gleichungen zu verstehen, ist es zunächst nützlich, den Fall zu betrachten, in dem μ = 1 ist, d. H. Wenn keine Reibung vorliegt. In diesem Fall zeigt die Untersuchung der Gleichungen, dass nun die „Kraft“ ∇C die Geschwindigkeit v ändert und die Geschwindigkeit die Änderungsrate w steuert. Intuitiv kann Geschwindigkeit gewonnen werden, indem ständig Gradientenelemente hinzugefügt werden. Dies bedeutet, dass wir eine ausreichend hohe Bewegungsgeschwindigkeit in diese Richtung erreichen können, wenn sich der Gradient während mehrerer Trainingsphasen in ungefähr eine Richtung bewegt. Stellen Sie sich zum Beispiel vor, was passiert, wenn Sie bergab fahren:



Mit jedem Schritt den Hang hinunter steigt die Geschwindigkeit und wir bewegen uns immer schneller zum Talboden. Dies ermöglicht es der Geschwindigkeitstechnik, viel schneller als beim normalen Gradientenabstieg zu laufen. Das Problem ist natürlich, dass wir, nachdem wir den Talboden erreicht haben, durch das Tal schlüpfen werden. Wenn sich der Gradient zu schnell ändert, kann sich herausstellen, dass wir uns in die entgegengesetzte Richtung bewegen. Dies ist der Punkt, an dem der Hyperparameter μ in (107) eingeführt wird. Ich habe vorhin gesagt, dass μ das Ausmaß der Reibung im System steuert. genauer gesagt muss das Ausmaß der Reibung als 1 & mgr; m vorgestellt werden. Wenn μ = 1 ist, gibt es, wie wir gesehen haben, keine Reibung, und die Geschwindigkeit wird vollständig durch den Gradienten ∇C bestimmt. Und umgekehrt, wenn μ = 0 ist, gibt es viel Reibung, es wird keine Geschwindigkeit gewonnen und die Gleichungen (107) und (108) werden auf die üblichen Gradientenabstiegsgleichungen w → w '= w - η∇C reduziert. In der PraxisDie Verwendung des Wertes von μ im Intervall zwischen 0 und 1 kann uns den Vorteil bieten, dass wir schneller werden können, ohne dass die Gefahr eines Minimums besteht. Wir können einen solchen Wert für μ unter Verwendung der ausstehenden Bestätigungsdaten auf die gleiche Weise wählen, wie wir die Werte für η und λ gewählt haben.

Bisher habe ich es vermieden, den Hyperparameter μ zu benennen. Tatsache ist, dass der Standardname für μ schlecht gewählt wurde: Er wird als Impulskoeffizient bezeichnet. Dies kann verwirrend sein, da μ dem Konzept des Impulses aus der Physik überhaupt nicht entspricht. Es ist viel stärker mit Reibung verbunden. Der Begriff „Impulskoeffizient“ ist jedoch weit verbreitet, daher werden wir ihn auch weiterhin verwenden.

Ein schönes Merkmal der Impulstechnik ist, dass fast nichts getan werden muss, um die Implementierung des Gradientenabfalls zu ändern und diese Technik in sie aufzunehmen. Wir können die Rückausbreitung nach wie vor verwenden, um Gradienten wie zuvor zu berechnen und Ideen wie das Überprüfen stochastisch ausgewählter Minipacks zu verwenden. In diesem Fall können wir einige der Vorteile der hessischen Optimierung anhand von Informationen über Gradientenänderungen nutzen. All dies geschieht jedoch ohne Fehler und mit nur geringfügigen Codeänderungen. In der Praxis ist die Impulstechnik weit verbreitet und beschleunigt häufig das Lernen.

Übungen

• Was wird schief gehen, wenn wir in der Impulstechnik μ> 1 verwenden?
• Was wird schief gehen, wenn wir in der Impulstechnik μ <0 verwenden?

Herausforderung

• Fügen Sie network2.py einen impulsbasierten stochastischen Gradientenabstieg hinzu.

Andere Ansätze zur Minimierung der Kostenfunktion

Es wurden viele andere Ansätze entwickelt, um die Kostenfunktion zu minimieren, und es wurde keine Einigung über den besten Ansatz erzielt. Wenn Sie sich eingehender mit neuronalen Netzen befassen, ist es hilfreich, sich mit anderen Technologien zu befassen, zu verstehen, wie sie funktionieren, welche Stärken und Schwächen sie haben und wie sie in die Praxis umgesetzt werden können. In der zuvor erwähnten Arbeit werden verschiedene solche Techniken vorgestellt und verglichen, einschließlich des gepaarten Gradientenabfalls und der BFGS-Methode (und auch der eng verwandten BFGS-Methode mit Speicherbeschränkung oder L-BFGS ). Eine weitere Technologie, die kürzlich vielversprechende Ergebnisse gezeigt hat .Dies ist Nesterovs beschleunigter Gradient, der die Impulstechnik verbessert. Ein einfacher Gradientenabstieg eignet sich jedoch gut für viele Aufgaben, insbesondere bei Verwendung des Impulses. Daher bleiben wir bis zum Ende des Buches beim stochastischen Gradientenabstieg.

Andere Modelle künstlicher Neuronen

Bisher haben wir unsere NS mit Sigmoid-Neuronen erstellt. Im Prinzip kann NS, das auf Sigmoidneuronen aufgebaut ist, jede Funktion berechnen. In der Praxis sind Netzwerke, die auf anderen Neuronenmodellen basieren, manchmal den Sigmoid-Modellen voraus. Je nach Anwendung können Netzwerke, die auf solchen alternativen Modellen basieren, schneller lernen, besser auf Verifizierungsdaten verallgemeinern oder beides tun. Lassen Sie mich einige alternative Modelle von Neuronen erwähnen, um Ihnen eine Vorstellung von einigen häufig verwendeten Optionen zu geben.

Die vielleicht einfachste Variante wäre ein Tang-Neuron, das eine Sigmoidfunktion durch eine hyperbolische Tangente ersetzt. Die Ausgabe eines Tang-Neurons mit der Eingabe x, einem Vektor der Gewichte w und einem Versatz b wird als angegeben

$$

$$\tanh(w \cdot x+b) \tag{109}$$

wo Tanh natürlich hyperbolische Tangente ist . Es stellt sich heraus, dass er sehr eng mit dem Sigmoid-Neuron verbunden ist. Denken Sie daran, dass tanh definiert ist als

$$

$$\tanh(z) \equiv \frac{e^z-e^{-z}}{e^z+e^{-z}} \tag{110}$$

Mit ein wenig Algebra ist das leicht zu erkennen

$$

$$\sigma(z) = \frac{1+\tanh(z/2)}{2} \tag{111}$$

Das heißt, Tanh skaliert nur das Sigmoid. Grafisch können Sie auch sehen, dass die Tanh-Funktion dieselbe Form wie das Sigmoid hat: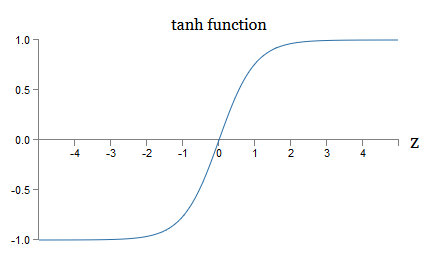



Ein Unterschied zwischen Tang-Neuronen und Sigmoid-Neuronen besteht darin, dass sich die Ausgabe der ersten von -1 bis 1 und nicht von 0 bis 1 erstreckt. Dies bedeutet Wenn Sie ein Netzwerk erstellen, das auf Tang-Neuronen basiert, müssen Sie möglicherweise Ihre Ausgaben (und, abhängig von den Details der Anwendung, möglicherweise die Eingaben) etwas anders normalisieren als in Sigmoid-Netzwerken.

Wie Sigmoid-Neuronen können Tang-Neuronen im Prinzip jede Funktion berechnen (obwohl es einige Tricks gibt) und Eingaben von -1 bis 1 markieren. Darüber hinaus lassen sich die Ideen der Rückausbreitung und des stochastischen Gradientenabfalls genauso einfach auf Tang anwenden -neurons sowie zu Sigmoid.

Übung

• Man beweise Gleichung (111).

Welche Art von Neuron sollte in Netzwerken, Tang oder Sigmoid verwendet werden? Die Antwort ist, gelinde gesagt, nicht offensichtlich! Es gibt jedoch theoretische Argumente und einige empirische Beweise dafür, dass Tang-Neuronen manchmal besser funktionieren. Lassen Sie uns kurz eines der theoretischen Argumente für Tang-Neuronen durchgehen. Angenommen, wir verwenden Sigmoid-Neuronen und alle Aktivierungen im Netzwerk sind positiv. Betrachten Sie die Gewichte w ^{l + 1} _jk, die für das Neuron Nr. J in der Schicht Nr. 1 + 1 enthalten sind. Backpropagation-Regeln (BP4) sagen uns, dass der damit verbundene Gradient gleich a ^l _k δ ^{l + 1} _{j ist} . Da die Aktivierungen positiv sind, ist das Vorzeichen dieses Gradienten dasselbe wie das von δ ^{l + 1} _j. Dies bedeutet, dass, wenn δ ^{l + 1} _j positiv ist, alle Gewichte w ^{l + 1} _jk während des Gradientenabfalls abnehmen, und wenn δ ^{l + 1} _j negativ ist, dann alle Gewichte w ^{l + 1} _jkerhöht sich während des Gefälles. Mit anderen Worten, alle mit demselben Neuron verbundenen Gewichte nehmen zusammen zu oder ab. Dies ist ein Problem, da Sie möglicherweise einige Gewichte erhöhen und andere reduzieren müssen. Dies kann jedoch nur passieren, wenn einige Eingabeaktivierungen unterschiedliche Vorzeichen haben. Dies legt die Notwendigkeit nahe, das Sigmoid durch eine andere Aktivierungsfunktion zu ersetzen, beispielsweise eine hyperbolische Tangente, die es ermöglicht, dass Aktivierungen sowohl positiv als auch negativ sind. Da tanh in Bezug auf Null symmetrisch ist, tanh (−z) = −tanh (z), kann man erwarten, dass Aktivierungen in verborgenen Schichten grob gesagt gleichmäßig zwischen positiv und negativ verteilt sind. Dies wird dazu beitragen, sicherzustellen, dass die Aktualisierungen der Skalen in die eine oder andere Richtung nicht systematisch verzerrt sind.

Wie ernst sollte dieses Argument genommen werden? Immerhin ist es heuristisch, liefert keinen strengen Beweis dafür, dass Tang-Neuronen Sigmoid-Neuronen überlegen sind. Vielleicht haben Sigmoidneuronen einige Eigenschaften, die dieses Problem kompensieren? In der Tat zeigte die Tanh-Funktion in vielen Fällen minimale bis keine Vorteile gegenüber dem Sigmoid. Leider haben wir keine einfachen und schnell implementierten Methoden, um zu überprüfen, welcher Neuronentyp schneller lernt oder sich bei der Verallgemeinerung für einen bestimmten Fall als effektiver erweist.

Eine andere Variante eines Sigmoidneurons ist ein gleichgerichtetes lineares Neuron oder eine gleichgerichtete lineare Einheit, ReLU. Die Ausgabe ReLU mit Eingabe x, dem Vektor der Gewichte w und Offset b wird wie folgt angegeben:

$$

$$\max(0, w \cdot x+b) \tag{112}$$

Die grafische Richtfunktion max (0, z) sieht folgendermaßen aus:



Solche Neuronen unterscheiden sich offensichtlich stark von Sigmoid- und Tang-Neuronen. Sie sind jedoch insofern ähnlich, als sie auch zur Berechnung einer beliebigen Funktion verwendet werden können, und sie können unter Verwendung von Rückausbreitung und stochastischem Gradientenabstieg trainiert werden.

Wann sollte ich ReLU anstelle von Sigmoid- oder Tang-Neuronen verwenden? In neueren Arbeiten zur Bilderkennung ( 1 , 2 , 3 , 4) In fast dem gesamten Netzwerk wurden schwerwiegende Vorteile der Verwendung von ReLU festgestellt. Wie bei Tang-Neuronen haben wir jedoch noch kein wirklich tiefes Verständnis dafür, wann genau welche ReLUs vorzuziehen sind und warum. Um sich ein Bild von einigen Problemen zu machen, denken Sie daran, dass Sigmoidneuronen nicht mehr lernen, wenn sie gesättigt sind, dh wenn die Ausgabe nahe 0 oder 1 liegt. Wie wir in diesem Kapitel oft gesehen haben, besteht das Problem darin, dass die σ'-Mitglieder den Gradienten verringern das verlangsamt das Lernen. Tang-Neuronen leiden unter ähnlichen Schwierigkeiten bei der Sättigung. Gleichzeitig wird eine Erhöhung der gewichteten Eingabe in ReLU niemals zu einer Sättigung führen, sodass keine entsprechende Verlangsamung des Trainings auftritt. Wenn andererseits die gewichtete Eingabe auf der ReLU negativ ist, verschwindet der Gradient und das Neuron hört überhaupt auf zu lernen.Dies ist nur ein paar der vielen Probleme, die es nicht trivial machen zu verstehen, wann und wie sich ReLUs besser verhalten als Sigmoid- oder Tang-Neuronen.

Ich habe ein Bild der Unsicherheit gemalt und betont, dass wir noch keine solide Theorie über die Wahl der Aktivierungsfunktionen haben. In der Tat ist dieses Problem noch komplizierter als ich beschrieben habe, da es unendlich viele mögliche Aktivierungsfunktionen gibt. Welches gibt uns das am schnellsten lernende Netzwerk? Welches ergibt die größte Genauigkeit bei den Tests? Ich bin überrascht, wie wenige wirklich gründliche und systematische Studien zu diesen Themen durchgeführt wurden. Idealerweise sollten wir eine Theorie haben, die uns detailliert erklärt, wie wir unsere Aktivierungsfunktionen auswählen (und möglicherweise im laufenden Betrieb ändern). Andererseits sollten wir nicht durch das Fehlen einer vollständigen Theorie aufgehalten werden! Wir haben bereits leistungsstarke Tools und können mit ihrer Hilfe erhebliche Fortschritte erzielen. Bis zum Ende des Buches werde ich Sigmoidneuronen als Hauptneuronen verwenden.da sie gut funktionieren und konkrete Illustrationen der wichtigsten Ideen im Zusammenhang mit der Nationalversammlung geben. Beachten Sie jedoch, dass dieselben Ideen auch auf andere Neuronen angewendet werden können und diese Optionen ihre Vorteile haben.

: , , ? ?

: , . , . . : , , ?

—

Einmal auf einer Konferenz über die Grundlagen der Quantenmechanik bemerkte ich, was wie eine lustige Sprachgewohnheit schien: Am Ende des Berichts begannen die Fragen des Publikums oft mit dem Satz: "Ich mag Ihren Standpunkt wirklich, aber ..." Quantengrundlagen sind nicht ganz mein übliches Fachgebiet, und ich habe auf diese Art des Fragens aufmerksam gemacht, weil ich mich auf anderen wissenschaftlichen Konferenzen praktisch nicht getroffen habe, damit der Fragesteller Sympathie für den Standpunkt des Sprechers zeigt. Zu dieser Zeit entschied ich, dass die Verbreitung solcher Fragen darauf hindeutete, dass Fortschritte bei den Quantengrundlagen erzielt wurden und dass die Menschen gerade erst anfingen, an Dynamik zu gewinnen. Später stellte ich fest, dass diese Einschätzung zu hart war. Die Redner hatten mit einigen der schwierigsten Probleme zu kämpfen, auf die der menschliche Geist jemals gestoßen ist. Der Fortschritt war natürlich langsam!Es war jedoch immer noch wertvoll, Nachrichten über das Denken der Menschen über diesen Bereich zu hören, auch wenn sie wenig bis gar nichts hatten.

In diesem Buch haben Sie möglicherweise eine „nervöse Zecke“ bemerkt, die dem Satz „Ich bin sehr beeindruckt“ ähnelt. Um zu erklären, was wir haben, habe ich oft auf Wörter wie „heuristisch“ oder „grob gesprochen“ zurückgegriffen, gefolgt von einer Erklärung eines bestimmten Phänomens. Diese Geschichten sind glaubwürdig, aber empirische Beweise waren oft recht oberflächlich. Wenn Sie die Forschungsliteratur studieren, werden Sie feststellen, dass Geschichten dieser Art in vielen Forschungsarbeiten über neuronale Netze erscheinen, oft in Begleitung einer kleinen Menge von Beweisen, die sie unterstützen. Wie verhalten wir uns zu solchen Geschichten?

In vielen Bereichen der Wissenschaft - insbesondere wenn einfache Phänomene betrachtet werden - kann man sehr strenge und verlässliche Beweise für sehr allgemeine Hypothesen finden. In der Nationalversammlung gibt es jedoch eine Vielzahl von Parametern und Hyperparametern, und es bestehen äußerst komplexe Beziehungen zwischen ihnen. In solch unglaublich komplexen Systemen ist es unglaublich schwierig, verlässliche allgemeine Aussagen zu treffen. Das Verständnis des NS in seiner ganzen Fülle, wie Quantengrundlagen, testet die Grenzen des menschlichen Geistes. Oft müssen wir auf Beweise für oder gegen mehrere bestimmte Einzelfälle einer allgemeinen Aussage verzichten. Infolgedessen müssen diese Aussagen manchmal geändert oder aufgegeben werden, wenn neue Beweise auftauchen.

Einer der Ansätze für diese Situation besteht darin, zu berücksichtigen, dass jede heuristische Geschichte über die NS eine gewisse Herausforderung beinhaltet. Betrachten Sie zum Beispiel die Erklärung, die ich zitiert habe, warum eine Ausnahme (Abbruch) von der Arbeit im Jahr 2012 funktioniert.: „Diese Technik reduziert die komplexe Gelenkanpassung von Neuronen, da sich ein Neuron nicht auf die Anwesenheit bestimmter Nachbarn verlassen kann. Am Ende muss er zuverlässigere Eigenschaften lernen, die bei der Zusammenarbeit mit vielen verschiedenen zufälligen Untergruppen von Neuronen nützlich sein können. “ Eine reichhaltige und provokative Aussage, auf deren Grundlage Sie ein ganzes Forschungsprogramm erstellen können, in dem Sie herausfinden müssen, was wahr ist, wo es falsch ist und was geklärt und geändert werden muss. Und jetzt gibt es wirklich eine ganze Branche von Forschern, die die Ausnahme (und ihre vielen Variationen) untersuchen und versuchen zu verstehen, wie sie funktioniert und welche Einschränkungen sie hat. So haben wir mit vielen anderen heuristischen Ansätzen diskutiert. Jeder von ihnen ist nicht nur eine mögliche Erklärung,aber auch eine Herausforderung für die Forschung und ein detaillierteres Verständnis.

Natürlich wird nicht eine Person genug Zeit haben, um all diese heuristischen Erklärungen gründlich genug zu untersuchen. Die gesamte Gemeinschaft von NS-Forschern wird Jahrzehnte brauchen, um eine wirklich leistungsfähige Theorie des NS-Trainings zu entwickeln, die auf Beweisen basiert. Bedeutet dies, dass es sich lohnt, heuristische Erklärungen als lasch und ohne Beweise abzulehnen? Nein!Wir brauchen eine Heuristik, die unser Denken anregt. Dies ähnelt der Ära großer geografischer Entdeckungen: Frühe Gelehrte handelten (und machten Entdeckungen) oft auf der Grundlage von Überzeugungen, die ernsthaft falsch waren. Später haben wir diese Fehler korrigiert und unser geografisches Wissen wieder aufgefüllt. Wenn Sie etwas schlecht verstehen - wie die Forscher die Geographie verstanden haben und wie wir die NS heute verstehen -, ist es wichtiger, das Unbekannte kühn zu studieren, als bei jedem Schritt Ihrer Argumentation gewissenhaft richtig zu sein. Daher sollten Sie diese Geschichten als nützliche Anweisungen betrachten, wie Sie über NS nachdenken, ein gesundes Bewusstsein für ihre Grenzen bewahren und die Zuverlässigkeit der Beweise in jedem Fall sorgfältig überwachen können. Mit anderen Worten, wir brauchen gute Geschichten für Motivation und Inspiration und sorgfältige gründliche Untersuchungen - umechte Fakten entdecken.