Physik und Wirtschaft. Gnoseologischer Unterschied und seine Manifestation in der IT

Ich bin aus der theoretischen Physik in die Welt der IT gekommen. Er war hauptsächlich in wirtschaftlichen Aufgaben tätig. Engagiert - dies: Analyse, TK, Aussage, Design, Programmierung. Natürlich habe ich die ganze Zeit die physischen und wirtschaftlichen Ansätze verglichen, um die Natur- bzw. Wirtschaftsgesetze zu verstehen. Ein bestimmter Standpunkt ist zu diesem Thema gereift. Über sie und wird diskutiert.

1. Über das Erkennen im Allgemeinen

Es gibt zwei Ansätze zur Erkenntnis:

Aristoteles 'Ansatz . Dies ist ein ganzheitlicher Ansatz und behandelt das Objekt als Black Box. Das Phänomen, das Objekt, wird in der gesamten Realität als Ganzes untersucht. Und die Realität sagt zum Beispiel, dass schwere Körper schneller zu Boden fallen als leichte; das ließ sich selbst ein sich bewegender Körper stoppt allmählich. Aristoteles 'Ansatz behandelt das Phänomen als integrale Realität, daher kann es als phänomenologisch bezeichnet werden.

Galileos Ansatz . Dies ist ein analytischer Systemansatz. Dies ist der Divide and Conquer-Ansatz. Das Phänomen, das Objekt, wird in seine Bestandteile zerlegt und jeder von ihnen wird separat untersucht, wobei vom Rest abstrahiert wird (Analyse). Dann können die resultierenden Bilder unter Berücksichtigung des Zusammenspiels der Komponenten zu einem zusammengefasst werden (Synthese). Zum Beispiel wird der Fall von Körpern als der Fall von Körpern in die Leere betrachtet. Und dort fallen sie mit der gleichen Beschleunigung. In Wirklichkeit verhindert die Reibung gegen Luft, dass sie gleichermaßen fallen. Nachdem wir diese Kraft separat untersucht haben, können wir das Ergebnis von Aristoteles erklären. Wenn wir uns von den Reibungskräften lösen, bewegt sich der sich bewegende Körper ohne anzuhalten. Und wenn wir die Reibungskraft berücksichtigen, erhalten wir das Ergebnis von Aristoteles. Galileos Ansatz führt sofort dazu, dass Kräfte untersucht werden müssen. Dies führt letztendlich zu einem kohärenten System der klassischen Physik.

Noch einmal zur Klarheit.

Aristoteles 'Ansatz . Es wird ein Phänomen untersucht: „Der Fall eines Körpers in der Luft auf den Boden“ - das F.-Phänomen. Wir nehmen verschiedene Körper und stellen fest, dass schwerere Körper schneller auf den Boden fallen als leichte.

Galileos Ansatz . Bei der Untersuchung des Phänomens F muss nicht nur das Gewicht berücksichtigt werden. Wir untersuchen den Fall in der Luft. Und ändern wir nicht nur das Gewicht, sondern auch die Luft. Versuchen wir, die Dichte so zu reduzieren, dass am Ende keine Luft mehr vorhanden ist. Dann stellen wir fest, dass alle Körper mit der gleichen Beschleunigung in die Leere fallen. Wir finden die Einflussparameter auf das Phänomen und versuchen, Bedingungen zu schaffen, unter denen nur ein Parameter von Bedeutung ist. Das liegt nicht in der Natur. Ein Physiker benötigt daher ein Labor, in dem er die Parameter variieren kann. Nachdem wir den Einfluss eines Parameters untersucht haben, können wir den Einfluss eines anderen Parameters untersuchen. Wir versuchen, die Komplexität des gesamten Ansatzes auf die Zusammensetzung einfacherer Ansätze zu reduzieren. Durch Variation der Form des fallenden Körpers können wir die Abhängigkeit der Reibungskraft von der Luft in Abhängigkeit von der Form des Körpers untersuchen. Durch Variation der Fallrate können wir die Abhängigkeit der Reibungskraft von der Geschwindigkeit erkennen. Durch Variieren der Fallhöhe können wir die Abhängigkeit der Beschleunigung von der Höhe erkennen. Durch Variation der geografischen Lage auf der Erde finden wir die Abhängigkeit der Beschleunigung des Sturzes von der Geografie.

Grob gesagt studieren sie in der Herangehensweise von Aristoteles die Realität, und in der Herangehensweise von Galileo studieren sie Abstraktionen, und von ihnen gelangen sie durch Synthese in die Realität.

2. Das Modell des physischen Wissens

Die Physik ist eine ideale Theorie für viele Wissenschaften, einschließlich der Wirtschaftswissenschaften. In physikalischen Experimenten werden diskrete Werteserien erhalten. Sie werden jedoch als Annäherung an kontinuierliche Funktionen angesehen, die in Wirklichkeit physikalische Indikatoren sind. Und Physiker versuchen, diese Funktionen zu erraten. Also vermutete Galileo die Parabel für die Flugbahn eines Steins, der in einem Winkel zum Horizont geworfen wurde. Kepler vermutete die Flugbahnen der Planeten - Ellipsen usw. Nachdem wir die Flugbahn erraten haben, erhalten wir einen Vorhersageapparat - die Fähigkeit, den Wert für unerforschte Koordinaten der Flugbahn zu berechnen. Zum Testen stellen sie ein Experiment auf - schaffen Sie die Bedingungen für das Experimentieren, um den interessierenden Wert zu erhalten. Nachdem wir den vorhergesagten und den experimentellen Wert verifiziert haben, erhalten wir eine Bestätigung oder Widerlegung der Theorie. Hier spielt manchmal der Fehler des experimentellen Fehlers eine wichtige Rolle. Physisches Wissen beruht auf der Identifizierung des Determinismus - dem Gesetz, einen Zustand aus einem Anfangszustand zu erhalten:

$$

$$S (t) = D (Q, S (0))$$

S(0) -   D –  – ,  S(t)  S(0) Q –       . ,  ,      . 

Also für einen geworfenen Stein von einem Punkt (0,0) mit einer Geschwindigkeit $$$v_0$in einem Winkel $$$α$bis zum Horizont haben wir

$$$$ Anzeige $$ x (t) = v_0 t cos⁡ (α), y (t) = v_0 t sin⁡ (α) - (gt ^ 2) / 2 $$ Anzeige $$

Der Anfangszustand S (0) wird durch drei Parameter eingestellt: Abfahrtspunkt (0,0), Anfangsgeschwindigkeit $$$v_0$Winkel $$$α$.
Die Auswirkung der Umgebung Q ist durch die Beschleunigung der Schwerkraft g gegeben. Bei Erweiterung des Problembereichs (hohe Anfangsgeschwindigkeit) ist g nicht mehr konstant.
Der Determinismus D ist durch die obige Formel gegeben.

Für eine realistischere Aufgabe muss die Reibung gegen die Luft berücksichtigt werden. Dies erschwert die Mathematik des Problems, aber das Prinzip bleibt dasselbe. Anstelle von Stein können Sie auch ein Flugzeug betrachten. Dann kommt die Schubkraft des Flugzeugs ins Spiel und ihre Regulierung durch den Piloten. Ein nicht-physischer Faktor erscheint ebenfalls - der Wille des Piloten. Wir können es nicht berücksichtigen. Aber wir wissen, dass es nicht unbegrenzt ist: Traktion kann nicht unendlich sein, Beschleunigung kann nicht unendlich sein. Dies bringt ein Element der Sicherheit in die Bewegung. Sie verwenden es zum Beispiel, um die Flugbahn einer Luftverteidigungsrakete aufzubauen.

Gehen wir zurück zum fliegenden Stein. Es zeichnet sich durch eine unendliche Anzahl physikalischer Parameter aus. Beispielsweise kann nur seine Form beliebig komplex sein. Wir sind uns jedoch sicher, dass wir den Stein in einem nützlichen Bereich als materiellen Punkt betrachten können. Dies ist die Hauptabstraktion der klassischen Mechanik. Alle Systeme werden als Sätze interagierender Materialpunkte dargestellt. Dies macht die hauptsächliche kognitive Reduktion - die Reduzierung des Verhaltens eines komplexen Systems auf das Verhalten seiner elementaren Komponenten.

Im Zusammenhang mit der erwähnten kognitiven Reduktion können zwei erkenntnistheoretische Ansätze unterschieden werden - Reduktionismus und Holismus.

3. Reduktionismus und Holismus

Reduktionismus ist das Prinzip, die Eigenschaften eines Systems von den Eigenschaften von Subsystemen und den Eigenschaften der Interaktion von Subsystemen zu reduzieren. Arbeitet erfolgreich in der Physik.
Betrachten Sie zum Beispiel Gas. Ohne es in Teilsysteme zu zerlegen, können wir mit experimentellen, phänomenologischen Konzepten arbeiten: Druck P, Temperatur T, Volumen V. Empirisch finden wir die Beziehung, die diese Parameter verbindet - die Zustandsgleichung des Gases:

$$

$$PV = constT$$

Dies ist die sogenannte phänomenologische Ebene - arbeiten Sie mit Phänomenen (Phänomenen), ohne auf deren Struktur einzugehen. Dies ist Aristoteles 'Ansatz.

Wenden Sie nun den Ansatz von Galileo an. Wir zerlegen das „Gas“ -System: Stellen Sie es sich als eine Ansammlung kollidierender Moleküle vor. Dann definieren wir P und T durch die mechanischen Parameter des Moleküls. Dies geschieht in der Molekularphysik. Daher reduzieren wir das Gassystem auf Teilsysteme von Molekülen. Dies wird die Zustandsgleichung klären oder für neue Systeme ableiten.

Dementsprechend haben wir in der Wirtschaft eine Analogie: Die Makroökonomie wird in Unternehmen und Haushalte zerlegt. Aber hier ist die Reduktion noch nicht perfekt. Leider gibt es kein wirtschaftliches Newton. Das Problem ist die Komplexität und Verfügbarkeit eines subjektiven Faktors, der nicht in der Physik liegt (obwohl es eine Debatte über die Rolle des Subjekts in der Quantenmechanik gibt).

Und jetzt zum Holismus.

Holismus ist das Prinzip, dass es in einem System nicht reduzierbare Eigenschaften geben kann. In der Biologie basiert die Lehre vom Vitalismus auf dem Konzept der Entelechie, der Lebenskraft, die dem gesamten Körper innewohnt und nicht reduzierbar ist.

Die Physik verzichtet bisher auf das Konzept des Holismus.

4. Formel- und Algorithmusmodelle

Ein Formelmodell ist ein durch eine Formel definiertes Modell. Das Konzept der "Formel" wird als bekannt angesehen.

Beispiele in der Physik: Newton-Gleichungen, Lagrange-Gleichungen, Maxwell-Gleichungen, Navier-Stokes-Gleichungen, Heisenberg-Schrödinger-Gleichungen, Einstein-Gleichungen.

Beispiele aus der Wirtschaft: Black-Scholes-Formel für den Optionspreis, Geldmengenformel, lineares Programmiermodell zur Optimierung des Finanzportfolios, Zinsberechnungsformeln, Risikoberechnungsformeln.

Mit einem Formelmodell kann eine Person ohne Computer arbeiten. Das ist fast alles reine Mathematik. Hier spielt der Algorithmus jedoch eine immer wichtigere Rolle. Die Lösung des Problems der vier Farben wurde also nicht auf eine Formel reduziert, sondern erforderte für viele Sonderfälle eine Brute-Force-Lösung. Diese Büste wurde von Computern gemacht.

Algorithmisches Modell - ein durch einen Algorithmus definiertes Modell, das möglicherweise nicht auf eine Formel reduziert werden kann. Natürlich ist es möglich, den Algorithmus als Formeln zu klassifizieren, aber dies sind nicht die gleichen klassischen Formeln. Das algorithmische Modell ist zunächst nur mit einem Computer realistisch
Ein formales Modell kann immer auf ein algorithmisches reduziert werden.

Ein Beispiel für das erste algorithmische Modell ist das Fermi-Pasta-Ulam-Problem. Hier ist ein Zitat aus Ulams Buch The Adventures of Mathematics.

Und hier ist ein Artikel über Habré, der über den aktuellen Stand des Fermi-Pasta-Ulam-Problems berichtet:
Mathematiker lösten das Fermi-Pasta-Ulam-Problem

5. Koordination

Mit Systemkoordination meine ich die Definition grundlegender Parameter, die im Prinzip die Entwicklung des Systems bestimmen. In der Mechanik eines Materialpunkts wird die Koordination beispielsweise definiert durch:

• Äußere Kraft F.
  
  • Masse m Materialpunkt
  • Raumkoordinaten (x, y, z) = r des Materialpunktes
  • Zeit t

Die Entwicklung des Systems ist durch die Newtonsche Gleichung gegeben

$$

$$(d ^ 2 r (t)) / (dt ^ 2) = (F (t)) / m$$

Wie ist die Koordination der wirtschaftlichen Einheit? Ich habe einmal an einem Business-Intelligence-System gearbeitet. Sein Hauptbegriff ist Indikator. Die Basis des Systems ist eine Scorecard. Hunderte von Indikatoren. Aber ich habe im Internet vergeblich nach einer Beschreibung der Basis von Indikatoren gesucht - einer Reihe von Indikatoren, die nicht auf andere reduziert werden können und die im Prinzip die Entwicklung einer wirtschaftlichen Einheit vollständig bestimmen. Das heißt, so wie ich es verstehe, wurde in der Wirtschaft keine Koordinierung vorgenommen. Daher ist es noch nicht möglich, über ein grundlegendes dynamisches Gesetz zu sprechen. Basierend auf der Verbindung von Indikatoren ist es nur möglich, eine Szenarioanalyse durchzuführen, um die Frage zu beantworten: "Was passiert mit den abgeleiteten Indikatoren, wenn sich die zugrunde liegenden Indikatoren entsprechend dem gegebenen Szenario ändern?"

6. Abstraktes Beispiel. Zeitreihenprognose wie Physik

Sie können das Prognoseproblem anhand der tatsächlichen Zeitreihen stellen: Wenn Sie eine Reihe von realen Werten haben, müssen Sie den vorhergesagten Wert des Indikators ermitteln - den Wert in der Zukunft. Dies impliziert eine Art versteckten Determinismus der Zeitreihen. Es gab viele wissenschaftliche und pseudowissenschaftliche Spekulationen zu diesem Thema. Ich selbst habe mich mit Wissenschaftsärzten befasst, die behaupteten, ihre Methodik würde es ihnen ermöglichen, eine Wechselkursprognose zu erhalten, und die entsprechenden Dissertationen mit allen möglichen Konfidenzintervallen und anderen Attributen der Verteilungsgesetze gezeigt. Aber als sie mit der Realität konfrontiert wurden, waren die Techniken weggeblasen.

Um eine Prognose zu erhalten, gehen Sie manchmal folgendermaßen vor:

1. Nehmen Sie die Echtzeitreihe {V (ti)}. Zeitplan - Schritt unterbrochene Linie.
2. Nehmen Sie eine stetige Funktion W (t), so dass W (ti) = V (ti). Das Diagramm ist eine kontinuierliche Kurve.
3. Es wird ein Polynom P (t) ausgewählt, das W (t) mit einem ausreichenden Genauigkeitsgrad approximiert. Ein Polynom kann für alle t berücksichtigt werden.
4. Dann haben wir eine Vorhersage für die zukünftige Zeit T: V (T) = P (T)
   All dies vermittelt den Eindruck von Wissenschaft, aber nur auf den ersten Blick. Ja, die Existenz eines approximierenden Polynoms für W (t) wird durch den Weierstrass-Satz aus der Matanalyse garantiert. Wir können W (t) beliebig genau polynomisieren. Es kann jedoch nicht für Vorhersagen verwendet werden.

Der ungefähre Wert für die reale Reihe beträgt 100% und der Vorhersagewert ist Null. Polynome können beliebig erfunden werden, aber sie geben alle unterschiedliche Vorhersagen.

Wenn Tag T eintrifft und wir das reale V (T) herausfinden, können wir für die Reihe {{V (ti)}, V (T)} ein neues Polynom Q (t) konstruieren, das diese Reihe beliebig genau approximiert, aber die Zeit T ist nicht mehr in Die Zukunft und Q (T) ist keine Prognose mehr, sondern Realität. Die Polynome P (t) und Q (t) müssen absolut nicht zusammenfallen und für die neue Vorhersagezeit T '> T zeigen sie unterschiedliche Ergebnisse. Das heißt, es gibt keine Prognose. Es scheint Wissenschaft zu geben, aber keine Prognose. Es ist wie eine mittelalterliche Theorie der Engel. Sie kann alles erklären, aber sie kann nichts vorhersagen.

Der Unterschied zwischen physikalischer Interpolation und Extrapolation aus wirtschaftlicher:

• Die Genauigkeit empirischer Daten : ungefähr in der Physik, genau in der Wirtschaft
• Domänenfunktionen : kontinuierlich in der Physik, diskontinuierlich, schrittweise in der Wirtschaft
• Empirische Daten : in der Physik diskret, in der Wirtschaft kontinuierlich mit diskreten Diskontinuitäten
• Grundgesetze : in der Physik dort. F = ma zum Beispiel; in der Wirtschaft noch

7. Wirtschaft und Physik

In der Wirtschaft sind reale Trajektorien - im Wesentlichen diskontinuierlich - stückweise konstante Funktionen. Beispielsweise kann der Indikator „Währungskurs“ jederzeit einen Sprung machen. Kontinuierliche wirtschaftliche Funktionen - Annäherungen zum Zwecke der Matanalyse (wenn Sie einen Hammer in der Hand haben, möchten Sie jedes Objekt wie einen Nagel betrachten ...). Jede Buchhaltungstransaktion führt zu Wertsprüngen von Indikatoren für Derivate von Konten. Und sie sind die Mehrheit der Indikatoren. Ferner ist jede Änderung der Anzahl der Arbeitnehmer diskret usw. Die Kontinuität der wirtschaftlichen Flugbahnen steht im Gegensatz zur Kontinuität der meisten physischen Flugbahnen. Daher ist der Apparat der Matanalyse nicht direkt auf wirtschaftliche Flugbahnen anwendbar.

Bild für die körperliche Wahrnehmung. Die Flugbahn eines Steins, der schräg zum Horizont geworfen wird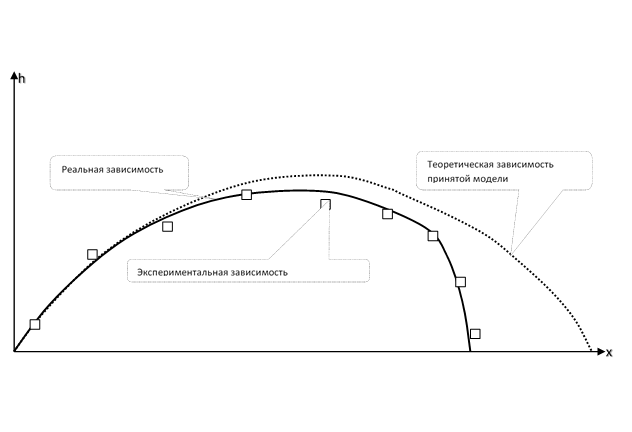

Bild für wirtschaftliches Wissen. Wechselkurs bei der Zentralbank.

Dies ist eine echte experimentelle exakte Funktion. Sie ist zu Zeitpunkten, zu denen sich der Wechselkurs ändert, diskontinuierlich.

In der Physik:

• Experimentelle physikalische Werte sind fast immer ungefähr
• Experimentelle physikalische Werte bilden eine diskrete Reihe.
• Eine experimentelle diskrete Reihe wird als Polygon für die kontinuierliche Approximation betrachtet, da die Realität kontinuierlich ist. Der Begriff der Kontinuität kann sich als Lüge auf kleinen räumlichen und zeitlichen Skalen herausstellen. Dann wird die Physik ihr Gesicht verändern.
• Gut definierte Basisindikatoren
• Theoretische und reale Trajektorien sind fast immer kontinuierlich und fast immer differenzierbar (die Trajektorie eines materiellen Punktes ist zeitlich immer zweimal differenzierbar).
• Aufgrund der Kontinuität der realen Dynamik und der realen Flugbahn hat ihre gute kontinuierliche Approximation Vorhersagekraft: In einer ausreichend kleinen Nachbarschaft wird die Funktion nicht weit von ihrem letzten realen Wert entfernt sein.

In der Wirtschaft:

• Experimentelle wirtschaftliche Werte können als genau angesehen werden. Nur in der Makroökonomie gibt es aufgrund der großen Anzahl von Geschäftseinheiten ein Genauigkeitsproblem.
• Experimentelle ökonomische Werte bestehen aus Konstanzintervallen, die zu bestimmten Zeitpunkten unterbrochen werden, wenn sich der Wert abrupt ändert
• Experimentelle Daten können nicht als Testgelände für die kontinuierliche Approximation angesehen werden, da die Realität diskontinuierlich ist.
• Nicht vollständig definierte Basisindikatoren. Es ist nicht klar, warum man tanzen soll.
• Aufgrund der Diskontinuität der realen Flugbahn garantiert eine beliebig gute kontinuierliche Annäherung keine Vorhersagen in einer beliebig kleinen Nachbarschaft.
• Reale Trajektorien sind fast immer diskontinuierlich. Dies bedeutet, dass die wirtschaftliche Bestimmung einen Ansatz erfordert, der sich von der klassischen Mechanik unterscheidet.
• In der Wirtschaft gibt es zunächst einen Faktor des freien Willens einer wirtschaftlichen Einheit. Seine Reichweite wird vom Staat geregelt. Die äußersten Grenzen dieser Freiheit:
  - Vollständige Freiheit in einem nicht staatlich regulierten Markt
  - Teilfreiheit in einem teilweise staatlich regulierten Markt
  - Völliger Mangel an Freiheit in einem vollständig zentralisierten Staat, in dem es keinen freien Markt gibt

Das ökonomische Wissen hat kein ähnliches Niveau wie die klassische Mechanik erreicht:

1. Die Elementarkomponenten der Art des Materialpunktes sind nicht definiert
2. Nicht definiertes Q (Umgebungsparameter), es ist nicht klar, was wichtig ist, was nicht wichtig ist,
3. ,
4. ; .

. – . – . ? , . . . . , – .

, . , , - .

8. IT

8.1.

. . . . , . . . . . . . , , . . … , . . , . . . , . . . . . . . . . . . – " . - "!? , . -1840( , ). . . , . , . , . , . . , , . (). . , , , : ", . ". ! . , , - .

8.2. -

. — . , , .. . . , . . – . , . , . – . . …

. . , . , , , . , . . . . . , - . . . . , : , . . . , , . . ? . . , .

. - , .

, , . , . . , .

. . . , . , . , : , . , . . .

, – Jump Processing. , . .

, . “ ”. , – . , , . – , . . , – .

8.3.

( ). . “”. . , . , . . – . . , . . . . , . . – . . , . … . ? , . , - . . . , . , , . . .

. , . , . , – . , . , – ( – ?).

8.4.

_{“ ”}

. () . . . , , . . , . . , , . . . – . , , . , . . , . Schön. . – . , . – . . , (, ). , . . , . . , , , . . . – . . . . . . . . . : , , , , , , , , … . 100 . ( , , ) . , ( , (SQL-) ). , . Das heißt, . . . , . . , : ”, . . . ”.

. , . , . : . , , .

. . . , , . . . . -.

() . , , ( ), . , . , – . , , , , , . . . , , . , “” “”. , “” “”. ? , .

: . . . , . . . . — . . : . : , …

. . , . . .

Zusammenfassung

, . . - . . — . Warum ist das so? .

: IT. .