Wir fahren mit der Berechnung der logischen Funktionen gemäß dem Diagramm für eine breitere Klasse von Verhaltensweisen fort. Wir betrachten zyklische autonome Verhaltensweisen, die nicht mehrere Signale enthalten (oder auf andere Weise: keine indizierten Ereignisse enthalten). Eine weitere Einschränkung: Der Einfachheit halber wird die Verbindung paralleler Zweige im OP nicht berücksichtigt. Wir betrachten nur eine Verbindung durch UND, dh ein Ereignis wird nur ausgelöst, wenn alle Vorgängerereignisse ausgelöst werden.
Wir werden STG verwenden, um das Verhalten zu beschreiben, jedoch mit zusätzlichen Einschränkungen. Für jeden Ort ist die Anzahl der Bögen, die ihn betreten und verlassen, genau gleich einem. Dementsprechend kann ein Ort mit ankommenden und ausgehenden Bögen als ein Bogen betrachtet werden, der zwei Ereignisse (Übergänge) verbindet. Dementsprechend bewegt sich die Markierung entlang von Bögen. Da Verhaltensweisen mit mehreren Signalen derzeit nicht berücksichtigt werden, sind Ereignisindizes verboten und werden nicht benötigt. Leere Ereignisse sind verboten. Die Situation ist auch verboten, wenn zwei in einem Ereignis enthaltene Bögen aus Ereignissen stammen, die nicht parallel zueinander sind (ein Sonderfall stammt aus demselben Ereignis). Dies dient dazu, Bögen zu entfernen, die keine semantische Last tragen. Der Rest wird unter dem Gesichtspunkt des STG-Verhaltens unter Berücksichtigung der oben genannten Einschränkungen als korrekt (normal, lebendig, sicher) angesehen. Das Verhalten enthält keine CSC-Konflikte.
Definition 1. Das Ereignis, in das der Bogen eintritt, ist eine Folge des Ereignisses, aus dem dieser Bogen austritt. Umgekehrt ist das Ereignis, aus dem der Bogen austritt, die Ursache für das Ereignis, in das dieser Bogen eintritt.
Definition 2. Ein Pfad - eine endlose Folge von Ereignissen - das Ergebnis von Änderungen in der Beschriftung eines Diagramms, beginnend mit einem bestimmten. Jedes Ereignis tritt unendlich oft in die Sequenz ein. Jeder solche Eintrag ist einzigartig.
Definition 3. Die Spur von Ereignis A ist der Pfad, auf dem alle Ereignisse entweder die direkte Folge von Ereignis A oder das Ergebnis des vorübergehenden Schließens der Beziehung der Folge von Ereignissen in Bezug auf Ereignis A sind. Die anfängliche Markierung für die Spur von Ereignis A wird wie folgt festgelegt. Wenn die Markierung willkürlich geändert wird, werden nach dem Auslösen von Ereignis A die Markierungen in den Ausgabebögen von Ereignis A festgelegt. Dann bewegen sich die restlichen Marker, bis die Bewegung der Marker unmöglich wird, ohne die Marker in den Ausgabebögen von Ereignis A freizugeben. Die resultierende Markierung ist die anfängliche Markierung für die Spur von Ereignis A.
Definition 4. Wir führen die Ordnungsrelation für drei Ereignisse (A, B, C) ein. Drei Ereignisse werden genau dann geordnet (geschrieben A> B> C), wenn für eine Spur von Ereignis A das erste Auftreten von Ereignis B in der Sequenz immer früher als das erste Auftreten von Ereignis C auftritt.
Bemerkung. Ereignis A kann parallel zu beiden Ereignissen B und C (oder nur C) sein, oder beide Ereignisse A und B können parallel zu Ereignis C sein.
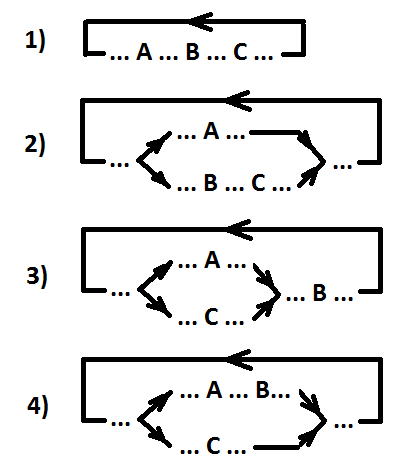
Standortoptionen für geordnete Ereignisse A, B und C (A> B> C).
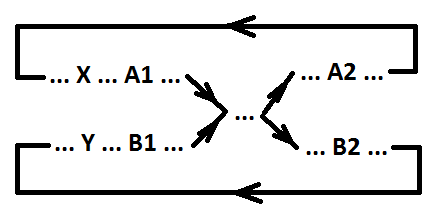
Definition 5. Das Signal b (Umschalten von B1 und B2) nimmt das Signal a (Umschalten von A1 und A2) in Bezug auf die Ereignisse X und Y (Ereignisse X und Y sind parallel oder fallen zusammen) auf, wenn die folgenden Bedingungen erfüllt sind:
1) X> A1> A2;
2) wenn Ereignis A2 parallel zu Ereignis X und nicht parallel zu Ereignis Y ist, dann ist X> A2> Y;
3) Y> B1> B2;
4) wenn Ereignis B2 parallel zu Ereignis Y und nicht parallel zu Ereignis X ist, dann ist Y> B2> X;
5) Y> B1> A2;
6) Wenn Ereignis A2 parallel zu Ereignis Y und nicht parallel zu Ereignis X ist, dann ist Y> A2> X.
Bemerkung 1. Die Bedingungen 1, 2 und 3, 4 bestimmen die Reihenfolge des Schaltens der Signale a bzw. b. Die Bedingungen 5, 6 spezifizieren die Reihenfolge des Fangereignisses B1 und des Fangereignisses A2.
Bemerkung 2. Ereignis X kann Ereignis A1 sein. In diesem Fall degenerieren die Bedingungen 1 und 2.
Bemerkung 3. Ereignis Y kann Ereignis B1 sein. In diesem Fall degenerieren die Bedingungen 3, 4 und 5.
Bemerkung 4. Ereignis X kann Ereignis A1 sein, und auch Ereignis B1 kann Ereignis Y sein. In diesem Fall degenerieren die Bedingungen 1, 2, 3, 4 und 5.
Nun beginnen wir zu überlegen, was ein Implantat ist. Der Implikant ist durch Ereignisse gekennzeichnet, durch die der Implikant seine Bedeutung ändert.
Definition 6. Ein Ereignis, bei dem der Implikant AND (OR) seinen Wert von 1 (0) auf 0 (1) ändert, nennen wir die rechte Grenze des Implikanten. Das diesem Ereignis entsprechende Signal wird als Einschalten bezeichnet. Der Implikant schaltet sich ein.
Definition 7. Ein Ereignis, bei dem das implizite AND (OR) seinen Wert von 0 (1) auf 1 (0) ändert, nennen wir den linken Rand des Implikanten. Das diesem Ereignis entsprechende Signal wird abgeschaltet. Der Implikant schaltet sich aus.
Definition 8. Ein Implikant, bei dem zwei rechte (oder zwei linke) Grenzen nicht parallel zueinander sind, wird als diskontinuierlich bezeichnet.
Vorerst werden unterbrochene Implantate nicht berücksichtigt. Wir werden auf ihre Betrachtung weiter unten zurückkommen.
Wir haben also: Alle rechten Ränder der Implikanten sind paarweise parallel zueinander, und die linken Ränder der Implikanten sind paarweise parallel zueinander.
Eine wichtige Eigenschaft. Der Implikant wird eingeschaltet, wenn mindestens ein Ereignis eintritt, nämlich der rechte Rand des Implikanten. Der Implikant wird nur ausgeschaltet, wenn alle Ereignisse auftreten, die die linken Grenzen des Implikanten darstellen.
Nun müssen die Eigenschaften der das Implantat bildenden Signale identifiziert werden.
Definition 9. Das im Implantat enthaltene Signal wird als Variable bezeichnet.
Die erste Eigenschaft von Variablen. Ein- und Ausschaltsignale sind variabel.
Die zweite Eigenschaft von Variablen. Für jede Schaltvariable (einer der Schalter ist der linke Rand des Implikanten L, der andere ist ein Ereignis X) muss ein Ereignis vorliegen - ein rechter Rand R desselben Implikanten ist so, dass entweder X und R dasselbe Ereignis oder R sind > X> L.
Die dritte Eigenschaft von Variablen. Für jede inklusive Variable (einer ihrer Schalter ist der rechte Rand des Implikanten R, der andere ist ein Ereignis X) muss es ein Ereignis geben - ein linker Rand L desselben Implikanten ist so, dass entweder X und L dasselbe Ereignis oder R sind > X> L.
Die vierte Eigenschaft von Variablen. Für jede Variable (Umschalten von X1 und X2), die nicht ein- oder ausgeschaltet wird, müssen zwei Ereignisse vorliegen: ein linker Rand des Implikanten L und ein rechter Rand des Implikanten R, so dass R> X1> L und R> X2> L. . Andernfalls könnte der Implikant in der Aus-Position keinen konstanten Wert halten.
Die fünfte Eigenschaft von Variablen. Für jedes Paar: eine Schaltvariable und eine Schaltvariable muss eine Folge von Variablen vorhanden sein, die sich relativ zu einigen rechten Rändern des Implikanten gegenseitig aufnehmen (bei verschiedenen Tonabnehmern können die rechten Ränder variieren), beginnend mit dieser Schaltvariablen und endend mit dieser Schaltvariablen . Andernfalls könnte der Implikant keinen konstanten Wert in der Ein-Position halten.
Sechste Eigenschaft von Variablen. Wenn für jede inklusive Variable a die rechte Grenze des Implikanten das Ereignis a + (a-) ist, wird eine solche Variable in die Aufzeichnung des Implikanten AND (OR) mit Inversion und in die Aufzeichnung des Implikanten OR (AND) ohne Inversion aufgenommen. Wenn für jede Schaltvariable a die linke Grenze des Implikanten das Ereignis a- (a +) ist, wird eine solche Variable in die Aufzeichnung des Implikanten AND (OR) mit Inversion und in die Aufzeichnung des Implikanten OR (AND) ohne Inversion aufgenommen.
Die siebte Eigenschaft von Variablen. Aufgrund der vierten Eigenschaft von Variablen gibt es für jede Variable a, die nicht ein- oder ausgeschaltet wird, eine rechte Grenze für die Implikanten R und eine linke Grenze für die Implikanten L, so dass R> a +> L und R> a-> L. Wenn R> a +> a-, dann tritt eine solche Variable mit Inversion in den Implikanten von Und und ohne Inversion in den Implikanten von OR ein. Wenn R> a-> a +, dann tritt eine solche Variable ohne Inversion in das implizite UND und in das implizite ODER mit Inversion ein.
Die sieben aufgelisteten Eigenschaften von Variablen sind notwendige Eigenschaften des Implikanten. Diese Eigenschaften reichen auch aus, um die Implantate zu beschreiben.
Bemerkung. Die obige Beschreibung des Implantats verbietet nicht die Situation, in der ein linker Rand des Implantats parallel zu einem rechten Rand desselben Implantats sein kann. Die Bedeutung dieses Phänomens besteht darin, dass ein solches Implantat in Abhängigkeit von der Geschwindigkeit paralleler Prozesse für die Implementierung des entsprechenden Signals in Echtzeit optional werden kann und sich in Echtzeit möglicherweise nicht ausschaltet (wenn die rechte Grenze früher als die linke Grenze arbeitet).
Nun werden wir betrachten, wie die normale Form einer logischen Funktion aus dem Implikanten aufgebaut wird.
Definition 10. Wenn sich das Implikant für einen bestimmten Zustand in der Aus-Position befindet (der Wert des Implantats AND (OR) ist 1 (0)), sagen wir, dass das Implikant diesen Zustand abdeckt.
Betrachten Sie ein bestimmtes Signal x, für das wir eine logische Funktion berechnen müssen. Um einen DNF (CNF) zu konstruieren, müssen AND (OR) -Implikanten alle Zustände abdecken, in denen die Funktion x 1 (0) ist. In diesem Fall ist es notwendig, dass keiner dieser UND (ODER) -Implikanten Zustände abdeckt, in denen die Funktion x 0 (1) ist. Bei der Berechnung logischer Funktionen müssen außerdem die Besonderheiten der Schaltkreise berücksichtigt werden: Implikanten sollten sich „überlappen“. Das heißt, wenn sich in einem bestimmten Zustand der Implikant einschalten kann (dh ein Ereignis, das die rechte Grenze dieses Implikanten darstellt, kann ausgelöst werden) und sich der Wert der Signalfunktion x während dieser Umschaltung nicht ändert, muss es einen anderen Implikanten geben, der diesen Zustand und abdeckt wird nicht eingeschaltet, wenn dieses Ereignis ausgelöst wird.
Jetzt müssen wir drei Fragen klären. Was ist ein Zustand in Bezug auf ein Diagramm? Wie bestimme ich die Zustände, in denen die Signalfunktion x 1 (0) ist? Wie kann man die Bedingungen bestimmen, die das Implantat abdeckt?
Beginnen wir mit den Staaten. Jede erreichbare Kennzeichnung ist Voraussetzung. Da es keine CSC-Konflikte gibt, entspricht jedes erreichbare Label einem eindeutigen Status (erreichbar). In unerreichbaren Zuständen ist der Wert der Funktion beliebig und es besteht keine Notwendigkeit, sie zu berücksichtigen. Somit wird jeder Zustand, den wir betrachten, durch die entsprechende Kennzeichnung eindeutig beschrieben. Die Position jedes Markers wird eindeutig durch den von ihm markierten Bogen bestimmt. Jeder Bogen ist eindeutig einem Paar (geordneter) Ereignisse zugeordnet: dem Ereignis, aus dem der Bogen austritt, und dem Ereignis, in das der Bogen eintritt. Somit wird jeder erreichbare Zustand eindeutig durch eine Menge beschrieben, die aus geordneten Ereignispaaren besteht.
Definition 11. Ein Ereignispaar, das einen markierten Bogen bezeichnet, wird {P, S} geschrieben, wobei P das Ursachenereignis und S das Folgeereignis ist.
Definition 12. MM wird die Menge der geordneten Paare {P, S} genannt, die einen erreichbaren Zustand beschreibt.
Bestimmen wir nun, für welche Zustände der Wert der Funktion x 1 und für welchen 0 ist. Die Ereignisse x + werden durch n Ereignisse A1, A2, ..., An und die Ereignisse x- durch m Ereignisse B1, B2, ..., verursacht. Bm.
Der Wert der Funktion x ist 1, wenn:
oder 1) für jedes i von 1 bis n gehört das Paar {Ai, x +} zur Menge MM;
oder 2) ein Paar {x +, S}, so dass x +> S> x- zur Menge MM gehört;
oder 3) ein Paar {P, S}, so dass x +> P> x- und x +> S> x- zur Menge MM gehören;
oder 4) ein Paar {P, x-}, so dass x +> P> x- zur Menge MM gehört und i von 1 bis m existiert, so dass das Paar {Bi, x-} nicht zur Menge MM gehört.
Der Wert der Funktion x ist 0, wenn:
oder 1) für jedes i von 1 bis m gehört das Paar {Bi, x-} zur Menge MM;
oder 2) ein Paar {x-, S}, so dass x-> S> x + zur Menge MM gehört;
oder 3) ein Paar {P, S}, so dass x-> P> x + und x-> S> x + zur Menge MM gehören;
oder 4) ein Paar {P, x +}, so dass x-> P> x + zur Menge MM gehört und es i von 1 bis n gibt, so dass das Paar {Ai, x +} nicht zur Menge MM gehört.
Jetzt finden wir heraus, welche Bedingungen das Implantat abdeckt. Der Implikant habe n linke Grenzen L1, L2, ..., Ln und m rechte Grenzen R1, R2, ..., Rm.
Der Implikant deckt den durch die Menge MM beschriebenen Zustand nicht ab, wenn mindestens eines der zur Menge MM gehörenden Paare {P, S} die folgende Bedingung erfüllt: Es gibt i von 1 bis n und j von 1 bis m, so dass
entweder 1) Li und S sind das gleiche Ereignis und Rj> P> Li,
oder 2) Rj und P sind das gleiche Ereignis und Rj> S> Li,
oder 3) Rj> P> Li und Rj> S> Li.
Diese Aussage gilt aufgrund der fünften Eigenschaft von Variablen.
Der Implikant deckt den durch die Menge MM beschriebenen Zustand ab, wenn für keines der zur Menge MM gehörenden Paare {P, S} die folgende Bedingung erfüllt ist: Es gibt i von 1 bis n und j von 1 bis m, so dass
entweder 1) Li und S sind das gleiche Ereignis und Rj> P> Li,
oder 2) Rj und P sind das gleiche Ereignis und Rj> S> Li,
oder 3) Rj> P> Li und Rj> S> Li.
Diese Aussage trifft aufgrund der zweiten, dritten und vierten Eigenschaft von Variablen zu.
Im übertragenen Sinne deckt ein Implikant den Zustand ab, wenn sich alle Marker zwischen der linken und rechten Grenze des Implikanten befinden. Befindet sich mindestens ein Marker außerhalb dieser Grenzen, deckt das Implantat diesen Zustand nicht ab.
Jetzt haben wir ein Werkzeug zur Berechnung normaler Formen (es ist immer noch nicht klar, es gibt jedoch immer noch eine Frage mit intermittierenden Implantaten). Wir sind jedoch an minimalen Normalformen interessiert (unter Berücksichtigung der Besonderheiten der Schaltung). Bevor wir fortfahren, kehren wir zur Betrachtung intermittierender Implikanten zurück. Betrachten Sie den I-Implikanten für das DNF-Signal x (der Fall mit dem OR-Implikanten für CNF ist ähnlich). Angenommen, die beiden linken Grenzen derselben Implikanten L1 und L2 sind nicht parallel zueinander und L1> L2> x- (der Fall für zwei rechte Grenzen wird ähnlich betrachtet). Dann muss es zwei rechte Grenzen der Implikanten R1 und R2 geben, so dass für Paare von L1 und R2 und L2 und R1 die zweite, dritte, vierte und fünfte Eigenschaft der Variablen erfüllt sein muss. Wenn es eine linke Grenze L3 parallel zu L1 gibt, müssen für das Paar L3 und R2 auch die obigen Eigenschaften erfüllt sein (ähnlich, im Fall der Existenz entsprechender Grenzen Implikanten, die parallel zu den Grenzen L2, R1 und R2 sind). Da jedoch nicht mehrere Signale verwendet werden, muss es einen nicht diskontinuierlichen Implikanten mit den Grenzen L1 und R2 geben (und mit parallelen entsprechenden Grenzen, falls einer der unterbrochenen Implikanten sie hatte). Darüber hinaus besteht der nicht-diskontinuierliche Implikant aus weniger Variablen und deckt alle Zustände ab, die vom diskontinuierlichen Implikanten abgedeckt werden, für den die Signalfunktion x den Wert 1 hat. Daher die Schlussfolgerung: Diskontinuierliche Implikanten sind keine Extremale und können nicht zur Berechnung von Minimalfunktionen verwendet werden.
Mehr zur Berechnung von Minimalfunktionen im nächsten Teil.