Stadt ohne Stau

Kapitel zwei
( Link zum ersten Kapitel )

Die Kunst, Straßennetze zu gestalten

Verkehrsprobleme der Stadt mit den Augen einer Person aus der Informatik

Wenn mir ein Artikel mit dem Titel „Die Kunst, Straßennetze zu entwerfen“ empfohlen würde, würde ich sofort fragen, wie viele Straßennetze unter Beteiligung des Autors gebaut wurden. Ich muss zugeben, meine berufliche Tätigkeit war weit vom Straßenbau entfernt und wurde kürzlich mit dem Entwurf von Mikroprozessoren in Verbindung gebracht, bei denen ich unter anderem mit dem Ressourcenverbrauch der Datenvermittlung befasst war. So kam es, dass mein Tisch genau gegenüber dem Panoramafenster stand, das von morgens bis abends von Horizont zu Horizont einen schönen Blick auf den langen Abschnitt des Wolgograd Highway und einen Teil des dritten Transportrings mit seinen endlosen Staus eröffnete. Und dann, eines Tages, wurde mir plötzlich klar: „Verdammt, denn die Komplexität des Datenwechselprozesses, mit dem ich auf einem Chip zu kämpfen habe, sollte genau den Schwierigkeiten entsprechen, auf die der Fluss von Autos im Netz von Straßenstraßen stößt.“
Wahrscheinlich war es nur ein Blick von außen und die Anwendung von Methoden, die für das untersuchte Gebiet nicht traditionell waren, die mir die Möglichkeit gaben, die Ursache von Staus zu verstehen und Empfehlungen zur Überwindung ihres Problems in der Praxis abzugeben.

Was ist die Neuheit des Ansatzes?

Historisch gesehen wird der Hauptzweck von Straßen als die Möglichkeit angesehen, schnell lange Strecken (zwischen Rom und den Provinzen) zurückzulegen. Ein solches Urteil ist gerechtfertigt, wenn es um das Intercity-Autobahnnetz auf Bundesebene geht: Die Städte, die sie verbinden, sehen aus wie kleine seltene Punkte auf dem Atlas, und die meisten Autos, die zwischen diesen Städten fahren, fahren ihren Weg, ohne irgendwo abzubiegen.

Es ist jedoch nur erforderlich, mehrere Seiten umzublättern und eine detaillierte Karte einer Großstadt zu öffnen, da sich das Bild sofort ändert: Allein die Adressen, an denen die Reise begonnen oder abgeschlossen werden kann, sind bereits etwa zehntausend, alle ziemlich dicht und relativ klein. Gleichzeitig können Hunderttausende von Autos gleichzeitig auf den Straßen einer solchen Stadt in Bewegung sein. Darüber hinaus besteht das Ziel eines jeden von ihnen nicht nur darin, bereits leere Straßen zu füllen, sondern eine Person oder Fracht von einem Punkt mit einer bestimmten Adresse " X " zu einem Punkt mit einer bestimmten Adresse zu bewegen. " Y ". Alles in allem bedeutet dies, dass das städtische Verkehrssystem angepasst werden muss, um das Problem der mehrfachen parallelen Adressierung effektiv zu lösen . Dadurch werden die Funktionen des städtischen Verkehrssystems dem Telefon- oder Computernetz noch ähnlicher als dem innerstädtischen Straßennetz.

Das Straßennetz als Vermittlungsschema für einen Hardwareentwickler oder -ingenieur auf dem Gebiet der Informationstransfertechnologien zu betrachten, ist eine völlig natürliche Art, über ein Problem zu sprechen, aber unter den an der Erforschung von Verkehrsproblemen beteiligten Personen ist diese Ansicht meines Wissens neu.

Die Theorie der Signalumschaltung ist eine enge Ingenieurwissenschaft, und sie allein reicht natürlich nicht aus, um eine separate Straße oder Straßenkreuzung zu planen oder das Verhalten eines Verkehrsstroms auf einem geraden, isolierten Abschnitt einer Autobahn vorherzusagen. Glücklicherweise sind die oben aufgeführten Probleme heute gut erforscht, und die zu ihrer Lösung entwickelten Methoden wurden bereits erfolgreich eingesetzt. Die Theorie des Wechsels wiederum ermöglicht es dem Architekten, das Risiko zu beseitigen, wenn alle Elemente des Straßennetzes perfekt ausgeführt sind und die Stadt immer noch in einen Zustand des Verkehrszusammenbruchs gerät. Dieses Risiko besteht, weil die gleichzeitige gleichzeitige Adressierung ressourcenintensiv ist.
zeitaufwändige Aufgabe, deren Schlüssel zu einer wirksamen Lösung nicht so sehr die Breite der Straßen und die Bequemlichkeit der Verkehrsknotenpunkte ist, sondern die kompetente Wahl des jeweiligen Vermittlungsschemas, das das vorgeschlagene Straßennetz umsetzen wird.

Anhand dieser Arbeit erfahren Sie beispielsweise, warum die in modernen Städten noch häufig genutzten „arteriellen“ Verkehrsnetze „schlecht“ sind und mit dem Bevölkerungswachstum zwangsläufig zu Staus führen. Ein weiteres interessantes Ergebnis, das gut mit den Beobachtungen übereinstimmt, erklärt, warum der Ausbau von Straßen allein, wenn zuvor alle Staus ausschließlich in der Nähe von Kreuzungen auftraten, die Situation wahrscheinlich nicht verbessern wird, selbst wenn die Anzahl der Autos in der Stadt gleich bleibt.

Als ich diesen Artikel schrieb, war es mir wichtig, dass er für den gewöhnlichsten Architekten verständlich war und durch seine Arbeit nützlich sein konnte. Ich habe versucht, den Leser in einer einfachen Sprache in Schaltprobleme einzuführen, um Kriterien zu entwickeln, anhand derer beurteilt werden kann, wie gut ein bestimmtes Straßennetz die Aufgabe der parallelen Adressierung bewältigen kann. Anhand von Modellbeispielen habe ich gezeigt, wie dieses Wissen in der Praxis eingesetzt werden kann.

Der Artikel richtet sich an einen breiten Kreis von Lesern, die mit dem universitätsweiten Mathematikkurs und der Theorie der Algorithmen ein wenig vertraut sind und bereit sind, sich 1 bis 5 Tage damit zu befassen.

Trennung und Zusammenlegung von Automobilströmen

Für viele Fahrer ist die Beobachtung offensichtlich, dass Verkehrsschwierigkeiten hauptsächlich an den Stellen der Straße auftreten, an denen Autos aus irgendeinem Grund gezwungen sind, die Spur zu wechseln. Beispiele hierfür sind Gabeln, Verengungen, Kreuzungsbereiche und Zufahrtsstraßen zu Autobahnen, Abschnitte einer Autobahn, auf denen einige Fahrspuren durch einen Unfall oder eine Straßenreparatur blockiert sind.
In diesem Abschnitt wird versucht, eine quantitative Beschreibung der in solchen Fällen ablaufenden Prozesse zu geben, und wir werden zunächst verstehen, wie Autos von einer Spur zur anderen rekonstruiert werden.

Zwei Strategien zum Wiederaufbau in einer benachbarten Reihe

Die Bewegung des Verkehrs entlang der Autobahn hat eine natürliche Unebenheit: Jemand fährt lieber etwas schneller, jemand etwas langsamer, der Abstand zwischen einem Auto nimmt ab und wird für das Fahren kaum komfortabler, während er zwischen den anderen so stark zunimmt, dass Autos hineinpassen können von benachbarten Fahrspuren. Das Auftreten solcher Lücken im Fluss der benachbarten Fahrspur direkt auf der Seite des zufälligen Fahrers kann häufig oder nicht sehr häufig sein. Wenn in dem Moment, in dem er ein Manöver durchführen muss, keine Lücke besteht, kann der Fahrer auf mindestens zwei Verhaltensstrategien zurückgreifen:

Strategie Nr. 1
Mehrere geeignete Lücken können einfach in der Nähe ihres Standorts angeordnet sein. Wenn die Bewegung dicht genug ist, ist es unwahrscheinlich, dass der Fahrer in der Lage ist, die Geschwindigkeit zu erhöhen und die erforderliche Lücke zu erreichen. Verlangsamen Sie jedoch die Bewegung ein wenig und lassen Sie den benachbarten Strom sich selbst überholen, um die ursprünglich zurückliegende Lücke auszugleichen - es wird keine großen Probleme geben. Die Kosten dieser Strategie liegen auf der Hand: Der Fahrer selbst und die Autos, die auf seiner Fahrspur zurückfahren, verlieren aufgrund der Notwendigkeit, die Geschwindigkeit zu reduzieren, einige Zeit.

Strategie Nr. 2
Um zu warten, müssen Sie Geduld haben und die notwendige Zeit dafür haben. Eine Alternative kann ein Versuch sein, das notwendige Manöver "hier" und "jetzt" durchzuführen. Nach dieser Idee gibt der Fahrer den Autos hinter ihm ein Zeichen für den Streifen, in dem er sich bewegen wird. Diejenigen wiederum, die auf sein Signal reagieren, sollten etwas langsamer fahren und vorwärts "loslassen", wobei sich die vor ihnen fahrenden Autos in ihrem Fluss bilden, wodurch die Lücke die erforderliche Größe erhält. Die Zeitkosten werden in diesem Fall auf die Autos der Fahrspur verteilt, auf der der Fahrer schließlich umgebaut hat.

Im wirklichen Leben sind beide Strategien gleichzeitig involviert: Erstens verlangsamt sich der Fahrer, wartet auf eine relativ große Lücke im Strom der benachbarten Fahrspur und gibt erst dann den darin fahrenden Autos ein Signal über ihre Absicht, ein Wiederaufbaumanöver durchzuführen.

Natürlich sind Eingänge, Rampen und Verengungen nicht der einzige Grund für den Spurwechsel, der bei der Gestaltung von Straßen berücksichtigt werden sollte. Die Fähigkeit von Autos mit höheren Geschwindigkeiten, den gemächlichen Verkehr zu überholen, ist erforderlich, damit sich die Situation auf der Autobahn nicht zu einer großen Warteschlange verschlechtert, die mit der Geschwindigkeit des langsamsten Traktors kriecht. Das Problem der Koexistenz von Fahrzeugen, die sich mit unterschiedlichen Geschwindigkeiten auf der Straße bewegen, ist jedoch etwas anderer Natur und kann von den in diesem Artikel behandelten Themen getrennt werden, da der Überholprozess und die damit verbundenen Umlagerungen keine erzwungenen Fahreraktionen sind, bei denen er sich beeilen muss . Wenn Zeit zum Warten bleibt, ist es nach der Wahrscheinlichkeitstheorie eine bequeme Gelegenheit, ein Manöver durchzuführen, das dem Fahrer selbst überlassen bleibt, und dies beeinträchtigt nicht unbedingt die Bewegung anderer Autofahrer.

Kosten für einen Zug
Das Verhalten der Fahrer in der Realität kann sehr schwierig sein, aber es ist für uns zunächst wichtig, dass das unter Modellbedingungen erzielte Ergebnis plausibel bleibt: Jede erzwungene Bewegung eines Autos von einer Spur zur anderen führt zu einer vorübergehenden Strafe für die Verkehrsteilnehmer.

Lassen Sie uns nun bewerten, wie viel Zeit von der Dichte der Autos auf der Straße abhängt.

Wir werden die Bewegung entlang jeder Spur als separaten Strom betrachten. Beim Versuch, einen bequemen Abstand zu Autos zu halten, die sich auf derselben Spur befinden, reservieren die Fahrer dabei einen Teil einer bestimmten charakteristischen Länge d im Strom. Lassen Sie ρ Autos pro Längeneinheit in einen Strom fallen. Wir stimmen zu, die Flussdichte klein zu nennen oder dasselbe zu sagen, dass ρ klein ist, wenn das Produkt ρ × d viel kleiner als eins ist.

In dem Moment, in dem der Fahrer erkennt, dass er in die nächste Reihe wechseln muss, ist die Wahrscheinlichkeit, dass der Abschnitt der Menge d , den er dort einnehmen würde, nicht frei ist, bei kleinem ρ ungefähr proportional zu ρ selbst. Wenn das beschriebene Ereignis tatsächlich stattfindet, werden insgesamt zwei Autos, die um einen Platz kämpfen, infolge von Manövern eine gewisse Verzögerung des durchschnittlichen konstanten Wertes δ erfahren.

Unter der Annahme, dass ρ klein ist, kann die Wahrscheinlichkeit, dass ihre Aktionen in diesem Moment die Bewegung anderer Autos beeinflussen, vernachlässigt werden. Somit ist in der ersten Ordnung der Kleinheit in Bezug auf ρ der Zeitverlust aus einer Bewegung α ⋅ ρ , wobei der Koeffizient α eine empirisch messbare Größe ist, abhängig von Kultur, Wetter, Geschwindigkeitsgrenzen (usw.), aber lokal zeitlich und für ungefähr konstant bleibt diese Stadt als Ganzes.

Die Intensität der Verluste auf dem Gelände vor dem Ausgang
Die Autos, die zum Kongress fahren, bevor sie die Rampe erreichen (Abb. 2), müssen in der angrenzenden Reihe rechts manchmal sogar mehrmals rekonstruiert werden. Jedes dieser Manöver macht es schwierig, sich zu bewegen, und infolgedessen ist die Durchschnittsgeschwindigkeit in dem Abschnitt vor der Ausfahrt merklich niedriger als in den Abschnitten „Transit“ (ohne Ausfahrten, „Einfahrten“ und Gabeln) der Autobahn.


Abb. 2

Um einen Teil des Weges mit einer niedrigeren Geschwindigkeit zu passieren, müssen die Fahrer (und ihre Passagiere) eine zusätzliche Zeit auf der Reise verbringen. Mit anderen Worten, der Bereich der Autobahn direkt neben der Rampe ist ein ständiger Erzeuger vorübergehender Verluste.

Angenommen, die durchschnittliche Maschinengeschwindigkeit ν und die Flussdichte ρ an der Frontalgrenze dieses Bereichs sind für alle Bänder gleich.

Nehmen wir außerdem an, dass die Dichte ρ und die Durchflussrate q, die den Ausgang verlassen (die durchschnittliche Anzahl von Autos, die pro Zeiteinheit auf die Rampe fahren), gleichzeitig klein sind und s die Anzahl von Fahrspuren auf der Autobahn ist. Um zum Ausgang zu gelangen, führt der Fahrer 1 bis s Wiederherstellungsmanöver durch. Wenn die Flussdichte auf der Rampe viel niedriger als ρ ist , kostet ihn nur das letzte Manöver praktisch "kostenlos", während der Rest in jedem Fall Verluste von α ⋅ ρ verursacht . Im Durchschnitt müssen Sie (0 + 1 + 2 + ... + s - 1) / s = ( s - 1) / 2 "teure" Manöver ausführen.

Angesichts der Schwierigkeiten, die durch alle Autos verursacht werden, die zum Kongress fahren, können wir die Formel für die Intensität vorübergehender Verluste aufschreiben:

I _out = q ⋅ α ρ ⋅ ( s - 1) / 2 = ( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 - 1 / s )

Der Wert p = ( sρν ) ist nichts anderes als die Durchflussrate aller Autos, die sich entlang der Autobahn in die betreffende Richtung bewegen (die durchschnittliche Anzahl von Autos, die pro Zeiteinheit an der Säule vorbeifahren). Die letzte Bemerkung gibt uns die Möglichkeit, die Formel für I in einer symmetrischeren Form umzuschreiben:

I _out = ( α / 2 ν ) ⋅ pq ⋅ (1 - 1 / s )

Verlustrate am angrenzenden Abschnitt der Zufahrtsstraße
Die Situation auf der Autobahn hinter dem Ort, an dem die Zufahrtsstraße mit ihr verbunden ist, wiederholt weitgehend die Situation auf dem Gelände vor dem Kongress, obwohl es einige Unterschiede gibt.
Lassen Sie einen kleinen Strom von Kraftfahrzeugen q durch die seitliche Rampe in den Hauptverkehr der Autobahn strömen (Abb. 3).


Abb. 3

Die Rampe hat nur eine begrenzte Länge, daher sollten alle neu ankommenden Autos wohl oder übel in die rechte Spur der Autobahn eingebaut werden. Infolgedessen ist die Verkehrsdichte auf der Fahrspur ganz rechts lokal höher als der Durchschnitt auf der Straße, sodass einige der Fahrer beschließen, die Fahrspur in eine weniger belebte benachbarte Reihe auf der linken Seite zu wechseln, was wiederum bereits in der zweiten zu einer lokalen Erhöhung der Dichte führt Streifen. Dieser Prozess der Interband-Migration wird fortgesetzt, bis die Flussdichte über die gesamte Breite der Autobahn ausgeglichen ist. Unter der Annahme, dass die Durchschnittsgeschwindigkeit ν für alle n Bänder gleich ist, können wir erwarten, dass nach Abschluss der Migrationsprozesse die Strömungsleistung in jedem von ihnen um genau (1 / s ) ⋅ q zunimmt.

Um zu sehen, wie viel eine solche „Rochade“ für die Fahrer kostet, berechnen wir zunächst die Leistung aller Migrationsströme. Die Strömung von der Rampe zur ersten Spur der Autobahn kennen wir bereits: Sie ist gleich q . Um ein Gleichgewicht in Form einer Erhöhung von (1 / s ) ⋅ q zu erhalten , sollte der Fluss in die zweite Spur von der Seite der ersten bereits (1 - 1 / s ) ⋅ q sein , von der zweiten in die dritte - (1 - 2 / s ) ⋅ q , von der k-ten Seite zur ( k + 1) -ten - (1 - k / s ) ⋅ q . Nach der letzten Formel beträgt die Leistung des Migrationsflusses zur Spur ganz links (1 - ( s - 1) / s ) ⋅ q = (1 / s ) ⋅ q , wie vom gesunden Menschenverstand vorgegeben.

Da wir die Zeitstrafe einer einzelnen Rekonstruktion und die Leistung aller Migrationsströme kennen, können wir nun die Gesamtintensität der von ihnen verursachten Verluste berechnen:

I _in = α ρ ⋅ q + α ρ ⋅ (1 - 1 / s ) ⋅ q + α ρ ⋅ (1 - 2 / s ) ⋅ q + ... + α ρ ⋅ (1 / s ) ⋅ q =

α ρ q (1 + 2 + ... + s ) / s =

α ρ q ( s + 1) / 2 =

( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 + 1 / s ).

Wenn wir uns noch einmal daran erinnern, dass sρν die Kraft p des Flusses aller Autos entlang der Autobahn ist, erhalten wir die Kostenformel in ihrer endgültigen Form:

I _in = ( α / 2 ν ) ⋅ pq ⋅ (1 + 1 / s ).

Symmetrische Gabelverlustrate
In den vorhergehenden Absätzen haben wir Verluste durch die Wechselwirkung von Strömungen festgestellt, von denen einer notwendigerweise groß und der andere notwendigerweise klein war. Um den Ansatz zur Lösung von Problemen zu demonstrieren, wenn die Kapazitäten beider Flüsse in ihrer Größe vergleichbar sind, betrachten wir ein weiteres Extrem: eine Gabel, in der beide „Tochter“ -Richtungen bei Fahrern gleichermaßen beliebt sind (Abb. 4).


Abb. 4

Der Einfachheit halber werden Autos, die auf der Gabelung nach rechts fahren, als "blau" und Autos, die nach links fahren, als "rot" bezeichnet. Anfänglich bewegen sich Autos beider "Farben" gemischt und verteilt auf alle zwei Fahrspuren der Autobahn. Wenn sie sich der Kreuzung nähern, driften die roten Autos langsam in Richtung der linken n Fahrspuren und die blauen in Richtung der rechten Fahrspur: Die Migration fließt in beide Richtungen zwischen benachbarten Fahrspuren. Im Gegensatz zum Beispiel der Zufahrtsstraße sind diese Ströme nicht mehr „relativ klein“. Übrigens gibt es nur zwischen den beiden zentralen Fahrspuren einen erzwungenen Verkehrsaustausch, dessen Intensität in einer der Richtungen (von links nach rechts oder von rechts nach links) einem Viertel der Leistung des gesamten Stroms entspricht, der sich entlang der Autobahn von Autos bewegt. Glücklicherweise gibt es in dieser Situation eine gute Möglichkeit, die generierten Kosten abzuschätzen. Erstens stellen wir fest, dass der Prozess der Aufteilung von Autos in „rot“ und „blau“ höchstwahrscheinlich lange vor der Gabelung beginnt und langsam verläuft. Daher sollte er einerseits nur geringe Auswirkungen auf die Verkehrsdichte in einer separaten Reihe haben und andererseits die Migration bewirken Strömungen, die sich über große Entfernungen erstrecken, bieten die Möglichkeit, jede von ihnen als eine Kombination einer großen Anzahl von Strömungen mit geringer Leistung darzustellen (Abb. 5).


Abb. 5

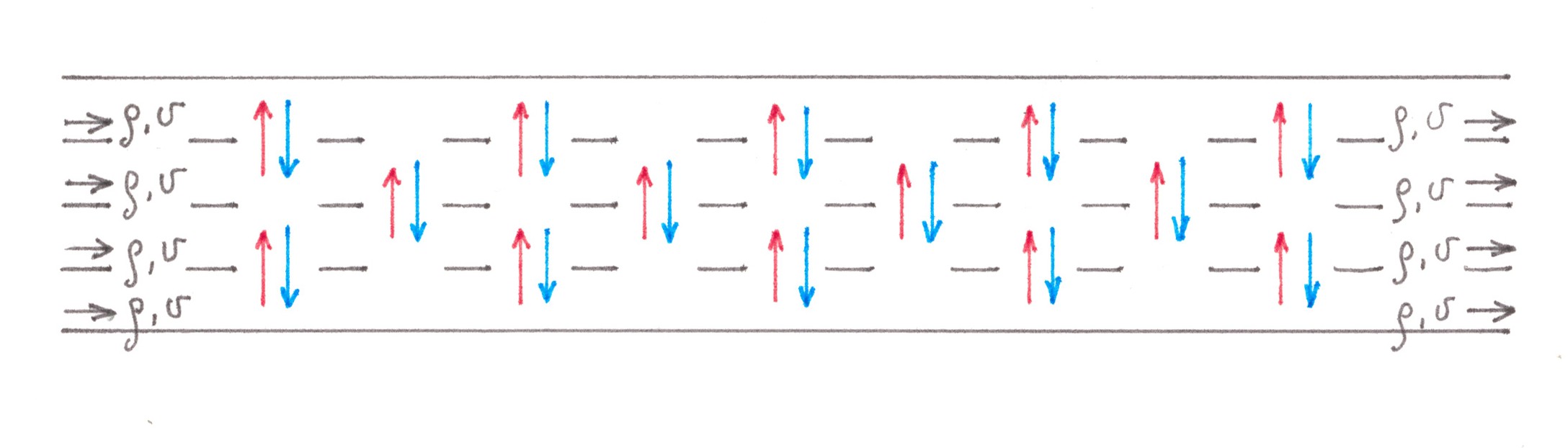
Da es sich jetzt um kleine Ströme handelt, wenn auch in größerer Anzahl, hindert uns nichts daran, das betrachtete Problem auf bereits gelöste zu reduzieren. Teilen Sie die Autobahn in der Mitte mental in zwei gleiche Teile und verbinden Sie sie dann mit einer großen Anzahl einspuriger Überbrückungsstraßen, sodass rote Autos auf die linke Seite und blaue Autos auf die rechte Seite gelangen (Abb. 6). Aufgrund der offensichtlichen Symmetrie können wir uns bei der Berechnung der erzeugten Verluste auf Maschinen jeder Farbe konzentrieren, z. B. Blau, und am Ende nur das Ergebnis verdoppeln.


Abb. 6

Lassen Sie also Geschwindigkeit ν und Dichte ρ für alle Fahrspuren gleich sein und bleiben Sie in dem gesamten Bereich, in dem Autos durch Farben getrennt sind, konstant.In diesem Fall beträgt die Durchflussrate aller Autos, die sich entlang der Autobahn bewegen ,:

p = 2 sρv . Q ₁ , q ₂ , ... q _m

bezeichnen die Ströme blauer Autos, die sich entlang imaginärer Springer zur rechten Hälfte der Autobahn bewegen. Angenommen, kurz vor der Trennstelle in jeder Fahrspur der Autobahn werden beide Farben mit gleichen Anteilen von 50% dargestellt, was impliziert, dass insgesamt q ₁ + q ₂ + ... + q _m gleich sρv / 2 sind, was p / 4 ist. Vom Strom erzeugte Verluste q


_i kann aufgrund seiner Kleinheit nach folgender Formel berechnet werden:

I _i =I _out +I _in = (α/ 2ν)⋅(p/ 2)⋅ q _i (1 - 1 /s) + (α/ 2ν)⋅(p/ 2)⋅ q _i (1 + 1 /s) = (α/ 2ν)p q _i

Summieren des letzten Ausdrucks über alleiFinden, der Verlust nur blaue Autos erzeugt:

I _blau = ( α / 2 ν ) ⋅ p ⋅ ( q ₁ + q ₂ + ... + q _m ) = ( α / 2 ν ) p ² /4 ist .

Vollständiger Verlust, wie bereits erwähnt, wird verdoppelt und die Menge doppelt so:

Ich _div = ( α / 2 ν ) p ² /2.

Analyse der erhaltenen Formeln
Wenn wir die Intensität I trennenDas heißt, die Zeit, die die Gesamtteilnehmer pro Sekunde durch die Menge des Seitenflusses q verloren haben , die per Definition gleich der Anzahl der Autos ist, die den Verkehr auf der Autobahn in einer Sekunde verbinden oder verlassen. Wir erhalten die durchschnittlichen Verluste, die von einem solchen Auto erzeugt werden:

i _in = I. _in / q = ( α / 2 ν ) ⋅ p ⋅ (1 + 1 / s )

i _out = I _out / q = ( α / 2 ν ) ⋅ p ⋅ (1 - 1 /s ) Das

vielleicht wichtigste in diesen Formeln ist die direkte Proportionalität zwischen dem Leistungsfluss von Autos auf der Autobahn p und den Stückkosten i . Alles sieht so aus, als würde ein Auto nachfahren wollen oder umgekehrt - um den Fluss der Hauptbewegung zu verlassen und so jedem Fahrer in der Nähe ständigen Schaden zuzufügen.

Die zweite interessante und sehr unerwartete Beobachtung betrifft den äußerst schwachen Effekt auf die Intensität der erzeugten Verluste der Anzahl der Fahrspuren in der Nähe der Autobahn direkt neben der Kreuzung. Wie Sie sehen können , ist der Kongress bei Betrachtung der Formel für I _out im Allgemeinen der billigste für eine einspurige Straße ( s = 1, d.h. _out = 0), und die Schwierigkeiten, die durch die angrenzende Zufahrtsstraße für eine dreispurige und eine sechsspurige Autobahn verursacht werden, unterscheiden sich nur um

100% ⋅ [(1 + 1/3) - (1 + 1/6)] / (1 + 1/3) = 12,5%.

Wenn wir berücksichtigen, dass jedes Auto, das jemals in den Verkehr auf der Autobahn eingetreten ist, es irgendwann verlassen muss, erscheint es rechtmäßig,den einheitlichen Wert i _av = ( i _in + i _in anstelle von i _in und i _{out zu verwenden)} ) / 2 = ( α / 2 ν ) ⋅ p .



Trotz des Fehlens einer expliziten Abhängigkeit von der Anzahl der Fahrspuren in der Formel für i _av muss daran erinnert werden, dass seine Schlussfolgerung (siehe die Annahmen für I _in und I _out ) stark von der Annahme einer geringen Dichte von Autos auf der Straße abhängt, so dass es unwahrscheinlich ist, dass zufriedenstellende Ergebnisse erzielt werden angewendet auf eine zu schmale Autobahn mit zu viel Verkehr.

Vorläufige Ergebnisse
In Gebieten in der Nähe von Kreuzungen kommt es unweigerlich zu Verkehr, der den Fahrern Zeit nimmt, die Durchschnittsgeschwindigkeit verringert. Letzteres führt zu einer Erhöhung der Fahrzeugdichte und infolgedessen zu einem möglichen Auftreten von Staus. Die mit der Trennung und Zusammenlegung von Automobilströmen verbundenen Zeitkosten werden als Umschaltung bezeichnet.

Verluste ähnlicher Art treten auf die eine oder andere Weise in jedem Vermittlungsschema auf: sei es ein Telefon- oder Computernetzwerk, ein Mehrkern-Mikroprozessor oder ein Postzustelldienst.

Wenn sich ein Fahrer dem Verkehr auf der Autobahn anschließt oder umgekehrt verlässt, sind die durch seine Handlungen verursachten Umstellungskosten proportional zur Leistung des zu diesem Zeitpunkt auf der Autobahn beobachteten Strom von Autos.

Um die Schaltverluste in der ganzen Stadt zu verringern, muss das in der Entwurfsphase implementierte Straßennetz sorgfältig abgewogen werden. Etwas später werden wir diese Aufgabe im Detail analysieren, aber einige offensichtliche Empfehlungen können jetzt aufgelistet werden:

1. Schaltverluste sind proportional zur Durchflusskapazität auf der Autobahn - es ist nicht erforderlich, die Straßen ohne Notwendigkeit zu vergrößern, zwei kleine Autobahnen sind doppelt so gut wie eine große;
2. Schaltverluste sind proportional zur Leistung der Seitenströme - es lohnt sich, das Netzwerk so zu gestalten, dass der Fahrer während seiner Fahrt so oft wie möglich zur Seite drehen musste;
3. Die gegenseitigen Störungen, die die Fahrer des Haupt- und des Nebenstroms zueinander verursachen, sollten im gesamten Stadtgebiet kleiner werden, wenn Sie versuchen, Routen zu vermeiden, die sich nur in einem kurzen Abschnitt der Strecke in einem Strom überschneiden.

Wirtschaftliche Voraussetzungen für die Existenz von Städten.
Stadtmodell mit einheitlichem Zugang

Vielleicht ist das erste, was ein Projekt zur Planung (oder Neuplanung) des Stadtverkehrssystems startet, zu versuchen, festzustellen, welche Art von Migration die Stadt jetzt wirklich braucht und wie sich ihre Bedürfnisse in Zukunft ändern werden.

Eine solche Analyse kann durchgeführt werden, wenn Sie die Stadt zuerst in nicht zu große, aber nicht zu kleine Gebietszonen unterteilen und dann für jedes Paar solcher Zonen angeben, welche ungefähre Anzahl von Fahrten zur einen oder anderen Seite die Einwohner zu dem einen oder anderen Zeitpunkt benötigen des Tages. Wenn Sie die gemachten Vorhersagen in eine quadratische Tabelle einfügen, erhalten Sie eine Matrix der Migrationsbedürfnisse der Stadtbewohner.

Für diese Matrix lohnt es sich dann, nach einem Netzwerk zu suchen, das es Fahrern und Fahrgästen ermöglicht, so wenig Zeit wie möglich auf einer separaten Reise zu verbringen und von den Stadtbehörden so wenig Ressourcen wie möglich für ihren Bau zu benötigen.

Wenn es um bestehende Städte geht, ist es hier wichtig, keinen Fehler zu machen und die Anzahl der Reisen, die Menschen wirklich benötigen, nicht durch die Anzahl der Reisen zu ersetzen, die historisch unter dem Einfluss einiger Hindernisse oder Schwierigkeiten zum Zeitpunkt der Entwurfsarbeit eingerichtet wurden. Wahrscheinlich kann das Berliner Verkehrsnetz „vor“ und „nach“ dem Fall der Trennmauer das auffälligste Beispiel für das Gesagte sein.

Dieser Abschnitt befasst sich hauptsächlich mit humanitären Fragen, auf die ich kein Spezialist bin, aber ich denke, dass es korrekter ist, sie als Amateur zu diskutieren, als das Problem einfach zu vermeiden.

Um die Migrationsbedürfnisse der Bevölkerung besser darzustellen, lohnt es sich, mit der grundlegenden Frage zu beginnen: „Warum brauchen Städte wirklich und welche nützliche Funktion erfüllen sie?“ .

Versuchen wir, dies nicht als normale Bewohner von Städten (und Dörfern) zu beantworten, sondern aus der Perspektive der Person, die für den Urbanisierungsprozess in einem großen und entwickelten Staat verantwortlich ist. Unter diesem Gesichtspunkt ist es nicht mehr wichtig, welche historischen Motive einst so viele Menschen auf ein winziges Stück Land drängten oder warum sie es jetzt weiterhin tun, es ist wichtig - welche wirtschaftlichen Auswirkungen Städte der einen oder anderen Größe und für was schaffen Aufgrund welcher Mechanismen wird dieser Effekt erzielt.

Meiner Meinung nach ist der Hauptgrund für die Existenz von Großstädten einerseits die Möglichkeit für Technologieunternehmen, Mitarbeiter seltener Berufe zu finden, und andererseits die Möglichkeit für Menschen, die seltene Berufe beherrschen, ihre Dienstleistungen zu wettbewerbsfähigen Bedingungen an an ihnen interessierte Unternehmen zu verkaufen. In einer kleinen (nicht spezialisierten) Stadt ist die Produktion vieler Waren und Dienstleistungen entweder einfach unmöglich oder versetzt die Technologieunternehmen und ihre Mitarbeiter, die sie umsetzen, in die Position gegenseitiger Geiseln, ohne dem einen oder anderen Alternativen zu geben.

Nehmen Sie zum Beispiel den nicht so seltenen Beruf eines Literaturlehrers. Laut Statistik werden sie benötigt: ungefähr 1 Lehrer pro 1000 Einwohner. In einer regulären Schule unterrichten 3-4 Personen Literatur. Die Wahl eines Arbeitsplatzes für einen Literaturlehrer kann als wettbewerbsfähig bezeichnet werden, wenn es in seiner Stadt mindestens 4-5 weiterführende Schulen gibt, die in Bezug auf die Bevölkerung etwa 15.000 Einwohner haben.

Anscheinend fühlen sich Menschen mit einer technischen Spezialität auf dem Arbeitsmarkt in Städten mit mindestens 100.000 Einwohnern wohl. Natürlich gibt es auch solche Berufe, deren Nachfrage nur in Städten mit einer Million Einwohnern auftritt, aber der wirtschaftliche Sinn von mehreren Millionen Städten bleibt mir ein Rätsel.

Nach alledem sehen zwei Hypothesen ziemlich motiviert aus (deren Gültigkeit jedoch die Wahrheit des Hauptinhalts des Artikels nicht beeinflusst):

1. Bei den häufigsten Reisen muss ein durchschnittlicher Erwachsener über Entfernungen reisen, die 4-5 der für ihn vielversprechendsten Jobs erfassen.
2. Für einen bedeutenden Teil der Bevölkerung, der die seltenen und wirtschaftlich wertvollsten Berufe besitzt, kann die Entfernung der häufigsten Reisen durchaus mit dem Radius der Stadt vergleichbar sein.

Als verstärkte Reflexion der Hypothesen 1) und 2) werde ich in meinen Beispielen häufig das Modell der Stadt mit „einheitlichem Zugang“ verwenden, vorausgesetzt, dass die Kraft der geforderten Reiseströme zwischen zwei Vierteln davon oder mit anderen Worten in allen Zellen der Matrix gleich ist Migrationsbedürfnisse sind die gleiche positive Zahl wert. Wenn Sie sich zufällig Aufzeichnungen über Reisen ansehen, die tagsüber in einer solchen Stadt unternommen wurden, haben alle Viertel für die nächste markierte Reise die gleichen Chancen, der Beginn dieser Reise zu sein und als Ende zu dienen, und es besteht keine Beziehung zwischen der Position des „Anfangs“ und des „Endes“. »Viertel sollten nicht beachtet werden.

Einfache Netzwerktopologie Netzwerke

Versuchen wir, die in den vorhergehenden Absätzen beschriebenen Ideen auf einige Arten von Stadtplänen anzuwenden, die aus dem Leben stammen.

Lineare Stadt
Die ersten großen Siedlungen entstanden überwiegend entlang der Küste, in Gebieten eines dünnen Landstreifens zwischen dem Meer und den Klippen oder entlang der Wege stark befahrener Straßen, so dass sie im Zuge des Wachstums enge, längliche Grenzen erlangten. Viele dieser Siedlungen haben bis heute überlebt, ihre längliche Form beibehalten und sich in moderne Städte verwandelt (Abbildung unten).


(abgelegenes Gebiet von Rio de Janeiro, Autor unbekannt)

Oft gibt es in einer solchen Stadt nur eine breite Straße, um die sie gebaut wird. Angenommen, jedes Viertel (Zone der territorialen Teilung) erzeugt einen Strom von Reisen mit einer einzigen Kapazität aller dieser Viertel - n , und die Stadt selbst folgt dem Migrationsmodell des „einheitlichen Zugangs“.


Abb. 7

Versuchen wir für die oben aufgeführten Bedingungen herauszufinden, wie sich die durchschnittliche Reisezeit und die erforderliche Straßenfläche mit zunehmendem n ändern.

Lassen Sie also alle Viertel die gleiche Form und Größe haben und ihre Anzahl erhöht sich um das λ (Lambda) -fache. Offensichtlich

• Die Länge der Hauptstraße erhöht sich um den Faktor λ .

Aufgrund des angenommenen Modells des „einheitlichen Zugangs“ enden 50% der Fahrten, die in der rechten Hälfte der Stadt begannen, in der linken Hälfte (genau das Gegenteil). Mit einer Erhöhung der Anzahl der Viertel um den Faktor λ erhöht sich daher auch die Leistung des Stroms, der durch die Mitte der Stadt fließt λ mal Eine ähnliche Argumentation mit derselben Schlussfolgerung wird zutreffen, wenn wir anstelle der Mitte einen Punkt nehmen, der die Stadt in einem bestimmten Verhältnis (1: 3, 2: 5) teilt, was dies impliziert

• Der Kraftfluss von Autos entlang der Hauptstraße erhöht sich um den Faktor λ .
• Die Anzahl der in jedem Abschnitt erforderlichen Fahrspuren der Hauptstraße erhöht sich um das λ- fache.

Mehr oder weniger offensichtlich, dass die durchschnittliche Länge der Reise und damit

• Die Nettoreisezeit für die Entfernung erhöht sich um den Faktor λ .

Wir müssen nur noch berechnen, wie oft sich der Zeitverlust aufgrund von Umstellungskosten auf einer Reise erhöht. In jedem Quartal tritt ein Nebenstrom von Einheitsleistung ein und aus, der zusammen vorübergehende Intensitätsverluste erzeugt:

I = I _in + I _out = ( α / 2 ν ) p ⋅ 2,

Dabei ist p die Durchflussrate auf der Hauptstraße. Wir wissen bereits, dass die Anzahl der Viertel und die Durchflussrate auf der Hauptstraße mit λ zunehmen. Daher erhöhen sich die vom Netzwerk verursachten Gesamtzeitverluste um den Faktor ² . Andererseits erhöht sich die Anzahl der vom Netzwerk erzeugten Fahrten, auf die sich infolgedessen alle diese Verluste verteilen, um den Faktor λ , woraus wir das erhalten

• Die durch die Schaltkosten verlorene Nettoreisezeit erhöht sich um den Faktor λ .

Lassen Sie uns alle Ergebnisse auf einer Platte zusammenfassen:

Lineare Topologie
Die Anzahl der Adresspunkte (Viertel) der Einheitskapazität ................................. n
Die Gesamtfläche der Straßen ............................................... ........................................ O ( n ² )
Reine Reisezeit
für das Zurücklegen der Strecke ausgegeben .............................................. ..... O ( n )
Reine Reisezeit
verloren aufgrund von Umstellungskosten ............................................ ......... O ( n )
Die Anzahl der Vermittlungsknoten ............................................... .................................... O ( n )
Die Anzahl der Schaltknoten unter Berücksichtigung der Leistung der Seitenflüsse ..................... O ( n )

Verwendete Notation: " y = O ( x )" bedeutet, dass die Größen x und y funktional abhängig sind, und wenn x unbegrenzt wächst, tendiert das Verhältnis x / y zu einer endlichen Zahl ungleich Null.

Zellstadt
Die zweite, ziemlich übliche Planungsmethode besteht darin, die Blöcke in Form einer rechteckigen Matrix anzuordnen, ähnlich wie portionierte Stücke in einem Schokoriegel platziert werden.

Wir sind damit einverstanden, solche Städte "Cellular" zu nennen.


(Los Angeles, Foto: Stepanov Glory)

Fig. 8 zeigt ein Diagramm der Zellularstadt, bestehend aus n (unter Berücksichtigung der "Hälften") der Viertel, die zusammen ein regelmäßiges Quadrat bilden. Die Viertel sind durch insgesamt √ n Straßen voneinander getrennt, die bedingt von West nach Ost verlaufen, und durch weitere √ n Straßen, die sich von Süd nach Nord erstrecken. Insgesamt bilden diese Straßen √ n × √ n Kreuzungen, von denen jede entweder als Ampelkreuzung oder über eine Straßenbrücke und Überführungen ausgeführt werden kann.


Abb. 8

Unabhängig davon, ob der Straßenverkehr in eine Richtung oder in zwei Richtungen verläuft, kann jede Fahrt von Punkt „A“ nach Punkt „B“ in einer karierten Stadt entlang einer Route durchgeführt werden, die nicht mehr als zwei Straßen durchläuft und an der Kreuzung nicht mehr als eine Kurve erfordert Liebes.

Angenommen, wie im vorherigen Beispiel erzeugt jedes Quartal einen Strom von Reisen mit Kapazitätseinheiten, und die Migrationsbedürfnisse der Bevölkerung werden durch das Modell des „einheitlichen Zugangs“ beschrieben. Berechnen wir nun für die Cellular City die Gesetze, nach denen sich die durchschnittliche Reisezeit und der Ressourcenverbrauch beim Aufbau eines Straßennetzes mit zunehmender Anzahl von Quartalen ändern.

Wenn die Anzahl der Viertel um einen Faktor von λ zunimmt, dann:

• Die Fläche der Stadt nimmt in λ- Zeiten zu und ihre linearen Dimensionen unter Beibehaltung der Proportionen -
  in √ λ ,
• Die durchschnittliche Verfahrlänge und die Nettodauer zum Zurücklegen der Strecke sind proportional zu den linearen Abmessungen.
• Die Anzahl der Straßen und die Anzahl der an eine Straße angrenzenden Stadtteile nimmt √ λ- mal zu.
• Die Leistung des Verkehrsflusses, die proportional zur Anzahl der Viertel ist, mit denen der Fluss „in Kontakt“ ist (eine Erklärung dieser Tatsache wird später gegeben), erhöht sich um das √ λ- fache.
• Die erforderliche Fläche aller Straßen wächst als (Anzahl der Straßen) × (Länge einer Straße) × (Kraft des Straßenflusses) = √ λ ⋅ √ λ ⋅ √ λ = λ √ λ

Seitliche Flüsse sind unterteilt in solche, die von oder in Richtung der Viertel verlaufen, und Verkehrsströme, die an ihren Kreuzungen von einer Straße zur anderen wechseln. Die erste bleibt je nach den Bedingungen immer gleich der Einheit, nach der zweiten, wenn wir berücksichtigen, dass es in der Stadt viel mehr Viertel als Viertel auf einer einzelnen Straße gibt, kommt oder verlässt fast der gesamte Verkehr, der sich entlang der Straße bewegt, die Straßenautobahn. Infolgedessen kann die Änderung der Größe der seitlichen Strömungen der Sekunde durch die Formel (Änderung der Leistung der Straßenströmung) / (Zunahme der Anzahl der Kreuzungen auf einer einzelnen Straße) = √ λ / √ λ = 1 geschätzt werden. Die Gleichheit des letzten Verhältnisses zur Konstante legt nahe, dass sich diese Strömungen nicht besonders ändern mit Bei einer Erhöhung der Anzahl der Quartale beträgt die Erhöhung der vom gesamten Netzwerk verursachten Vermittlungskosten daher: (Erhöhung der Gesamtzahl der Quartale + Kreuzungen) × (Änderung des Werts des Flusses auf einer einzelnen Straße) = λ √ λ . Da die Kraft des von allen Vierteln erzeugten Fahrflusses in λ zunahm, dann

• Die durch Schaltkosten verlorene Nettoreisezeit erhöht sich um √ λ

Stellen Sie sich das Ergebnis in Form einer Tablette vor:

"Zelltopologie"
Die Anzahl der Adresspunkte (Viertel) der Einheitskapazität ................................. n
Die Gesamtfläche der Straßen ............................................... .................................... O ( n √ n )
Reine Reisezeit
für das Zurücklegen der Strecke ausgegeben .............................................. ... O (√ n )
Reine Reisezeit
verloren aufgrund von Umstellungskosten ............................................ ....... O (√ n )
Die Anzahl der Vermittlungsknoten ............................................... .................................... O ( n )
Die Anzahl der Schaltknoten unter Berücksichtigung der Leistung der Seitenflüsse ..................... O ( n )

Wenn man das lineare und das zellulare Netzwerk miteinander vergleicht, fällt es schwer, nicht zu bemerken, dass die Zunahme der für den Bau benötigten Ressourcen und die Zeit, die für eine Reise mit dem Wachstum der Stadt für das erste Netzwerk aufgewendet wird, viel schneller ist als für das zweite. Zum Beispiel benötigt eine Mobilfunkstadt von 100 Vierteln zehnmal weniger Asphalt, und eine Fahrt durch sie erfordert durchschnittlich zehnmal weniger Zeit als in einer linearen Stadt derselben Größe. Daher ist es sinnvoll, Straßennetze mit linearer Topologie nur in sehr kleinen Städten zu verwenden.

Wenn Sie für eine Weile das Vorhandensein von Umstellungskosten vergessen, kann die Mobilfunktopologie als idealer Weg zum Entwerfen von Straßennetzen angesehen werden, da sie eine asymptotisch optimale O-Schätzung sowohl für die durchschnittliche Fahrtlänge als auch für die erforderliche Straßenfläche liefert. In der Tat wird für jede mehr oder weniger „kompakte“ Lage der Stadt (mit einheitlichem Zugang) die Länge der Reise nicht langsamer als die Quadratwurzel ihrer Fläche, die normalerweise direkt proportional zur Bevölkerung ist. Als Ergebnis erhalten wir alle das gleiche O (√ n ).

Die Tatsache, dass eine typische Route in der Cellular City eher an einer „Ecke“ als an einer geraden Linie verläuft, gibt im Prinzip das Recht, nach besseren Möglichkeiten für die Planung von Städten zu suchen, aber 20% Einsparungen (so viel können Sie im Limit gewinnen, wenn Autos lernen, durch Mauern zu fahren) sind unwahrscheinlich Eines Tages werden sie Architekten zwingen, die rechteckige Anordnung von Straßen und Wegen aufzugeben.

Die untere mögliche Grenze der Kosten für den Bau (und die Wartung) des Netzwerks kann erreicht werden, indem berücksichtigt wird, dass jedes Auto einen Teil der Fahrspur für seine Bewegung reserviert. Infolgedessen ist die Gesamtfläche der Straßen proportional zum Produkt der durchschnittlichen Reisezeit (durchschnittliche Reisedauer) durch die Anzahl der Autos in der Stadt : O (√ n ) × O ( n ) = O ( n √ n ) (vergleiche mit der Tabelle für die Zellenstadt).

Wenn wir über die Zeit sprechen, die aufgrund von Umstellungskosten auf Reisen verloren geht, hängt das Verhältnis zur Zeit, die zum Zurücklegen der Entfernung benötigt wird, überraschenderweise nicht asymptotisch von der Anzahl der einzelnen Viertel in der zellularen oder linearen Stadt ab (O (√ n )). / O (√ n ) = O (1), O ( n ) / O ( n ) = O (1)). Mit anderen Worten, der Prozentsatz der Reisezeit, die durch Wechselereignisse in der Großstadt und in der Kleinstadt verloren geht, ist gleich. Daraus können wir schließen, dass wenn es in einer kleinen Stadt keine ernsthaften Probleme mit den Umstellungskosten gab (sagen wir, sie betrugen 10 bis 20%), sie in einer großen Stadt immer noch nicht beobachtet werden sollten, und wenn ja, dann selbst Sie werden nirgendwo hingehen, egal wie die Stadt wuchs und sich vergrößerte.

Da wir nicht wissen, welche der Alternativen zutrifft (oder besser gesagt, dass es Probleme mit dem Autoverkehr in Großstädten gibt), lohnt es sich, die Topologie der Mobilfunkstadt so zu verbessern, dass die Umstellungskosten in ihr mindestens um eine konstante Zeit sinken.

Nützliche Beispiele für unrealistische Netzwerke

Mal sehen, ob die Zelltopologie den Empfehlungen entspricht, die wir durch Analyse der Umschaltung von Flüssen auf der Autobahn entwickelt haben.

1) Vergrößern Sie Straßen nicht ohne Notwendigkeit.
- Ja. Der Verkehr ist auf viele Straßen verteilt (vergleiche mit Linear City).

2) Vermeiden Sie es, Bedingungen zu schaffen, wenn Sie eine große Anzahl von Kurven in einer Fahrt machen müssen.
- Ja. Jede Reise wird höchstwahrscheinlich entlang einer Route durchgeführt, die nur eine Kurve auf den Straßen der Stadt erfordert.

3) Vermeiden Sie Situationen, wenn Sie auf einem Straßenabschnitt fahren, dessen Routen nur einen kleinen Abschnitt des gemeinsamen Pfades haben.
- Hier gibt es vielleicht etwas zu arbeiten. Trotz der minimalen Anzahl von Abbiegungen pro Fahrt führt die Route als Teil des Hauptautobahnflusses durch eine große Anzahl von Vermittlungsknoten (O ( n )), in denen jeweils wertvolle Zeit verschwendet wird.

Die letzte Bemerkung motiviert dazu, die folgende Frage zu untersuchen: „Was ist der Mindestwert der durchschnittlichen Anzahl von Vermittlungsknoten, durch die eine Fahrt innerhalb eines Straßennetzes verlaufen muss, das n Blöcke verbindet?“

Die Suche nach einem solchen Netzwerk ist natürlich nur unter der Bedingung sinnvoll, dass die Anzahl der von einem Vermittlungsknoten kombinierten oder gemeinsam genutzten Streams von oben vorläufig um einen bestimmten festen Wert begrenzt ist. Andernfalls können Sie immer ein Straßennetz mit n Adresspunkten und einer einzelnen Mega-Kreuzung präsentieren.


(Autor unbekannt)

Es ist viel einfacher, das eigentliche Problem zu untersuchen, wenn Sie zuvor zumindest einen Teil der Muster anhand einiger einfacher, wenn auch nicht realistischer Modellbeispiele aufgedeckt haben. Nach dieser Logik werden wir vorübergehend die geometrischen Einschränkungen beim Bau einer Straße für Reisende vergessen, um Entfernungen zurückzulegen, und ihre ganze Aufmerksamkeit darauf konzentrieren, wie abstrakte Netzwerke das Problem der parallelen Adressierung lösen. In Bezug auf die Vermittlungsknoten nehmen wir vorerst an, dass jeder von ihnen entweder den Strom in zwei Teile (den Teilungsknoten) teilt oder zwei Flüsse zu einem kombiniert.


Abb. 9


, , n , ( 9).

, .

( ) , , — , , n ( 10). .


Abb. 10

Wenn Sie die Richtungen aller Flüsse im direkten Adressbaum in die entgegengesetzte Richtung ändern, erhalten Sie den umgekehrten Adressbaum, dessen Zweck darin besteht, n Startpunkte mit einem einzigen Ende zu verbinden.

In Fällen, in denen n eine Zweierpotenz ist, verläuft jede Route innerhalb des Adressbaums genau durch log ₂ n Vermittlungsknoten, was zweifellos (asymptotisch) weniger ist als der gleiche Indikator für ein Netzwerk mit Mobilfunk (O (√ n )) oder Linear ( ( )). O ( n )) Topologie.

Die zwei einfachsten Arten von logarithmischen Netzwerken
Unter Verwendung von "baumartigen" Netzwerken als Bausteine ​​ist es nicht schwierig, die vorherige Lösung auf den Fall zu verallgemeinern, wenn es mehr als einen Ausgangspunkt gibt, aber -k . Es gibt zwei einfache Möglichkeiten, dies zu tun.

Die erste Möglichkeit besteht darin, den umgekehrten Adressbaum zu verwenden, um zuerst die Routen aller Fahrten in einem gemeinsamen Stream zu erfassen und diesen Stream dann mithilfe des direkten Adressbaums in Unterflüsse zu unterteilen, die jeweils an ihr Ziel adressiert sind (Netzwerk oben in Abb. 11) )


Abb. 11

Wenn k und n Zweierpotenzen sind, verläuft am Ende jede Route genau durch log ₂ k + log ₂ n Vermittlungsknoten. Netzwerke, die nach dem gerade beschriebenen Algorithmus aufgebaut sind, vereinbaren wir, (unidirektionales) Logarithmus mit vorläufiger Zusammenführung aufzurufen .

Der zweite Weg zur Lösung des gleichen Problems kann erhalten werden, indem in der ersten Lösung die Reihenfolge der Fusions- und Trennungsvorgänge umgekehrt wird. Die Implementierung lautet wie folgt: Erstellen Sie für jeden Startpunkt einen eindeutigen Satz imaginärer Duplikate aller Endadresspunkte und verbinden Sie ihn dann mit diesen Duplikaten (überhaupt nicht imaginär) mit einem direkten Adressbaum.

Um den Aufbau des Netzwerks abzuschließen, muss nur noch jeder Endpunkt mit einem umgekehrten Adressbaum mit k imaginären Duplikaten verbunden werden (das Netzwerk von unten in Abb. 11).

Immer wenn n und k Zweierpotenzen sind, ist die Anzahl der Vermittlungsknoten auf dem Pfad einer Route innerhalb des neu aufgebauten Netzwerks wieder gleich log ₂ k + log ₂ n . Wir erklären uns damit einverstanden, Netzwerke dieser Art (unidirektional) logarithmisch mit vorläufiger Trennung zu nennen .

Umwandlung von unidirektionalen Netzwerken in symmetrische
Im Allgemeinen unidirektionale NetzwerkeWir rufen jedes Netzwerk an, wenn die damit verbundenen Adresspunkte streng in Start und Ziel unterteilt sind. Standardmäßig wird für unidirektionale Netzwerke angenommen, dass mindestens eine Route möglicher Bewegungen von einem Startpunkt zu einem Endpunkt bereitgestellt wird.

Neben einer lebenslangen Reise ist es schwierig, Beispiele zu nennen, bei denen einige Adresspunkte nur am Anfang als Routen dienen und andere nur ihr Ende sein könnten. Wir werden unsere Argumentation der Realität näher bringen, wenn wir auch Netzwerke einbeziehen, in denen zwei beliebige Adresspunkte durch Routen in beide Richtungen verbunden sind. Wir stimmen zu, solche Netzwerke als symmetrisch zu bezeichnen .

Tatsächlich gibt es keine ideologische Lücke zwischen unidirektionalen und symmetrischen Netzwerken: Jedes symmetrische Netzwerk kann auch als unidirektionales Netzwerk verwendet werden, und jedes unidirektionale Netzwerk, das anfänglich eine gleiche Anzahl von Start- und Endpunkten verbindet, kann in ein symmetrisches Netzwerk umgewandelt werden (Abb. 12).


Abb. 12

Die 13a und 13b zeigen die "symmetrischen" Formen des logarithmischen Netzwerks mit vorläufiger Verschmelzung und des logarithmischen Netzwerks mit vorläufiger Trennung. Ihre Beispiele zeigen die grundlegende Möglichkeit, n Blöcke mit diesem Netzwerktyp zu verbinden, wobei die Anzahl der besuchten Vermittlungsknoten während einer Fahrt proportional zum Logarithmus der Anzahl der Blöcke in der Stadt ist.


Abb. 13 a


Abb. 13 b

Genaue untere Schätzung
Bisher wurde bereits eine umfangreiche Sammlung von Netzwerken mit verschiedenen Funktionen gesammelt, abhängig von der durchschnittlichen Anzahl der während der Reise besuchten Knoten und der Anzahl der Adresspunkte in der Stadt. Wir wissen jedoch immer noch nicht, wie klein diese Zahl für eine bestimmte Anzahl von Quartalen grundsätzlich sein kann. Die Untergrenze für ihren Wert kann unter Verwendung des Informationsansatzes erhalten werden.

Selbst wenn ein bestimmtes Straßennetz n Adresspunkte verbindet und die Migrationsbedürfnisse der Bevölkerung so sind, dass jede Reise, egal wo sie begonnen hat, die gleiche Chance hat, irgendwo in der Stadt zu enden.

Um das beabsichtigte Problem zu lösen, generieren wir nach diesem Rezept eine zusätzliche Informationsnachricht: Über einen langen Zeitraum sammeln wir Aufzeichnungen aller Reisen, die zu Beginn einen festen Punkt haben, und notieren in zufälliger Reihenfolge die Adressen, an die diese Reisen endeten. Die resultierende Nachricht ist eine zufällige Folge, die sich aus den Namen von n Adresspunkten der Stadt zusammensetzt.

Eine Möglichkeit, diese Nachricht an Mars zu senden, besteht darin, zuerst alle Namen mit Binärwörtern gleicher Länge zu codieren, wodurch die ursprüngliche Nachricht in eine Folge von Nullen und Einsen umgewandelt wird, und erst dann die resultierende Folge über einen digitalen Kommunikationskanal zu senden. Da zur unterscheidbaren Codierung die Menge nWenn Binärnamen mit der Länge log ₂ n erforderlich sind , beträgt die Länge der digitalen Nachricht:

(Anzahl der Datensätze) × log ₂ n Zeichen.

Das Interessanteste ist, dass es nach der Informationstheorie unabhängig vom verwendeten Codierungsalgorithmus einfach unmöglich ist, dieselbe Nachricht im Durchschnitt mit einer geringeren Anzahl von Binärzeichen zu übertragen.

Eine Alternative zum direkten Übertragen der codierten Namen der Endpunkte kann eine Methode sein, bei der für jede Fahrt angegeben wird, in welche der möglichen Richtungen die Route an der nächsten Weggabelung gedreht wurde. Nach unseren Annahmen können alle Gabeln im Netzwerk nur doppelt sein, daher ist zur Angabe der Richtung jeweils genau 1 Bit erforderlich. Jeder, der einen Stadtplan hat und den Startpunkt kennt, reicht aus, um jede Route zu verfolgen und die ursprüngliche Reihenfolge seiner Ziele wiederherzustellen. Wenn die durchschnittliche Anzahl der während einer Fahrt besuchten Gabeln (Teilungsknoten) x beträgt , beträgt die Länge der Binärnachricht mit der neuen Codierungsmethode: (Anzahl der Datensätze) × x.

Wie bereits erwähnt, kann ein neues Codierungsverfahren nicht effizienter sein als das direkte binäre Adressübertragungsverfahren. Daher: (Anzahl der Datensätze) × x ≥ (Anzahl der Datensätze) × log ₂ n , woher:

x ≥ log ₂ n .

Obwohl die letzte Ungleichung ursprünglich für eine Gruppe von Reisen mit einem gemeinsamen festen Ausgangspunkt abgeleitet wurde, stellte sich heraus, dass ihr Erscheinungsbild von der spezifischen Wahl dieses Punkts unabhängig war. Wir haben daher das Recht, das Ergebnis sofort auf alle Reisen in der Stadt auszudehnen und so den ersten Teil der gewünschten Schätzung zu erhalten:

P1 ) Vorausgesetzt, jede neue Reise hat die gleiche Chance, in einem von n zu endenAdresspunkte der Stadt, die durchschnittliche Anzahl der Teilungsknoten pro Route darf nicht weniger als log ₂ n betragen .

Wenn Sie die Uhr mental zurückdrehen, wird jeder Reiseendpunkt zum Startpunkt und jeder binäre Netzwerkteilungsknoten zu einem binären Zusammenführungsknoten. Mit diesem kleinen Trick können Sie automatisch den zweiten fehlenden Teil der Schätzung aus P1 abrufen:

P2 ) Vorausgesetzt, dass jede abgeschlossene Reise die gleichen Chancen hat, an einem der n Adresspunkte der Stadt zu beginnen, kann die durchschnittliche Anzahl der Fusionsknoten pro Route nicht geringer als log sein ₂ n .

Wenn wir uns an die Existenz eines logarithmischen Netzwerks mit vorläufiger Zusammenführung und eines logarithmischen Netzwerks mit vorläufiger Trennung erinnern, erhalten wir sofort zwei Beispiele für Netzwerke, die hinsichtlich der Anzahl der Vermittlungsknoten optimal sind, die im Durchschnitt während einer Fahrt in ihnen besucht werden. Mal sehen, ob diese Qualität ihnen hilft, die Intensität der erzeugten Schaltverluste zu reduzieren.

Switching-Kosten in logarithmischen Netzwerken

Wenn wir die Netzwerke mit vorläufiger Zusammenführung und vorläufiger Trennung vergleichen, dann sieht das erste aufgrund seiner Einfachheit viel attraktiver aus. Leider hat diese Einfachheit auch eine Kehrseite der Medaille: Die Kombination aller Routen zu einem Strom widerspricht der Empfehlung i1 und wird dadurch zu einer potenziellen Ursache für große Zeitverluste. Ein Netzwerk mit vorläufiger Trennung scheint den Empfehlungen i1 - i3 zu folgen. Nach Abbildung 13b erhöht es jedoch tendenziell schnell die Anzahl der verwendeten Straßenkanten und Schaltknoten. Die letztere Qualität kann Netzwerke dieses Typs für den praktischen Gebrauch zu teuer machen.

Wir werden diese Probleme genauer analysieren. Zunächst sind wir uns einig, dass die Stadt dem Migrationsmodell des einheitlichen Zugangs unterliegt und der von einem ihrer Adresspunkte erzeugte Reisefluss eine Einheitskapazität hat.

Verluste in einem Netzwerk mit vorläufiger Fusion
In Abbildung 14 sehen Sie ein Diagramm der Flüsse, die sich aus den angegebenen Vereinbarungen innerhalb des Netzwerks mit vorläufiger Fusion ergeben.


Abb. 14

Es erschien mir zweckmäßig, das Netzwerk in seiner unidirektionalen Form darzustellen, was bedeutet, dass jeder Start- und Endpunkt, der nicht mit denselben Nummern signiert ist, tatsächlich denselben Adresspunkt in der Stadt bedeutet.

Basierend auf dem Diagramm berechnen wir die Intensität der im Netzwerk generierten Vermittlungskosten. Beginnen wir mit der linken Hälfte, in der durch den umgekehrten Adressbaum alle Routen in einem Stream gesammelt werden. Jeder Vermittlungsknoten in diesem Teil des Netzwerks stellt den Ort dar, an dem zwei unidirektionale Autobahnen zu einer verschmelzen (Abb. 15).


Abb. 15

Wenn anfänglich jede der Straßen effizient beladen ist, besteht nach ihrer Vereinheitlichung keine Notwendigkeit, die Anzahl der Fahrspuren zu verringern, so dass die Umstellungskosten nicht reduziert werden sollten.

Angenommen, ein Stromfluss pro Einheit reicht bereits aus, um die Straße in mindestens zwei Fahrspuren effektiv zu füllen. In diesem Fall kommen wir zu einem eher unerwarteten Ergebnis: Die Vereinigung der Fahrzeugströme innerhalb des logarithmischen Netzwerks mit der vorläufigen Zusammenführung erfolgt absolut „kostenlos“, ohne vorübergehende Verluste zu verursachen.

Die Berechnung der Kosten, die in der rechten rechten Hälfte anfallen, ist nicht viel schwieriger. Dieser Teil des Netzwerks ist ein direkter Adressbaum, von dem jeder Knoten eine symmetrische Gabelung in den Straßen ist, die wir bereits untersucht haben. Wenn die Leistung der einfallenden Strömungs p Intensität an der Gabelung Verlust Schwellen gleich ( α / 2 ν ) ⋅ p ² /2. Die Leistung des in die Wurzelgabel eintretenden Stroms beträgt: n , daher beträgt die Intensität der Verluste im Wurzelknoten: ( α / 2 ν ) ⋅ n ²/ 2. In jeder nächsten Generation des Adressbaums verdoppelt sich die Anzahl der Gabeln, und die Leistung des auf ihnen laufenden Streams wird halbiert. Infolgedessen hat die Verlustformel innerhalb des gesamten Baums die Form:

I _{t_div1} = ( α / 2 ν ) ⋅ (1/2) ⋅ [ n ² + 2 ( n / 2) ² + 4 ( n / 4) ² + ... + ( n / 2) ⋅ 2 ² ] =

( α / 2 ν ) ⋅ ( n / 2) ² [1 + 1/2 + 1/4 + ... + 2 /n ] ≈ ( α /2 ν ) ⋅ n ²

, , n , ́ , ( α /2 ν ) ⋅ n , .

Wenn es um abstrakte Netze geht, ist es schwierig, eine aussagekräftige Schätzung der Fläche der von ihnen genutzten Straßen abzugeben. Als alternatives Maß für die strukturelle Komplexität kann die Gesamtleistung aller Seitenströme berechnet werden. Wie geplant sollte der resultierende Wert die Ressourcenkosten für die Errichtung aller vom Netzwerk benötigten Austauschstellen widerspiegeln. Ich kann nicht sagen, dass diese Methode in der Praxis immer eine gute Interpretation haben wird, aber ich werde wahrscheinlich eine ungefähre Vorstellung davon bekommen, wie viel Arbeit vor mir liegt.

Innerhalb des logarithmischen Netzwerks mit vorläufiger Zusammenführung sind Seitenströme nur im direkten Adressbaum vorhanden, und ihre Gesamtleistung für jede Knotengeneration ist dieselbe: n / 2. Gesamtbaumprotokoll ₂ nGenerationen von Knoten, daher liefert eine neue Methode zur Bewertung der Komplexität eine Schätzung der Komplexität: O ( n log ₂ n ).

Logarithmisches Netzwerk mit vorläufiger Zusammenführung
Anzahl der Adresspunkte der Einheitsleistung ........................................ ............ n
Durchschnittlicher Reiseverlust
aufgrund von Umstellungskosten:
asymptotisches Verhalten ........................ .................................................. ............................ O ( n )
exakter Wert ................ .................................................. ........................... ( α / 2 ν ) ⋅ n
Die Anzahl der Vermittlungsknoten ............................................... .................................. O ( n )
Die Anzahl der Schaltknoten unter Berücksichtigung der Leistung von Seitenströmen .... ............... O ( n log ₂ n )

Verluste im Netzwerk mit vorläufiger Trennung
Fahren wir nun mit der Analyse des logarithmischen Netzwerks mit vorläufiger Trennung fort, wobei wir erneut davon ausgehen, dass das Netzwerk zum Verbinden von Adresspunkten der Einheitsleistung verwendet wird in der Stadt des "einheitlichen Zugangs".

Fig. 16 zeigt ein Fragment davon, das aus einem Adresspunkt zusammen mit direkten und umgekehrten Adressbäumen neben diesem Punkt besteht.


Abb. 16

Zunächst schätzen wir die Intensität der durch das Fragment erzeugten Schaltverluste.
Die Kosten, die bei der Aufteilung der Flüsse anfallen, können durch Ersetzen der Formel I _{t_div1} = ( α / 2 ν ) ⋅ n ^{2 ermittelt werden} , die im vorherigen Beispiel für den direkten _Adressbaum anstelle von n - eins abgeleitet wurde. In der Tat haben die direkten Adressbäume in den 16 und 14 die gleiche Tiefe und leiten Ströme mit ähnlicher Leistung entlang sich selbst ( _{ca. ,} ). , , n n ² , ( α /2 ν ) ⋅ n ² :

I _{t_div2} = ( α /2 ν ).

Wir berechnen nun den Wert der Kosten in der linken Hälfte des Fragments.
Aufgrund der geringen Anzahl der kombinierten Straßenflüsse innerhalb des umgekehrten Adressbaums wäre es diesmal nicht sinnvoll, mehr als zwei Fahrspuren zu bauen. Fusionen unter diesen Bedingungen sind nicht mehr kostenlos: Im Gegensatz zum vorherigen Beispiel gibt es auf der Autobahn Engstellen (Abb. 17), an denen Umstellungskosten erforderlich sind.


Abb. 17

Unter der Annahme, dass der Fahrer die bevorstehende Verengung im Voraus bemerkt, können wir davon ausgehen, dass der Prozess des Bewegens von Autos von der Sackgasse langsam ist und sich über Hunderte von Metern entlang der Autobahn erstreckt. In diesem Fall haben wir das Recht, auf den Trick zurückzugreifen, den wir zuvor zur Berechnung der Verluste an der symmetrischen Gabel verwendet haben - den gesamten Migrationsfluss q in viele kleine Teile q _i zu teilen und dann jeden von ihnen als Seitenstrom von der Seite der Rampe zu interpretieren. Die durch jeden solchen Teilstrom erzeugten Verluste werden nach der Formel berechnet:
I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s) gibt es jedoch zwei Feinheiten.

Die erste davon ist, dass Autos nicht weiter als bis zur nächsten Reihe migrieren.
Und tatsächlich: Die Strömungen in den beiden zentralen Fahrspuren sollten aufgrund der offensichtlichen Symmetrie immer ungefähr die gleiche Dichte haben, damit die Fahrer nicht viel Grund haben, die Mittellinie zu überqueren. Aus der gemachten Beobachtung folgt, dass in der Formel für Verluste, die durch partielle seitliche Strömung verursacht werden, s gleich 1 ist.

Wenn die Maschinen die extremen Fahrspuren verlassen und sich in zwei zentralen Reihen neu anordnen, wächst die Strömungsleistung innerhalb der zentralen Bänder allmählich und ändert sich jeweils von P / 2 bis P . Somit ist die zweite Subtilität eine signifikante Abhängigkeit von paus der Zahl des Teilstroms i , die uns zwingt, nicht zu schreiben:

I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s ),
sondern:
I _i = ( α / 2 ν ) p ( i ) ⋅ q _i ⋅ (1 + 1 / s ).
In dem Fall, in dem viele kleine Teile, in die der Migrationsstrom aufgeteilt wurde, alle gleich groß waren, wird die Abhängigkeit p ( i ) durch einen linearen Graphen ausgedrückt (Fig. 18).


Abb. 18

Um die Intensität der Gesamtverluste zu berechnen, muss entweder auf die Integration zurückgegriffen werden oder (dies ermöglicht es, eine besonders einfache Form einer integrierbaren Funktion zu erstellen), da p ( i ) den Durchschnittswert in der Grafik gleich 3 P / 4 nimmt. Da der gesamte Migrationsfluss von der Seite jedes extremen Streifens P / 2 beträgt, beträgt die Intensität der Verluste bei einer separaten Verschmelzung:

I _{Verschmelzung} = 2 ⋅ ( α / 2 ν ) ⋅ (3 P / 4) ⋅ ( P / 2)

= ( α / 2 ν ) 3 P ²/ 4.

Um die im Fragment erzeugten Zeitverluste im umgekehrten Adressbaum zu ermitteln, wenden wir die Formel für I _merge auf jeden seiner _{Knoten an} :

I _{t_merge} = (3/4) ⋅ ( α / 2 ν ) [1 ⋅ (1/2) ² + 2 ⋅ (1/4) ² + 4 ⋅ (1/8) ² + ... + ( n / 2) ⋅ (1 / n ) ² ] ≈

≈ (3/4) ⋅ ( α / 2 ν ) [1/4 + 1/8 + 1/16 + ...] =

= (3/8)⋅ ( α / 2 ν ) [1/2 + 1/4 + 1/8 + ...] =

= (3/8) ⋅ ( α / 2 ν ).

Die Gesamtkosten, die innerhalb des Fragments aufgrund der Zusammenführung und Trennung von Strömungen entstehen, _betragen :

I _{t_merge} + I _{t_div2} = ( α / 2 ν ) [1 + 3/8] = 11/8 ( α / 2 ν ).

Ein vorläufiges geteiltes logarithmisches Netzwerk enthält nur n solcher Fragmente und genau nEinheitenflüsse werden durch ihre Adresspunkte erzeugt, daher ist der Wert, den wir gerade gefunden haben, gerade gleich den Schaltverlusten, die durchschnittlich pro Fahrt auftreten.

Tatsächlich ist es für uns wichtiger, nicht einmal eine bestimmte Anzahl, die den spezifischen Umstellungskosten entspricht, sondern die Tatsache, dass diese Kosten mit zunehmendem n konstant bleiben . Der letztere Umstand macht das logarithmische Netzwerk mit vorläufiger Trennung asymptotisch zum wirtschaftlichsten in Bezug auf Schaltverluste unter allen Arten von Netzwerken, die wir zuvor untersucht haben.

Leider kostet Führung nicht „kostenlos“. Trotz der verschwindend geringen Größe der überwältigenden Anzahl von Flows enthält jeder im Netzwerk enthaltene Adressbaum etwa 2 nzweispurige Straßenrippen und ungefähr n Schaltknoten voller Größe. Es gibt 2 n Bäume im Netzwerk , was O ( n ² ) Kanten und Knoten bedeutet, was es unter allen betrachteten Beispielen nicht nur zum wirtschaftlichsten, sondern auch zum teuersten Netzwerk macht.

Was die Summe der seitlichen Strömungen betrifft , so wächst ihr Wert, wie leicht zu berechnen ist, mit der Geschwindigkeit O ( n log2 n ) und hat in diesem Fall keine große Bedeutung.

Logarithmisches Netzwerk mit vorläufiger Trennung
Anzahl der Adresspunkte der Einheitsleistung ........................................ ............ n
Durchschnittliche Reisezeit,
verloren durch Wechselkosten:
Asymptotik .......................................... .................................................. .......... O (1)
exakter Wert .................................. .................................................. ........... 11/8 ( α / 2 ν ).
Die Anzahl der Vermittlungsknoten ............................................... .................................. O ( n ² )
Die Anzahl der Schaltknoten unter Berücksichtigung der Leistung der Seitenflüsse ... ................ O ( n log ₂ n )

Logarithmisch ausgeglichenes Netzwerk

Außergewöhnlich kleine Schaltverluste mit der möglichen Verwendung des logarithmischen Netzwerks mit vorläufiger Trennung, aber gleichzeitig zu ressourcenintensiv für seinen Aufbau, führen zu dem Wunsch, eine Möglichkeit zu finden, sein Design so zu ändern, dass der Ressourcenverbrauch erheblich reduziert wird und die Schaltkosten nicht wesentlich steigen.

Offensichtlich ist der Hauptschuldige für eine übermäßig große Anzahl von Straßen im Netz die äußerst geringe Effizienz ihrer Nutzung. Letzteres ist deutlich in Abbildung 19 zu sehen, die ein detailliertes Diagramm der Flüsse innerhalb eines direkten Adressbaums neben dem i- ten Adresspunkt zeigt.


Abb. 19

In dem Diagramm gibt die Zahl, die über dem Rand des Baums steht, die Leistung des entlang des Randes fließenden Reisestroms an, und das Intervall darunter ist der Satz von Adresspunkten, zwischen denen dieser Strom schließlich verteilt wird. Es wird angenommen, dass alle im Diagramm vorhandenen Kanten zweispurige Autobahnen sind. Die Anzahl der Kanten in jeder Generation des Baums ist am unteren Rand der Abbildung angegeben.

Bei sorgfältiger Prüfung stellen Sie möglicherweise fest, dass die Regel, nach der der Reisefluss in einen bestimmten Knoten aufgeteilt wird, ausschließlich durch die Position dieses Knotens im Adressbaum bestimmt wird und nicht von der Nummer des Adresspunkts abhängt, der diese Reisen ausgelöst hat.

Wenn es mehrere Streams gibt, die an denselben Satz von Punkten adressiert sind, und jeder von ihnen nicht stark genug ist, um seinen zugewiesenen Pfad zu füllen, warum sollten Sie sie dann nicht auf einer Autobahn miteinander kombinieren? Tatsächlich ermöglicht diese im Wesentlichen einfache Idee den Aufbau eines guten abstrakten Netzwerks, das relativ geringe Schaltverluste erzeugt und bei der Anzahl der verwendeten Straßen wirtschaftlich ist.

Wenn wir zum Adressbaum des i- ten Punkts zurückkehren, sehen wir, dass der in den Wurzelknoten eintretende Stream in zwei untergeordnete Streams mit einer Kapazität von jeweils 1/2 unterteilt ist. Der erste Stiefsohnstrom besteht aus Fahrten, die an Punkte aus dem Intervall [1; n / 2], die zweite - an Punkte aus dem Intervall [( n / 2) + 1;n ].
Nach der oben beschriebenen Idee kombinieren wir an jedem ungeraden Punkt und am nächsten Adresspunkt dieselbe Art von Stiefsohnströmen mit einer geraden Zahl, die der Reihe nach folgt. Eine solche Technik ermöglicht es, dass jedes ausgewählte Punktpaar anstelle von vier Strömen mit einer Potenz von 1/2 nur zwei Ströme mit Einheitsgröße aufweist (Abbildung 20). Wir werden die Abkürzung BN ₂ [i; i +1].


Abb. 20

Wenn die Stiefsohnflüsse nicht kombiniert würden, sondern sich noch innerhalb des Adressbaums befänden, würde bei der nächsten erreichten Knotengeneration jeder von ihnen erneut in zwei Teile unterteilt, die sowohl in der Leistung als auch in der Größe der Punktmengen gleich sind, zu denen sie gehören Komponenten ihrer Reisen.

Warum die etablierte Tradition brechen, weil wir nach der Vereinigung immer noch die gleichen Stream-Typen wie zuvor haben, aber nur weniger Vertreter für jeden Typ? - anwendbar auf jeden der Ausgangsströme BN ₂ [i; i +1] genau dieselbe Trennungsregel, die für einen Stream seines Typs im Adressbaum gelten würde.

Es gibt keinen Grund, warum die oben beschriebene logische Konstruktion zum Kombinieren und Aufteilen derselben Flüsse nicht induktiv wiederholt werden konnte. Fig. 21 zeigt ein Diagramm der Kombination von zwei Fragmenten von
BN ₂ zu einem Fragment von BN ₄ , und Fig. 22 zeigt, wie der Algorithmus im allgemeinen Fall aussieht.


Abb. 21


Abb. 22

Am Ende wird der Prozess der Fragmentierungsvergrößerung abgeschlossen sein und uns zum einzigen Element BN _{n führen} [1; n ] nennen wir es das ausgeglichene Netzwerk vom logarithmischen Typ (Abb. 23).


Abb. 23

Untersuchen wir dieses Netzwerk auf die Komplexität und Größe der erzeugten Schaltverluste.
Basierend auf der induktiven Natur des Balanced Network-Konstruktionsverfahrens kann die Anzahl der in seiner Struktur enthaltenen Schaltknoten durch die Rückgabegleichung beschrieben werden:

Knoten (BN _k ) = 2 Knoten (BN _{k / 2} ) + 2 k ,

mit der Randbedingung:

Knoten (BN ₁ ) = 0. Die

Lösung für dieses Gleichungssystem ist die Funktion:

Knoten (BN _n ) = 2 n log ₂ n .

Da BN _n zu bauenWenn log ₂ n Induktionsschritte erforderlich sind , durchläuft jede Fahrt log ₂ n Trennungsknoten und die gleiche Anzahl von Zusammenführungsknoten, wobei sie sich auf ihrem Weg abwechseln (Abb. 24).


Abb. 24

, :
( α /2 ν ) ⋅ (1) ² /2.

, :
( α /2 ν ) ⋅ 3 ⋅ (1/2) ² /4 = 3/16 ( α /2 ν ).

, , — n log ₂ n , :
11/16 ( α /2 ν ) n log ₂ n ,

was pro Fahrt gilt:
11/16 ( α / 2 ν ) log ₂ n

Ausgeglichenes Netzwerk vom logarithmischen Typ
Anzahl der Adresspunkte der Einheitsleistung ................... ................................. n
Durchschnittlicher Reisezeitverlust
aufgrund von Umstellungskosten:
asymptotisches Verhalten ... .................................................. ................................................. O. (log ₂ n )
exakter Wert ........................................... .................................................. ..11 / 16 ( α / 2 ν ) log₂ n
Anzahl der Vermittlungsknoten ............................................. .................................... O ( n log ₂ n )
Die Anzahl der Schaltknoten unter Berücksichtigung der Leistung der Seite Threads ................... O ( n log ₂ n )

́ . , . , , — , , , , . , . , , .

Warum historische Städte zum Stau verurteilt sind

Meine Aussage mag unerwartet erscheinen, aber die Antwort darauf, warum sich natürlich entwickelnde Städte normalerweise unter Staus leiden, haben wir bereits in den vorhergehenden Absätzen gefunden. Woraus besteht es also?

Tatsache ist, dass viele historische Städte, die die Ära der mittelalterlichen Festungen überlebten (zum Beispiel fast alle Hauptstädte der „Alten Welt“), aus dieser Zeit die radiale Struktur der Straßen erbten. Leider (für ihre modernen Bewohner) lässt sich ein Straßennetz mit einer ähnlichen Topologie nicht gut skalieren: Die dichte Lage radialer Straßen in der Nähe des Zentrums wird an der Peripherie zu selten. Infolgedessen wurden im Zuge des Bevölkerungswachstums die Straßen, die sich ursprünglich am Rande der wenigen Straßen befanden, die zur Festung führten, größer, und die Straßen, die an der Peripherie erschienen, waren kurz und hatten keine ausreichende Transitbedeutung, um an Breite zu gewinnen. Infolgedessen bezieht sich das Straßennetz, das wir heute in großen historischen Städten sehen, meistens auf arterielle Transportsysteme.und in unserer Terminologie auf die Art der logarithmischen Netzwerke mit (unvollständiger) vorläufiger Zusammenführung.


( , : )

, , : , , «» , O( √ n ). , : , - , , O( n ). , nDiese Zeit wird sich gegen die reine Zeit durchsetzen, um die Entfernung zu überwinden. Mit anderen Worten, es werden Staus in der Stadt auftreten.

Zweifellos ist die Umstrukturierung des Verkehrssystems in historischen Großstädten eine Aufgabe, die gelöst werden kann. Es ist jedoch wichtig zu verstehen, dass der Bau einer weiteren, zwei oder fünf großen Verkehrsadern die Situation in der Stadt zwar geringfügig verbessert, die Grundursache für Staus jedoch nicht beseitigt. Anscheinend besteht die einzige Möglichkeit, die Mängel des logarithmischen Netzwerks durch vorläufiges Zusammenführen zu überwinden, darin, ein anderes Netzwerk zu verwenden. Ein guter Kandidat kann hier ein Netzwerk mit zellularen Topologien sein, bei dem die Wachstumsrate der Zeit zum Abdecken der Entfernung zumindest mit der Wachstumsrate der Schaltverluste übereinstimmt.


(Nacht Berlin, Foto: Vincent Laforet)

Vielleicht zeichnet sich das moderne Berlin deshalb, obwohl es große Ausfallstraßen hat, bereits durch eine deutlich sichtbare Maschenstruktur aus.

Es gibt weltweit viele interessante Lösungen, wie die Bewohner historischer Städte mobiler werden können, aber der Hauptpreis im Kampf um die Zugänglichkeit des Verkehrs sollte wahrscheinlich den Ingenieuren von Barcelona verliehen werden.


(Barcelona aktualisiert Straßennetz, Foto: Vincent Laforet)

Ein detaillierter Blick auf die linearen und zellularen Stadtnetzwerke

, , . , , , , .


, : ( 25).


Abb. 25

. , , 1/ n .

.
, i
( n − i ) , , , i ( i − 1) , . , i - :

q _{W_out} = ( n − i )/ n — , ,
q _{W_in} = ( i − 1)/ n — , . , i :
q _{E_out} = ( i − 1)/ n — ,
q _{E_in} = ( n − i )/ n — .

, i - :

q _{E_in} + q _{W_in} = ( n − 1)/ n ,
, :
q _{E_out} + q _{E_out} = ( n − 1)/ n ,
i ( 1/ n , , ).

, i - . :
( )×( ) = ( n − i )( i − 1) , :

P _W ( i ) = ( n − i )( i − 1)/ n .

:
( )×( )/ n ,
P _E , :

P _E ( i ) = P _W( i ) = P ( i ).

Wenn wir die Leistung aller Haupt- und Nebenflüsse kennen, können wir die Intensität der Verluste berechnen, die im Netzwerk in der Nähe des i- ten Quartals auftreten:

I ( i ) = ( α / 2 ν ) ⋅ P ( i ) ⋅ [( q _{E_in} + q _{W_in} ) ⋅ (1 + 1 / s ) + ( q _{E_out} + q _{E_out} ) ⋅ (1 - 1 / s )] =
= ( α /2 ν ) ⋅ P ( i ) ⋅ [ (1 − 1/ n ) ⋅ (1 + 1/ s ) + (1 − 1/ n ) ⋅ (1 − 1/ s ) ] =
= ( α /2 ν ) ⋅ 2 P ( i ) ⋅ (1 − 1/ n ) =
= 2( α /2 ν ) ⋅ (1 − 1/ n ) ⋅ ( n − i) ( i - 1) / n =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i ) ⋅ ( i - 1) ⋅ (1 / n ).

Wenn wir den letzten Ausdruck über i zusammenfassen , erhalten wir die Intensität der Verluste, die vom gesamten Netzwerk als Ganzes erzeugt werden.

I = ∑ _i I ( i )
= ∑ _i 2 ( α / 2 ν ) ⋅ (1 - 1 /n ) ⋅ ( n − i ) ⋅ ( i − 1) ⋅ (1/ n ) =
= 2( α /2 ν ) ⋅ (1 − 1/ n ) ⋅ n ² ⋅ ∑ _i (1 − i / n ) ⋅ ( i / n − 1/ n ) ⋅ (1/ n ) ≈
≈ 2( α /2 ν ) ⋅ n ² ⋅ ∑ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ).

Die Summe ∑ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ) mit jedem großen n kann mit guter Genauigkeit durch das Integral ersetzt werden:

∫ t (1 - t ) d t ( t ∈ [0; 1]) = 1/2 - 1/3 = 1/6.

, n :

I = ( α /2 ν ) n ² /3.

, . , , , — λ ( λ ).

m . 1, ( α /2 ν ) m ² /3. λ λ , , λ ² , :

I = ( α /2 ν ) m ² ⋅ λ ² /3.

, , , — , , n . n m ⋅ λ , :

I = ( α /2 ν ) m ² ⋅ λ ² /3 =
= ( α /2 ν ) ( m ⋅ λ ) ² /3 =
= ( α /2 ν ) n ² /3.

, .


, . , , , , , , , . , ( 26).

Hier geht es natürlich nicht darum, das oben beschriebene Netzwerk ernsthaft in die Praxis umzusetzen: Es würde vor dem Hintergrund der Stadtlandschaft nicht allzu ästhetisch aussehen und darüber hinaus aufgrund der Notwendigkeit eines mehrstufigen Austauschs eine gute Hälfte des Straßenraums verschlingen. Dennoch ist dieses rein hypothetische Netz ein guter Weg, um die notwendigen Schätzungen zu erhalten, die später leicht auf Straßennetze ausgedehnt werden können, die im Hinblick auf ihre Anwendbarkeit in realen Städten wirklich interessant sind.

Wie üblich gehen wir davon aus, dass die Migrationsbedürfnisse der Bewohner durch das Modell des „einheitlichen Zugangs“ beschrieben werden, und beginnen unsere Betrachtung mit dem Fall, dass die Kapazität aller von einem separaten Quartal generierten Reiseströme 1 beträgt.

, , . 27 . , , , , .


Abb. 26

Um den Wert der von der Stadt verursachten Umstellungskosten zu ermitteln, berechnen wir die Leistung aller Haupt- und Nebenflüsse in jeder ihrer Gebietszonen. Die Form und die gegenseitige Anordnung der Zonen ermöglichen es uns, auf eine Schachanalogie zurückzugreifen, um das letzte Problem zu lösen, wobei die Zonen als Feldzellen betrachtet werden und die Bewegung von Autos zwischen ihnen - Bewegungen des Bootes (Abb. 27). Von einer Zelle zur anderen, sofern sie sich in einer „allgemeinen Position“ zueinander befinden, kann der Turm in zwei Zügen bewegt werden, und wenn beide Zellen auf derselben Horizontalen oder einer Vertikalen liegen, dann in einer.


Abb. 27

Um viele unbequeme Vorbehalte zu vermeiden, gehen wir davon aus, dass die Bewegung, bei der sich der Turm nirgendwo bewegt, auch nach unseren Regeln zulässig ist. Die Bewegungsroute des Turms, die aus zwei Bewegungen besteht, von denen eine notwendigerweise vertikal und die andere horizontal ausgeführt wird, wird als die einfachste bezeichnet. Es ist sinnvoll, die vertikale und horizontale Bewegung gleichzeitig als „an Ort und Stelle“ zu betrachten. In diesem Fall stellt sich heraus, dass zwei beliebige Zellen auf der Platine auf genau zwei verschiedenen einfachsten Wegen miteinander verbunden sind.

«» , , . ( ) « » n = d ² , 1/(2 n ).

, ( i , j ) . ( i , j ) . ( 28 ):

1a) ( d − i ) ();
2a) ( i − 1) j - ();
3a) , j - .


Abb. 28

, ( 28 ):

1b) ( d − i ) j - ;
2b) ( i − 1)
3b) , j - .

2× [ d ⋅ ( i − 1) + 1 ⋅ ( i − 1) ] × ( d − i ) , :

P _SN ( i , j ) = ( d + 1) ⋅ ( i − 1) ⋅ ( d − i ) / n ( = P _SN ( i ) ).

j ,

( P _SN ) _j ( i ) = P _SN ( i , j = Const ),

, j - , , .
- , ( P _SN ) _j ( i ), .

, , , : P _SN ( i , j ) . , ( P _SN ) _j ( i ) = P _SN ( i ) j , , . , , , - .

P _SN ( i ):

( d + 1) ⋅ ( i − 1) ⋅ ( d − i ) /(2 n ).

, P _SN i ( i − 1) ⋅ ( d − i ). , d i - ( 29a).


Abb. 29a


Abb. 29b

, «» «», «» «» ( 29b) . :

1. P _SN ( i ) i = ( d + 1)/2, , Δ , Δ .
2. - , ( P _NS ) _j ( i ), j - , , - ( P _SN ) _j ( i ) i = ( d + 1)/2. ( P _SN ) _j ( i ) = P _SN ( i ), P _SN ( i ) i = ( d + 1)/2 , ( P _NS ) _j ( i ) = P _SN ( i ) = P _vert ( i ), , . P _SN ( i ) 30 (, d >> 1, i >> 1, d − i >> 1).

Abb. 30

, i j P _SN ( i ) .

, — . , ( i , j ), :

1. q _{in_transit} : — i - , — j - , ( i , j ) ( 31a);
2. q _{out_transit} : — j - , ( i , j ), — i - ( 31b);
3. q _in : — ( i , j ), — i - ( 31c);
4. q _out : — i - . — ( i , j ) ( 31d).

Abb. 32: abcd

, , , :

q ₀ = d ⋅ ( d − 1) /(2 n )

, , . ( i , j ) :

I _vert ( i , j ) = ( α /2 ν ) ⋅ P _vert ( i ) ⋅ [ ( q _in + q _{in_transit} ) ⋅ (1 + 1/ s ) + ( q _out + q _{out_transit} ) ⋅ (1 − 1/ s ) ] =
= 4 ( α /2 ν ) ⋅ ( d + 1)( i − 1)( d − i ) ⋅ d ( d − 1) /2 n ² ≈
≈ 2 ( α /2 ν ) ⋅ d ⁵ ⋅ ( i / d )(1 − i / d ) ⋅ (1/ d ) ⁴ =
= 2 ( α /2 ν ) ⋅ d ² ⋅ ( i / d )(1 − i / d ) ⋅ (1/ d ).

, , I _vert ( i , j ) :

I _vert = ∑ _ij I _vert ( i , j ) =
= 2 ( α /2 ν ) ⋅ d ² ⋅ ∑ _ij ( i / d )(1 − i / d ) ⋅ (1/ d ).

j , d :

∑ _ij ( i / d )(1 − i / d ) ⋅ (1/ d ) = d ⋅ ∑ _i ( i / d )(1 − i / d ) ⋅ (1/ d ).

:

∑ _i ( i / d )(1 − i / d ) ⋅ (1/ d ) ≈ ∫ t (1 − t ) d t ( t ∈[0; 1] ) = 1/2 − 1/3 = 1/6.

,

I _vert = ( α /2 ν ) ⋅ d ³ /3 = ( α /2 ν ) ⋅ n √ n /3.

, I _horiz , , , :

I _horiz = I _vert = ( α /2 ν ) ⋅ n √ n /3.

, :

I = I _vert + I _horiz = 2/3 ⋅ ( α /2 ν ) ⋅ n √ n ,



2/3 ⋅ ( α /2 ν ) ⋅ √ n


, — . , λ .
m . , I ₁ = 2/3 ⋅ ( α /2 ν ) ⋅ m √ m . λ λ , λ ² . :

I = 2/3 ⋅ ( α /2 ν ) λ ² ⋅ m √ m

, λ , : n = λ m . I n λ :

I = 2/3 ⋅ ( α /2 ν ) λ ² ⋅ m √ m =
= 2/3 ⋅ ( α /2 ν ) ⋅ √ λ ⋅ ( λ √ λ ) ⋅ ( m √ m ) =
= 2/3 ⋅ √ λ ( α /2 ν ) ⋅ ( λ m )√( λ m ) =
= 2/3 ⋅ √ λ ( α /2 ν ) ⋅ n √ n .

, , 2/3 ⋅ √ λ ( α /2 ν ) ⋅ √ n , √ λ , .

, , , . , , , , , , .


( - : Vincent Laforet)

. - , , . , , .


, , : , , , . , , , .


( - , : )

. 1 , , , : . . , : . , , «» , , , — ( 33).


Abb. 33

.

33, , . , , .

, , : ( ) ( , ), 500 . , , .

, , . , , - ( «1» 34a).


Abb. 34

, - , , , , ( «2» 34a), , , .

, ( 34b). , , , . , - , . «» «» , , .


. , ( 35) .


Abb. 35

, , — ( 36).


Abb. 36
, , , , () . , .

«» .

? .

, , , , , : , .

, , .

, ( i , j ) , , : 1/4 , 1/4 — , 1/4 ⋅ i / d
1/4 ⋅ (1 − i / d ) — ( 37).

Abb. 37

, , , , , , ( i , j ) . , ( i , j ) , , .

, ( i , j ), , ( 38).


Abb. 38

( i , j ) ( 38). , :
1/2 ⋅ ( )×( ( i , j )) ⋅ 1/ d ² =
= 1/2 ⋅ d ⋅ i / d ² =
= 1/2 ⋅ i / d .
:
1/2 ⋅ ( ( i , j ))×( ) ⋅ 1/ d ² =
= 1/2 ⋅ ( d − i ) ⋅ d / d ² =
= 1/2 ⋅ (1 − i / d ).

- , My_street. , , My_street ( 39).


Abb. 39

40 My_street, , , ( 26).



Abb. 40

, My_street , , . , , . , .


, , , «». , , . Q . , , , , Q ( 41a) Q .


. 41

, — , -, . , , «» , ( 41b).

. , . , r _k , Δ _k = ( x _k , x _{k +1} ] () x _k (, ). , () x _k , r _k q _in | Δ _k |/ n ( 1/ n Δ _k ), , r _k , - .

[1, x _k ] Δ _k , , , Δ _k , q _out x _k / n ( 42).


Abb. 42

Tatsächlich findet auch der Beitrag von „internen“ Reisen zur Kraft der seitlichen Strömungen statt, jedoch überschreitet der Wert dieses Beitrags niemals | Δ _k | / n ; daher in dem Fall, wenn x _k >> | Δ _k | kann einfach vernachlässigt werden. Die Leistung p _{k des} Hauptstroms entlang r _k mit vorgenommenen Vereinfachungen wird durch einen Graphen von zwei geraden Abschnitten mit einem Maximum P _k gleich x _k ⋅ | dargestellt Δk | / n . Der ungefähre Wert der Schaltverluste bei r _k kann durch die Formel ermittelt werden:

I _k = ( α / 2 ν ) ⋅ _x [ q _in ( x ) ⋅ p _k ( x ) ⋅ (1 + 1 / s )] + ( α / 2 ν ) ⋅ _x [ q _out ( x ) ⋅ p _k ( x ) ⋅ (1 - 1 / s )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ∑ _x [| Δ _k | / n ⋅ p _k ( x )] + ( α / 2 ν ) ⋅ (1 - 1 / s ) ∑ _x [ x _k / n ⋅ p _k ( x )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / x _k + ( α / 2 ν ) ⋅ (1 - 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / | Δ _k |,

wobei die erste Summe über die Fläche x ∈ [1, x _k ] und die zweite über x ∈ Δ _{k genommen wird} . Ausdrücke:

( ∑ _x p _k ( x )) / x _k , x ∈ [1, x _k ] und

( ∑ _x p _k ( x )) / | Δk |, x ∈ Δk

es gibt nichts mehr als die durchschnittliche Leistung des Stroms entlang r _k innerhalb der angegebenen Intervalle. Da der Leistungsgraph innerhalb dieser Intervalle die Form einer geraden Linie hat, beträgt die durchschnittliche Leistung in beiden Fällen P _k / 2. Ersetzen
x _k ⋅ | Δ _k | / n ein
P _k
Wir geben schließlich die Formel für die Verlustintensität in ihrer einfachsten Form:

I _k = 2 ( α / 2 ν ) ⋅ P _k ⋅ P _k / 2 = ( α / 2 ν ) ⋅ P _k ²

Versuchen wir nun, die Folge x _{k der} Zahlen jener Viertel zu berechnen, durch die die lineare Stadt in Segmente unterteilt werden soll. Als Kriterium für die Auswahl der Segmente nehmen wir an, dass die maximale Leistung der Verkehrsströme P _k auf geeigneten Straßen unabhängig von k , also der Gleichheit, den gleichen Wert hat

x _k ⋅ | Δ _k | = Konst.

Daran erinnern | Δ _k | = x _{k + 1} - x _k , wir kommen zu der Differenzgleichung:

x _{k + 1} - x _k = Konst / x _k .

Angenommen, x und k sind stetige Variablen, und ersetzen

x _{k + 1} - x _k = x ( k + 1) - x ( k )

auf d x / d k ⋅ 1,

Wir können die Differenzgleichung durch Differential approximieren:

d x / d k = Konst / x <=> x d x = Konst ⋅ d k .

Woher erhalten wir für x _{k eine} Lösung in der allgemeinen Form:

x _k = C ₁ √ ( k + C ₂ ).

Es bleibt uns überlassen, den Wert der Konstanten C ₁ und C ₂ aus den Randbedingungen zu bestimmen, es gibt jedoch eine wichtige Subtilität in dieser Angelegenheit. Anders als in den übrigen Segmenten begannen alle Autos, die von der Westautobahn zu den Vierteln des Segments Nummer 1 innerhalb desselben Segments kamen, ihre Reise. Infolgedessen hat der Graph der Strömungsleistung auf der ersten Autobahn nach Norden die Form einer regelmäßigen umgekehrten Parabel.

Gleichzeitig deuteten die a priori-Bedingungen, aus denen die Formel für x _{k erhalten} wurde, im Wesentlichen darauf hin, dass die Strömungsleistungsgraphen auf allen Autobahnen nahe an einer Dreiecksansicht liegen sollten und die Fahrten selbst hauptsächlich außerhalb des Segments beginnen sollten, in das sie gerichtet sind. Diese Anforderungen können mit angemessener Genauigkeit erfüllt werden, wenn wir das erste Segment formal in zwei gleiche Teile teilen (eine Parabel nähert sich einem gleichschenkligen Dreieck und die meisten Fahrten entlang der ersten Autobahn werden tatsächlich von der südlichen Hälfte des Segments Nummer 1 in die nördliche Hälfte geleitet), ohne die Anzahl der Straßen zu erhöhen ( Abb. 43).


Abb. 43

Es ist die Mitte des ersten Segments, die als Punkt x ₁ in der Formel für x _{k betrachtet werden sollte} . Von hier erhalten wir die erste Randbedingung:

x ₂ = 2 x ₁ oder

√ (2 + C ₂ ) = 2 ⋅ √ (1 + C ₂ ) =>

C ₂ = - 2/3.

Die zweite Randbedingung ergibt sich aus der Anforderung, dass die Straßen und Segmente genau Q sind , was bedeutet, dass x _{Q + 1} gleich dem nächsten Quartal mit der größten Anzahl in der Stadt sein sollte:

C ₁ √ ( Q + 1 - 2/3) = n + 1, woher

C ₁ ≈ ( n + 1) / √ Q.

Auf diese Weise:

x _k ≈ ( n + 1) ⋅ √ ( k - 2/3) / √ Q ,

| Δ _k | ≈ d x / d k = ( n + 1) / 2√ ( k - 2/3) ⋅ √ Q.

P _k = x _k ⋅ | Δk | / n =

= ( n + 1) 2/2 n ≤ Q ≤ n / 2 Q.

I _k = ( α / 2 ν ) ⋅ P _k ² =

= ( α / 2 ν ) ⋅ ( n / 2 Q ) ² .

Da alle 2 Q- Straßenautobahnen Verluste gleicher Intensität verursachen, beträgt der Wert der Vermittlungskosten innerhalb des gesamten Netzes:

I = 2 Q ⋅ ( α / 2 ν ) ⋅ ( n / 2 Q ) ² = ( α / 2 ν ) ⋅ n 2/2 Q.

Wie Sie sehen, wird das gewünschte Ziel erreicht: Nach der Aufteilung der Hauptautobahnen in Q- Teile verringerten sich die Verluste tatsächlich um den Faktor Q (mit Ausnahme des konstanten Koeffizienten von 1/3 bis 1/2, der im Vergleich zur Formel für die übliche lineare Stadt zunahm). Nun, die halbe Arbeit ist erledigt, es bleibt das Ergebnis anzuwenden, um die Stadt mit zellularer Architektur zu verbessern.

Wolkenkratzeraufzug in der Zellularstadt
Der Einfachheit halber werden wir uns mit einem Beispiel einer Stadt zufrieden geben, in der alle Straßen einseitig sind. Unter Verwendung der Analogie zwischen Linear City und den einzelnen Straßen der Cellular City teilen wir die Autobahn entlang dieser in Q- Teile. Standardmäßig wird angenommen, dass Sie das Viertel verlassen und auf jede Autobahn fahren können, die in der Nähe des Viertels vorbeiführt. Gleichzeitig gibt es unter allen Autobahnen, die entlang einer Straße verlegt sind, eine Kurve in Richtung eines bestimmten Viertels mit genau einer davon. Bei der Festlegung von Regeln sind deren Einheitlichkeit und Einfachheit äußerst wichtig. Schauen Sie sich Abbildung 44 an:


Abb. 44

Alle Straßen haben das gleiche Erscheinungsbild und die gleichen Regeln. Welche ihrer Straßen in welchen Kontoblöcken öffnet den Zugang? Abbildung 45 zeigt ein Diagramm der zulässigen Abbiegungen zwischen Autobahnen. Ein Blick auf dieses Bild ist schwer zu verwechseln. Das gleiche wird oft über das U-Bahn-System in einer Großstadt gesagt. In beiden Fällen wird jedoch alles klar und einfach, wenn Sie die Logik der Idee kennen. Die logische Regel für zulässige Abbiegungen klingt recht einfach: Wenn Sie auf einer Autobahn fahren, überqueren Sie Straßen senkrecht zu Ihrer Bewegung und können in ein Viertel direkt dahinter abbiegen. Sie können auf jede dieser Straßen abbiegen.


Abb. 45

Die Skyscraper Lift-Topologie ist sowohl mit Ampeln als auch mit Überführungen kompatibel. Es ist schwierig, kann aber auf Netzwerke verallgemeinert werden, die nicht unbedingt eine zelluläre oder lineare Struktur haben. Letzteres ist wirklich wichtig für historische Städte, in denen es unwahrscheinlich ist, dass es richtig ist, die Hälfte der historischen Denkmäler abzureißen, um viele kleine gerade Straßen zu legen, in denen es jedoch bereits ziemlich große Straßen gibt, die mehrere zwei- oder dreispurige Autobahnen aufnehmen können.

Über die Probleme des Verkehrs und die Arbeit der Mathematik

Es ist angenehm, die halbjährliche sorgfältige Arbeit abzuschließen. Die Arbeit, die ich geschrieben habe, löst natürlich nicht alle Probleme und Schwierigkeiten der Straßenplanung - dieses Geschäft erfordert eine große Anzahl sehr unterschiedlicher Menschen. Dennoch bieten die Ergebnisse die Möglichkeit, wichtige Fehler in bereits gebauten Städten zu erkennen und Methoden zur Vermeidung solcher Fehler in der Zukunft bereitzustellen. Dieser Artikel war nicht als Nachschlagewerk gedacht, das alle möglichen Fälle abdeckt, denen ein Ingenieur in der Praxis begegnen kann. Ich betrachtete meine Hauptaufgabe darin, einen neuen Standpunkt zu vertreten, einen neuen Weg zu finden, um über das Problem nachzudenken und darüber zu sprechen, um das notwendige Minimum an einfachen Modellbeispielen bereitzustellen, die vom Leser erstellt wurden könnte mich schon erweitern.

Es wird traurig, wenn man merkt, wie viel Zeit die Stadtbewohner im Stau verloren haben, nur weil es zur richtigen Zeit keinen Mathematiker gab, der den Abend mit einem vollständig lösbaren Problem verbringen konnte. Wie viele dieser Probleme umgeben noch unser Leben oder verstecken sich in Ihrem Beruf? Sitzt eine Person bei der Arbeit in Ihrer Nähe, deren Werkzeuge einen Bleistift und ein Blatt Papier haben?

Ich hoffe, dass sich alles zum Besseren ändert.

Vielen Dank für Ihre Aufmerksamkeit und viel Glück!
Sergey Kovalenko.

2019 Jahr
magnolia@bk.ru


(Foto: Vincent Laforet)