Gieriger Ansatz und Spielautomaten. Analyse der Aufgaben der ML-Strecke der Programmiermeisterschaft

Wir veröffentlichen weiterhin Analysen der Aufgaben, die bei der letzten Meisterschaft vorgeschlagen wurden. Als nächstes folgen Aufgaben aus der Qualifikationsrunde für Spezialisten für maschinelles Lernen. Dies ist der dritte von vier Tracks (Backend, Frontend, ML, Analytics). Die Teilnehmer mussten ein Modell für die Korrektur von Tippfehlern in Texten erstellen, eine Strategie für das Spielen an Spielautomaten vorschlagen, ein System von Empfehlungen für Inhalte in Erinnerung rufen und mehrere weitere Programme erstellen.

A. Tippfehler

Zustand

(Epigraph) (aus einem Forum)
- Wer hat diesen Unsinn komponiert?
- Astrophysiker. Sie sind auch Menschen.
- Sie haben 10 Fehler im Wort "Journalisten" gemacht.

Viele Benutzer machen Tippfehler, einige aufgrund von Tastenanschlägen und andere aufgrund ihres Analphabetismus. Wir möchten prüfen, ob der Benutzer tatsächlich an ein anderes Wort als das von ihm eingegebene denken kann.

Nehmen wir formeller an, dass das folgende Fehlermodell auftritt: Der Benutzer beginnt mit einem Wort, das er schreiben möchte, und macht anschließend eine Reihe von Fehlern. Jeder Fehler ist eine Ersetzung eines Teilstrings des Wortes durch einen anderen Teilstring. Ein Fehler entspricht dem Ersetzen nur an einer Position (dh wenn der Benutzer einen einzelnen Fehler durch die Regel "abc" → "cba" machen möchte, kann er aus der Zeichenfolge "abcabc" entweder "cbaabc" oder "abccba" erhalten). Nach jedem Fehler wird der Vorgang wiederholt. Dieselbe Regel könnte mehrmals in verschiedenen Schritten verwendet werden (im obigen Beispiel könnte beispielsweise "cbacba" in zwei Schritten erhalten werden).

Es ist erforderlich, die Mindestanzahl von Fehlern zu bestimmen, die ein Benutzer machen kann, wenn er ein bestimmtes Wort im Auge hat und ein anderes schreibt.

Lösung

Versuchen wir, aus der richtigen Schreibweise alle möglichen Wörter mit nicht mehr als 4 Fehlern zu generieren. Im schlimmsten Fall kann O ((L﹒N) ⁴ ) vorliegen. In den Grenzen des Problems ist dies eine ziemlich große Zahl, daher müssen Sie herausfinden, wie Sie die Komplexität reduzieren können. Stattdessen können Sie den Meet-in-the-Middle-Algorithmus verwenden: Generieren Sie Wörter mit nicht mehr als 2 Fehlern sowie Wörter, aus denen Sie ein vom Benutzer geschriebenes Wort mit nicht mehr als 2 Fehlern erhalten können. Beachten Sie, dass die Größe jedes dieser Sätze 10 ⁶ nicht überschreitet. Wenn die Anzahl der vom Benutzer gemachten Fehler 4 nicht überschreitet, überschneiden sich diese Sätze. Ebenso können wir überprüfen, ob die Anzahl der Fehler 3, 2 und 1 nicht überschreitet.

 struct FromTo { std::string from; std::string to; }; std::pair<size_t, std::string> applyRule(const std::string& word, const FromTo &fromTo, int pos) { while(true) { int from = word.find(fromTo.from, pos); if (from == std::string::npos) { return {std::string::npos, {}}; } int to = from + fromTo.from.size(); auto cpy = word; for (int i = from; i < to; i++) { cpy[i] = fromTo.to[i - from]; } return {from, std::move(cpy)}; } } void inverseRules(std::vector<FromTo> &rules) { for (auto& rule: rules) { std::swap(rule.from, rule.to); } } int solve(std::string& wordOrig, std::string& wordMissprinted, std::vector<FromTo>& replaces) { std::unordered_map<std::string, int> mapping; std::unordered_map<int, std::string> mappingInverse; mapping.emplace(wordOrig, 0); mappingInverse.emplace(0, wordOrig); mapping.emplace(wordMissprinted, 1); mappingInverse.emplace(1, wordMissprinted); std::unordered_map<int, std::unordered_set<int>> edges; auto buildGraph = [&edges, &mapping, &mappingInverse](int startId, const std::vector<FromTo>& replaces, bool dir) { std::unordered_set<int> mappingLayer0; mappingLayer0 = {startId}; for (int i = 0; i < 2; i++) { std::unordered_set<int> mappingLayer1; for (const auto& v: mappingLayer0) { auto& word = mappingInverse.at(v); for (auto& fromTo: replaces) { size_t from = 0; while (true) { auto [tmp, wordCpy] = applyRule(word, fromTo, from); if (tmp == std::string::npos) { break; } from = tmp + 1; { int w = mapping.size(); mapping.emplace(wordCpy, w); w = mapping.at(wordCpy); mappingInverse.emplace(w, std::move(wordCpy)); if (dir) { edges[v].emplace(w); } else { edges[w].emplace(v); } mappingLayer1.emplace(w); } } } } mappingLayer0 = std::move(mappingLayer1); } }; buildGraph(0, replaces, true); inverseRules(replaces); buildGraph(1, replaces, false); { std::queue<std::pair<int, int>> q; q.emplace(0, 0); std::vector<bool> mask(mapping.size(), false); int level{0}; while (q.size()) { auto [w, level] = q.front(); q.pop(); if (mask[w]) { continue; } mask[w] = true; if (mappingInverse.at(w) == wordMissprinted) { return level; } for (auto& v: edges[w]) { q.emplace(v, level + 1); } } } return -1; } 

B. Vielarmiger Bandit

Zustand

Dies ist eine interaktive Aufgabe.

Sie selbst wissen nicht, wie es passiert ist, aber Sie befanden sich in einer Halle mit Spielautomaten mit einer ganzen Tüte Token. Leider lehnen sie es an der Abendkasse ab, Token zurückzunehmen, und Sie haben beschlossen, Ihr Glück zu versuchen. Es gibt viele Spielautomaten in der Halle, die Sie spielen können. Für ein Spiel mit einem Spielautomaten verwenden Sie einen Token. Im Falle eines Gewinns gibt Ihnen die Maschine einen Dollar, im Falle eines Verlustes - nichts. Jede Maschine hat eine feste Gewinnwahrscheinlichkeit (die Sie nicht kennen), die jedoch für verschiedene Maschinen unterschiedlich ist. Nachdem Sie die Website des Herstellers dieser Maschinen studiert haben, haben Sie festgestellt, dass die Gewinnwahrscheinlichkeit für jede Maschine in der Herstellungsphase zufällig aus der Beta-Verteilung mit bestimmten Parametern ausgewählt wird.

Sie möchten Ihre erwarteten Gewinne maximieren.

Lösung

Dieses Problem ist bekannt und kann auf verschiedene Arten gelöst werden. Die Hauptentscheidung der Jury setzte die Thompson-Stichprobenstrategie um. Da jedoch die Anzahl der Schritte zu Beginn des Programms bekannt war, gibt es optimalere Strategien (z. B. UCB1). Darüber hinaus könnte man sogar mit der Epsilon-Greedy-Strategie auskommen: Mit einer bestimmten Wahrscheinlichkeit ε eine zufällige Maschine spielen und mit einer Wahrscheinlichkeit (1 - ε) eine Maschine mit der besten Siegesstatistik spielen.

 class SolverFromStdIn(object): def __init__(self): self.regrets = [0.] self.total_win = [0.] self.moves = [] class ThompsonSampling(SolverFromStdIn): def __init__(self, bandits_total, init_a=1, init_b=1): """ init_a (int): initial value of a in Beta(a, b). init_b (int): initial value of b in Beta(a, b). """ SolverFromStdIn.__init__(self) self.n = bandits_total self.alpha = init_a self.beta = init_b self._as = [init_a] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self._bs = [init_b] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self.last_move = -1 random.seed(int(time.time())) def move(self): samples = [random.betavariate(self._as[x], self._bs[x]) for x in range(self.n)] self.last_move = max(range(self.n), key=lambda x: samples[x]) self.moves.append(self.last_move) return self.last_move def set_reward(self, reward): i = self.last_move r = reward self._as[i] += r self._bs[i] += (1 - r) return i, r while True: n, m = map(int, sys.stdin.readline().split()) if n == 0 and m == 0: break alpha, beta = map(float, sys.stdin.readline().split()) solver = ThompsonSampling(m) for _ in range(n): print >> sys.stdout, solver.move() + 1 sys.stdout.flush() reward = int(sys.stdin.readline()) solver.set_reward(reward) 

C. Ausrichtung der Sätze

Zustand

Eine der wichtigsten Aufgaben für das Training eines guten maschinellen Übersetzungsmodells ist ein guter Fall von parallelen Sätzen. In der Regel sind parallele Angebote die Quelle für parallele Angebote. Es stellt sich heraus, dass Sie häufig nur ihre Länge kennen müssen, um ein bestimmtes Korpus paralleler Sätze zu bilden. Insbesondere stellen Sie möglicherweise fest, dass der Satz in der Ausgangssprache umso länger übersetzt wird, je länger er ist. Einige Schwierigkeiten liegen in der Tatsache, dass sich während der Übersetzung die Anzahl der Sätze im Text ändern kann: Manchmal können zwei benachbarte Sätze in der Übersetzung zu einem kombiniert werden oder umgekehrt - ein Satz kann in zwei Sätze geteilt werden. In einigen seltenen Fällen können Sätze in einer Übersetzung vollständig weggelassen werden, oder eine Übersetzung kann in einer Übersetzung erscheinen, die nicht im Original enthalten war.

Nehmen wir formeller an, dass das folgende generative Modell für parallele Gehäuse wahr ist. Bei jedem Schritt führen wir einen der folgenden Schritte aus:

1. Stoppen Sie

Mit der Wahrscheinlichkeit p _h endet _die Erzeugung der Rümpfe.

2. [1-0] Angebote überspringen

Mit der Wahrscheinlichkeit p _d schreiben _wir dem Originaltext einen Satz zu. Wir schreiben der Übersetzung nichts zu. Die Länge des Satzes in der Originalsprache L ≥ 1 wird aus der diskreten Verteilung ausgewählt:

.

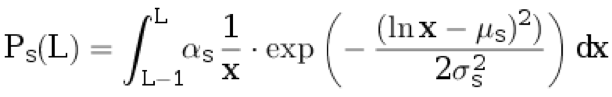
Hier sind μs , σs die Verteilungsparameter und αs der so gewählte Normalisierungskoeffizient .

3. [0-1] Vorschlag einfügen

Mit der Wahrscheinlichkeit p _i weisen _wir der Übersetzung einen Satz zu. Wir schreiben dem Original nichts zu. Die Länge eines Satzes in einer Übersetzungssprache L ≥ 1 wird aus einer diskreten Verteilung ausgewählt:

.

Hier sind μ _t , σ _t die Verteilungsparameter und α _t der so gewählte Normalisierungskoeffizient .

4. Übersetzung

Mit der Wahrscheinlichkeit (1 - p _d - p _i - p _h ) nehmen wir die Länge des Satzes in der Originalsprache L _s ≥ 1 aus der Verteilung p _s (mit Aufrundung). Als nächstes erzeugen wir die Länge des Satzes in der Übersetzungssprache L _t ≥ 1 aus der bedingten diskreten Verteilung:

.

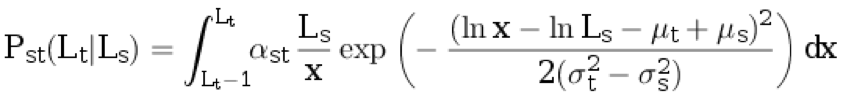
Hier ist α _st der Normalisierungskoeffizient, und die verbleibenden Parameter sind in den vorhergehenden Absätzen beschrieben.

Weiter ist ein weiterer Schritt:

1. [2-1] Mit der Wahrscheinlichkeit p _{split s} teilt sich _der erzeugte Satz in der Originalsprache in zwei nicht leere auf, so dass sich die Gesamtzahl der Wörter um genau eins erhöht . Die Wahrscheinlichkeit, dass ein Satz der Länge L _s in Teile der Länge L ₁ und L ₂ zerfällt (dh L ₁ + L ₂ = L _s + 1), ist proportional zu P _s (L ₁ ) ⋅ P _s (L ₂ ).

2. [1-2] Mit der Wahrscheinlichkeit p _{split t} teilt sich _der erzeugte Satz in der Zielsprache in zwei nicht leere Sätze auf, so dass sich die Gesamtzahl der Wörter um genau eins erhöht. Die Wahrscheinlichkeit, dass ein Satz der Länge L _t in Teile der Länge L1 und L2 zerfällt (dh L ₁ + L ₂ = L _t + 1), ist proportional zu P _t (L ₁ ) ⋅ P _t (L ₂ ).

3. 3. [1-1] Mit einer Wahrscheinlichkeit von (1 - p _{split s} - p _{split t} ) zerfällt keiner der generierten Sätze.

Lösung

Die Aufgabe ist ein Sonderfall der Ausrichtung mit Hidden-Markov-Modellen (HMM-Ausrichtung). Die Hauptidee ist, dass Sie die Wahrscheinlichkeit berechnen können, mit diesem Modell und dem Vorwärtsalgorithmus ein bestimmtes Dokumentpaar zu generieren: In diesem Fall ist der Status ein Paar von Dokumentpräfixen. Dementsprechend kann die erforderliche Wahrscheinlichkeit der Ausrichtung eines bestimmten Paares paralleler Sätze durch den Vorwärts-Rückwärts- Algorithmus berechnet werden.

D. Band mit Empfehlungen

Zustand

Betrachten Sie einen Feed mit Empfehlungen für heterogene Inhalte. Es mischt Objekte verschiedener Typen (Bilder, Videos, Nachrichten usw.). Diese Objekte sind normalerweise nach Relevanz für den Benutzer geordnet: Je relevanter (interessanter) das Objekt für den Benutzer ist, desto näher am Anfang der Empfehlungsliste. Bei einer solchen Reihenfolge treten jedoch häufig Situationen auf, in denen mehrere Objekte desselben Typs in der Liste der Empfehlungen aufgeführt sind. Dies verschlechtert die externe Vielfalt unserer Empfehlungen erheblich und daher gefällt es den Benutzern nicht. Es ist erforderlich, einen Algorithmus zu implementieren, der gemäß der Liste der Empfehlungen eine neue Liste erstellt, die frei von diesem Problem ist und am relevantesten ist.

Eine erste Liste von Empfehlungen sei a = [a ₀ , a ₁ , ..., a _{n - 1} ] mit der Länge n> 0. Ein Objekt mit der Nummer i hat den Typ mit der Nummer b _i ∈ {0, ..., m - 1}. Zusätzlich hat ein Objekt unter der Nummer i die Relevanz r (a _i ) = 2 _−i . Betrachten Sie die Liste, die aus der ersten Liste erhalten wird, indem Sie eine Teilmenge von Objekten auswählen und neu anordnen: x = [a _{i 0} , a _{i 1} , ..., a _{i k - 1} ] mit der Länge k (0 ≤ k ≤ n). Eine Liste wird als zulässig bezeichnet, wenn keine zwei aufeinanderfolgenden Objekte in ihrem Typ übereinstimmen, d. H. B _{i j} ≠ b _{i j + 1} für alle j = 0, ..., k - 2. Die Relevanz der Liste wird durch die Formel berechnet $$$\ sum_ {j = 0} ^ {k-1} 2 _ {- j} r (a_ {i_j})$. Sie müssen die Liste der maximalen Relevanz unter allen gültigen finden.

Lösung

Mit einfachen mathematischen Berechnungen kann gezeigt werden, dass das Problem durch einen „gierigen“ Ansatz gelöst werden kann, dh in der optimalen Liste von Empfehlungen hat jeder Punkt das relevanteste Objekt von allen, die am selben Anfang der Liste gültig sind. Die Implementierung dieses Ansatzes ist einfach: Wir nehmen Objekte in einer Reihe und fügen sie, wenn möglich, der Antwort hinzu. Wenn ein ungültiges Objekt gefunden wird (dessen Typ mit dem Typ des vorherigen übereinstimmt), legen wir es in einer separaten Warteschlange beiseite, aus der wir es so schnell wie möglich in die Antwort einfügen. Beachten Sie, dass zu jedem Zeitpunkt alle Objekte in dieser Warteschlange einen übereinstimmenden Typ haben. Am Ende verbleiben möglicherweise mehrere Objekte in der Warteschlange. Sie werden nicht in die Antwort aufgenommen.

  std::vector<int> blend(int n, int m, const std::vector<int>& types) { std::vector<int> result; std::queue<int> repeated; for (int i = 0; i < n; ++i) { if (result.empty() || types[result.back()] != types[i]) { result.push_back(i); if (!repeated.empty() && types[repeated.front()] != types[result.back()]) { result.push_back(repeated.front()); repeated.pop(); } } else { repeated.push(i); } } return result; } 

D. Clusterisierung von Zeichenfolgen

Es gibt ein endliches Alphabet A = {a ₁ , a ₂ , ..., a _{K - 1} , a _K = S}, a _i ∈ {a, b, ..., z}, S ist das Ende der Zeile.

Betrachten Sie die folgende Methode zum Generieren von zufälligen Zeichenfolgen über dem Alphabet A:

1. Das erste Zeichen x ₁ ist eine Zufallsvariable mit der Verteilung P (x ₁ = a _i ) = q _i (es ist bekannt, dass q _K = 0 ist).
2. Jedes nächste Zeichen wird basierend auf dem vorherigen gemäß der bedingten Verteilung P (x _i = a _j || x _{i - 1} = a _l ) = p _{jl erzeugt} .
3. Wenn x _i = S ist, stoppt die Erzeugung und das Ergebnis ist x ₁ x ₂ ... x _{i - 1} .

Der Satz von Linien, die aus einer Mischung von zwei beschriebenen Modellen mit unterschiedlichen Parametern erzeugt werden, ist angegeben. Für jede Zeile muss der Index der Kette angegeben werden, aus der sie generiert wurde.

Lösung

Das Problem wird mithilfe des EM-Algorithmus gelöst: Es wird angenommen, dass die dargestellte Probe aus einer Mischung von zwei Markov-Ketten generiert wird, deren Parameter während der Iterationen wiederhergestellt werden. Eine Einschränkung von 80% der richtigen Antworten wird vorgenommen, damit die Richtigkeit der Lösung nicht durch Beispiele beeinträchtigt wird, die in beiden Ketten eine hohe Wahrscheinlichkeit haben. Diese Beispiele können daher bei ordnungsgemäßer Wiederherstellung einer Kette zugewiesen werden, die hinsichtlich der generierten Antwort falsch ist.

 import random import math EPS = 1e-9 def empty_row(size): return [0] * size def empty_matrix(rows, cols): return [empty_row(cols) for _ in range(rows)] def normalized_row(row): row_sum = sum(row) + EPS return [x / row_sum for x in row] def normalized_matrix(mtx): return [normalized_row(r) for r in mtx] def restore_params(alphabet, string_samples): n_tokens = len(alphabet) n_samples = len(string_samples) samples = [tuple([alphabet.index(token) for token in s] + [n_tokens - 1, n_tokens - 1]) for s in string_samples] probs = [random.random() for _ in range(n_samples)] for _ in range(200): old_probs = [x for x in probs] # probs fixed p0, A = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) q0, B = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) for prob, sample in zip(probs, samples): p0[sample[0]] += prob q0[sample[0]] += 1 - prob for t1, t2 in zip(sample[:-1], sample[1:]): A[t1][t2] += prob B[t1][t2] += 1 - prob A, p0 = normalized_matrix(A), normalized_row(p0) B, q0 = normalized_matrix(B), normalized_row(q0) trans_log_diff = [ [math.log(b + EPS) - math.log(a + EPS) for b, a in zip(B_r, A_r)] for B_r, A_r in zip(B, A) ] # A, p0, B, q0 fixed probs = empty_row(n_samples) for i, sample in enumerate(samples): value = math.log(q0[sample[0]] + EPS) - math.log(p0[sample[0]] + EPS) for t1, t2 in zip(sample[:-1], sample[1:]): value += trans_log_diff[t1][t2] probs[i] = 1.0 / (1.0 + math.exp(value)) if max(abs(x - y) for x, y in zip(probs, old_probs)) < 1e-9: break return [int(x > 0.5) for x in probs] def main(): N, K = list(map(int, input().split())) string_samples = [] alphabet = list(input().strip()) + [''] for _ in range(N): string_samples.append(input().rstrip()) result = restore_params(alphabet, string_samples) for r in result: print(r) if __name__ == '__main__': main() 

---

.