Eine leicht zugängliche Erklärung des Wellenfunktionskollapsalgorithmus

Der Wavefunction Collapse-Algorithmus bringt einem Computer das Improvisieren bei. Bei der Eingabe empfängt es archetypische Daten und erstellt prozedural generierte Daten ähnlich dem Original.


( Quelle )

Meistens wird es verwendet, um Bilder zu erstellen, aber es kann auch Städte bauen, Skateparks bauen und schreckliche Gedichte schreiben.


( Quelle )

Der Zusammenbruch der Wellenfunktion ist ein sehr unabhängig denkender Algorithmus, der praktisch keine Hilfe oder Anweisungen von außen benötigt. Sie brauchen nur ein Beispiel für den Stil, den Sie erreichen möchten, und er wird den Rest erledigen. Trotz seiner Selbstversorgung ist er überraschend einfach. Es werden keine neuronalen Netze, zufälligen Wälder oder andere Elemente verwendet, die dem maschinellen Lernen ähneln. Wenn Sie sich mit der Idee beschäftigen, wird sie für Sie sehr verständlich und intuitiv.

Die meisten Implementierungen und Erklärungen des Zusammenbruchs der Wellenfunktion sind eine vollständige, geschwindigkeitsoptimierte Version des Algorithmus. Natürlich sind alle wichtig und notwendig, aber es ist schwierig, sie von Grund auf zu verstehen. In diesem Beitrag werde ich alles in einer einfachen Sprache erklären, die ich verstehe, wobei ich mich auf die limitierte Wavefunction-Version konzentriere, die ich Even Simpler Tiled Model nannte . Außerdem habe ich eine Beispielimplementierung von ESTM auf Github veröffentlicht . Der darin enthaltene Code ist ineffizient und langsam, aber sehr gut lesbar und ausführlich kommentiert. Sobald Sie die ESTM zugrunde liegende Technologie verstanden haben, werden Sie dem Verständnis komplexerer Versionen des Algorithmus näher kommen. Wenn Sie den Kollapsalgorithmus für Wellenfunktionen verstehen möchten, ist dieser Artikel ein guter Anfang.

Beginnen wir mit der Geschichte.

Die Hochzeit

Stellen Sie sich vor, Sie planen Ihre Hochzeit. Zusätzlich zur Auswahl an Schmuck und Musik müssen Sie einen Sitzplan für die Gäste zum Abendessen erstellen. Ihre Familie mag es zu streiten und ungezogen zu sein, daher kann es schwierig sein. Ein Vater kann nicht näher als zwei Tische von seiner Mutter sitzen. Eine Cousine wird einsam, wenn sie nicht mit einer anderen Cousine zusammensitzt. Und es ist besser, Onkel Roy nicht neben den umweltfreundlichen Mitgliedern der Familie Ihres Partners zu pflanzen. Es bleibt nur 5 Stunden vor dem Eintreffen des Essens, also entscheiden Sie sich, diese hartnäckige Aufgabe mit dem Wellenfunktions-Kollaps-Algorithmus anzugreifen.

Sie beginnen mit einer langen Liste von Regeln und einem leeren Sitzplan.


Sie erstellen die ursprüngliche Wellenfunktion des Plans. Sie bindet jeden Stuhl an eine Liste von Personen, die darauf sitzen können. Während jede Person auf jedem Stuhl sitzen kann. Die Wellenfunktion von Sitzgästen beginnt mit einer vollständigen Überlagerung (das Konzept ist der Quantenphysik entlehnt) jedes möglichen Schemas.


Schrödingers Katze war gleichzeitig tot und lebendig, bis jemand die Schachtel öffnete und nachschaute; Ihr Plan ist gleichzeitig jedes mögliche Schema, bis Sie die Dinge in Ordnung bringen. Eine vollständige Überlagerung ist ein nützliches theoretisches Konstrukt, aber es hilft Ihrer Großmutter nicht herauszufinden, wo sie sitzen muss. Sie müssen die Wellenfunktion des Aufenthaltsorts der Gäste auf einen bestimmten Zustand bringen, der dann in gewöhnliche Nicht-Quanten-Visitenkarten umgewandelt werden kann.

Wir beginnen dies, indem wir den Zusammenbruch der Wellenfunktion für einen Stuhl durchführen. Wir wählen einen Stuhl aus, sehen uns die Liste der Personen an, die darauf sitzen können, und weisen ihn zufällig einer von ihnen zu. In diesem Fall wird die Wellenfunktion des Stuhls zusammengebrochen.


Diese Wahl hat Konsequenzen, die sich auf die Wellenfunktionen der verbleibenden Stühle erstrecken. Wenn Onkel Roy an Tisch 2 sitzt, werden Cousin Frank und Michelle Obama (eine Freundin der Familie Ihres Partners) definitiv nicht neben ihm sein. Und wenn Michelle nicht an Tisch 2 sitzt, wird Barack auch nicht hinter ihm sein. Wir aktualisieren die Wellenfunktion des Lageplans, indem wir Personen aus den Listen möglicher Kandidaten löschen.


Sobald sich die Schwingungen gelegt haben, wiederholen wir diesen Vorgang. Wir wählen einen anderen Stuhl mit mehreren möglichen Kandidaten aus und reduzieren seine Wellenfunktion, indem wir zufällig eine der für ihn akzeptablen Personen auswählen. Wieder erweitern wir die durch diese Wahl verursachten Vibrationen auf den Rest des Plans und entfernen Personen aus der Wellenfunktion des Stuhls, wenn sie nicht mehr darauf sitzen können.

Wir wiederholen diesen Vorgang entweder, bis die Wellenfunktion zusammenbricht (dh genau 1 sitzende Person bleibt darin) oder bis wir einen Widerspruch erreichen . Widerspruch ist ein Stuhl, auf dem niemand sitzen kann, weil sie alle aufgrund früherer Wahlen ausgewiesen wurden. Der Widerspruch macht es unmöglich, die gesamte Wellenfunktion zusammenzubrechen.

Wenn Sie einen Widerspruch erreicht haben, ist es am einfachsten, von vorne zu beginnen. Verwerfen Sie alle vorherigen Arbeiten, suchen Sie einen neuen leeren Plan und starten Sie den Algorithmus erneut, um den Zusammenbruch der Wellenfunktion für einen anderen zufälligen Stuhl abzuschließen. Sie können auch ein Backtracking-System implementieren, mit dem Sie eine bestimmte Auswahl stornieren können, anstatt alles sofort aufzugeben ("Was ist, wenn Sheila auf den Stuhl 54 versetzt wird?").

Nach einigen Fehlstarts erreichen Sie endlich einen vollständig zusammengebrochenen Zustand, in dem jeder Stuhl genau einer Person zugeordnet ist und alle Regeln befolgt werden. Fertig!

Von der Hochzeit bis zu Bitmaps

Dies ist kein theoretisches Beispiel. Sie können wirklich eine Variante des Zusammenbruchs der Wellenfunktion realisieren, die einen Sitzplan für die Gäste für die Hochzeit erstellt. Beim traditionelleren Wavefunction Collapse versuchen wir jedoch normalerweise, keine Personen bei der Hochzeit zu setzen, sondern die Pixel im Ausgabebild anzuordnen. Der Prozess wird jedoch sehr ähnlich sein. Wir bringen dem Algorithmus eine Reihe von Regeln bei, die die Ausgabe erfüllen sollte. Wir initialisieren die Wellenfunktion. Wir führen den Zusammenbruch eines Elements durch und erweitern die Konsequenzen auf den Rest der Wellenfunktion. Und das tun wir so lange, bis die Wellenfunktion vollständig zusammenbricht oder bis wir einen Widerspruch erreichen.

Der traditionelle Zusammenbruch der Wellenfunktion unterscheidet sich vom Zusammenbruch der Hochzeit darin, wie wir dem Algorithmus die Regeln beibringen, denen er folgen muss. In der Hochzeitsversion mussten wir die Regeln selbst aufschreiben. In der traditionellen Version geben wir dem Algorithmus jedoch nur ein Beispielbild, und basierend darauf erstellt der Algorithmus den Rest. Er analysiert ein Beispiel, analysiert seine Muster und findet heraus, wie Pixel oder Kacheln ausgerichtet werden sollen.

Beginnen wir mit der Untersuchung des tatsächlichen Zusammenbruchs einer Wellenfunktion, indem wir einen einfachen Sonderfall betrachten, den ExUtumno (der Ersteller des Algorithmus) als Simple Tiled Model bezeichnet .

Einfaches gekacheltes Modell

Im einfachen gekachelten Modell werden Eingabe- und Ausgabebilder aus einer kleinen Anzahl vordefinierter Kacheln erstellt, und jedes Quadrat im Ausgabebild ist nur auf seine vier nächsten Nachbarn beschränkt. Angenommen, wir generieren zufällige Welten für ein zweidimensionales Spiel mit einer Draufsicht. Wir können Kacheln für Land, Küste und Meer haben sowie eine Reihe von Regeln wie "Die Küste kann in der Nähe des Meeres sein", "Land kann in der Nähe der Küste sein" und "Das Meer kann neben einem anderen Meer sein".


Das einfache gekachelte Modell berücksichtigt die Symmetrie und Drehung seiner Kacheln. Beispielsweise kann sich Land in Küstennähe befinden, jedoch nur in der richtigen Ausrichtung.


Diese Symmetrieverarbeitung liefert bessere Ausgabebilder, kompliziert jedoch den Code. Um die Dinge einfach zu halten, schauen wir uns eine noch einfachere Ansicht des Zusammenbruchs der Wellenfunktion an, die ich Even Simpler Tiled Model nannte .

Noch einfacher gekacheltes Modell

Selbst das einfachere gekachelte Modell („ein noch einfacheres Kachelmodell“) ähnelt dem einfachen gekachelten Modell, aber seine Kacheln haben keine Symmetrieeigenschaften. Jede Kachel ist ein Pixel derselben Farbe, das heißt, wir können ihre Kanten in keiner Weise verwechseln.


Selbst einfachere Regeln für gekachelte Modelle bestimmen, welche Kacheln in welcher Ausrichtung nebeneinander platziert werden können. Jede Regel ist ein Tupel aus drei Elementen (3-Tupel): zwei Kacheln und eine Richtung. Zum Beispiel bedeutet (SEA, COAST, LEFT) , dass die SEA Kachel (Meer) von der COAST Kachel (Küste) COAST kann. Diese Regel muss von einer anderen Regel begleitet sein, die die Situation in Bezug auf COAST - (COAST, SEA, RIGHT) .


Wenn Sie möchten, dass sich die SEA Kacheln nicht nur , sondern auch von den COAST Kacheln befinden. dann brauchen sie zusätzliche Regeln: (SEA, COAST, RIGHT) und (COAST, SEA, LEFT) .

Wie ich oben sagte, müssen wir nicht selbst eine Liste all dieser Regeln erstellen. Durch das Zusammenfallen der Wellenfunktion können Regeln für ein noch einfacheres Kachelmodell erstellt werden, indem ein Beispielbild analysiert und eine Liste aller darin enthaltenen 3-Tupel gesammelt wird.


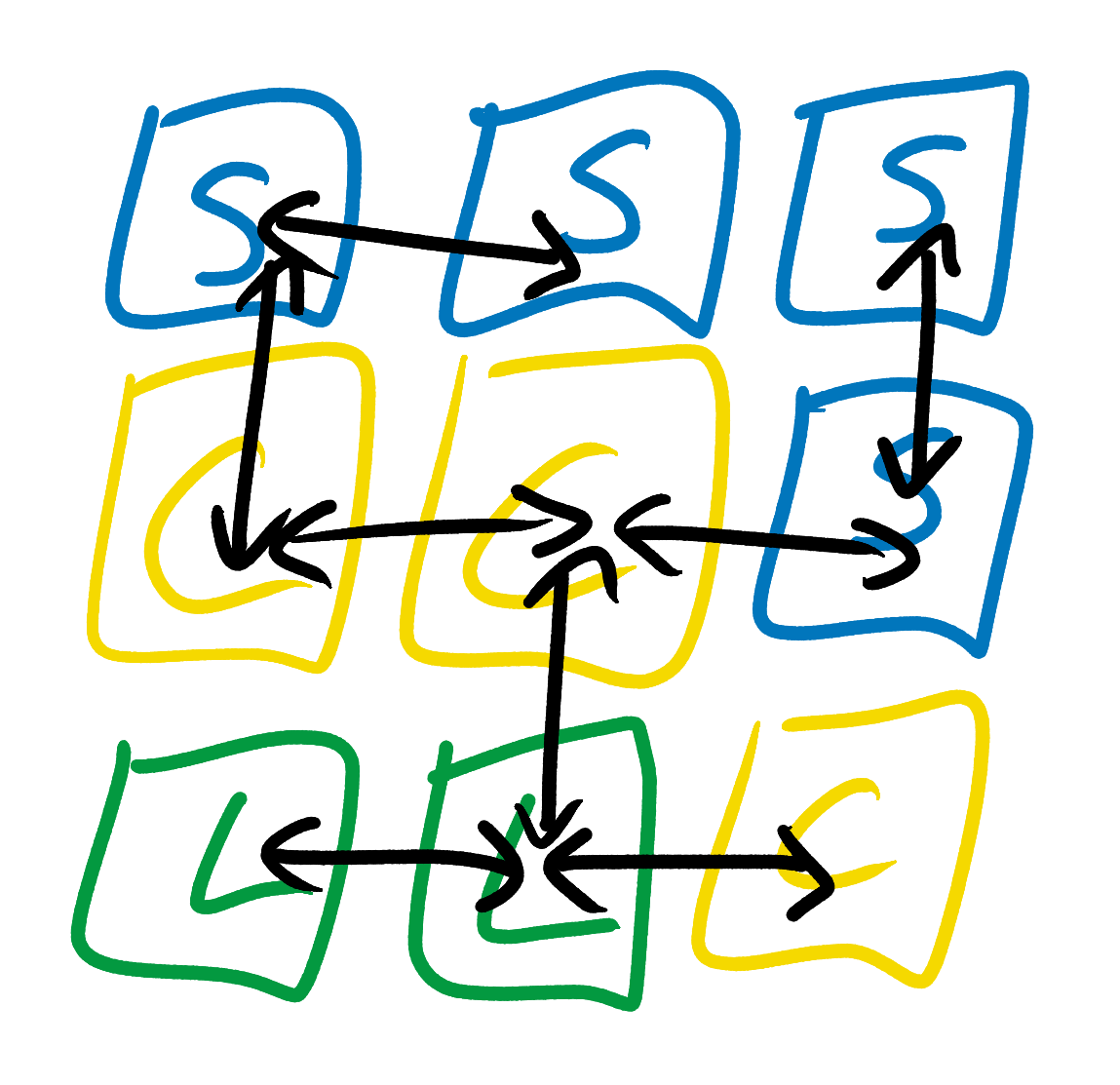
Nachdem das oben gezeigte Beispielbild untersucht wurde, stellt Even Simpler Tiled Model fest, dass sich die Seekacheln nur unter oder neben den Küstenkacheln oder in der Nähe anderer Seekacheln befinden dürfen. Sie stellt außerdem fest, dass sich Küstenplättchen neben Land-, See- oder anderen Küstenplättchen befinden können, jedoch nur über Seekacheln und unter Landkacheln. Sie versucht nicht, komplexere Regeln abzuleiten, zum Beispiel "Seekacheln sollten sich in der Nähe von mindestens einer Seekachel befinden" oder "Jede Insel muss mindestens eine Landkachel enthalten". Keine der Kacheln kann die Tatsache beeinflussen, dass einige Kacheltypen zwei oder mehr Quadrate von ihnen entfernt sein können oder nicht. Dies ähnelt einem Hochzeitsplanmodell, bei dem die einzige Regel lautet: „X kann neben Y sitzen“.

Bei der Analyse des eingehenden Bildes müssen wir auch die Häufigkeit aufzeichnen, mit der sich jede der Kacheln trifft. Später verwenden wir diese Zahlen als Gewichte bei der Auswahl der Wellenfunktion des Quadrats, deren Zusammenbruch durchgeführt werden muss, sowie bei der Auswahl der Kachel, die dem Quadrat beim Zusammenbruch zugewiesen ist.

Nachdem wir die Regeln gelernt haben, denen das Ausgabebild entsprechen muss, sind wir bereit, den Zusammenbruch der Wellenfunktion des Ausgabebildes aufzubauen.

Zusammenbruch

Wie im Hochzeitsbeispiel beginnen wir den Kollaps mit einer Wellenfunktion, bei der sich jedes Quadrat des Ausgabebildes in einer Überlagerung jedes Kacheltyps befindet.


Wir beginnen mit der Auswahl eines Quadrats, dessen Wellenfunktion zusammenbricht. Im Hochzeitsbeispiel wurde diese Wahl zufällig getroffen. Wie ExUtumno feststellte, gehen die Menschen diese Aufgaben normalerweise anders an. Stattdessen suchen sie nach Quadraten mit der niedrigsten Entropie . Die Entropie ist ein Maß für Unsicherheit und Unordnung. Im Allgemeinen ist ein Quadrat mit hoher Entropie ein Quadrat mit vielen möglichen Kacheln, die in seiner Wellenfunktion verbleiben. Es ist immer noch nicht klar, auf welcher Fliese er letztendlich zusammenbricht. Ein Quadrat mit niedriger Entropie ist ein Quadrat mit möglichst wenigen Kacheln in der Wellenfunktion. Der Satz von Kacheln, auf die er dadurch zusammenbricht, ist bereits sehr begrenzt.

Im Modell mit noch einfacheren Kacheln ist beispielsweise ein Quadrat ohne Informationen zu den umgebenden Quadraten unbegrenzt und kann zu einer beliebigen Kachel werden. Daher hat es eine sehr hohe Entropie. Für ein Quadrat, um das bereits mehrere Quadrate zusammengebrochen sind, können jedoch nur 2 Kacheln ausgewählt werden.


Die Wellenfunktion des zentralen Quadrats in der obigen Abbildung ist nicht vollständig zusammengebrochen, aber wir wissen bereits, dass es sich nicht um ein Landplättchen handeln kann. Es ist jedoch bereits begrenzt, was bedeutet, dass es eine Entropie hat, die niedriger ist als die des oberen rechten Platzes, der immer noch Land, Meer oder Küste sein kann.

Es sind so begrenzte Kacheln mit geringer Entropie, dass die Leute normalerweise darauf achten, wenn sie solche Probleme manuell lösen. Auch wenn Sie den Zusammenbruch der Wellenfunktion nicht verwenden, um einen Plan für die Platzierung von Gästen bei der Hochzeit zu erstellen, und ihn selbst erstellen, konzentrieren Sie sich dennoch auf die Bereiche des Plans, die bereits die meisten Einschränkungen aufweisen. Sie werden Dwayne nicht an Tisch 1 setzen und dann zufällig springen, um Katie an Tisch 7 zu bringen (der bisher leer ist). Sie setzen zuerst Dwayne ein, dann werden Sie herausfinden, wer neben ihm sitzen kann, wer dann neben dieser Person sitzen kann und so weiter. Ich habe noch keine Rechtfertigung dafür gesehen, aber meine Intuition besagt, dass die Verwendung dieser Heuristik der minimalen Entropie wahrscheinlich weniger Widersprüche erzeugt, als wenn Sie zufällig Quadrate für den Zusammenbruch auswählen.

Die Shannon-Formel wird als Entropieformel im Wellenfunktionskollapsalgorithmus verwendet. Es werden die Gewichte der Kacheln verwendet, die wir im vorherigen Schritt aus dem eingehenden Bild analysiert haben:

 # Sums are over the weights of each remaining # allowed tile type for the square whose # entropy we are calculating. shannon_entropy_for_square = log(sum(weight)) - (sum(weight * log(weight)) / sum(weight)) 

Nachdem wir das Quadrat der Wellenfunktion mit der kleinsten Entropie berechnet haben, kollabieren wir ihre Wellenfunktion. Dazu wählen wir zufällig eine der Kacheln aus, die für das Quadrat noch verfügbar sind, gewichtet mit den Gewichten der Kacheln, die wir aus dem eingehenden Bild analysiert haben. Gewichte werden verwendet, weil sie ein realistischeres Ausgabebild liefern. Angenommen, die Wellenfunktion eines Quadrats gibt an, dass es sich um Land oder Küste handeln kann. Wir müssen nicht immer eine der Optionen mit einer Wahrscheinlichkeit von 50% auswählen. Wenn das Eingabebild mehr Landkacheln als die Küste hat, sollten wir diesen Vorteil im Ausgabebild widerspiegeln. Dies wird mit einfachen globalen Gewichten realisiert. Wenn im Beispielbild 20 Landplättchen und 10 Küstenplättchen vorhanden sind, kollabiert das Quadrat mit einer Wahrscheinlichkeit von 2/3 und an der Küste mit der verbleibenden Wahrscheinlichkeit von 1/3 .

Dann erweitern wir die Konsequenzen der Wahl auf den Rest der Wellenfunktion des Ausgangs („Wenn sich herausstellt, dass dieses Plättchen das Meer ist, kann dieses Plättchen kein Land sein, das heißt, dies kann nicht die Küste sein“). Wenn sich alle diese Erschütterungen gelegt haben, wiederholen wir den Vorgang unter Verwendung der minimalen Entropieheuristik, um die nächste kollabierende Kachel auszuwählen. Wir wiederholen diesen Kollaps-Ausbreitungszyklus, entweder bis die gesamte Wellenfunktion des Ausgabebildes vollständig kollabiert und wir das Ergebnis zurückgeben können, oder bis wir einen Widerspruch erreichen und einen Fehler zurückgeben.

Als Ergebnis haben wir eine Welt (oder einen Fehler) geschaffen.

Wohin als nächstes gehen

Nachdem Sie sich mit dem Modell mit noch einfacheren Kacheln befasst haben, können Sie die Leistungsleiter und die Komplexität des Algorithmus erklimmen. Beginnen Sie mit dem einfachen gekachelten Modell, das wir am Anfang dieses Beitrags erwähnt haben, und fahren Sie dann mit dem vollständigen überlappenden Modell fort. Im überlappenden Modell beeinflussen sich Kacheln oder Pixel aus der Ferne gegenseitig. Wenn Sie solche Dinge verstehen, stellt ExUtumno , dass das Simple Tiled Model der Markov-Kette der Ordnung 1 ähnelt und komplexere Modelle Ketten größerer Ordnung ähneln.

Wavefunction Collapse kann sogar zusätzliche Einschränkungen berücksichtigen, z. B. "Diese Kachel muss Meer sein" oder "Dieses Pixel muss rot sein" oder "Es kann nur ein Monster in der Ausgabe sein". All dies ist in der README des Hauptprojekts beschrieben . Sie können auch die Geschwindigkeitsoptimierungen untersuchen, die für die vollständige Implementierung vorgenommen wurden. Es ist nicht notwendig, die Entropie jedes Quadrats in jeder Iteration neu zu berechnen, und die Verbreitung von Informationen durch die Wellenfunktion kann viel schneller erfolgen. Diese Aspekte werden mit zunehmender Größe der Ausgabebilder wichtiger.

Der Zusammenbruch der Wellenfunktion ist ein schönes und mächtiges Werkzeug, das es wert ist, gemeistert zu werden. Denken Sie darüber nach, wenn Sie das nächste Mal eine Hochzeit planen oder eine prozedurale Welt schaffen.