Die manuelle Lungensegmentierung dauert etwa 10 Minuten und erfordert eine bestimmte Fähigkeit, um das gleiche qualitativ hochwertige Ergebnis wie bei der automatischen Segmentierung zu erzielen. Die automatische Segmentierung dauert ca. 15 Sekunden.
Ich nahm an, dass es ohne ein neuronales Netzwerk möglich wäre, eine Genauigkeit von nicht mehr als 70% zu erreichen. Ich nahm auch an, dass morphologische Operationen nur die Erstellung eines Bildes für komplexere Algorithmen sind. Als Ergebnis der Verarbeitung dieser, wenn auch nur wenigen, 40 Proben tomographischer Daten, segmentierte der Algorithmus die Lungen fehlerfrei. Darüber hinaus änderte sich der Algorithmus nach dem Testen in den ersten fünf Fällen nicht signifikant und funktionierte bei den anderen 35 Studien korrekt, ohne die Einstellungen zu ändern.
Auch neuronale Netze haben einen Nachteil: Für ihr Training benötigen wir Hunderte von Trainingsmustern der Lunge, die manuell markiert werden müssen.
Inhalt
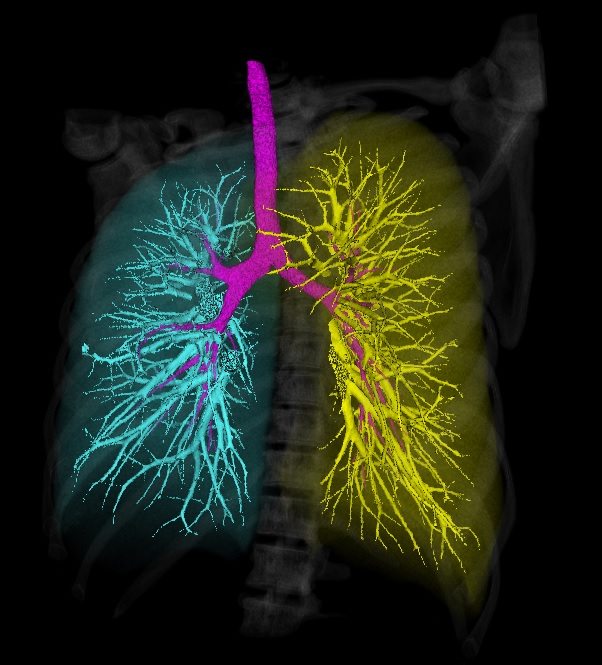
Struktur der Atemwege
Das Atmungssystem umfasst die Atemwege und Lungen. Die Atemwege sind in die oberen und unteren Atemwege unterteilt. Der Trennungspunkt zwischen den unteren und oberen Atemwegen ist der Schnittpunkt von Speiseröhre und Atemwegen. Alle Organe, die sich über dem Kehlkopf befinden, sind der obere Trakt und der Kehlkopf und die Organe darunter sind der untere Trakt.
Liste der Atmungsorgane:
Die Nasenhöhle ist eine luftgefüllte Höhle zwischen Nase und Rachen.
Der Pharynx ist ein Kanal, durch den Nahrung und Luft gelangen.
Die Luftröhre ist ein Schlauch, der mit dem Kehlkopf und den Bronchien verbunden ist.
Der Kehlkopf ist für die Stimmbildung verantwortlich. Es befindet sich auf der Höhe der Halswirbel C4-C6.
Die Bronchien sind die Atmungskanäle, deren Hauptteil sich in der Lunge befindet.
Die Lunge ist das Hauptorgan der Atemwege.

Haunsfield-Skala
Godfrey Hounsfield war ein englischer Elektrotechniker, der zusammen mit dem amerikanischen Theoretiker Allan Cormack die Computertomographie entwickelte, für die er 1979 den Nobelpreis erhielt.

Die Hounsfield-Skala - ist eine quantitative Skala zur Beschreibung der Radiodichte, die in Hounsfield-Einheiten gemessen wird und als HU bezeichnet wird.
Die Radiodichte wird auf Basis des Strahlungsdämpfungskoeffizienten berechnet. Der Dämpfungskoeffizient gibt an, wie leicht die Strahlung in ein Materialvolumen eindringen kann.
Die Radiodichte wird nach folgender Formel berechnet:
$$ Anzeige $$ {μ_ {X} -μ_ {Wasser} \ über μ_ {Wasser} -μ_ {Luft}} \ mal 1000 $$ Anzeige $$
wo sind lineare Dämpfungskoeffizienten für das gemessene Material, Wasser und Luft.
Die Radiodichte kann negativ sein, da die Radiodichte Null dem Wasser entspricht. Dies bedeutet, dass alle Materialien mit einem niedrigeren Dämpfungskoeffizienten als dem Wasserschwächungskoeffizienten (z. B. Lungengewebe, Luft) eine negative Radiodichte aufweisen.
Die ungefähren Radiodichten für verschiedene Gewebe sind nachstehend aufgeführt:
- Luft: -1000 HU.
- Atmungsorgane: von -950 bis -300 HE.
- Blut (ohne Kontrast der Gefäße): von 0 bis 100 HE.
- Knochen: 100 bis 1000 HU.

Links zu Wikipedia: Hounsfield-Skala , Godfrey Hounsfield , Dämpfungskoeffizient .
Mathematische Morphologie
Morphologische Operationen sind die Hauptwerkzeuge, die im Algorithmus verwendet wurden.
Im Bereich der Bildverarbeitung werden morphologische Operationen als eine Gruppe von Algorithmen zur Transformation der Form von Objekten bezeichnet. Am häufigsten werden morphologische Operationen auf binärisierte Bilder angewendet, bei denen Einheiten Objektvoxeln entsprechen und Nullen leer sind.
Die wichtigsten morphologischen Operationen umfassen:
Morphologische Dilatation ist das Hinzufügen neuer Voxel zu allen Randvoxeln der Objekte. Mit anderen Worten, der Algorithmus scannt alle Voxel, die der Kante des Objekts entsprechen, und vergrößert sie mithilfe eines Kernels mit einer bestimmten Form (Kugel, Würfel, Kreuz usw.). Der Kernel hat einen eigenen Radius (für die Kugel) oder die Breite der Seite (für den Würfel). Diese Operation wird häufig verwendet, um mehrere Objekte in der Nähe zu einem einzigen Objekt zusammenzuführen.
Morphologische Erosion ist das Abschneiden aller Voxel, die an der Grenze der Objekte liegen. Dieser Vorgang ist umgekehrt zur Dilatation. Diese Operation ist nützlich, um Rauschen zu entfernen, das die Form vieler kleiner miteinander verbundener Objekte hat. Diese Methode zur Geräuschentfernung sollte jedoch nur angewendet werden, wenn das interessierende Objekt eine Dicke aufweist, die viel größer als der Erosionsradius ist. Andernfalls gehen die nützlichen Informationen verloren.
Das morphologische Schließen ist eine Erweiterung, gefolgt von einer Erosion. Es wird verwendet, um Löcher in Objekten zu schließen und Objekte in der Nähe zusammenzuführen.
Die morphologische Öffnung ist eine Erosion, gefolgt von einer Erweiterung. Es wird verwendet, um kleine Rauschobjekte zu entfernen und die Objekte in mehrere Objekte aufzuteilen.

Lee-Algorithmus und RLE-Komprimierung
Zur Auswahl von Objekten im binärisierten Voxelvolumen wird der Lie-Algorithmus verwendet. Ursprünglich wurde dieser Algorithmus erfunden, um den kürzesten Weg aus dem Labyrinth zu finden. Wir verwenden es, um das Objekt auszuwählen und es von einem dreidimensionalen Array von Voxeln zu einem anderen zu verschieben. Die Grundidee des Algorithmus besteht in einer parallelen Bewegung in alle möglichen Richtungen vom Startpunkt aus. Für einen dreidimensionalen Fall ist es möglich, sich von einem Voxel aus in 26 oder 6 Richtungen zu bewegen.
Um die Leistung zu optimieren, wurde der Lauflängencodierungsalgorithmus angewendet. Die Hauptidee des Algorithmus besteht darin, dass die Folge von Einsen und Nullen durch eine Ziffer ersetzt wird, die der Anzahl der Elemente in der Folge entspricht. Beispielsweise kann die Zeichenfolge "00110111" ersetzt werden durch: "2; 2; 1; 3 ". Dies reduziert die Anzahl der Speicherzugriffe.
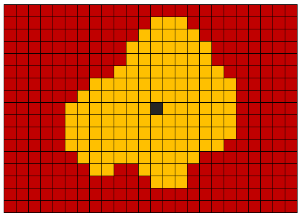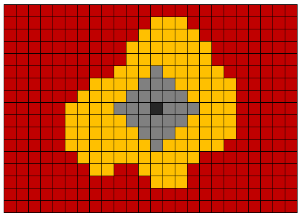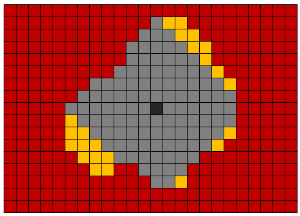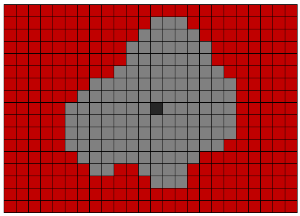

Wikipedia-Links: Lee-Algorithmus , RLE-Algorithmus .
Schwellentransformation des Basisvolumens
Unter Verwendung des Tomographen wurden die Daten über eine Radiodichte an jedem Punkt des gescannten Raums erhalten. Luftvoxel haben eine Radiodichte im Bereich von -1100 bis -900 HE, und Voxel von Atmungsorganen haben eine Radiodichte von -900 bis -300 HE. Daher können wir alle unnötigen Voxel mit einer Radiodichte von mehr als -300 HE entfernen. Als Ergebnis erhalten wir ein binärisiertes Voxelvolumen, das nur die Atmungsorgane und Luft enthält.
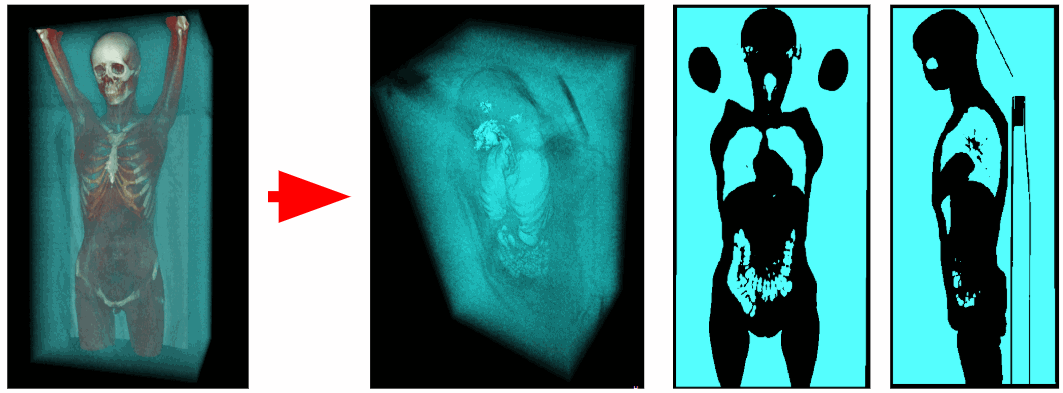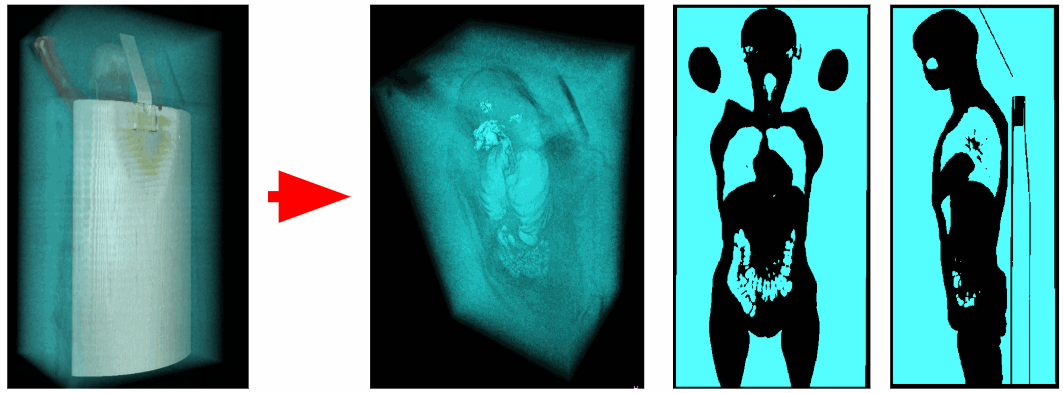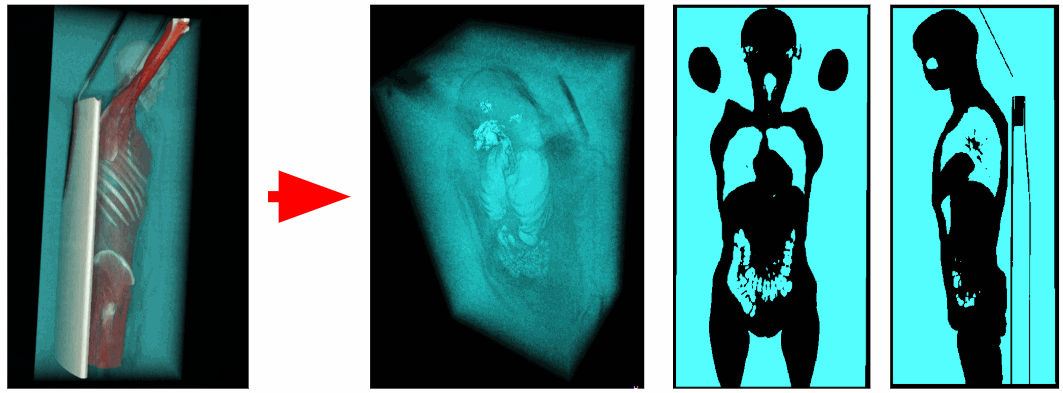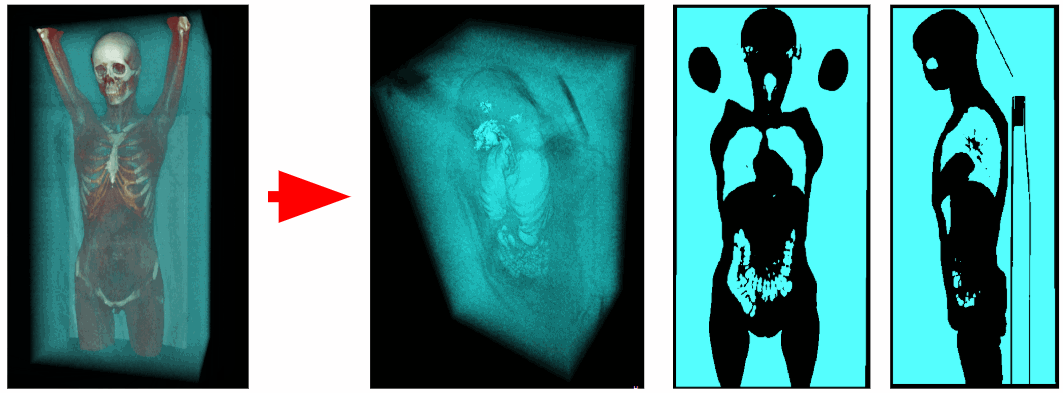
Externe Luftentfernung
Um die innere Luft des Körpers zu segmentieren, löschen wir alle Objekte, die an die Ecken des 3D-Volumens angrenzen. So entfernen wir die Außenluft.

In nicht allen Fällen wird jedoch die Luft im Tomographentisch entfernt, da möglicherweise keine Verbindung zu den Ecken des 3D-Volumens besteht.

Daher scannen wir nicht nur die Ecken, sondern auch alle Voxel, die auf einer der Kantenebenen des f liegen. Wie wir im Bild unten sehen können, wurden auch die Lungen entfernt. Es stellt sich heraus, dass die Luftröhre auch eine Verbindung mit der oberen Ebene des 3D-Volumens hatte.
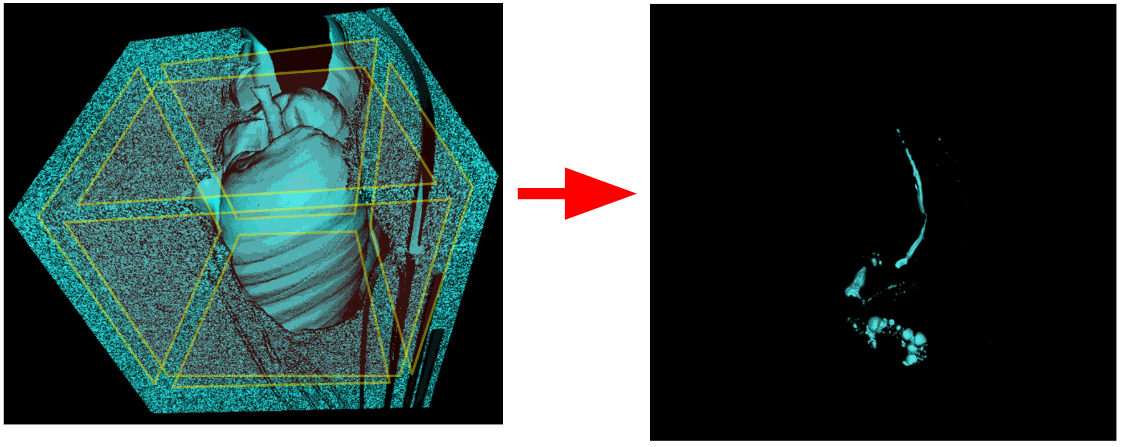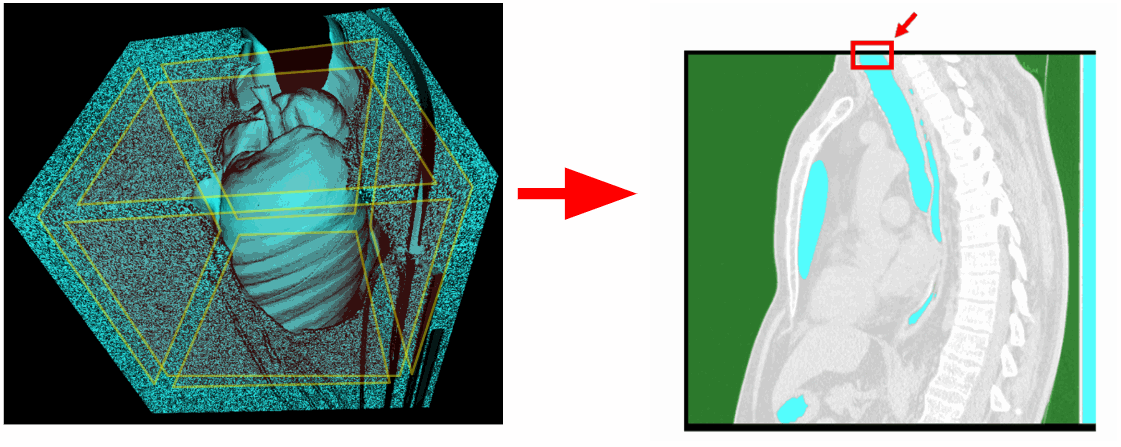
Wir müssen die oberste Ebene aus dem Scanbereich ausschließen. Es gibt auch Studien, bei denen die Lunge nicht vollständig erfasst wurde und die untere Ebene mit der Lunge verbunden ist.
Wenn Sie möchten, können Sie auch die untere Ebene ausschließen.

Diese Methode betrifft jedoch nur Brustuntersuchungen. Bei der Erfassung des gesamten Körpervolumens tritt die Verbindung von innerer und äußerer Luft durch die Nasenhöhle auf. Daher ist es notwendig, morphologische Erosion anzuwenden, um die innere und äußere Luft zu trennen.
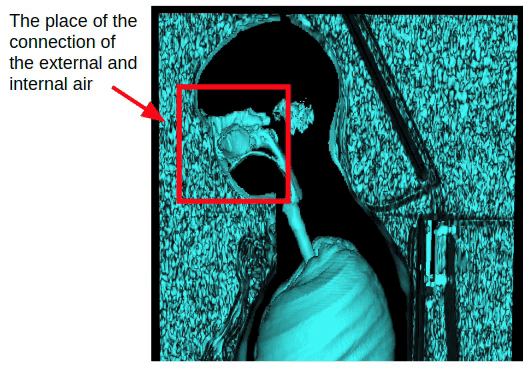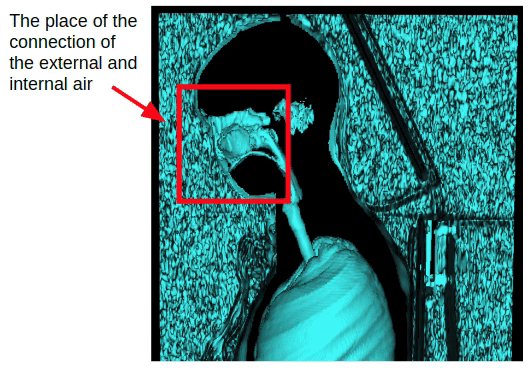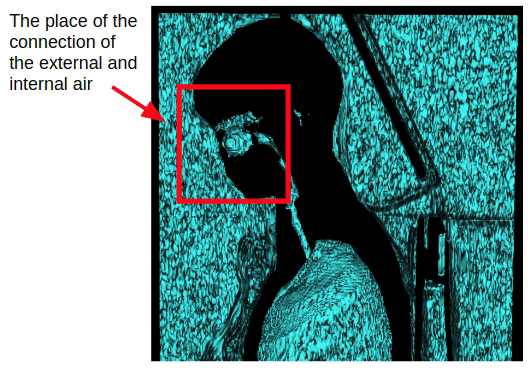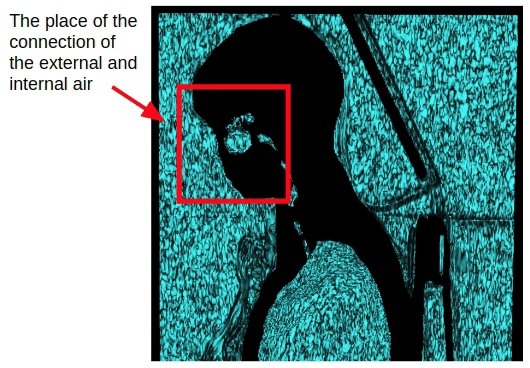
Nach dem Anwenden der Erosion können wir zu der zuvor erhaltenen Methode zur Segmentierung der Außenluft zurückkehren, die auf der Konnektivität der Außenluft mit den Seitenebenen des 3D-Volumens basiert.

Nach der Segmentierung der Außenluft konnten wir die Außenluft sofort vom gesamten Luft- und Lungenvolumen abziehen und die Innenluft von Körper und Lunge abrufen. Es gibt jedoch ein Problem. Nach der Erosion gingen einige Informationen über die Außenluft verloren. Um es wiederherzustellen, wenden wir eine Erweiterung der Außenluft an.

Als nächstes subtrahieren wir die Außenluft von der gesamten Luft und den Atmungsorganen und erhalten die Innenluft und die Atmungsorgane.


Segmentierung des Objekts mit maximalem Volumen
Als nächstes segmentieren wir die Atmungsorgane als maximales Volumenobjekt. Die Atmungsorgane haben keine Verbindung zur Luft im Magen-Darm-Trakt.


Es ist anzumerken, dass die richtige Wahl der Radiodensitätsschwelle im ersten Schritt wichtig ist. Andernfalls besteht in einigen Fällen aufgrund der geringen Auflösung möglicherweise keine Verbindung zwischen den beiden Lungen. Wenn wir beispielsweise annehmen, dass Voxel der Atmungsorgane eine Radiodichte von -500 HE und weniger aufweisen, führt die Segmentierung der Atmungsorgane als größtes Volumenobjekt im folgenden Fall zu einem Fehler, da kein Zusammenhang zwischen diesen besteht die zwei Lungen. Daher sollte der Schwellenwert auf -300 HE erhöht werden.

Schließen der Gefäße in der Lunge
Um die Gefäße in der Lunge zu erfassen, verwenden wir den morphologischen Verschluss, dh die Erweiterung, gefolgt von der Erosion mit demselben Radius. Die Radiodichte der Gefäße (ohne Kontrastmittel) beträgt etwa 0..100 HU.

Auf dem Bild sehen wir, dass große Blutkanäle nicht geschlossen sind. Dies ist jedoch nicht erforderlich. Der Zweck dieser Operation war es, die vielen kleinen Löcher in der Lunge zu zerstören, um den Lungensegmentierungsprozess in den nächsten Schritten zu vereinfachen.
Segmentierungsalgorithmus für Atmungsorgane
Als Ergebnis erhalten wir den folgenden Segmentierungsalgorithmus für Atmungsorgane:
- Schwellenwerttransformation des Basisvolumens mit dem Schwellenwert "<-300 HU".
- Morphologische Erosion mit einem Radius von 3 mm zur Trennung von Außen- und Innenluft.
- Segmentierung der Außenluft basierend auf der Außenluftverbindung mit den Grenzseitenebenen des 3D-Volumens.
- Morphologische Erweiterung der Außenluft zur Wiederherstellung der nach der Erosion verlorenen Informationen.
- Subtraktion der Außenluft von der gesamten Luft und den Atmungsorganen, um die Innenluft und die Atmungsorgane zu erhalten.
- Segmentierung des Objekts mit maximalem Volumen.
- Morphologisches Schließen der Gefäße in der Lunge.

Algorithmusimplementierung in MATLAB
Funktion "getRespiratoryOrgans"
Funktion "getExternalAir"
Funktion "getMaxObject"
Der Quellcode kann über die Referenz heruntergeladen werden.
Fazit
Die folgenden Artikel werden sein:
- Segmentierung der Luftröhre und der Bronchien;
- Lungensegmentierung;
- Segmentierung der Lungenlappen.
Die folgenden Algorithmen werden berücksichtigt:
- Entfernungstransformation;
- Transformation des nächsten Nachbarn, auch als Feature-Transformation bekannt;
- Berechnung der Eigenwerte der Hessischen Matrix zur Segmentierung flacher 3D-Objekte;
- Segmentierung von Wassereinzugsgebieten.