Neuronale Netze und Deep Learning, Kapitel 4: Visueller Beweis, dass neuronale Netze jede Funktion berechnen können

In diesem Kapitel gebe ich eine einfache und meist visuelle Erklärung des Universalitätstheorems. Um dem Material in diesem Kapitel zu folgen, müssen Sie die vorherigen nicht lesen. Es ist als eigenständiger Aufsatz aufgebaut. Wenn Sie das grundlegendste Verständnis von NS haben, sollten Sie in der Lage sein, die Erklärungen zu verstehen.


Eine der erstaunlichsten Tatsachen über neuronale Netze ist, dass sie jede Funktion überhaupt berechnen können. Nehmen wir an, jemand gibt Ihnen eine komplexe und kurvenreiche Funktion f (x):



Und unabhängig von dieser Funktion ist ein solches neuronales Netzwerk garantiert, dass für jede Eingabe x der Wert f (x) (oder eine nahe liegende Annäherung) die Ausgabe dieses Netzwerks ist, dh:



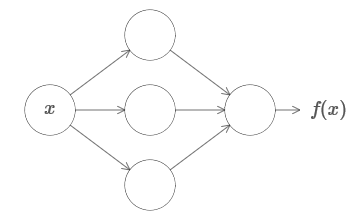
Dies funktioniert auch dann, wenn es sich um eine Funktion vieler Variablen f = f (x ₁ , ..., x _m ) und mit vielen Werten handelt. Hier ist zum Beispiel ein Netzwerk, das eine Funktion mit m = 3 Eingängen und n = 2 Ausgängen berechnet:



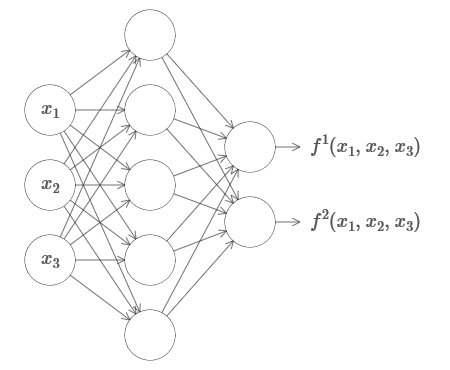
Dieses Ergebnis legt nahe, dass neuronale Netze eine gewisse Universalität aufweisen. Egal welche Funktion wir berechnen möchten, wir wissen, dass es ein neuronales Netzwerk gibt, das dies kann.

Darüber hinaus gilt der Universalitätstheorem auch dann, wenn wir das Netzwerk auf eine einzige Schicht zwischen eingehenden und ausgehenden Neuronen beschränken - die sogenannten in einer versteckten Schicht. So können auch Netzwerke mit einer sehr einfachen Architektur extrem leistungsfähig sein.

Der Universalitätstheorem ist Menschen, die neuronale Netze verwenden, gut bekannt. Obwohl dies so ist, ist ein Verständnis dieser Tatsache nicht so weit verbreitet. Und die meisten Erklärungen dafür sind technisch zu komplex. In einer der ersten Arbeiten, die dieses Ergebnis belegen, wurden beispielsweise der Hahn-Banach-Satz , der Riesz-Repräsentationssatz und einige Fourier-Analysen verwendet. Wenn Sie Mathematiker sind, ist es für Sie leicht, diese Beweise zu verstehen, aber für die meisten Menschen ist es nicht so einfach. Schade, denn die Hauptgründe für die Universalität sind einfach und schön.

In diesem Kapitel gebe ich eine einfache und meist visuelle Erklärung des Universalitätstheorems. Wir werden Schritt für Schritt die zugrunde liegenden Ideen durchgehen. Sie werden verstehen, warum neuronale Netze wirklich jede Funktion berechnen können. Sie werden einige der Einschränkungen dieses Ergebnisses verstehen. Und Sie werden verstehen, wie das Ergebnis mit tiefem NS verbunden ist.

Um dem Material in diesem Kapitel zu folgen, müssen Sie die vorherigen nicht lesen. Es ist als eigenständiger Aufsatz aufgebaut. Wenn Sie das grundlegendste Verständnis von NS haben, sollten Sie in der Lage sein, die Erklärungen zu verstehen. Aber ich werde manchmal Links zu vorherigem Material bereitstellen, um Wissenslücken zu schließen.

Universalsätze finden sich oft in der Informatik, deshalb vergessen wir manchmal sogar, wie erstaunlich sie sind. Aber es lohnt sich, sich daran zu erinnern: Die Fähigkeit, eine beliebige Funktion zu berechnen, ist wirklich erstaunlich. Fast jeder Prozess, den Sie sich vorstellen können, kann auf die Berechnung einer Funktion reduziert werden. Betrachten Sie die Aufgabe, den Namen einer Musikkomposition anhand einer kurzen Passage zu finden. Dies kann als Funktionsberechnung angesehen werden. Oder überlegen Sie, ob Sie einen chinesischen Text ins Englische übersetzen möchten. Und dies kann als Funktionsberechnung betrachtet werden (in der Tat viele Funktionen, da es viele akzeptable Optionen für die Übersetzung eines einzelnen Textes gibt). Oder betrachten Sie die Aufgabe, eine Beschreibung der Handlung des Films und der Qualität des Schauspiels basierend auf der mp4-Datei zu erstellen. Auch dies kann als Berechnung einer bestimmten Funktion angesehen werden (die Bemerkung zu den Textübersetzungsoptionen ist auch hier richtig). Universalität bedeutet, dass NS im Prinzip alle diese und viele andere Aufgaben ausführen können.

Nur aus der Tatsache, dass wir wissen, dass es NS gibt, die beispielsweise vom Chinesischen ins Englische übersetzen können, folgt natürlich nicht, dass wir über gute Techniken zum Erstellen oder sogar Erkennen eines solchen Netzwerks verfügen. Diese Einschränkung gilt auch für traditionelle Universalitätstheoreme für Modelle wie Boolesche Schemata. Wie wir bereits in diesem Buch gesehen haben, verfügt der NS über leistungsstarke Algorithmen zum Lernen von Funktionen. Die Kombination aus Lernalgorithmen und Vielseitigkeit ist eine attraktive Mischung. Bisher haben wir uns in dem Buch auf Trainingsalgorithmen konzentriert. In diesem Kapitel konzentrieren wir uns auf die Vielseitigkeit und deren Bedeutung.

Zwei Tricks

Bevor ich erkläre, warum der Universalitätstheorem wahr ist, möchte ich zwei Tricks erwähnen, die in der informellen Aussage „Ein neuronales Netzwerk kann jede Funktion berechnen“ enthalten sind.

Erstens bedeutet dies nicht, dass das Netzwerk verwendet werden kann, um eine Funktion genau zu berechnen. Wir können nur eine so gute Annäherung bekommen, wie wir brauchen. Indem wir die Anzahl der versteckten Neuronen erhöhen, verbessern wir die Approximation. Zum Beispiel habe ich zuvor ein Netzwerk dargestellt, das eine bestimmte Funktion f (x) unter Verwendung von drei versteckten Neuronen berechnet. Für die meisten Funktionen kann unter Verwendung von drei Neuronen nur eine Annäherung von geringer Qualität erhalten werden. Durch Erhöhen der Anzahl versteckter Neuronen (z. B. bis zu fünf) können wir normalerweise eine verbesserte Annäherung erhalten:



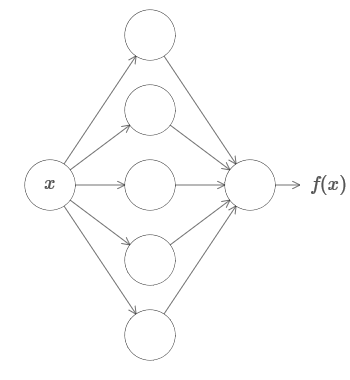
Und um die Situation zu verbessern, indem die Anzahl der versteckten Neuronen weiter erhöht wird.

Nehmen wir zur Verdeutlichung dieser Aussage an, wir hätten eine Funktion f (x) erhalten, die wir mit der notwendigen Genauigkeit ε> 0 berechnen wollen. Es besteht die Garantie, dass bei Verwendung einer ausreichenden Anzahl versteckter Neuronen immer ein NS gefunden werden kann, dessen Ausgabe g (x) die Gleichung | g (x) - f (x) | <ε für jedes x erfüllt. Mit anderen Worten wird die Annäherung mit der gewünschten Genauigkeit für jeden möglichen Eingabewert erreicht.

Der zweite Haken ist, dass Funktionen, die mit der beschriebenen Methode approximiert werden können, zu einer kontinuierlichen Klasse gehören. Wenn die Funktion unterbrochen wird, dh plötzlich scharfe Sprünge macht, ist es im allgemeinen Fall unmöglich, mit Hilfe von NS eine Annäherung vorzunehmen. Dies ist nicht überraschend, da unsere NS kontinuierliche Funktionen von Eingabedaten berechnen. Selbst wenn die Funktion, die wir wirklich berechnen müssen, diskontinuierlich ist, ist die Approximation oft ziemlich kontinuierlich. Wenn ja, dann können wir NS verwenden. In der Praxis ist diese Einschränkung normalerweise nicht wichtig.

Infolgedessen wird eine genauere Aussage des Universalitätstheorems sein, dass NS mit einer verborgenen Schicht verwendet werden kann, um jede kontinuierliche Funktion mit jeder gewünschten Genauigkeit zu approximieren. In diesem Kapitel beweisen wir eine etwas weniger strenge Version dieses Theorems, bei der zwei verborgene Schichten anstelle einer verwendet werden. In Aufgaben werde ich kurz beschreiben, wie diese Erklärung mit geringfügigen Änderungen an einen Beweis angepasst werden kann, der nur eine verborgene Ebene verwendet.

Vielseitigkeit mit einem Eingabe- und einem Ausgabewert

Um zu verstehen, warum der Universalitätstheorem wahr ist, verstehen wir zunächst, wie eine NS-Approximationsfunktion mit nur einem Eingabe- und einem Ausgabewert erstellt wird:



Es stellt sich heraus, dass dies die Essenz der Aufgabe der Universalität ist. Sobald wir diesen Sonderfall verstanden haben, wird es ziemlich einfach sein, ihn auf Funktionen mit vielen Eingabe- und Ausgabewerten zu erweitern.

Um zu verstehen, wie ein Netzwerk zum Zählen von f aufgebaut wird, beginnen wir mit einem Netzwerk, das eine einzelne verborgene Schicht mit zwei verborgenen Neuronen und eine Ausgangsschicht mit einem Ausgangsneuron enthält:



Um uns vorzustellen, wie die Netzwerkkomponenten funktionieren, konzentrieren wir uns auf das obere versteckte Neuron. Im Diagramm des Originalartikels können Sie das Gewicht interaktiv mit der Maus ändern, indem Sie auf „w“ klicken und sofort sehen, wie sich die vom oberen versteckten Neuron berechnete Funktion ändert:



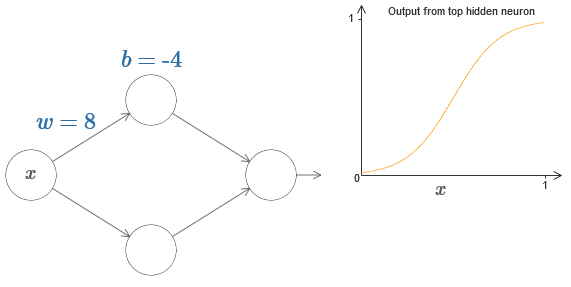
Wie wir früher in diesem Buch erfahren haben, zählt ein verstecktes Neuron σ (wx + b), wobei σ (z) ≡ 1 / (1 + e ^−z ) ein Sigmoid ist . Bisher haben wir diese algebraische Form ziemlich oft verwendet. Um die Universalität zu beweisen, ist es jedoch besser, diese Algebra vollständig zu ignorieren und stattdessen die Form im Diagramm zu manipulieren und zu beobachten. Dies hilft Ihnen nicht nur, besser zu fühlen, was passiert, sondern gibt uns auch einen Beweis für die Universalität, die für andere Aktivierungsfunktionen neben Sigmoid gilt.

Genau genommen wird der von mir gewählte visuelle Ansatz traditionell nicht als Beweis angesehen. Ich glaube jedoch, dass der visuelle Ansatz mehr Einblick in die Wahrheit des Endergebnisses bietet als herkömmliche Beweise. Und natürlich ist ein solches Verständnis der eigentliche Zweck des Beweises. In den von mir vorgeschlagenen Beweisen treten gelegentlich Lücken auf; Ich werde vernünftige, aber nicht immer strenge visuelle Beweise liefern. Wenn Sie dies stört, betrachten Sie es als Ihre Aufgabe, diese Lücken zu schließen. Verlieren Sie jedoch nicht das Hauptziel aus den Augen: zu verstehen, warum der Universalitätstheorem wahr ist.

Klicken Sie zunächst auf den Versatz b im Originaldiagramm und ziehen Sie ihn nach rechts, um ihn zu vergrößern. Sie werden sehen, dass sich das Diagramm mit zunehmendem Versatz nach links bewegt, aber seine Form nicht ändert.

Ziehen Sie es dann nach links, um den Versatz zu verringern. Sie werden sehen, dass sich das Diagramm nach rechts bewegt, ohne die Form zu ändern.

Gewicht auf 2-3 reduzieren. Sie werden sehen, dass sich die Kurve mit abnehmendem Gewicht gerade richtet. Damit die Kurve nicht vom Diagramm abweicht, müssen Sie möglicherweise den Versatz korrigieren.

Erhöhen Sie schließlich das Gewicht auf Werte größer als 100. Die Kurve wird steiler und nähert sich schließlich dem Schritt. Stellen Sie den Versatz so ein, dass sein Winkel im Bereich des Punktes x = 0,3 liegt. Das folgende Video zeigt, was passieren soll:



Wir können unsere Analyse erheblich vereinfachen, indem wir das Gewicht erhöhen, sodass die Ausgabe wirklich eine gute Annäherung an die Schrittfunktion darstellt. Unten habe ich die Ausgabe des oberen versteckten Neurons für das Gewicht w = 999 erstellt. Dies ist ein statisches Bild:



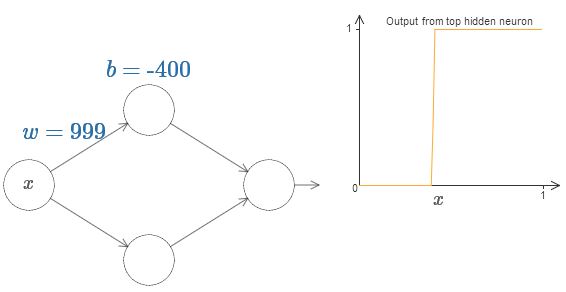
Die Verwendung von Schrittfunktionen ist etwas einfacher als bei einem typischen Sigmoid. Der Grund ist, dass Beiträge aller versteckten Neuronen in der Ausgabeschicht addiert werden. Die Summe einer Reihe von Schrittfunktionen ist leicht zu analysieren, es ist jedoch schwieriger, darüber zu sprechen, was passiert, wenn eine Reihe von Kurven in Form eines Sigmoid hinzugefügt wird. Daher ist es viel einfacher anzunehmen, dass unsere versteckten Neuronen schrittweise Funktionen produzieren. Genauer gesagt fixieren wir dazu das Gewicht w auf einen sehr großen Wert und weisen dann die Position der Stufe durch den Versatz zu. Natürlich ist die Arbeit mit einer Ausgabe als Schrittfunktion eine Annäherung, aber sie ist sehr gut, und bis jetzt werden wir die Funktion als echte Schrittfunktion behandeln. Später werde ich auf die Auswirkung von Abweichungen von dieser Annäherung zurückkommen.

Welcher Wert von x ist der Schritt? Mit anderen Worten, wie hängt die Position der Stufe von Gewicht und Verschiebung ab?

Versuchen Sie zur Beantwortung der Frage, das Gewicht und den Versatz im interaktiven Diagramm zu ändern. Können Sie verstehen, wie die Position des Schritts von w und b abhängt? Wenn Sie ein wenig üben, können Sie sich selbst davon überzeugen, dass seine Position proportional zu b und umgekehrt proportional zu w ist.

Tatsächlich liegt der Schritt bei s = –b / w, wie zu sehen sein wird, wenn wir das Gewicht und die Verschiebung auf die folgenden Werte einstellen:



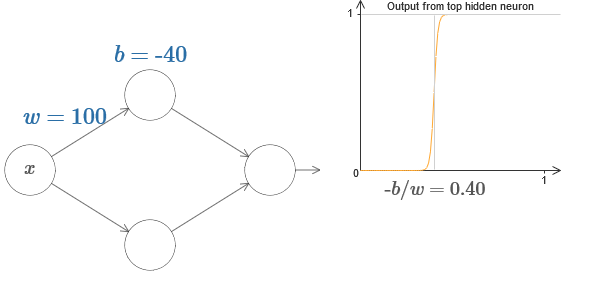
Unser Leben wird stark vereinfacht, wenn wir versteckte Neuronen mit einem einzigen Parameter s beschreiben, dh durch die Position des Schritts s = −b / w. Im folgenden interaktiven Diagramm können Sie einfach s ändern:



Wie oben erwähnt, haben wir einem sehr großen Wert speziell ein Gewicht w am Eingang zugewiesen - groß genug, damit die Schrittfunktion eine gute Annäherung darstellt. Und wir können das parametrisierte Neuron auf diese Weise leicht in seine übliche Form zurückversetzen, indem wir den Bias b = −ws wählen.

Bisher haben wir uns nur auf die Ausgabe des überlegenen versteckten Neurons konzentriert. Betrachten wir das Verhalten des gesamten Netzwerks. Angenommen, versteckte Neuronen berechnen die Schrittfunktionen, die durch die Parameter der Schritte s ₁ (oberes Neuron) und s ₂ (unteres Neuron) definiert sind. Ihre jeweiligen Ausgangsgewichte sind w ₁ und w ₂ . Hier ist unser Netzwerk:



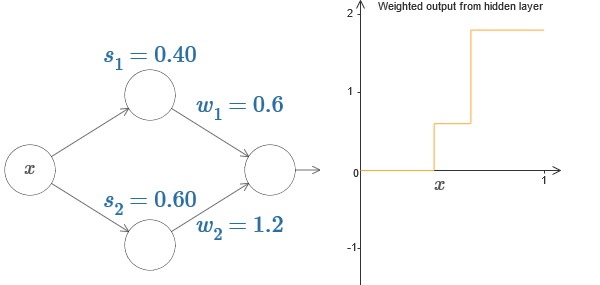
Rechts ist ein Diagramm der gewichteten Ausgabe w ₁ a ₁ + w ₂ a _{2 der} verborgenen Schicht. Hier sind a ₁ und a ₂ die Ausgänge der oberen bzw. unteren versteckten Neuronen. Sie werden mit "a" bezeichnet, da sie oft als neuronale Aktivierungen bezeichnet werden.

Übrigens stellen wir fest, dass der Ausgang des gesamten Netzwerks σ ist (w ₁ a ₁ + w ₂ a ₂ + b), wobei b die Vorspannung des Ausgangsneurons ist. Dies ist offensichtlich nicht dasselbe wie die gewichtete Ausgabe der verborgenen Ebene, deren Diagramm wir erstellen. Im Moment konzentrieren wir uns jedoch auf die ausgeglichene Ausgabe der verborgenen Schicht und denken erst später darüber nach, wie sie sich auf die Ausgabe des gesamten Netzwerks bezieht.

Versuchen Sie, den Schritt s _{1 des} oberen versteckten Neurons im interaktiven Diagramm im Originalartikel zu erhöhen und zu verringern. Sehen Sie, wie dies die gewichtete Ausgabe der verborgenen Ebene ändert. Es ist besonders nützlich zu verstehen, was passiert, wenn s ₁ s ₂ überschreitet. Sie werden sehen, dass der Graph in diesen Fällen seine Form ändert, wenn wir von einer Situation, in der das obere versteckte Neuron zuerst aktiviert wird, zu einer Situation übergehen, in der das untere versteckte Neuron zuerst aktiviert wird.

Versuchen Sie in ähnlicher Weise, den Schritt s _{2 des} unteren verborgenen Neurons zu manipulieren, und sehen Sie, wie dies die Gesamtleistung der verborgenen Neuronen verändert.

Versuchen Sie, die Ausgangsgewichte zu reduzieren und zu erhöhen. Beachten Sie, wie dies den Beitrag der entsprechenden versteckten Neuronen skaliert. Was passiert, wenn eines der Gewichte gleich 0 ist?

Versuchen Sie abschließend, w ₁ auf 0,8 und w ₂ auf -0,8 einzustellen. Das Ergebnis ist eine "Vorsprung" -Funktion mit einem Anfang bei s ₁ , einem Ende bei s ₂ und einer Höhe von 0,8. Eine gewichtete Ausgabe könnte beispielsweise folgendermaßen aussehen:



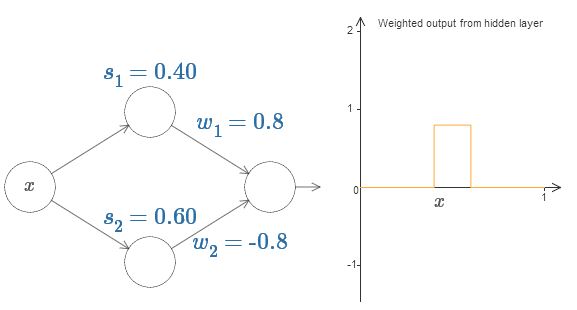
Natürlich kann der Vorsprung auf jede Höhe skaliert werden. Verwenden wir einen Parameter, h, der die Höhe bezeichnet. Der Einfachheit halber werde ich auch die Notation "s ₁ = ..." und "w ₁ = ..." entfernen.



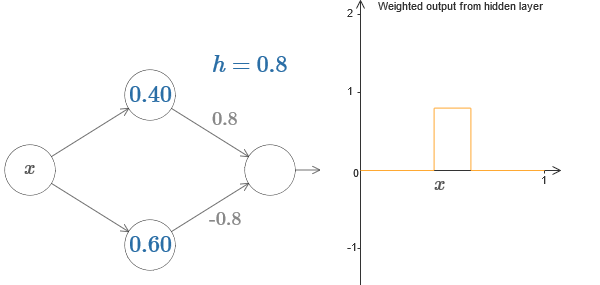
Versuchen Sie, den h-Wert zu erhöhen und zu verringern, um zu sehen, wie sich die Höhe des Vorsprungs ändert. Versuchen Sie, h negativ zu machen. Versuchen Sie, die Punkte der Schritte zu ändern, um zu beobachten, wie sich dadurch die Form des Vorsprungs ändert.

Sie werden sehen, dass wir unsere Neuronen nicht nur als grafische Grundelemente verwenden, sondern auch als Einheiten, die Programmierern vertrauter sind - so etwas wie eine Wenn-Dann-Sonst-Anweisung in der Programmierung:

wenn Eingabe> = Schrittbeginn:
addiere 1 zur gewichteten Ausgabe
sonst:
Addiere 0 zur gewichteten Ausgabe

Zum größten Teil werde ich mich an die grafische Notation halten. Manchmal ist es jedoch hilfreich, zur Wenn-Dann-Sonst-Ansicht zu wechseln und darüber nachzudenken, was in diesen Begriffen geschieht.

Wir können unseren Protrusionstrick verwenden, indem wir zwei Teile versteckter Neuronen im selben Netzwerk zusammenkleben:



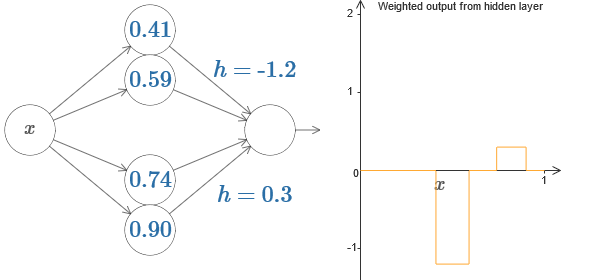
Hier ließ ich die Gewichte fallen, indem ich einfach die h-Werte für jedes Paar versteckter Neuronen aufschrieb. Versuchen Sie, mit beiden h-Werten zu spielen, und sehen Sie, wie sich das Diagramm ändert. Verschieben Sie die Registerkarten und ändern Sie die Punkte der Schritte.

In einem allgemeineren Fall kann diese Idee verwendet werden, um eine beliebige Anzahl von Spitzen einer beliebigen Höhe zu erhalten. Insbesondere können wir das Intervall [0,1] in eine große Anzahl von (N) Teilintervallen unterteilen und N Paare versteckter Neuronen verwenden, um Peaks beliebiger Höhe zu erhalten. Mal sehen, wie das bei N = 5 funktioniert. Dies sind bereits ziemlich viele Neuronen, daher bin ich etwas enger dargestellt. Entschuldigung für das komplexe Diagramm - ich könnte die Komplexität hinter zusätzlichen Abstraktionen verbergen, aber es scheint mir, dass es eine kleine Qual mit Komplexität wert ist, um besser zu fühlen, wie die neuronalen Netze funktionieren.



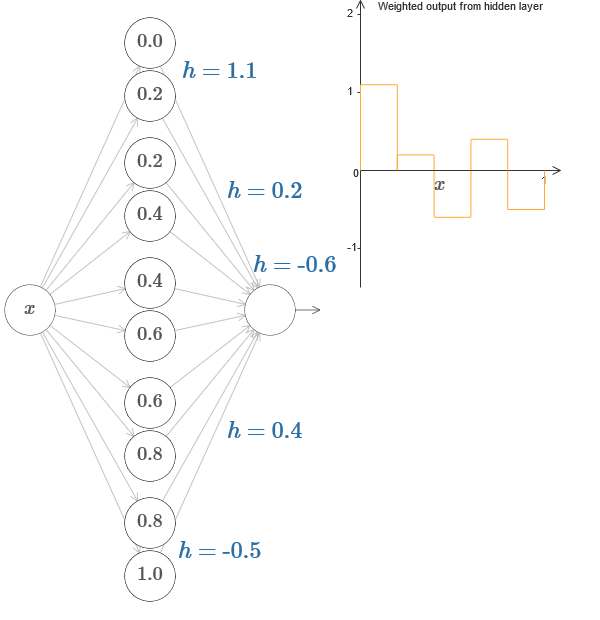
Sie sehen, wir haben fünf Paare versteckter Neuronen. Die Punkte der Schritte der entsprechenden Paare liegen bei 0,1 / 5, dann bei 1 / 5,2 / 5 usw. bis zu 4 / 5,5 / 5. Diese Werte sind fest - wir erhalten fünf Vorsprünge gleicher Breite in der Grafik.

Jedem Neuronenpaar ist ein Wert h zugeordnet. Denken Sie daran, dass Ausgangsneuronenverbindungen die Gewichte h und –h haben. Im Originalartikel im Diagramm können Sie auf die h-Werte klicken und sie von links nach rechts verschieben. Mit einer Änderung der Höhe ändert sich auch der Zeitplan. Durch Ändern der Ausgabegewichte konstruieren wir die endgültige Funktion!

Im Diagramm können Sie weiterhin auf das Diagramm klicken und die Höhe der Schritte nach oben oder unten ziehen. Wenn Sie die Höhe ändern, sehen Sie, wie sich die Höhe des entsprechenden h ändert. Die Ausgabegewichte + h und –h ändern sich entsprechend. Mit anderen Worten, wir manipulieren direkt eine Funktion, deren Grafik rechts angezeigt wird, und sehen diese Änderungen in den Werten von h links. Sie können auch die Maustaste an einem der Vorsprünge gedrückt halten und dann die Maus nach links oder rechts ziehen. Die Vorsprünge werden dann an die aktuelle Höhe angepasst.

Es ist Zeit, die Arbeit zu erledigen.

Erinnern Sie sich an die Funktion, die ich ganz am Anfang des Kapitels gezeichnet habe:



Dann habe ich das nicht erwähnt, aber tatsächlich sieht es so aus:

$$

$$f (x) = 0,2 + 0,4 x ^ 2 + 0,3x \ sin (15 x) + 0,05 \ cos (50 x) \ tag {113}$$

Es ist für x-Werte von 0 bis 1 konstruiert und Werte entlang der y-Achse variieren von 0 bis 1.

Offensichtlich ist diese Funktion nicht trivial. Und Sie müssen herausfinden, wie Sie es mithilfe neuronaler Netze berechnen können.

In unseren obigen neuronalen Netzen haben wir eine gewichtete Kombination ∑ _j w _j a _j der Ausgabe versteckter Neuronen analysiert. Wir wissen, wie wir diesen Wert maßgeblich kontrollieren können. Wie bereits erwähnt, entspricht dieser Wert jedoch nicht der Netzwerkausgabe. Die Ausgabe des Netzwerks ist σ (∑ _j w _j a _j + b), wobei b die Verschiebung des Ausgangsneurons ist. Können wir direkt die Kontrolle über die Netzwerkausgabe erlangen?

Die Lösung besteht darin, ein neuronales Netzwerk zu entwickeln, in dem die gewichtete Ausgabe der verborgenen Schicht durch die Gleichung σ ⁻¹ ⋅f (x) gegeben ist, wobei σ ⁻¹ die Umkehrfunktion von σ ist. Das heißt, wir möchten, dass die gewichtete Ausgabe der verborgenen Ebene folgendermaßen aussieht:



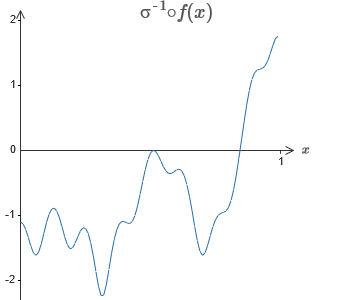Wenn dies erfolgreich ist, ist die Ausgabe des gesamten Netzwerks eine gute Annäherung an f (x) (ich setze den Versatz des Ausgangsneurons auf 0).

Dann besteht Ihre Aufgabe darin, einen NS zu entwickeln, der sich der oben gezeigten Zielfunktion annähert. Um besser zu verstehen, was passiert, empfehle ich Ihnen, dieses Problem zweimal zu lösen. Klicken Sie zum ersten Mal im Originalartikel auf das Diagramm und passen Sie die Höhen der verschiedenen Vorsprünge direkt an. Es wird für Sie ziemlich einfach sein, eine gute Annäherung an die Zielfunktion zu erhalten. Der Approximationsgrad wird durch die durchschnittliche Abweichung, die Differenz zwischen der Zielfunktion und der vom Netzwerk berechneten Funktion geschätzt. Ihre Aufgabe ist es, die durchschnittliche Abweichung auf einen Mindestwert zu bringen. Die Aufgabe gilt als erledigt, wenn die durchschnittliche Abweichung 0,40 nicht überschreitet.



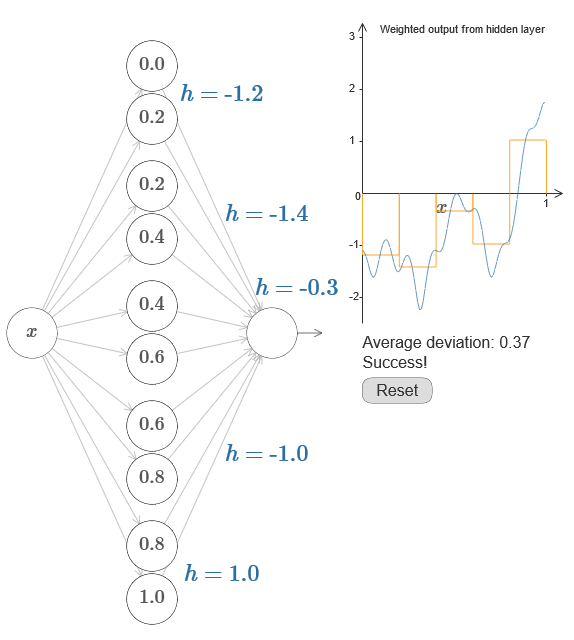Wenn Sie erfolgreich sind, klicken Sie auf die Schaltfläche Zurücksetzen, wodurch die Registerkarten zufällig geändert werden. Berühren Sie beim zweiten Mal nicht das Diagramm, sondern ändern Sie die h-Werte auf der linken Seite des Diagramms, um die durchschnittliche Abweichung auf einen Wert von 0,40 oder weniger zu bringen.

Sie haben also alle Elemente gefunden, die das Netzwerk benötigt, um die Funktion f (x) näherungsweise zu berechnen! Die Annäherung stellte sich als grob heraus, aber wir können das Ergebnis leicht verbessern, indem wir einfach die Anzahl der Paare versteckter Neuronen erhöhen, wodurch die Anzahl der Vorsprünge erhöht wird.

Insbesondere ist es einfach, alle gefundenen Daten mit der für NS verwendeten Parametrierung wieder in die Standardansicht umzuwandeln. Lassen Sie mich schnell daran erinnern, wie das funktioniert.

In der ersten Schicht haben alle Gewichte einen großen konstanten Wert, zum Beispiel w = 1000.

Die Verschiebungen versteckter Neuronen werden durch b = −ws berechnet. So wird beispielsweise für das zweite versteckte Neuron s = 0,2 zu b = –1000 × 0,2 = –200.

Die letzte Schicht der Skala wird durch die Werte von h bestimmt. So bedeutet beispielsweise der Wert, den Sie für das erste h wählen, h = -0,2, dass die Ausgabegewichte der beiden oberen versteckten Neuronen -0,2 bzw. 0,2 betragen. Und so weiter für die gesamte Ebene der Ausgabegewichte.

Schließlich ist der Versatz des Ausgangsneurons 0.

Und das war's: Wir haben eine vollständige Beschreibung des NS erhalten, die die anfängliche Zielfunktion gut berechnet. Und wir verstehen es, die Qualität der Approximation zu verbessern, indem wir die Anzahl der versteckten Neuronen verbessern.

Außerdem ist in unserer ursprünglichen Zielfunktion f (x) = 0,2 + 0,4x ²+ 0,3sin (15x) + 0,05cos (50x) ist nichts Besonderes. Ein ähnliches Verfahren könnte für jede kontinuierliche Funktion in den Intervallen von [0,1] bis [0,1] angewendet werden. Tatsächlich verwenden wir unseren einschichtigen NS, um eine Nachschlagetabelle für eine Funktion zu erstellen. Und wir können diese Idee als Grundlage nehmen, um einen allgemeinen Beweis der Universalität zu erhalten.

Funktion vieler Parameter

Wir erweitern unsere Ergebnisse auf den Fall einer Reihe von Eingabevariablen. Es klingt kompliziert, aber alle Ideen, die wir brauchen, können bereits für den Fall mit nur zwei eingehenden Variablen verstanden werden. Daher betrachten wir den Fall mit zwei eingehenden Variablen.

Schauen wir uns zunächst an, was passiert, wenn ein Neuron zwei Eingänge hat: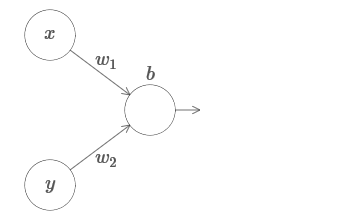



Wir haben Eingänge x und y mit den entsprechenden Gewichten w ₁ und w ₂ und dem Offset b des Neurons. Wir setzen das Gewicht von w ₂ auf 0 und spielen mit dem ersten, w ₁ , und versetzen b, um zu sehen, wie sie die Ausgabe des Neurons beeinflussen:



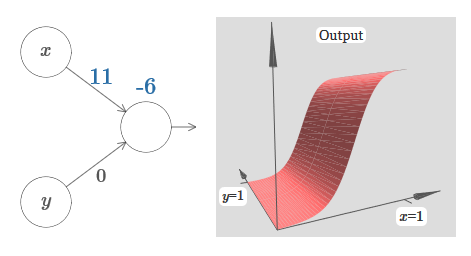Wie Sie sehen können , beeinflusst die Eingabe y bei w ₂ = 0 nicht die Ausgabe des Neurons. Alles geschieht so, als wäre x die einzige Eingabe.

Was wird Ihrer Meinung nach passieren, wenn wir das Gewicht von w ₁ auf w ₁ = 100 erhöhen und w ₂ 0 belassen? Wenn Ihnen dies nicht sofort klar ist, denken Sie ein wenig über dieses Problem nach. Dann schauen Sie sich das folgende Video an, das zeigt, was passieren wird:



Wie zuvor nähert sich die Ausgabe mit einer Erhöhung des Eingabegewichts der Form der Stufe an. Der Unterschied besteht darin, dass sich unsere Schrittfunktion jetzt in drei Dimensionen befindet. Nach wie vor können wir die Position der Schritte verschieben, indem wir den Versatz ändern. Der Winkel liegt am Punkt s _x ≡ - b / w1.

Wiederholen wir das Diagramm so, dass der Parameter der Ort des Schritts ist:



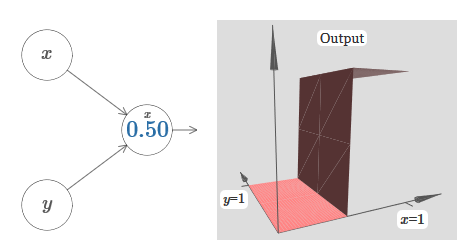Wir nehmen an, dass das Eingabegewicht von x von großer Bedeutung ist - ich habe w ₁ = 1000 verwendet - und das Gewicht w ₂ = 0. Die Zahl auf dem Neuron ist die Position des Schritts, und das x darüber erinnert uns daran, dass wir den Schritt entlang der x-Achse bewegen. Natürlich ist es durchaus möglich, eine Schrittfunktion entlang der y-Achse zu erhalten, wodurch das eingehende Gewicht für y groß wird (zum Beispiel w ₂₎= 1000), und das Gewicht für x ist 0, w ₁ = 0:



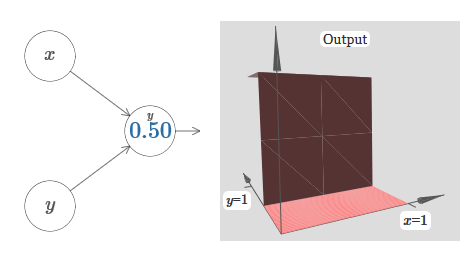Die Zahl auf dem Neuron gibt wiederum die Position des Schritts an, und y darüber erinnert uns daran, dass wir den Schritt entlang der y-Achse bewegen. Ich könnte die Gewichte für x und y direkt bestimmen, habe es aber nicht getan, da dies das Diagramm verunreinigen würde. Beachten Sie jedoch, dass der y-Marker anzeigt, dass das Gewicht für y groß und für x 0 ist.

Wir können die soeben entworfenen Schrittfunktionen verwenden, um die dreidimensionale Vorsprungsfunktion zu berechnen. Dazu nehmen wir zwei Neuronen, von denen jedes eine Schrittfunktion entlang der x-Achse berechnet. Dann kombinieren wir diese Schrittfunktionen mit den Gewichten h und –h, wobei h die gewünschte Vorsprungshöhe ist. All dies ist im folgenden Diagramm zu sehen:



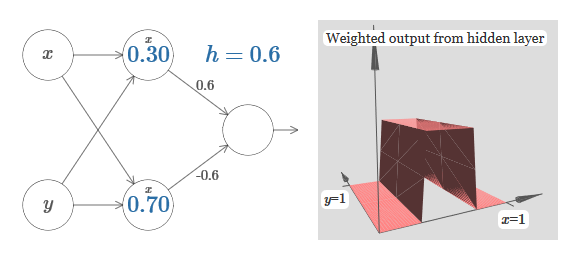Versuchen Sie, den Wert von h zu ändern. Sehen Sie, wie es sich auf Netzwerkgewichte bezieht. Und wie sie die Höhe der Vorsprungsfunktion rechts verändert.

Versuchen Sie auch, den Punkt des Schritts zu ändern, dessen Wert im oberen versteckten Neuron auf 0,30 eingestellt ist. Sehen Sie, wie sich die Form des Vorsprungs ändert. Was passiert, wenn Sie es über den 0,70-Punkt hinaus bewegen, der dem unteren versteckten Neuron zugeordnet ist?

Wir haben gelernt, wie man die Vorsprungsfunktion entlang der x-Achse aufbaut. Natürlich können wir die Vorsprungsfunktion leicht entlang der y-Achse ausführen, indem wir zwei Schrittfunktionen entlang der y-Achse verwenden. Denken Sie daran, dass wir dies tun können, indem wir am Eingang y große Gewichte machen und am Eingang x das Gewicht 0 setzen. Und so, was passiert:



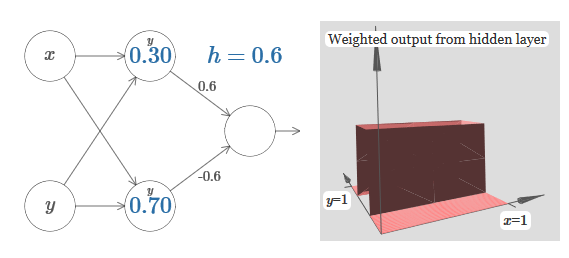Es sieht fast identisch mit dem vorherigen Netzwerk aus! Die einzige sichtbare Veränderung sind kleine y-Marker auf versteckten Neuronen. Sie erinnern uns daran, dass sie Schrittfunktionen für y und nicht für x erzeugen, sodass das Gewicht am Eingang y sehr groß ist und am Eingang x Null ist und nicht umgekehrt. Nach wie vor habe ich beschlossen, es nicht direkt zu zeigen, um das Bild nicht zu überladen.

Mal sehen, was passiert, wenn wir zwei Vorsprungsfunktionen hinzufügen, eine entlang der x-Achse, die andere entlang der y-Achse, beide mit der Höhe h:



Um das Verbindungsdiagramm mit dem Gewicht Null zu vereinfachen, habe ich weggelassen. Bisher habe ich kleine x- und y-Marker auf versteckten Neuronen hinterlassen, um mich daran zu erinnern, in welche Richtungen die Protrusionsfunktionen berechnet werden. Später werden wir sie ablehnen, da sie durch die eingehende Variable impliziert werden.

Versuchen Sie, den Parameter h zu ändern. Wie Sie sehen können, ändern sich aus diesem Grund die Ausgangsgewichte sowie die Gewichte der beiden Vorsprungsfunktionen x und y.

Unsere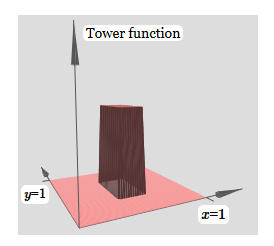



Erstellung ist ein bisschen wie eine „Turmfunktion“: Wenn wir solche Turmfunktionen erstellen können, können wir sie verwenden, um beliebige Funktionen zu approximieren, indem wir einfach Türme unterschiedlicher Höhe an verschiedenen Stellen hinzufügen:



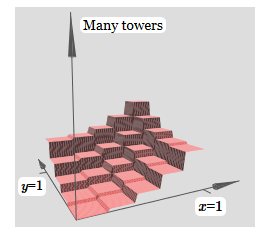Natürlich haben wir die Erstellung einer beliebigen Turmfunktion noch nicht erreicht. Bisher haben wir so etwas wie einen zentralen Turm der Höhe 2h mit einem Plateau der Höhe h um ihn herum gebaut.

Aber wir können einen Turm zum Funktionieren bringen. Denken Sie daran, dass wir zuvor gezeigt haben, wie Neuronen verwendet werden können, um die if-then-else-Anweisung zu implementieren:

if  >= :  1 else:  0 

Es war ein Neuron mit einem Eingang. Und wir müssen eine ähnliche Idee auf die kombinierte Ausgabe versteckter Neuronen anwenden:

  if     >= :  1 else:  0 

Wenn wir die richtige Schwelle wählen - zum Beispiel 3h / 2, die zwischen der Höhe des Plateaus und der Höhe des zentralen Turms gedrückt wird - können wir das Plateau auf Null drücken und nur einen Turm belassen.

Stellen Sie sich vor, wie das geht? Versuchen Sie, mit dem folgenden Netzwerk zu experimentieren. Jetzt zeichnen wir die Ausgabe des gesamten Netzwerks und nicht nur die gewichtete Ausgabe der verborgenen Schicht. Dies bedeutet, dass wir den Offset-Term zur gewichteten Ausgabe der verborgenen Ebene hinzufügen und das Sigmoid anwenden. Können Sie die Werte für h und b finden, für die Sie einen Turm erhalten? Wenn Sie an dieser Stelle nicht weiterkommen, sind hier zwei Tipps: (1) Damit das ausgehende Neuron das Wenn-Dann-Sonst-Verhalten zeigt, müssen die eingehenden Gewichte (alle h oder –h) groß sein. (2) Der Wert von b bestimmt die Skala der Wenn-Dann-Sonst-Schwelle.



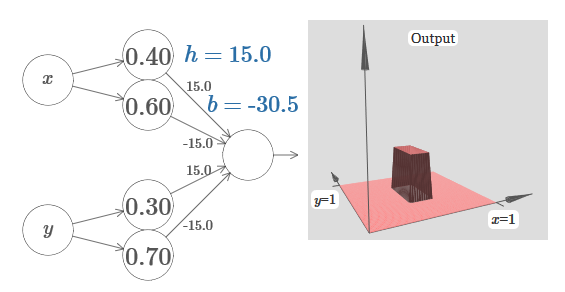
Mit Standardparametern ähnelt die Ausgabe einer abgeflachten Version des vorherigen Diagramms mit einem Turm und einem Plateau. Um das gewünschte Verhalten zu erzielen, müssen Sie den Wert von h erhöhen. Dies gibt uns das Schwellenverhalten von Wenn-Dann-Sonst. Zweitens muss man b ≈ −3h / 2 wählen, um den Schwellenwert korrekt einzustellen.

So sieht es für h = 10 aus:


Selbst für relativ bescheidene Werte von h erhalten wir eine schöne Turmfunktion. Und natürlich können wir ein beliebig schönes Ergebnis erzielen, indem wir h weiter erhöhen und die Vorspannung auf dem Niveau b = –3h / 2 halten.

Versuchen wir, zwei Netzwerke zusammenzukleben, um zwei verschiedene Turmfunktionen zu zählen. Um die jeweiligen Rollen der beiden Subnetze zu verdeutlichen, habe ich sie in separate Rechtecke eingefügt: Jedes von ihnen berechnet die Turmfunktion mit der oben beschriebenen Technik. Die Grafik rechts zeigt die gewichtete Ausgabe der zweiten verborgenen Schicht, dh die gewichtete Kombination von Turmfunktionen.



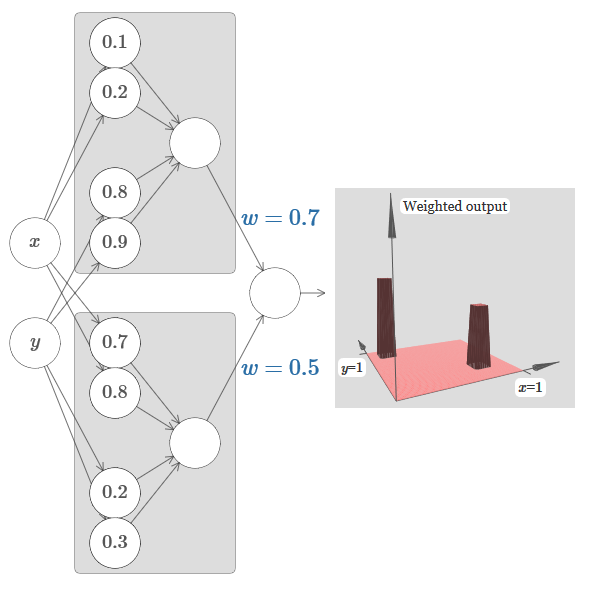
Insbesondere ist zu sehen, dass Sie durch Ändern des Gewichts in der letzten Schicht die Höhe der Ausgangstürme ändern können.

Mit derselben Idee können Sie so viele Türme berechnen, wie Sie möchten. Wir können sie beliebig dünn und groß machen. Infolgedessen garantieren wir, dass sich die gewichtete Ausgabe der zweiten verborgenen Schicht jeder gewünschten Funktion zweier Variablen annähert:



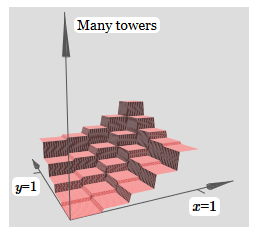
Insbesondere wenn wir die gewichtete Ausgabe der zweiten verborgenen Schicht zwingen, sich gut σ ⁻¹ ⋅f anzunähern, garantieren wir, dass die Ausgabe unseres Netzwerks eine gute Annäherung an die gewünschte Funktion f ist.

Was ist mit den Funktionen vieler Variablen?

Versuchen wir drei Variablen zu nehmen: x ₁ , x ₂ , x ₃ . Kann das folgende Netzwerk verwendet werden, um die Turmfunktion in vier Dimensionen zu berechnen?



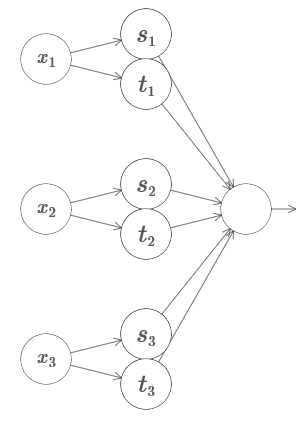
Hier bezeichnen x ₁ , x ₂ , x ₃ den Netzwerkeingang. s ₁ , t ₁ usw. - Schrittpunkte für Neuronen - das heißt, alle Gewichte in der ersten Schicht sind groß, und die Offsets werden so zugewiesen, dass die Punkte der Schritte s ₁ , t ₁ , s ₂ , ... sind. Die Gewichte in der zweiten Schicht wechseln sich ab, + h, −h, wobei h eine sehr große Zahl ist. Der Ausgangsoffset beträgt −5h / 2.

Das Netzwerk berechnet unter drei Bedingungen eine Funktion gleich 1: x ₁ liegt zwischen s ₁ und t ₁ ; x ₂ liegt zwischen s ₂ und t ₂ ; x ₃ liegt zwischen s ₃ und t ₃ . Das Netzwerk ist an allen anderen Orten 0. Dies ist ein Turm, in dem 1 einen kleinen Teil des Eingangsraums darstellt und 0 alles andere ist.

Wenn wir viele solcher Netzwerke zusammenkleben, können wir so viele Türme erhalten, wie wir möchten, und eine beliebige Funktion von drei Variablen approximieren. Die gleiche Idee funktioniert in m Dimensionen. Nur der Ausgangsversatz (−m + 1/2) h wird geändert, um die gewünschten Werte richtig zu drücken und das Plateau zu entfernen.

Nun wissen wir, wie man NS verwendet, um die reale Funktion vieler Variablen zu approximieren. Was ist mit den Vektorfunktionen f (x ₁ , ..., x _m ) ∈ R ⁿ ? Natürlich kann eine solche Funktion einfach als n separate reelle Funktionen f1 (x ₁ , ..., x _m ), f2 (x ₁ , ..., x _m ) usw. betrachtet werden. Und dann kleben wir einfach alle Netzwerke zusammen. Es ist also einfach, es herauszufinden.

Herausforderung

• Wir haben gesehen, wie man neuronale Netze mit zwei verborgenen Schichten verwendet, um eine beliebige Funktion zu approximieren. Können Sie beweisen, dass dies mit einer verborgenen Schicht möglich ist? Tipp - Versuchen Sie, nur mit zwei Ausgabevariablen zu arbeiten, und zeigen Sie Folgendes: (a) Es ist möglich, die Funktionen der Schritte nicht nur entlang der x- oder y-Achse, sondern auch in einer beliebigen Richtung abzurufen. (b) Addiert man viele Konstruktionen aus Schritt (a), ist es möglich, die Funktion eines runden statt eines rechteckigen Turms zu approximieren; © Mit runden Türmen kann eine beliebige Funktion angenähert werden. Schritt © wird mit dem in diesem Kapitel vorgestellten Material etwas einfacher.

Über sigmoidale Neuronen hinausgehen

Wir haben bewiesen, dass ein Netzwerk von Sigmoidneuronen jede Funktion berechnen kann. Denken Sie daran, dass sich in einem Sigmoid-Neuron die Eingänge x ₁ , x ₂ , ... am Ausgang in σ (∑ _j w _j x _{j j} + b) verwandeln, wobei w _j die Gewichte sind, b die Verschiebung ist, σ das Sigmoid ist.



Was ist, wenn wir einen anderen Neuronentyp mit einer anderen Aktivierungsfunktion betrachten, s (z):



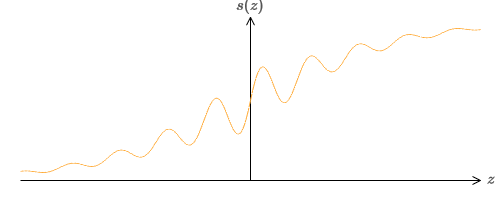
Das heißt, wir nehmen an, dass wenn ein Neuron x ₁ , x ₂ , ... Gewichte w ₁ , w ₂ , ... und Vorspannung b hat, s (∑ _j w _j x _j + b) ausgegeben wird.

Wir können diese Aktivierungsfunktion verwenden, um Schritt zu machen, genau wie im Fall des Sigmoid. Versuchen Sie (im Originalartikel ) im Diagramm, das Gewicht auf beispielsweise w = 100 anzuheben:





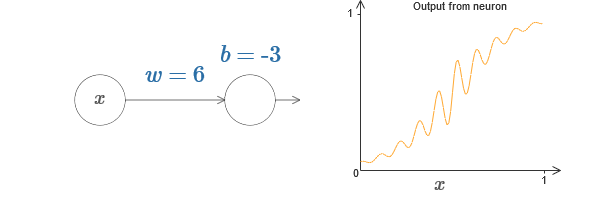
Wie im Fall des Sigmoid wird dadurch die Aktivierungsfunktion komprimiert, was zu einer sehr guten Annäherung an die Schrittfunktion führt. Wenn Sie den Versatz ändern, werden Sie feststellen, dass wir die Position des Schritts in eine beliebige ändern können. Daher können wir dieselben Tricks wie zuvor verwenden, um jede gewünschte Funktion zu berechnen.

Welche Eigenschaften sollte s (z) haben, damit dies funktioniert? Wir müssen annehmen, dass s (z) gut definiert ist als z → −∞ und z → ∞. Diese Grenzwerte sind zwei Werte, die von unserer Schrittfunktion akzeptiert werden. Wir müssen auch davon ausgehen, dass diese Grenzen unterschiedlich sind. Wenn sie sich nicht unterscheiden würden, würden die Schritte nicht funktionieren, es würde einfach einen flachen Zeitplan geben! Wenn jedoch die Aktivierungsfunktion s (z) diese Eigenschaften erfüllt, sind die darauf basierenden Neuronen universell für Berechnungen geeignet.

Die Aufgaben

• Zu Beginn des Buches haben wir einen anderen Neuronentyp kennengelernt - ein begradigtes lineares Neuron oder eine gleichgerichtete lineare Einheit, ReLU. Erklären Sie, warum solche Neuronen die für die Universalität erforderlichen Bedingungen nicht erfüllen. Finden Sie Beweise für die Vielseitigkeit, die zeigen, dass ReLUs universell für die Datenverarbeitung geeignet sind.
• Angenommen, wir betrachten lineare Neuronen mit der Aktivierungsfunktion s (z) = z. Erklären Sie, warum lineare Neuronen die Bedingungen der Universalität nicht erfüllen. Zeigen Sie, dass solche Neuronen nicht für Universal Computing verwendet werden können.

Schrittfunktion korrigieren

Vorläufig gingen wir davon aus, dass unsere Neuronen genaue Schrittfunktionen erzeugen. Dies ist eine gute Annäherung, aber nur eine Annäherung. Tatsächlich gibt es eine enge Fehlerlücke, die in der folgenden Grafik dargestellt ist und in der sich die Funktionen überhaupt nicht wie eine Schrittfunktion verhalten:



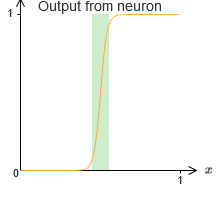
In dieser Zeit des Scheiterns funktioniert meine Erklärung der Universalität nicht.

Das Scheitern ist nicht so beängstigend. Durch Einstellen ausreichend großer Eingabegewichte können diese Lücken beliebig klein gemacht werden. Wir können sie viel kleiner als auf der Karte machen und für das Auge unsichtbar machen. Vielleicht müssen wir uns also keine Sorgen um dieses Problem machen.

Trotzdem hätte ich gerne einen Weg, es zu lösen.

Es stellt sich heraus, dass es leicht zu lösen ist. Schauen wir uns diese Lösung zur Berechnung von NS-Funktionen mit nur einer Eingabe und Ausgabe an. Dieselben Ideen werden funktionieren, um das Problem mit einer großen Anzahl von Ein- und Ausgängen zu lösen.

Angenommen, wir möchten, dass unser Netzwerk eine Funktion f berechnet. Nach wie vor versuchen wir dies, indem wir das Netzwerk so gestalten, dass die gewichtete Ausgabe der verborgenen Neuronenschicht σ ⁻¹ ⋅f (x) ist:



Wenn wir dies mit der oben beschriebenen Technik tun, werden wir die verborgenen Neuronen zwingen, eine Folge von Vorsprungsfunktionen zu erzeugen:



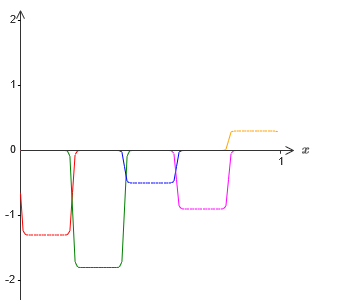
Natürlich habe ich die Größe der Ausfallintervalle übertrieben, damit es leichter zu sehen war. Es sollte klar sein, dass wir, wenn wir alle diese Funktionen der Vorsprünge addieren, überall eine ziemlich gute Annäherung von σ ⁻¹ ⋅f (x) erhalten, mit Ausnahme der Ausfallintervalle.

Nehmen wir jedoch an, dass wir anstelle der gerade beschriebenen Näherung eine Reihe versteckter Neuronen verwenden, um die Näherung der Hälfte unserer ursprünglichen Zielfunktion zu berechnen, dh σ ⁻¹ ⋅f (x) / 2. Natürlich sieht es genauso aus wie eine skalierte Version des neuesten Diagramms:



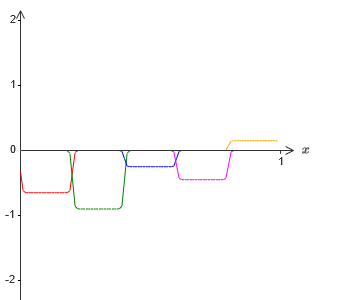
Nehmen wir an, wir lassen einen weiteren Satz versteckter Neuronen die Annäherung an σ ⁻¹ ⋅f (x) / 2 berechnen. An ihrer Basis werden die Vorsprünge jedoch um die Hälfte ihrer Breite verschoben:



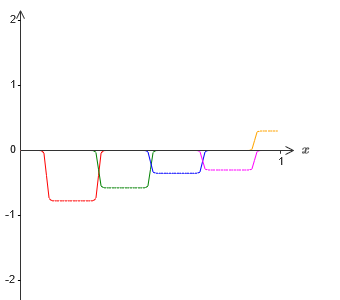
Jetzt haben wir zwei verschiedene Näherungen für σ - 1⋅f (x) / 2. Wenn wir diese beiden Näherungen addieren, erhalten wir eine allgemeine Näherung an σ - 1⋅f (x). Diese allgemeine Annäherung weist in kleinen Intervallen immer noch Ungenauigkeiten auf. Das Problem wird jedoch geringer sein als zuvor - da die Punkte, die in die Intervalle des Versagens der ersten Näherung fallen, nicht in die Intervalle des Versagens der zweiten Näherung fallen. Daher ist die Annäherung in diesen Intervallen ungefähr zweimal besser.

Wir können die Situation verbessern, indem wir eine große Anzahl M überlappender Approximationen der Funktion σ - 1⋅f (x) / M hinzufügen. Wenn alle ihre Ausfallintervalle eng genug sind, wird jeder Strom nur in einem von ihnen sein. Wenn Sie eine ausreichend große Anzahl überlappender Näherungen von M verwenden, ist das Ergebnis eine ausgezeichnete allgemeine Näherung.

Fazit

Die hier diskutierte Erklärung der Universalität kann definitiv nicht als praktische Beschreibung des Zählens von Funktionen unter Verwendung neuronaler Netze bezeichnet werden! In diesem Sinne ist es eher ein Beweis für die Vielseitigkeit von NAND-Logikgattern und mehr. Daher habe ich im Grunde versucht, dieses Design klar und einfach zu befolgen, ohne seine Details zu optimieren. Der Versuch, dieses Design zu optimieren, kann jedoch eine interessante und lehrreiche Übung für Sie sein.

Obwohl das erhaltene Ergebnis nicht direkt zum Erstellen von NS verwendet werden kann, ist es wichtig, da es die Frage nach der Berechenbarkeit einer bestimmten Funktion unter Verwendung von NS beseitigt. Die Antwort auf eine solche Frage wird immer positiv sein. Daher ist es richtig zu fragen, ob eine Funktion berechenbar ist, aber wie kann sie richtig berechnet werden?

Unser universelles Design verwendet nur zwei versteckte Schichten, um eine beliebige Funktion zu berechnen. Wie bereits erwähnt, ist es möglich, dasselbe Ergebnis mit einer einzelnen verborgenen Ebene zu erzielen. Vor diesem Hintergrund fragen Sie sich vielleicht, warum wir tiefe Netzwerke benötigen, dh Netzwerke mit einer großen Anzahl versteckter Schichten. Können wir diese Netzwerke nicht einfach durch flache Netzwerke mit einer verborgenen Schicht ersetzen?

Obwohl es im Prinzip möglich ist, gibt es gute praktische Gründe für die Verwendung tiefer neuronaler Netze. Wie in Kapitel 1 beschrieben, haben tiefe NS eine hierarchische Struktur, die es ihnen ermöglicht, sich gut anzupassen, um hierarchisches Wissen zu studieren, das zur Lösung realer Probleme nützlich ist. Insbesondere bei der Lösung von Problemen wie der Mustererkennung ist es nützlich, ein System zu verwenden, das nicht nur einzelne Pixel, sondern auch immer komplexere Konzepte versteht: von Rändern über einfache geometrische Formen und darüber hinaus bis hin zu komplexen Szenen mit mehreren Objekten. In späteren Kapiteln werden wir Beweise dafür sehen, dass tiefe NS besser mit dem Studium solcher Wissenshierarchien umgehen können als flache. Zusammenfassend: Die Universalität sagt uns, dass NS jede Funktion berechnen kann; Empirische Erkenntnisse legen nahe, dass tiefe NS besser an die Untersuchung von Funktionen angepasst sind, die zur Lösung vieler realer Probleme nützlich sind.