Eine neue Methode der Clusteranalyse wird vorgeschlagen. Sein Vorteil liegt in einem weniger rechenintensiven Algorithmus. Die Methode basiert auf der Berechnung von Stimmen für die Tatsache, dass sich ein Objektpaar in derselben Klasse befindet, aus Informationen über den Wert einzelner Koordinaten.
Einführung
Ein großer Bedarf an Datenanalyse ist die Entwicklung effektiver Klassifizierungsmethoden. Bei solchen Methoden ist es erforderlich, den gesamten Satz von Objekten in die optimale Anzahl von Klassen zu unterteilen, basierend nur auf Informationen über den Wert einzelner Indikatoren [Zagoruyko 1999].
Die Clusteranalyse ist eine der beliebtesten Methoden der Datenanalyse und der mathematischen Statistik. Mit der Clusteranalyse können Sie automatisch Objektklassen finden, wobei nur Informationen zu den quantitativen Indikatoren von Objekten verwendet werden (Training ohne Lehrer). Jede solche Klasse kann durch eines ihrer charakteristischsten Objekte definiert werden, beispielsweise durch Indikatoren gemittelt. Es gibt eine Vielzahl von Methoden und Ansätzen zur Klassifizierung von Daten.
Moderne Forschungen auf dem Gebiet der Clusteranalyse werden durchgeführt, um Methoden zur Bestimmung von Klassen komplexer Topologie zu verbessern [Furaoa 2007, Zagoruiko 2013] sowie die Geschwindigkeit von Algorithmen bei Big Data zu verbessern.
In diesem Artikel schlagen wir eine Klassifizierungsmethode vor, die darauf basiert, Stimmen für ein Objektpaar in derselben Klasse zu erhalten, basierend auf Informationen über den Wert einzelner Indikatoren. Es wird vorgeschlagen zu berücksichtigen, dass ein Objektpaar zur selben Klasse gehört, wenn die Werte ihrer einzelnen Indikatoren in einem Intervall liegen, dessen Länge einen bestimmten Wert nicht überschreitet.
K-Mittel-Methode
Die k-means-Methode ist eine der beliebtesten Clustering-Methoden. Ziel ist es, solche Rechenzentren zu erhalten, die der Hypothese der Kompaktheit von Datenklassen mit ihrer symmetrischen radialen Verteilung entsprechen. Eine Möglichkeit, die Positionen solcher Zentren anhand ihrer Anzahl \ textit {k} zu bestimmen, ist der EM-Ansatz.
Bei diesem Verfahren werden zwei Verfahren nacheinander ausgeführt.
- Definition für jedes Datenobjekt $ inline $ X_ {i} $ inline $ das nächste Zentrum $ inline $ C_ {j} $ inline $ und Zuweisen einer Klassenbezeichnung zu diesem Objekt $ inline $ X_ {i} ^ {j} $ inline $ . Ferner wird für alle Objekte ihre Zugehörigkeit zu verschiedenen Klassen bestimmt.
- Berechnung der neuen Position der Zentren aller Klassen.
Wenn wir diese beiden Prozeduren iterativ von der anfänglichen zufälligen Position der Zentren der \ textit {k} -Klassen wiederholen, können wir die Trennung von Objekten in Klassen erreichen, die der Hypothese der radialen Kompaktheit von Klassen am ehesten entsprechen würden.
Der Klassifizierungsalgorithmus eines neuen Autors wird mit der k-means-Methode verglichen.
Neue Methode
Der neue Clusteranalysealgorithmus basiert auf Stimmen für die Zugehörigkeit zu verschiedenen Clustern aus Informationen über die Werte der einzelnen Koordinaten von Datenpunkten.
- Es wird ein Wert d angegeben , der die Länge des Intervalls von Indikatoren kennzeichnet, innerhalb dessen zwei Objekte als zur selben Klasse gehörend betrachtet werden.
- Ausgewählte Metrik $ inline $ x_ {i} $ inline $ und alle Objektpaare werden berücksichtigt $ inline $ \ left \ {O_ {l}, O_ {k} \ right \} $ inline $ wo $ inline $ l, k = 1 \ ldots N $ inline $ .
- Wenn $ inline $ \ left | x_ {i} ^ {l} -x_ {i} ^ {k} \ right | \ le d $ inline $ dann die Größe $ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (Stimme hinzugefügt).
- Die Aktionen 2) und 3) werden für alle Indikatoren wiederholt $ inline $ i = 1 \ ldots M $ inline $ .
- Der Wert p , der die Mindestanzahl von Stimmen für die Zugehörigkeit zu denselben Klassen kennzeichnet, wird eingestellt.
- Unter Verwendung der Schlüsselmethode von Wertepaaren werden alle Objektklassen so bestimmt, dass innerhalb einer Sprachklasse für Objektpaare aus diesen Klassen > = p .
- Iteriert alle Werte von d und p und wiederholt die Punkte 1) - 6), um die Anzahl der Klassen zu erhalten, die der angegebenen Anzahl von Klassen g am nächsten kommt.
Um die Komplexität des Algorithmus auf
N zu reduzieren, können Sie
T- Intervalle für einzelne Indikatoren verwenden und Klausel 2) und 3) im Algorithmus durch Folgendes ersetzen:
1. Der Indikator ist ausgewählt
$ inline $ x_ {i} $ inline $ und alle Intervalle werden berücksichtigt
$ inline $ \ left [u_ {l}, w_ {l} \ right] $ inline $ wo
$ inline $ l = 1 \ ldots T $ inline $ ::
$$ display $$ u_ {0} = \ min (x_ {i}); u_ {0} = \ min (x_ {i}); $$ display $$
$$ display $$ w_ {T} = \ max (x_ {i}); $$ display $$
$$ display $$ s_ {i} = w_ {T} -u_ {0}; $$ display $$
$$ display $$ u_ {l} = u_ {0} + l \ cdot s_ {i}; $$ display $$
$$ display $$ w_ {l} = u_ {l} + d; $$ display $$
2. Wenn
$ inline $ x_ {i} ^ {k} \ in \ left [u_ {j}, w_ {j} \ right] $ inline $ und
$ inline $ x_ {i} ^ {l} \ in \ left [u_ {j}, w_ {j} \ right] $ inline $ wo
$ inline $ j = 1 \ ldots T $ inline $ dann die Größe
$ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (Die Stimme wird mit einer eindeutigen Taste
l ,
k für die
i- te Anzeige hinzugefügt.)
Numerisches Experiment
Die Daten mit der für den Menschen intuitiven Klassifizierung wurden als Anfangsdaten verwendet.
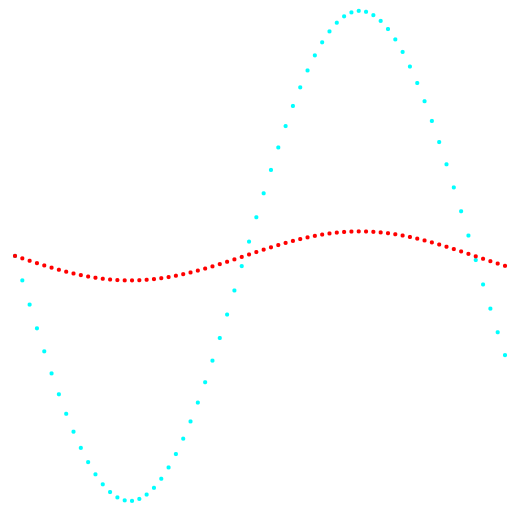
Die Abbildungen 1 und 2 zeigen die Ergebnisse der Klassifizierung der k-Mittelwert-Methode und der neuen Klassifizierungsmethode.
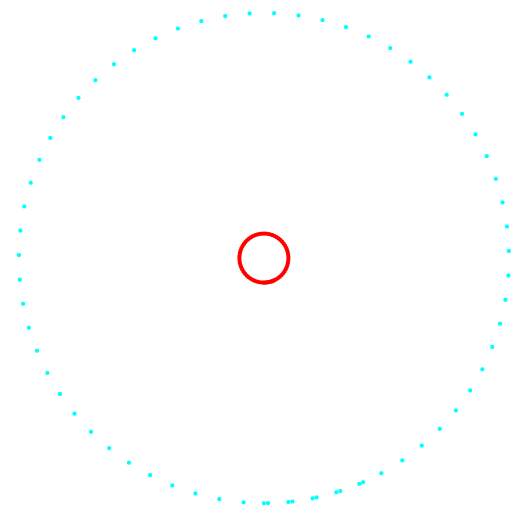Abb. 1. Projektion 1-2 und Datenklassifizierung.Links ist die k-means-Methode, rechts die Methode des Autors.
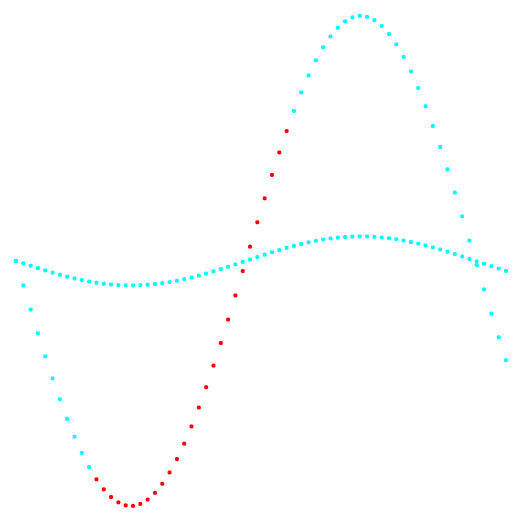
Abb. 2. Projektion 2-3 und Datenklassifizierung.Links ist die k-means-Methode, rechts die Methode des Autors.
Das Ergebnis des Vergleichs der beiden Methoden zeigt den offensichtlichen Vorteil der Methode des Autors in ihrer Fähigkeit, Cluster komplexer Topologie zu erkennen.
Software-Implementierung
Die k-means Clustering-Methode wurde programmgesteuert als Webanwendung implementiert. Der Computerteil der Anwendung wird unter Verwendung des Zend-Frameworks an einen in PHP geschriebenen Server gesendet. Die Anwendungsoberfläche wurde mit HTML, CSS, JavaScript und jQuery geschrieben. Die Anwendung ist nach der Registrierung eines neuen Benutzers unter
http://svlaboratory.org/application/klaster2 verfügbar. Mit der Anwendung können Sie die Zugehörigkeit von Objekten zu verschiedenen Clustern in einer bestimmten Koordinatenebene visualisieren.
Fazit
Eine neue Klassifizierungsmethode wird vorgeschlagen. Die Vorteile dieser Methode sind die Erkennung von Klassen komplexer Topologie, nicht radialer Verteilung sowie eine geringere Komplexität des Algorithmus und weniger Aktionen, was insbesondere bei Arrays mit großen Datenmengen von Vorteil ist.
Referenzen- Zagoruyko N.G. Angewandte Methoden der Daten- und Wissensanalyse. Nowosibirsk: Verlag des Instituts für Mathematik, 1999.270 p.
- Zagoruyko N.G., Borisova I.A., Kutnenko O.A., Levanov D.A. Erkennung von Mustern in experimentellen Datenfeldern // Computertechnologien. - 2013.Vol. 18. Nr. S1. S. 12-20.
- Shen Furaoa, Tomotaka Ogurab, Osamu Hasegawab Ein verbessertes selbstorganisierendes inkrementelles neuronales Netzwerk für unbeaufsichtigtes Online-Lernen. Hasegawa Lab, 2007.