Die Übersetzung wurde für Studenten des Kurses „Applied Analytics on R“ erstellt .
Dies war mein erster Versuch, Clients basierend auf realen Daten zu gruppieren, und es gab mir wertvolle Erfahrungen. Es gibt viele Artikel im Internet über das Clustering mit numerischen Variablen, aber es war nicht so einfach, Lösungen für kategoriale Daten zu finden, was etwas schwieriger ist. Clustering-Methoden für kategoriale Daten befinden sich noch in der Entwicklung, und in einem anderen Beitrag werde ich einen anderen ausprobieren.
Auf der anderen Seite denken viele Menschen, dass das Clustering kategorialer Daten möglicherweise keine aussagekräftigen Ergebnisse
liefert - und dies ist teilweise richtig (siehe die
ausgezeichnete Diskussion zu CrossValidated ). Irgendwann dachte ich: „Was mache ich? Sie können einfach in Kohorten unterteilt werden. “ Eine Kohortenanalyse ist jedoch auch nicht immer ratsam, insbesondere bei einer signifikanten Anzahl von kategorialen Variablen mit einer großen Anzahl von Ebenen: Sie können problemlos mit 5-7 Kohorten umgehen, aber wenn Sie 22 Variablen haben und jede 5 Ebenen hat (z. B. eine Kundenumfrage mit diskreten Schätzungen 1) , 2, 3, 4 und 5), und Sie müssen verstehen, mit welchen charakteristischen Gruppen von Kunden Sie es zu tun haben - Sie erhalten 22x5 Kohorten. Niemand möchte sich mit einer solchen Aufgabe beschäftigen. Und hier könnte Clustering helfen. In diesem Beitrag werde ich darüber sprechen, was ich selbst wissen möchte, sobald ich mit dem Clustering begonnen habe.
Der Clustering-Prozess selbst besteht aus drei Schritten:
- Der Aufbau einer Matrix der Unähnlichkeit ist zweifellos die wichtigste Entscheidung beim Clustering. Alle nachfolgenden Schritte basieren auf der von Ihnen erstellten Unähnlichkeitsmatrix.
- Die Wahl der Clustering-Methode.
- Cluster-Evaluierung.
Dieser Beitrag ist eine Art Einführung, die die Grundprinzipien des Clustering und seiner Implementierung in der Umgebung R beschreibt.
Unähnlichkeitsmatrix
Die Basis für das Clustering wird die Unähnlichkeitsmatrix sein, die mathematisch beschreibt, wie unterschiedlich die Punkte im Datensatz voneinander entfernt sind. Sie können die Punkte, die am nächsten beieinander liegen, weiter in Gruppen zusammenfassen oder die am weitesten voneinander entfernten Punkte voneinander trennen - dies ist die Hauptidee der Clusterbildung.
In diesem Stadium sind Unterschiede zwischen Datentypen wichtig, da die Unähnlichkeitsmatrix auf den Abständen zwischen einzelnen Datenpunkten basiert. Die Abstände zwischen den Punkten numerischer Daten sind leicht vorstellbar (ein bekanntes Beispiel sind
euklidische Abstände ), aber bei kategorialen Daten (Faktoren in R) ist nicht alles so offensichtlich.
Um in diesem Fall eine Unähnlichkeitsmatrix zu erstellen, sollte der sogenannte Gover-Abstand verwendet werden. Ich werde nicht auf den mathematischen Teil dieses Konzepts eingehen, sondern nur Links bereitstellen:
hier und
da . Aus diesem
metric = c("gower") bevorzuge ich die Verwendung von
daisy() mit der
metric = c("gower") aus dem
cluster .
Die Unähnlichkeitsmatrix ist fertig. Für 200 Beobachtungen wird es schnell erstellt, erfordert jedoch möglicherweise einen sehr großen Rechenaufwand, wenn Sie mit einem großen Datensatz arbeiten.
In der Praxis ist es sehr wahrscheinlich, dass Sie zuerst den Datensatz bereinigen, die erforderlichen Transformationen aus den Zeilen in Faktoren durchführen und die fehlenden Werte verfolgen müssen. In meinem Fall enthielt der Datensatz auch Zeilen mit fehlenden Werten, die jedes Mal wunderschön gruppiert wurden. Es schien also ein Schatz zu sein - bis ich mir die Werte ansah (leider!).
Clustering-Algorithmen
Möglicherweise wissen Sie bereits, dass Clustering
k-means und hierarchisch ist . In diesem Beitrag konzentriere ich mich auf die zweite Methode, da sie flexibler ist und verschiedene Ansätze ermöglicht: Sie können entweder einen
agglomerativen (von unten nach oben) oder einen
abteilungsweisen (von oben nach unten) Clustering-Algorithmus wählen.
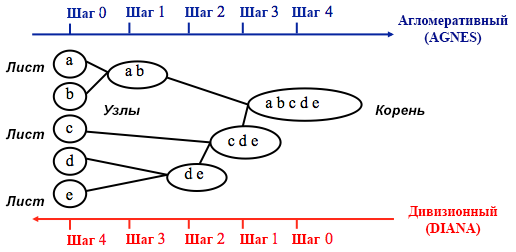Quelle: Programmierhandbuch für UC Business Analytics R.Agglomeratives Clustering beginnt mit
n Clustern, wobei
n die Anzahl der Beobachtungen ist: Es wird angenommen, dass jeder von ihnen ein separater Cluster ist. Dann versucht der Algorithmus, die ähnlichsten Datenpunkte untereinander zu finden und zu gruppieren - so beginnt die Clusterbildung.
Divisional Clustering wird in umgekehrter Weise durchgeführt - es wird zunächst angenommen, dass alle n Datenpunkte, die wir haben, ein großer Cluster sind, und dann werden die am wenigsten ähnlichen in separate Gruppen unterteilt.
Bei der Entscheidung, welche dieser Methoden ausgewählt werden soll, ist es immer sinnvoll, alle Optionen auszuprobieren. Im Allgemeinen
eignet sich agglomeratives Clustering jedoch besser zur Identifizierung kleiner Cluster und wird von den meisten Computerprogrammen verwendet, und Divisionsclustering ist besser zur Identifizierung großer Cluster geeignet .
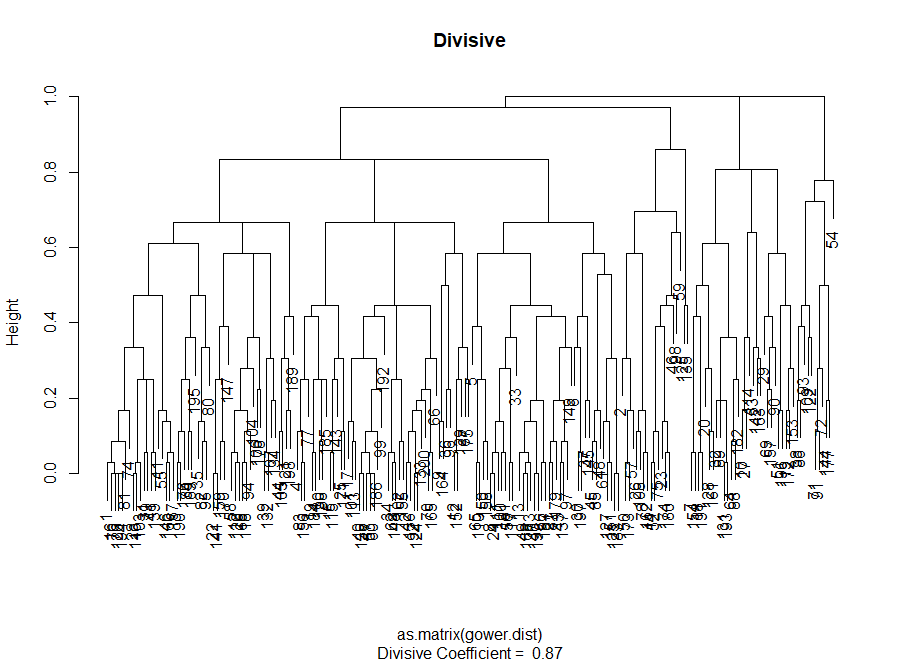
Bevor ich mich für eine Methode entscheide, schaue ich mir lieber Dendrogramme an - eine grafische Darstellung von Clustering. Wie Sie später sehen werden, sind einige Dendrogramme gut ausbalanciert, während andere sehr chaotisch sind.
# Die Haupteingabe für den folgenden Code ist die Unähnlichkeit (Distanzmatrix)
Bewertung der Clusterqualität
In diesem Stadium muss zwischen verschiedenen Clustering-Algorithmen und einer unterschiedlichen Anzahl von Clustern gewählt werden. Sie können verschiedene Bewertungsmethoden anwenden, ohne zu vergessen, sich vom
gesunden Menschenverstand leiten zu lassen. Ich habe diese Wörter fett und kursiv hervorgehoben, da die Aussagekraft der Auswahl
sehr wichtig ist - die Anzahl der Cluster und die Methode zur Aufteilung von Daten in Gruppen sollten aus praktischer Sicht praktisch sein. Die Anzahl der Kombinationen von Werten kategorialer Variablen ist endlich (da sie diskret sind), aber keine darauf basierende Aufschlüsselung ist sinnvoll. Möglicherweise möchten Sie auch nicht sehr wenige Cluster haben - in diesem Fall sind sie zu verallgemeinert. Am Ende hängt alles von Ihrem Ziel und den Aufgaben der Analyse ab.
Im Allgemeinen möchten Sie beim Erstellen von Clustern klar definierte Gruppen von Datenpunkten erhalten, damit der Abstand zwischen solchen Punkten innerhalb des Clusters (
oder die Kompaktheit ) minimal und der Abstand zwischen Gruppen (
Trennbarkeit ) maximal möglich ist. Dies ist intuitiv leicht zu verstehen: Der Abstand zwischen Punkten ist ein Maß für ihre Unähnlichkeit, die auf der Grundlage der Unähnlichkeitsmatrix erhalten wird. Daher basiert die Bewertung der Qualität der Clusterbildung auf der Bewertung der Kompaktheit und Trennbarkeit.
Als nächstes werde ich zwei Ansätze demonstrieren und zeigen, dass einer von ihnen bedeutungslose Ergebnisse liefern kann.
- Ellbogenmethode : Beginnen Sie damit, wenn der wichtigste Faktor für Ihre Analyse die Kompaktheit der Cluster ist, d. H. Die Ähnlichkeit innerhalb der Gruppen.
- Bewertungsmethode für Silhouetten : Das als Maß für die Datenkonsistenz verwendete Silhouettendiagramm zeigt, wie nahe die einzelnen Punkte innerhalb eines Clusters an den Punkten in benachbarten Clustern liegen.
In der Praxis führen diese beiden Methoden häufig zu unterschiedlichen Ergebnissen, was zu Verwirrung führen kann. Die maximale Kompaktheit und die klarste Trennung werden mit einer unterschiedlichen Anzahl von Clustern erreicht, sodass der gesunde Menschenverstand und das Verständnis dessen, was Ihre Daten wirklich bedeuten, eine wichtige Rolle spielen bei der endgültigen Entscheidung.
Es gibt auch eine Reihe von Metriken, die Sie analysieren können. Ich werde sie direkt zum Code hinzufügen.
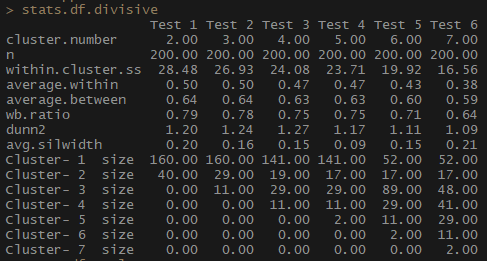
Der Mittelwert innerhalb des Indikators, der den durchschnittlichen Abstand zwischen Beobachtungen innerhalb von Clustern darstellt, nimmt ebenso ab wie innerhalb von Cluster.ss (die Summe der Quadrate der Abstände zwischen Beobachtungen in einem Cluster). Die durchschnittliche Breite der Silhouette (durchschnittliche Silberbreite) variiert nicht so eindeutig, es ist jedoch immer noch eine umgekehrte Beziehung zu erkennen.
Beachten Sie, wie unverhältnismäßig die Clustergrößen sind. Ich würde mich nicht beeilen, mit einer unvergleichlichen Anzahl von Beobachtungen innerhalb von Clustern zu arbeiten. Einer der Gründe ist, dass der Datensatz möglicherweise unausgewogen ist und einige Beobachtungsgruppen alle anderen in der Analyse überwiegen - dies ist nicht gut und führt höchstwahrscheinlich zu Fehlern.
stats.df.aggl <-cstats.table(gower.dist, aggl.clust.c, 7) #stats.df.aggl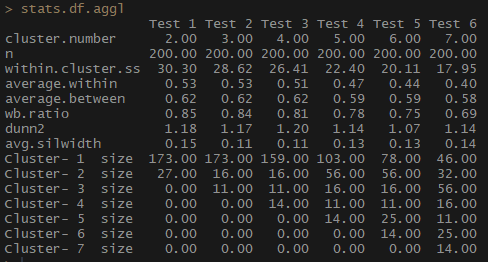
Beachten Sie, wie viel besser die Anzahl der Beobachtungen pro Gruppe durch agglomeratives hierarchisches Clustering auf der Grundlage der vollständigen Kommunikationsmethode ausgeglichen wird.
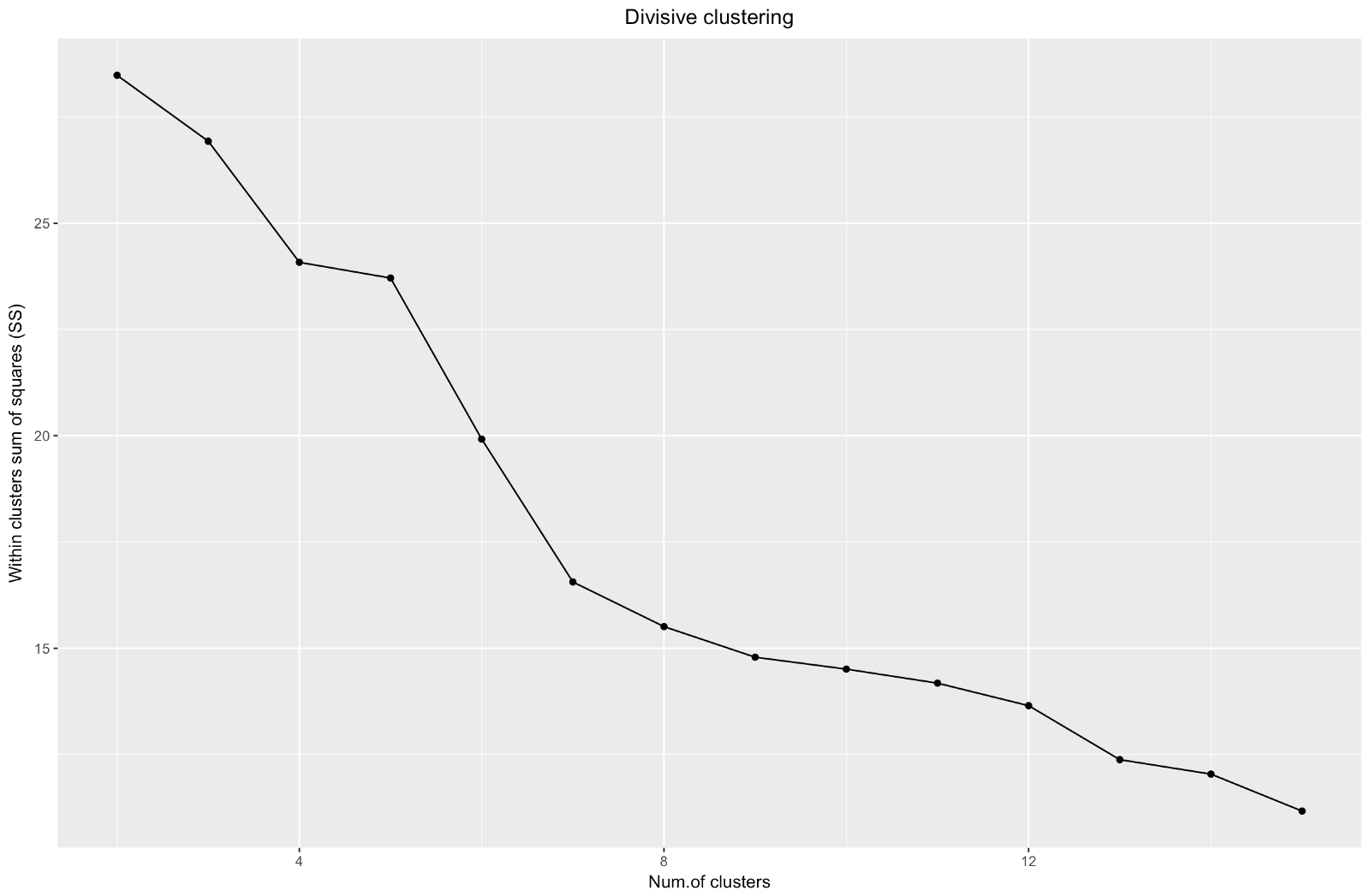
Also haben wir ein Diagramm des "Ellbogens" erstellt. Es zeigt, wie die Summe der quadratischen Abstände zwischen den Beobachtungen (wir verwenden sie als Maß für die Nähe der Beobachtungen - je kleiner sie sind, desto näher sind die Messungen innerhalb des Clusters) für eine unterschiedliche Anzahl von Clustern variieren. Idealerweise sollten wir an der Stelle, an der eine weitere Clusterbildung nur eine geringfügige Abnahme der Quadratsumme (SS) ergibt, eine deutliche „Ellbogenbiegung“ sehen. Für die folgende Grafik würde ich bei ungefähr 7 anhalten. Obwohl in diesem Fall einer der Cluster nur aus zwei Beobachtungen besteht. Mal sehen, was beim agglomerativen Clustering passiert.
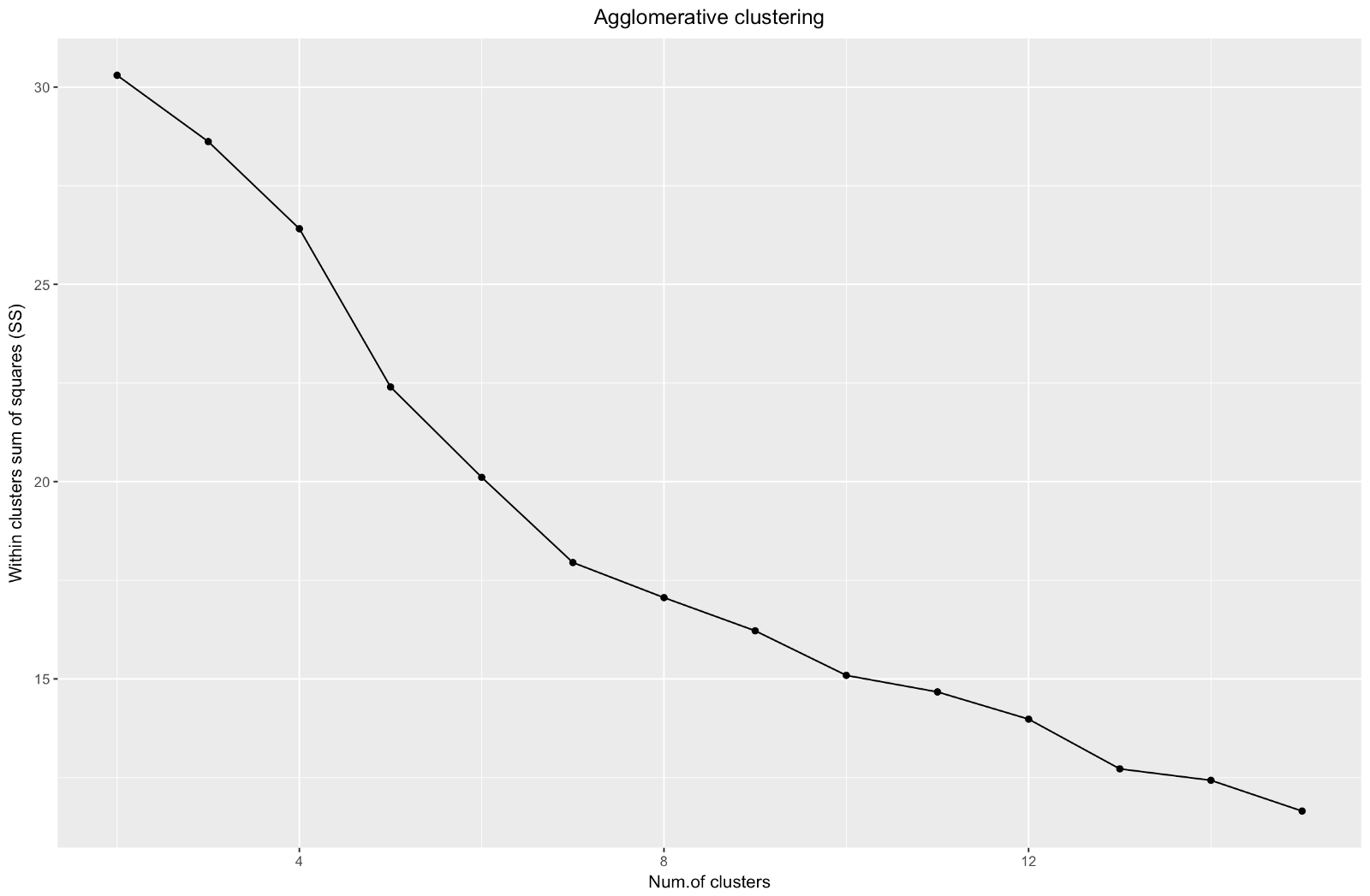
Agglomerativer „Ellbogen“ ähnelt dem Teilungsbogen, aber die Grafik sieht glatter aus - Biegungen sind nicht so ausgeprägt. Wie beim Divisionsclustering würde ich mich auf 7 Cluster konzentrieren. Wenn ich jedoch zwischen diesen beiden Methoden wähle, mag ich die Clustergrößen, die durch die agglomerative Methode erhalten werden, mehr - es ist besser, dass sie miteinander vergleichbar sind.
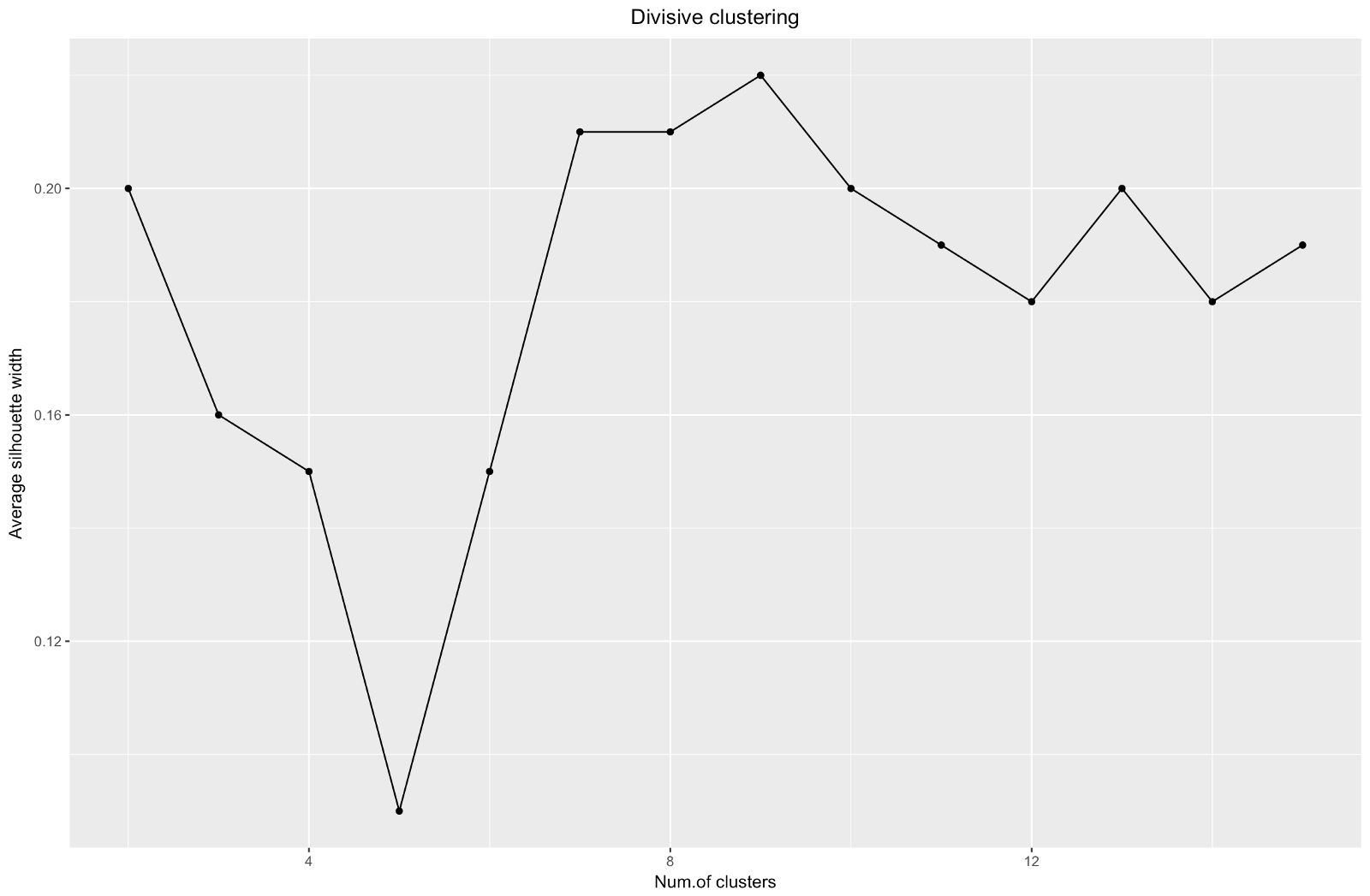
Wenn Sie die Silhouette-Schätzmethode verwenden, sollten Sie den Betrag auswählen, der den maximalen Silhouette-Koeffizienten ergibt, da Sie Cluster benötigen, die weit genug voneinander entfernt sind, um als getrennt betrachtet zu werden.
Der Silhouette-Koeffizient kann zwischen –1 und 1 liegen, wobei 1 einer guten Konsistenz innerhalb der Cluster entspricht und –1 nicht sehr gut.
Im Fall des obigen Diagramms würden Sie 9 statt 5 Cluster auswählen.
Zum Vergleich: Im „einfachen“ Fall ähnelt das Silhouettendiagramm dem folgenden. Nicht ganz wie bei uns, aber fast.
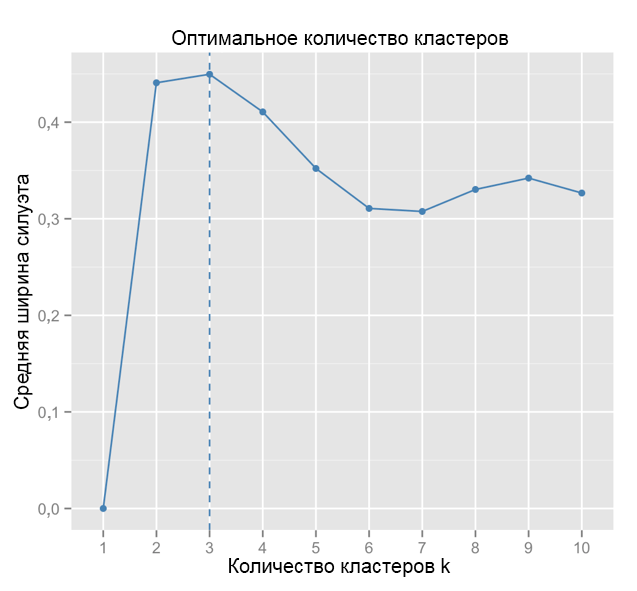Quelle: Data Sailors ggplot(data = data.frame(t(cstats.table(gower.dist, aggl.clust.c, 15))), aes(x=cluster.number, y=avg.silwidth)) + geom_point()+ geom_line()+ ggtitle("Agglomerative clustering") + labs(x = "Num.of clusters", y = "Average silhouette width") + theme(plot.title = element_text(hjust = 0.5))
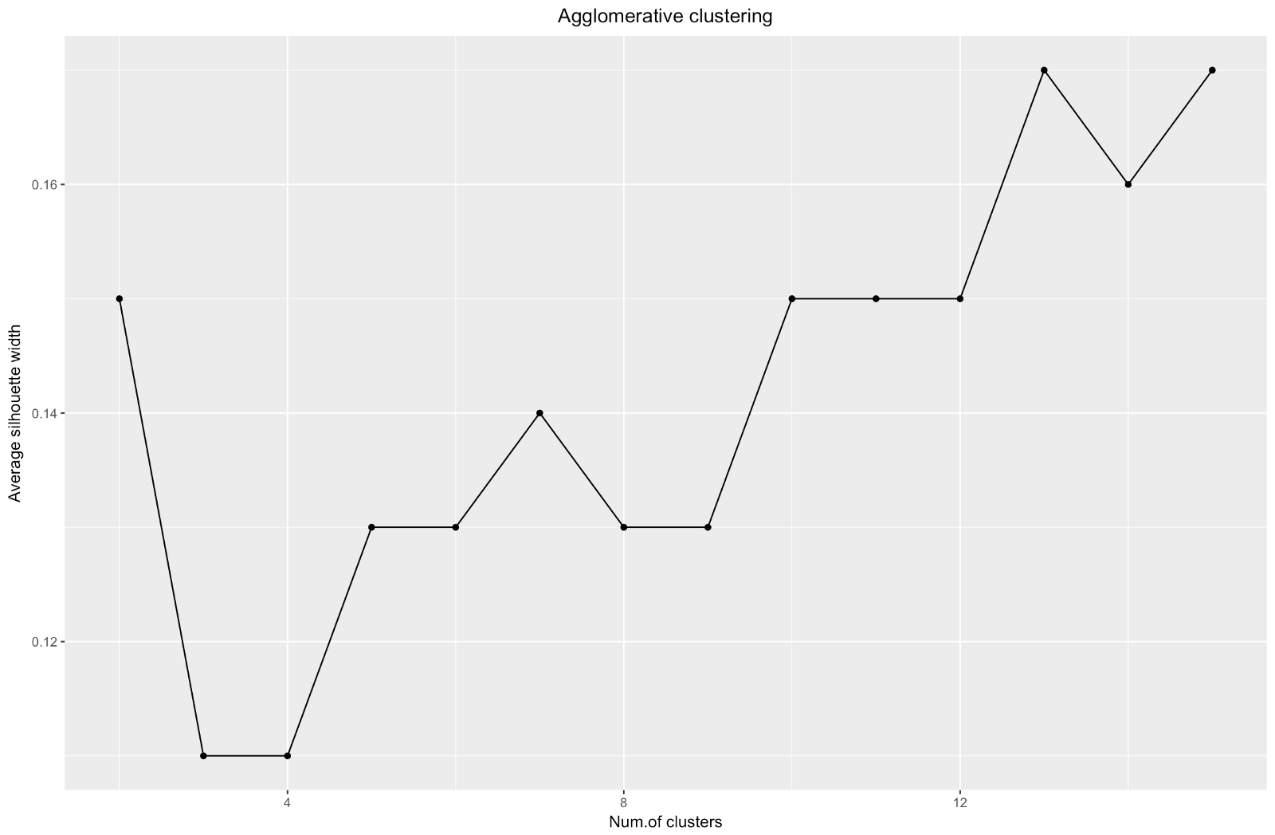
Das Diagramm der Silhouette-Breite zeigt uns: Je mehr Sie den Datensatz teilen, desto klarer werden die Cluster. Am Ende erreichen Sie jedoch einzelne Punkte, die Sie nicht benötigen. Dies ist jedoch genau das, was Sie sehen werden, wenn Sie beginnen, die Anzahl der Cluster
k zu erhöhen. Zum Beispiel habe ich für
k=30 das folgende Diagramm erhalten:
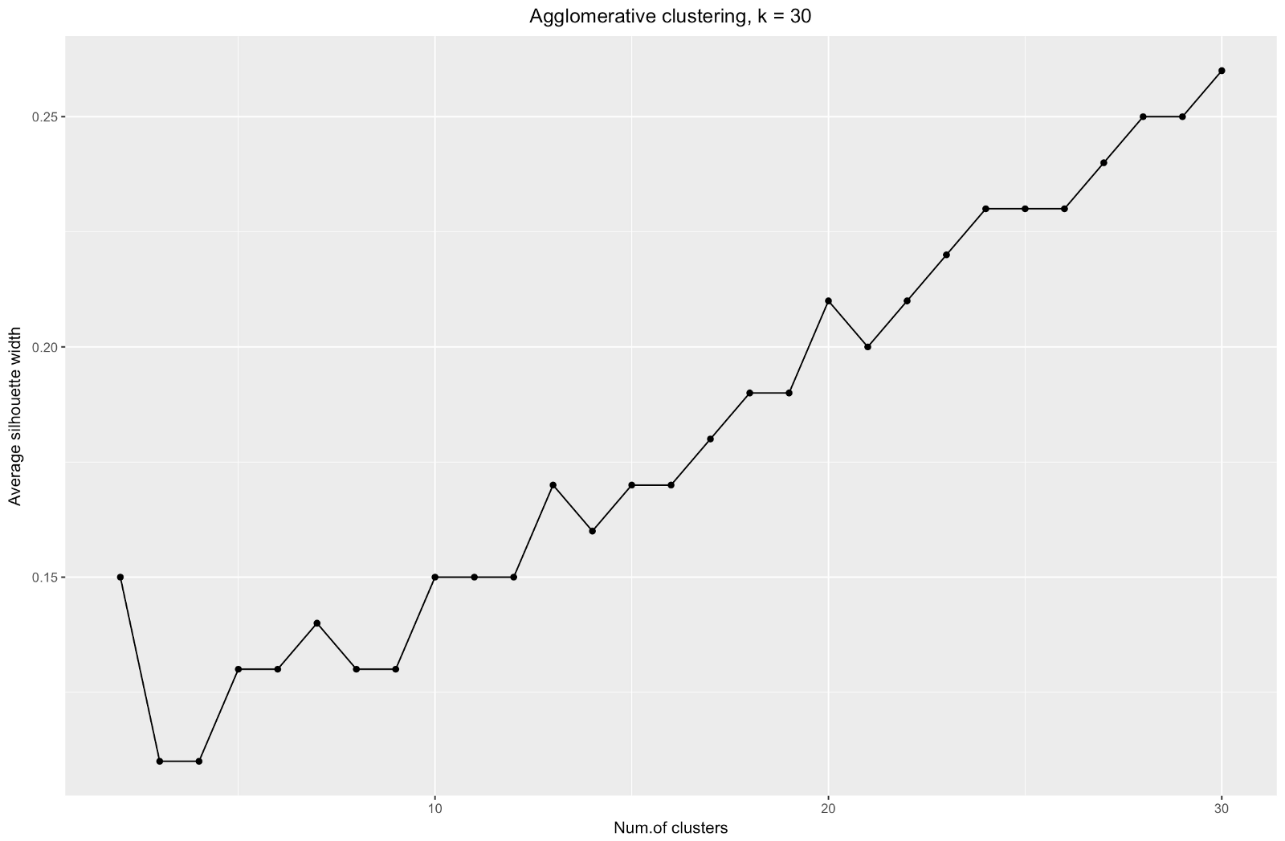
Zusammenfassend: Je mehr Sie den Datensatz teilen, desto besser sind die Cluster, aber wir können keine einzelnen Punkte erreichen (in der obigen Tabelle haben wir beispielsweise 30 Cluster ausgewählt und wir haben nur 200 Datenpunkte).
Agglomeratives Clustering scheint mir in unserem Fall also viel ausgewogener zu sein: Clustergrößen sind mehr oder weniger vergleichbar (sehen Sie sich nur einen Cluster mit nur zwei Beobachtungen an, wenn Sie nach der Divisionsmethode dividieren!), Und ich würde bei 7 Clustern aufhören, die mit dieser Methode erhalten wurden. Mal sehen, wie sie aussehen und woraus sie bestehen.
Der Datensatz besteht aus 6 Variablen, die in 2D oder 3D visualisiert werden müssen, sodass Sie hart arbeiten müssen! Die Art der kategorialen Daten unterliegt auch einigen Einschränkungen, sodass vorgefertigte Lösungen möglicherweise nicht funktionieren. Ich muss: a) sehen, wie die Beobachtungen in Cluster unterteilt sind, b) verstehen, wie die Beobachtungen kategorisiert werden. Daher habe ich a) ein Farbdendrogramm, b) eine Wärmekarte der Anzahl der Beobachtungen pro Variable in jedem Cluster erstellt.
library("ggplot2") library("reshape2") library("purrr") library("dplyr")
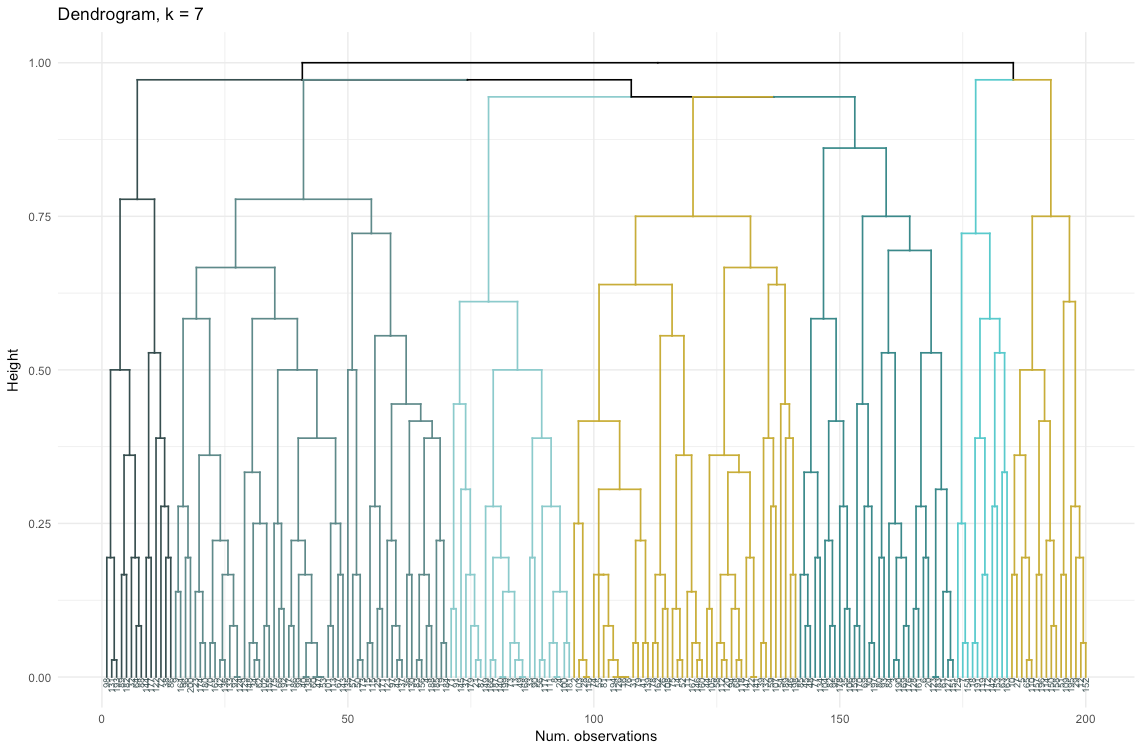
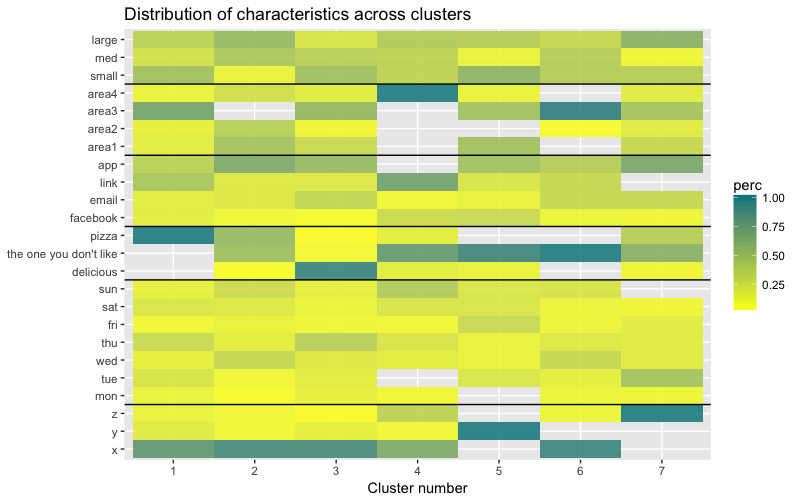
Die Wärmekarte zeigt grafisch, wie viele Beobachtungen für jede Faktorstufe für die Anfangsfaktoren (die Variablen, mit denen wir begonnen haben) gemacht werden. Die dunkelblaue Farbe entspricht einer relativ großen Anzahl von Beobachtungen innerhalb des Clusters. Diese Wärmekarte zeigt auch, dass für den Wochentag (Sonne, Samstag, Montag) und die Korbgröße (groß, mittel, klein) die Anzahl der Kunden in jeder Zelle nahezu gleich ist - dies kann bedeuten, dass diese Kategorien für die Analyse nicht bestimmend sind, und Vielleicht müssen sie nicht berücksichtigt werden.
Fazit
In diesem Artikel haben wir die Unähnlichkeitsmatrix berechnet, die agglomerativen und Divisionsmethoden der hierarchischen Clusterbildung getestet und uns mit den Ellbogen- und Silhouettenmethoden zur Bewertung der Qualität von Clustern vertraut gemacht.
Divisions- und agglomeratives hierarchisches Clustering ist ein guter Anfang, um das Thema zu untersuchen, aber hören Sie hier nicht auf, wenn Sie die Clusteranalyse wirklich beherrschen möchten. Es gibt viele andere Methoden und Techniken. Der Hauptunterschied zum Clustering numerischer Daten besteht in der Berechnung der Unähnlichkeitsmatrix. Bei der Beurteilung der Clusterqualität liefern nicht alle Standardmethoden zuverlässige und aussagekräftige Ergebnisse - die Silhouette-Methode ist höchstwahrscheinlich nicht geeignet.
Und schließlich, da einige Zeit vergangen ist, seit ich dieses Beispiel gemacht habe, sehe ich jetzt eine Reihe von Mängeln in meinem Ansatz und freue mich über jedes Feedback. Eines der wesentlichen Probleme meiner Analyse hing nicht mit dem Clustering als solchem zusammen -
mein Datensatz war in vielerlei Hinsicht
unausgewogen , und dieser Moment blieb unberücksichtigt. Dies hatte spürbare Auswirkungen auf das Clustering: 70% der Kunden gehörten einer Ebene des Faktors „Staatsbürgerschaft“ an, und diese Gruppe dominierte die meisten der erhaltenen Cluster, sodass es schwierig war, die Unterschiede innerhalb anderer Ebenen des Faktors zu berechnen. Das nächste Mal werde ich versuchen, den Datensatz auszugleichen und die Clustering-Ergebnisse zu vergleichen. Aber mehr dazu in einem anderen Beitrag.
Wenn Sie meinen Code klonen möchten, finden Sie hier den Link zu github:
https://github.com/khunreus/cluster-categoricalIch hoffe dir hat dieser Artikel gefallen!
Quellen, die mir geholfen haben:
Hierarchisches Clustering-Handbuch (Datenaufbereitung, Clustering, Visualisierung) - Dieser Blog ist interessant für diejenigen, die sich für Business Analytics in der R-Umgebung interessieren:
http://uc-r.imtqy.com/hc_clustering und
https: // uc-r. imtqy.com/kmeans_clusteringClustering:
http://www.sthda.com/english/articles/29-cluster-validation-essentials/97-cluster-validation-statistics-must-know-methods/( k-):
https://eight2late.wordpress.com/2015/07/22/a-gentle-introduction-to-cluster-analysis-using-r/denextend, :
https://cran.r-project.org/web/packages/dendextend/vignettes/introduction.html#the-set-function, :
https://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/:
https://jcoliver.imtqy.com/learn-r/008-ggplot-dendrograms-and-heatmaps.html,
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5025633/ ( GitHub:
https://github.com/khunreus/EnsCat ).