Fast unsichtbar sehen, auch in Farbe: Eine Technik zur Visualisierung von Objekten durch einen Diffusor

Eine der berühmtesten Fähigkeiten von Superman ist die Supersicht, die es ihm ermöglichte, Atome zu betrachten, im Dunkeln und in großen Entfernungen zu sehen und auch durch Objekte zu sehen. Diese Fähigkeit wird auf Bildschirmen äußerst selten demonstriert, ist es aber. In unserer Realität ist es auch möglich, durch Anwendung einiger wissenschaftlicher Tricks fast vollständig undurchsichtige Objekte zu durchschauen. Die empfangenen Bilder waren jedoch bis vor kurzem immer schwarzweiß. Heute werden wir eine Studie kennenlernen, in der Wissenschaftler der Duke University (USA) mit einer einzigen Belichtung ein Farbbild von Objekten aufnehmen konnten, die hinter einer undurchsichtigen Wand versteckt sind. Was ist diese Supertechnologie, wie funktioniert sie und in welchen Bereichen kann sie angewendet werden? Der Bericht der Forschungsgruppe wird uns darüber berichten. Lass uns gehen.

Studienbasis

Trotz aller möglichen "Brötchen" der Technologie zur Visualisierung von Objekten in Streumedien gibt es eine Reihe von Problemen bei der Implementierung dieser Technologie. Das wichtigste ist die Tatsache, dass die Wege der Photonen, die durch den Streuer laufen, stark variieren, was zu zufälligen Speckle- Mustern * auf der anderen Seite führt.

Speckle * ist ein zufälliges Interferenzmuster, das durch gegenseitige Interferenz kohärenter Wellen mit zufälligen Phasenverschiebungen und / oder einem zufälligen Satz von Intensität gebildet wird. Meistens sieht es aus wie eine Reihe heller Flecken (Punkte) auf einem dunklen Hintergrund.

In den letzten Jahren wurden verschiedene Visualisierungstechniken entwickelt, um die Auswirkungen des Diffusors zu umgehen und Informationen über das Objekt aus dem Speckle-Muster zu extrahieren. Das Problem bei diesen Techniken sind ihre Einschränkungen - Sie müssen bestimmte Kenntnisse über das Objekt haben, Zugriff auf ein Streumedium oder Objekt usw. haben.

Gleichzeitig gibt es laut Wissenschaftlern eine viel weiter fortgeschrittene Methode - die Visualisierung mit Memory-Effekt (ME). Mit dieser Methode können Sie das Objekt ohne Vorkenntnisse bezüglich seines eigenen oder Streumediums visualisieren. Wie wir wissen, hat jeder Nachteile, und die ME-Methode ist keine Ausnahme. Um kontrastreiche Speckle-Muster und dementsprechend genauere Bilder zu erhalten, sollte die Beleuchtung schmalbandig sein, d.h. weniger als 1 nm.

Das Überlisten der Einschränkungen der ME-Methode ist ebenfalls möglich, aber auch diese Tricks beinhalten den Zugriff auf eine optische Quelle oder ein optisches Objekt auf den Diffusor oder die direkte Messung der PSF * .

PSF * ist eine Punktstreufunktion, die das Bild beschreibt, das das Formationssystem bei der Beobachtung einer Punktlichtquelle oder eines Punktobjekts empfängt.

Forscher nennen diese Methoden funktionierend, aber nicht perfekt, da eine PSF-Messung beispielsweise aufgrund der Dynamik des Diffusors oder seiner Unzugänglichkeit für das Bildgebungsverfahren nicht immer möglich ist. Mit anderen Worten, es gibt noch viel zu tun.

In ihrer Arbeit schlagen Forscher einen anderen Ansatz vor. Sie demonstrieren uns eine Methode zur Implementierung einer multispektralen Visualisierung von Objekten durch ein Streumedium unter Verwendung einer einzelnen Speckle-Messung mit einer Monochromkamera. Im Gegensatz zu anderen Techniken erfordert diese keine Vorkenntnisse des PSF-Systems oder des Quellenspektrums.

Mit der neuen Methode können Sie qualitativ hochwertige Bilder des Zielobjekts in fünf gut getrennten Spektralkanälen zwischen 450 nm und 750 nm erstellen, was durch Berechnungen bestätigt wurde. In der Praxis war es bisher möglich, drei gut getrennte Spektralkanäle zwischen 450 nm und 650 nm und sechs benachbarte Spektralkanäle zwischen 515 und 575 nm sichtbar zu machen.

Das Prinzip der neuen Methode

Bild Nr. 1: Lampe - räumlicher Lichtmodulator - Diffusor (mit Irisblende) - Codieröffnung - Prisma - optisches Relais (1: 1-Visualisierung) - Monochromkamera.

Die Forscher stellen drei Hauptelemente jeder Visualisierung durch einen Diffusor fest: ein interessierendes Objekt (von außen beleuchtet oder unabhängig leuchtend), einen Diffusor und einen Detektor.

Wie bei Standard-ME-Systemen wird in dieser Studie ein Objekt betrachtet, dessen Winkelgröße sich innerhalb des ME-Sichtfelds und in einem Abstand u hinter dem Diffusor befindet. Nach der Wechselwirkung mit dem Diffusor breitet sich das Licht bis zu einer Entfernung v aus, bevor es den Detektor erreicht.

Bei der herkömmlichen ME-Bildgebung werden Standardkameras verwendet, und bei diesem Verfahren wird ein Codierungsdetektormodul verwendet, das aus einer Codierungsapertur und einem von der Wellenlänge abhängigen optischen Element besteht. Der Zweck dieses Elements besteht darin, jeden Spektralkanal eindeutig zu modulieren, bevor er kombiniert und in einen Monochromdetektor umgewandelt wird.

Anstatt einfach einen kontrastarmen Fleck zu messen, dessen Spektralkanäle untrennbar gemischt sind, wurde ein spektral gemultiplextes Signal aufgezeichnet, das für die Trennung gut geeignet war.

Die Forscher betonen erneut, dass ihre Methode keine zuvor bekannten Eigenschaften oder Annahmen in Bezug auf einen Diffusor oder eine Lichtquelle erfordert.

Nach vorläufigen Messungen des gemultiplexten Speckles wurde der bekannte Tλ-Wert (wellenlängenabhängiges Codierungsmuster) verwendet, um den Speckle in jedem Spektralband individuell zu rekonstruieren.

In ihrer Arbeit in der Phase der Berechnung und Modellierung verwendeten die Wissenschaftler bestimmte Methoden des maschinellen Lernens, die bei der Implementierung einer zuvor nicht berücksichtigten Methode hilfreich sein können. Zunächst wurden die Merkmale einer spärlichen Matrix trainiert, um Speckle darzustellen.

Training in Zeichen * - ermöglicht es dem System, automatisch die Darstellungen zu finden, die zum Identifizieren von Zeichen der Quelldaten erforderlich sind.

Als Ergebnis wurde eine Basis auf Speckle-Bildern aus verschiedenen Messkonfigurationen trainiert. Diese Basis ist ziemlich verallgemeinert und hängt nicht von bestimmten Objekten und Streuern ab, die an der Erzeugung der Maske Iλx, y beteiligt sind. Mit anderen Worten wird das System basierend auf einem Diffusor trainiert, der in der experimentellen Konfiguration nicht verwendet wird, d.h. Das System hat keinen Zugriff darauf, wie die Forscher wollten.

Um Speckle-Bilder bei jeder Wellenlänge zu erhalten, wurde der OMP-Algorithmus ( Orthogonal Matching Pursuit ) verwendet.

Am Ende wurden durch unabhängige Berechnung der Autokorrelation jedes Spektralkanals und der Inversion der Autokorrelation bei jeder Wellenlänge Bilder des Objekts erhalten. Die resultierenden Bilder bei jeder Wellenlänge werden dann kombiniert, um ein Farbbild des Objekts zu erzeugen.


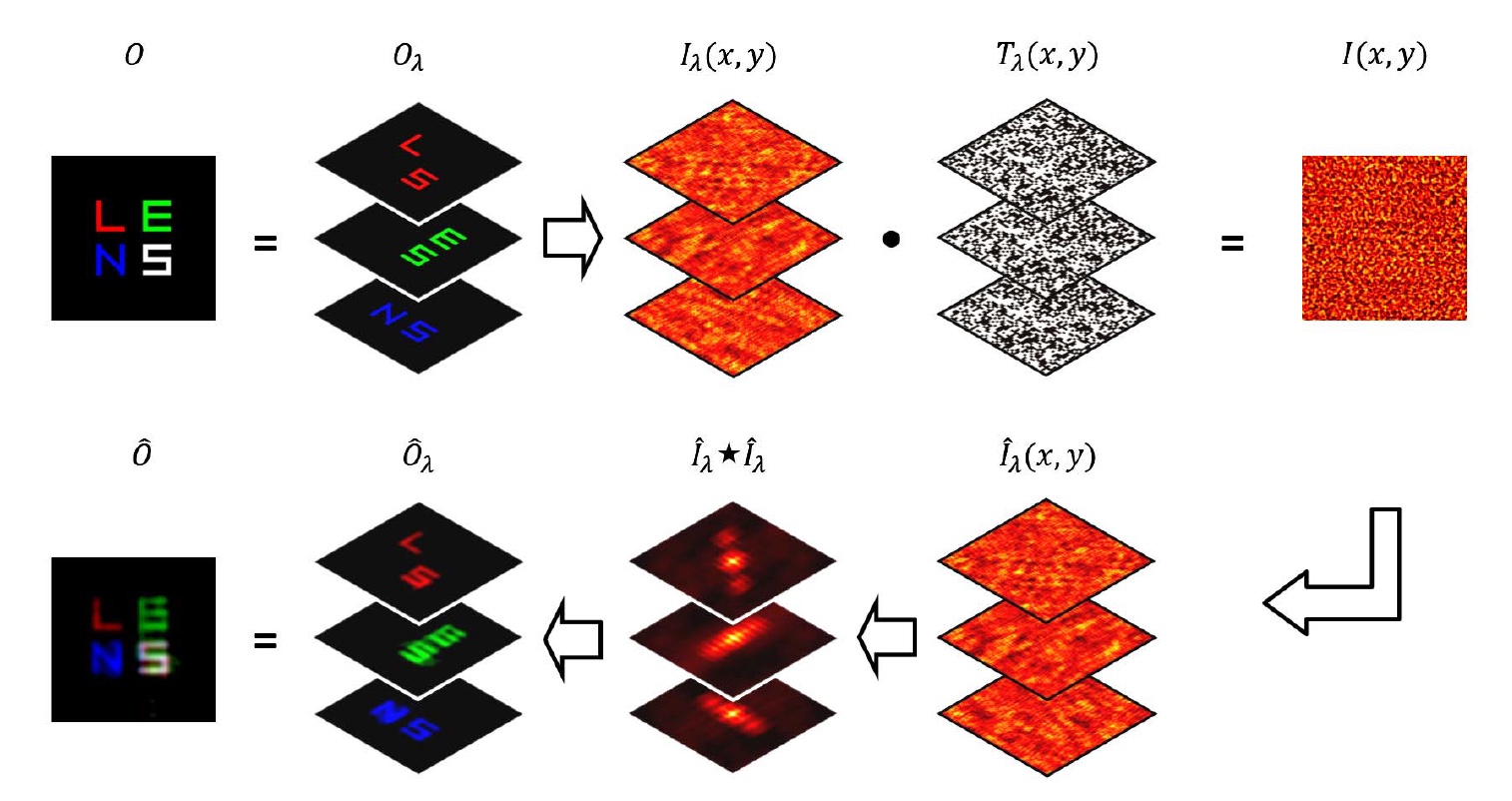
Bild 2: Ein schrittweiser Prozess zum Kompilieren eines Bildes eines Objekts.
Diese Technik macht nach Ansicht ihrer Schöpfer keine Annahmen über die Korrelationen zwischen den Spektralkanälen und erfordert nur die Annahme, dass der Wert der Wellenlänge ziemlich zufällig ist. Darüber hinaus erfordert dieses Verfahren nur Informationen über den Codierungsdetektor, die auf der vorläufigen Kalibrierung der Codierungsapertur und einer vorab trainierten Datenbibliothek beruhen. Solche Eigenschaften machen diese Bildgebungstechnik sehr vielseitig und nicht invasiv.

Simulationsergebnisse

Betrachten Sie zunächst die Simulationsergebnisse.


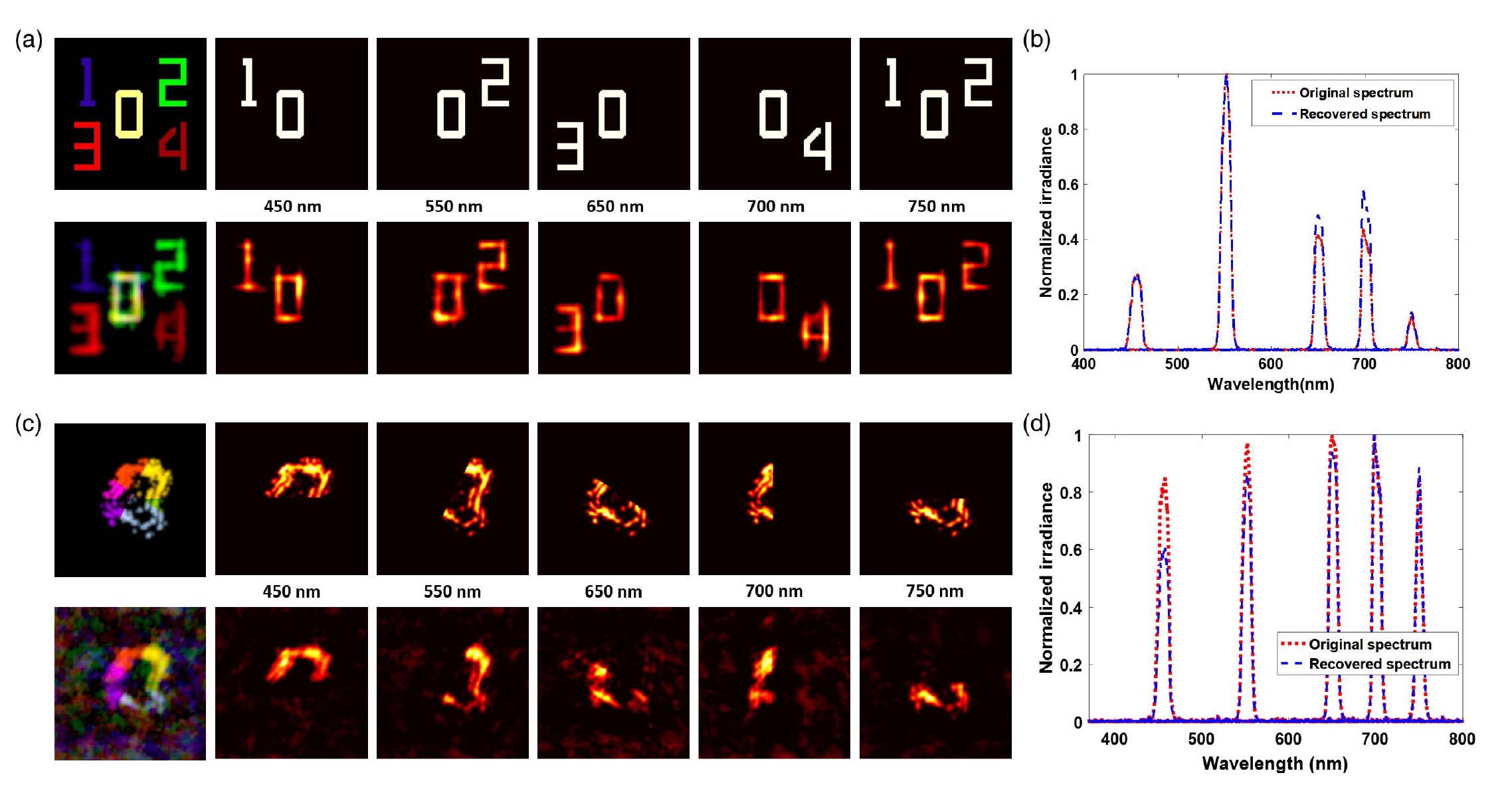Bild Nr. 3

Das obige Bild zeigt Beispiele eines multispektralen Bildes von zwei Objekten, die durch einen Diffusor aufgenommen wurden. Die obere Reihe bei 3a enthält ein interessierendes Objekt, das aus mehreren Zahlen besteht, die sowohl in Falschfarbe als auch in einer Aufteilung nach dem Spektralkanal gezeigt sind. Bei der Erstellung eines Objekts in Falschfarbe wird das Intensitätsprofil jeder Wellenlänge im CIE 1931 RGB-Raum angezeigt.

Das rekonstruierte Objekt (untere Reihe bei 3a ) sowohl in Falschfarbe als auch aus Sicht einzelner Spektralkanäle zeigt, dass die Technik eine hervorragende Visualisierung und nur eine unbedeutende Kreuzinteraktion zwischen Spektralkanälen bietet, die dabei keine besondere Rolle spielt.

Nach dem Empfang des rekonstruierten Objekts, d.h. Nach der Visualisierung war es notwendig, den Genauigkeitsgrad durch Vergleichen der spektralen Intensität (gemittelt über alle hellen Pixel) des realen Objekts und des rekonstruierten ( 3b ) zu bewerten.

Die Bilder 3c zeigen ein reales Objekt (obere Reihe) und ein rekonstruiertes Bild (untere Reihe) für eine Zelle aus einem Baumwollstamm, und 3d zeigt eine Analyse der Visualisierungsgenauigkeit.

Um die Genauigkeit der Visualisierung beurteilen zu können, mussten für jeden Spektralkanal die Werte des strukturellen Ähnlichkeitskoeffizienten (SSIM) und des Spitzensignal-Rausch-Verhältnisses (pSNR) dieses Objekts berechnet werden.



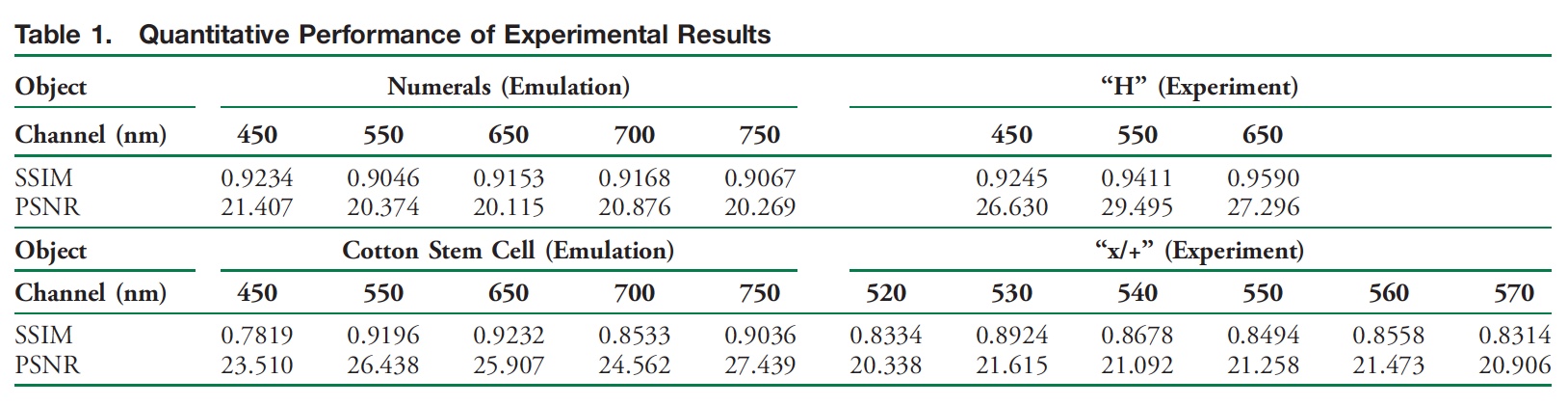
Die obige Tabelle zeigt, dass jeder der fünf Kanäle einen SSIM-Koeffizienten von 0,8–0,9 und ein PSNR von mehr als 20 aufweist. Daraus folgt, dass trotz des geringen Kontrasts des Speckle-Signals die Überlagerung von fünf Spektralbändern mit einer Breite von 10 nm auf dem Detektor eine ziemlich genaue Rekonstruktion ermöglicht räumliche und spektrale Eigenschaften des untersuchten Objekts. Mit anderen Worten, die Technik funktioniert, dies sind jedoch nur Simulationsergebnisse. Um das Vertrauen in ihre Arbeit zu stärken, führten die Wissenschaftler eine Reihe praktischer Experimente durch.

Versuchsergebnisse

Einer der bedeutendsten Unterschiede zwischen Modellierung und realen Experimenten ist die Umgebung, d.h. die Bedingungen, unter denen beide durchgeführt werden. Im ersten Fall gibt es kontrollierte Bedingungen, im zweiten unvorhersehbare Bedingungen, d.h. wie kommt es?

Es wurden drei Spektralkanäle mit einer Breite von 8-12 nm mit einem Zentrum von 450, 550 und 650 nm untersucht, die in Kombination mit verschiedenen relativen Werten einen weiten Farbbereich erzeugen.


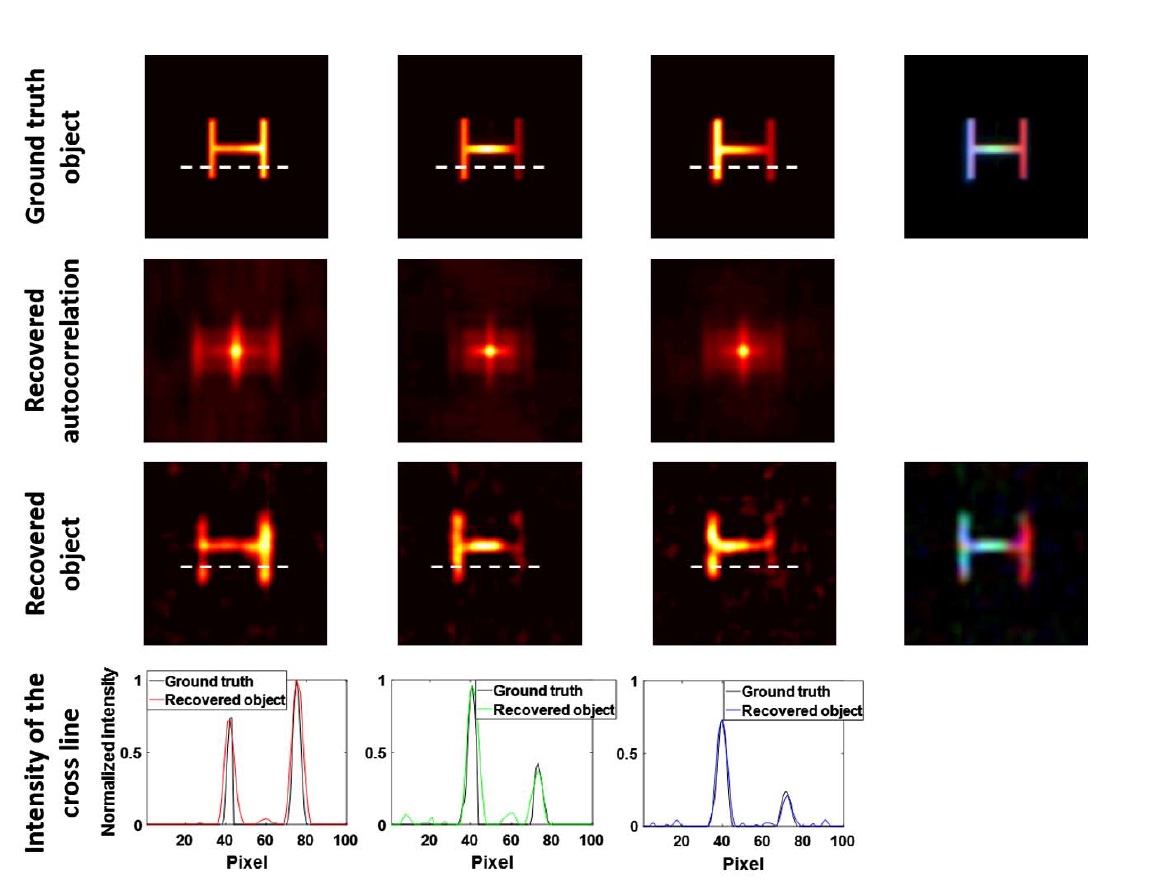Bild Nr. 4

Das Bild oben zeigt einen Vergleich zwischen dem realen Objekt (mehrfarbiger Buchstabe "H") und dem rekonstruierten. Die Zeit der Belichtung (Belichtung, d. H. Belichtung) wurde auf 1800 s eingestellt, wodurch wir ein SNR im Bereich von 60 bis 70 dB erhalten konnten. Ein solches SNR ist nach Ansicht von Wissenschaftlern für die Erfahrung nicht besonders wichtig, dient jedoch als zusätzliche Bestätigung für die Effizienz ihrer Methodik, insbesondere bei komplexen Objekten. In der Realität und nicht unter Laborbedingungen kann diese Methode eine Größenordnung schneller sein.

Die obere Reihe von Bild Nr. 4 zeigt ein Objekt bei jeder Wellenlänge (von links nach rechts) und ein echtes Vollfarbenobjekt.

Um ein Bild eines realen Objekts als Ergebnis der Visualisierung zu erhalten, wurde eine Bildverarbeitungskamera mit entsprechenden Bandpassfiltern verwendet, um Spektralkomponenten direkt anzuzeigen und ein Vollfarbbild durch Summieren der resultierenden Spektralkanäle zu erhalten.

Die zweite Zeile des obigen Bildes zeigt die Autokorrelationsmuster jedes rekonstruierten Spektralkanals, der Multiplexmessungen bildet, die Eingabedaten für den Datenverarbeitungsschritt sind.

Die dritte Reihe ist ein rekonstruiertes Objekt in jedem Spektralkanal sowie ein rekonstruiertes Vollfarbenobjekt, d.h. Endergebnis der Visualisierung.

Das Vollfarbbild zeigt, dass die relativen Werte zwischen den Spektralkanälen ebenfalls korrekt sind, da die Farbe des kombinierten rekonstruierten Bildes dem realen Wert entspricht und der SSIM-Koeffizient für jeden Kanal mehr als 0,92 erreicht.

Die untere Reihe ist eine Bestätigung dieser Aussage und zeigt einen Vergleich der Intensität des realen Objekts und des rekonstruierten. Die Daten von beiden stimmen in allen Spektralbereichen überein.

Daraus folgt, dass selbst das Vorhandensein von Rauschen und potenziellen Modellierungsfehlern das Erhalten eines qualitativ hochwertigen Bildes nicht verhinderte und die experimentellen Ergebnisse gut mit den Simulationsergebnissen korrelieren.

Die obige Erfahrung wurde unter Berücksichtigung der geteilten Spektralkanäle eingestellt. Die Wissenschaftler führten ein weiteres Experiment durch, jedoch mit benachbarten Kanälen und genauer mit einem kontinuierlichen Spektralbereich von 60 nm.


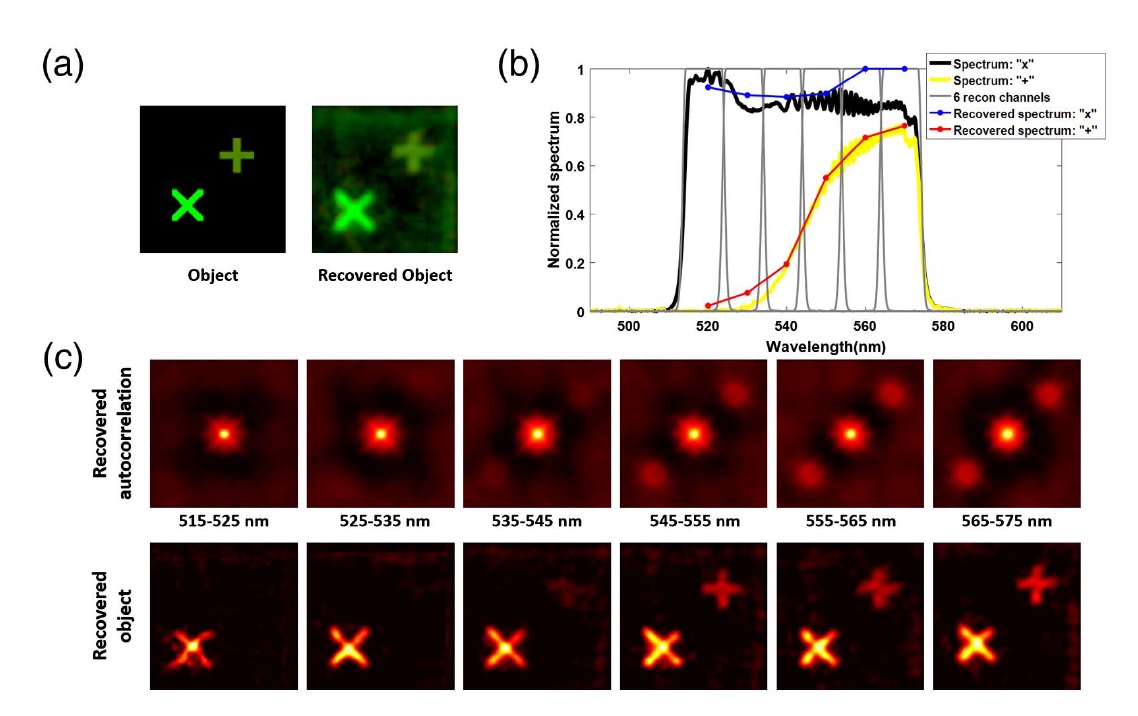Bild Nr. 5

Der Buchstabe "X" und das "+" Zeichen ( 5a ) fungierten als reales Objekt. Das Spektrum des Buchstabens „X“ ist relativ gleichmäßig und kontinuierlich - zwischen 515 und 575 nm, aber das „+“ hat ein strukturiertes Spektrum, das hauptsächlich zwischen 535 und 575 nm liegt ( 5b ). Für dieses Experiment betrug die Belichtung 120 s, um das gewünschte (wie zuvor) SNR von 70 dB zu erreichen.

Ein 60 nm breites Bandpassfilter über dem gesamten Objekt und ein Tiefpassfilter über dem "+" - Zeichen wurden ebenfalls verwendet. Während der Rekonstruktion von 60 nm wird das Spektrum in 6 benachbarte Kanäle mit einer Breite von 10 nm unterteilt ( 5b ).

Wie wir aus den Bildern 5c sehen können , stimmen die resultierenden Bilder hervorragend mit dem realen Objekt überein. Dieses Experiment zeigte, dass das Vorhandensein oder Fehlen von spektralen Korrelationen im gemessenen Speckle die Wirksamkeit der untersuchten Bildgebungstechnik nicht beeinflusst. Wissenschaftler selbst glauben, dass eine viel größere Rolle im Visualisierungsprozess und genauer in seinem Erfolg weniger die spektralen Eigenschaften des Objekts als vielmehr die Kalibrierung des Systems und die Details seines Codierungsdetektors spielen.

Um sich eingehender mit den Nuancen der Studie vertraut zu machen, empfehle ich Ihnen, den Bericht von Wissenschaftlern und zusätzliche Materialien zu lesen.

Nachwort

In dieser Arbeit beschrieben Wissenschaftler eine neue Methode der multispektralen Bildgebung durch einen Diffusor. Die Modulation der Speckle in Abhängigkeit von der Wellenlänge unter Verwendung einer Codierungsapertur ermöglichte es, eine Multiplexmessung durchzuführen und die Speckle unter Verwendung des OMP-Algorithmus basierend auf maschinellem Lernen zu berechnen.

Am Beispiel des mehrfarbigen Buchstabens „H“ haben Wissenschaftler gezeigt, dass die Fokussierung auf fünf Spektralkanäle, die Violett, Grün und drei Rottönen entsprechen, eine Rekonstruktion des Bildes ermöglicht, das alle Farben des Originals enthält (Blau, Gelb usw.).

Laut den Forschern kann ihre Technik sowohl in der Medizin als auch in der Astronomie nützlich sein. Farbe enthält wichtige Informationen in beide Richtungen: in der Astronomie - der chemischen Zusammensetzung der untersuchten Objekte, in der Medizin - der molekularen Zusammensetzung von Zellen und Geweben.

Derzeit stellen Wissenschaftler nur ein Problem fest, das zu Ungenauigkeiten bei der Visualisierung führen kann: Modellierungsfehler. Aufgrund der ausreichend langen Zeit, die erforderlich ist, um den Prozess abzuschließen, können Umweltveränderungen auftreten, die eigene Anpassungen vornehmen, die in der Vorbereitungsphase nicht berücksichtigt wurden. In Zukunft ist jedoch geplant, einen Weg zu finden, um dieses Problem zu lösen, wodurch die beschriebene Visualisierungstechnik nicht nur genau, sondern auch unter allen Bedingungen stabil wird.



Vielen Dank für Ihren Aufenthalt bei uns. Gefällt dir unser Artikel? Möchten Sie weitere interessante Materialien sehen? Unterstützen Sie uns, indem Sie eine Bestellung aufgeben oder Ihren Freunden empfehlen, einen Rabatt von 30% für Habr-Benutzer auf ein einzigartiges Analogon von Einstiegsservern, das wir für Sie erfunden haben: Die ganze Wahrheit über VPS (KVM) E5-2650 v4 (6 Kerne) 10 GB DDR4 240 GB SSD 1 Gbit / s von $ 20 oder wie teilt man den Server? (Optionen sind mit RAID1 und RAID10, bis zu 24 Kernen und bis zu 40 GB DDR4 verfügbar).

Dell R730xd 2 mal günstiger? Nur wir haben 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2,6 GHz 14C 64 GB DDR4 4 x 960 GB SSD 1 Gbit / s 100 TV von 199 US-Dollar in den Niederlanden! Dell R420 - 2x E5-2430 2,2 GHz 6C 128 GB DDR3 2x960 GB SSD 1 Gbit / s 100 TB - ab 99 US-Dollar! Lesen Sie mehr über den Aufbau eines Infrastrukturgebäudes. Klasse mit Dell R730xd E5-2650 v4 Servern für 9.000 Euro für einen Cent?