Neuronale Netze und tiefes Lernen, Kapitel 5: Warum sind tiefe neuronale Netze so schwer zu trainieren?

Stellen Sie sich vor, Sie sind Ingenieur und wurden gebeten, einen Computer von Grund auf neu zu entwickeln. Sobald Sie im Büro sitzen, haben Sie Probleme, logische Schaltkreise zu entwerfen, die UND- ODER ODER-Ventile zu verteilen usw. - und plötzlich kommt Ihr Chef herein und teilt Ihnen die schlechten Nachrichten mit. Der Client hat gerade beschlossen, dem Projekt eine unerwartete Anforderung hinzuzufügen: Das Schema des gesamten Computers sollte nicht mehr als zwei Ebenen haben:



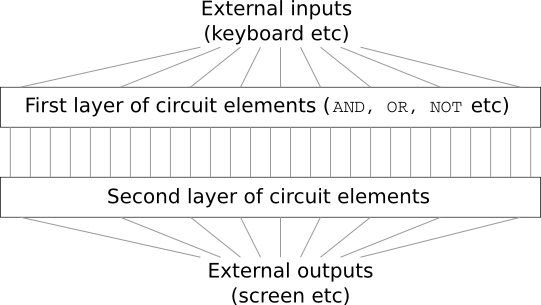
Sie sind erstaunt und sagen dem Chef: "Ja, der Kunde ist verrückt!"

Der Chef antwortet: „Das denke ich auch. Aber der Kunde muss bekommen, was er will. "

Tatsächlich ist der Klient im engeren Sinne nicht völlig verrückt. Angenommen, Sie dürfen ein spezielles Logikgatter verwenden, mit dem Sie eine beliebige Anzahl von Eingängen über UND verbinden können. Und Sie dürfen das NAND-Gatter mit einer beliebigen Anzahl von Eingängen verwenden, d. H. Einem Gatter, das viele Eingaben durch UND addiert und dann das Ergebnis umkehrt. Es stellt sich heraus, dass Sie mit solchen Spezialventilen jede Funktion mit nur einer zweischichtigen Schaltung berechnen können.

Nur weil etwas getan werden kann, heißt das noch lange nicht, dass es sich lohnt, es zu tun. In der Praxis beginnen wir bei der Lösung von Problemen im Zusammenhang mit dem Entwurf von Logikschaltungen (und fast allen algorithmischen Problemen) normalerweise mit der Lösung von Unteraufgaben und stellen dann schrittweise eine vollständige Lösung zusammen. Mit anderen Worten, wir bauen eine Lösung auf vielen Abstraktionsebenen auf.

Angenommen, wir entwerfen eine Logikschaltung zum Multiplizieren von zwei Zahlen. Es ist wahrscheinlich, dass wir es aus Teilschaltungen erstellen möchten, die Operationen wie das Hinzufügen von zwei Zahlen implementieren. Additionsunterschaltungen bestehen wiederum aus Unterschaltungen, die zwei Bits hinzufügen. Grob gesagt wird unser Schema so aussehen:



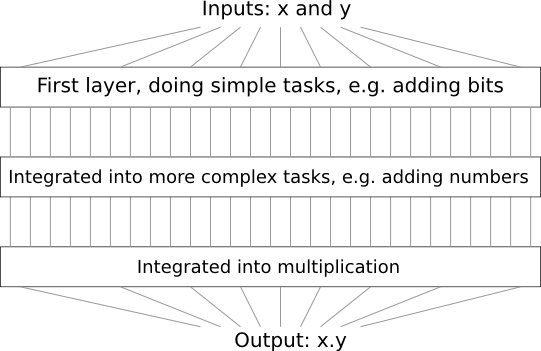
Das heißt, die letzte Schaltung enthält mindestens drei Schichten von Schaltungselementen. In der Tat wird es wahrscheinlich mehr als drei Ebenen haben, wenn wir die Unteraufgaben in kleinere als die von mir beschriebenen aufteilen. Aber du hast das Prinzip verstanden.

Daher erleichtern tiefe Schemata den Entwurfsprozess. Sie helfen aber nicht nur beim Design. Es gibt mathematische Beweise dafür, dass zur Berechnung einiger Funktionen in sehr flachen Schaltkreisen eine exponentiell größere Anzahl von Elementen verwendet werden muss als in tiefen. Zum Beispiel gibt es eine berühmte Reihe wissenschaftlicher Arbeiten der 1980er Jahre, in denen gezeigt wurde, dass die Berechnung der Parität eines Satzes von Bits eine exponentiell größere Anzahl von Gates mit einer flachen Schaltung erfordert. Wenn Sie jedoch tiefe Schemata verwenden, ist es einfacher, die Parität mit einem kleinen Schema zu berechnen: Sie berechnen einfach die Parität der Bitpaare und verwenden dann das Ergebnis, um die Parität der Bitpaare usw. zu berechnen, um schnell die allgemeine Parität zu erreichen. Daher können tiefe Schemata viel leistungsfähiger sein als flache.

Bisher hat dieses Buch einen Ansatz für neuronale Netze (NS) verwendet, ähnlich den Anforderungen eines verrückten Kunden. Fast alle Netzwerke, mit denen wir gearbeitet haben, hatten eine einzige verborgene Schicht von Neuronen (plus die Eingabe- und Ausgabeschichten):



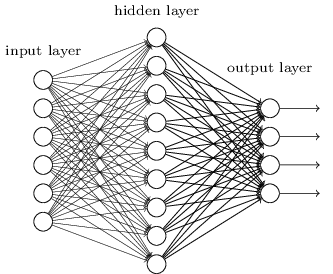
Diese einfachen Netzwerke haben sich als sehr nützlich erwiesen: In früheren Kapiteln haben wir solche Netzwerke verwendet, um handgeschriebene Zahlen mit einer Genauigkeit von mehr als 98% zu klassifizieren! Es ist jedoch intuitiv klar, dass Netzwerke mit vielen verborgenen Schichten viel leistungsfähiger sind:



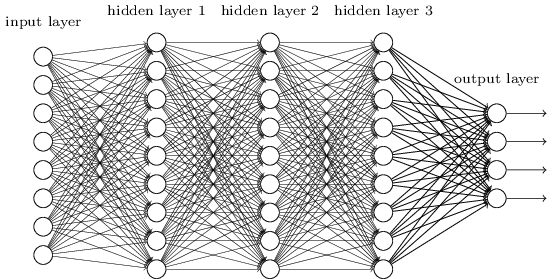
Solche Netzwerke können Zwischenschichten verwenden, um viele Abstraktionsebenen zu erstellen, wie dies bei unseren Booleschen Schemata der Fall ist. Beispielsweise können bei der Mustererkennung Neuronen der ersten Schicht lernen, Gesichter zu erkennen, Neuronen der zweiten Schicht - komplexere Formen, beispielsweise Dreiecke oder Rechtecke, die aus Gesichtern erzeugt werden. Dann kann die dritte Schicht noch komplexere Formen erkennen. Usw. Es ist wahrscheinlich, dass diese vielen Abstraktionsebenen tiefen Netzwerken einen überzeugenden Vorteil bei der Lösung von Problemen beim Erkennen komplexer Muster verschaffen. Darüber hinaus gibt es, wie im Fall von Schaltungen, theoretische Ergebnisse, die bestätigen, dass tiefe Netzwerke von Natur aus mehr Fähigkeiten haben als flache.

Wie trainieren wir diese tiefen neuronalen Netze (GNSs)? In diesem Kapitel werden wir versuchen, STS mit unserem Arbeitstier unter den Trainingsalgorithmen zu trainieren - stochastischer Gradienten-Rückwärtsausbreitungsabstieg. Wir werden jedoch auf ein Problem stoßen - unser STS wird nicht viel besser funktionieren (wenn überhaupt übertroffen) als flache.

Dieser Fehler erscheint angesichts der obigen Diskussion seltsam. Aber anstatt das STS aufzugeben, werden wir uns eingehender mit dem Problem befassen und versuchen zu verstehen, warum das STS schwer zu trainieren ist. Wenn wir uns das Problem genauer ansehen, werden wir feststellen, dass verschiedene Ebenen im STS mit sehr unterschiedlichen Geschwindigkeiten lernen. Insbesondere wenn die letzten Schichten des Netzwerks gut trainiert sind, bleiben die ersten oft während des Trainings stecken und lernen fast nichts. Und es ist nicht nur Pech. Wir werden grundlegende Gründe für die Verlangsamung des Lernens finden, die mit der Verwendung von gradientenbasierten Lerntechniken zusammenhängen.

Wenn wir uns tiefer mit diesem Problem befassen, stellen wir fest, dass auch das gegenteilige Phänomen auftreten kann: Die frühen Schichten können gut lernen und die späteren bleiben stecken. Tatsächlich werden wir die interne Instabilität entdecken, die mit dem Gradientenabstiegstraining in tiefen mehrschichtigen NS verbunden ist. Und aufgrund dieser Instabilität bleiben die frühen oder späten Schichten oft im Training stecken.

Das klingt alles ziemlich unangenehm. In diese Schwierigkeiten geraten, können wir beginnen, Ideen darüber zu entwickeln, was für ein effektives Training von STS getan werden muss. Daher werden diese Studien eine gute Vorbereitung für das nächste Kapitel sein, in dem wir tiefes Lernen nutzen werden, um die Probleme der Bilderkennung anzugehen.

Fading Gradientenproblem

Was geht also schief, wenn wir versuchen, ein tiefes Netzwerk zu trainieren?

Um diese Frage zu beantworten, kehren wir zu dem Netzwerk zurück, das nur eine verborgene Schicht enthält. Wie üblich werden wir das MNIST-Ziffernklassifizierungsproblem als Sandbox zum Lernen und Experimentieren verwenden.

Wenn Sie alle diese Schritte auf Ihrem Computer wiederholen möchten, müssen Sie Python 2.7 installiert haben, die Numpy-Bibliothek und eine Kopie des Codes, der aus dem Repository entnommen werden kann:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git 

Sie können auf Git verzichten, indem Sie einfach die Daten und den Code herunterladen . Wechseln Sie in das Unterverzeichnis src und laden Sie aus der Python-Shell die MNIST-Daten:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Konfigurieren Sie das Netzwerk:

 >>> import network2 >>> net = network2.Network([784, 30, 10]) 

Ein solches Netzwerk hat 784 Neuronen in der Eingangsschicht, was 28 × 28 = 784 Pixel des Eingabebildes entspricht. Wir verwenden 30 versteckte Neuronen und 10 Wochenenden, was zehn möglichen Klassifizierungsoptionen für die Zahlen MNIST ('0', '1', '2', ..., '9') entspricht.

Versuchen wir, unser Netzwerk für 30 ganze Epochen zu trainieren, indem wir Mini-Pakete mit jeweils 10 Trainingsbeispielen verwenden, wobei die Lerngeschwindigkeit η = 0,1 und der Regularisierungsparameter λ = 5,0 sind. Während des Trainings werden wir die Genauigkeit der Klassifizierung durch validation_data verfolgen:

 >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Wir erhalten eine Klassifizierungsgenauigkeit von 96,48% (oder so - die Zahlen variieren bei verschiedenen Starts), vergleichbar mit unseren früheren Ergebnissen mit ähnlichen Einstellungen.

Fügen wir eine weitere versteckte Ebene hinzu, die ebenfalls 30 Neuronen enthält, und versuchen, das Netzwerk mit denselben Hyperparametern zu trainieren:

 >>> net = network2.Network([784, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Die Klassifizierungsgenauigkeit verbessert sich auf 96,90%. Es ist inspirierend - eine leichte Erhöhung der Tiefe hilft. Fügen wir eine weitere versteckte Schicht von 30 Neuronen hinzu:

 >>> net = network2.Network([784, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Es hat nicht geholfen. Das Ergebnis fiel sogar auf 96,57%, ein Wert nahe dem ursprünglichen flachen Netzwerk. Und wenn wir eine weitere versteckte Ebene hinzufügen:

 >>> net = network2.Network([784, 30, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Dann sinkt die Klassifizierungsgenauigkeit wieder auf 96,53%. Statistisch gesehen ist dieser Rückgang wahrscheinlich unbedeutend, aber es ist nichts Gutes daran.

Dieses Verhalten scheint seltsam. Es scheint intuitiv, dass zusätzliche verborgene Schichten dem Netzwerk helfen sollten, komplexere Klassifizierungsfunktionen zu erlernen und die Aufgabe besser zu bewältigen. Natürlich sollte sich das Ergebnis nicht verschlechtern, da im schlimmsten Fall zusätzliche Schichten einfach nichts bewirken. Dies ist jedoch nicht der Fall.

Also, was ist los? Nehmen wir an, dass zusätzliche versteckte Ebenen im Prinzip helfen können und dass das Problem darin besteht, dass unser Trainingsalgorithmus nicht die richtigen Werte für Gewichte und Offsets findet. Wir möchten verstehen, was mit unserem Algorithmus nicht stimmt und wie wir ihn verbessern können.

Um zu verstehen, was schief gelaufen ist, visualisieren wir den Lernprozess im Netzwerk. Unten habe ich einen Teil des Netzwerks aufgebaut [784,30,30,10], in dem es zwei versteckte Schichten gibt, von denen jede 30 versteckte Neuronen hat. In dem Diagramm hat jedes Neuron einen Balken, der die Änderungsrate beim Lernen des Netzwerks angibt. Ein großer Balken bedeutet, dass sich die Gewichte und Verschiebungen des Neurons schnell ändern, und ein kleiner bedeutet, dass sie sich langsam ändern. Genauer gesagt bezeichnet der Balken den ∂C / ∂b-Gradienten des Neurons, dh die Änderungsrate der Kosten in Bezug auf den Versatz. In Kapitel 2 haben wir gesehen, dass dieser Gradientenwert nicht nur die Änderungsrate der Verschiebung während des Trainings steuert, sondern auch die Änderungsrate der eingegebenen Neuronengewichte. Machen Sie sich keine Sorgen, wenn Sie sich nicht an diese Details erinnern können: Sie müssen nur bedenken, dass diese Balken angeben, wie schnell sich die Gewichte und Verschiebungen der Neuronen während des Trainings des Netzwerks ändern.

Um das Diagramm zu vereinfachen, habe ich nur sechs obere Neuronen in zwei versteckten Schichten gezeichnet. Ich habe die ankommenden Neuronen gesenkt, weil sie keine Gewichte oder Vorurteile haben. Ich habe auch Ausgangsneuronen weggelassen, da wir zwei Schichten vergleichen und es sinnvoll ist, Schichten mit der gleichen Anzahl von Neuronen zu vergleichen. Das Diagramm wurde mit dem Programm generate_gradient.py zu Beginn des Trainings erstellt, dh unmittelbar nach der Initialisierung des Netzwerks.



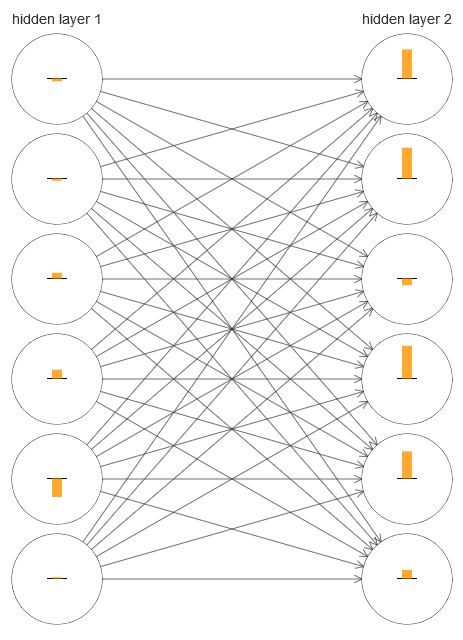
Das Netzwerk wurde zufällig initialisiert, daher ist diese Vielfalt in der Geschwindigkeit des Trainings von Neuronen nicht überraschend. Es fällt jedoch sofort auf, dass in der zweiten verborgenen Schicht die Streifen im Grunde viel mehr sind als in der ersten. Infolgedessen lernen Neuronen in der zweiten Schicht viel schneller als in der ersten. Ist dies ein Zufall oder lernen Neuronen in der zweiten Schicht im Allgemeinen schneller als die Neuronen in der ersten?

Um genau zu wissen, ist es gut, eine allgemeine Methode zum Vergleichen der Lerngeschwindigkeit in der ersten und zweiten verborgenen Ebene zu haben. Dazu bezeichnen wir den Gradienten als δlj = ∂C / ∂blj, dh als Gradienten des Neurons Nr. J in der Schicht Nr. 1. Im zweiten Kapitel haben wir es einen "Fehler" genannt, aber hier werde ich es informell einen "Gradienten" nennen. Informell - da dieser Wert nicht explizit partielle Ableitungen der Gewichtskosten enthält, ist ∂C / ∂w. Der Gradient δ ¹ kann als ein Vektor betrachtet werden, dessen Elemente bestimmen, wie schnell die erste verborgene Schicht lernt, und δ ² als ein Vektor, dessen Elemente bestimmen, wie schnell die zweite verborgene Schicht lernt. Wir verwenden die Längen dieser Vektoren als ungefähre Schätzungen der Lerngeschwindigkeit der Schichten. Das ist zum Beispiel die Länge || δ ¹ || misst die Lerngeschwindigkeit der ersten verborgenen Ebene und die Länge || δ ² || misst die Lerngeschwindigkeit der zweiten verborgenen Schicht.

Mit solchen Definitionen und der gleichen Konfiguration wie oben finden wir, dass || δ ¹ || = 0,07 und || δ ² || = 0,31. Dies bestätigt unseren Verdacht: Die Neuronen in der zweiten verborgenen Schicht lernen viel schneller als die Neuronen in der ersten verborgenen Schicht.

Was passiert, wenn wir mehr versteckte Ebenen hinzufügen? Mit drei versteckten Schichten im Netzwerk [784,30,30,30,10] betragen die entsprechenden Lerngeschwindigkeiten 0,012, 0,060 und 0,283. Wieder lernen die ersten verborgenen Schichten viel langsamer als die letzten. Füge eine weitere versteckte Ebene mit 30 Neuronen hinzu. In diesem Fall betragen die entsprechenden Lerngeschwindigkeiten 0,003, 0,017, 0,070 und 0,285. Das Muster bleibt erhalten: Die frühen Schichten lernen langsamer als die späteren.

Wir haben die Lerngeschwindigkeit gleich zu Beginn untersucht - direkt nach der Initialisierung des Netzwerks. Wie ändert sich diese Geschwindigkeit beim Lernen? Gehen wir zurück und betrachten das Netzwerk mit zwei versteckten Schichten. Die Lerngeschwindigkeit ändert sich folgendermaßen:



Um diese Ergebnisse zu erhalten, habe ich einen Batch-Gradientenabstieg mit 1000 Trainingsbildern und ein Training für 500 Epochen verwendet. Dies unterscheidet sich geringfügig von unseren üblichen Verfahren - ich habe keine Minipakete verwendet und nur 1000 Trainingsbilder anstelle eines vollständigen Satzes von 50.000 Teilen aufgenommen. Ich versuche nicht, Sie auszutricksen und zu täuschen, aber es stellt sich heraus, dass die Verwendung eines stochastischen Gradientenabfalls mit Minipaketen viel mehr Rauschen zu den Ergebnissen führt (aber wenn Sie das Rauschen mitteln, sind die Ergebnisse ähnlich). Mit den von mir gewählten Parametern ist es einfach, die Ergebnisse zu glätten, damit wir sehen können, was passiert.

Wie wir sehen, beginnen auf jeden Fall zwei Schichten mit zwei sehr unterschiedlichen Geschwindigkeiten (die wir bereits kennen) mit dem Training. Dann fällt die Geschwindigkeit beider Schichten sehr schnell ab, wonach ein Rückprall auftritt. Während dieser ganzen Zeit lernt die erste verborgene Ebene jedoch viel langsamer als die zweite.

Was ist mit komplexeren Netzwerken? Hier sind die Ergebnisse eines ähnlichen Experiments, jedoch mit einem Netzwerk mit drei verborgenen Schichten [784,30,30,30,10]:



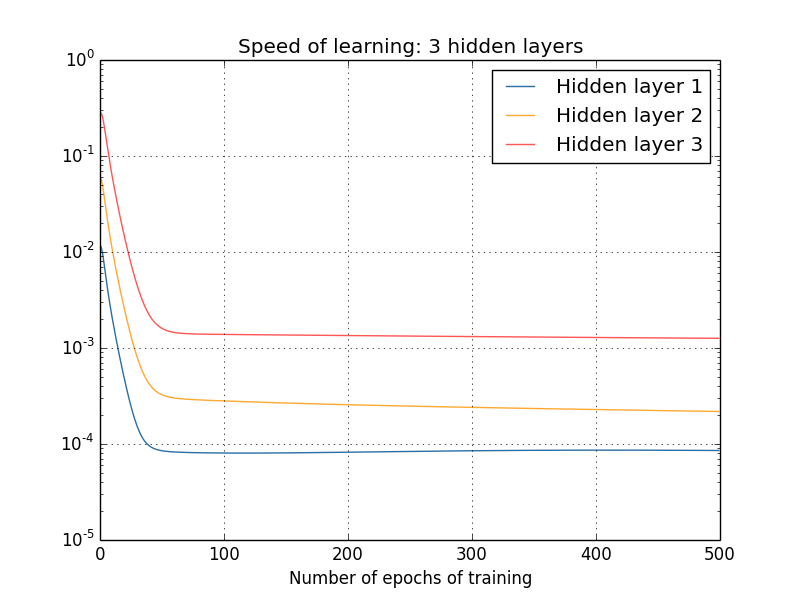
Und wieder lernen die ersten verborgenen Schichten viel langsamer als die letzten. Lassen Sie uns abschließend versuchen, eine vierte verborgene Ebene (Netzwerk [784,30,30,30,30,10]) hinzuzufügen und zu sehen, was passiert, wenn es trainiert wird:



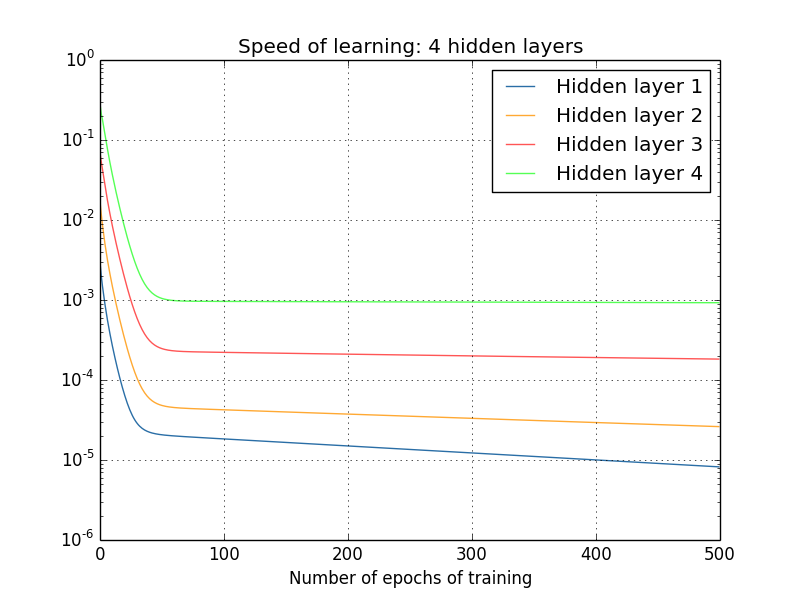
Und wieder lernen die ersten verborgenen Schichten viel langsamer als die letzten. In diesem Fall lernt die erste verborgene Ebene etwa 100-mal langsamer als die letzte. Kein Wunder, dass wir solche Probleme hatten, diese Netzwerke zu lernen!

Wir haben eine wichtige Beobachtung gemacht: Zumindest bei einigen GNS nimmt der Gradient ab, wenn man sich entlang versteckter Schichten in die entgegengesetzte Richtung bewegt. Das heißt, die Neuronen in den ersten Schichten werden viel langsamer trainiert als die Neuronen in der letzten. Und obwohl wir diesen Effekt nur in einem Netzwerk beobachtet haben, gibt es grundlegende Gründe, warum dies in vielen NS passiert. Dieses Phänomen ist als „verschwindendes Gradientenproblem“ bekannt (siehe Arbeiten 1 , 2 ).

Warum gibt es ein Problem mit dem verblassenden Gradienten? Gibt es Möglichkeiten, dies zu vermeiden? Wie gehen wir damit um, wenn wir STS trainieren? Tatsächlich werden wir bald feststellen, dass dies nicht unvermeidlich ist, obwohl die Alternative für sie nicht sehr attraktiv erscheint: Manchmal ist der Gradient in den ersten Schichten viel größer! Dies ist bereits ein Problem des explosiven Gradientenwachstums, und es ist darin nicht besser als im Problem eines verschwindenden Gradienten. Im Allgemeinen stellt sich heraus, dass der Gradient im STS instabil ist und entweder zu explosivem Wachstum neigt oder in den ersten Schichten verschwindet. Diese Instabilität ist ein grundlegendes Problem für das Gradienten-GNS-Training. Dies ist es, was wir verstehen und möglicherweise irgendwie lösen müssen.

Eine der Reaktionen auf einen verblassenden (oder instabilen) Gradienten besteht darin, darüber nachzudenken, ob dies tatsächlich ein ernstes Problem ist. Lassen Sie uns kurz vom NS ablenken und uns vorstellen, dass wir versuchen, die Funktion f (x) einer Variablen numerisch zu minimieren. Wäre es nicht schön, wenn die Ableitung f '(x) klein wäre? Würde das nicht bedeuten, dass wir schon dem Extrem nahe sind? Und bedeutet ein kleiner Gradient in den ersten Schichten des GNS nicht, dass wir Gewichte und Verschiebungen nicht mehr stark anpassen müssen?

Natürlich nicht. Denken Sie daran, dass wir die Gewichte und Offsets des Netzwerks zufällig initialisiert haben. Es ist höchst unwahrscheinlich, dass unsere ursprünglichen Gewichte und Mischungen gut mit dem übereinstimmen, was wir von unserem Netzwerk erwarten. Betrachten Sie als spezifisches Beispiel die erste Schicht von Gewichten im Netzwerk [784,30,30,30,10], die die Zahlen MNIST klassifiziert. Zufällige Initialisierung bedeutet, dass die erste Ebene die meisten Informationen über das eingehende Bild auswirft. Selbst wenn die späteren Schichten sorgfältig trainiert würden, wäre es für sie äußerst schwierig, die eingehende Nachricht zu bestimmen, einfach weil es an Informationen mangelt. Es ist daher absolut unmöglich sich vorzustellen, dass die erste Schicht einfach nicht trainiert werden muss. Wenn wir STS trainieren wollen, müssen wir verstehen, wie das Problem eines verschwindenden Gradienten gelöst werden kann.

Was verursacht das Problem des Fading-Gradienten? Instabile Gradienten in GNS

Um zu verstehen, wie das Problem eines verschwindenden Gradienten auftritt, betrachten Sie die einfachste NS: mit nur einem Neuron in jeder Schicht. Hier ist ein Netzwerk mit drei versteckten Schichten:



Hier sind w ₁ , w ₂ , ... Gewichte, b ₁ , b ₂ , ... Verschiebungen, C ist eine bestimmte Kostenfunktion. Zur Erinnerung möchte ich sagen, dass die Ausgabe a _j von Neuron Nr. J gleich σ (z _j ) ist, wobei σ die übliche Sigmoidaktivierungsfunktion ist und z _j = w _j a _{j - 1} + b _j die gewichtete Eingabe des Neurons ist. Ich habe die Kostenfunktion am Ende dargestellt, um zu betonen, dass die Kosten eine Funktion der Netzwerkleistung sind, und ₄ : Wenn die tatsächliche Leistung nahe an dem liegt, was Sie möchten, sind die Kosten gering, und wenn weit, sind sie groß.

Wir untersuchen den Gradienten ∂C / ∂b ₁ , der mit dem ersten versteckten Neuron assoziiert ist. Wir finden den Ausdruck für ∂C / ∂b ₁ und nachdem wir ihn untersucht haben, werden wir verstehen, warum das Problem des verschwindenden Gradienten auftritt.

Wir beginnen mit der Demonstration des Ausdrucks für ∂C / ∂b ₁ . Es sieht uneinnehmbar aus, aber tatsächlich ist seine Struktur einfach und ich werde es bald beschreiben. Hier ist dieser Ausdruck (ignorieren Sie vorerst das Netzwerk selbst und beachten Sie, dass σ nur eine Ableitung der Funktion σ ist):



Die Struktur des Ausdrucks ist wie folgt: Für jedes Neuron im Netzwerk gibt es einen Multiplikationsterm σ '(z _j ), für jedes Gewicht gibt es w _j und es gibt auch den letzten Term ∂C / ∂a ₄ , der der Kostenfunktion entspricht. Beachten Sie, dass ich die entsprechenden Mitglieder über den entsprechenden Teilen des Netzwerks platziert habe. Daher ist das Netzwerk selbst eine mnemonische Ausdrucksregel.

Sie können diesen Ausdruck auf Glauben nehmen und seine Diskussion direkt an die Stelle überspringen, an der erklärt wird, wie er sich auf das Problem des verblassenden Gradienten bezieht. Daran ist nichts auszusetzen, da dieser Ausdruck ein Sonderfall aus unserer Diskussion über die Rückausbreitung ist. Es ist jedoch leicht, seine Treue zu erklären, so dass es für Sie sehr interessant (und vielleicht lehrreich) sein wird, diese Erklärung zu studieren.

Stellen Sie sich vor, wir hätten eine kleine Änderung von Δb ₁ zum Versatz b _{1 vorgenommen} . Dadurch werden eine Reihe von kaskadierenden Änderungen im Rest des Netzwerks gesendet. Erstens bewirkt dies, dass sich die Ausgabe des ersten versteckten Neurons Δa ₁ ändert. Dies wiederum zwingt Δz ₂ , sich in der gewichteten Eingabe in das zweite versteckte Neuron zu ändern. Dann ändert sich Δa ₂ in der Ausgabe des zweiten versteckten Neurons. Und so weiter bis zu einer Änderung von ΔC im Ausgangswert. Es stellt sich heraus, dass:

$$

$$\ frac {\ partielles C} {\ partielles b_1} \ approx \ frac {\ Delta C} {\ Delta b_1} \ tag {114}$$

Dies legt nahe, dass wir einen Ausdruck für den Gradienten ∂C / ∂b ₁ ableiten können, indem wir den Einfluss jedes Schritts in dieser Kaskade sorgfältig überwachen.

Lassen Sie uns dazu überlegen, wie Δb ₁ bewirkt, dass sich die Ausgabe a _{1 des} ersten versteckten Neurons ändert. Wir haben also a ₁ = σ (z ₁ ) = σ (w ₁ a ₀ + b ₁ )

$$

$$\ Delta a_1 \ approx \ frac {\ partielles \ Sigma (w_1 a_0 + b_1)} {\ partielles b_1} \ Delta b_1 \ tag {115}$$

$$

$$= \ sigma '(z_1) \ Delta b_1 \ tag {116}$$

Der Term σ ′ (z ₁ ) sollte bekannt vorkommen: Dies ist der erste Term unseres Ausdrucks für den Gradienten ∂C / ∂b ₁ . Intuitiv wandelt es die Änderung des Offsets & Dgr; b ₁ in die Änderung & Dgr; a _{1 der} Ausgangsaktivierung um. Die Änderung von Δa ₁ bewirkt wiederum eine Änderung der gewichteten Eingabe z ₂ = w ₂ a ₁ + b _{2 des} zweiten versteckten Neurons:

$$

$$\ Delta z_2 \ approx \ frac {\ teilweise z_2} {\ teilweise a_1} \ Delta a_1 \ tag {117}$$

$$

$$= w_2 \ Delta a_1 \ tag {118}$$

Wenn wir die Ausdrücke für Δz ₂ und Δa ₁ kombinieren, sehen wir, wie sich die Änderung der Vorspannung b ₁ entlang des Netzwerks ausbreitet und z _{2 beeinflusst} :

$$

$$\ Delta z_2 \ approx \ sigma '(z_1) w_2 \ Delta b_1 \ tag {119}$$

Und das sollte auch bekannt sein: Dies sind die ersten beiden Begriffe in unserem angegebenen Ausdruck für den Gradienten ∂C / ∂b ₁ .

Dies kann weiter fortgesetzt werden, indem überwacht wird, wie sich Änderungen im Rest des Netzwerks verbreiten. Auf jedem Neuron wählen wir den Term σ '(z _j ) und durch jedes Gewicht den Term w _j . Als Ergebnis wird ein Ausdruck erhalten, der die endgültige Änderung & Dgr; C der Kostenfunktion mit der anfänglichen Änderung & Dgr; b _{1 der} Vorspannung in Beziehung setzt:

$$

$$\ Delta C \ approx \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ partielles C} {\ partielles a_4} \ Delta b_1 \ tag {120}$$

Wenn wir es durch Δb ₁ teilen, erhalten wir wirklich den gewünschten Ausdruck für den Gradienten:

$$

$$\ frac {\ partielles C} {\ partielles b_1} = \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ partielles C} {\ partielles a_4} \ tag { 121}$$

Warum gibt es ein Problem mit dem verblassenden Gradienten?

Um zu verstehen, warum das Problem des verschwindenden Gradienten auftritt, schreiben wir unseren gesamten Ausdruck für den Gradienten im Detail:

$$

$$\ frac {\ partielles C} {\ partielles b_1} = \ sigma '(z_1) \ w_2 \ sigma' (z_2) \ w_3 \ sigma '(z_3) \, w_4 \ sigma' (z_4) \ \ frac {\ partielles C} {\ partielles a_4} \ tag {122}$$

Zusätzlich zum letzten Term ist dieser Ausdruck das Produkt von Termen der Form w _j σ ′ (z _j ). Um zu verstehen, wie sich jeder von ihnen verhält, betrachten wir den Graphen der Funktion σ:



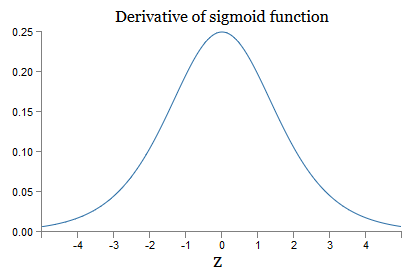
Der Graph erreicht ein Maximum am Punkt σ '(0) = 1/4. Wenn wir den Standardansatz zum Initialisieren der Netzwerkgewichte verwenden, wählen wir die Gewichte unter Verwendung der Gaußschen Verteilung aus, dh des quadratischen Mittelwerts Null und der Standardabweichung 1. Daher erfüllen die Gewichte normalerweise die Ungleichung | w _j | <1. Wenn wir all diese Beobachtungen vergleichen, sehen wir, dass die Terme w _j σ '(z _j ) normalerweise die Ungleichung | w _j σ' (z _j ) | <1/4 erfüllen. Und wenn wir das Produkt aus der Menge solcher Begriffe nehmen, wird es exponentiell abnehmen: Je mehr Begriffe, desto kleiner das Produkt. Es scheint eine mögliche Lösung für das Problem des verschwindenden Gradienten zu sein.

Um dies genauer zu schreiben, vergleichen wir den Ausdruck für ∂C / ∂b ₁ mit dem Ausdruck des Gradienten in Bezug auf den nächsten Versatz, zum Beispiel ∂C / ∂b ₃ . Natürlich haben wir keinen detaillierten Ausdruck für ∂C / ∂b ₃ aufgeschrieben, aber er folgt den gleichen Gesetzen wie oben für ∂C / ∂b _{1 beschrieben} . Und hier ist ein Vergleich zweier Ausdrücke:



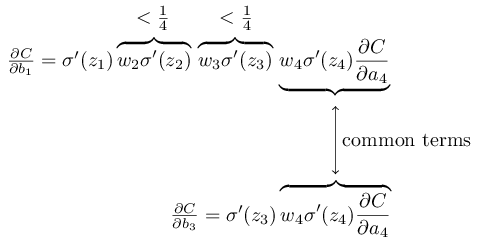
Sie haben mehrere gemeinsame Mitglieder. Der Gradient ∂C / ∂b ₁ enthält jedoch zwei zusätzliche Terme, von denen jeder die Form w _j σ ′ (z _j ) hat. Wie wir gesehen haben, überschreiten solche Begriffe normalerweise nicht 1/4. Daher ist der Gradient ∂C / ∂b ₁ normalerweise 16 (oder mehr) Mal kleiner als ∂C / ∂b ₃ . Und dies ist die Hauptursache für das Problem des verschwindenden Gradienten.

Dies ist natürlich kein genauer, aber informeller Beweis für das Problem. Es gibt mehrere Einschränkungen. Insbesondere könnte man daran interessiert sein, ob die Gewichte w _j während des Trainings zunehmen werden. In diesem Fall erfüllen die Terme w _j σ '(z _j ) im Produkt nicht mehr die Ungleichung | w _j σ' (z _j ) | <1/4. Und wenn sich herausstellt, dass sie groß genug sind, mehr als 1, haben wir nicht mehr das Problem eines verblassenden Gradienten. Stattdessen wächst der Farbverlauf exponentiell, wenn Sie sich durch die Ebenen zurückbewegen. Und anstelle des Problems des verschwindenden Gradienten erhalten wir das Problem des explosiven Gradientenwachstums.

Das Problem des explosiven Gradientenwachstums

Schauen wir uns ein konkretes Beispiel für einen explosiven Gradienten an. Das Beispiel wird etwas künstlich sein: Ich werde die Netzwerkparameter anpassen, um das Auftreten eines explosiven Wachstums zu gewährleisten. Obwohl das Beispiel künstlich ist, zeigt es deutlich, dass das explosive Wachstum des Gradienten keine hypothetische Möglichkeit ist, aber es kann wirklich passieren.

Für ein explosives Gradientenwachstum müssen Sie zwei Schritte ausführen. Zunächst wählen wir große Gewichte im gesamten Netzwerk aus, z. B. w1 = w2 = w3 = w4 = 100. Dann wählen wir solche Verschiebungen so, dass die Terme σ ′ (z _j ) nicht zu klein sind. Und das ist ganz einfach: Wir müssen nur solche Verschiebungen so auswählen, dass die gewichtete Eingabe jedes Neurons zj = 0 ist (und dann σ ′ ( _zj ) = 1/4). Daher brauchen wir zum Beispiel z ₁ = w ₁ a ₀ + b ₁ = 0. Dies kann erreicht werden, indem b ₁ = −100 ∗ a _{0 gesetzt wird} . Die gleiche Idee kann verwendet werden, um andere Offsets auszuwählen. Als Ergebnis werden wir sehen, dass alle Terme w _j σ '(z _j ) gleich 100 ∗ 14 = 25 sind. Und dann bekommen wir ein explosives Gradientenwachstum.

Instabiles Gradientenproblem

Das grundlegende Problem ist nicht das verschwindende Gradientenproblem oder das explosive Wachstum des Gradienten. Es ist so, dass der Gradient in den ersten Schichten das Produkt von Elementen aus allen anderen Schichten ist. Und wenn es viele Schichten gibt, wird die Situation im Wesentlichen instabil. Und die einzige Möglichkeit, mit der alle Ebenen ungefähr gleich schnell lernen können, besteht darin, solche Mitglieder der Arbeit auszuwählen, die sich gegenseitig ausgleichen. Und da es keinen Mechanismus oder Grund für einen solchen Ausgleich gibt, ist es unwahrscheinlich, dass dies zufällig geschieht.Kurz gesagt, das eigentliche Problem ist, dass NS unter dem Problem eines instabilen Gradienten leidet. Und am Ende lernen verschiedene Schichten des Netzwerks mit furchtbar unterschiedlichen Geschwindigkeiten, wenn wir standardmäßige gradientenbasierte Lerntechniken verwenden.

Übung

• , |σ′(z)|<1/4. , , . ?

Wir haben gesehen, dass der Gradient in den ersten Schichten eines tiefen Netzwerks verschwinden oder explosionsartig wachsen kann. Tatsächlich verschwindet bei Verwendung von Sigmoidneuronen der Gradient normalerweise. Um zu verstehen, warum, betrachten Sie erneut den Ausdruck | wσ ′ (z) |. Um das Problem des verschwindenden Gradienten zu vermeiden, benötigen wir | wσ ′ (z) | ≥1. Sie können entscheiden, dass dies mit sehr großen Werten von w leicht zu erreichen ist. In Wirklichkeit ist es jedoch nicht so einfach. Der Grund ist, dass der Term σ '(z) auch von w abhängt: σ' (z) = σ '(wa + b), wobei a die Eingangsaktivierung ist. Und wenn wir w groß machen, müssen wir versuchen, σ ′ (wa + b) nicht parallel klein zu machen. Und dies stellt sich als ernsthafte Einschränkung heraus. Der Grund ist, dass wenn wir w groß machen, wir wa + b sehr groß machen. Wenn Sie sich den Graphen von σ 'ansehen, können Sie sehen, dass dies uns zu den „Flügeln“ der Funktion σ' führt.wo es sehr kleine Werte annimmt. Die einzige Möglichkeit, dies zu vermeiden, besteht darin, die eingehende Aktivierung in einem relativ engen Wertebereich zu halten. Manchmal passiert das zufällig. Aber öfter passiert das nicht. Daher haben wir im allgemeinen Fall das Problem eines verschwindenden Gradienten.

Die Aufgaben

• |wσ′(wa+b)|. , |wσ′(wa+b)|≥1. , , |w|≥4.
• , |w|≥4, , |wσ′(wa+b)|≥1.
• , , ,

  $$

  $$\frac{2}{|w|} \ln\left( \frac{|w|(1+\sqrt{1-4/|w|})}{2}-1\right) \tag{123}$$
• , |w|≈6.9, ≈0,45. , , , .
• . x, w ₁ , b w ₂ . , , , w ₂ σ(w ₁ x+b)≈x for x∈[0,1]. , , ( ). : x=1/2+Δ, , w ₁ , w ₁ Δ .

Wir haben Spielzeugnetzwerke mit nur einem Neuron in jeder verborgenen Schicht untersucht. Was ist mit komplexeren tiefen Netzwerken, die viele Neuronen in jeder verborgenen Schicht haben?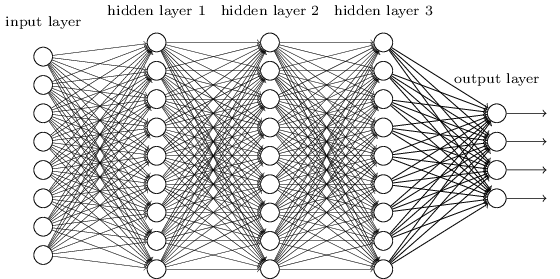



In solchen Netzwerken passiert fast dasselbe. Zu Beginn des Kapitels über die Rückausbreitung haben wir gesehen, dass der Gradient in Schicht #l eines Netzwerks mit L Schichten wie folgt angegeben wird:

$$

$$\delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C \tag{124}$$

Hier ist Σ '(z ^l ) die Diagonalmatrix, deren Elemente die Werte von σ' (z) für die gewichteten Eingaben der Schicht Nr. 1 sind. w ^l sind Gewichtsmatrizen für verschiedene Schichten. Und ∇ _a C ist der Vektor partieller Ableitungen von C in Bezug auf Ausgangsaktivierungen.

Dieser Ausdruck ist viel komplizierter als bei einem Neuron. Und doch, wenn Sie genau hinschauen, wird seine Essenz sehr ähnlich sein, mit einer Reihe von Paaren der Form (w ^j ) ^T Σ ′ (z ^j ). Darüber hinaus haben die Matrizen Σ '(z ^j ) diagonal kleine Werte, nicht mehr als 1/4. Wenn die Gewichtsmatrizen w ^j nicht zu groß sind, ist jeder zusätzliche Term (w ^j ) ^T Σ ′ (z ^l) neigt dazu, den Gradientenvektor zu reduzieren, was zu einem verschwindenden Gradienten führt. Im allgemeinen Fall führt eine größere Anzahl von Multiplikationstermen zu einem instabilen Gradienten, wie in unserem vorherigen Beispiel. In der Praxis, empirisch normalerweise in Sigmoid-Netzwerken, verschwinden Gradienten in den ersten Schichten exponentiell schnell. Infolgedessen verlangsamt sich das Lernen in diesen Ebenen. Und die Verlangsamung ist kein Unfall oder eine Unannehmlichkeit: Sie ist eine grundlegende Folge unseres gewählten Lernansatzes.

Andere Hindernisse für tiefes Lernen

In diesem Kapitel habe ich mich auf das Verblassen von Verläufen - und allgemein auf instabile Verläufe - als Hindernis für tiefes Lernen konzentriert. In der Tat sind instabile Gradienten nur ein Hindernis für die Entwicklung des Zivilschutzes, wenn auch ein wichtiges und grundlegendes. Ein wesentlicher Teil der aktuellen Forschung versucht, die Probleme, die beim Unterrichten von GO auftreten können, besser zu verstehen. Ich werde nicht alle diese Werke im Detail beschreiben, aber ich möchte kurz einige Werke erwähnen, um Ihnen eine Vorstellung von einigen Fragen zu geben, die von Menschen gestellt werden.

Als erstes Beispiel im Jahr 2010Es wurden Beweise dafür gefunden, dass die Verwendung von Sigmoid-Aktivierungsfunktionen zu Problemen beim Lernen von NS führen kann. Insbesondere wurde festgestellt, dass die Verwendung eines Sigmoid dazu führt, dass die Aktivierungen der letzten verborgenen Schicht während des Trainings in der Region 0 gesättigt sind, was das Training ernsthaft verlangsamt. Es wurden mehrere alternative Aktivierungsfunktionen vorgeschlagen, die nicht so stark unter dem Sättigungsproblem leiden (siehe auch ein anderes Diskussionspapier ).

Als erstes Beispiel wurde 2013 der Effekt der zufälligen Initialisierung von Gewichten und des Impulsgraphen in einem stochastischen Gradientenabstieg basierend auf einem Impuls auf dem GO untersucht. In beiden Fällen beeinflusste eine gute Wahl die Fähigkeit, STS zu trainieren, erheblich.

Diese Beispiele legen nahe, dass die Frage „Warum ist STS so schwer zu trainieren?“ sehr kompliziert. In diesem Kapitel haben wir uns auf die Instabilitäten konzentriert, die mit dem Gradiententraining von GNS verbunden sind. Die Ergebnisse der beiden vorhergehenden Absätze zeigen, dass die Wahl der Aktivierungsfunktion, die Methode zum Initialisieren der Gewichte und sogar die Details der Durchführung des Trainings basierend auf dem Gradientenabstieg ebenfalls eine Rolle spielen. Und natürlich wird die Wahl der Netzwerkarchitektur und anderer Hyperparameter wichtig sein. Daher können viele Faktoren eine Rolle bei der Schwierigkeit spielen, tiefe Netzwerke zu lernen, und das Problem des Verständnisses dieser Faktoren ist Gegenstand laufender Forschung. Aber das alles wirkt eher düster und führt zu Pessimismus. Es gibt jedoch gute Nachrichten - im nächsten Kapitel werden wir alles zu unseren Gunsten einpacken und verschiedene Ansätze in GO entwickeln.die in gewissem Maße in der Lage sein wird, all diese Probleme zu überwinden oder zu umgehen.