
1985 richtete das Institut für Elektrotechnik- und Elektronikingenieure (
IEEE ) den
IEEE 754- Standard ein, der für
Gleitkomma- und Rechenformate zuständig
ist und in den nächsten 30 Jahren zum Modell für die gesamte Hardware und Software wird.
Und obwohl die meisten Programmierer zu jeder Zeit wahllos einen Gleitkommawert verwenden, lassen die Geschwindigkeit und Genauigkeit solcher Operationen oft zu wünschen übrig, wenn sie mathematische Operationen mit reellen Zahlen ausführen müssen, aufgrund bestimmter Einschränkungen bei der Darstellung dieser Zahlen.
Viele Jahre lang wurde der Standard von Informatikern, die mit diesen Problemen vertraut waren, scharf kritisiert, aber
John Gustafson war der prominenteste unter ihnen, der allein einen Kreuzzug führte, um den Gleitkomma durch etwas Passenderes zu ersetzen. In diesem Fall wird Posit oder
Unum als geeignetere Option angesehen - die dritte Option ist das Ergebnis seiner Untersuchung von „universellen Zahlen“. Er sagt, dass Posit-Zahlen die meisten Hauptprobleme des IEEE 754-Standards lösen, die Leistung und Genauigkeit verbessern und weniger Bits verwenden werden. Was noch besser ist, er gibt an, dass das neue Format Standard-Gleitkommazahlen "on the fly" ersetzen kann, ohne den Quellcode von Anwendungen ändern zu müssen.
Wir haben uns mit Gustafson auf der ISC19-Konferenz getroffen. Und für die dort ansässigen Supercomputerspezialisten besteht einer der Hauptvorteile des Posit-Formats darin, dass Sie mit weniger Bits als Zahlen aus IEEE 754 eine größere Genauigkeit und einen größeren Dynamikbereich erzielen können. Und das nicht nur ein bisschen weniger. Gustafson sagte, dass 32-Bit-Posit in fast allen Fällen 64-Bit-Float ersetzt, was schwerwiegende Konsequenzen für das wissenschaftliche Rechnen haben könnte. Wenn Sie die Anzahl der Bits halbieren, können Sie nicht nur den Cache, den Speicher und den Speicher für diese Nummern reduzieren, sondern auch die Kanalbreite, die für die Übertragung an den Prozessor erforderlich ist, erheblich reduzieren und umgekehrt. Dies ist der Hauptgrund, warum die Posit-basierte Arithmetik seiner Meinung nach im Vergleich zu IEEE-Gleitkommazahlen eine doppelte bis vierfache Berechnungsgeschwindigkeit ergibt.
Die Beschleunigung kann durch eine kompakte Darstellung reeller Zahlen erreicht werden. Anstelle des Exponenten und des Bruchteils einer festen Größe, die im IEEE-Standard verwendet werden, codiert posit den Exponenten mit einer variablen Anzahl von Bits (eine Kombination aus Modusbits und Exponentenbits), so dass sie in den meisten Fällen weniger benötigt werden. Infolgedessen verbleiben mehr Bits auf dem Bruchteil, was eine größere Genauigkeit ergibt. Ein dynamischer Exponent lohnt sich aufgrund seiner Verjüngungsgenauigkeit. Dies bedeutet, dass Werte mit einem kleinen Exponenten, die am häufigsten verwendet werden, eine größere Genauigkeit aufweisen können und weniger häufig verwendete sehr große und sehr kleine Zahlen eine geringere Genauigkeit aufweisen.
Gustafsons 2017er
Arbeit , die das Posit-Format beschreibt, gibt eine detaillierte Beschreibung, wie dies funktioniert.
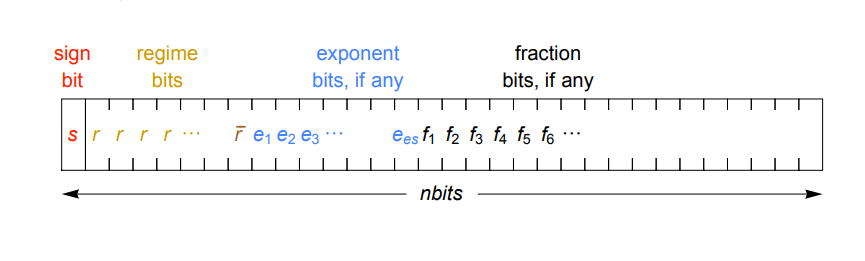
Ein weiterer wichtiger Vorteil des Formats besteht darin, dass Posit im Gegensatz zu gewöhnlichen Gleitkommazahlen auf jedem System dieselben bitweisen Ergebnisse liefert, was mit dem IEEE-Format oft nicht garantiert werden kann (hier können sogar dieselben Berechnungen auf demselben System unterschiedliche Ergebnisse liefern Ergebnisse). Das neue Format befasst sich auch mit Rundungsfehlern, Überlaufen und Verschwinden signifikanter Ziffern, denormalisierten Zahlen und vielen Werten vom Typ Nicht-Zahl (NaN). Außerdem vermeidet pos solche Seltsamkeiten wie die nicht übereinstimmenden Werte 0 und -0. Stattdessen verwendet das Format ein binäres Komplement für das Zeichen, wie z. B. Ganzzahlen, was bedeutet, dass der bitweise Vergleich korrekt funktioniert.
Etwas, das als Quire bezeichnet wird, ist mit Posit-Zahlen verbunden - einem Akkumulationsmechanismus, mit dem Programmierer reproduzierbare lineare Algebra durchführen können - ein Prozess, auf den reguläre IEEE-Zahlen nicht zugreifen können. Es unterstützt die verallgemeinerte Operation der kombinierten Multiplikationsaddition und anderer kombinierter Operationen, mit denen Sie skalare Produkte oder Summen ohne Rundungsfehler oder Überläufe berechnen können. An der University of California in Berkeley gestartete Tests haben gezeigt, dass Quire-Operationen 3-6-mal schneller sind als sequentielle Ausführung. Gustafson sagt, dass sie positiven Zahlen erlauben, "außerhalb ihrer Gewichtsklasse zu kämpfen".
Obwohl dieses Zahlenformat erst seit einigen Jahren besteht, hat die HPC-Community (High Performance Computing) bereits ein Interesse daran, ihre Anwendungen zu untersuchen. Im Moment bleibt die gesamte Arbeit experimentell und basiert auf der erwarteten Geschwindigkeit der zukünftigen Hardware oder auf der Verwendung von Werkzeugen, die die Positivarithmetik auf herkömmlichen Prozessoren emulieren. Während der Produktion gibt es keine Chips, die Posit auf Hardwareebene implementieren.
Eine der möglichen Anwendungen des Formats ist das im Bau befindliche Funkinterferometer
Square Kilometer Array (SKA). Bei seiner Entwicklung werden Positivzahlen als eine Möglichkeit betrachtet, die Kanalbreite und die Rechenlast für die Verarbeitung von Daten, die vom Radioteleskop kommen, radikal zu reduzieren. Es ist notwendig, dass die Supercomputer, die ihn bedienen, nicht mehr als 10 MW verbrauchen, und eine der vielversprechendsten Möglichkeiten, dies zu erreichen, besteht nach Ansicht der Konstrukteure darin, das dichtere Positivformat zu verwenden, um die geschätzte Speicherkanalbreite (200 PB / s), den Übertragungskanal, zu halbieren Daten (10 TB / s) und Netzwerkverbindung (1 TB / s). Die Rechenleistung sollte ebenfalls zunehmen.
Eine andere Anwendung ist zur Verwendung in Wettervorhersagen und Klimavorhersagen. Das britische Team hat
gezeigt, dass 16-Bit-Positivzahlen den Standard-16-Bit-Gleitkommazahlen deutlich voraus sind und "ein großes Potenzial für die Verwendung in komplexeren Modellen haben". Die 16-Bit-Posit-Emulation in diesem Modell funktionierte ebenso wie 64-Bit-Gleitkommazahlen.
Das Livermore National Laboratory
wertet Posit- und andere Zahlenformate aus und untersucht Möglichkeiten, um die Datenmenge zu reduzieren, die in Exaflops-Supercomputern der Zukunft verschoben wird. In einigen Fällen erzielten sie auch bessere Ergebnisse. Zum Beispiel konnten Positivzahlen bei physikalischen Berechnungen wie der Schockhydrodynamik eine überlegene Genauigkeit liefern und übertrafen im Allgemeinen Gleitkommazahlen in verschiedenen Dimensionen.

Vielleicht hat Posit das größte Potenzial beim maschinellen Lernen, bei dem 16-Bit-Zahlen zum Lernen und 8-Bit-Zahlen zur Verifizierung verwendet werden können. Laut Gustafson sind 32-Bit-Gleitkommazahlen für das Training zu viel des Guten und zeigen in einigen Fällen nicht einmal so gute Ergebnisse wie 16-Bit-Positiv, was erklärt, dass der IEEE 754-Standard „absolut nicht für die Verwendung mit KI vorgesehen war“. .
Es ist nicht überraschend, dass die KI-Community ihnen Aufmerksamkeit geschenkt hat. Facebook Jeff Johnson hat eine experimentelle Plattform mit FGPA unter Verwendung von Posit entwickelt, die eine bessere Energieeffizienz im Vergleich zu float16 und IEEE bfloat16 für maschinelle Lernaufgaben zeigt. Sie planen, die Verwendung von 16-Bit-Quire-Hardware für das Training zu untersuchen und sie mit konkurrierenden Formaten zu vergleichen.
Es ist erwähnenswert, dass Facebook mit Intel am Nervana Neural Network (NNP) -Prozessor arbeitet, was einige der AI-bezogenen Aufgaben des sozialen Riesen beschleunigen sollte. Die Verwendung des Posit-Formats ist nicht ausgeschlossen, obwohl es wahrscheinlicher ist, dass Intel sein ursprüngliches FlexPoint-Format für Nervana beibehält. In jedem Fall lohnt es sich, diesen Punkt zu verfolgen.
Gustafson kennt mindestens einen KI-Chip, in dem versucht wird, Positivzahlen im Design zu verwenden, obwohl er nicht das Recht hat, den Namen des Unternehmens preiszugeben. Das französische Unternehmen Kalray, das mit der European Processor Initiative (EPI) zusammenarbeitet, hat auch Interesse daran gezeigt, die Position seines MPPA-Beschleunigers (Massively Parallel Processor Array) der nächsten Generation zu unterstützen, damit diese Technologie an
europäische Exaflop-Supercomputer gehen kann.
Für Gustafson inspiriert dies natürlich alles und er glaubt, dass dieser dritte Versuch, seine universellen Zahlen voranzutreiben, erfolgreich sein könnte. Im Gegensatz zu den Versionen eins und zwei ist posit einfach in Hardware zu implementieren. Und angesichts des harten Wettbewerbs auf dem Gebiet der KI sollten wir vielleicht den kommerziellen Erfolg des neuen Formats erwarten. Unter anderen Plattformen, auf denen Posit eine glänzende Zukunft erwarten kann, sind digitale Signalverarbeitung, GPU (für Grafiken und andere Computer), Geräte für das Internet der Dinge, Edge-Computing. Und natürlich HPC.
Wenn die Technologie kommerziell vertrieben wird, ist es unwahrscheinlich, dass Gustafson von ihrem Erfolg profitieren kann. Sein Projekt, wie im 10-seitigen Standard angegeben, ist vollständig offen und steht jedem Unternehmen zur Verfügung, das geeignete Software und Hardware entwickeln möchte. Dies erklärt wahrscheinlich die Aufmerksamkeit von Unternehmen wie IBM, Google, Intel, Micron, Rex Computing, Qualcomm, Fujitsu, Huawei und vielen anderen auf Technologie.
Das Ersetzen des IEEE 754 durch etwas Passenderes ist jedoch ein großes Projekt, selbst für eine Person mit einem so beeindruckenden Lebenslauf wie dem von Gustafson. Noch bevor er bei ClearSpeed, Intel und AMD arbeitete, untersuchte er Möglichkeiten zur Verbesserung wissenschaftlicher Berechnungen auf modernen Prozessoren. "Ich habe in den letzten 30 Jahren versucht, dieses Problem zu lösen", sagte er.